固体物理第四章课件
- 格式:pdf
- 大小:989.97 KB
- 文档页数:38






第四章半导体的导电性本章重点1. 迁移率 2. 载流子的散射 3. 电导率 4. 迁移率和电阻率与杂质浓度和温度的关系§ 4.1 载流子的漂移运动 迁移率4.1.1 欧姆定律El ES V I= = = =σ E S R ρl / S ρ欧姆定律的微分形式J =σ Eσ=1ρ为电导率,单位:西门子/米, 西门子/厘米电阻率ρ的单位Ω ⋅ m,Ω ⋅ cm4.1.2 漂移速度和迁移率载流子在电场力作用下作定向运动叫漂移运动,平均漂移 速度−vd。
电子浓度为n的导体,电子漂移运动形成电流A O E vd×1 sJ = − nq v d (2)−J =σ E , 电流密度随电场增加而增大 又J = − nq vd−vd = μ E−μ = v d / E (3)−J = nqμ Eσ = nqμ(4)μ 为电子迁移率,表示单位电场下电子的平均漂移速度。
描述载流子在电场中漂移运动的难易程度。
单位:(m2/V.s或cm2/V.s)4.1.3 半导体的电导率和迁移率 复杂性:电子和空穴两种载流子,且其浓度随温度、掺杂而变化。
电场方向电子漂移方向 电子电流 空穴电流 空穴漂移方向漂移电流示意图半导体中电流:J = J n + J p = (nqμn + pqμ p ) E = σ E半导体中电导率与载流子浓度和迁移率的关系:σ = nqμ n + pqμ p电导率主要取决于多子对N型半导体n>>pσ = nq μnσ = pq μ pσ = ni q ( μ n + μ p )对P型半导体p>>n 对本征半导体p=n=ni电子迁移率大于空穴迁移率,高速开关器件主要依靠 电子导电。
§ 4.2 载流子的散射4.2.1 载流子散射与漂移运动 1、载流子的散射——改变速度的方向和大小 散射的根本原因:周期性势场遭到破坏,产生了附加势场。
平均自由程 l :连续两次散射间自由运动的平均路程。


第四章 晶格振动和晶体的热学性质● 晶格振动:晶体中的原子在格点附近作热振动● 原子的振动以波的形式在晶体传播(原子的振动波称为格波) ● 晶格振动对晶体的性质有重要影响 主要内容● 晶格动力学(经典理论,1912年由波恩和卡门建立)晶格振动的模式数量(有多少种基本的波动解) 晶格振动的色散关系(波动的频率和波数的关系)● 晶格振动的量子理论 ● 固体的热容量 4.1 一维单原子链的振动原子链共有N 个原胞,每个原胞只有一个原子,每个原子具有相同的质量m,平衡时原子间距等于晶格常数a,原子沿链方向运动,第n 个原子离开平衡位置的位移用x n 表示,第n 个原子和第n+1个原子间的相对位移为 一维单原子链原子振动时,相邻两个原子之间的间距: 基本假设● 平衡时原子位于Bravais 格点上 ● 原子围绕平衡位置作微振动●简谐近似:原子间的相互作用势能只考虑到平方项 微振动时:简谐近似:势能展开式保留到二次项微振动:原子离开平衡位置的位移与原子间距相比是小量。
晶体中原子的平衡位置由原子结合能(势)决定。
任何一种晶体,原子间的相互作用势能可以表述成原子之间距离的函数。
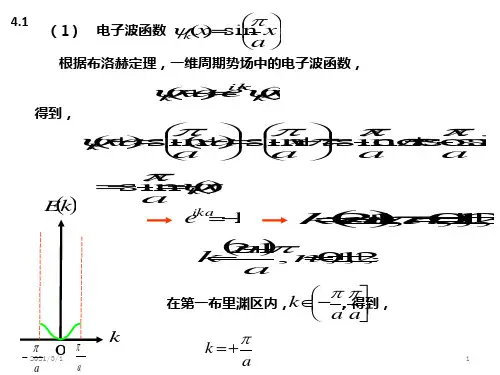
n n x x -=+1δδ+=a x ()()⋅⋅⋅+⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛+=+=222 21 )(δδδa ax d U d x d U d a U a U x U把qa改变一个2π的整数倍,原子的振动相同,因此可以把qa限制负pi和正pi之间,此范围以外的q值,并不提供新的物理内容.群速度是指波包的传播速度,dw/dq,也就是能量在介质中的传播速度。
在布里渊区的边界上,群速度为零,波是一个驻波。
4.2 一维双原子链的振动q趋于0时,w也趋于零,称为声学波4.3 三维晶格的振动(略) 一个原胞中有n 个原子晶格基矢: 原胞数目: 原子的质量: 对于一个波矢q,有3n 个ω(即有3n 支色散曲线) 在3n 支色散关系中,当q→0时(长波):有三支ω →0,且各原子的振幅趋于相同,这三支为声学波。
