编译原理实验报告记录FIRST集和FOLLOW集
- 格式:doc
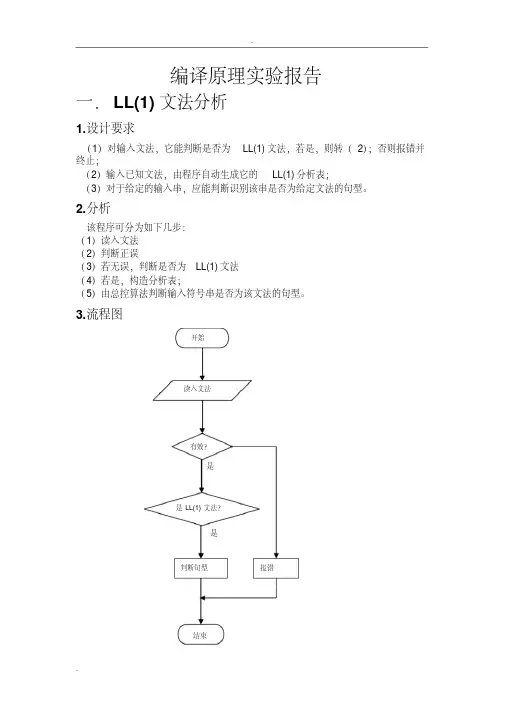
- 大小:148.00 KB
- 文档页数:12

编译原理实验报告姓名:叶玉虎班级:计122班指导老师:王森玉实验日期:2015/5/11实验内容:1.求出每个非终结符的FIRST集合2.求出每个产生式右部的FIRST集合3.求出每个非终结符的Follow集合实验环境:Visual Studio2010实验目的:让同学们掌握FIRST集合和FOLLOW集合的求法实验代码:#include<stdio.h>#include<string.h>#define MAX 50char css[MAX][MAX];//保存所有的产生式int count=0;int cnt=0;struct L{//保存所有的终结符char ch;int flag;//1:能推出ε,0:不能,初值:-1int num;char first[MAX];int s;//first的长度char follow[MAX];int l;//follow的长度}l[MAX];//对输入的格式进行控制,并校验输入是否符合格式int handle(char a[]){int len,i=0,j,k;len=strlen(a);while(a[i]!=10){if(a[i]=='$')return 2;if((' '==a[i])||(9==a[i])){i++;continue;}if((a[i]>='A')&&(a[i]<='Z')){if((a[i+1]!='-')||(a[i+2]!='>')){printf("产生式格式错误\n");return -1;}else{j=i;k=0;while((a[j]!=' ')&&(a[j]!=9)&&(a[j]!='$')&&(a[j]!=10)){if(a[j]=='|'){css[count][k]='\0';count++;if((a[j+1]=='')||(a[j]==9)||(a[j]=='$')||(a[j]==10)){printf("产生式格式错误\n");return 0;}css[count][0]=a[i];css[count][1]=a[i+1];css[count][2]=a[i+2];k=3;j++;continue;}css[count][k]=a[j];k++;j++;}css[count][k]='\0';i=j;count++;}}else{printf("产生式格式错误\n");return -1;}}return 0;}//从键盘获得输入int input(){char a[MAX*MAX];int v;printf("输入产生式,产生式之间以空格回车或Tab键分隔,并以$键结束.\n");printf("用@表示虚拟符号ε,终结符用大写字母表示,其他字符表示非终结符\n");while(1){fgets(a,MAX*MAX,stdin);v=handle(a);if(v==-1)return -1;if(v==2)return 0;}}//求出能推出ε的非终结符void seekEmpty(){int i,j,k,t;int flag=0,flag2=0;int len,c;char a[MAX][MAX],ch;for(i=0;i<count;i++){strcpy(a[i],css[i]);}//求出含有的非终结符的个数,并把各终结符保存起来for(i=0;i<count;i++){for(j=0;j<cnt;j++){if(l[j].ch==a[i][0]){l[j].num++;flag=1;break;}elseflag=0;}if((!cnt)||(!flag)){l[cnt].ch=a[i][0];l[cnt].flag=-1;l[cnt].num=1;l[cnt].s=0;l[cnt].l=0;cnt++;flag=1;continue;}}c=count;while(c){for(i=0;i<c;i++){//如果该终结符推出ε,从a[]中删除所有带有该终结符的产生式if(a[i][3]=='@'){ch=a[i][0];for(j=0;j<c;j++){if(ch==a[j][0]){if(j!=c-1){for(k=j;k<c-1;k++)strcpy(a[k],a[k+1]);c--;j--;}else{c--;j--;}}}for(j=0;j<cnt;j++){if(ch==l[j].ch){l[j].flag=1;break;}}i--;continue;}len=strlen(a[i]);for(j=3;j<len;j++){//当该产生式右边含有非终结符时从a[]中删除该条记录if((a[i][j]<'A')||(a[i][j]>'Z')){flag2=1;break;}}if(flag2){for(k=0;k<cnt;k++){if(a[i][0]==l[k].ch){l[k].num--;if(l[k].num==0)l[k].flag=0;break;}}if(i!=c-1)for(k=i;k<c-1;k++){strcpy(a[k],a[k+1]);}c--;i--;flag2=0;continue;}//如果产生式右边为非终结符看看该终结符能不能推出εfor(j=3;j<len;j++){if((a[i][j]>='A')&&(a[i][j]<='Z')){for(k=0;k<cnt;k++){if(a[i][j]==l[k].ch){if(l[k].flag==0){flag2=1;break;}else if(l[k].flag==1){for(t=j;t<len-1;t++)a[i][t]=a[i][t+1];a[i][len-1]='\0';j--;len--;break;}break;}}if(flag2)break;}}if(a[i][3]=='\0'){ch=a[i][0];for(j=0;j<c;j++){if(ch==a[j][0]){if(j!=c-1){for(k=j;k<c-1;k++)strcpy(a[k],a[k+1]);c--;j--;}else{c--;j--;}}}i--;for(k=0;k<cnt;k++){if(ch==l[k].ch){l[k].flag=1;break;}}}if(flag2){for(k=0;k<cnt;k++){if(a[i][0]==l[k].ch){l[k].num--;if(l[k].num==0)l[k].flag=0;}}if(i!=c-1)for(k=i;k<c-1;k++){strcpy(a[k],a[k+1]);}c--;i--;flag2=0;continue;}}}}//求每个非终结符的First集合void seekFirstVn(){int i,j,k,t,t1,t2,c,item;int len,s,flag=0,flag2=0,fchange;char a[MAX][MAX],ch[MAX];for(i=0;i<count;i++){strcpy(a[i],css[i]);}c=count;while(1){fchange=0;for(i=0;i<c;i++){//右部为ε,将ε并入到左部的First中if(a[i][3]=='@'){/*for(j=0;j<cnt;j++){if(l[j].ch==a[i][0]){for(k=0;k<l[j].s;k++)if(l[j].first[k]==a[i][3]){flag=1;break;}if(!flag){l[j].first[l[j].s]=a[i][3];l[j].s++;l[j].first[l[j].s]='\0';fchange=1;break;}flag=0;}}*///从当前列表a[]中删除if(i!=c-1)for(j=i;j<c-1;j++)strcpy(a[j],a[j+1]);c--;i--;continue;}len=strlen(a[i]);//产生式右边符号为终结符时,将该终结符并入到左部的First集合中for(j=3;j<len;j++){if((a[i][j]<'A')||(a[i][j]>'Z')){for(k=0;k<cnt;k++){if(a[i][0]==l[k].ch){for(t=0;t<l[k].s;t++){if(a[i][j]==l[k].first[t]){flag=1;break;}}if(!flag){l[k].first[l[k].s]=a[i][j];l[k].s++;l[k].first[l[k].s]='\0';fchange=1;}flag=0;break;}}//从a[][]中删除该条产生式if(i!=c-1)for(k=i;k<c-1;k++)strcpy(a[k],a[k+1]);c--;i--;break;}//产生式右边符号为非终结符时else if((a[i][j]>='A')&&(a[i][j]<='Z')){/*将该非终结符的FIRST集合除去ε并入到当前非终结符的FIRST集合中*/for(k=0;k<cnt;k++){if(a[i][j]==l[k].ch){for(t=0;t<cnt;t++){if(a[i][0]==l[t].ch){for(t1=0;t1<l[k].s;t1++){for(t2=0;t2<l[t].s;t2++){if(l[k].first[t1]==l[t].first[t2]){break;}}if((t2==l[t].s)&&(l[k].first[t1])!='@'){fchange=1;l[t].first[l[t].s]=l[k].first[t1];l[t].s++;l[t].first[l[t].s]='\0';}}break;}}break;}}if(l[k].flag)continue;elsebreak;}}}if(!fchange){for(i=0;i<cnt;i++){if(l[i].flag){l[i].first[l[i].s]='@';l[i].s++;l[i].first[l[i].s]='\0';}printf("FIRST(%c): %s\n",l[i].ch,l[i].first);}printf("\n");break;}}}//求产生式右部的First集合void seekFirstRight(){struct Right{char a[MAX];char first[MAX];int s;}r[MAX];int i,j,k,t;int cnt=0,len,len1,flag=0;for(i=0;i<count;i++){for(j=0;j<cnt;j++){if(!strcmp(css[i]+3,r[j].a)){flag=1;break;}}if(flag){flag=0;continue;}strcpy(r[j].a,css[i]+3);r[j].s=0;cnt++;}for(i=0;i<cnt;i++){len=strlen(r[i].a);for(j=0;j<len;j++){//遇到终结符if(r[i].a[j]=='@'){r[i].first[r[i].s]='@';r[i].s++;r[i].first[r[i].s]='\0';break;}else if((r[i].a[j]<'A')||(r[i].a[j]>'Z')){r[i].first[r[i].s]=r[i].a[j];r[i].s++;r[i].first[r[i].s]='\0';break;}else{for(k=0;k<cnt;k++){if(r[i].a[j]==l[k].ch){len1=strlen(l[k].first);for(t=0;t<len1;t++){if(l[k].first[t]!='@'){r[i].first[r[i].s]=l[k].first[t];r[i].s++;r[i].first[r[i].s]='\0';}}break;}}if(l[k].flag){if(j==len-1){r[i].first[r[i].s]='@';r[i].s++;r[i].first[r[i].s]='\0';}continue;}elsebreak;}}}for(i=0;i<cnt;i++){printf("FIRST(%s): %s\n",r[i].a,r[i].first);}printf("\n");}//求每个非终极符的Follow集合void seekFollow(){int i,j,k,t,t1,t2,t3,c=0;int flag=0,len;int fchange;//判断一次循环是否有改动的地方char a[MAX][MAX],ch[MAX];for(i=0;i<count;i++){len=strlen(css[i]);for(j=3;j<len;j++){if((css[i][j]>='A')&&(css[i][j]<='Z')){break;}}if(j!=len){strcpy(a[c],css[i]);c++;}}l[0].follow[l[0].l]='#';l[0].l++;l[0].follow[l[0].l]='\0';while(1){fchange=0;for(i=0;i<c;i++){len=strlen(a[i]);for(j=3;j<len;j++){if((a[i][j]>='A')&&(a[i][j]<='Z')){//判断该非终结符的前一位是否为非终结符,是的话,//将其First集合去ε后并到其前一位非终结符的Follow集合中if((a[i][j-1]>='A')&&(a[i][j-1]<='Z')){for(k=0;k<cnt;k++){if(a[i][j-1]==l[k].ch){for(t=0;t<cnt;t++){if(a[i][j]==l[t].ch){for(t1=0;t1<l[t].s;t1++){if(l[t].first[t1]=='@')continue;for(t2=0;t2<l[k].l;t2++)if(l[t].first[t1]==l[k].follow[t2])break;if(t2==l[k].l){fchange=1;l[k].follow[l[k].l]=l[t].first[t1];l[k].l++;l[k].follow[l[k].l]='\0';}}break;}}break;}}}//如果该非终结符是最后一位,//将该产生式左部非终结符的Follow集合//加入到当前非终结符的Follow集合中.//然后从当前终结符开始向右判断是否为非终结符,是的话,进行相应处理//循环直到当前非终结符推不出ε或当前为终结符时退出if(j==len-1){t3=j;strcpy(ch,a[i]);while(!flag){if((ch[t3]>='A')&&(ch[t3]<='Z')){for(k=0;k<cnt;k++){if(ch[0]==l[k].ch){for(t=0;t<cnt;t++){if(ch[t3]==l[t].ch){for(t1=0;t1<l[k].l;t1++){for(t2=0;t2<l[t].l;t2++)if(l[k].follow[t1]==l[t].follow[t2])break;if(t2!=l[t].l)continue;else{fchange=1;l[t].follow[l[t].l]=l[k].follow[t1];l[t].l++;l[t].follow[l[t].l]='\0';}}if(l[t].flag)ch[t3--]='\0';else{flag=1;t3--;}break;}}break;}}}elsebreak;}flag=0;}}//如果当前位为终结符,判断其前一位是否为非终结符//是的话,将该终结符并到该非终结符的Follow集合中else{if((a[i][j-1]>='A')&&(a[i][j-1]<='Z')){for(k=0;k<cnt;k++){if(a[i][j-1]==l[k].ch){for(t=0;t<l[k].l;t++)if(a[i][j]==l[k].follow[t])break;if(t==l[k].l){fchange=1;l[k].follow[l[k].l]=a[i][j];l[k].l++;l[k].follow[l[k].l]='\0';}}}}}}}if(!fchange){for(i=0;i<cnt;i++)printf("FOLLOW(%c): %s\n",l[i].ch,l[i].follow);break;}}}int main(){int i;if(input()==-1)return -1;seekEmpty();seekFirstVn();seekFirstRight();seekFollow();return 0;}实验演示:因为不知道怎么用电脑输出’ε’符号,我在代码里用’@’来表示‘ε’.以‘$’来结束输入测试数据1:S->MH|aH->LSo|@K->dML|@L->eHfM->K|bLM测试数据2:S->aHH->aMd|dM->Ab|@A->aM|e实验感想:经过这几次的实验,不仅让我们更加深刻的知道了first集合和follow集合的计算步骤和方法,还很好的培养了我们动手能力。


【编译原理】语法分析LL(1)分析法的FIRST和FOLLOW集 近来复习编译原理,语法分析中的⾃上⽽下LL(1)分析法,需要构造求出⼀个⽂法的FIRST和FOLLOW集,然后构造分析表,利⽤分析表+⼀个栈来做⾃上⽽下的语法分析(递归下降/预测分析),可是这个FIRST集合FOLLOW集看得我头⼤。
教课书上的规则如下,⽤我理解的语⾔描述的:任意符号α的FIRST集求法:1. α为终结符,则把它⾃⾝加⼊FIRSRT(α)2. α为⾮终结符,则:(1)若存在产⽣式α->a...,则把a加⼊FIRST(α),其中a可以为ε(2)若存在⼀串⾮终结符Y1,Y2, ..., Yk-1,且它们的FIRST集都含空串,且有产⽣式α->Y1Y2...Yk...,那么把FIRST(Yk)-{ε}加⼊FIRST(α)。
如果k-1抵达产⽣式末尾,那么把ε加⼊FIRST(α) 注意(2)要连续进⾏,通俗地描述就是:沿途的Yi都能推出空串,则把这⼀路遇到的Yi的FIRST集都加进来,直到遇到第⼀个不能推出空串的Yk为⽌。
重复1,2步骤直⾄每个FIRST集都不再增⼤为⽌。
任意⾮终结符A的FOLLOW集求法:1. A为开始符号,则把#加⼊FOLLOW(A)2. 对于产⽣式A-->αBβ: (1)把FIRST(β)-{ε}加到FOLLOW(B) (2)若β为ε或者ε属于FIRST(β),则把FOLLOW(A)加到FOLLOW(B)重复1,2步骤直⾄每个FOLLOW集都不再增⼤为⽌。
⽼师和同学能很敏锐地求出来,⽽我只能按照规则,像程序⼀样⼀条条执⾏。
于是我把这个过程写成了程序,如下:数据元素的定义:1const int MAX_N = 20;//产⽣式体的最⼤长度2const char nullStr = '$';//空串的字⾯值3 typedef int Type;//符号类型45const Type NON = -1;//⾮法类型6const Type T = 0;//终结符7const Type N = 1;//⾮终结符8const Type NUL = 2;//空串910struct Production//产⽣式11 {12char head;13char* body;14 Production(){}15 Production(char h, char b[]){16 head = h;17 body = (char*)malloc(strlen(b)*sizeof(char));18 strcpy(body, b);19 }20bool operator<(const Production& p)const{//内部const则外部也为const21if(head == p.head) return body[0] < p.body[0];//注意此处只适⽤于LL(1)⽂法,即同⼀VN各候选的⾸符不能有相同的,否则这⾥的⼩于符号还要向前多看⼏个字符,就不是LL(1)⽂法了22return head < p.head;23 }24void print() const{//要加const25 printf("%c -- > %s\n", head, body);26 }27 };2829//以下⼏个集合可以再封装为⼀个⼤结构体--⽂法30set<Production> P;//产⽣式集31set<char> VN, VT;//⾮终结符号集,终结符号集32char S;//开始符号33 map<char, set<char> > FIRST;//FIRST集34 map<char, set<char> > FOLLOW;//FOLLOW集3536set<char>::iterator first;//全局共享的迭代器,其实觉得应该⽤局部变量37set<char>::iterator follow;38set<char>::iterator vn;39set<char>::iterator vt;40set<Production>::iterator p;4142 Type get_type(char alpha){//判读符号类型43if(alpha == '$') return NUL;//空串44else if(VT.find(alpha) != VT.end()) return T;//终结符45else if(VN.find(alpha) != VN.end()) return N;//⾮终结符46else return NON;//⾮法字符47 }主函数的流程很简单,从⽂件读⼊指定格式的⽂法,然后依次求⽂法的FIRST集、FOLLOW集1int main()2 {3 FREAD("grammar2.txt");//从⽂件读取⽂法4int numN = 0;5int numT = 0;6char c = '';7 S = getchar();//开始符号8 printf("%c", S);9 VN.insert(S);10 numN++;11while((c=getchar()) != '\n'){//读⼊⾮终结符12 printf("%c", c);13 VN.insert(c);14 numN++;15 }16 pn();17while((c=getchar()) != '\n'){//读⼊终结符18 printf("%c", c);19 VT.insert(c);20 numT++;21 }22 pn();23 REP(numN){//读⼊产⽣式24 c = getchar();25int n; RINT(n);26while(n--){27char body[MAX_N];28 scanf("%s", body);29 printf("%c --> %s\n", c, body);30 P.insert(Production(c, body));31 }32 getchar();33 }3435 get_first();//⽣成FIRST集36for(vn = VN.begin(); vn != VN.end(); vn++){//打印⾮终结符的FIRST集37 printf("FIRST(%c) = { ", *vn);38for(first = FIRST[*vn].begin(); first != FIRST[*vn].end(); first++){39 printf("%c, ", *first);40 }41 printf("}\n");42 }4344 get_follow();//⽣成⾮终结符的FOLLOW集45for(vn = VN.begin(); vn != VN.end(); vn++){//打印⾮终结符的FOLLOW集46 printf("FOLLOW(%c) = { ", *vn);47for(follow = FOLLOW[*vn].begin(); follow != FOLLOW[*vn].end(); follow++){48 printf("%c, ", *follow);49 }50 printf("}\n");51 }52return0;53 }主函数其中⽂法⽂件的数据格式为(按照平时做题的输⼊格式设计的):第⼀⾏:所有⾮终结符,⽆空格,第⼀个为开始符号;第⼆⾏:所有终结符,⽆空格;剩余⾏:每⾏描述了⼀个⾮终结符的所有产⽣式,第⼀个字符为产⽣式头(⾮终结符),后跟⼀个整数位候选式的个数n,之后是n个以空格分隔的字符串为产⽣式体。


华东交通大学课程设计(论文)任务书软件学院专业项目管理班级2005-4一、课程设计(论文)题目正规文法的First集合Follow集求解过程动态模拟二、课程设计(论文)工作:自2008年6月23 日起至2008年 6 月27 日止。
三、课程设计(论文)的内容要求:1、基本要求:进一步培养学生编译器设计的思想,加深对编译原理和应用程序的理解,针对编译过程的重点和难点内容进行编程,独立完成有一定工作量的程序设计任务,同时强调好的程序设计风格,并综合使用程序设计语言、数据结构和编译原理的知识,熟悉使用开发工具VC 6.0 或其它软件编程工具。
为了使学生从课程设计中尽可能取得比较大的收获,对课程设计题目可根据自己的兴趣选题(须经老师审核),或从老师给定题目中选择完成(具体见编译原理课程设计题目要求)。
通过程序实现、总结报告和学习态度综合考评,并结合学生的动手能力,独立分析解决问题的能力和创新精神。
成绩分优、良、中、及格和不及格五等。
2、具体要求设计一个由正规文法生成Fisrt集Follow集的动态过程模拟动态模拟算法的基本功能是:●输入一个正规文法;●输出由文法构造的First集的算法;●输出First集;●输出由文法构造的Follow集的算法;●输出Follow集;学生签名:2008 年 6 月 27 日课程设计(论文)评阅意见评阅人职称副教授2008 年 6 月 27 日目录一、需求分析 (3)二、总体设计 (4)三、详细设计 (9)四、课设小结 (12)五、谢辞 (13)六、参考文献 (14)一、 需求分析问题描述设计一个由正规文法生成First 集和Follow 集并进行简化的算法动态模拟。
(算法参见教材) 【基本要求】动态模拟算法的基本功能是: (1) 输入一个文法G ;(2) 输出由文法G 构造FIRST 集的算法; (3) 输出First 集;(4) 输出由文法G 构造FOLLOW 集的算法; (5) 输出FOLLOW 集。

计算f i r s t集合和f o l l o w集合--编译原理计算first 集合和follow 集合姓名:彦清 学号:E10914127一、实验目的输入:任意的上下文无关文法。
输出:所输入的上下文无关文法一切非终结符的first 集合和follow 集合。
二、实验原理设文法G[S]=(V N ,V T ,P ,S ),则首字符集为:FIRST (α)={a | α⇒*a β,a ∈V T ,α,β∈V *}。
若α⇒*ε,ε∈FIRST (α)。
由定义可以看出,FIRST (α)是指符号串α能够推导出的所有符号串中处于串首的终结符号组成的集合。
所以FIRST 集也称为首符号集。
设α=x 1x 2…x n ,FIRST (α)可按下列方法求得:令FIRST (α)=Φ,i =1;(1)若x i ∈V T ,则x i ∈FIRST (α); (2) 若x i ∈V N ;① 若ε∉FIRST (x i ),则FIRST (x i )∈FIRST (α);② 若ε∈FIRST (x i ),则FIRST (x i )-{ε}∈FIRST (α);(3) i =i+1,重复(1)、(2),直到x i ∈V T ,(i =2,3,…,n )或x i ∈V N 且若ε∉FIRST (x i )或i>n 为止。
当一个文法中存在ε产生式时,例如,存在A →ε,只有知道哪些符号可以合法地出现在非终结符A 之后,才能知道是否选择A →ε产生式。
这些合法地出现在非终结符A 之后的符号组成的集合被称为FOLLOW 集合。
下面我们给出文法的FOLLOW 集的定义。
设文法G[S]=(V N ,V T ,P ,S ),则FOLLOW (A )={a | S ⇒… Aa …,a ∈V T }。
若S ⇒*…A ,#∈FOLLOW (A )。
由定义可以看出,FOLLOW (A )是指在文法G[S]的所有句型中,紧跟在非终结符A 后的终结符号的集合。

First集合的求法:First集合最终是对产生式右部的字符串而言的,但其关键是求出非终结符的First集合,由于终结符的First集合就是它自己,所以求出非终结符的First集合后,就可很直观地得到每个字符串的First集合。
1. 直接收取:对形如U-a…的产生式(其中a是终结符),把a收入到First(U)中2. 反复传送:对形入U-P…的产生式(其中P是非终结符),应把First(P)中的全部内容传送到First(U)中。
Follow集合的求法:Follow集合是针对非终结符而言的,Follow(U)所表达的是句型中非终结符U所有可能的后随终结符号的集合,特别地,“#”是识别符号的后随符。
1. 直接收取:注意产生式右部的每一个形如“…Ua…”的组合,把a直接收入到Follow(U)中。
2.直接收取:对形如“…UP…”(P是非终结符)的组合,把First(P)除ε直接收入到Follow(U)中。
3.反复传送:对形如P-…U的产生式(其中U是非终结符),应把Follow(P)中的全部内容传送到Follow(U)中。
(或 P-…UB且First(B)包含ε,则把First(B)除ε直接收入到Follow(U)中,并把Follow(P)中的全部内容传送到Follow(U)中)例1:判断该文法是不是LL(1)文法,说明理由 S→ABc A→a|ε B→b|ε?First集合求法就是:能由非终结符号推出的所有的开头符号或可能的ε,但要求这个开头符号是终结符号。
如此题A可以推导出a和ε,所以FIRST(A)={a,ε};同理FIRST (B)={b,ε};S可以推导出aBc,还可以推导出bc,还可以推导出c,所以FIRST(S)={a,b,c}。
Follow集合的求法是:紧跟随其后面的终结符号或#。
但文法的识别符号包含#,在求的时候还要考虑到ε。
具体做法是把所有包含你要求的符号的产生式都找出来,再看哪个有用。


摘要:编译原理是计算机科学与技术专业最重要的一门专业基础课程,内容庞大,涉及面广,知识点多。
由于该课程教、学难度都非常大,往往费了大量时间而达不到预期教学效果俗语说:学习的最好方法是实践。
本次课程设计的目的正是基于此,力求为学生提供一个理论联系实际的机会,通过布置一定难度的课题,要求学生独立完成。
我们这次课程设计的主要任务是编程实现对给定文法的FIRST 集和FOLLOW集的求解。
通过实践,建立系统设计的整体思想,锻炼编写程序、调试程序的能力,学习文档编写规范,培养独立学习、吸取他人经验、探索前言知识的习惯,树立团队协作精神。
同时,课程设计可以充分弥补课堂教学及普通实验中知识深度与广度有限的缺陷,更好地帮助学生从全局角度把握课程体系。
关键词:编译原理;FIRST集;FOLLOW集目录1 课题综述 (1)1.1 课题来源 (1)1.2 课题意义 (1)1.3 预期目标 (1)1.4 面对的问题 (1)1.5 需解决的关键技术 (1)2 系统分析 (2)2.1 基础知识 (2)2.1.1 FIRST集定义 (2)2.1.2FIRST集求解算法.................................................................... 错误!未定义书签。
2.1.3FOLLOW集的定义 (4)2.1.4 FOLLOW集算法 (4)2.2 解决问题的基本思路 (4)2.3 总体方案 (4)3 系统设计 (5)3.1 算法实现 (5)3.2 流程图 (6)4 代码编写 (10)5 程序调试 (15)6 运行与测试 (15)1 课题综述1.1 课题来源文法:包含若干终结符,非终结符,由终结符与非终结符组成的产生式。
本次课程设计就是对产生式进行左递归分析,待无左递归现象后进行FIRST集与FOLLOW集的求解。
1.2 课题意义由文法产生的若干个句子有可能是合法的或者不合法的,也有可能产生歧义,所以要消除歧义先消除文法左递归,然后根据求得的FIRST集与FOLLOW 集构造分析表,分析给定句子的合法性。

《编译原理》实验报告
专业班级:计101班
学号:109074002
姓名:卞恩会
指导老师:王森玉
实验内容:
1.求出每个非终结符的FIRST集合
2.求出每个产生式右部的FIRST集合
3.求出每个非终结符的Follow集合实验环境:
Visual Studio2010
实验目的:
掌握FIRST集合和FOLLOW集合的求法
测试数据1:
S->aH
H->aMd|d
M->Ab|@
A->aM|e
输出结果:
测试数据2:S->AB
S->bC
A->@
A->b
B->@
B->aD
C->AD
C->b
D->aS
D->c
测试数据3:E->TX
X->+TX|@ T->FY
Y->*FY|@ F->i|(E)
输出结果:
感受:通过上机调试代码让我对书上的单纯的理论的知识有了一个更深的理解同时让我明白了对待一个问题我们应该全面的去理解它,这样才能学到的更多。
程序清单:。
编译原理课设报告ll0编译原理课设报告LL(0)。
一、引言。
编译原理是计算机科学与技术领域的重要课程之一,它研究如何将高级程序语言翻译成机器语言。
LL(0)是一种重要的语法分析方法,它是一种自顶向下的分析方法,通过构建语法树来实现对程序语言的分析和翻译。
本报告将介绍LL(0)语法分析的原理、算法以及课设的设计与实现。
二、LL(0)语法分析原理。
LL(0)语法分析是一种基于预测分析表的自顶向下语法分析方法。
它通过预测下一个输入符号,根据文法规则进行推导,最终构建出语法树。
LL(0)的意思是“左侧扫描、左推导、0个向前看符号”。
LL(0)语法分析的关键是构建预测分析表,该表包含了文法的非终结符和终结符的组合,以及对应的产生式。
通过分析输入串和预测分析表,可以确定下一个推导所使用的产生式,从而构建语法树。
三、LL(0)语法分析算法。
1. 构建First集和Follow集。
在LL(0)语法分析中,需要先构建每个非终结符的First集和Follow集。
First集表示该非终结符能够推导出的终结符集合,Follow集表示在该非终结符的右侧能够出现的终结符集合。
2. 构建预测分析表。
根据文法的产生式和First集、Follow集,构建预测分析表。
预测分析表的行表示文法的非终结符,列表示文法的终结符。
表中的每个格子填写对应的产生式。
3. 进行语法分析。
根据输入串和预测分析表,进行语法分析。
从左到右扫描输入串,根据当前输入符号和栈顶符号,在预测分析表中查找对应的产生式。
将产生式右侧的符号入栈,并将输入串向右移动一个位置。
重复这个过程,直到输入串为空或者出现错误。
四、课设设计与实现。
1. 文法设计。
根据课设要求,设计符合LL(0)语法分析方法的文法。
文法应该满足左递归消除、左因子消除等要求,以便于构建预测分析表。
2. 构建预测分析表。
根据设计的文法,构建预测分析表。
根据文法的非终结符和终结符,填写预测分析表中的产生式。
FIRST集合、FOLLOW集合及LL(1)⽂法求法FIRST集合定义可从α推导得到的串的⾸符号的集合,其中α是任意的⽂法符号串。
规则计算⽂法符号 X 的 FIRST(X),不断运⽤以下规则直到没有新终结符号或ε可以被加⼊为⽌:(1)如果 X 是⼀个终结符号,那么 FIRST(X) = X。
(2)如果 X 是⼀个⾮终结符号,且 X ->Y1 Y2 … Y k是⼀个产⽣式,其中 k≥1,那么如果对于某个i,a在 FIRST(Y1)、FIRST(Y2)… FIRST(Y i-1)中,就把a加⼊到 FIRST(X) 中。
(3)如果 X ->ε是⼀个产⽣式,那么将ε加⼊到 FIRST(X)中。
以上是书上的官⽅规则,不仅读起来很拗⼝,理解也很累。
下⾯看⼀下精简版的规则(从别⼈ @ 那⾥看来的,感觉很棒,这⾥引⽤⼀下):(1)如果X是终结符,则FIRST(X) = { X } 。
(2)如果X是⾮终结符,且有产⽣式形如X → a…,则FIRST( X ) = { a }。
(3)如果X是⾮终结符,且有产⽣式形如X → ABCdEF…(A、B、C均属于⾮终结符且包含ε,d为终结符),需要把FIRST( A )、FIRST( B )、FIRST( C )、FIRST( d )加⼊到 FIRST( X )中。
(4)如果X经过⼀步或多步推导出空字符ε,将ε加⼊FIRST( X )。
实践记得,曾经有⼈说过:只读,就会⽩给下⾯以这个⽂法为例讲解⼀波,会⽤精简版规则,更容易理解⼀些:E -> T E'E' -> + T E' | εT -> F T'T' -> * F T' | εF -> ( E ) | id12345FIRST(E) = FIRST(T)根据规则3,很容易理解,这⾥要注意的由于T不含ε,所以遍历到T就停⽌了,E’不会加⼊进来FIRST(E’) = FIRST(+) ∪ FIRST(ε)= { +, ε }根据规则2和4,,很好理解FIRST(T) = FIRST(F)根据规则3,和第⼀条推导过程⼀样FIRST(T’) = FIRST() ∪ FIRST(ε)= { , ε }根据规则2和4,和第⼆条推导⼀样FIRST(F) = FIRST( ( ) ∪ FIRST(id)= { ( , id }根据规则2结果:FIRST(E) = FIRST(T) = FIRST(F) = { ( , id }FIRST(E') = FIRST(+) ∪ FIRST(ε)= { + , ε }FIRST(E') = FIRST(*) ∪ FIRST(ε)= { * , ε }123FOLLOW集合定义对于⾮终结符号A,FOLLOW(A)被定义为可能在某些句型中紧跟在A右边的终结符号集合。
编译原理实验⼆:LL(1)语法分析器⼀、实验要求 1. 提取左公因⼦或消除左递归(实现了消除左递归) 2. 递归求First集和Follow集 其它的只要按照课本上的步骤顺序写下来就好(但是代码量超多...),下⾯我贴出实验的⼀些关键代码和算法思想。
⼆、基于预测分析表法的语法分析 2.1 代码结构 2.1.1 Grammar类 功能:主要⽤来处理输⼊的⽂法,包括将⽂法中的终结符和⾮终结符分别存储,检测直接左递归和左公因⼦,消除直接左递归,获得所有⾮终结符的First集,Follow集以及产⽣式的Select集。
#ifndef GRAMMAR_H#define GRAMMAR_H#include <string>#include <cstring>#include <iostream>#include <vector>#include <set>#include <iomanip>#include <algorithm>using namespace std;const int maxn = 110;//产⽣式结构体struct EXP{char left; //左部string right; //右部};class Grammar{public:Grammar(); //构造函数bool isNotTer(char x); //判断是否是终结符int getTer(char x); //获取终结符下标int getNonTer(char x); //获取⾮终结符下标void getFirst(char x); //获取某个⾮终结符的First集void getFollow(char x); //获取某个⾮终结符的Follow集void getSelect(char x); //获取产⽣式的Select集void input(); //输⼊⽂法void scanExp(); //扫描输⼊的产⽣式,检测是否有左递归和左公因⼦void remove(); //消除左递归void solve(); //处理⽂法,获得所有First集,Follow集以及Select集void display(); //打印First集,Follow集,Select集void debug(); //⽤于debug的函数~Grammar(); //析构函数protected:int cnt; //产⽣式数⽬EXP exp[maxn]; //产⽣式集合set<char> First[maxn]; //First集set<char> Follow[maxn]; //Follow集set<char> Select[maxn]; //select集vector<char> ter_copy; //去掉$的终结符vector<char> ter; //终结符vector<char> not_ter; //⾮终结符};#endif 2.1.2 AnalyzTable类 功能:得到预测分析表,判断输⼊的⽂法是否是LL(1)⽂法,⽤预测分析表法判断输⼊的符号串是否符合刚才输⼊的⽂法,并打印出分析过程。
编译原理课程实验报告实验2:语法分析
三、系统设计得分
要求:分为系统概要设计和系统详细设计。
(1)系统概要设计:给出必要的系统宏观层面设计图,如系统框架图、数据流图、功能模块结构图等以及相应的文字说明。
1)系统的数据流图:
说明
说明:本语法分析器是基于上一个实验词法分析器的基础上,通过在界面写或者是导入源程序,词法分析器将源程序识别的词法单元传递给语法分析器,语法分析器验证这个词法单元组成的串是否可以由源语言的文法生成,能够输出语法分析的结果,文法的first集、follow 集和预测分析表,当然也可以以易于理解的方式报告语法错误。
2)系统框架图
本系统框架主要是三部分,一部分是词法分析,负责识别源程序的词法单元识别,并将其存
因为预测分析表实在是过于庞大,因此本处分段截取预测分析表,下面的表是接在上面表的右侧。
(3)针对一测试程序输出其句法分析结果;
测试程序:
语法分析结果:
语法分析树:
(4)输出针对此测试程序对应的语法错误报告;
带错误的测试程序:
语法错误报告:
(5)对实验结果进行分析。
总结:
本语法分析器具有强大的语法分析功能
●允许变量的连续声明,比如int a,b,c;
●允许声明的同时赋值,比如string c = “你好”;
●允许对数组的声明和引用,同时进行赋值,比如char[4] a = {‘a’,’b’,’c’,’d’};a[0] = ‘m’;
●支持多种类型的声明和赋值,比如int,short,long,flaot,double,char,string,boolean
的声明和赋值;
●允许声明和使用一个过程函数,比如:。
【编译原理】FIRST集、FOLLOW集算法原理和实现书中⼀些话,不知是翻译的原因。
还是我个⼈理解的原因感觉不是⾮常好理解。
个⼈重新整理了⼀下。
不过相对于消除左递归和提取左公因,FIRST集和FOLLOW集的算法相对来说⽐较简单。
书中的重点给出:FIRST:⼀个⽂法符号的FIRST集就是这个符号能推导出的第⼀个终结符号的集合, 包括空串。
例: A -> abc | def | ε那么FIRST(A) 等于 { a, d, ε }。
FOLLOW:蓝线画的部分很重要。
特别是这句话:请注意,在这个推导的某个阶段,A和a之间可能存在⼀些⽂法符号。
单如果这样,这些符号会推导得到ε并消失。
这句话的意思就是好⽐说: S->ABa B->c | ε 这个⽂法 FOLLOW(A)的值应该是FIRST(B)所有的终结符的集合(不包含ε),但是FIRST(B)是包含ε的,说明B是可空的,既然B是可空的S->ABa 也可以看成 S->Aa。
那么a就可以跟在A的后⾯.所以在这种情况下,FOLLOW(A)的值是包含a的。
换句话说就是。
⼀个⽂法符号A的FOLLOW集合就是它的下⼀个⽂法符号B的FIRST集合。
如果下⼀个⽂法符号B的FIRST集合包含ε,那么我们就要获取下⼀个⽂法符号B的FOLLOW集添加到FOLLOW(A)中代码中的注释已经很详细// 提取First集合func First(cfg []*Production, sym *Symbolic) map[string] *Symbolic {result := make(map[string] *Symbolic)// 规则⼀如果符号是⼀个终结符号,那么他的FIRST集合就是它⾃⾝if sym.SymType() == SYM_TYPE_TERMINAL || sym.SymType() == SYM_TYPE_NIL {result[sym.Sym()] = symreturn result}// 规则⼆如果⼀个符号是⼀个⾮终结符号// (1) A -> XYZ 如果 X 可以推导出nil 那么就去查看Y是否可以推导出nil// 如果 Y 推导不出nil,那么把Y的First集合加⼊到A的First集合// 如果 Y 不能推导出nil,那么继续推导 Z 是否可以推导出nil,依次类推// (2) A -> XYZ 如果XYZ 都可以推导出 nil, 那么说明A这个产⽣式有可能就是nil,这个时候我们就把nil加⼊到FIRST(A)中for _, production := range cfg {if production.header == sym.Sym() {nilCount := 0for _, rightSymbolic := range production.body { // 对于⼀个产⽣式ret := First(cfg, rightSymbolic) // 获取这个产⽣式体的First集合hasNil := falsefor k, v := range ret {if v.SymType() == SYM_TYPE_NIL { // 如果推导出nil, 标识当前产⽣式体的符号可以推导出nilhasNil = true} else {result[k] = v}}if false == hasNil { // 当前符号不能推导出nil, 那么这个产⽣式的FIRST就计算结束了,开始计算下⼀个产⽣式break}// 当前符号可以推导出nil,那么开始推导下⼀个符号nilCount++if nilCount == len(production.body) { // 如果产⽣式体都可以推导出nil,那么这个产⽣式就可以推导出nilresult["@"] = &Symbolic{sym: "@", sym_type: SYM_TYPE_NIL}}}}}return result}// 提取FOLLOW集合func Follow(cfg []*Production, sym string) [] *Symbolic {fmt.Printf("Follow ------> %s\n", sym)result := make([] *Symbolic, 0)// ⼀个⽂法符号的FOLLOW集就是可能出现在这个⽂法符号后⾯的终结符// ⽐如 S->ABaD, 那么FOLLOW(B)的值就是a。
编译原理实验报告记录FIRST集和FOLLOW集————————————————————————————————作者:————————————————————————————————日期:编译原理实验报告实验名称计算first集合和follow集合实验时间院系计算机科学与技术班级软件工程1班学号姓名输入:任意的上下文无关文法。
输出:所输入的上下文无关文法一切非终结符的first 集合和follow 集合。
2. 实验原理设文法G[S]=(V N ,V T ,P ,S ),则首字符集为: FIRST (α)={a | α⇒*a β,a ∈V T ,α,β∈V *}。
若α⇒*ε,ε∈FIRST (α)。
由定义可以看出,FIRST (α)是指符号串α能够推导出的所有符号串中处于串首的终结符号组成的集合。
所以FIRST 集也称为首符号集。
设α=x 1x 2…x n ,FIRST (α)可按下列方法求得:令FIRST (α)=Φ,i =1;(1) 若x i ∈V T ,则x i ∈FIRST (α);(2) 若x i ∈V N ;① 若ε∉FIRST (x i ),则FIRST (x i )∈FIRST (α);② 若ε∈FIRST (x i ),则FIRST (x i )-{ε}∈FIRST (α);(3) i =i+1,重复(1)、(2),直到x i ∈V T ,(i =2,3,…,n )或x i∈V N 且若ε∉FIRST (x i )或i>n 为止。
当一个文法中存在ε产生式时,例如,存在A →ε,只有知道哪些符号可以合法地出现在非终结符A 之后,才能知道是否选择A →ε产生式。
这些合法地出现在非终结符A 之后的符号组成的集合被称为FOLLOW 集合。
下面我们给出文法的FOLLOW 集的定义。
设文法G[S]=(V N ,V T ,P ,S ),则FOLLOW (A )={a | S ⇒… Aa …,a ∈V T }。
若S ⇒*…A ,#∈FOLLOW (A )。
由定义可以看出,FOLLOW (A )是指在文法G[S]的所有句型中,紧跟在非终结符A 后的终结符号的集合。
FOLLOW 集可按下列方法求得:(1) 对于文法G[S]的开始符号S ,有#∈FOLLOW (S );(2) 若文法G[S]中有形如B →xAy 的规则,其中x ,y ∈V *,则FIRST(y )-{ε}∈FOLLOW (A );(3) 若文法G[S]中有形如B →xA 的规则,或形如B →xAy 的规则且ε∈FIRST (y ),其中x ,y ∈V *,则FOLLOW (B )∈FOLLOW (A );计算first集合和follow集合4.实验心得通过上机实验我对文法符号的FIRST集和FOLLOW集有了更深刻的理解,已经熟练的掌握了求解的思想和方法,同时也锻炼了自己的动手解决问题的能力,对编程能力也有所提高。
5.实验代码与结果#include<iostream>#include<string>#include<algorithm>using namespace std;#define MAXS 50int NONE[MAXS]={0};string strings;//产生式string Vn;//非终结符string Vt;//终结符string first[MAXS];// 用于存放每个终结符的first集string First[MAXS];// 用于存放每个非终结符的first集string Follow[MAXS]; // 用于存放每个非终结符的follow集int N;//产生式个数struct STR{string left;string right;};//求VN和VTvoid VNVT(STR *p){int i,j;for(i=0;i<N;i++){for(j=0;j<(int)p[i].left.length();j++){if((p[i].left[j]>='A'&&p[i].left[j]<='Z')){if(Vn.find(p[i].left[j])>100)Vn+=p[i].left[j];}else{if(Vt.find(p[i].left[j])>100)Vt +=p[i].left[j];}}for(j=0;j<(int)p[i].right.length();j++){if(!(p[i].right[j]>='A'&&p[i].right[j]<='Z')){if(Vt.find(p[i].right[j])>100)Vt +=p[i].right[j];}else{if(Vn.find(p[i].right[j])>100)Vn+=p[i].right[j];}}}}void getlr(STR *p,int i){int j;for(j=0;j<strings.length();j++){if(strings[j]=='-'&&strings[j+1]=='>'){p[i].left=strings.substr(0,j);p[i].right=strings.substr(j+2,strings.length()-j);}}}//对每个文法符号求first集string Letter_First(STR *p,char ch){int t;if(!(Vt.find(ch)>100)){first[Vt.find(ch)]="ch";return first[Vt.find(ch)-1];}if(!(Vn.find(ch)>100)){for(int i=0;i<N;i++){if(p[i].left[0]==ch){if(!(Vt.find(p[i].right[0])>100)){if(First[Vn.find(ch)].find(p[i].right[0])>100){First[Vn.find(ch)]+=p[i].right[0];}}if(p[i].right[0]=='*'){if(First[Vn.find(ch)].find('*')>100){First[Vn.find(ch)]+='*';}}if(!(Vn.find(p[i].right[0])>100)){if(p[i].right.length()==1){string ff;ff=Letter_First(p,p[i].right[0]);for(int i_i=0;i_i<ff.length();i_i++){if( First[Vn.find(ch)].find(ff[i_i])>100){First[Vn.find(ch)]+=ff[i_i];}}}else{for(int j=0;j<p[i].right.length();j++){string TT;TT=Letter_First(p,p[i].right[j]);if(!(TT.find('*')>100)&&(j+1)<p[i].right.length()){sort(TT.begin(),TT.end());string tt;for(int t=1;t<TT.length();t++){tt+=TT[t];}TT=tt;tt="";for(t=0;t<TT.length();t++){if( First[Vn.find(ch)].find(TT[t])>100){First[Vn.find(ch)]+=TT[t];}}}else{for(t=0;t<TT.length();t++){if( First[Vn.find(ch)].find(TT[t])>100){First[Vn.find(ch)]+=TT[t];}}break;}}}}}}return First[Vn.find(ch)];}}// 求每个非终结符的Follow集string Letter_Follow(STR *p,char ch){int t,k;NONE[Vn.find(ch)]++;if(NONE[Vn.find(ch)]==2){NONE[Vn.find(ch)]=0;return Follow[Vn.find(ch)];}for(int i=0;i<N;i++){for(int j=0;j<p[i].right.length();j++){if(p[i].right[j]==ch){if(j+1==p[i].right.length()){string gg;gg=Letter_Follow(p,p[i].left[0]);NONE[Vn.find(p[i].left[0])]=0;for(int k=0;k<gg.length();k++){if(Follow[Vn.find(ch)].find(gg[k])>100){Follow[Vn.find(ch)]+=gg[k];}}}else{string FF;for(int jj=j+1;jj<p[i].right.length();jj++){string TT;TT=Letter_First(p,p[i].right[jj]);if(!(TT.find('*')>100)&&(jj+1)<p[i].right.length()){sort(TT.begin(),TT.end());string tt;for(int t=1;t<TT.length();t++){tt+=TT[t];}TT=tt;tt="";for(t=0;t<TT.length();t++){if( FF.find(TT[t])>100&&TT[t]!='*'){FF+=TT[t];}}}else{for(t=0;t<TT.length();t++){if( FF.find(TT[t])>100){FF+=TT[t];}}break;}}if(FF.find('*')>100){for(k=0;k<FF.length();k++){if(Follow[Vn.find(ch)].find(FF[k])>100){Follow[Vn.find(ch)]+=FF[k];}}}else{for(k=0;k<FF.length();k++){if((Follow[Vn.find(ch)].find(FF[k])>100)&&FF[k]!='*'){Follow[Vn.find(ch)]+=FF[k];}}string dd;dd=Letter_Follow(p,p[i].left[0]);NONE[Vn.find(p[i].left[0])]=0;for(k=0;k<dd.length();k++){if(Follow[Vn.find(ch)].find(dd[k])>100){Follow[Vn.find(ch)]+=dd[k];}}}}}}}return Follow[Vn.find(ch)];}void result(){cout<<"\n该文法不是LL(1)型文法"<<endl;}//主函数int main(){int i,j,k;cout<<"请输入产生式总数:";cin>>N;cout<<"\n请输入各产生式(*代表空):"<<endl;STR *p=new STR[MAXS];for(i=0;i<N;i++){cin>>strings;getlr(p,i);}VNVT(p);cout<<endl;cout<<"\n========================================="<<endl;cout<<"非终结符"<<"\t"<<"FIRST"<<"\t\t"<<"FOLLOW"<<endl;for(i=0;i<Vn.length();i++){cout<<" "<<Vn[i]<<"\t\t{";string pp;pp=Letter_First(p,Vn[i]);for(j=0;j+1<pp.length();j++){cout<<pp[j]<<",";}cout<<pp[pp.length()-1]<<"} ";Follow[0]+='#';cout<<" {";string ppp;ppp=Letter_Follow(p,Vn[i]);for(k=0;k+1<ppp.length();k++){cout<<ppp[k]<<",";}cout<<ppp[ppp.length()-1]<<"}"<<endl;}result();cout<<"\n========================================="<<endl;return 0;}。