湘教版九年级下册数学:11 二次函数
- 格式:pptx
- 大小:1.16 MB
- 文档页数:18


湘教版数学九年级下册第1章《二次函数》教学设计一. 教材分析湘教版数学九年级下册第1章《二次函数》是学生在学习了初中阶段函数知识后,进一步深入研究函数性质的重要内容。
本章主要介绍二次函数的定义、性质、图象及其应用。
通过学习二次函数,学生可以更好地理解数学与实际生活的联系,提高解决问题的能力。
教材内容安排合理,由浅入深,逐步引导学生掌握二次函数的知识。
二. 学情分析九年级的学生已经具备了一定的函数知识,对函数的概念、性质有所了解。
但二次函数相对于一次函数和反比例函数,其性质和图象更具复杂性,需要学生在已有的知识基础上,通过观察、分析、归纳等方法,自主探究二次函数的性质。
此外,学生在生活中接触到的一些现象和问题,也需要用二次函数来解释和解决。
三. 教学目标1.理解二次函数的定义,掌握二次函数的表示方法。
2.掌握二次函数的性质,能够分析二次函数图象的特点。
3.会利用二次函数解决实际问题,提高数学应用能力。
4.培养学生的观察、分析、归纳、总结能力,提高学生的自主学习能力。
四. 教学重难点1.二次函数的定义和表示方法。
2.二次函数的性质及其图象特点。
3.二次函数在实际问题中的应用。
五. 教学方法1.采用问题驱动法,引导学生主动探究二次函数的性质。
2.利用数形结合法,让学生直观地理解二次函数的图象特点。
3.运用实例分析法,让学生学会将二次函数应用于实际问题。
4.采用小组合作学习法,培养学生的团队协作能力。
六. 教学准备1.准备相关课件、图片、实例等教学资源。
2.安排适当的时间让学生进行自主学习和小组讨论。
3.准备一些练习题,用于巩固所学知识。
七. 教学过程1.导入(5分钟)利用一个实际问题引入二次函数的概念,激发学生的兴趣。
例如:抛物线运动中,物体上升和下降的轨迹为什么是抛物线?2.呈现(10分钟)介绍二次函数的定义和表示方法,展示二次函数的一般形式:y=ax^2+bx+c(a≠0)。
通过示例,让学生理解二次函数的各项参数代表的意义。

湘教版数学九年级下册1.1《二次函数》教学设计一. 教材分析湘教版数学九年级下册1.1《二次函数》是本册教材中的重要内容,主要介绍了二次函数的定义、图像和性质。
通过本节课的学习,学生能够理解二次函数的概念,掌握二次函数的图像特点,了解二次函数的性质,并为后续学习二次方程和二次不等式打下基础。
二. 学情分析学生在学习本节课之前,已经掌握了函数的基本概念和一次函数的知识,具备了一定的函数思维。
但二次函数相对于一次函数来说,概念较为抽象,图像和性质的理解也需要一定的空间想象能力。
因此,在教学过程中,需要关注学生的学习困难,引导学生通过观察、操作、思考、交流等方式,逐步理解二次函数的概念和性质。
三. 教学目标1.理解二次函数的定义,掌握二次函数的图像特点;2.了解二次函数的性质,能够运用二次函数解决实际问题;3.培养学生的空间想象能力,提高学生的数学思维能力。
四. 教学重难点1.二次函数的定义和图像特点;2.二次函数的性质及其运用。
五. 教学方法1.情境教学法:通过生活实例引入二次函数,激发学生的学习兴趣;2.启发式教学法:引导学生主动思考、探究二次函数的性质;3.小组合作学习:培养学生团队合作精神,提高学生的交流能力;4.动手操作:让学生通过实际操作,加深对二次函数图像和性质的理解。
六. 教学准备1.教学课件:制作精美的课件,辅助讲解和展示二次函数的图像和性质;2.教学素材:准备一些实际问题,供学生练习和讨论;3.板书设计:设计清晰、简洁的板书,便于学生记录和复习。
七. 教学过程1.导入(5分钟)利用生活实例,如抛物线射击、自行车刹车等问题,引导学生思考二次函数的应用,激发学生的学习兴趣。
2.呈现(10分钟)讲解二次函数的定义,通过课件展示二次函数的图像,让学生观察和理解二次函数的图像特点。
3.操练(10分钟)让学生通过实际操作,尝试绘制一些简单的二次函数图像,加深对二次函数图像特点的理解。
4.巩固(10分钟)讲解二次函数的性质,引导学生通过思考、交流,总结二次函数的性质。


九年级下册《1.1二次函数》(湘教版)数学教案
标题:九年级下册《1.1二次函数》数学教案
一、教学目标:
1. 理解二次函数的基本概念。
2. 掌握二次函数的一般形式及特殊形式。
3. 能够运用二次函数解决实际问题。
二、教学重点与难点:
1. 教学重点:二次函数的概念和一般形式。
2. 教学难点:理解并掌握二次函数的图像和性质。
三、教学过程:
(一) 导入新课
通过回顾一次函数的相关知识,引出二次函数的概念。
(二) 新知探究
1. 二次函数的概念和表示方法
让学生自行阅读课本,然后引导他们总结二次函数的定义,并用公式表示出来。
2. 二次函数的一般形式和特殊形式
讲解二次函数的一般形式y=ax^2+bx+c(a≠0),并通过实例让学生了解二次函数的三种特殊形式:顶点式、零点式和完全平方式。
(三) 巩固练习
设计一些习题,包括基础题和提高题,帮助学生巩固所学知识。
四、课堂小结
引导学生对本节课的内容进行总结,强化记忆。
五、课后作业
布置适量的课后作业,以检查学生的学习效果。
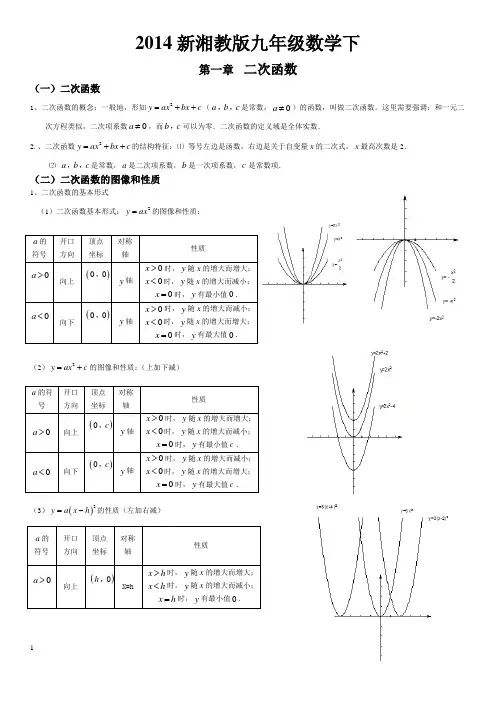
2014新湘教版九年级数学下第一章 二次函数(一)二次函数1、二次函数的概念:一般地,形如2y ax bx c =++(a b c ,,是常数,0a ≠)的函数,叫做二次函数。
这里需要强调:和一元二 次方程类似,二次项系数0a ≠,而b c ,可以为零.二次函数的定义域是全体实数.2. 、二次函数2y ax bx c =++的结构特征:⑴ 等号左边是函数,右边是关于自变量x 的二次式,x 最高次数是2. ⑵ a b c ,,是常数,a 是二次项系数,b 是一次项系数,c 是常数项.(二)二次函数的图像和性质1、二次函数的基本形式(1)二次函数基本形式:2y ax =的图像和性质:(2)2y ax c =+的图像和性质:(上加下减)(3)()2y a x h =-的性质(左加右减)a 的符号开口方向顶点坐标对称轴性质a >向上()00,y 轴 0x >时,y 随x 的增大而增大;0x <时,y 随x 的增大而减小;0x =时,y 有最小值0. 0a <向下()00,y 轴 0x >时,y 随x 的增大而减小;0x <时,y 随x 的增大而增大;0x =时,y 有最大值0.a 的符号开口方向顶点坐标对称轴性质0a >向上()0c ,y 轴 0x >时,y 随x 的增大而增大;0x <时,y 随x 的增大而减小;0x =时,y 有最小值c . 0a < 向下()0c ,y 轴 0x >时,y 随x 的增大而减小;0x <时,y 随x 的增大而增大;0x =时,y 有最大值c .a 的符号开口方向顶点坐标对称轴性质a >向上()0h ,X=hx h >时,y 随x 的增大而增大;x h <时,y 随x 的增大而减小;x h =时,y 有最小值0.(4)二次函数()2y a x h k=-+的图象与性质(5)二次函数c bx ax y ++=2的图像与性质2、二次函数2y ax bx c =++图象的画法 ①画精确图:五点绘图法(列表-描点-连线)利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+,2-32确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图. ②画草图:抓住以下几点:开口方向,对称轴,与x 轴y 轴的交点,顶点.3、二次函数图象的平移: 平移步骤:⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+,确定其顶点坐标()h k ,; ⑵ 保持抛物线2y ax =的形状不变,将其顶点平移到()h k ,处,具体平移方法如下:平移规律: 在原有函数的基础上“h 值正右移,负左移;k 值正上移,负下移” 概括成八个字“左加右减,上加下减”.4、二次函数()2y a x h k =-+与2y ax bx c =++的比较:从解析式上看,()2y a x h k =-+与2y ax bx c =++是两种不同的 表达形式,后者通过配方可以得到前者,即22424b ac b y a x a a -⎛⎫=++⎪⎝⎭,其中2424b ac b h k a a -=-=,. 5、求抛物线的顶点、对称轴的方法①公式法:a b ac a b x a c bx ax y 442222-+⎪⎭⎫ ⎝⎛+=++=,顶点是),(a b ac a b 4422--,对称轴是a b x 2-=. ②配方法:将抛物线的解析式化为()k h x a y +-=2的形式,得到顶点为(h ,k ),对称轴是直线h x =.③运用抛物线的对称性:由于抛物线是以对称轴为轴的轴对称图形,所以对称轴的连线的垂直平分线是抛物线的对称轴,对称轴与抛物线的交点是顶点.④抛物线2y ax bx c =++的图象与y 轴一定相交,交点坐标为(0,)c ;6、二次函数的图象与各项系数之间的关系(1)二次项系数a :二次函数2y ax bx c =++中,a 作为二次项系数,显然0a ≠a 决定了抛物线开口的大小和方向,a 的正负决定开口方向,的a 的值越大,抛物线的开口越小. (2) 一次项系数b :在二次项系数a 确定的前提下,b 决定了抛物线的对称轴的位置. 在0a >的前提下:当0b >时,02b a -<,即抛物线的对称轴在y 轴左侧;当0b =时,02ba-=, 即抛物线的对称轴就是y 轴;当0b <时,02ba->,即抛物线对称轴在y 轴的右侧. 在0a <的前提下:当0b >时,02b a ->,即抛物线的对称轴在y 轴右侧;当0b =时,02ba-=,y 轴的左侧.ab 左同右异” 【或左(h <0)】(3)常数项c:决定了抛物线与y轴交点的位置.当0c>时,抛物线与y轴的交点在x轴上方,即抛物线与y轴交点的纵坐标为正;当0c=时,抛物线与y轴的交点为坐标原点,即抛物线与y轴交点的纵坐标为0;当0c<时,抛物线与y轴的交点在x轴下方,即抛物线与y轴交点的纵坐标为负.(三)不共线三点确定二次函数的表达式1、用待定系数法求二次函数的解析式①一般式:.已知图象上三点或三对、的值,通常选择一般式.②顶点式:.已知图象的顶点或对称轴或抛物线上纵坐标相同的两点,通常选择顶点式.③交点式:.已知图象与轴的交点坐标、,通常选择交点式.2、二次函数图象的对称:二次函数图象的对称一般有五种情况,可以用一般式或顶点式表达(1)关于x轴对称:2y ax bx c=++关于x轴对称后,得到的解析式是2y ax bx c=---;()2y a x h k=-+关于x轴对称后,得到的解析式是()2y a x h k=---;(2)关于y轴对称:2y ax bx c=++关于y轴对称后,得到的解析式是2y ax bx c=-+;()2y a x h k=-+关于y轴对称后,得到的解析式是()2y a x h k=++;(3)关于原点对称:2y ax bx c=++关于原点对称后,得到的解析式是2y ax bx c=-+-;()2y a x h k=-+关于原点对称后,得到的解析式是()2y a x h k=-+-;(4)关于顶点对称(即:抛物线绕顶点旋转180°)2y ax bx c=++关于顶点对称后,得到的解析式是222by ax bx ca =--+-;()2y a x h k=-+关于顶点对称后,得到的解析式是()2y a x h k=--+.(5)关于点()m n,对称:()2y a x h k=-+关于点()m n,对称后,得到的解析式是()222y a x h m n k=-+-+-根据对称的性质,显然无论作何种对称变换,抛物线的形状一定不会发生变化,因此a永远不变.习惯上是先确定原抛物线(或表达式已知的抛物线)的顶点坐标及开口方向,再确定其对称抛物线的顶点坐标及开口方向,然后再写出其对称抛物线的表达式.(四)二次函数与一元二次方程的关系二次函数与一元二次方程的关系:函数cbxaxy++=2,当y=时,得到一元二次方程20ax bx c++=,那么一元二次方程的解就是二次函数的图象与x轴交点的横坐标,因此二次函数图象与x轴的交点情况决定一元二次方程根的情况.(五)二次函数的应用二次函数解决实际问题的一般步骤是:(1)建立适当的平面直角坐标系;(2)把实际问题中的一些数据与点的坐标联系起来;(3)用待定系数法求出抛物线的关系式;(4)利用二次函数的图象及其性质去分析问题、解决问题.的图象与x 轴有两个交点 y 为全体实数与x 轴有一个交点y ≥0与x 轴有无交点y>0的解方程有两个不等实数解方程有两个相等实数解方程没有实数解。




湘教版数学九年级下册《1.1 二次函数》教学设计一. 教材分析湘教版数学九年级下册《1.1 二次函数》是学生在学习了函数、方程等知识后,进一步对函数的性质进行探究。
本节内容主要介绍二次函数的定义、性质及图象。
教材通过生活中的实例引入二次函数的概念,让学生感受数学与实际的联系,提高学习兴趣。
教材内容由浅入深,逐步引导学生掌握二次函数的图象和性质,为后续学习打下基础。
二. 学情分析九年级的学生已经掌握了函数、方程等基本知识,具备一定的逻辑思维能力和抽象思维能力。
但二次函数的内容较为抽象,学生对其理解和运用可能存在一定的困难。
因此,在教学过程中,教师需要关注学生的学习情况,针对学生的实际水平进行教学。
三. 教学目标1.理解二次函数的定义,掌握二次函数的一般形式。
2.了解二次函数的图象特征,会绘制二次函数的图象。
3.掌握二次函数的性质,会运用二次函数解决实际问题。
四. 教学重难点1.二次函数的定义和一般形式。
2.二次函数的图象特征和性质。
五. 教学方法1.情境教学法:通过生活中的实例引入二次函数,让学生感受数学与实际的联系。
2.引导发现法:教师引导学生发现二次函数的图象和性质,培养学生的观察能力和发现能力。
3.实践操作法:让学生动手绘制二次函数的图象,提高学生的动手能力。
六. 教学准备1.教学课件:制作二次函数的图象和性质的课件,便于学生直观理解。
2.练习题:准备相应的练习题,巩固所学知识。
七. 教学过程1.导入(5分钟)利用生活中的实例,如抛物线运动,引出二次函数的概念。
让学生思考:二次函数是如何描述实际问题的?2.呈现(10分钟)呈现二次函数的一般形式,引导学生观察二次函数的图象,了解二次函数的顶点、开口方向等特征。
3.操练(10分钟)让学生动手绘制二次函数的图象,观察图象的变化,体会二次函数的性质。
同时,教师进行讲解,解答学生的疑问。
4.巩固(10分钟)针对所学内容,进行课堂练习,让学生运用二次函数的知识解决问题。
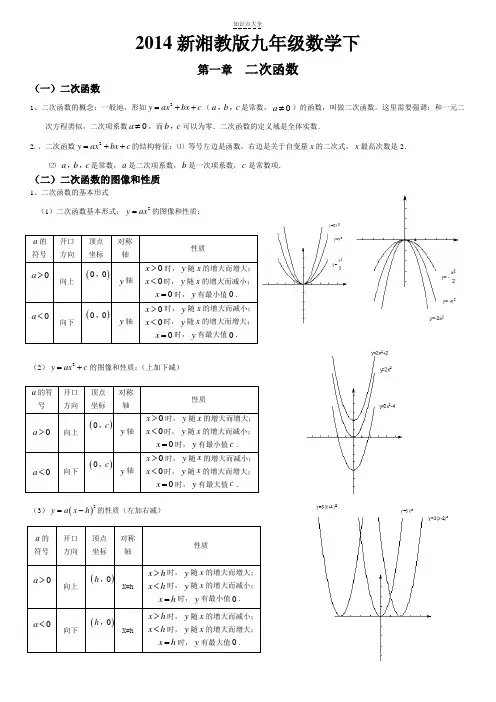
2014新湘教版九年级数学下第一章 二次函数(一)二次函数1、二次函数的概念:一般地,形如2y ax bx c =++(a b c ,,是常数,0a ≠)的函数,叫做二次函数。
这里需要强调:和一元二 次方程类似,二次项系数0a ≠,而b c ,可以为零.二次函数的定义域是全体实数.2. 、二次函数2y ax bx c =++的结构特征:⑴ 等号左边是函数,右边是关于自变量x 的二次式,x 最高次数是2. ⑵ a b c ,,是常数,a 是二次项系数,b 是一次项系数,c 是常数项.(二)二次函数的图像和性质1、二次函数的基本形式(1)二次函数基本形式:2y ax =的图像和性质:(2)2y ax c =+的图像和性质:(上加下减)(3)()2y a x h =-的性质(左加右减)a 的符号开口方向顶点坐标对称轴性质a >向上()00,y 轴 0x >时,y 随x 的增大而增大;0x <时,y 随x 的增大而减小;0x =时,y 有最小值0. 0a <向下()00,y 轴 0x >时,y 随x 的增大而减小;0x <时,y 随x 的增大而增大;0x =时,y 有最大值0.a 的符号开口方向顶点坐标对称轴性质0a > 向上()0c ,y 轴 0x >时,y 随x 的增大而增大;0x <时,y 随x 的增大而减小;0x =时,y 有最小值c . 0a < 向下()0c ,y 轴 0x >时,y 随x 的增大而减小;0x <时,y 随x 的增大而增大;0x =时,y 有最大值c .a 的符号开口方向顶点坐标对称轴性质a >向上()0h ,X=hx h >时,y 随x 的增大而增大;x h <时,y 随x 的增大而减小;x h =时,y 有最小值0.a <向下()0h ,X=hx h >时,y 随x 的增大而减小;x h <时,y 随x 的增大而增大;x h =时,y 有最大值0.(4)二次函数()2y a x h k=-+的图象与性质(5)二次函数c bx ax y ++=2的图像与性质2、二次函数2y ax bx c =++图象的画法 ①画精确图:五点绘图法(列表-描点-连线)利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图. ②画草图:抓住以下几点:开口方向,对称轴,与x 轴y 轴的交点,顶点.3、二次函数图象的平移: 平移步骤:⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+,确定其顶点坐标()h k ,; ⑵ 保持抛物线2y ax =的形状不变,将其顶点平移到()h k ,处,具体平移方法如下:a 的符号开口方向顶点坐标对称轴性质a >向上()h k ,X=h x h >0a <时,y 随x 的增大而增大;x h <时,y 随x 的增大而减小;x h =时,y 有最小值k .a <向下()h k ,X=hx h >时,y 随x 的增大而减小;x h <时,y 随x 的增大而增大;x h =时,y 有最大值k .a 的符号开口 方向顶点 坐标对称 轴性质0a > 向上2424b ac b a a ⎛⎫-- ⎪⎝⎭, 2bx a=-2bx a>-时,y 随x 的增大而增大; 2bx a<-时,y 随x 的增大而减小; 2bx a=-时,y 有最小值244ac b a -. 0a < 向下2424b ac b a a ⎛⎫-- ⎪⎝⎭, 2bx a=-2bx a<-时,y 随x 的增大而增大; 2bx a>-时,y 随x 的增大而减小; 2bx a=-时,y 有最大值244ac b a -. 向右(h >0)【或左(h <0)】平移 |k|个单位向上(k >0)【或下(k <0)】平移|k |个单位向右(h >0)【或左(h <0)】平移|k|个单位向右(h >0)【或左(h <0)】平移|k|个单位向上(k >0)【或下(k <0)】平移|k |个单位向上(k >0)【或向下(k <0)】平移|k |个单位y=a (x-h )2+ky=a (x-h )2y=ax 2+ky=ax 2y=2(x-4)2-3y=2(x-4)2y=2x 2平移规律: 在原有函数的基础上“h 值正右移,负左移;k 值正上移,负下移” 概括成八个字“左加右减,上加下减”.4、二次函数()2y a x h k =-+与2y ax bx c =++的比较:从解析式上看,()2y a x h k =-+与2y ax bx c =++是两种不同的 表达形式,后者通过配方可以得到前者,即22424b ac b y a x a a -⎛⎫=++⎪⎝⎭,其中2424b ac b h k a a -=-=,. 5、求抛物线的顶点、对称轴的方法①公式法:a b ac a b x a c bx ax y 442222-+⎪⎭⎫ ⎝⎛+=++=,顶点是),(a b ac a b 4422--,对称轴是a b x 2-=. ②配方法:将抛物线的解析式化为()k h x a y +-=2的形式,得到顶点为(h ,k ),对称轴是直线h x =.③运用抛物线的对称性:由于抛物线是以对称轴为轴的轴对称图形,所以对称轴的连线的垂直平分线是抛物线的对称轴,对称轴与抛物线的交点是顶点.④抛物线2y ax bx c =++的图象与y 轴一定相交,交点坐标为(0,)c ;6、二次函数的图象与各项系数之间的关系(1)二次项系数a :二次函数2y ax bx c =++中,a 作为二次项系数,显然0a ≠a 决定了抛物线开口的大小和方向,a 的正负决定开口方向,的a 的值越大,抛物线的开口越小. (2) 一次项系数b :在二次项系数a 确定的前提下,b 决定了抛物线的对称轴的位置. 在0a >的前提下:当0b >时,02b a -<,即抛物线的对称轴在y 轴左侧;当0b =时,02ba-=, 即抛物线的对称轴就是y 轴;当0b <时,02ba->,即抛物线对称轴在y 轴的右侧. 在0a <的前提下:当0b >时,02b a ->,即抛物线的对称轴在y 轴右侧;当0b =时,02ba-=, 即抛物线的对称轴就是y 轴;当0b <时,02ba-<,即抛物线对称轴在y 轴的左侧. ab 的符号的判定:对称轴abx 2-=在y 轴左边则0>ab ,在y 轴的右侧则0<ab ,概括的说就是“左同右异” (3)常数项c :决定了抛物线与y 轴交点的位置.当0c >时,抛物线与y 轴的交点在x 轴上方,即抛物线与y 轴交点的纵坐标为正;当0c =时,抛物线与y 轴的交点为坐标原点,即抛物线与y 轴交点的纵坐标为0; 当0c <时,抛物线与y 轴的交点在x 轴下方,即抛物线与y 轴交点的纵坐标为负.(三)不共线三点确定二次函数的表达式1、用待定系数法求二次函数的解析式①一般式:.已知图象上三点或三对、的值,通常选择一般式.②顶点式:.已知图象的顶点或对称轴或抛物线上纵坐标相同的两点,通常选择顶点式.③交点式:.已知图象与轴的交点坐标、,通常选择交点式.2、二次函数图象的对称:二次函数图象的对称一般有五种情况,可以用一般式或顶点式表达(1) 关于x 轴对称:2y ax bx c =++关于x 轴对称后,得到的解析式是2y ax bx c =---;()2y a x h k=-+关于x 轴对称后,得到的解析式是()2y a x h k=---;(2)关于y 轴对称:2y ax bx c =++关于y 轴对称后,得到的解析式是2y ax bx c =-+; ()2y a x h k=-+关于y 轴对称后,得到的解析式是()2y a x h k =++;(3)关于原点对称:2y ax bx c =++关于原点对称后,得到的解析式是2y ax bx c =-+-; ()2y a x h k=-+关于原点对称后,得到的解析式是()2y a x h k=-+-;(4)关于顶点对称(即:抛物线绕顶点旋转180°)2y ax bx c =++关于顶点对称后,得到的解析式是222b y ax bx c a =--+-;()2y a x h k=-+关于顶点对称后,得到的解析式是()2y a x h k=--+.(5)关于点()m n ,对称:()2y a x h k=-+关于点()m n ,对称后,得到的解析式是()222y a x h m n k=-+-+-根据对称的性质,显然无论作何种对称变换,抛物线的形状一定不会发生变化,因此a永远不变.习惯上是先确定原抛物线(或表达式已知的抛物线)的顶点坐标及开口方向,再确定其对称抛物线的顶点坐标及开口方向,然后再写出其对称抛物线的表达式.(四)二次函数与一元二次方程的关系二次函数与一元二次方程的关系: 函数c bx ax y ++=2,当0y =时,得到一元二次方程20ax bx c ++=,那么一元二次方程的解就是二次函数的图象与x 轴交点的横坐标,因此二次函数图象与x 轴的交点情况决定一元二次方程根的情况.(五)二次函数的应用二次函数解决实际问题的一般步骤是:(1)建立适当的平面直角坐标系;(2)把实际问题中的一些数据与点的坐标联系起来;(3)用待定系数法求出抛物线的关系式;(4)利用二次函数的图象及其性质去分析问题、解决问题.的图象与x 轴有两个交点 y 为全体实数 与x 轴有一个交点y ≥0与x 轴有无交点y>0的解方程有两个不等实数解方程有两个相等实数解方程没有实数解。