5.6.1 匀速圆周运动的数学模型
- 格式:pptx
- 大小:193.24 KB
- 文档页数:6

高一物理教案:解析匀速圆周运动的数学模型匀速圆周运动作为一种经典的运动形式,在物理学中具有重要的地位。
在解析匀速圆周运动的过程中,正弦函数和余弦函数被广泛应用。
本教案通过对匀速圆周运动的数学模型进行分析,旨在帮助学生深入理解这一运动形式的特性。
1.圆周运动基本概念(1)圆周的概念圆周是由一个定点O和到该点的距离等于定值的点P所构成的图形。
定点O称为圆心,定值称为圆的半径。
圆周上的每一点P均与圆心O的距离相等。
(2)圆周运动的概念当一个质点以半径为r的圆周作匀速运动时,其圆心角的大小是恒定的,即该运动是匀速圆周运动。
匀速圆周运动也称为等速圆周运动。
2.解析匀速圆周运动的数学模型(1)描述匀速圆周运动的物理量匀速圆周运动可以通过以下物理量进行全面描述:-角速度ω-线速度v-周期T-频率f-圆周位移s-圆周位移角度θ-圆周位移速度vθ-圆周位移加速度aθ这些物理量的表示方法如下:-角速度ω:单位时间内圆周位移角度θ的大小,通常用弧度数计量,即ω=θ/T。
-线速度v:单位时间内质点在圆周上运动的线路长度,通常用m/s表示,即v=2πr/T。
-周期T:质点绕圆周一周所需的时间,通常用秒数计量。
-频率f:质点绕圆周所做的运动在单位时间内重复的次数,通常用Hz计量,即f=1/T。
-圆周位移s:质点在圆周上的位移长度,通常用m表示,即s=rθ,其中r为圆的半径。
-圆周位移角度θ:质点在圆周上所绕的角度大小,通常用弧度表示,即θ=ωt。
-圆周位移速度vθ:质点在圆周运动中的位移速度,通常用m/s表示,即vθ=rsin(θ)/t。
-圆周位移加速度aθ:质点在圆周运动中的位移加速度,通常用m/s²表示,即aθ=rω²cos(θ)。
(2)运用数学模型描述匀速圆周运动匀速圆周运动的数学模型由一个以圆心为原点的直角坐标系形成。
以运动方向为正方向,将质点在$t=0$时刻所处的位置记为$(r,0)$,$t$时刻质点的位置为$(r\cos{\theta},r\sin{\theta})$。

匀速圆周运动数学模型正余弦选择匀速圆周运动是物理学中的一个重要概念,其数学模型可以用正余弦函数来描述。
在本文中,我们将探讨匀速圆周运动的数学模型,以及正余弦函数在描述该运动中的应用。
让我们回顾一下匀速圆周运动的基本概念。
匀速圆周运动是指物体在圆周上以恒定的速度做运动的情况。
在这种运动中,物体的速度大小保持不变,但方向不断变化。
我们可以用角速度来描述物体在圆周上的运动状态。
角速度是指物体单位时间内绕圆心转过的角度,通常用希腊字母ω(omega)表示。
接下来,让我们来看一下匀速圆周运动的数学模型。
假设物体在半径为r的圆周上以角速度ω做匀速圆周运动,则物体的位移可以用下面的公式来表示:S = r * θ其中,S表示位移,r表示圆周的半径,θ表示物体绕圆心转过的角度。
这个公式的推导非常简单,只需要考虑到位移与半径和角度之间的关系即可。
接下来,让我们来看一下正余弦函数在描述匀速圆周运动中的应用。
正余弦函数是描述周期性变化的函数,可以很好地描述物体在匀速圆周运动中的位置变化。
我们来看正弦函数的应用。
正弦函数可以表示物体在圆周上的垂直位置的变化。
假设物体在圆周上的初始位置为0度,那么物体在任意时刻t的垂直位置可以用下面的公式来表示:y = r * sin(ωt)其中,y表示物体的垂直位置,r表示圆周的半径,ω表示角速度,t表示时间。
这个公式告诉我们,物体在圆周上的垂直位置随时间呈正弦变化。
接下来,我们来看余弦函数的应用。
余弦函数可以表示物体在圆周上的水平位置的变化。
假设物体在圆周上的初始位置为0度,那么物体在任意时刻t的水平位置可以用下面的公式来表示:x = r * cos(ωt)其中,x表示物体的水平位置,r表示圆周的半径,ω表示角速度,t表示时间。
这个公式告诉我们,物体在圆周上的水平位置随时间呈余弦变化。
通过正余弦函数的应用,我们可以很好地描述匀速圆周运动中物体的位置变化。
正弦函数描述了物体在圆周上的垂直位置的变化,而余弦函数描述了物体在圆周上的水平位置的变化。

物理匀速圆周运动公式知识介绍
高中物理匀速圆周运动公式
匀速圆周运动公式
1.线速度V=s/t=2πr/T
2.角速度&omega 高中学习方法;=Φ/t =2π/T=2πf
3.向心加速度a=V2/r=ω2r=(2π/T)2r
4.向心力F心=mV2/r=mω2r=mr(2π/T)2=mωv=F合
5.周期与频率:T=1/f
6.角速度与线速度的关系:V=ωr
7.角速度与转速的'关系ω=2πn(此处频率与转速意义相同)
8.主要物理量及单位:弧长(s):米(m);角度(Φ):弧度(rad);频率(f):赫(Hz);周期(T):秒(s);转速(n):r/s;半径(r):米(m);线速度(V):m/s;角速度(ω):rad/s;向心加速度:m/s2。
注:
(1)向心力可以由某个具体力提供,也可以由合力提供,还可以由分力提供,方向始终与速度方向垂直,指向圆心;
(2)做匀速圆周运动的物体,其向心力等于合力,并且向心力只改变速度的方向,不改变速度的大小,因此物体的动能保持不变,向心力不做功,但动量不断改变。
【物理匀速圆周运动公式知识介绍】。


匀速圆周运动的数学模型
匀速圆周运动是物理学中的一种基本运动形式,其数学模型是描述一个点绕圆心做速度大小不变的圆周运动。
该模型在数学上通常使用极坐标系来描述,其中半径r和角度θ是两个重要的参数。
在这个模型中,点在圆周上运动,其速度v的大小恒定,方向始终垂直于半径。
因此,速度v可以表示为:v = w×r,其中w是角速度,表示单位时间内转过的角度。
同时,向心加速度a n表示点向圆心运动的趋势,其大小为a n = v²/r。
另外,向心力F表示点受到的使它做圆周运动的力,其大小为F = m ×v²/r,其中m是点的质量。
而离心力则表示点离开圆心运动的趋势,其大小为F = m×w²×r。
这些公式构成了匀速圆周运动的数学模型,可以用来描述和分析圆周运动的各种性质和规律。
例如,通过向心加速度和向心力公式可以推导出角速度和半径之间的关系,也可以用来计算物体在圆周运动中的轨迹和运动规律。
总之,匀速圆周运动的数学模型是一个重要的工具,可以用来描述和分析圆周运动的各种性质和规律,在物理学、工程学等领域有着广泛的应用。
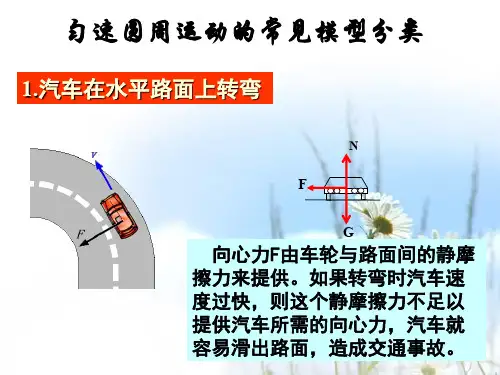


常见的圆周运动模型物体做匀速圆周运动时,向心力才是物体受到的合外力.物体做非匀速圆周运动时,向心力是合外力沿半径方向的分力(或所有外力沿半径方向的分力的矢量和).具体运动类型如下。
一、匀速圆周运动模型及处理方法1.随盘匀速转动模型(无相对滑动,二者有共同的角速度)例4. 如图所示,质量为m 的小物体系在轻绳的一端,轻绳的另一端固定在转轴上。
轻绳长度为L 。
现在使物体在光滑水平支持面上与圆盘相对静止地以角速度ω(1)物体运动一周所用的时间T ; (2)绳子对物体的拉力。
2。
火车转弯模型(或汽车拐弯外侧高于内侧时)汽车做匀速圆周运动,向心力由重力与斜面对汽车的支持力的合力提供,且向心力的方向水平,向心力大小F 向=mg tanθ,根据牛顿第二定律:F 向=m v 2R,tan θ=hd,例.在高速公路的拐弯处,通常路面都是外高内低.如图所示,在某路段汽车向左拐弯,司机左侧的路面比右侧的路面低一些.汽车的运动可看作是做半径为R 的圆周运动.设内外路面高度差为h ,路基的水平宽度为d ,路面的宽度为L .已知重力加速度为g .要使车轮与路面之间的横向摩擦力(即垂直于前进方向)等于零,则汽车转弯时的车速应等于( )A.gRhL B. gRhd C. gRLh D. gRdhB 对. 3。
圆锥摆模型小球在水平面内是匀速圆周运动,重力和拉力合力提供向心力θtan mg例6.如图所示,用细绳系着一个小球,使小球在水平面内做匀速圆周运动,不计空气阻力,关于小球受力有以下说法,正确的是( ) A.只受重力 B.只受拉力 C.受重力.拉力和向心力 D.受重力和拉力 4.双星模型练习.如图所示,长为L 的细绳一端固定,另一端系一质量为m 的小球。
给小球一个合适的初速度,小球便可在水平面内做匀速圆周运动,这样就构成了一个圆锥摆,设细绳与竖直方向的夹角为θ。
下列说法中正确的是OωLθA.小球受重力、绳的拉力和向心力作用B.小球只受重力和绳的拉力作用C.θ越大,小球运动的速度越大D.θ越大,小球运动的周期越大练习.有一种叫“飞椅”的游乐项目,示意图如图所示,长为L的钢绳一端系着座椅,另一端固定在半径为r的水平转盘边缘.转盘可绕穿过其中心的竖直轴转动.当转盘以角速度ω匀速转动时,钢绳与转轴在同一竖直平面内,与竖直方向的夹角为θ.不计钢绳的重力,求转盘转动的角速度ω与夹角θ的关系.二、匀速圆周运动中实例分析例.如图所示,是双人花样滑冰运动中男运动员拉着女运动员做圆锥摆运动的精彩场面.若女运动员做圆锥摆运动时和竖直方向的夹角为B,女运动员的质量为m,转动过程中女运动员的重心做匀速圆周运动的半径为r,求这时男运动员对女运动员的拉力大小及两人转动的角速度。


