轴向拉(压)杆截面上的应力

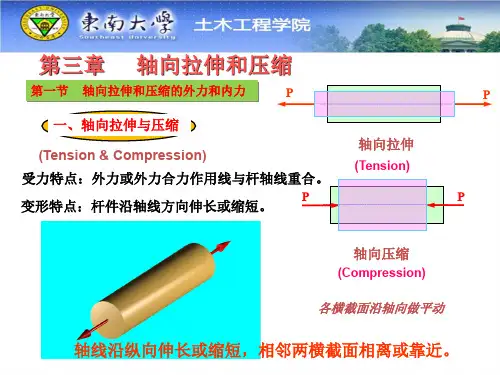
第七章轴向拉伸和压缩一、内容提要轴向拉伸与压缩是杆件变形的基本形式之一，是建筑工程中常见的一种变形。

(一)、基本概念1. 内力 由于外力的作用，而在构件相邻两部分之间产生的相互作用力。

这里要注意产生内力的前提条件是构件受到外力的作用。

2. 轴力 轴向拉（压）时，杆件横截面上的内力。

它通过截面形心，与横截面相垂直。

拉力为正，压力为负。

3. 应力 截面上任一点处的分布内力集度称为该点的应力。

与截面相垂直的分量σ称为正应力，与截面相切的分量τ称为切应力。

轴拉（压）杆横截面上只有正应力。

4. 应变 单位尺寸上构件的变形量。

5. 轴向拉（压） 杆件受到与轴线相重合的合外力作用，产生沿着轴线方向的伸长或缩短的变形，称为轴向拉（压）。

6. 极限应力 材料固有的能承受应力的上限，用σ0表示。

7. 许用应力与安全系数 材料正常工作时容许采用的最大应力，称为许用应力。

极限应力与许用应力的比值称为安全系数。

8. 应力集中 由于杆件截面的突然变化而引起局部应力急剧增大的现象，称为应力集中。

(二)、基本计算1. 轴向拉（压）杆的轴力计算求轴力的基本方法是截面法。

用截面法求轴力的三个步骤：截开、代替和平衡。

求出轴力后要能准确地画出杆件的轴力图。

画轴向拉（压）杆的轴力图是本章的重点之一，要特别熟悉这一内容。

2. 轴向拉（压）杆横截面上应力的计算任一截面的应力计算公式 AF N =σ 等直杆的最大应力计算公式 AF max N max =σ 3. 轴向拉（压）杆的变形计算虎克定律 A E l F l N =∆εσE =或 虎克定律的适用范围为弹性范围。

泊松比 εε=μ'4. 轴向拉（压）杆的强度计算强度条件塑性材料：σma x ≤[σ] 脆性材料： σt ma x ≤[σt ]σ c ma x ≤[σc ]强度条件在工程中的三类应用（1）对杆进行强度校核在已知材料、荷载、截面的情况下，判断σma x是否不超过许用值[σ]，杆是否能安全工作。

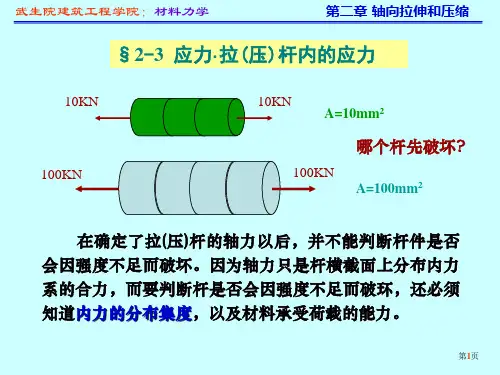
§4-3 轴向拉(压)杆的应力1．应力的概念为了解决杆件的强度问题，不仅要知道当外力达到一定值时杆件可能沿哪个截面破坏，而且还要知道该截面上哪个点首先开始破坏。

因而仅仅知道杆件截面上内力的合力是不够的，还需要进一步研究截面上内力的分布情况，从而引入了应力的概念。

应力就是杆件截面上分布内力的集度。

若考察某受力杆截面m-m 上M 点处的应力，如图4-8所示。

图4-8 一点的应力在M 点周围取一很小的面积A ∆，设A ∆面积上分布内力的合力为F ∆，则面积A ∆上内力F ∆的平均集度为A F p m ∆∆= (4-1) 式中m p 称为面积A ∆上的平均应力。

当微小面积A ∆趋近于零时，就得到截面上M 点处的总应力，即dA dFA Fp A =∆∆==∆lim 0(4-2) 由于F 是矢量，故P 也是矢量，其方向一般不与截面垂直或平行，因此可以分解成与截面垂直的法向分量正应力σ和与截面向切的切向分量切应力(剪应力)τ。

从应力的定义可知，应力是与“截面”和“点”这两个因素分不开的。

一般地说，杆件在外力作用下，任一截面上不同点的应力值是不同的，同一点位于不同截面上的应力值也是不同的。

因此在谈内力时，应明确是哪个截面哪个点处的应力。

应力的量纲为⎥⎦⎤⎢⎣⎡2长度力，其国际单位为Pa(帕斯卡)，1Pa=1牛顿/米2。

工程中常用MPa ，1MPa=106Pa 。

2．拉(压)杆横截面上的应力对于拉(压)杆，横截面上的内力为轴力F N ，与轴力对应的应力为正应力σ。

观察受拉等直杆(图4-9(a))的变形情况。

首先在等直杆侧面作两条横向线ab 和cd ，代表其横截面，然后在杆的两端施加一对轴向拉力F 使杆发生变形。

可以观察到，横向线ab 和cd 移动到a’b’和c’d’的位置了，如图4-9(b)所示。

对于压杆，同样可以观察到该现象。

根据这一现象，可以假设原为平面的横截面在杆变形后仍为平面，即平面假设。

根据这一假设，拉(压)杆变形后两横截面将沿杆轴线方向作相对平移，也就是说，拉(压)杆在其任意两个横截面之间纵向线段的伸长变形是均匀的。

轴向拉压杆件横截面上的应力在工程设计和材料力学中，轴向拉压杆件是一种经常使用的结构元件，其横截面上的应力分布是一个重要的研究内容。

在此，将介绍轴向拉压杆件横截面上的应力分布，并给出相关参考内容。

轴向拉压杆件是指受到拉力或压力作用的杆件，其横截面形状可以是圆形、方形、矩形、椭圆形等。

在讨论轴向拉压杆件横截面上的应力分布时，我们假设该杆件是均匀材料、轴对称且受到等径向拉力或压力作用。

根据这些假设，我们可以得到以下结论。

首先，对于圆形横截面的轴向拉压杆件，应力沿着截面的半径方向是均匀的。

这意味着，在横截面上的任何一点，杆件的应力大小是相同的，只是方向不同。

具体而言，在拉力作用下，横截面上的应力大小为σ = F/A，其中F是作用于杆件上的拉力，A是横截面的面积。

而在压力作用下，横截面上的应力大小为σ = -F/A。

其次，对于矩形或方形横截面的轴向拉压杆件，其应力分布是非均匀的。

在拉力作用下，杆件的边缘处应力最大，中心处应力最小。

具体而言，在矩形或方形横截面的边缘处，应力计算公式为σ = F/2A，其中F是作用于杆件上的拉力，A是横截面的面积。

而在中心处，应力计算公式为σ = F/A。

此外，对于椭圆形横截面的轴向拉压杆件，其应力分布也是非均匀的。

在拉力作用下，杆件的长轴方向应力最大，短轴方向应力最小。

具体而言，在椭圆形横截面的长轴方向，应力计算公式为σ = F/2A，其中F是作用于杆件上的拉力，A是横截面的面积。

而在短轴方向，应力计算公式为σ = F/A。

综上所述，轴向拉压杆件横截面上的应力分布与杆件的形状密切相关。

在实际工程中，根据结构的要求，可以选择合适的截面形状来平衡应力分布，以提高杆件的强度和稳定性。

参考文献：1. 程训文等著. 材料力学. 北京：清华大学出版社，2016年2. 韩良辉等著. 结构力学. 北京：中国建筑工业出版社，2019年3. 林万善等著. 实用结构力学基础. 北京：中国水利水电出版社，2014年4. Beer, Ferdinand P., Johnston, E. Russell, DeWolf, John T. Mechanics of Materials. New York: McGraw-Hill Education, 2017.5. Popov, Egor P. Engineering Mechanics of Solids. Upper Saddle River, NJ: Pearson, 2015.。

1拉压杆横截面上的应力6.1.1 应力的概念同一种材料制成横截面积不同的两根直杆，在相同轴向拉力的作用下，其杆内的轴力相同。

但随拉力的增大，横截面小的杆必定先被拉断。

这说明单凭轴力F N 并不能判断拉（压）杆的强度，即杆件的强度不仅与内力的大小有关， 图6-1而且还与截面面积有关，即与内力在横截面上分布的密集程度（简称集度）有关，为此引入应力的概念。

要了解受力杆件在截面m-m 上的任意一点C 处的分布内力集度，可假想将杆件在m-m 处截开，在截面上围绕C 点取微小面积ΔA ，ΔA 上分布内力的合力为Δp (图6-1a)，将Δp 除以面积ΔA ，即Ap p ∆∆=m （6-1） p m 称为在面积ΔA 上的平均应力，它尚不能精确表示C 点处内力的分布状况。

当面积无限趋近于零时比值Ap ∆∆的极限，才真实地反映任意一点C 处内力的分布状况，即 lim 0dAdp A p p A =∆∆=→∆ （6-2） 上式p 定义为C 点处内力的分布集度，称为该点处的总应力。

其方向一般既不与截面垂直，也不与截面相切。

通常，将它分解成与截面垂直的法向分量和与截面相切的切向分量（图6-1b ），法向分量称为正应力，用σ 表示；切向分量称为切应力，用τ表示。

将总应力用正应力和切应力这两个分量来表达具有明确的物理意义，因为它们和材料的两类破坏现象——拉断和剪切错动——相对应。

因此，今后在强度计算中一般只计算正应力和切应力而不计算总应力。

应力的单位为“帕”，用Pa 表示。

1Pa=1N/m 2, 常用单位为兆帕MPa ，1MPa=106Pa=1MN/mm 2=1N/mm 2，1GPa=109Pa 。

6.1.2 轴向拉伸和压缩时横截面上的正应力取一等截面直杆，在其侧面作两条垂直于杆轴的直线ab 和 cd ，然后在杆两端施加一对轴向拉力F 使杆发生变形，此时直线ab 、 cd分别平移至a 'b '、 c 'd '且仍保持为直线（图6-2a ）。