优化设计答案

第一题考察温度对烧碱产品得率的影响，选了四种不同温度进行试验，在同一温度下进行了5次试验（三数据见下表）。

希望在显着性水平为0.05。

1.SSE的公式2.SSA的公式3.将表格粘贴进Excel，然后进行数据分析，勾选标于第一行，显示在下面P=0.001799，远小于0.05，所以是显着的4.打开Minitab，复制表格，“统计”“方差分析”“选单因素未重叠”“响应C1C2C3C4”点击“比较”勾选第一个，确定结果: 工作表 3单因子方差分析: 60度, 65度, 70度, 75度来源自由度 SS MS F P因子 3 84.15 28.05 7.96 0.002误差 16 56.40 3.52合计 19 140.55S = 1.877 R-Sq = 59.87% R-Sq（调整） = 52.35%平均值（基于合并标准差）的单组 95% 置信区间水平 N 平均值标准差 ------+---------+---------+---------+---60度 5 90.200 1.789 (------*------)65度 5 93.200 1.789 (------*------)70度 5 95.000 2.000 (------*------)75度 5 90.200 1.924 (------*------)------+---------+---------+---------+---90.0 92.5 95.0 97.5合并标准差 = 1.877Tukey 95% 同时置信区间所有配对比较单组置信水平 = 98.87%60度减自:下限中心上限 ------+---------+---------+---------+---65度 -0.401 3.000 6.401 (------*------)70度 1.399 4.800 8.201 (------*-----)75度 -3.401 0.000 3.401 (------*------)------+---------+---------+---------+----5.0 0.0 5.0 10.065度减自:下限中心上限 ------+---------+---------+---------+---70度 -1.601 1.800 5.201 (------*-----)75度 -6.401 -3.000 0.401 (------*------)------+---------+---------+---------+----5.0 0.0 5.0 10.070度减自:下限中心上限 ------+---------+---------+---------+---75度 -8.201 -4.800 -1.399 (-----*------)------+---------+---------+---------+----5.0 0.0 5.0 10.0获得结果，区间相交包含0.0的不明显，反之明显第二题为研究线路板焊点拉拔力与烘烤温度、烘烤时间和焊剂量之间关系。

优化设计考试题目及答案一、单项选择题（每题2分，共10分）1. 在优化设计中，目标函数通常表示为：A. 约束条件B. 目标函数C. 优化变量D. 优化算法答案：B2. 以下哪项不是优化设计中的常见约束类型？A. 线性约束B. 非线性约束C. 静态约束D. 动态约束答案：D3. 优化算法中的梯度下降法主要适用于哪种类型的优化问题？A. 线性规划问题B. 非线性规划问题C. 整数规划问题D. 动态规划问题答案：B4. 在多目标优化中，帕累托最优解是指：A. 一个目标函数的最优解B. 所有目标函数的最优解C. 无法进一步改善任何一个目标而不损害其他目标的解集D. 所有解中目标函数值最小的解答案：C5. 以下哪个算法不是用于解决组合优化问题的？A. 遗传算法B. 模拟退火算法C. 粒子群优化算法D. 线性规划算法答案：D二、多项选择题（每题3分，共15分）1. 优化设计中的目标函数可能具有哪些特性？A. 连续性B. 可微性C. 凸性D. 非凸性答案：A, B, C, D2. 以下哪些因素会影响优化算法的性能？A. 算法的初始点B. 算法的参数设置C. 问题的规模D. 计算机的硬件配置答案：A, B, C, D3. 在优化设计中，以下哪些方法可以用于处理约束条件？A. 拉格朗日乘数法B. 罚函数法C. 增广拉格朗日法D. 直接忽略约束条件答案：A, B, C4. 以下哪些是优化算法的常见特点？A. 收敛性B. 鲁棒性C. 计算效率D. 易于实现答案：A, B, C, D5. 在多目标优化中，以下哪些是常用的优化准则？A. 权重法B. 目标规划法C. 帕累托优化法D. 遗传算法答案：A, B, C, D三、计算题（每题10分，共20分）1. 给定一个优化问题，目标函数为 \( f(x) = x^2 + 2y^2 \) ，约束条件为 \( x + y \leq 10 \) ，\( x \geq 0 \) ，\( y \geq 0 \) 。

二年级语文下册优化设计89页答案1、1“小王一把拽住正准备闯红灯的老伯说：‘你活得不耐烦了？真是为老不尊！’”这句话中小王使用的语言不得体。

[判断题] *对错(正确答案)2、《望岳》的作者是（）[单选题] *李白杜甫(正确答案)李贺李商隐3、下列选项中加着重号字注音有错误的一项是（）[单选题] *A、一幢房屋dòng 眉黛hēi(正确答案)B、一声嗥叫háo 灵动língC、旮旮旯旯gā点缀zhuìD、一抹金黄mǒ盛开shèng4、1《拿来主义》运用了先立后破的写作方法。

[判断题] *对(正确答案)错5、1“欢迎你到我家来拜访！”这句话表达得体。

[判断题] *对错(正确答案)6、袅娜中的娜读作（）[单选题] *nānǎnuó(正确答案)nuò7、1祥林嫂是孙犁《荷花淀》中的人物形象。

[判断题] *对(正确答案)错8、关于《红楼梦》的文化常识，选出表述正确的一项( ) [单选题] *A.林黛玉与贾宝玉二人关系为姨表兄妹。

B.在黛玉初进贾府拜过贾母后不久，贾母就让元春、迎春、探春、惜春四姐妹和黛玉相见。

C.《红楼梦》的别名除《石头记》外，还有另外几个，例如《情僧录》《风月宝鉴》《金陵十二钗》《金玉缘》《刘姥姥进大观园》等。

D.《红楼梦》中的贾宝玉的前身是全书开篇神话中的神瑛侍者，黛玉的前身为灵河畔的绛珠仙草。

神瑛侍者下凡造历，绛珠仙草便也投胎入世，用一世眼泪还灌溉之情。

(正确答案)9、下列中括号内字的注音有误的一项是（）[单选题] *A.油[腻]（nì）[嘟]囔（dū）[腊]肉（là）B.[肿]胀（zhǒng）[沸]腾（fèi）[孥孥]（nú）C.锅[铲]（chǎn）[搁]置（gē）[栗]子（sù）(正确答案)D.[唾]沫（tuò）[焖]饭（mèn）[奈]何（nài）10、下列词语中，加着重号字的注音正确的一项是（）[单选题] *A、狭隘（ài）言简意赅（hài）B、笑靥（yǎn）心宽体胖（pán）C、脸颊（jiá）诲人不倦（huǐ）D、酝酿（niàng）一蹴而就（cù）(正确答案)11、1《劝学》的作者是荀子，名况，字卿，是我国春秋时期著名的思想家、教育家，先秦儒家最后的代表，朴素唯物主义思想的集大成者。

高一优化设计参考答案高一优化设计参考答案高一是学生们迈入高中阶段的重要一年，也是他们开始接触到更加深入的学科知识和学习方法的一年。

优化设计作为高中数学的一部分，是培养学生分析问题、解决问题的能力的重要环节。

本文将为大家提供一份高一优化设计的参考答案，希望能够帮助同学们更好地理解和掌握这一知识点。

优化设计题目一：求解最大值题目描述：一块铁板长100厘米，要制作一个无盖的长方体容器，使得容器的体积最大。

求容器的最大体积。

解题思路：假设长方体的底边长为x厘米，高为h厘米，则长为100-2x厘米。

根据体积公式V=xh(100-2x)，我们可以将体积的表达式化简为V=-2x^2+100x。

为了求解最大值，我们需要对体积的表达式进行求导。

V'=-4x+100。

令V'=0，解得x=25。

将x=25代入体积的表达式，得到V=6250。

因此，容器的最大体积为6250立方厘米。

优化设计题目二：求解最小值题目描述：一个矩形花坛的周长为20米，求解花坛的最小面积。

解题思路：假设矩形的长为x米，宽为y米，则根据周长的条件可得2x+2y=20。

将该条件代入面积公式S=xy，得到S=x(10-x)。

为了求解最小值，我们需要对面积的表达式进行求导。

S'=10-2x。

令S'=0，解得x=5。

将x=5代入面积的表达式，得到S=25。

因此，花坛的最小面积为25平方米。

优化设计题目三：求解最短路径题目描述：一只蚂蚁在一条长为10米的直线上，从点A出发，要爬到点B。

蚂蚁的爬行速度为1米/分钟，但在距离点C的5米范围内，蚂蚁的速度会减慢为0.5米/分钟。

求解蚂蚁从点A到点B所需的最短时间。

解题思路：假设蚂蚁从A点到C点的距离为x米，则从C点到B点的距离为(10-x)米。

根据速度和距离的关系，我们可以得到蚂蚁从A点到C点所需的时间t1=x分钟，从C点到B点所需的时间t2=(10-x)/0.5分钟。

因此，蚂蚁从A点到B点所需的总时间为T=t1+t2=x+(10-x)/0.5分钟。

人教版数学优化设计必修一答案人教版数学优化设计必修一答案一、选择题：(本大题共12小题，每小题5分，共60分，在每个小题给出的四个选项中，只有一项是符合题目要求的.)解析：此题不需要计算，同学如果熟知对数函数性质，知道同底数的对数函数图像关于x轴对称，那么无论0 a 1，还是a 1，对应的函数值都有小于1的可能，则答案必定包含大于0小于1的一个和大于1的一个，答案D。

解析：a,c属于指数函数赋值形式，b属于对数函数赋值形式。

b 0很容易通过图像或函数增减性判断。

a,b均通过图像与1比较大小即可，a小于1大于0，c大于1.。

正确答案C。

解析：抛物线最好画，所以我们先判断BC选项，考试时优先选择排除容易确定的选项也会节省时间。

很容易发现C在x大于0时是减函数。

解析：对于这种图像判断题，我们分两次假设进行，假设0 a 1和a 1两种情况分别画出草图比较，注意题中给出的对数函数的负号，画出图像要延x轴翻折。

B中指数函数图像表示0 a 1，而对数函数图像应该过2,4象限递增。

C 答案如B中解释。

D指数函数图像表示a 1，对数函数图像应沿着x轴翻折才是正确的。

解析：只有②一个正确的，任何不是0的数的0次幂都等于1. ②中的关于a的二次方程通过我们计算永远大于0. ①中n为偶数a为负数时不成立。

解析：定义是R上的奇函数，则一定有f(x)=0，且f(-x)=-f(x)，图像关于y轴对称。

所以f(-2)=-f(2)，将f(2)由已知函数计算得出，那么f(-2)就很容易了。

怎么样，奇函数的应用你了解了么欢迎留言讨论。

解析：基础题，保证对数函数有意义，真数大于0.x 5.每道大题都有相应的考察知识点，你要学会先从题干中找出考察点，然后回顾，从而破题。

下面先来道简单的计算，复习下基本公式。

注：不要忽略N是空集的情况。

注：第一问中求定义域，使得对数函数有意义即真数大于0.第二问求奇偶性注意先判断定义域关于原点对称，在用定义法证明奇偶性。

1. 已知函数f(x) = 2x - 1，则f(3)的值为（）A. 5B. 6C. 7D. 8答案：C解析：将x=3代入函数f(x) = 2x - 1中，得f(3) = 2×3 - 1 = 6 - 1 = 5。

2. 若|a| = 5，则a的取值范围是（）A. a > 0B. a < 0C. a = 5D. -5 ≤ a ≤ 5答案：D解析：绝对值表示一个数到0的距离，所以|a| = 5意味着a到0的距离是5，即a可以是5或者-5，所以取值范围是-5 ≤ a ≤ 5。

3. 下列各数中，有理数是（）A. √2B. πC. 3/2D. √-1答案：C解析：有理数是可以表示为两个整数之比的数，所以3/2是有理数。

而√2、π和√-1都是无理数。

4. 若a、b、c是等差数列，且a+b+c=15，则b的值为（）A. 5B. 7C. 8D. 10答案：A解析：等差数列中，任意两项之和等于它们中间项的两倍，即a+b = 2b，所以a+b+c = 3b，由题意知3b=15，解得b=5。

5. 下列方程中，无解的是（）A. 2x + 3 = 7B. 3x - 4 = 5C. 5x + 2 = 0D. 2x + 3 = 0答案：D解析：对于方程2x + 3 = 0，移项得2x = -3，解得x = -3/2，所以方程有解。

其他方程均可以找到x的值。

6. 若m^2 - 4m + 3 = 0，则m的值为______。

答案：1 或 3解析：这是一个一元二次方程，可以通过因式分解或者使用求根公式求解。

因式分解得(m-1)(m-3) = 0，所以m的值为1或3。

7. 已知等差数列{an}的第一项为a1，公差为d，第n项an = 5，则a3的值为______。

答案：a3 = 5 - 2d解析：等差数列的通项公式为an = a1 + (n-1)d，代入an = 5，得a1 + (n-1)d= 5，解得a1 = 5 - (n-1)d。

９．图6-39所示为一对称的两杆支架，在支架的顶点承受一个载荷为2F=300000N ， 支架之间的水平距离2B=1520mm ，若已选定壁厚T=2.5mm 钢管，密度/1083-6mm Kg ⨯=.7ρ，屈服极限700=s σMpa ，要求在满足强度与稳定性条件下设计最轻的支架尺寸。

[解] 1．建立数学模型 设计变量：⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=H D x x x 21目标函数：221422577600101.2252)(x x HB D T x f +⨯=+=πρ 约束条件： １）圆管杆件中的压应力σ应小于或等于y ο，即y TDHHB F σπσ≤+=22于是得2122157760019098.59)(x x x x g +=２）圆管杆件中的压应力α应小于或等于压杆稳定的临界应力c σ，由欧拉公式得钢管的压杆温度应力c σ222152222225776006.25102.6)8()(x x H B T D E AL EIC ++⨯=++==ππσ2式中 A ――圆管的截面积；L ――圆管的长度。

于是得0)6006.25)/(577(102.657760019098.59)(2221521222≤++⨯-+=-=x x x x x x g c σσ３） 设计变量的值不得小于或等于0于是得)(0)(2213≤-=≤-=x x g x x g2．从以上分析可知，该优化设计问题具有2个设计变量，4个约束条件，按优化方法程序的规定编写数学模型的程序如下：subroutine ffx(n,x,fx) dimension x(n) fx=1.225e-4*x(1)*sqrt(577600.0+x(2)*x(2)) endsubroutine ggx(n,kg,x,gx) dimension x(n),gx(kg)gx(1)=19098.59*sqrt(577600.0+x(2)*x(2))/(x(1)*x(2))-700.0 gx(2)=19098.59*sqrt(577600.0+x(2)*x(2))/(x(1)*x(2))- 1 2.6e5*(x(1)*x(1)+6.25)/(577600.0+x(2)*x(2)) gx(3)=-x(1) gx(4)=-x(2) end3．利用惩罚函数法（SUMT 法）计算，得到的最优解为：============== PRIMARY DATA ============== N= 2 KG= 4 KH= 0 X : .7200000E+02 .7000000E+03 FX: .9113241E+01GX: -.3084610E+03 -.8724784E+03 -.7200000E+02 -.7000000E+03 PEN = .9132947E+01R = .1000000E+01 C = .4000000E+00 T0= .1000000E-01 EPS1= .1000000E-05 EPS2= .1000000E-05=============== OPTIMUM SOLUTION ============== IRC= 18 ITE= 39 ILI= 39 NPE= 229 NFX= 0 NGR= 57 R= .1717988E-06 PEN= .6157225E+01 X : .4868305E+02 .6988214E+03 FX: .6157187E+01GX: -.1204029E+03 -.1266042E-01 -.4868305E+02 -.6988207E+0310．图6-40所示为一箱形盖板，已知长度L=6000mm ，宽度b=600mm ，厚度mm t s 5承受最大单位载荷q=0.01Mpa ，设箱形盖板的材料为铝合金，其弹性模量MPa E 4107⨯=，泊松比3.0=μ，许用弯曲应力[]MPa 70=σ，许用剪应力[]MPa 45=τ，要求在满足强度、刚度和稳定性条件下，设计重量最轻的结构方案。

八年级上册数学优化设计119页答案题目描述：一个长方体的长、宽、高分别为x、y、z，且它们的和为30，求长方体的最大表面积。

解题思路：
设长方体的长、宽、高分别为x、y、z，其表面积为S，则有：
S = 2xy + 2xz + 2yz
又因为x + y + z = 30，因此可以用一个变量表示出其中的一个变量，比如z = 30 - x - y，代入表面积公式中得：
S = 2xy + 2x(30 - x - y) + 2y(30 - x - y)
= -2x^2 - 2y^2 + 60x + 60y
求解表面积的极大值，可以先对公式进行简化，得到：
S = -2(x - 15)^2 - 2(y - 15)^2 + 900
由于表面积是由正数平方项相加减得，因此表面积的最大值为900，当x = 15，y = 15时，长方体的表面积最大。

答案：
1. 解题思路
2. 表面积公式
3. 将z代入表面积公式得简化公式
4. 确定表面积的极大值
5. 最大表面积的解析式
6. 结论：当x = 15，y = 15时，长方体的表面积最大，为900。

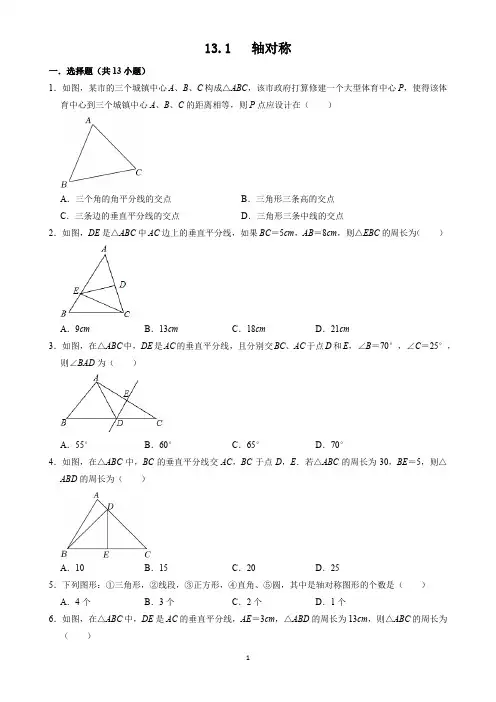
13.1 轴对称一．选择题（共13小题）1．如图，某市的三个城镇中心A、B、C构成△ABC，该市政府打算修建一个大型体育中心P，使得该体育中心到三个城镇中心A、B、C的距离相等，则P点应设计在（）A．三个角的角平分线的交点B．三角形三条高的交点C．三条边的垂直平分线的交点D．三角形三条中线的交点2．如图，DE是△ABC中AC边上的垂直平分线，如果BC＝5cm，AB＝8cm，则△EBC的周长为（）A．9cm B．13cm C．18cm D．21cm3．如图，在△ABC中，DE是AC的垂直平分线，且分别交BC、AC于点D和E，∠B＝70°，∠C＝25°，则∠BAD为（）A．55°B．60°C．65°D．70°4．如图，在△ABC中，BC的垂直平分线交AC，BC于点D，E．若△ABC的周长为30，BE＝5，则△ABD的周长为（）A．10B．15C．20D．255．下列图形：①三角形，②线段，③正方形，④直角、⑤圆，其中是轴对称图形的个数是（）A．4个B．3个C．2个D．1个6．如图，在△ABC中，DE是AC的垂直平分线，AE＝3cm，△ABD的周长为13cm，则△ABC的周长为（）A．16cm B．13cm C．19cm D．10cm7．如图，电信部门要在公路l旁修建一座移动信号发射塔．按照设计要求，发射塔到两个城镇M，N的距离必须相等，则发射塔应该建在（）A．A处B．B处C．C处D．D处8．在△ABC中，∠ABC＝45°，AD，BE分别为BC、AC边上的高，AD、BE相交于点F，下列结论：①∠FCD＝45°，②AE＝EC，③S△ABF：S△AFC＝BD：CD，④若BF＝2EC，则△FDC周长等于AB的长．正确的是（）A．①②B．①③C．①④D．①③④9．如图，点P是∠AOB内一点，OP＝m，∠AOB＝α，点P关于直线OA的对称点为点Q、关于直线OB 的对称点为点T，连接QT，分别交OA、OB于点M、N，连接PM、PN，下列结论：①∠OTQ＝90°﹣α；②当α＝30°时，△PMN的周长为m；③0＜QT＜2m；④∠MPN＝180°﹣2α，其中正确的是（）A．①②B．③④C．①②④D．①②③④10．如图，在△ABC中，∠C＝90°，AB的垂直平分线交BC于点D，交AB于点E，已知∠CAD：∠DAB＝1：2，则∠B＝（）A．34°B．36°C．60°D．72°11．如图，△ABC中，D、E、F三点分别在AB、BC、AC上，且四边形BEFD是以DE为对称轴的轴对称图形，四边形CFDE是以FE为对称轴的轴对称图形．若∠C＝40°，则∠DFE的度数为何？（）A．65°B．70°C．75°D．80°12．如图所示，光线L照射到平面镜I上，然后在平面镜Ⅰ、Ⅱ之间来回反射，已知∠α＝55°，∠γ＝75°，则∠β为（）A．50°B．55°C．60°D．65°13．如图，点A在直线l上，△ABC与△AB′C′关于直线l对称，连接BB′分别交AC，AC′于点D，D′，连接CC′，下列结论不一定正确的是（）A．∠BAC＝∠B′AC′B．CC′∥BB′C．BD＝B′D′D．AD＝DD′二．填空题（共6小题）14．如图，在△ABC中，BC＝8，AB的中垂线交BC于E，AC的中垂线交BC于G，则△AGE的周长等于．15．如图所示，弹性小球从点P（0，3）出发，沿所示方向运动，每当小球碰到矩形OABC的边时反弹，反弹时反射角等于入射角，当小球第1次碰到矩形的边时的点为P1，第2次碰到矩形的边时的点为P2，…，第n次碰到矩形的边时的点为P n，则点P2021的坐标是．16．如图，把一张长方形纸片ABCD的一角沿AE折叠，点D的对应点D′落在∠BAC的内部，若∠CAE ＝2∠BAD′，且∠CAD′＝n，则∠DAE的度数为（用含n的式子表示）．17．已知：如图，P是∠AOB内的一点，P1，P2分别是点P关于OA、OB的对称点，P1P2交于点OA于点M，交OB于点N，若P1P2＝5cm，则△PMN的周长是cm．18．如图是一个风筝的图案，它是轴对称图形，EF是对称轴．∠A＝90°，∠AED＝130°，∠C＝45°，则∠BFC的度数为．19．如图，线段AB、BC的垂直平分线l1、l2相交于点O．若∠B＝39°，则∠AOC＝°．三．解答题（共9小题）20．如图，Rt△ABC中，∠ACB＝90°，D是AB上一点，BD＝BC，过点D作AB的垂线交AC于点E，求证：BE垂直平分CD．21．如图，△ABC中，∠ACB＝90°，AD平分∠BAC，DE⊥AB于E．（1）若∠BAC＝50°，求∠EDA的度数；（2）求证：直线AD是线段CE的垂直平分线．22．如图已知：E是∠AOB的平分线上一点，EC⊥OA，ED⊥OB，垂足分别为C、D．求证：（1）∠ECD＝∠EDC；（2）OE是CD的垂直平分线．23．如图，△ABC中，EF垂直平分AC，交AC于点F，交BC于点E，AD⊥BC，垂足为D，且BD＝DE，连接AE．（1）求证：AB＝CE；（2）若△ABC的周长为14cm，AC＝6cm，则DC的长为cm．24．如图，在四边形ABCD中，BD所在的直线垂直平分线段AC，过点A作BC的平行线AF交CD于F，延长AB、DC交于点E．求证：（1）AC平分∠EAF；（2）∠F AD＝∠E．25．如图，△ABC中，AB的垂直平分线分别交AB，BC于点D，E，AC的垂直平分线分别交AC，BC于点F，G，连接AE，AG．（1）若△AEG的周长为10，求线段BC的长；（2）若∠BAC＝104°，求∠EAG的度数．26．如图，△ABC中，∠ABC＝30°，∠ACB＝50°，DE、FG分别为AB、AC的垂直平分线，E、G分别为垂足．（1）求∠DAF的度数；（2）若△DAF的周长为10，求BC的长．27．如图，AD为△ABC的角平分线，AD的中垂线交AB于点E、BC的延长线于点F，AC于EF交于点O．（1）求证：∠3＝∠B；（2）连接OD，求证：∠B+∠ODB＝180°．28．如图，△ABC中，AB，AC边的垂直平分线分别交BC于点D，E，垂足分别为点F，G，△ADE的周长为6cm（1）求△ABC中BC边的长度；（2）若∠B+∠C＝64°，求∠DAE的度数．13.1 轴对称一．选择题（共13小题）1．如图，某市的三个城镇中心A、B、C构成△ABC，该市政府打算修建一个大型体育中心P，使得该体育中心到三个城镇中心A、B、C的距离相等，则P点应设计在（）A．三个角的角平分线的交点B．三角形三条高的交点C．三条边的垂直平分线的交点D．三角形三条中线的交点【解答】解：∵体育中心到城镇中心A、B的距离相等，∴P A＝PB，∴点P在线段AB的垂直平分线上，同理，点P在线段AC的垂直平分线上，∴P点应设计在三条边的垂直平分线的交点，故选：C．2．如图，DE是△ABC中AC边上的垂直平分线，如果BC＝5cm，AB＝8cm，则△EBC的周长为（）A．9cm B．13cm C．18cm D．21cm【解答】解：∵DE是AC边上的垂直平分线，∴AE＝CE，∵BC＝5cm，AB＝8cm，∴△EBC的周长＝EB+EC+BC＝EB+AE+BC＝AB+BC＝13（cm），故选：B．3．如图，在△ABC中，DE是AC的垂直平分线，且分别交BC、AC于点D和E，∠B＝70°，∠C＝25°，则∠BAD为（）A．55°B．60°C．65°D．70°【解答】解：在△ABC中，∠B＝70°，∠C＝25°，则∠BAC＝180°﹣∠B﹣∠C＝180°﹣70°﹣25°＝85°，∵DE是AC的垂直平分线，∴DA＝DC，∴∠DAC＝∠C＝25°，∴∠BAD＝85°﹣25°＝60°，故选：B．4．如图，在△ABC中，BC的垂直平分线交AC，BC于点D，E．若△ABC的周长为30，BE＝5，则△ABD的周长为（）A．10B．15C．20D．25【解答】解：∵BC的垂直平分线分别交AC，BC于点D，E，∴DB＝DC，BE＝EC．∵BE＝5，∴BC＝2BE＝10．∵△ABC的周长为30，∴AB+AC+BC＝30．∴AB+AC＝20．∴△ABD的周长＝AB+AD+BD＝AB+AD+DC＝AB+AC＝20，故选：C．5．下列图形：①三角形，②线段，③正方形，④直角、⑤圆，其中是轴对称图形的个数是（）A．4个B．3个C．2个D．1个【解答】解：根据轴对称图形的定义可知：线段，正方形，圆、直角是轴对称图形，三角形不一定是轴对称图形．故选：A．6．如图，在△ABC中，DE是AC的垂直平分线，AE＝3cm，△ABD的周长为13cm，则△ABC的周长为（）A．16cm B．13cm C．19cm D．10cm【解答】解：∵DE是AC的垂直平分线，AE＝3cm，∴AC＝2AE＝6cm，AD＝DC，∵△ABD的周长为13cm，∴AB+BD+AD＝13cm，∴AB+BD+DC＝AB+BC＝13cm，∴△ABC的周长为AB+BC+AC＝13cm+6cm＝19cm，故选：C．7．如图，电信部门要在公路l旁修建一座移动信号发射塔．按照设计要求，发射塔到两个城镇M，N的距离必须相等，则发射塔应该建在（）A．A处B．B处C．C处D．D处【解答】解：根据作图可知：EF是线段MN的垂直平分线，所以EF上的点到M、N的距离相等，即发射塔应该建在C处，故选：C．8．在△ABC中，∠ABC＝45°，AD，BE分别为BC、AC边上的高，AD、BE相交于点F，下列结论：①∠FCD＝45°，②AE＝EC，③S△ABF：S△AFC＝BD：CD，④若BF＝2EC，则△FDC 周长等于AB的长．正确的是（）A．①②B．①③C．①④D．①③④【解答】解：∵△ABC中，AD，BE分别为BC、AC边上的高，∴AD⊥BC，而△ABF和△ACF有一条公共边，∴S△ABF：S△AFC＝BD：CD，∴③正确；∵∠ABC＝45°，∴AD＝BD，∠DAC和∠FBD都是∠ACD的余角，而∠ADB＝∠ADC＝90°，∴△BDF≌△ADC，∴FD＝CD，∴∠FCD＝∠CFD＝45°，∴①正确；若AE＝EC，BE⊥AC，可得AB＝BC，与题意不符合，故②错误．若BF＝2EC，根据①得BF＝AC，∴AC＝2EC，即E为AC的中点，∴BE为线段AC的垂直平分线，∴AF＝CF，BA＝BC，∴AB＝BD+CD＝AD+CD＝AF+DF+CD＝CF+DF+CD，即△FDC周长等于AB的长，∴④正确．故选：D．9．如图，点P是∠AOB内一点，OP＝m，∠AOB＝α，点P关于直线OA的对称点为点Q、关于直线OB 的对称点为点T，连接QT，分别交OA、OB于点M、N，连接PM、PN，下列结论：①∠OTQ＝90°﹣α；②当α＝30°时，△PMN的周长为m；③0＜QT＜2m；④∠MPN＝180°﹣2α，其中正确的是（）A．①②B．③④C．①②④D．①②③④【解答】解：∵点P关于直线OA的对称点为点Q、关于直线OB的对称点为点T，∴OQ＝OO＝OT，∠AOP＝∠AOQ，∠POB＝∠BOT，∵∠AOB＝α，∴∠QOT＝2α，∴∠OQT＝∠OQT＝（180°﹣2α）＝90°﹣α，故①正确，当α＝30°时，∵∠TOQ＝60°，OQ＝OT，∴△OPQ是等边三角形，∴QT＝OQ＝m，∵MP＝MQ，NP＝NT，∴△PMN的周长＝PM+MN+PN＝QM+MN+NT＝QT＝m，故②正确，∵OQ＝OT＝m，∴0＜QT≤2m，故③错误，∠MPN＝∠OPM+∠OPN＝∠OQM+∠OTN＝180°﹣2α，故④正确，故选：C．10．如图，在△ABC中，∠C＝90°，AB的垂直平分线交BC于点D，交AB于点E，已知∠CAD：∠DAB＝1：2，则∠B＝（）A．34°B．36°C．60°D．72°【解答】解：∵D是线段AB垂直平分线上的点，∴AD＝BD，∴△DAB是等腰三角形，∠B＝∠DAB，∵∠CAD：∠DAB＝1：2，∴设∠DAC＝x，则∠B＝∠DAB＝2x，∴x+2x+2x＝90°，∴x＝18°，即∠B＝36°，故选：B．11．如图，△ABC中，D、E、F三点分别在AB、BC、AC上，且四边形BEFD是以DE为对称轴的轴对称图形，四边形CFDE是以FE为对称轴的轴对称图形．若∠C＝40°，则∠DFE的度数为何？（）A．65°B．70°C．75°D．80°【解答】解：∵四边形BEFD是以DE为对称轴的轴对称图形，四边形CFDE是以FE为对称轴的轴对称图形，∴∠BED＝∠DEF＝∠CEF＝，∠EDF＝∠C＝40°，∴∠DFE＝180°﹣∠DEF﹣∠EDF＝80°，故选：D．12．如图所示，光线L照射到平面镜I上，然后在平面镜Ⅰ、Ⅱ之间来回反射，已知∠α＝55°，∠γ＝75°，则∠β为（）A．50°B．55°C．60°D．65°【解答】解：∠β所在的顶点处是一个平角为180°，α，γ经过反射后，与β所在的顶点处的一个角组成三角形的内角和180°，即180°﹣2β+α+γ＝180°，∴2β＝∠α+∠γ。

第一、填空题1.组成优化设计数学模型的三要素是设计变量 、 目标函数 、 约束条件。

2.函数()22121212,45f x x x x x x =+-+在024X ⎡⎤=⎢⎥⎣⎦点处的梯度为120-⎡⎤⎢⎥⎣⎦，海赛矩阵 为2442-⎡⎤⎢⎥-⎣⎦3.目标函数是一项设计所追求的指标的数学反映，因此对它最基本的要求是能用 来评价设计的优劣，，同时必须是设计变量的可计算函数。

4.建立优化设计数学模型的基本原则是确切反映工程实际问题，的基础上力求简洁。

5.约束条件的尺度变换常称规格化，这是为改善数学模型性态常用的一种方法。

6.随机方向法所用的步长一般按加速步长法来确定，此法是指依次迭代的步 长按一定的比例递增的方法。

7.最速下降法以负梯度方向作为搜索方向，因此最速下降法又称为梯度法，其收敛速度较 慢 。

8.二元函数在某点处取得极值的充分条件是()00f X ∇=必要条件是该点处的海赛矩阵正定9.拉格朗日乘子法的基本思想是通过增加变量将等式约束优化问题变成无 约束优化问题，这种方法又被称为升维法。

10改变复合形形状的搜索方法主要有反射，扩张，收缩，压缩11坐标轮换法的基本思想是把多变量 的优化问题转化为单变量的优化问题 12．在选择约束条件时应特别注意避免出现相互矛盾的约束，，另外应当尽量减少不必要的约束。

13．目标函数是n 维变量的函数，它的函数图像只能在n+1,空间中描述出来，为了在n 维空间中反映目标函数的变化情况，常采用目标函数等值面的方法。

14.数学规划法的迭代公式是1k k k k X X d α+=+，其核心是建立搜索方向，和计算最佳步长15协调曲线法是用来解决设计目标互相矛盾的多目标优化设计问题的。

16.机械优化设计的一般过程中，建立优化设计数学模型是首要和关键的一步，它是取得正确结果的前提。

二、名词解释1．凸规划对于约束优化问题()min f X..s t ()0j g X ≤(1,2,3,,)j m =⋅⋅⋅若()f X 、()j g X (1,2,3,,)j m =⋅⋅⋅都为凸函数，则称此问题为凸规划。

七年级上册数学优化设计答案优化设计(1)1。

有人买了一包七宝粥和一包菊花茶，先称出菊花茶的质量是七宝粥的3倍，再过一段时间，发现剩下的菊花茶在减少，则下列说法中正确的是( ) A．菊花茶的质量比七宝粥多B．菊花茶的质量与时间成反比C．七宝粥的数量是菊花茶的2倍D．七宝粥的数量是菊花茶的3倍解析：第1题：先把2种饮料的总质量看作100，再求出这100的倍数．从而得出： 50÷5=5（袋）．答：正确．2。

若A和B分别为两种不同食品的生产成本和售价，当成本A和售价B的函数关系式为： R(B)一一一t（ A）时，根据A和B的成本函数表达式，求出的利润最大值和最小值．4。

若零件批量生产总成本函数表达式为： C=f(q)(c)其中： f(q)代表生产该零件所需要的劳动数量； c代表生产每一件该零件的生产成本； q代表生产零件所耗用的原材料的数量； k代表工资费用的增长率。

请根据上述资料，以下各项对零件批量生产时的总成本影响较小的是（） A．制造费用B．原材料消耗C．单位变动成本D．单位劳动成本E．工资支出F．劳动力的报酬解析：6。

甲厂在某年6月份生产某种产品500件，每件的固定成本是8元，该产品的售价是每件10元。

为使该产品的销售收入达到总成本的80%，该企业应采取的最佳销售方案是（） A．高价位B．低价位C．稳定价格D．保持不变E．降低售价解析：由于产品的固定成本为8元，如果将产品的价格降低到固定成本以下，会亏损，故此题选D。

答案： D 7。

甲、乙两个服装厂商定，如果提供的服装符合消费者的要求，就按预定的单价接受订货。

开始时甲厂只接受订货1000套，乙厂只接受订货2000套，过了几天，甲厂共接受订货2800套，已经超过了乙厂能够提供的服装数量。

则下列判断正确的是（） A．甲、乙服装厂都可获得总收益B．甲厂盈利，乙厂亏损C．甲厂的盈利一定大于乙厂的亏损D．甲厂的亏损一定小于乙厂的盈利解析：第1题：本题属于数字运算题，根据题意知，甲厂获得总收益1000×7/12=100×7/6=70（万元）。

四年级优化设计参考答案四年级优化设计参考答案在四年级的学习中，优化设计是一个重要的课程内容。

通过优化设计，学生可以培养解决问题的能力，提高思维和创新能力。

本文将为四年级的优化设计提供一些参考答案，帮助学生更好地完成任务。

一、数学优化设计1. 设计一个游戏：在一个正方形的房间里，有一只小猫和一只老鼠。

小猫的速度是老鼠的两倍，老鼠可以随意移动，而小猫只能在房间的四个角落之间移动。

请设计一个游戏规则，使得小猫永远无法抓住老鼠。

解答：游戏规则可以是，老鼠每次移动的距离是小猫的两倍。

这样，无论小猫如何移动，老鼠总能够保持足够的距离，从而永远无法被小猫抓住。

2. 设计一个数学题：有一根长为10厘米的绳子，要将其剪成两段，使得其中一段的长度是另一段的两倍。

请问应该在哪个位置剪断绳子？解答：将绳子剪断的位置应该在2:1的比例处，即距离绳子一端的1/3处。

这样，剪断后的两段绳子长度比例为2:1。

二、科学优化设计1. 设计一个实验：请设计一个实验，通过改变水的温度来观察冰的融化速度。

你可以使用不同温度的水和相同大小的冰块进行实验。

解答：可以将冰块放在不同温度的水中，例如冷水、温水和热水。

记录下冰块在不同温度下的融化时间，并比较结果。

通过实验可以得出结论：温度越高，冰块融化的速度越快。

2. 设计一个发明：在夏天，人们常常会因为热而感到不舒服。

请设计一种可以降低室内温度的发明，可以帮助人们更好地度过炎热的夏天。

解答：可以设计一种太阳能驱动的空调系统。

通过太阳能板收集太阳能，将其转化为电能，然后用电能驱动空调系统。

这样，可以在不消耗额外能源的情况下，降低室内温度，提供舒适的环境。

三、语言优化设计1. 设计一个故事情节：请设计一个故事情节，要求故事中的主人公面临困境，通过自己的努力和智慧解决问题。

解答：故事情节可以是，主人公在森林中迷路了，他唯一的指南针遗失了。

为了找到回家的路，主人公决定利用自己对自然的了解，观察树木的生长方向和太阳的位置，最终成功找到回家的路。

2023年高考优化设计化学答案
一、原题
1. 下列有关离子方程式的叙述中，正确的是（）
A. 对于溶液中的每种离子，都可以用一个离子方程式来表示
B. 离子方程式可以用来描述溶液中离子的变化
C. 离子方程式可以用来描述溶液中离子的比例
D. 离子方程式可以用来描述溶液中离子的浓度
答案：A、B、D
2. 下列有关溶解度的叙述中，正确的是（）
A. 溶解度是指溶质在溶剂中的溶解量
B. 溶解度越大，溶质在溶剂中的溶解量越小
C. 溶解度受温度的影响较大
D. 溶解度受压强的影响较大
答案：A、C
3. 下列有关溶质的叙述中，正确的是（）
A. 溶质是指溶解在溶剂中的物质
B. 溶质可以是固体、液体或气体
C. 溶质可以是有机物或无机物
D. 溶质可以是混合物或单质
答案：A、C、D
二、解析
1. 离子方程式是一种用来描述溶液中离子的变化的数学方程式，它可以用来表示溶液中每种离子的浓度，以及离子之间的比
例关系。

离子方程式可以用来描述溶液中离子的变化，以及离子之间的比例关系，但不能用来描述溶液中离子的比例。

2. 溶解度是指溶质在溶剂中的溶解量，它受温度和压强的影响较大，温度升高时，溶解度通常会增加；压强升高时，溶解度通常会减小。

溶解度越大，溶质在溶剂中的溶解量越大，反之亦然。

3. 溶质是指溶解在溶剂中的物质，它可以是固体、液体或气体，也可以是有机物或无机物，甚至可以是混合物或单质。

优化设计6年级上册答案优化设计6年级上册答案【篇一：单元测试优化设计(六年级数学)】lass=txt>一、认真思考，仔细填空。

（20分）1、3?3388?8?38?（??2、30个5?6的和是（）；15米的23是（）米。

??3、10的倒数是（）；（）和1互为倒数。

?134号?4、1?2?（）=3座5??5、在○里填上“”“”或“=”。

?5?6?4○562○2338○8线?6、比24多1 ）。

?6的数是（）；比56少34的数是（? ?7、边长为1分米的正方形的周长是（）分米。

?2?8、六（1）班有50人，女生占全班人数的2 名?5，女生有（）人，男生有（）人。

姓? ?9、一袋大米25千克，已经吃了它的2 ?5，吃了（）千克，还剩（）千克。

?10、看一本书180页，每天看全书的1 ?9，3天看了全书的（）。

? 二、精打细选。

（选择正确答案的序号填在括号里）（10分）封? 1、“羊的只数是牛的只数的3?8”，（）是单位“1”。

? ?a、羊的只数b、牛的只数c、无法确定?2、（）的倒数一定大于1。

?级?a、真分数b、假分数c、任何数班?3、今年的产量比去年多1 ?10，今年的产量相当于去年的（）。

??a、110b、910c、1110?1 ?43）=3+4=7，这是根据（）计算的。

密?a、乘法交换律b、乘法分配律c、乘法结合律? ?5、比28的2 7多7的数是（）。

? ? a、15 b、14c、1?校三、注意审题，细心计算。

（32分）学??1、直接写得数。

?1?4?25?5 73376?24=12?14=29?2?93?10310?425?10?16?2、能简算的要简算。

（3?55351489?4?9?454?18?16?29?310512四、认真看图，列式计算。

（10分）五、走进生活，实践运用。

（28分）1、甲乙两地相距420千米，一辆汽车4小时行驶了全程的57，行驶了多少千米？种苹果树，14种梨树，苹果树比梨树多多少平方米？3、某鞋店进来运动鞋200双。

优化设计七年级上册语文答案一、基础知识(5分)1.下列加点字的读音有误的一项是(2分) ( )a. 机杼(zhù) 辔头(pèi) 单于(kè) 扑朔(shuò)b. 邮票(yōu) 汹涌(yǒng) 窄窄(zhǎi) 嘶哑(yǎ)c. TNUMBERG63至(xué) 摇晃(huàng) 黝黑(yǒu) 余永亮(qiāng)d. 晾晒(shài) 疏忽(shū) 腻了(nì) 匆遽(jù)2. 以下字形完全正确的一项就是(2分后) ( )a. 疖子泱泱田滕熠熠b. 牙崽踉跄滑稽舔着c. 呢喃害羞缴喙疯癫 c. 行政处罚哽住场屋隘直立3. 下列文学常识不正确的一项是(1分) ( )a. 贾尼·罗大里，就是意大利知名的儿童文学作家，年国际安徒生奖获得者。

b. 屠格涅夫，德国作家，主要作品有长篇小说《罗亭》《父与子》。

c. 《最后一课》Lizier《都德短篇小说优选》，作者都德，法国著名作家。

d. 《乡愁》选自《百年中国文学经典》，作者余光中，台湾讲坛“回头浪子”，当代诗人、评论家二、名句累积与运用(10分后)4. 无为在歧路，□□□□□。

(王勃《送杜少府之任蜀州》)5. 读天地之悠悠，□□□□□□。

(陈子昂《尼里幽州台歌》)6. □□□□□□□，绝胜烟柳满皇都。

(韩愈《早春呈水部张十八员外》)7. □□□□□□□，获得生前身后名。

(辛弃疾《破阵子·为陈同甫诗赋青词以递之》8.《送杜少府之任蜀州》中道出千山万水也隔不断朋友情谊的诗句是：□□□□□，□□□□□。

9.《破阵子·为陈同甫壮词以寄之》词中表现词人愿为国家效力，梦中也不忘戍边报国志愿的句子是：□□□□□□，□□□□□□。

10. 《陋室铭》中注重陋室环境之雅的语句就是：□□□□□，□□□□□。

三、阅读(45分)(一)课内文言文写作(10分后)爱莲说水陆草木之花，调皮者甚红头。

大学实验优化设计考试题及答案一、选择题（每题2分，共10分）1. 实验设计中的正交试验设计法主要用于解决什么问题？A. 实验成本B. 实验时间C. 实验变量的优化D. 实验数据的统计分析答案：C2. 在实验设计中，若要研究的因素有n个水平，每个因素有k个可能的状态，则该实验设计需要进行多少次实验？A. n * kB. n + kC. k^nD. n^k答案：C3. 下列哪项不是实验设计中的基本原则？A. 随机化B. 局部控制C. 重复性D. 单一变量答案：B4. 实验优化设计的目的是什么？A. 减少实验次数B. 提高实验精度C. 确定最优实验条件D. 所有上述选项答案：D5. 在实验设计中，若某一因素的水平增加会导致其他因素的水平必须相应增加，这样的因素称为：A. 主要因素B. 次要因素C. 约束因素D. 独立因素答案：C二、填空题（每题2分，共10分）6. 实验设计中的________是用来评估实验结果可靠性的一种方法。

答案：重复试验7. 在进行实验设计时，若实验结果受到非研究因素的随机干扰，可以通过________来减少这种干扰。

答案：随机化8. 拉丁方设计是一种特殊类型的________，它可以平衡实验中的某些非研究因素的影响。

答案：因子设计9. 实验设计中的响应面法是一种用于________的实验设计方法。

答案：多变量优化10. 在实验设计中，通过________可以确定实验中各因素的最佳组合。

答案：方差分析三、简答题（每题10分，共20分）11. 简述实验设计中的Box-Behnken设计方法及其应用场景。

答案：Box-Behnken设计是一种旋转中心组合设计，它允许实验者在多维空间中进行实验，同时保持实验次数相对较少。

该方法特别适用于当实验的因素数量较多，而每个因素的水平数不是很多时。

它广泛应用于制药、化学工艺优化等领域。

12. 解释什么是田口方法（Taguchi方法），并说明其在实验优化设计中的作用。

第一、填空题1.构成优化设计数学模型的三因素是设计变量、目标函数、拘束条件。

2.函数 f x1 , x2 x12x224x1x2 5 在 X02点处的梯度为12 ，海赛矩阵40为24 423.目标函数是一项设计所追求的指标的数学反应，所以对它最基本的要求是能用来评论设计的好坏，，同时一定是设计变量的可计算函数。

4.成立优化设计数学模型的基来源则是切实反应工程本质问题，的基础上力争简短。

5.拘束条件的尺度变换常称规格化，这是为改良数学模型性态常用的一种方法。

6.随机方向法所用的步长一般按加快步长法来确立，此法是指挨次迭代的步长按必定的比率递加的方法。

7.最速降落法以负梯度方向作为搜寻方向，所以最速降落法又称为梯度法，其收敛速度较慢。

8.二元函数在某点处获得极值的充足条件是 f X 00 必需条件是该点处的海赛矩阵正定9.拉格朗日乘子法的基本思想是经过增添变量将等式拘束优化问题变为无拘束优化问题，这类方法又被称为升维法。

10改变复合形形状的搜寻方法主要有反射，扩充，缩短，压缩11坐标轮换法的基本思想是把多变量的优化问题转变为单变量的优化问题12 ．在选择拘束条件时应特别注意防止出现相互矛盾的拘束，，此外应当尽量减少不用要的拘束。

13 ．目标函数是 n 维变量的函数，它的函数图像只好在n+1,空间中描绘出来，为了在 n 维空间中反应目标函数的变化状况，常采纳目标函数等值面的方法。

14. 数学规划法的迭代公式是X k 1X k k d k，其中心是成立搜寻方向，和计算最正确步长15 协调曲线法是用来解决设计目标相互矛盾的多目标优化设计问题的。

16. 机械优化设计的一般过程中，成立优化设计数学模型是首要和重点的一步，它是获得正确结果的前提。

二、名词解说1．凸规划关于拘束优化问题min f Xst..g j X0( j1,2,3,,m)若 f X 、g j X( j1,2,3,, m) 都为凸函数，则称此问题为凸规划。