【高中数学选择性必修】求曲线的方程
- 格式:doc
- 大小:937.50 KB
- 文档页数:7





2020-2021年高二数学选择性必修一尖子生同步培优题典2.5直线与圆、圆与圆 解析版学校:___________姓名:___________班级:___________考号:___________ 注意事项:本卷共16小题,6道单选题,3道多选题,3道填空题,4道解答题。
一、单项选择题(本题共6小题,每小题满分5分)1.“1k =”是“直线0x y k -+=与圆221x y +=相交”的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分也不必要条件【答案】A 【解析】 【分析】 【详解】 圆的圆心为原点,半径,原点到直线的距离,当时,,所以,直线与圆相交;反之,若直线与圆相交,则有,即,解得:,因此,根据充分、必要条件的概念,“”是“直线与圆相交”的充分不必要条件,故选A .主要考查充要条件的概念及充要条件的判定方法.2.若关于x 24430x x kx k -+-=有且只有两个不同的实数根,则实数k 的取值范围是( )A .55,126⎛⎫⎪⎝⎭B .23,34⎛⎤⎥⎝⎦C .50,12⎛⎤⎥⎝⎦D .53,124【答案】D 【解析】 【分析】()2443x x k x -=-+由且只有两个不同的实数根,看成24y x x =-与()43y k x =-+有且只有两个不同的交点,即过()4,3的直线与以()2,0为圆心,2为半径的半圆有且只有两个交点,从而得到斜率k 的范围. 【详解】24430x x kx k -+-=有且只有两个不同的实数根,得()2443x x k x -=-+有且只有两个不同的实数根, 即24y x x =-与()43y k x =-+有且只有两个不同的交点,即过()4,3的直线与以()2,0为圆心,2为半径的半圆有且只有两个交点, 当直线与半圆相切时,圆心()2,0到直线430kx y k --+=的距离为2即22321k k -+=+,解得512k =, 当直线过()0,0时,斜率为34, 所以k 的取值范围为53,124. 故选:D. 【点睛】本题考查根据直线与圆相切求斜率的值,函数与方程,属于中档题.3.已知圆229x y +=的弦过点P (1,2),当弦长最短时,该弦所在直线方程为 ( )A .250x y +-=B .20y -=C .20x y -=D .10x -=【答案】A 【解析】由题意可得该直线与直线OP 垂直,又2OP k =,所以直线的斜率为12-,由点斜式可求得直线方程为250x y +-=,故选A.4.已知直线l :10()x ay a R +-=∈是圆22:4210C x y x y +--+=的对称轴.过点(4,)A a -作圆C 的一条切线,切点为B ,则||AB =( )A .2B .42C .6D .210【答案】C 【解析】试题分析:直线l 过圆心,所以1a =-,所以切线长2(4)14(4)216AB =-+-⨯-++=,选C.考点:切线长5.过直线:240l x y ++=与圆22:2410C x y x y ++-+=的交点,且面积最小的圆的方程为( ).A .22136165525x y ⎛⎫⎛⎫++-= ⎪ ⎪⎝⎭⎝⎭ B .221364555x y ⎛⎫⎛⎫++-= ⎪ ⎪⎝⎭⎝⎭C .22138165525x y ⎛⎫⎛⎫++-= ⎪ ⎪⎝⎭⎝⎭ D .221384555x y ⎛⎫⎛⎫++-= ⎪ ⎪⎝⎭⎝⎭ 【答案】B 【解析】 【分析】由已知圆的标准方程,可得圆心、半径,再求出过圆心且垂直于已知直线的直线方程,解方程组可得圆心,再根据点到直线的距离公式和勾股定理可求出半径,由此即可求出圆的方程. 【详解】由题知,圆22:2410C x y x y ++-+=的圆心为(1,2)C -,半径2r.设直线l 与圆C 的交点为A 、B ,如图所示,过C 作CD AB ⊥,则经过A 、B 两点面积最小的圆是以AB 为直径的圆. 由直线l 的方程为240x y ++=,CD AB ⊥可得,12CD k =, 所以CD 所在直线的方程为12(1)2y x -=+, 联立24012(1)2x y y x ++=⎧⎪⎨-=+⎪⎩,得13565x y ⎧=-⎪⎪⎨⎪=⎪⎩,即136,55D ⎛⎫- ⎪⎝⎭,即D 为以AB 为直径的圆的圆心.又圆心C 到直线l 的距离5d ==,所以||BD ===,所以以AB ; 所以以AB 为直径的圆的方程为221364555x y ⎛⎫⎛⎫++-= ⎪ ⎪⎝⎭⎝⎭. 故选:B. 【点睛】本题主要考查直线和圆的位置关系,点到直线的距离公式,弦长公式的应用,属于中档题.6.已知圆22:(1)2C x y +-=,若点P 在圆C 上,并且点P 到直线y x =的距离为2,则满足条件的点P 的个数为( ) A .1 B .2 C .3 D .4【答案】C 【解析】 【分析】设()00,P x y ,根据点到直线的距离公式得出22000021x y x y +-=,再结合点P 在圆C上,得出2200021x y y +-=,联立两式,求解方程组,即可得出答案. 【详解】设()00,P x y ,由点P 到直线y x =的距离为22=两边平方整理得到22000021x y x y +-=①()00,x y 在圆C 上,()220012x y ∴+-=,即2200021x y y +-=②联立①②得()0010y x -= 解得00y =或01x =当00y =时,由①②可得201x =,解得01x =或01x =-,即(1,0)P 或(1,0)P -当01x =时,由①②可得20020y y -=,解得00y =或02y =,即(1,0)P 或()1,2P综上,满足条件的点P 的个数为3个 故选:C 【点睛】本题主要考查了直线与圆的位置关系的应用,点到直线距离公式的应用,属于中档题. 7.已知圆C 的圆心为原点O ,且与直线420x y ++=相切.点P 在直线8x =上,过点P 引圆C 的两条切线PA ,PB ,切点分别为A ,B ,如图所示,则直线AB 恒过定点的坐标为( )A .(2,0)B .(0,2)C .(1,0)D .(0,1)【答案】A 【解析】 【分析】由圆C 的圆心为原点且与直线420x y ++=相切即得圆的方程,又PA ,PB 是它的切线,可知A ,B 一定在以OP 为直径4,2b ⎛⎫⎪⎝⎭为圆心的圆上,即AB 为两圆的公共弦,即可求出直线AB 的方程,进而找到定点 【详解】依题意知,圆C 的半径2242411r ==+且圆心为O∴圆C 的方程为2216x y += ∵PA ,PB 是圆C 的两条切线∴OA AP ⊥,OB BP ⊥,即A ,B 在以OP 为直径的圆上若设点P 的坐标为(8,)b ,b R ∈,则线段OP 的中点坐标为4,2b ⎛⎫⎪⎝⎭∴以OP 为直径的圆的方程为2222(4)422b b x y ⎛⎫⎛⎫-+-=+ ⎪ ⎪⎝⎭⎝⎭,b R ∈,化简得2280x y x by +--=,b R ∈∵AB 为两圆的公共弦∴直线AB 的方程为816x by +=,b R ∈,即8(2)0x by -+= ∴直线AB 恒过定点(2,0) 故选:A 【点睛】本题考查了圆的切点弦过定点问题,首先根据已知条件求出两圆方程,由两圆过相同的两点,即有公共直线求出切点弦的直线方程,进而确定定点 8.已知点(,1),P t t t R -∈,点E 是圆2214x y +=上的动点,点F 是圆229(3)(1)4x y -++=上的动点,则PF PE -的最大值为( ) A .2 B .52C .3D .4【答案】D 【解析】 【分析】由于两圆不在直线的同侧,先做出圆O 关于直线对称的圆1O ,把PF PE -转化为PF PE '-,若PF PE '-最大,必须PF 最大,PE '最小.【详解】 如图:依题意得点(,1),P t t t R -∈在直线1y x =-上, 点E 关于直线1y x =-对称的点E ', 点E '在圆2214x y +=关于直线1y x =-对称的圆2211:(1)(1)4O x y ++-=上,则PE PE '=,设圆229(3)(1)4x y -++=的圆心为2O , 因为11PE PO E O ''≥-,22PF PO FO ≤+, 所以22112112()()224PF PE PF PE PO FO PO E O PO PO OO ''-=-≤+--=-+≤+=,当12,,,,P E F O O '五点共线,E '在线段1O 上,2O 在线段PF 上时“=”成立. 因此,PF PE -的最大值为4. 【点睛】本题主要考查圆与圆的位置关系,直线与圆的位置关系,距离和差的最值问题对称变换是常采用的方法.二、多选题(3道小题,每小题满分5分,答漏得3分,答错得0分)9.已知圆22:(cos )(sin )1M x y θθ++-=,直线:l y kx =.下列命题中,正确的命题是( )A .对任意实数k 和θ,直线l 和圆M 有公共点B .对任意实数θ,必存在实数k ,使得直线l 与圆M 相切C .对任意实数k ,必存在实数θ,使得直线l 与圆M 相切D .存在实数k 与θ,使得圆M 上有一点到直线l 的距离为3 【答案】AC 【解析】 【分析】由已知可得圆心(cos ,sin )M θθ-,半径1r =,且圆过原点,求出圆心到直线的距离,逐项判断,即可得出结论. 【详解】选项A ,圆22:(cos )(sin )1M x y θθ++-=恒过原点(0,0)O , 所以A 正确;圆心(cos ,sin )M θθ-到直线l 的距离为d ,|sin()|1d θϕ==+≤∴对于任意实数k ,直线l 与圆相交或相切,所以选项C 正确,选项B 不正确;圆上的点到直线l 距离最大值为12d +≤, 所以选项D 不正确. 故选:AC. 【点睛】本题考查直线与圆的位置关系,注意点到直线距离公式的合理应用,属于中档题. 10.以下四个命题表述正确的是( ) A .直线()4120mx y m R +-=∈恒过定点()0,3B .圆C :2228130+--+=x y x y 的圆心到直线4330x y -+=的距离为2 C .圆1C :2220x y x ++=与圆2C :224840x y x y +--+=恰有三条公切线D .两圆22440x y x y ++-=与222120x y x ++-=的公共弦所在的直线方程为:260x y ++=【答案】AC 【解析】 【分析】根据直线过的定点判断A 选项的正确性,根据圆心到直线的距离判断B 选项的正确性,根据两个圆的位置关系判断C 选项的正确性,根据相交弦所在直线方程判断D 选项的正确性. 【详解】对于A 选项,当0x =时3y =,所以直线过定点()0,3,故A 选项正确. 对于B 选项,圆C 的圆心为()1,4,到直线4330x y -+=的距离为412315-+=,所以B 选项错误.对于C 选项,圆1C 的圆心为()1,0-,半径为11r =;圆2C 的圆心为()2,4,半径为24r =.125r r ==+,所以两圆外切,故恰有三条公切线,故C 正确.对于D 选项,由22224402120x y x y x y x ⎧++-=⎨++-=⎩两式相减并化简得260x y -+=,所以D 选项错误.综上所述,正确的选项为AC. 故选:AC【点睛】本小题主要考查直线和圆的位置关系,圆和圆的位置关系,考查直线过定点问题,属于中档题.11.如图()()()()2,0,1,11,12,0A B C D --,,,CD 是以OD 为直径的圆上一段圆弧,CB 是以BC 为直径的圆上一段圆弧,BA 是以OA 为直径的圆上一段圆弧,三段弧构成曲线Ω.则下面说法正确的是( )A .曲线Ω与x 轴围成的面积等于32π B .CB 与BA 的公切线方程为:12=0x y +-- C .AB 所在圆与CB 所在圆的交点弦方程为:0x y -= D .用直线y x =截CD 2 【答案】BC 【解析】 【分析】由题知曲线Ω与x 轴围成的图形为一个半圆、一个矩形和两个四分之一圆,求面积和,可判断A ;设CB 与BA 的公切线方程,由直线与圆相切的条件,列方程组,可求得直线方程,即可判断B ;由两圆方程联立相减,则可求出AB 所在圆与CB 所在圆的交点弦方程,可判断C ;由弦长公式求出弦长,可判断D. 【详解】各段圆弧所在圆方程分别为:CD :22(1)1x y ++=,CB :22(1)1y x +-=,BA :22(1)1x y -+=曲线Ω与x 轴围成的图形为一个半圆、一个矩形和两个14圆,面积为22224πππ++⨯=+,故选项A 错误;设CB 与BA 的公切线方程为:(0,0)y kx b k b =+<>, 则221111b k b k k -++==++,解得1,12k b =-=+,所以CB 与BA 的公切线方程为:12y x =-++, 即120x y +--=,故选项B 正确;由22(1)1y x +-=及22(1)1x y -+=两式相减得:0x y -=即为交点弦所在直线方程,故选项C 正确;CD 所在圆的方程为22(1)1x y ++=,圆心为(1,0)-,圆心到直线y x =的距离为1222d -==, 则弦长为2221()22-=,故选项D 错误. 故选:BC.【点睛】本题考查圆的方程的运用,直线与圆的位置关系,考查数形结合思想和运算能力,综合性较强,运算较繁杂..评卷人得分三、填空题12.以圆C 1:x 2+y 2-12x -2y -13=0和圆C 2:x 2+y 2+12x +16y -25=0公共弦为直径的圆的方程为________. 【答案】x 2+y 2-4x +4y -17=0 【解析】试题分析:解法一:先两圆方程相减,得到公共弦方程,再联立直线和圆的方程求出公共点坐标,进而求出圆的半径和圆心,写出圆的方程即可;解法二:先两圆方程相减,得到公共弦方程,再利用圆系方程进行求解.试题解析:解法一:联立两圆方程22221221301216250x y x y x y x y ⎧+---=⎨+++-=⎩, 相减得公共弦所在直线方程为4x +3y -2=0.再由221221304320x y x y x y ⎧+---=⎨+-=⎩, 联立得两圆交点坐标(-1,2)、(5,-6). ∵所求圆以公共弦为直径,∴圆心C 是公共弦的中点(2,-2),半径为221(51)(62)52++--=, ∴圆C 的方程为(x -2)2+(y +2)2=25.解法二:由解法一可知公共弦所在直线方程为4x +3y -2=0.设所求圆的方程为x 2+y 2-12x -2y -13+λ(x 2+y 2+12x +16y -25)=0(λ为参数). 可求得圆心1212162(,)2(1)2(1)C λλλλ----++.∵圆心C 在公共弦所在直线上, ∴121216243202(1)2(1)λλλλ---⨯+⨯-=++,解得λ=12. ∴圆C 的方程为x 2+y 2-4x +4y -17=0.13.2020年是中国传统的农历“鼠年”,有人用3个圆构成“卡通鼠”的形象,如图:(0,3)Q -是圆Q 的圆心,圆Q 过坐标原点O ;点L 、S 均在x 轴上,圆L 与圆S 的半径都等于2,圆S 、圆L 均与圆Q 外切.已知直线l 过点O .(1)若直线l 与圆L 、圆S 均相切,则l 截圆Q 所得弦长为__________; (2)若直线l 截圆L 、圆S 、圆Q 所得弦长均等于d ,则d =__________.【答案】3 125【解析】 【分析】(1)设出公切线方程,利用圆心到直线的距离等于半径列出方程求解即可; (2)设出方程,分别表示出圆心到直线的距离1d,2d =,3d =,结合弦长公式求得k ,m 即可【详解】解:(1)根据条件得到两圆的圆心坐标分别为(4,0)-,(4,0),设公切线方程为(0)y kx m k =+≠且k 存在,则22==,解得3k =±,0m =,故公切线方程为y x =,则Q 到直线l的距离d =, 故l 截圆Q的弦长3==; (2)设方程为(0)y kx m k =+≠且k 存在,则三个圆心到该直线的距离分别为:1d2d,3d ,则22221234(4)4(4)4(9)d d d d =-=-=-,即有22=,①2249-=-,②解①得0m =,代入②得2421k =, 则2416144214(4)425121d ⨯=-=+,即125d =,故答案为:3;125. 【点睛】本题考查直线与圆的位置关系,圆与圆的位置关系,公切线方程,方程思想,数形结合思想,属于中档题.14.定义:点()00,M x y 到直线22:0(0)l ax by c a b ++=+≠的有向距离为已知点(2,0)A-,(2,0)B,直线m过点(4,0)P,若圆22(6)36x y+-=上存在一点C,使得A,B,C三点到直线m的有向距离之和为0,则直线m的斜率的取值范围是________.【答案】4,03⎡⎤-⎢⎥⎣⎦【解析】【分析】首先设直线m的方程为(4)y k x=-,(,)C x y,根据A,B,C三点到直线m的有向距离之和为0得到120kx y k--=,再根据点C在圆22(6)36x y+-=上,即可得到直线m的斜率的取值范围.【详解】因为直线m的斜率存在,设直线m的方程为(4)y k x=-,即40kx y k--=,设(,)C x y,则A,B,C三点到直线m的有向距离之和为++=,化简得120kx y k--=.又点C在圆22(6)36x y+-=上,所以直线120kx y k--=与圆22(6)36x y+-=有交点,6≤,解得403k-≤≤.故答案为:4,03⎡⎤-⎢⎥⎣⎦【点睛】本题主要考查点到直线的距离公式,同时考查学生的分析问题的能力,属于中档题. 四、解答题(4道小题,每小题满分10分)15.在直角坐标系xOy中,直线l:40x-=交x轴于M,以O为圆心的圆与直线l相切.(1)求圆O的方程;(2)设点()00,N x y 为直线3y x =-+上一动点,若在圆O 上存在点P ,使得45ONP ∠=︒,求0x 的取值范围;(3)是否存在定点S ,对于经过点S 的直线L ,当L 与圆O 交于A ,B 时,恒有AMO BMO ∠=∠若存在,求点S 的坐标;若不存在,说明理由.【答案】(1)224x y +=;(2)03322x -≤≤;(3)()1,0,证明见解析 【解析】 【分析】(1)已知圆心()0,0O ,由点到直线的距离为半径,求出半径,即可得到圆O 的方程; (2)当NP 与圆O 相切时ONP ∠最大,可得2sin 452ON ≥︒=,求解出0x 的取值范围;(3)讨论直线斜率存在与不存在两种情况,当斜率不存在时,易知点S 存在;当斜率存在时,由AMO BMO ∠=∠可得0AM BM k k +=,设直线方程并代入圆方程,由韦达定理求出m k =-,即可求出定点S . 【详解】(1)由题意,圆心()0,0O ,直线l 与圆O 相切,所以圆心到直线l 的距离即半径422r ===, 所以圆O :224x y +=;(2)由题意,当NP 与圆O 相切时ONP ∠最大, 此时2sin OP ONP ON ON∠==, 在圆O 上存在点P ,使得45ONP ∠=︒,即2sin 45ON ≥︒=,ON ≤ 设点()00,3N x x -,则ON =,≤0x ≤≤(3)当直线L 斜率不存在时,L 与圆O 交于A 、B 两点, 则点A 和点B 关于x 轴对称,点M 在x 轴上,当0y =时,4x =,所以()4,0M , 所以AMO BMO ∠=∠成立,点S 存在; 当直线L 斜率存在时,设直线L :y kx m =+,代入圆O 方程,并整理得,()2221240k x kmx m +++-=, 设点()11,A x y ,点()22,B x y ,则12221km x x k +=-+,212241m x x k -⋅=+,若AMO BMO ∠=∠成立,即0AM BM k k +=,故1212044kx m kx m x x +++=--,整理得()()12122480kx x k m x x m --+-=, 将12221km x x k +=-+,212241m x x k -⋅=+代入得,()22242248011m kmk k m m k k -+--=++,化简得m k =-,所以直线L :()1y k x =-,恒过定点()1,0. 【点睛】本题主要考查直线与圆的位置关系和求定点问题,考查学生转化能力和计算能力,属于中档题.16.已知两个定点(4,0),(1,0)A B --,动点P 满足||2||PA PB =.设动点P 的轨迹为曲线E ,直线:4l y kx =-. (1)求曲线E 的轨迹方程;(2)若l 与曲线E 交于不同的,C D 两点,且90COD ∠=(O 为坐标原点),求直线l 的斜率;(3)若1,2k Q =是直线l 上的动点,过Q 作曲线E 的两条切线,QM QN ,切点为,M N ,探究:直线MN 是否过定点.【答案】(1)224x y +=(2)k =3)线MN 过定点1(,1)2-【解析】试题分析:(1)设点P 坐标为(),x y ,由2PA PB =,得:=整理即可得轨迹方程;(2)依题意圆心到直线l 的距离d =l 的斜率k ;(3)由题意可知:,,,O Q M N 四点共圆且在以OQ 为直径的圆上,设1,42Q t t ⎛⎫- ⎪⎝⎭,其方程为()1402x x t y y t ⎛⎫-+-+= ⎪⎝⎭,即:22402t x tx y y ⎛⎫-+--= ⎪⎝⎭,又,M N 在曲线22:4E x y +=上,4402MN t l tx y ⎛⎫=+--=⎪⎝⎭,即()4102y x t y ⎛⎫+-+= ⎪⎝⎭,由210y x y ⎧+=⎪⎨⎪+=⎩可解得定点坐标. 试题解析:(1)设点P 坐标为(),x y 由2PA PB ==整理得:曲线的E 轨迹方程为224x y += (2)依题意圆心到直线l的距离d ==k ∴=(3)由题意可知:,,,O Q M N 四点共圆且在以OQ 为直径的圆上,设1,42Q t t ⎛⎫- ⎪⎝⎭, 其方程为()1402x x t y y t ⎛⎫-+-+= ⎪⎝⎭,即:22402t x tx y y ⎛⎫-+--= ⎪⎝⎭又,M N 在曲线22:4E x y +=上,4402MN t l tx y ⎛⎫=+--= ⎪⎝⎭,即()4102y x t y ⎛⎫+-+= ⎪⎝⎭,由0210y x y ⎧+=⎪⎨⎪+=⎩得121x y ⎧=⎪⎨⎪=-⎩,∴直线MN 过定点1,12⎛⎫- ⎪⎝⎭.17.如图,一个湖的边界是圆心为O 的圆,湖的一侧有一条直线型公路l ,湖上有桥AB (AB 是圆O 的直径).规划在公路l 上选两个点P ,Q ,并修建两段直线型道路PB ,QA ,规划要求:线段PB ,QA 上的所有点到点O 的距离均不小于...圆O 的半径.已知点A ,B 到直线l 的距离分别为AC 和BD (C ,D 为垂足),测得10AB =,6AC =,12BD =(单位:百米).(1)若道路PB 和桥AB 垂直,求道路PB 的长;(2)在规划要求下,P 和Q 中能否有一个点选在D 处?并说明理由;(3)在规划要求下,若道路PB 和QA 的长度均为d (单位:百米),求当d 最小时,P ,Q 两点间的距离.【答案】(1)道路PB 的长为15(百米);(2)不能,答案见解析;(3)(17321)+百米. 【解析】 【分析】(1)当道路PB 和桥AB 垂直,先确定出点P 的位置,根据题目条件,采用几何法求解;(2)分别假设点P 或点Q 位于点D ,分析道路PB 和QA 上的点到圆心O 的距离是否均不小于...圆O 的半径; (3)由题意分析可知,当PB 上所有点到圆心的距离均不小于圆O 的半径时,90OPB ∠≥,且当PB AB ⊥时,PB 最小,验证PB QA d ==时,QA 上的点到圆心O 的距离均不.小于..圆O 的半径. 【详解】解:(1)过A 作AE BD ⊥,垂足为E . 由已知条件得,四边形ACDE 为矩形,6DE BE AC ===,8AE CD ==.因为PB AB ⊥,所以84cos sin 105PBD ABE ∠=∠==, 所以12154cos 5BD PB PBD ===∠. 因此道路PB 的长为15(百米).(2)不能,理由如下:①若P 在D 处,由(1)可得E 在圆上,则线段BE 上的点(除B ,E )到点O 的距离均小于圆O 的半径,所以P 选在D 处不满足规划要求. ②若Q 在D 处,连接AD ,由(1)知2210AD AE ED =+=,从而2227cos 0225AD AB BD BAD AD AB +-∠==>⋅,所以BAD ∠为锐角.所以线段AD 上存在点到点O 的距离小于圆O 的半径. 因此Q 选在D 处也不满足规划要求. 综上,P 和Q 均不能选在D 处. (3)先讨论点P 的位置.当90OBP ︒∠<时,线段PB 上存在点到点O 的距离小于圆O 的半径,点P 不符合规划要求;当90OBP ︒∠≥时,对线段PB 上任意一点F ,OF OB ≥,即线段PB 上所有点到点O 的距离均不小于圆O 的半径,点P 符合规划要求.设1P 为l 上一点,且1PB AB ⊥,由(1)知,115PB =, 此时11113sin cos 1595PD PB PBD PB EBA =∠=∠=⨯=; 当90OBP ︒∠>时,在1PPB △中,115PB PB >=. 由上可知,15d ≥. 再讨论点Q 的位置.由(2)知,要使得15QA ≥,点Q 只有位于点C 的右侧,才能符合规划要求.当15QA =时,2222156321CQ QA AC =-=-=.此时,线段QA 上所有点到点O 的距离均不小于圆O 的半径.综上,当PB AB ⊥点Q 位于点C 右侧,且321CQ =时,d 最小,此时P ,Q 两点间的距离17321PQ PD CD CQ =++=+.因此,d 最小时,P ,Q 两点间的距离为(17321)+百米. 【点睛】本题考查直线与圆的位置关系综合题,难度较大.解答时注意数形结合,灵活运用题目所给几何条件求解.18.已知()0,3A ,,B C 为222(0)x y r r +=>上三点.(1)求r 的值;(2)若直线BC 过点(0,2),求ABC 面积的最大值;(3)若D 为曲线22(1)4(3)x y y ++=≠-上的动点,且AD AB AC =+,试问直线AB 和直线AC 的斜率之积是否为定值?若是,求出该定值;若不是,说明理由. 【答案】(1)3r =;(25(3)定值为:15-.【解析】 【分析】(1)由(0,3)A 为圆222:()0O x y r r +=>上的点即可得r ;(2)设1(B x ,1)y ,2(C x ,2)y ,根据1211||2ABCSx x =-利用韦达定理即可求解; (3)直线AB 和直线AC 的斜率之积为m ,设1(B x ,1)y ,2(C x ,2)y ,0(D x ,0)y ,即可得121233y y m x x --=⇒2121223(1)()91m y y y y m +=-+--,12121(3)(3)x x y y m =--,由AD AB AC =+可得1212(3),D x x y y ++-,代入222125(1)4(3)()01m mx y y y y m +++=≠-⇒+=-,求得m 即可.【详解】解:(1)∵()0,3A 为圆()2220x y rr +=>上,所以()222030r r +=>∴3r =(2)由题意知直线BC 的斜率存在,设直线BC 的方程为2y kx =+,()11,B x y ,()22,C x y 将2y kx =+代人229x y +=得,()221450kx kx ++-=所以1211||2ABCS x x =⋅⋅-=△令21k t +=,则ABC S ==△1t ≥ 当1t=,即0k =时ABC (3)设直线AB 和直线AC 的斜率之积为(0)m m ≠ 设()11,B x y ,()22,C x y ,()00,D x y 则121233y y m x x --⋅= ()()1212133x x y y m =--①,()()22122221233y y m x x --=因为B ,C 为圆222:O x y r +=上,所以22119x y +=,22229x y +=()()()()22122221233y y mq y q y --=--化简得()()()()222113333y y m y y --=++整理得()()2222113191m y y y y m +=-+--② 因为AD AB AC =+,所以()()()112200,,3,33x y x y x y -+-=-从而()1212,3D x x y y ++-,又因为D 为曲线()2214(3)x y y +-=≠-的动点 所以()()22121224x x y y +++-=展开得 ()()22221122121212224()44x y x y x x y y y y +++++-++=将①代入得 ()()()21121229933240y y y y y y m++--+-+=化简得 ()()()()1212123910m y y m y y m +-++++=将②代人得()2121223(1)1()9(23)()9(1)01m m y y m y y m m ⎡⎤++-+--++++=⎢⎥-⎣⎦,整理得 ()212501m m y y m +⋅+=-, 因为2133y y +≠--所以120y y +≠从而250m m +=又0m ≠所以15m =-【点睛】本题考查了直线与圆的位置关系,考查两直线的斜率之积是否为定值的判断与证明,解题时要认真审题,注意韦达定理的合理运用,属于中档题.。
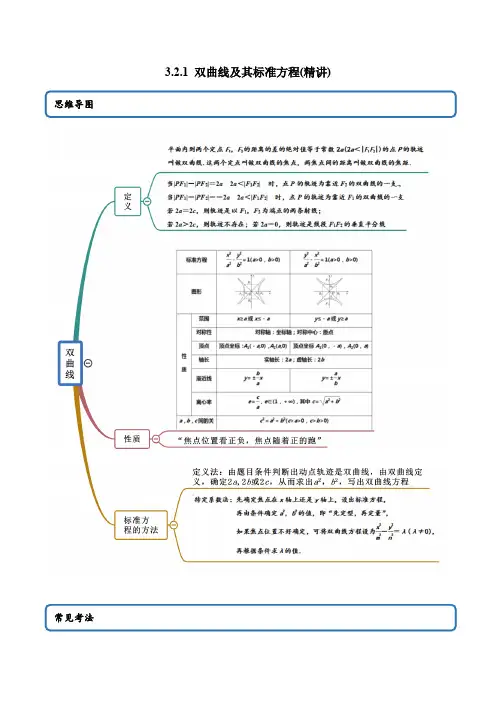
3.2.1 双曲线及其标准方程(精讲)考点一 双曲线的定义及运用【例1】2.(2021·全国高二课时练习)动点P 到点(1,0)M 及点(5,0)N 的距离之差为2a ,则当1a =和2a =时,点P 的轨迹分别是( ) A .双曲线和一条直线 B .双曲线和一条射线 C .双曲线的一支和一条射线D .双曲线的一支和一条直线(2)(2021·全国高二课时练习)已知F 是双曲线221412x y -=的左焦点,点(1,4)A ,P 是双曲线右支上的动点,则||||PF PA +的最小值为( ) A .9B .5C .8D .4(3)(2021·全国)设双曲线()2222:10,0x y C a b a b-=>>的左、右焦点分别为1F ,2F P 是双曲线C 上一点,且1260F PF ∠=︒.若12F PF △的面积为a =( )A .1B .2C .4D (4).(2021·全国高二课时练习)已知双曲线22:13y C x -=的右焦点为F ,P 是双曲线C 的左支上一点,()0,2M ,则PFM △的周长的最小值为( )A .2+B .4+C .D .3【答案】(1)C(2)A(3)D(4)A【解析】(1)由题意,知4MN =,当1a =时,||||224PM PN a -==<,此时点P 的轨迹是双曲线的一支;当2a =时,||||24||PM PN a MN -===, 点P 的轨迹为以N 为端点沿x 轴向右的一条射线.故选:C.(2)设右焦点为F ',则(4,0)F ',依题意,有||4PF PF '=+,||||||44549PF PA PF PA AF ''∴+=++≥+=+=,(当P 在线段AF '上时,取等号).故||||PF PA +的最小值为9. 故选:A.(3)设2PF m =,1PF n =.由1260F PF ∠=︒,12F PF △的面积为可得222242cos601sin 602n m a c m n mn mn ⎧⎪-=⎪=+-︒⎨⎪⎪︒=⎩,∴()2224416c n m mn a =-+=+①ca=a =故选:D.(4)设双曲线C 的左焦点为1F ,则12PF PF a -=.由题可知1a =,2c =, ∴12PF PF =+,()12,0F -,()2,0F ,∴MF =PFM △的周长为12MF MP PF MP PF ++=++. ∵当M ,P ,1F 三点共线时,1MP PF +最小,最小值为1MF = ∴PFM △的周长的最小值为2+ 故选:A 【一隅三反】1.(2021·河北定兴第三中学)已知双曲线221916x y -=的左右焦点1F ,2F ,P 是双曲线上一点,17PF =,则2PF =( ) A .1或13 B .1C .13D .9【答案】C【解析】根据双曲线定义可得1226PF PF a -==,又17PF =, 所以21PF =或213PF =, 又22225c a b =+=,解得5c =,即12210F F c ==, 又121210PF PF F F +≥=, 所以213PF =. 故选:C2.(2021·鹤山市第二中学)P 是双曲线x 2-y 2=16左支上一点,F 1,F 2分别是左、右焦点,则|PF 1|-|PF 2|=( ) A .4 B .-4C .8D .-8【答案】D【解析】因为双曲线方程为x 2-y 2=16,化为标准方程得2211616x y -=,即4a =,所以2128PF F a P -==,而点P 在双曲线左支上,于是12PF PF <, 所以218PF PF -=-. 故选:D .3(2021·全国)已知F 1,F 2为双曲线C :x 2-y 2=1的左、右焦点,点P 在C 上,∠F 1PF 2=60°,则|PF 1|·|PF 2|等于( ) A .2 B .4 C .6 D .8【答案】B【解析】不妨设P 是双曲线右支上一点,在双曲线x 2-y 2=1中,a =1,b =1,c则|PF 1|-|PF 2|=2a =2,|F 1F 2|=∵|F 1F 2|2=|PF 1|2+|PF 2|2-2|PF 1|·|PF 2|·cos ∠F 1PF 2, ∴8=|PF 1|2+|PF 2|2-2|PF 1|·|PF 2|·12, ∴8=(|PF 1|-|PF 2|)2+|PF 1|·|PF 2|,∴8=4+|PF 1|·|PF 2|,∴|PF 1|·|PF 2|=4.故选:B考点二 求曲线的轨迹方程【例2】(1)(2021·全国高二课时练习)已知动点(),P x y 2,则动点P 的轨迹是( ) A .椭圆B .双曲线C .双曲线的左支D .双曲线的右支(2)(2021·全国高二课时练习)已知1F ,2F 为平面内两个定点,P 为动点,若12-=PF PF a (a 为大于零的常数),则动点P 的轨迹为( ) A .双曲线 B .射线C .线段D .双曲线的一支或射线【答案】(1)D(2)D【解析】2=表示:动点(),P x y 到两定点()12,0F -,()22,0F 的距离之差等于2, 而1224F F <=,由双曲线的定义,知动点P 的轨迹是双曲线的右支. 故选:D (2)两个定点的距离为12F F ,当12a F F <,即1212PF PF F F -<时,点P 的轨迹为双曲线的一支; 当12a F F =,即1212PF PF F F -=时,点P 的轨迹为射线; 不存在1212PF PF F F ->的情况.综上所述,动点P 的轨迹为双曲线的一支或射线. 故选:D . 【一隅三反】1.(2021·浙江丽水·高二期中)已知点Q 是圆22:16O x y +=(O 为坐标原点)上一动点,点)(5,0P ,若线段PQ 的垂直平分线交直线OQ 于点M ,则点M 的轨迹是( ) A .直线 B .圆C .椭圆D .双曲线【答案】D【解析】依题意,||4,||5OQ OP ==,因线段PQ 的垂直平分线交直线OQ 于点M ,于是得||||MP MQ =, 当点M 在线段QO 的延长线上时,||||||||||4MP MO MQ MO QO -=-==,如图,当点M 在线段OQ 的延长线上时,||||||||||4MO MP MO MQ QO -=-==,如图,从而得||||||45||MP MO OP -=<=,由双曲线的定义知,点M 的轨迹是双曲线. 故选:D2.(2021·全国高二课时练习)已知圆1C :()2231x y ++=和圆2C :()2239x y -+=,动圆M 同时与圆1C 及圆2C 外切,则动圆的圆心M 的轨迹方程为______.【答案】()22118y x x -=≤-【解析】如图所示,设动圆M 与圆1C 及圆2C 分别外切于点A 和点B ,根据两圆外切的条件,得11MC AC MA -=,22MC BC MB -=. 因为MA MB =,所以1122MC AC MC BC -=-, 即21212MC MC BC AC -=-=,所以点M 到两定点2C ,1C 的距离的差是常数且小于126C C =.根据双曲线的定义,得动点M 的轨迹为双曲线的左支,其中1a =,3c =,则28b =.故点M 的轨迹方程为()22118y x x -=≤-.故答案为:()22118y x x -=≤-.考点三 双曲线的标准方程【例3】(1).(2021·全国高二课时练习)等轴双曲线的一个焦点是()16,0F -,则其标准方程为( )A .22199x y -=B .22199y x -=C .2211818y x -=D .2211818x y -=(2)(2021·全国高二课时练习)已知双曲线过点1⎛- ⎝⎭P和2⎫⎪⎪⎝⎭P ,则双曲线的标准方程为( ) A .221916x y -= B .221916y x -=C .221169x y -=D .221169y x -=(3)(2021·全国高二课时练习)中心在原点,焦点在x 轴上,且一个焦点在直线3x -4y +12=0上的等轴双曲线的方程是( ) A .x 2-y 2=8 B .x 2-y 2=4 C .y 2-x 2=8D .y 2-x 2=4【答案】(1)D(2)B(3)A【解析】(1)∵等轴双曲线的一个焦点为()16,0F -,∴6c =,且a=b ,又222c a b =+,∴2236a =,即218a =,∴双曲线的标准方程为2211818x y -=.故选:D(2)因为双曲线的焦点位置不正确的,所以设双曲线的方程为()2210mx ny mn +=<.因为1⎛- ⎝⎭P,2⎫⎪⎪⎝⎭P 两点在双曲线上, 所以454141121619m n m n ⎧+=⎪⎪⎨⎪+=⎪⎩,解得11619m n ⎧=-⎪⎪⎨⎪=⎪⎩,于是所求双曲线的标准方程为221916y x -=.故选:B .(3)设等轴双曲线的方程为2222x y a b-,且22a b =,令y =0,得x =-4,∴等轴双曲线的一个焦点为(-4,0), ∴c =4,a 2=b 2=12c 2=12×16=8,故选:A. 【一隅三反】1.(2021·内蒙古乌兰浩特一中高二期末(文))已知双曲线2222:1(0,0)x y C a b a b-=>>的焦点到顶点的距离为1,且双曲线的一条渐近线与直线430x y +=垂直,则双曲线C 的方程为( )A .22132x y -=B .221169x y -=C .22198x y -=D .22123x y -= 【答案】B【解析】由题意得222134c a b a a b c-=⎧⎪⎪=⎨⎪+=⎪⎩,解得43a b =⎧⎨=⎩,所以双曲线的方程为221169x y -=.故选:B .2.(2021·全国)已知等轴双曲线的中心在原点,焦点在x 轴上,与直线y =12x 交于A ,B 两点,若|AB |=( ) A .x 2-y 2=6 B .x 2-y 2=9 C .x 2-y 2=16 D .x 2-y 2=25【答案】B【解析】设等轴双曲线的方程为x 2-y 2=a 2(a >0),与y =12x 联立,得34x 2=a 2,∴|AB |=a =3,故选B.3.(2021·全国高二课前预习)已知双曲线的实轴和虚轴等长,且过点(5,3),则双曲线方程为( )A .2212525x y -=B .22199x y -=C .2211616y x -=D .2211616x y -=【答案】D【解析】解析由题意知,所求双曲线是等轴双曲线,设其方程为x 2-y 2=λ(λ≠0),将点(5,3)代入方程,可得λ=52-32=16,所以双曲线方程为x 2-y 2=16,即-=1.4.(2021·全国高二专题练习)已知双曲线22x a -22y b =1(a >0,b >0)的实轴长为4,离心率为线的标准方程为( )A.24x-216y=1 B.x2-24y=1C.22x-23y=1 D.x2-26y=1【答案】A【解析】因为双曲线22xa-22yb=1(a>0,b>0)的实轴长为4,所以a=2,cac=b4,则双曲线的标准方程为24x-216y =1.故选:A5.(2021·云南丽江第一高级中学高二月考(理))与椭圆C:2211612y x+=共焦点且过点(的双曲线的标准方程为( )A.2212yx-=B.2221y x-=C.22122y x-=D.2212yx-=【答案】C【解析】因为椭圆C:2211612y x+=的焦点为()()0,2,0,2-;所以设双曲线的标准方程为()222210,0y xa ba b-=>>,则有22224311a ba b⎧+=⎪⎨-=⎪⎩,解得222a b==,所以方程为22122y x-=.故选:C.6.(2021·云南昆明·高二期末(理))双曲线2222:1(0,0)x yC a ba b-=>>的顶点焦点到C的一条渐近线的距离分C的方程为( )A.221123yx-=B.22143x y-=C.221312x y-=D.221412x y-=【答案】D【解析】双曲线2222:1(0,0)x yC a ba b-=>>的焦点,()0F c±到渐近线0bx ay±=b==顶点(,0)A a±到渐近线0bx ay±=bac==由222b bac c a b ⎧=⎪⎪=⎨⎪=+⎪⎩解得224,12a b == 所以双曲线的方程为221412x y -=.故选:D。



2019新人教版高中数学选择性必修一全册重点知识点归纳总结(复习必背)第一章空间向量与立体几何一、知识要点1、空间向量的概念:在空间,我们把具有大小和方向的量叫做向量。
注:(1)向量一般用有向线段表示同向等长的有向线段表示同一或相等的向量。
(2)向量具有平移不变性2、空间向量的运算定义:与平面向量运算一样,空间向量的加法、减法与数乘运算如下(如图)。
OB OA AB a b =+=+ ;BA OA OB a b =-=- ;()OP a R λλ=∈运算律:(1)加法交换律:a b b a +=+(2)加法结合律:)()(c b a c b a ++=++(3)数乘分配律:ba b aλλλ+=+)(运算法则:三角形法则、平行四边形法则、平行六面体法则3、共线向量(1)如果表示空间向量的有向线段所在的直线平行或重合,那么这些向量也叫做共线向量或平行向量,a 平行于b ,记作b a//。
(2)共线向量定理:空间任意两个向量a 、b (b ≠0 ),a //b 存在实数λ,使a=λb 。
(3)三点共线:A 、B 、C 三点共线<=>ACAB λ=<=>OB y OA x OC +=(其中x +y =1)(4)与a 共线的单位向量为4、共面向量(1)定义:一般地,能平移到同一平面内的向量叫做共面向量。
说明:空间任意的两向量都是共面的。
(2)共面向量定理:如果两个向量,a b 不共线,p与向量,a b 共面的条件是存在实数x ,y 使p xa yb =+。
(3)四点共面:若A 、B 、C 、P 四点共面<=>ACy AB x AP +=<=>)1(=++++=z y x OC z OB y OA x OP 其中5、空间向量基本定理:如果三个向量,,a b c不共面,那么对空间任一向量p ,存在一个唯一的有序实数组,,x y z ,使p xa yb zc =++。


3.1.2 椭圆的简单几何性质(精讲)考点一离心率【例1】(1)(2021·四川高二期末(文))椭圆()222210x ya ba b+=>>的左右焦点分别是1F,2F,以2F为圆心的圆过椭圆的中心,且与椭圆交于点P,若直线1PF恰好与圆2F相切于点P,则椭圆的离心率为( ).A B C1D(2)(2021·黄冈天有高级中学高二月考)已知12,F F是椭圆的两个焦点,过1F且与椭圆长轴垂直的直线交椭圆于,A B两点,若2ABF是等腰直角三角形,则这个椭圆的离心率是( )A B.2C1D【答案】(1)C(2)C【解析】(1)由题意2PF c=,12PF PF⊥,所以1PF===,所以122PF PF c a++=,所以离心率为1cea=.故选:C.(2)不妨设椭圆方程为()222210x ya ba b+=>>,焦点()()12,0,,0F c F c-,离心率为e,将x c =代入22221c y a b +=可得2b y a =±,所以22bAB a =,又2ABF 是等腰直角三角形,所以212224bAB F F c a===,所以22b c a =即2220c a ac -+=,所以2210e e +-=,解得1e =(负值舍去).故选:C. 【一隅三反】1.(2021·河北石家庄二中高一期末)若焦点在x 轴上的椭圆 22116x y m +=+m = A .31 B .28 C .25 D .23【答案】D【解析】焦点在x 轴上,所以221,6a m b =+= 所以2165c m m =+-=-离心率e =,所以2225314c m e a m -===+解方程得m=23 所以选D2.(2021·江苏高二期末)设1F ,2F 为椭圆2222:1(0)x y C a b a b +=>>的两个焦点,点P 在C 上,且1122,,PF F F PF 成等比数列,则C 的离心率的最大值为( ) A .12 B .23C .34D .1【答案】A【解析】设()2120F F c c =>,122PF PF a +=, 因为1122,,PF F F PF 成等比数列, 所以2212124F F PF PF c =⨯=,由12PF PF +≥2a ≥ 即12c e a =≤,当且仅当12PF PF =等号成立, 所以椭圆C 的离心率最大值为12. 故选:A.3.(2021·全国高二课时练习)在Rt ABC 中,1AB AC ==,如果一个椭圆通过A 、B 两点,它的一个焦点为点C ,另一个焦点在AB 上,则这个椭圆的离心率e =( )A B 1C 1D -【答案】D【解析】设另一个焦点为F ,如图所示,∵||||1AB AC ==,||BC42AB AC BC a ++==a =,设FA x =,则12x a +=,12x a -=,∴x =2214c +=,c =c e a ==故选:D.考点二 点与椭圆的位置关系【例2】(1)(2021·广西平果二中(理))点(1,1)与椭圆22132x y +=的位置关系为( )A .在椭圆上B .在椭圆内C .在椭圆外D .不能确定(2)(【新教材精创】3.1.2 椭圆的简单几何性质(2) 导学案-人教A 版高中数学选择性必修第一册)若点(),1P a 在椭圆22123x y +=的外部,则a 的取值范围为( )A .⎛ ⎝⎭B .,⎫⎛+∞⋃-∞⎪ ⎪ ⎝⎭⎝⎭C .4,3⎛⎫+∞ ⎪⎝⎭D .4,3⎛⎫-∞- ⎪⎝⎭【答案】(1)B(2)B【解析】(1)1151326+=<,可知点(1,1)在椭圆内.故选:B.(2)因为点(),1P a 在椭圆22123x y +=的外部,所以221123a +>,即243a >,解得a >a <.故选:B. 【一隅三反】1.(2021·安徽定远二中)点()1,0.7P 与椭圆2212x y +=的位置关系为( )A .在椭圆内B .在椭圆上C .在椭圆外D .不能确定【答案】A【解析】2210.70.9912+=<,所以,点P 在椭圆2212x y +=内.故选:A.2.(2021·甘肃省民乐县第一中学高三二模(理))若直线9mx ny +=和圆229x y +=没有交点,则过点(,)m n 的直线与椭圆221916x y +=的交点个数为( )A .1个B .至多一个C .2个D .0个【答案】C【解析】因为直线9mx ny +=和圆229x y +=没有交点, 3>,即229m n +<,所以2222191699m n m n +≤+<,即点(,)m n 在椭圆221916x y +=内, 所以过点(,)m n 的直线与椭圆221916x y +=的交点个数为2个. 故选:C考点三 直线与椭圆的位置关系【例3】(2021·安徽省泗县第一中学)已知椭圆的长轴长是(,. (1)求这个椭圆的标准方程;(2)如果直线y x m =+与这个椭圆交于两不同的点,求m 的取值范围.【答案】(1)2213x y +=;(2)22m -<<.【解析】(1)由已知得2a =c = 解得a =2321b ∴=-=,∴椭圆的标准方程为2213x y +=. (2)由2213y x m x y =+⎧⎪⎨+=⎪⎩,解方程组并整理得2246330x mx m ++-=, 有两个不同的交点∴222(6)44(33)12(4)0m m m ∆=-⨯⨯-=-->.解不等式得22m -<<. m ∴的取值范围(2,2)-.【一隅三反】1.(2021·上海市长征中学)设直线与椭圆的方程分别为 2y x b =+与2217525x y +=,问b 为何值时,(1)直线与椭圆有一个公共点; (2)直线与椭圆有两个公共点; (3)直线与椭圆无公共点.【答案】(1)b =±(2)b -<(3)b <-b >【解析】设直线与椭圆的方程分别为 2y x b =+与2217525x y +=,问b 为何值时, 由22217525y x b x y =+⎧⎪⎨+=⎪⎩得2213172530x bx b ++=-.(1)当()()22124133075b b =--∆⨯⨯=,即b =±(2)当()()22124133075b b =--∆⨯⨯>,即b -<(3)()()22124133075b b =--∆⨯⨯<即b <-b >时直线与椭圆无公共点.2.(2021·广东高二期末)在平面直角坐标系xOy 中,已知点P到两点(M N 的距离之和等于4,设点P 的轨迹为曲线C .(1)求曲线C 的方程.(2)若直线2y kx =+与曲线C 有公共点,求实数k 的取值范围. 【答案】(1)2214x y +=;(2)|k k k ⎧⎪≤≥⎨⎪⎪⎩⎭.【解析】(1)由己知得4PM PN MN +=>=由椭圆定义可知,轨迹C 是以M ,N为焦点,焦距长2c =24a =的椭圆. 所以222431b a c =-=-=,所以曲线C 的方程是2214x y +=.(2)由22214y kx x y =+⎧⎪⎨+=⎪⎩得()221416120k x kx +++=. ()()22216412146448k k k ∆=-⨯⨯+=-,因为直线2y kx =+与曲线C 有公共点, 所以0∆≥,即264480k -≥,解得k ≤k ≥故实数k的取值范围是|k k k ⎧⎪≤≥⎨⎪⎪⎩⎭.3.(2021·莆田第十五中学高二期末)直线0x y m --=与椭圆2219xy +=有且仅有一个公共点,求m 的值.【答案】m =【解析】将直线方程0x y m --=代入椭圆方程2219x y +=, 消去x 得到:2210290y my m -++=,令0∆=,即()22441090m m -⨯-=解得m =考点四 弦长【例4-1】(2021·全国高二课时练习)直线x -y +1=0被椭圆23x +y 2=1所截得的弦长|AB |等于( )A.2BC.D.【答案】A【解析】由2210,1,3x y x y -+=⎧⎪⎨+=⎪⎩得交点为(0,1),31(,)22--,则|AB |故选:A.【例4-2】(2021·陕西高二期末(理))已知椭圆()2222:10y x E a b a b +=>>的焦距为⎫⎪⎪⎝⎭在椭圆E 上.(1)求椭圆E 的标准方程;(2)设直线1y kx =+与椭圆E 交于M 、N 两点,O 为坐标原点,求OMN 面积的取值范围. 【答案】(1)2214y x +=;(2)⎛ ⎝⎦. 【解析】(1)因为焦距为2c =c =因为点⎫⎪⎪⎝⎭在椭圆E 上,所以221314a b +=,联立222221314c a b a b c ⎧=⎪⎪+=⎨⎪=+⎪⎩,解得24a =,21b =,椭圆E 的标准方程为2214y x +=. (2)设()11,M x y ,()22,N x y ,联立22141y x y kx ⎧+=⎪⎨⎪=+⎩,整理得()224230k x kx ++-=,0∆>,则12224k x x k +=-+,12234x x k =-+,原点到直线1y kx =+,则MON △的面积12S ==令t =t ≥,22211t S t t t==++,令1y t t =+,则221t y t-'=,函数1yt t =+在)+∞上单调递增,故1t t +≥,201t t <≤+OMN 面积的取值范围为⎛ ⎝⎦. 【一隅三反】1.(2021·安徽省泗县第一中学高二开学考试(理))已知椭圆的长轴长是(),).(1)求这个椭圆的标准方程;(2)如果直线y x m =+与这个椭圆交于A 、B两不同的点,若2AB =,求m 的值. 【答案】(1)2213x y +=;(2)1m =±.【解析】(1)由已知得2a =a =c =2221b a c =-=所以椭圆的标准方程2213x y +=(2)由2213y x m x y =+⎧⎪⎨+=⎪⎩消除y 得2246330x mx m ++-= 因为有两个不同的交点,所以()222(6)44(33)1240m m m ∆=-⨯⨯-=-->得m 的取值范围为()2,2- 由韦达定理得:126342m m x x --+== ,212334m x x -=所以2AB ==解得1m =±2.(2021·四川高二期末(文))已知椭圆1C 以直线0x my +=所过的定点为一个焦点,且短轴长为4. (1)求椭圆1C 的标准方程;(2)过点()1,0C 的直线l 与椭圆1C 交于A ,B 两个不同的点,求OAB 面积的最大值. 【答案】(1)22194x y +=;【解析】(1)直线0x my +过定点),即椭圆的一个焦点为),依题意:椭圆1C 的半焦距c =2b =,长半轴长a 有2229a b c =+=, 所以椭圆1C 的标准方程为22194x y +=; (2)显然点()1,0C 在椭圆内部,即直线l 与椭圆必有两个不同的交点, 由题意得直线l 不垂直于y 轴,设直线l 的方程为1x ky =+,由2214936x ky x y =+⎧⎨+=⎩消去x 整理得()22498320k y ky ++-=, 设()11,A x y ,()22,B x y ,则122849k y y k -+=+,1223249y y k -=+, 从而有1212111||||222△△△OAB AOC BOC S S S OC y OC y y y =+=⋅⋅+⋅⋅=-421k =++121=,t 1()4f t t t=+在)+∞单调递增, 则t 0k=时,14t t =+≥=于是有129AOB S ≤△0k =时等号成立, 所以OAB 3.(2021·重庆字水中学高二期末)已知椭圆22:1y E x m +=的下焦点为1F 、上焦点为2F ,其离心率e =过焦点2F 且与x 轴不垂直的直线l 交椭圆于A 、B 两点 (1)求实数m 的值;(2)求ABO (O 为原点)面积的最大值. 【答案】(1)2m =;【解析】(1)由题意可得:21b =,2a m =,可得1b =,a =因为c e a ==c = 因为222a b c =+,所以12mm =+,可得2m =,(2)由(1)知:椭圆22:12y E x +=,上焦点()20,1F ,设()11,A x y ,()22,B x y ,直线:l 1y kx =+, 由22112y kx y x =+⎧⎪⎨+=⎪⎩可得:()222210k x kx ++-=,所以12222k x x k -+=+,12212-=+x x k ,所以()()()()222222121212222222442248842222k k k k x x x x x x k k k k ++-+⎛⎫-=+-=+== ⎪++⎝⎭++,可得:12x x -=所以12211122ABOSx x OF =⨯-⨯==≤即0k =时等号成立,所以ABO (O 为原点)面积的最大值为2. 考点五 中点弦与点差法【例5】(1)(2021·全国高二专题练习)已知椭圆2219x y +=,过点11,22P ⎛⎫ ⎪⎝⎭的直线与椭圆相交于A 、B 两点,且弦AB 被点P 平分,则直线AB 的方程为( ) A .950x y +-= B .940x y --= C .950x y +-=D .940x y -+=(2)(2021·南京市中华中学高二期中)已知椭圆C :22221x y a b +=(0a b >>)的左焦点为F ,过点F的直线0x y -与椭圆C 相交于不同的两点A ,B ,若P 为线段AB 的中点,O 为坐标原点,直线OP 的斜率为12-,则椭圆C 的方程为( )A .22132x y +=B .2214x y +=C .22142x y +=D .22163x y +=【答案】(1)C(2)D【解析】(1)设点()11,A x y 、()22,B x y ,由已知可得121211x x y y +=⎧⎨+=⎩, 因为点A 、B 都在椭圆上,则221122221919x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩,两式作差可得()()()()1212121209x x x x y y y y -++-+=,即()121209x x y y -+-=, 所以,直线AB 的斜率为121219AB y y k x x -==--,因此,直线AB 的方程为111292y x ⎛⎫-=-- ⎪⎝⎭,即950x y +-=. 故选:C.(2)直线0x y -过点F ,令0y =则x =()F,即c =设()()1122,,,A x y B x y ,则2222112222221,1x y x y a b a b +=+=,两式相减并化简得2121221212y y y y b a x x x x +--=⋅+-,所以222222111222b b a b a a ⎛⎫-=-⋅⇒=⇒= ⎪⎝⎭,22223,c a b b b a =-====所以椭圆C 的方程为22163x y +=.故选:D 【一隅三反】1.(2021·浙江嘉兴·高二期中)已知点P Q M ,,是椭圆2222:1(0)x y C a b a b +=>>上的三点,坐标原点O 是PQM的重心,若点M ⎫⎪⎪⎝⎭,直线PQ 的斜率恒为12-,则椭圆C 的离心率为( ) ABCD【答案】D【解析】设()()1122,,,P x y Q x y,又,M ⎫⎪⎪⎝⎭由原点O 是PQM的重心,得1212220,033x x y y ++==,即1212,x x y y +=+=, 又P Q ,是椭圆2222:1(0)x y C a b a b+=>>上的点,2222112222221,1x y x y a b a b∴+=+=, 作差可得:()()()()1212121222x x x x y y y y a b -+-+=-,即()()2212122121212b b x x y y x x a y y ⎛⎫⋅ ⎪+-=-=-=-+⎝⎭,即12b a =,∴c e a===, 故选:D2.(2021·河南新乡·高二期末(理))已知椭圆()2222:10x y G a b a b+=>>的右焦点为()F ,过点F 的直线交椭圆于A 、B 两点.若AB的中点坐标为,则G 的方程为( )A .2213214+=x yB .2213820+=x yC .2214830+=x yD .2213618x y +=【答案】D【解析】设点()11,A x y 、()22,B x y ,则22112222222211x y a b x y a b ⎧+=⎪⎪⎨⎪+=⎪⎩,两个等式作差得22221212220x x y y a b --+=, 整理可得2221222212y y b x x a-=--, 设线段AB的中点为M,即2121221212AB OMy y y y b k k x x x x a-+⋅=⋅=--+,另一方面12AB MFk k ==,1OM k =-,所以,()2211122b a -=⨯-=-,所以,22222182c a b a b ⎧=-=⎨=⎩,解得223618a b ⎧=⎨=⎩, 因此,椭圆G 的方程为2213618x y +=.故选:D.3.(2021·江苏)已知椭圆C 的方程为2214x y +=,直线AB 与椭圆C 交于A ,B 点,且线段AB 的中点坐标为1(1,)2,则直线AB 的方程为( )A .3220x y --=B .4230--=x yC .2230x y +-=D .+220x y -=【答案】D【解析】设,A B 两点的坐标分别为1122(,),(,)x y x y ,则有221122221414x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩,两式相减得12121212()()()()04x x x x y y y y -++-+=, ∴121212124()y y x xx x y y -+=--+. 又12122,1x x y y +=+=, ∴121221412y y x x -=-=--⨯,即直线AB 的斜率为12-, ∴直线AB 的方程为11(1)22y x -=--,即+220x y -=. 故选:D.4.(2021·河北辛集中学高二期中)过椭圆216x +24y =1内一点M (2,1)引一条弦,使弦被M 点平分.(1)求此弦所在的直线方程; (2)求此弦长.【答案】(1)x +2y -4=0;【解析】(1)设所求直线方程为y -1=k (x -2).代入椭圆方程并整理,得 (4k 2+1)x 2-8(2k 2-k )x +4(2k -1)2-16=0,① 又设直线与椭圆的交点为A (x 1,y 1),B (x 2,y 2), 则x 1,x 2是方程的两个根,于是x 1+x 2=228(2)41k k k -+.又M 为AB 的中点,∴122x x +=224(2)41k k k -+=2,解得k =-12,直线方程为11(2)2y x -=--,即x +2y -4=0.(2)由(1)将k =-12代入①得,x 2-4x =0, ∴120,4x x ==, ∴|AB |12|x x -=考点六 最值【例6】(1)(2021·浙江高二期末)点P 、Q 分别在圆(222x y +=和椭圆2214x y +=上,则P 、Q 两点间的最大距离是( )A .B .C .D .(2)(2021·江苏高二开学考试)已知椭圆22:194x y C +=的右顶点为2A ,直线:l x m =与椭圆C 相交于A ,B 两点,当2∠AA B 为钝角时,m 的取值范围是( ). A .150,13⎛⎫⎪⎝⎭B .15,313⎛⎫ ⎪⎝⎭C .1515,00,1313⎛⎫⎛⎫-⋃ ⎪ ⎪⎝⎭⎝⎭D .15153,,31313⎛⎫⎛⎫--⋃ ⎪ ⎪⎝⎭⎝⎭【答案】(1)C(2)B【解析】(1)圆(222x y +=的圆心为(C ,半径为r =设点(),Q x y ,则2244x y =-且11y -≤≤,CQ ==,当且仅当3y =-时,等号成立,所以,max max PQ CQ r =+=故选:C.(2)易知33m -<<,x m=代入22194x y +=得y =±AB =由对称性知2AA B 是等腰三角形,AB 是底,设AB 与x 轴交点为M ,如图, 2∠AA B 为钝角,则24AA M π∠>,∴2AM MA >,即3m >-,解得15313m <<.故选:B .【一隅三反】1.(【新东方】高中数学20210429—004【2020】【高二上】)已知P 为椭圆22221x y a b+=上一点,12,F F 是焦点,12F PF ∠取最大值时的余弦值为13,则此椭圆的离心率为_______.【解析】依题意12122,2PF PF a F F c +==,222a b c =+,当12F PF ∠取最大值时,即12cos F PF ∠最小,即12cos F PF ∠的最小值为13.而()222221212121212121224cos 22PF PF PF PF c PF PF F F F PF PF PF PF PF +-⋅-+-∠==⋅⋅222121212424212a PF PF c b PF PF PF PF -⋅-==-⋅⋅, 而()2122124PF PF PF PF a +⋅≤=,当且仅当12PF PF a ==时等号成立,故21222cos 1b F PF a∠≥-,当且仅当12PF PF a ==时等号成立,所以12cos F PF ∠的最小值为222113b a -=,即2223ba =,故c e a ===2.(2021·重庆西南大学附中高二期末)已知椭圆()2222:10x y C a b a b+=>>的左、右焦点为1F 、2F ,离心率为12,过2F 的直线l 交C于A 、B 两点,若1AF B △的周长为8.(1)求椭圆C 的标准方程;(2)若椭圆上存在两点关于直线4y x m =+对称,求m 的取值范围.【答案】(1)22143x y +=;(2)m <<【解析】(1)1AF B △周长为8,即48a =,2a ∴=.又因为12e =,1c ∴=,b =椭圆方程22143x y C +=:,(2)设椭圆上两点11(,)A x y ,22(,)B x y 关于4y x m =+对称,则AB 的方程为14y x t =-+,由2214143y x t x y ⎧=-+⎪⎪⎨⎪+=⎪⎩消去y 有:2213816480x tx t -+-= 由22(8)413(1648)0.t t ∆=--⨯⨯->得213,4t <① 又1212128124,()213413t tx x y y x x t +=+=-++=因为AB 的中点在直线4y x m =+上,所以1212422y y x x m ++=+,即12441313t tm =⨯+ 所以1340m t +=②,由①②得:2413m <,即m <<。
求曲线的方程(45分钟 100分)一、选择题(每小题6分,共30分)1.动点P到点(-1,2)的距离是3,则动点P的轨迹方程为( )A.(x+1)2+(y-2)2=9B.(x-1)2+(y+2)2=9C.(x+1)2+(y-2)2=3D.(x-1)2+(y+2)2=32.已知点P是直线2x-y+3=0上的一个动点,定点M(-1,2),Q是线段PM延长线上的一点,且|PM|=|MQ|,则Q点的轨迹方程是( )A.2x+y+1=0B.2x-y-5=0C.2x-y-1=0D.2x-y+5=03.等腰三角形ABC底边两端点是A(-错误!未找到引用源。
,0),B(错误!未找到引用源。
,0),顶点C的轨迹是( )A.一条直线B.一条直线去掉一点C.一个点D.两个点4.已知两定点A(-2,0),B(1,0),如果动点P满足条件|PA|=2|PB|,则动点P的轨迹所围成的图形的面积等于( )A.9πB.8πC.4πD.π5.在平面直角坐标系中,已知A(3,1),B(-1,3),若点C满足错误!未找到引用源。
=α错误!未找到引用源。
+β错误!未找到引用源。
,其中α,β∈R,且α+β=1,O 为坐标原点,则点C的轨迹为( )A.射线B.直线C.圆D.线段二、填空题(每小题8分,共24分)6.直角坐标平面xOy中,若定点A(1,2)与动点P(x,y)满足错误!未找到引用源。
·错误!未找到引用源。
=4,则点P的轨迹方程是.7.(2013·珠海高二检测)动点P与平面上两定点A(-错误!未找到引用源。
,0),B(错误!未找到引用源。
,0)连线的斜率的积为定值-错误!未找到引用源。
,则动点P的轨迹方程为.8.(2013·揭阳高二检测)已知直线l:错误!未找到引用源。
+错误!未找到引用源。
=1,M是直线l上的一个动点,过点M作x轴和y轴的垂线,垂足分别为A,B,点P 是线段AB的靠近点A的一个三等分点,点P的轨迹方程为.三、解答题(9题,10题14分,11题18分)9.等腰三角形的顶点是A(4,2),底边一个端点是B(3,5),求另一个顶点C的轨迹方程,试说明它的轨迹是什么?10.已知A,B分别是直线y=错误!未找到引用源。
x和y=-错误!未找到引用源。
x 上的两个动点,线段AB的长为2错误!未找到引用源。
,P是AB的中点.求动点P 的轨迹C的方程.11.(能力挑战题)在边长为1的正方形ABCD中,边AB,BC上分别有一个动点Q,R,且|BQ|=|CR|.求直线AR与DQ的交点P的轨迹方程.答案解析1.【解析】选A.由条件可知,点P的轨迹是以(-1,2)为圆心,以3为半径的圆,方程为(x+1)2+(y-2)2=9.2.【解析】选D.设Q(x,y),则P为(-2-x,4-y),代入2x-y+3=0,得2x-y+5=0. 【举一反三】若题中直线方程和点的坐标不变,其他条件改为“Q是PM的中点”,则结论如何?【解析】设Q(x,y),P(x0,y0),则x=错误!未找到引用源。
,y=错误!未找到引用源。
, ∴x0=2x+1,y0=2y-2.∵点P在直线2x-y+3=0上,∴2(2x+1)-(2y-2)+3=0.整理得4x-2y+7=0,即点Q的轨迹方程为4x-2y+7=0.3.【解题指南】利用等腰三角形的性质知|CA|=|CB|.【解析】选B.∵△ABC为等腰三角形,∴|CA|=|CB|,∴点C的轨迹应是AB的中垂线,又∵C为AB中点时不能构成三角形,∴C的轨迹应是一条直线去掉一点.4.【解析】选C.设P(x,y),由|PA|=2|PB|,知错误!未找到引用源。
=2错误!未找到引用源。
.化简整理,得(x-2)2+y2=4,所以动点P的轨迹是圆心为(2,0),半径为2的圆,此圆的面积为4π.5.【解题指南】利用向量的坐标运算,建立方程组,把α,β用动点坐标(x,y)表示后代入α+β=1,整理即得点C的轨迹.【解析】选B.设C(x,y).∵错误!未找到引用源。
=α错误!未找到引用源。
+β错误!未找到引用源。
,∴(x,y)=α(3,1)+β(-1,3),∴(x,y)=(3α-β,α+3β),∴错误!未找到引用源。
∴错误!未找到引用源。
∵α+β=1,∴错误!未找到引用源。
+错误!未找到引用源。
=1,即x+2y-5=0,∴点C的轨迹是一条直线.6.【解析】由错误!未找到引用源。
·错误!未找到引用源。
=4知,x+2y=4⇒x+2y-4=0,∴P点的轨迹方程是x+2y-4=0.答案:x+2y-4=07.【解析】设P(x,y),由题意知,x≠±错误!未找到引用源。
,k AP=错误!未找到引用源。
,k BP=错误!未找到引用源。
,由条件知k AP·k BP=-错误!未找到引用源。
,∴错误!未找到引用源。
×错误!未找到引用源。
=-错误!未找到引用源。
,整理得x2+2y2-2=0(x≠±错误!未找到引用源。
).答案:x2+2y2-2=0(x≠±错误!未找到引用源。
)【误区警示】解答本题时容易漏掉“x≠±错误!未找到引用源。
”这个条件.这是因为忽略了直线斜率的存在性所导致.所以做题时理解要到位,避免因隐含条件未挖掘出来而导致错误发生.【变式备选】与点A(-1,0)和点B(1,0)连线的斜率之和为-1的动点P的轨迹方程是.【解析】设P(x,y),则错误!未找到引用源。
+错误!未找到引用源。
=-1,整理得x2+2xy=1(x≠±1).答案:x2+2xy=1(x≠±1)8.【解题指南】利用相关点法.【解析】如图,设P(x,y),∵P是线段AB上靠近A的一个三等分点,∴A(错误!未找到引用源。
x,0),B(0,3y),也即M(错误!未找到引用源。
x,3y).又∵M在直线错误!未找到引用源。
+错误!未找到引用源。
=1上,∴错误!未找到引用源。
×错误!未找到引用源。
x+错误!未找到引用源。
×3y=1, 整理得3x+8y-8=0,这就是点P的轨迹方程.答案:3x+8y-8=09.【解析】设另一端点C的坐标为(x,y),依题意,得|AC|=|AB|,由两点间距离公式,得错误!未找到引用源。
=错误!未找到引用源。
.化简,得(x-4)2+(y-2)2=10. 因为A,B,C三点不共线,即点B,C不能重合,且B,C不能为☉A的一直径的两个端点.因为B,C不重合,所以点C的坐标不能为(3,5).又因为点B,C不能为☉A的一直径的两个端点,由错误!未找到引用源。
=4,错误!未找到引用源。
=2,得x=5,y=-1.点C的坐标不能为(5,-1).故点C的轨迹方程为(x-4)2+(y-2)2=10(点(3,5)和(5,-1)除外).点C的轨迹是以点A(4,2)为圆心,以错误!未找到引用源。
为半径的圆除去(3,5)和(5,-1)两点.【一题多解】∵△ABC为等腰三角形,∴|AB|=|AC|,又∵A(4,2),B(3,5)且|AB|=错误!未找到引用源。
,∴|CA|=错误!未找到引用源。
,即C的轨迹是以A为圆心,以错误!未找到引用源。
为半径的圆,∴方程为(x-4)2+(y-2)2=10.又A,B,C不能共线,故轨迹方程为(x-4)2+(y-2)2=10(x≠3,5),其轨迹是以A(4,2)为圆心,以错误!未找到引用源。
为半径的圆除去(3,5)和(5,-1)两点.【拓展提升】轨迹方程中的“补点”与“去点”曲线的方程、方程的曲线的定义中要满足以下两点:(1)曲线上点的坐标都是方程的解.(2)以方程的解为坐标的点都在曲线上.求动点轨迹方程要同时满足这两个条件,因此就要学会适时“补点”与“去点”:“补点”是指有时求轨迹方程时,会漏掉曲线上的部分点或个别点,应根据条件作出补充.“去点”是求轨迹方程时,有些方程整理、变形会产生不合题意的点,应去掉.10.【解析】设P(x,y),A(x1,y1),B(x2,y2).∵P是线段AB的中点,∴错误!未找到引用源。
∵A,B分别是直线y=错误!未找到引用源。
x和y=-错误!未找到引用源。
x上的点,∴y1=错误!未找到引用源。
x1,y2=-错误!未找到引用源。
x2,∴错误!未找到引用源。
又∵|AB|=2错误!未找到引用源。
,∴(x1-x2)2+(y1-y2)2=12.∴12y2+错误!未找到引用源。
x2=12,∴动点P的轨迹C的方程为错误!未找到引用源。
+y2=1.11.【解题指南】解答本题应首先建立适当的平面直角坐标系,分别设出动点P,Q,R的坐标,采用平面几何的知识构造等式,消去参数变量即可以得到P的轨迹方程.【解析】分别以AB,AD边所在的直线为x轴,y轴建立直角坐标系.如图所示,则点A(0,0),B(1,0),C(1,1),D(0,1),设动点P(x,y).设|AQ|=t(0≤t≤1),则Q(t,0),由|BQ|=|CR|知|AQ|=|BR|,所以R(1,t).当t≠0时,直线AR方程:y=tx ①直线DQ方程为错误!未找到引用源。
+y=1 ②由②式得1-y=错误!未找到引用源。
③①×③得y(1-y)=tx·错误!未找到引用源。
,化简得x2+y2-y=0.当t=0时,点P与原点重合,坐标(0,0)也满足上述方程.故点P的轨迹方程为x2+y2-y=0(0≤x≤错误!未找到引用源。
,0≤y≤错误!未找到引用源。
).关闭Word文档返回原板块。