经典:1.5-经济学中的几个常用函数
- 格式:ppt
- 大小:454.00 KB
- 文档页数:24


第五节经济学中常用函数教学目的:了解经济中常用函数的概念。
结合经济现象理解盂求函数、供给函数、成本函数、收入函数、利润函数的概念.教学重点:结合经济现象理解需求函数、供给函数、成本函数、收入函数、利润函数的概念. 教学难点:经济现象的理解.教学内容:一.需求函数与价格函数一种商品的需求量0与该种商品的价格“密切相关,如杲不考虑其它因素的影响,则商品的蛊求量Q可看作价格P的函数。
称为需求函数,记作Q = /(卫)。
评注:(1)一般地,当商品的价格增加时,商品的需求量将会减少,因此,需求函数Q = f(p) 是价格〃的减少函数。
如图(2)在企业管理和经济中常见的需求函数有线性需求函数:Q = a-bp,其中/?>0, a>0均为常数;二次需求函数:Q = a_bp_cp2,其中^>0, b>0, c>Q均为常数;指数需求函数:Q = A严,其中A>0, b>0均为常数;基函数需求函数:Q = AP-a ,其+ A>0, G>0均为常数。
二、供给函数“供给量”是在一定价格水平下,生产者愿意11!售并且有可供出售的商品量,如果不考虑价格以外的其它因素,则商品的供给量S是价格p的函数,记作S = S(p)0评注:(1) 一般地,供给量随价格的上升而增大,因此,供给函数S = S(p)是价格〃的单调增加函数。
(2)常见的供给函数有线性函数,二次函数,幕函数,指数函数等。
(3)如果市场上某种商品的需求量与供求量相等,则该商品市场处于平衡状态,这时的商品价格刁就是供、需平衡的价格,叫做均衡价格。
◎就是均衡数量。
2 4例1 :已知某商品的供给函数是S=-p-4,需求函数是Q = 50--p,试求该漓品处于市3 3场平衡状态下的均衡价格和均衡数量。
解: 令S=Q,解方程组< e=|/^-44 Q= 50--p得均衡价格p = 27,均衡数量e = 14o2 4说明供给函数S=-p-4与需求函数2 = 50-一0的图彖交点的横坐标就是市场均衡价格。

一、常用的经济函数1、总成本函数、总收入函数、总利润函数总成本函数是指在一定时期内,生产产品时所消耗的生产费用之总和。
常用C 表示,可以看作是产量x 的函数,记作()C C x =总成本包括固定成本和可变成本两部分,其中固定成本F 指在一定时期内不随产量变动而支出的费用,如厂房、设备的固定费用和管理费用等;可变成本V 是指随产品产量变动而变动的支出费用,如税收、原材料、电力燃料等。
固定成本和可变成本是相对于某一过程而言的。
在短期生产中,固定成本是不变的,可变成本是产量x 的函数,所以()()C x F V x =+,在长期生产中,支出都是可变成本,此时0F =。
实际应用中,产量x 为正数,所以总成本函数是产量x 的单调增加函数,常用以下初等函数来表示:(1)线性函数 C a bx =+, 其中0b >为常数.(2)二次函数 2C a bx cx =++,其中0,0c b ><为常数.(3)指数函数 ax C be =, 其中,0a b >为常数.平均成本:每个单位产品的成本,即 ()C x C x=. 总收益函数是指生产者出售一定产品数量(x )所得到的全部收入,常用R 表示,即 ()R R x =其中x 为销售量. 显然,0(0)0Q R R ===,即未出售商品时,总收益为0.若已知需求函数()Q Q p =,则总收益的为1()()R R Q P Q Q p Q -==⋅=⋅ 平均收益:()R x R x=,若单位产品的销售价格为p ,则R p x =⋅,且R p =. 总利润函数是指生产中获得的纯收入,为总收益与总成本之差,常用L 表示,即 ()()()L x R x C x =-例 某工厂生产某产品,每日最多生产100个单位。
日固定成本为130元,生产每一个单位产品的可变成本为6元,求该厂每日的总成本函数及平均单位成本函数.解 设每日的总成本函数为C 及平均单位成本函数为C ,因为总成本为固定成本与可变成本之和,据题意有()1306(0100)130()6(0100)C C x xx C C x x x ==+≤≤==+<≤例 设某商店以每件a 元的价格出售商品,若顾客一次购买50件以上,则超出部分每件优惠10%,试将一次成交的销售收入R 表示为销售量x 的函数。



03 第三节常用经济函数常用经济函数是经济学中用来描述经济变量之间关系的数学模型。
这些函数可以用来分析经济发展、预测经济趋势、制定经济政策等。
下面介绍几种常用的经济函数及其含义。
一、消费函数消费函数是指消费者在某一时期内消费的商品或服务的数量与收入之间的函数关系。
通常表示为C=f(Y),其中C表示消费,Y表示收入。
消费函数曲线是一条向右上方倾斜的曲线,表示随着收入的增加,消费也会增加。
但在达到一定收入后,消费增长速度会逐渐减缓,甚至出现零增长或负增长。
二、投资函数投资函数是指企业在某一时期内进行的投资数量与资本存量之间的函数关系。
通常表示为I=f(K),其中I表示投资,K表示资本存量。
投资函数曲线是一条向右上方倾斜的曲线,表示随着资本存量的增加,投资也会增加。
但在达到一定资本存量后,投资增长速度会逐渐减缓,甚至出现零增长或负增长。
三、总供给函数总供给函数是指某一时期内,企业愿意且有能力提供的商品和服务的总量与价格水平之间的函数关系。
通常表示为Y=f(P),其中Y表示总供给,P表示价格水平。
总供给函数曲线是一条向右下方倾斜的曲线,表示随着价格水平的提高,总供给会减少。
但在达到一定价格水平后,总供给增长速度会逐渐减缓,甚至出现零增长或负增长。
四、总需求函数总需求函数是指某一时期内,消费者愿意且有能力购买的商品和服务的总量与价格水平之间的函数关系。
通常表示为Y=f(P),其中Y表示总需求,P表示价格水平。
总需求函数曲线是一条向右下方倾斜的曲线,表示随着价格水平的提高,总需求会减少。
但在达到一定价格水平后,总需求增长速度会逐渐减缓,甚至出现零增长或负增长。
五、菲利普斯曲线菲利普斯曲线是指通货膨胀率与失业率之间的函数关系。
通常表示为π=f(u),其中π表示通货膨胀率,u表示失业率。
菲利普斯曲线是一条向右下方倾斜的曲线,表示随着失业率的降低,通货膨胀率会上升。
但在达到一定失业率后,通货膨胀率增长速度会逐渐减缓,甚至出现零增长或负增长。



微分学在经济中的应用§1 经济学中的常用函数一、需求函数消费者对商品有需求才是使商品在市场上得以流通的源动力。
这种源动力的核心主要有两个:一是购买商品的愿望,二是有购买商品的能力。
影响需求的因素有人口、收入、财产、价格和爱好等等。
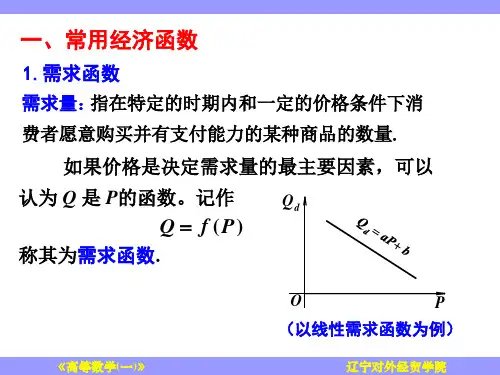
忽略其他因素,只考虑与价格的关系就得到了需求函数)(P f D =, (1-1)需求函数通常是单调下降函数(如图1-1所示)。
产生下降的原因有两个:一是收入效应,二是替代效应。
注:需求量与价格有时也是按上升方式变化的。
例如,古画、文物等珍品价格越高,越被人门人为是珍品,因而需求量就越大。
下列函数可作为需求函数:线性函数 )0,0(>>-=b a bP a D , 二次函数 )0,0,0(2>≥>--=c b a cP bP a D ,指数函数 )0,0(>>=-b A Ae D bP ,幂 函 数 )0,0(>>=-ααA AP D 。
二、供给函数供给是生产者在一定时间内,在一定的价格水平下对某种商品愿意并能够出售的数量,需求是对消费者而言,供给是对生产者而言。
所以,供给和需求是相对的概念,这就是 说产生了和生产者之间的一对永恒的矛盾。
产生供给的条件有个,一是有出售商品的愿望,二是有供给商品的能力。
影响供给的因素有生产成本、技术成本、劳动力及价格等等。
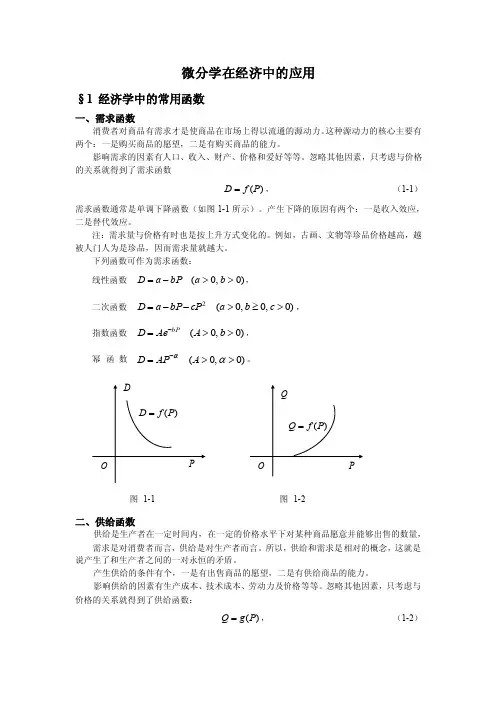
忽略其他因素,只考虑与 价格的关系就得到了供给函数:)(P g Q =, (1-2)供给函数通常是单调上升函数(如图1-2所示)。
注:供给量与价格有时也是按下降方式变化的。
例如,古画、文物等珍品价格上升后,人们就会把存货拿出来出售,供给量增加,当价格上升到一定程度后,人们以为它更珍贵,就不会再提供给市场。
因而价格上涨供给量反而减少。
经常采用的供给函数有如下形式:线性函数 )0,0(>>+-=d c dP c Q , 二次函数 )0,0,0(2>≥>++-=c b a cP bP a Q ,指数函数 ),0,0,0(A B k B A B Ae Q kP >>>>-=, 幂 函 数 )0,0,0(>>>-=-ααB A BAP D 。
第五节第五节 经济学中的常用函数经济学中的常用函数第一章一、需求函数二、供给函数三、总成本函数、总收益函数总利润函数四、库存函数一、需求函数如果价格是决定需求量的最主要因素,可以认为 Q 是 P 的函数。
记作)(P f Q =则 f 称为需求函数.需求的含义:消费者在某一特定的时期内,在一定的价格条件下对某种商品具有购买力的需要.,bP a Q −=线性需求函数:常见的需求函数:2cPbP a Q −−=二次曲线需求函数:( 其中 a , b , c , A > 0 )0,≥b a 幂函数:00A Q kP ,A ,k −=>>其中bP Q Ae−=指数需求函数:例 1设某商品的需求函数为)0,(>+−=b a b aP Q .00时的价格时的需求量和讨论==Q P 解,0b Q P ==时它表示价格为零时的需求量为 b ,称为饱和需求量;,0ab P Q ==时它表示价格为,时a b 无人愿意购买此商品.二、供给函数如果价格是决定供给量的最主要因素,可以认为 Q 是 P 的函数。
记作)(P G Q =则 G 称为供给函数.供给的含义:在某一时间内,在一定的价格条件下,生产者愿意并且能够售出的商品.一般地,供给函数可以用以下简单函数近似代替:线性函数:0,,>−=b a b aP Q 其中幂函数:指数函数:0,0,>>=k A kP Q A 其中0,0,>>=b A ae Q bP 其中例2 设产品的需求函数为供给函数为 ()s s Q Q P = 在同一个坐标系中作出需求曲线D 和供给曲线S(如图),如果曲线D和曲线S 的交点00(,)P Q (或记为(,)e e P Q )就是供需平衡点,而P 或e P 称为均衡价格,0Q 或e Q 称为均衡数量. 当0P P ¹时,市场力量会推动P 趋向0P 。
寻求0P 是金融经济学的主要问题之一。