第三章 群速度色散
- 格式:ppt
- 大小:933.50 KB
- 文档页数:4
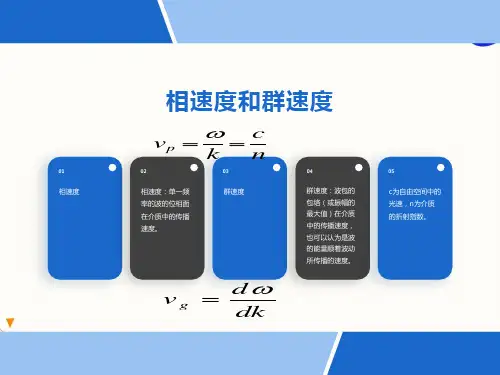



正常色散介质中群速度与相速度的相对关系
光的传播速度在不同介质中会发生改变,这种现象被称为光在介质中的折射,其中光传播的速度,在正常色散介质中群速度与相速度有一定的关系。
在正常色散介质中,介质中的光速度与频率之间呈现线性关系,也就是说在相同介质中,频率越高,光速度也越高。
根据自然的光学原理,光在介质中的传输速度是由群速度和相速度组成的。
群速度和相速度在正常色散介质中是有一定的关系的。
群速度表示的是光信号在介质中整体传播的速度,而相速度则是光的电场和磁场在介质中传播的速度。
在正常的色散介质中,群速度通常要大于相速度,也就是说,在介质中传输光信号的速度整体上要快于电场和磁场的传输速度。
这可以通过正常色散介质中材料的复合折射率来解释。
光的相位速度与群速度之间的差异是由折射率的频率依赖性造成的。
在正常色散材料中,较高频率的光会快速折射并且离开表面,而较低频率的光则会被材料捕获和重新释放,从而形成相对较慢的群速度。
在光纤通讯系统中,光速度和光的传输性能至关重要。
对于正常色散介质,光信号传播的快慢由材料的折射率决定,因此了解群速度和相速度之间的相对关系对于光纤通讯系统的设计和优化非常重要。
总之,在正常色散介质中,群速度和相速度之间存在一定程度的相对关系。
群速度比相速度更高,这是由于复合折射率的频率依赖性造成的。
这种相对关系在光学系统的优化中非常重要,因为光速和光的传输性能通常是光学系统设计和优化的关键因素之一。



一波包维基百科,自由的百科全书跳转到:导航搜索汉汉▼一个正在传播中,非色散的波包。
在物理学里,一个波包是一群平面波在空间的一个小区域内的叠和。
这些平面波都有不同的波数、波长、相位、波幅,都分别地建设性干涉于空间的一个小区域。
依据不同的演化方程,在传播的时候,波包的包络线(素描波包轮廓的曲线)可能会保持不变(没有色散,如图右),或者包络线会改变(有色散)。
在量子力学里,波包有个特别的意思:波包被铨释为粒子的概率波,而在任何位置,任何时间,概率波波幅的绝对值的平方,就是在那个位置,那个时间,找到粒子的概率密度。
在这方面,它的功能类似波函数。
类似在经典力学里的哈密顿表述,在量子力学里,应用薛定谔方程,我们可以追溯一个量子系统随着时间的演化。
波包是薛定谔方程的数学解答。
在某些区域内,波包所囊括的面积的平方,可以铨释为找到粒子处于那区域的概率密度。
采用坐标表现,波包的位置给出了粒子的位置。
波包越狭窄,粒子的位置越明确,而动量的分布越扩散。
这位置的明确性和动量的明确性,两者之间的轻重取舍是海森堡不确定原理的一个标准例子。
目录隐藏1 背景 2 波包计算范例 3 参考文献 4 参阅编辑背景早在十七世纪,牛顿就已创始地建议光的粒子观:光的移动是以离散的束包形式,称为光微粒。
可是,在许多实验中,光表现出了波动行为。
这使科学家们渐渐地倾向于波动观,认为光是一种传播于介质中的波动。
特别著名的一个实验是英国科学家托马斯杨在1801 年设计与研究成功的双缝实验。
这实验试图解答光到底是粒子还是波动的问题。
从这实验观测到的干涉图案给予光的粒子观一个致命的打击。
大多数的科学家从此接受了光的波动观。
在20 世纪初期,科学家开始发现经典力学内在的许多严重的问题,许多实验的结果,都无法用经典理论来解释。
一直到1930 年代,光的粒子性,才真正地被物理学家广泛接纳。
在这段时间,量子力学如火如荼的发展,造成了许多理论上的突破。
许多深奥的实验结果,都能够得到圆满合理的解释。



光纤色散在光纤中传输的光信号(脉冲)的不同频率成份或不同的模式分量以不同的速度传播,到达一定距离后必然产生信号失真(脉冲展宽),这种现象称为光纤的色散或弥散。
光纤中传输的光信号具有一定的频谱宽度,也就是说光信号具有许多不同的频率成分。
同时,在多模光纤中,光信号还可能由若干个模式叠加而成,也就是说上述每一个频率成份还可能由若干个模式分量来构成。
光纤的色散主要有材料色散、波导色散、偏振模色散和模间色散四种。
其中,模间色散是多模光纤所特有的。
这四种色散作用还相互影响,由于材料折射率n是波长λ(或频率w)的非线性函数,d2n/d2λ≠0,于是不同频率的光波传输的群速度不同,所导致的色散成为材料色散。
由于导引模的传播常数β是波长λ(或频率w)的非线性函数,使得该导引模的群速度随着光波长的变化而变化,所产生的色散成为波导色散(或结构色散)。
偏振模色散指光纤中偏振色散,简称PMD(polarization modedispersion),它是由于实际的光纤中基模含有两个相互垂直的偏振模,沿光纤传播过程中,由于光纤难免受到外部的作用,如温度和压力等因素变化或扰动,使得两模式发生耦合,并且它们的传播速度也不尽相同,从而导致光脉冲展宽,引起信号失真。
不同的导引模的群速度不同引起的色散成为模间色散,模间色散只存在与多模光纤中。
色散限制了光纤的带宽—距离乘积值。
色散越大,光纤中的带宽—距离乘积越小,在传输距离一定(距离由光纤衰减确定)时,带宽就越小,带宽的大小决定传输信息容量的大小。
光纤色散可以使脉冲展宽,而导致误码。
这是在通信网中必须避免的一个问题,也是长距离传输系统中需要解决的一个课题。
一般来说,光纤色散包括材料色散和波导结构色散两部分,材料色散取决于制造光纤的二氧化硅母料和掺杂剂的分散性,而波导色散通常是一种模式的有效折射率随波长而改变的倾向。
材料色散与波导色散都与波长有关,所以又统称为波长色散。
材料色散:是由光纤材料自身特性造成的。

群速度波的群速度,或简称群速,是指波的包络传播的速度。
实际上就是波实际前进的速度。
形象一点说,你拿电钻在一个很坚固的墙上钻洞,你会觉得电钻的钻头的螺纹在旋转时似乎以高速前进,但这只是你的错觉,因为你看到的是螺纹的“相速度”,虽然很快,但是你的电钻却很慢很慢地向墙内推进,也就是说电钻的总的向前推进的速度就是“群速度”。
如果墙壁很硬,你的电钻根本就钻不进去,电钻向前推进的速度为“0”,但是你从电钻的螺纹上看却总是觉得电钻是不断钻进去的。
实用系统的信号总是由许多频率分量组成,在色散介质中,各单色分量将以不同的相速传播,因此要确定信号在色散介质中的传播速度就发生困难,为此引入群速的概念,它描述信号的能量传播速度。
对于电离层(地球大气由下往上分为对流层、平流层、电离层、磁层),因折射指数n〈1,所以无线电波的相速度大于光速c,这一结论和相对论的理论并不矛盾,因为相速度只代表相位变化的快慢,并不代表电磁波能量的真正传播速度。
群速则总小于自由空间的光速c。
群速度:许多不同频率的正弦电磁波的合成信号在介质中传播的速度。
不同频率正弦波的振幅和相位不同,在色散介质中,相速不同,故在不同的空间位置上的合成信号形状会发生变化。
群速是一个代表能量的传播速度。
注意到波的相速度不必然与波的群速度相同;群速度代表的是“振幅变化”(或说波包)的传递速度。
电磁辐射的相速度可能在一些特定情况下(例如:出现异常色散的情形)超过真空中光速,但这不表示任何超光速的信息或者是能量移转。
物理学家阿诺·索末菲与里昂·布里于因(Léon Brillouin)对此皆有理论性描述。
波的相速度或相位速度,或简称相速,是指电磁波相位传播[1]的速度。
通俗地讲,就是电磁波形状向前变化的速度。
在波导中,相速度往往比群速度要大。
无线电波在介质中传播时,如果该介质的介电常数ε与频率无关,波的传播速度也与频率无关,这种介质称为非色散介质;与此相反,如果介质的ε或传播速度v与频率有关,则称为色散介质[1]。
色散关系公式推导首先,我们需要了解两个概念:相速度和群速度。
相速度是指在介质中传播的波最快的速度,而群速度是指一组波的平均速度。
假设在介质中传播的波的频率为ω,波长为λ,相速度为v,群速度为vg。
根据波动方程可知:v = ω / k其中,k为波数,k = 2π / λ。
因此,v = ωλ / 2π接下来,我们考虑介质中的折射率n与波长λ之间的关系。
根据光的波动理论,折射率与介质中电场的振幅成正比,即n = f(E)其中,E为电场的振幅。
根据经典电动力学理论,电场振幅与光波的振幅成正比,即E = Acos(ωt)其中,A为振幅。
因此,n = f(A)将波长λ表示为n和角频率ω的函数,可得λ = f(n, ω)对λ关于ω求导,得到dλ / dω = (f / ω) / (f / n)根据著名的几何光学理论,n与λ之间的关系可以用折射率的色散函数来表示,即n = f(λ)此时,色散函数的导数为dn / dλ = (f / λ)因此,dλ / dω = 1 / (c * dn / dλ)其中,c为真空中光速。
将折射率的色散函数展开,得到n(λ) = A + B / λ^2 + C / λ^4 + ...其中,A、B、C等为常数。
因此,dn / dλ = -2B / λ^3 - 4C / λ^5 - ...代入色散关系公式中,得到v = c / n = c / [A + B / λ^2 + C / λ^4 + ...] 群速度vg可以通过色散函数的二阶导数求得,即vg = dω / dk = dω / (dλ / dk) = c / [n + λ * dn / d λ] = c / [n + λ * (d^2n / dλ^2)]综上所述,色散关系公式的推导涉及相速度、群速度、折射率的色散函数以及偏微分等知识。
掌握这些关键概念和推导方法,有助于更深入地理解光的传播规律。
gvd计算公式
GVD(群速度色散)是一个物理概念,它可以用于描述波导中电磁波的传播特性。
根据不同的应用领域和具体波导结构,GVD的计算公式会有所不同。
例如,在计算Ag/PP介质空芯波导的色散系数时,可以使用公式:
$\beta_{2} = \frac{v \delta^{2} n_{eff}}{\delta v^{2}} + \frac{2 \delta
n_{eg}}{\delta v}$
其中,$n_{eff}$为实验有效折射率(由THz-TDS实验数据获得),v为太
赫兹频率,$\delta v$表示频率变化量。
通过这个公式,可以计算出波导在该范围内的色散系数,如-4\~ ps/GHz/cm。
请注意,以上公式仅供参考,如需更准确的信息,建议查阅相关领域的文献或咨询该领域的专家。