第一章晶体结构习题
- 格式:pdf
- 大小:834.00 KB
- 文档页数:12

第一章 晶体的结构习题一、填空题1.固体一般分为_____ _____ _____2.晶体的三大特征是_____ _____ _____3._____是晶格中最小的重复单元,_____既反映晶格的周期性又反映晶格的对称性。
4._____和_____均是表示晶体原子排列紧密程度。
5.独立的对称操作有______二、证明题1.试证明体心立方格子和面心立方格子互为正倒格子。
2.证明倒格子矢量112233G h b h b h b =++ 垂直于密勒指数为123()h h h 的晶面系。
3.对于简方晶格,证明密勒单立指数为(,,)h k l 的晶面系,面间距d 满足:22222()d a h k l =++,其中a 为立方边长;并说明面指数简单的晶面,其面密度较大,容易解理。
4.证明不存在5度旋转对称轴。
5.证明正格矢和倒格矢之间的关系式为:()为整数m m R G π2=⋅三、计算题1.已知某种晶体固体物理学原胞基矢为(1)求原胞体积。
(2)求倒格子基矢。
(3)求第一布里渊区体积。
2.一晶体原胞基矢大小m a 10104-⨯=,m b 10106-⨯=,m c 10108-⨯=,基矢间夹角90=α, 90=β, 120=γ。
试求:(1)倒格子基矢的大小; (2)正、倒格子原胞的体积; (3) 正格子(210)晶面族的面间距。
j 2a 3i 2a a 1+=j 2a 3i 2a -a 2+=k c a 3=3.如图1.所示,试求: (1) 晶列ED ,FD 和OF 的晶列指数;(2) 晶面AGK ,FGIH 和MNLK 的密勒指数;(3) 画出晶面(120),(131)。
a 2xy zA B D C G F E OIH y x Aa 2K O GLNM z图1.4.矢量a ,b ,c 构成简单正交系。
求:晶面族)(hkl 的面间距。
5.设有一简单格子,它的基矢分别为i a 31=,j a 32=,)(5.13k j i a ++=。



半导体物理习题 -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN附: 半导体物理习题第一章 晶体结构1. 指出下述各种结构是不是布拉伐格子。
如果是,请给出三个原基矢量;如果不是,请找出相应的布拉伐格子和尽可能小的基元。
(1) 底心立方(在立方单胞水平表面的中心有附加点的简立方); (2) 侧面心立方(在立方单胞垂直表面的中心有附加点的简立方); (3) 边心立方(在最近邻连线的中点有附加点的简立方)。
2. 证明体心立方格子和面心立方格子互为正、倒格子。
3. 在如图1所示的二维布拉伐格子中,以格点O 为原点,任意选取两组原基矢量,写出格点A 和B 的晶格矢量A R 和B R 。
4. 以基矢量为坐标轴(以晶格常数a 为度量单位,如图2),在闪锌矿结构的一个立方单胞中,写出各原子的坐标。
5.石墨有许多原子层,每层是由类似于蜂巢的六角形原子环组成,使每个原子有距离为a的三个近邻原子。
试证明在最小的晶胞中有两个原子,并画出正格子和倒格子。
第二章晶格振动和晶格缺陷1.质量为m和M的两种原子组成如图3所示的一维复式格子。
假设相邻原子间的弹性力常数都是β,试求出振动频谱。
2.设有一个一维原子链,原子质量均为m,其平衡位置如图4所示。
如果只考虑相邻原子间的相互作用,试在简谐近似下,求出振动频率ω与波矢q之间的函数关系。
3.若把聚乙烯链—CH=CH—CH=CH—看作是具有全同质量m、但力常数是以1β,2β交替变换的一维链,链的重复距离为a,试证明该一维链振动的特征频率为}])(2sin41[1{2/1221221212ββββββω+-±+=qam并画出色散曲线。
第三章 半导体中的电子状态1. 设晶格常数为a 的一维晶格,导带极小值附近的能量)(k E c 为mk k m k k E c 21222)(3)(-+=(3.1)价带极大值附近的能量)(k E v 为mk m k k E v 2221236)( -=(3.2)式中m 为电子质量,14.3,/1==a a k πÅ。

第一章晶体的结构简单回答下面的问题:1 a原胞与单胞有什么不同?何谓布拉菲格子?何谓倒格子?以一结点为顶点,以三个不同方向的周期为边长的平行六面体可作为晶格的一个重复单元.体积最小的重复单元,称为原胞或固体物理学原胞.它能反映晶格的周期性.原胞的选取不是惟一的,但它们的体积都相等.为了同时反映晶体对称的特征,结晶学上所取的重复单元,体积不一定最小,结点不仅在顶角上,还可以是体心或面心.这种重复单元称作晶胞、惯用晶胞或布喇菲原胞.晶体内部结构可以看成是由一些相同的点子在空间作规则的周期性无限分布,这些点子的总体称为布喇菲点阵。
布拉菲格子:由基元代表点(格点)在空间中的周期性排列所形成的晶格。
倒格子*(Reciprocal Lattice,Reciprocal有相互转换的含意)已知有正格子基矢,定义倒格矢基矢为:;; .其中为正格子原胞体积。
由平移操作所产生的格点叫倒格点:为倒格矢;倒格点的总体叫倒格子,叫一组倒格基矢。
由与所决定的点阵为互为倒格子b晶体的宏观对称性可以概括为多少点群?晶体中有几种基本对称素?多少个晶系?这些晶系分别包括哪些布拉菲格子?晶体学中共有32种点群八种基本对称素C1 (1)、C2 (2)、C3 (3)、C4 (4)、C6 (6)、Ci (i)、CS (m)和 S4七大晶系十四种布拉菲格子c什么是晶体、准晶体和非晶体?晶体:组成固体的原子(或离子)在微观上的排列具有长程周期性非晶体:组成固体的粒子只有短程序(在近邻或次近邻原子间的键合:如配位数、键长和键角等具有一定的规律性),无长程周期性准晶:有长程的取向序,沿取向序的对称轴方向有准周期性,但无长程周期性2试推导面心和体心立方点阵的x射线衍射的系统消光规律3多晶体与单晶体的x射线衍射图有什么区别?多晶(衍射环对应一个晶面);单晶(衍射点对应一个晶面)4a)何谓晶体、准晶体及非晶体?它们的x光或电子衍射有何区别?黄昆第45页晶体:衍射图样是一组组清晰的斑点非晶体:由于原子排列是长程无序的,衍射图样呈现为弥散的环,没有表征晶态的斑点准晶体:衍射图样具有五重对称的斑点分布,斑点的明锐程度不亚于晶体的情况(b)何谓布拉菲格子、晶体学点群、晶系和晶体学空间群?C1 (1)、C2 (2)、C3 (3)、C4 (4)、C6 (6)及S1,S2,S3,S4,S5这十种对称素组成32个不同的点群结晶学中把a, b, c满足同一类要求的一种或数种布喇菲格子称为一个晶系。
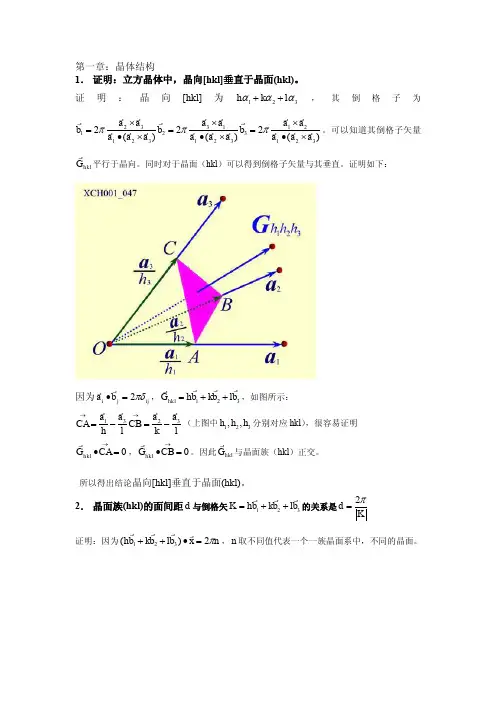

固体物理习题参考答案(部分)第一章 晶体结构1.氯化钠:复式格子,基元为Na +,Cl -金刚石:复式格子,基元为两个不等价的碳原子 氯化钠与金刚石的原胞基矢与晶胞基矢如下:原胞基矢)ˆˆ()ˆˆ()ˆˆ(213212211j i a a i k a a k j a a +=+=+= , 晶胞基矢 ka a j a a ia a ˆˆˆ321===2. 解:31A A O ':h:k;l;m==-11:211:11:111:1:-2:1 所以(1 1 2 1) 同样可得1331B B A A :(1 1 2 0); 5522A B B A :(1 1 0 0);654321A A A A A A :(0 0 0 1)3.简立方: 2r=a ,Z=1,()63434r 2r a r 3333πππ===F体心立方:()πππ833r4r 342a r 3422a 3r 4a r 4a 33333=⨯=⨯=∴===F Z ,,则面心立方:()πππ622r 4r 34434442r 4a r 4a 233ar 33=⨯=⨯=∴===F Z ,,则 六角密集:2r=a, 60sin 2c a V C = a c 362=,πππ622336234260sin 34223232=⨯⨯⨯=⨯=⎪⎭⎫ ⎝⎛a a c a r F a金刚石:()πππ163r 38r 348a r 3488Z r 8a 33333=⨯=⨯===F ,, 4. 解:'28109)31arccos(312323)ˆˆˆ()ˆˆˆ(cos )ˆˆˆ()ˆˆˆ(021*******12211=-=-=++-⋅+-=⋅=++-=+-=θθa a k j i a k j i a a a a a kj i a a kj i a a 5.解:对于(110)面:2a 2a a 2S =⋅=所包含的原子个数为2,所以面密度为22a2a22=对于(111)面:2a 2323a 22a 2S =⨯⨯= 所包含的原子个数为2,所以面密度为223a34a 232=8.证明:ABCD 是六角密堆积结构初基晶胞的菱形底面,AD=AB=a 。

晶体结构习题第一章晶体结构1.三维空间中有多少种brafi格?画一张图来说明这些布拉菲格子。
解:三维空间有14种布拉菲格子,分别如下图所示:2.石墨层中的碳原子排列成六角形网络结构,如图所示。
一个原电池包含多少个原子?为什么?么?解决方案:石墨层中的原电池包含两个原子。
在图中,a和B原子并不相等,它们的几何位置也不同,所以在一个原始细胞中至少有两个碳原子;如图所示,石墨单层可以通过周期性平移图中由点框包围的两个原子A和B的单元来获得。
它可以形成石墨单层的原细胞。
因此,石墨层中的一个原细胞包含两个原子。
3、利用刚球密堆模型,求证球可能占据的最大体积与总体积之比为:(1)简单立方体6(5)金刚石;(2)体心立方322(3)面心立方(4)六方密积?;?;?;8663?。
解:(1)在简单的立方晶体学原胞中,假设原子半径为r,则原胞的晶体学常数为a?2R,则简单立方体的密度(即球可能占据的最大体积与总体积的比率)为:441??r31??r333?33?6A(2R)(2)在体心立方晶体学原胞中,如果原子半径为r,则原胞的晶体学常数为a?4R/3,则BCC的密度为:442??r32??r33?3??33??38a(4r/3)(3)在面心立方的结晶学原胞中,设原子半径为r,则原胞的晶体学常数a?22r,则面心立方的致密度为:444?? r32??r33??33?? a(22r)32?6(4)在六方密积的晶体学原胞中,假设原子半径为r,那么原胞的晶体学常数a?2rc?(26/3)a?(46/3)r,则六角密积的致密度为:446?? r36??r333223a3(2r)6?c6?(46/3)r442?6(5)在金刚石晶胞中,如果原子半径为r,晶胞的晶胞常数为a?(8/3)r,那么钻石的密度是:448??r38??r33?3??33??3316a(8/3)r4.有一个简单的格,它的基向量是A1?3i,a2?3j,a3?1.5(i?j?k)。
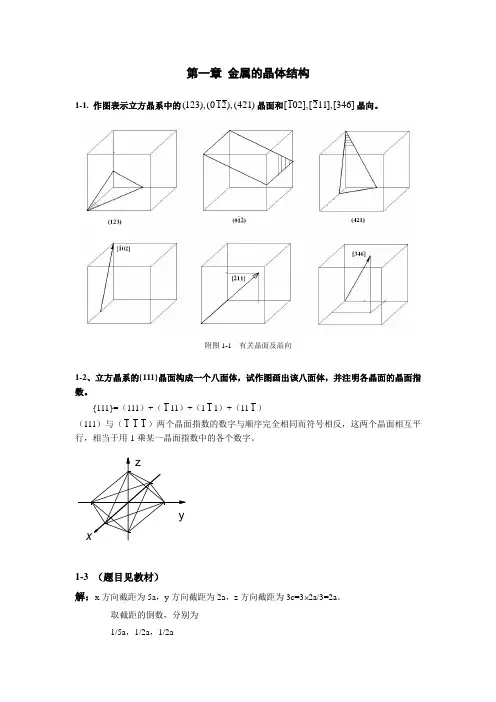
第一章金属的晶体结构1-1. 作图表示立方晶系中的(123),(012),(421)晶面和[102],[211],[346]晶向。
附图1-1 有关晶面及晶向1-2、立方晶系的{111}晶面构成一个八面体,试作图画出该八面体,并注明各晶面的晶面指数。
{111}=(111)+(111)+(111)+(111)(111)与(111)两个晶面指数的数字与顺序完全相同而符号相反,这两个晶面相互平行,相当于用-1乘某一晶面指数中的各个数字。
xy z1-3 (题目见教材)解:x方向截距为5a,y方向截距为2a,z方向截距为3c=3 2a/3=2a。
取截距的倒数,分别为1/5a,1/2a,1/2a化为最小简单整数分别为2,5,5 故该晶面的晶面指数为(2 5 5)1-4 (题目见课件)解:(100)面间距为a/2;(110)面间距为2a/2;(111)面间距为3a/3。
三个晶面中面间距最大的晶面为(110)。
1-5 (题目见课件)解:方法同1-4题1-7 证明理想密排六方晶胞中的轴比c/a=1.633。
证明:理想密排六方晶格配位数为12,即晶胞上底面中心原子与其下面的3个位于晶胞内的原子相切,构成正四面体,如图所示。
则OD=2c,AB=BC=CA=AD=BD=CD=a 因∆ABC 是等边三角形,所以有OC=32CE 因(BC)2=(CE)2+(BE)2则CE=23a ,OC=32×23a =33a又(CD)2=(OC)2+(21c )2,即(CD)2=(33a )2+(21c )2=(a )2因此,ac=38≈1.6331-8解:面心立方八面体间隙半径 r=a/2-2a/4=0.146a , 面心立方原子半径R=2a/4,则a=4R/2,代入上试有CBADEOr=0.146⨯4R/2=0.414R。
(其他的证明类似)1-9 a)设有一刚球模型,球的直径不变,当由面心立方晶格转变为体心立方晶格时,试计算其体积的膨胀?b)经X射线测定,在912℃时γ-Fe的晶格常数为0.3633nm,α-Fe的晶格常数为0.2892nm,当由γ-Fe转变为α-Fe时,试求其体积膨胀? c)分析实际体积膨胀小于理论体积膨胀的原因?解:a)令面心立方晶格与体心立方晶格的体积及晶格常数分别为V面、V体与a面、a体,刚球半径为r,由晶体结构可知,对于面心晶胞有4r=2a面,a面=22r,V面= (a面)3=(22r)3对于体心晶胞有4r=3a体,a体=334r,V体= (a体)3=(334r)3则由面心立方晶胞转变为体心立方晶胞的体积膨胀∆V为∆V=2×V体-V面=2.01r3b)按晶格常数计算实际转变体积膨胀∆V实,有∆V实=2×V体-V面=2×(0.2892)3-(0.3633)3=0.000425 nm3c)实际体积膨胀小于理论体积膨胀的原因在于由γ-Fe转变为α-Fe时,Fe 原子半径发生了变化,原子半径减小了。

第一章晶体结构习题1、晶体结构的堆积比率 在sc, bcc 和fcc 结构中,fcc 是原子排列最密积的,sc 是最稀疏的,它们的配位数分别是fcc-12;bcc-8;sc-6;而金刚石结构比简单立方结构还要稀疏,配位数是4。
如果把同样的硬球放置在这些结构原子所在的位置上,球的体积取得尽可能大,以使最近邻的球正好接触,但彼此并不重迭。
我们把一个晶胞中被硬球占据的体积和晶胞体积之比定义为结构的堆积比率(又叫最大空间利用率)。
试证明以上四种结构的堆积比率是fcc :74.062=π bcc :68.083=π sc :52.061=π 金刚石:34.0163=π 2、点阵常数的计算 已知氯化钠是立方晶体,其分子量为58.46,在室温下的密度是2.167×103 kg·m -3,试计算氯化钠结构的点阵常数。
3、立方晶系的晶面和晶向 证明立方晶系中方向[hkl ]垂直于平面(hkl )。
4、六角密堆积结构 (a) 证明理想的六角密堆积结构(hcp)的轴比c /a 是 (8/3)1/2=1.633。
(b) 钠在23K 附近从bcc 结构转变为hcp 结构(马氏体相变),假如在此相变过程中保持密度不变,求hcp 相的点阵常数a 。
已知bcc 相的点阵常数是4.23Å,且hcp 相的c /a 比值与理想值相同。
5、面间距 考虑晶体中一组互相平行的点阵平面 (hkl ),(a) 证明倒易点阵矢量G (hkl )=h b 1+k b 2+l b 3垂直于这组平面(hkl );(b) 证明两个相邻的点阵平面间的距离d (hkl )为:)(2)(hkl G hkl d π= (c) 证明对初基矢量a 1、a 2、a 3互相正交的晶体点阵,有 232221)/()/()/(1)(a l a k a h hkl d ++=(d) 证明对简单立方点阵有 )()()()(222l k h ahkl d ++=6、一个单胞的尺寸为a 1=4 Å ,a 2=6 Å ,a 3=8 Å ,α=β=90°,γ=120°,试求:(a) 倒易点阵单胞基矢;(b)倒易点阵单胞体积;(c) (210)平面的面间距。

《无机材料科学基础》习题和思考题第一章晶体1.球体按立方最紧密堆积方式堆积,取出立方晶胞,画出立方晶胞中的四面体空隙和八面体空隙的位置分布图。
2.用鲍林规则分析氧化镁晶体结构。
已知镁离子半径为0.65Å,氧离子半径为1.40Å。
(1)确定晶胞中质点的位置坐标;(2)计算每个晶胞中含氧化镁“分子”数,(3)已知晶胞常数a=4.20 Å,求氧化镁堆积系数和密度,(4)氧化镁晶体中最邻近的两个镁离子中心距为多少?次邻近的两个镁离子中心距为多少?最邻近和次邻近的两个氧离子中心距为多少?(5)画出氧化镁晶胞的(111)、(110)、(100)面的质点分布图并在图上标出氧离子的密排方向,求个面的面密度。
3.已知纤锌矿结构中存在两套硫离子和两套锌离子的六方底心格子,并已知锌离子填充在硫离子最紧密堆积体的四面体空隙中,现以一套硫离子的等同点为基准取六方晶胞,画出晶胞中的质点分布图,计算晶胞中所含式量分子数。
4.完成下表5. 六方最紧密堆积与四方最紧密堆积的堆积密度相同,为什么许多氧化物是以氧离子的立方最紧密堆积为基础,而较少以六方最紧密堆积为基础?6. 用鲍林规则分析镁橄榄石的结构:P48 图2-18(1)标记为50的Mg2+与哪几个氧离子配位形成[MgO6]八面体?写出O2+的标高;(2)标记为25的两个O2+与哪几个镁离子配位?写出Mg2+离子的标高;(3)标记为75的O2+离子与哪几个镁离子配位?写出Mg2+离子的标高;(4)标记为0和50的两个Mg2+的[MgO6] 八面体共用几个顶点?写出O2+的标高;(5)[SiO4] 和 [MgO6] 之间、[MgO6]和[MgO6] 八面体之间有那些连接方式?(6)镁橄榄石的晶胞是什么形状?计算晶胞中含有的式量分子数。
第二章晶体缺陷1.氧化镁为氯化钠型结构,氧化锂为反萤石型结构,在两种结构中氧离子都作立方最紧密堆积,为什么在氧化镁中主要的热缺陷是肖特基型,而在氧化锂中却是弗伦克尔型?萤石型结构的氧化物晶体中常见的热缺陷估计主要是什么类型?为什么?2.已知氯化钠晶体中肖特基缺陷形成焓为2.2ev,而氧化镁晶体中肖特基缺陷形成焓为6ev,试分别计算400℃时氯化纳晶体与氧化镁晶体中肖特基缺陷的浓度。
固体物理题库第⼀章晶体的结构第⼀章晶体的结构⼀、填空体(每空1分)1. 晶体具有的共同性质为长程有序、⾃限性、各向异性。
2. 对于简⽴⽅晶体,如果晶格常数为a,它的最近邻原⼦间距为 a ,次近邻原⼦间,原胞与晶胞的体积⽐1:1 ,配位数为 6 。
3. 对于体⼼⽴⽅晶体,如果晶格常数为a a2,次近邻原⼦间距为 a ,原胞与晶胞的体积⽐1:2 ,配位数为8 。
4. 对于⾯⼼⽴⽅晶体,如果晶格常数为a邻原⼦间距为 a ,原胞与晶胞的体积⽐1:4 ,配位数为12 。
5. ⾯指数(h1h2h3)所标志的晶⾯把原胞基⽮a1,a2,a3分割,其中最靠近原点的平⾯在a1,a2,a3上的截距分别为__1/h1_,_1/h2__,__1/h3_。
6. 根据组成粒⼦在空间排列的有序度和对称性,固体可分为晶体、准晶体和⾮晶体。
7. 根据晶体内晶粒排列的特点,晶体可分为单晶和多晶。
8. 常见的晶体堆积结构有简⽴⽅(结构)、体⼼⽴⽅(结构)、⾯⼼⽴⽅(结构)和六⾓密排(结构)等,例如⾦属钠(Na)是体⼼⽴⽅(结构),铜(Cu)晶体属于⾯⼼⽴⽅结构,镁(Mg)晶体属于六⾓密排结构。
9. 对点阵⽽⾔,考虑其宏观对称性,他们可以分为7个晶系,如果还考虑其平移对称性,则共有14种布喇菲格⼦。
10.晶体结构的宏观对称只可能有下列10种元素:1 ,2 ,3 ,4 ,6 ,i ,m ,3,4,6,其中3和6不是独⽴对称素,由这10种对称素对应的对称操作只能组成32个点群。
11. 晶体按照其基元中原⼦数的多少可分为复式晶格和简单晶格,其中简单晶格基元中有 1 个原⼦。
12. 晶体原胞中含有 1 个格点。
13. 魏格纳-塞茨原胞中含有 1 个格点。
⼆、基本概念1. 原胞原胞:晶格最⼩的周期性单元。
2. 晶胞结晶学中把晶格中能反映晶体对称特征的周期性单元成为晶胞。
3. 散射因⼦原⼦内所有电⼦在某⼀⽅向上引起的散射波的振幅的⼏何和,与某⼀电⼦在该⽅向上引起的散射波的振幅之⽐。
第一章晶体结构1.试述晶态、非晶态、准晶、多晶和单晶的特征性质。
解:晶态固体材料中的原子有规律的周期性排列,或称为长程有序。
非晶态固体材料中的原子不是长程有序地排列,但在几个原子的范围内保持着有序性,或称为短程有序。
准晶态是介于晶态和非晶态之间的固体材料,其特点是原子有序排列,但不具有平移周期性。
另外,晶体又分为单晶体和多晶体:整块晶体内原子排列的规律完全一致的晶体称为单晶体;而多晶体则是由许多取向不同的单晶体颗粒无规则堆积而成的。
2.晶格点阵与实际晶体有何区别和联系?解:晶体点阵是一种数学抽象,其中的格点代表基元中某个原子的位置或基元质心的位置,也可以是基元中任意一个等价的点。
当晶格点阵中的格点被具体的基元代替后才形成实际的晶体结构。
晶格点阵与实际晶体结构的关系可总结为:晶格点阵+基元=实际晶体结构3.晶体结构可分为Bravais格子和复式格子吗?解:晶体结构可以分为Bravais格子和复式格子,当基元只含一个原子时,每个原子的周围情况完全相同,格点就代表该原子,这种晶体结构就称为简单格子或Bravais格子;当基元包含2个或2个以上的原子时,各基元中相应的原子组成与格点相同的网格,这些格子相互错开一定距离套构在一起,这类晶体结构叫做复式格子。
4.图1.34所示的点阵是布喇菲点阵(格子)吗?为什么?如果是,指明它属于那类布喇菲格子?如果不是,请说明这种复式格子的布喇菲格子属哪类?(a)(b)(c)(d)图1.34(a)“面心+体心”立方;(b)“边心”立方;(c)“边心+体心”立方;(d)面心四方解:(a)“面心+体心”立方不是布喇菲格子。
从“面心+体心”立方体的任一顶角上的格点看,与它最邻近的有12个格点;从面心任一点看来,与它最邻近的也是12个格点;但是从体心那点来看,与它最邻近的有6个格点,所以顶角、面心的格点与体心的格点所处的几何环境不同,即不满足所有格点完全等价的条件,因此不是布喇菲格子,而是复式格子,此复式格子属于简立方布喇菲格子。
第一章晶体结构习题1、概念:晶体,晶体结构,空间点阵,离子半径,离子极化,配位数,固溶体,合金2、在正交简单点阵、底心点阵、体心点阵、面心点阵中分别画出(110)、(001两组晶面,并指出每个晶面上的结点数?3、设有某一晶面在x、y、z三个坐标轴上的截距分别为1a,2b,3c,求该晶面符号?4、在立方晶系中,一晶面在x轴的截距为1,在y轴的截距为1/2,且平行于z 轴,一晶向上某点坐标为x=1/2,y=0,z=1,求出其晶面指数和晶向指数,并绘图示之?答:根据晶面和晶向指数的标定方法可知,题中晶面指数为(120),如图中ABCD,晶向指数为[102]如图中OP。
6、画出立方晶系中下列晶面和晶向:(010),(011),(111),(231),(321),[010],[011],[111],[231],[321]7、什么叫离子极化?极化对晶体结构有什么影响?在离子紧密堆积时,带电荷的离子所产生的电场必然要对另一离子的电子云发生作用(吸引或排斥),因而使这个离子的大小和形状发生了改变,这种现象叫离子极化。
极化会对晶体结构产生显著影响,主要表现为极化会导致离子间距离缩短,离子配位数降低,同时变形的电子云相互重叠,使键性由离子键向共价键过渡,最终使晶体结构类型发生变化.8、氧化镁(MgO )与氯化钠(NaCl )具有相同结构。
求(1) MgO 的晶格常数;(2) MgO 的密度?(Ar(Mg)=24, Ar(O)=16) 解:(1)(2)每一个单位晶胞中含有4个Mg 2+及4个O 2-,1mol 的Mg 2+具有24g 的质量,1mol 的O 2-具有16g 的质量。
9、已知MgO 晶体中Mg 2+和O 2-在三维空间有规律地相间排列,其晶体结构相当于两套面心立方点阵互相套叠在一起,晶胞常数a=b=c=4.20, α=β=γ=90℃,请回20.078Mg r nm +=20.132O r nm-=222()2(0.0780.132)0.396Mg O a r r nm +-=+=+=232333732324164()4(2416)6.0210 6.02104.28/(0.39610) 6.0210g g g cm a ρ-++⨯⨯===⨯⨯⨯答:①画出MgO晶体二维和三维空间的晶体结构图.②从①的图形中抽象出MgO晶体的空间点阵图形.③从②中划分出单位空间格子,计算其结点数.12、画出MgO晶体(面心立方点阵)在(1 0 0)、(1 1 0)、(1 1 1)晶面上的结点和离子排布图.13、已知γCs+ = 0.169 nm,γCl- = 0.181 nm。
(一).填空题1.同非金属相比,金属的主要特性是__________2.晶体与非晶体的最根本区别是__________3.金属晶体中常见的点缺陷是__________ ,最主要的面缺陷是__________ 。
4.位错密度是指__________ ,其数学表达式为__________ 。
5.表示晶体中原子排列形式的空间格子叫做__________ ,而晶胞是指__________ 。
6.在常见金属晶格中,原子排列最密的晶向,体心立方晶格是__________ ,而面心立方晶格是__________ 。
7.晶体在不同晶向上的性能是__________,这就是单晶体的__________现象。
一般结构用金属为__________ 晶体,在各个方向上性能__________ ,这就是实际金属的__________现象。
8.实际金属存在有__________ 、__________ 和__________ 三种缺陷。
位错是__________ 缺陷。
实际晶体的强度比理想晶体的强度__________ 得多。
9.常温下使用的金属材料以__________ 晶粒为好。
而高温下使用的金属材料在一定范围内以__________ 晶粒为好。
‘10.金属常见的晶格类型是__________、__________ 、__________ 。
11.在立方晶格中,各点坐标为:A (1,0,1),B (0,1,1),C (1,1,1/2),D(1/2,1,1/2),那么AB晶向指数为__________ ,OC晶向指数为__________ ,OD晶向指数为__________ 。
12.铜是__________ 结构的金属,它的最密排面是__________ ,若铜的晶格常数a=0.36nm,那么最密排面上原子间距为__________ 。
13 α-Fe、γ-Fe、Al、Cu、Ni、Pb、Cr、V、Mg、Zn中属于体心立方晶格的有__________ ,属于面心立方晶格的有__________ ,属于密排六方晶格的有__________ 。
(一).填空题1.同非金属相比,金属的主要特性是__________2.晶体与非晶体的最根本区别是__________3.金属晶体中常见的点缺陷是__________ ,最主要的面缺陷是__________ 。
4.位错密度是指__________ ,其数学表达式为__________ 。
5.表示晶体中原子排列形式的空间格子叫做__________ ,而晶胞是指__________ 。
6.在常见金属晶格中,原子排列最密的晶向,体心立方晶格是__________ ,而面心立方晶格是__________ 。
7.晶体在不同晶向上的性能是__________,这就是单晶体的__________现象。
一般结构用金属为__________ 晶体,在各个方向上性能__________ ,这就是实际金属的__________现象。
8.实际金属存在有__________ 、__________ 和__________ 三种缺陷。
位错是__________ 缺陷。
实际晶体的强度比理想晶体的强度__________ 得多。
9.常温下使用的金属材料以__________ 晶粒为好。
而高温下使用的金属材料在一定范围内以__________ 晶粒为好。
‘10.金属常见的晶格类型是__________、__________ 、__________ 。
11.在立方晶格中,各点坐标为:A (1,0,1),B (0,1,1),C (1,1,1/2),D(1/2,1,1/2),那么AB晶向指数为__________ ,OC晶向指数为__________ ,OD晶向指数为__________ 。
12.铜是__________ 结构的金属,它的最密排面是__________ ,若铜的晶格常数a=0.36nm,那么最密排面上原子间距为__________ 。
13 α-Fe、γ-Fe、Al、Cu、Ni、Pb、Cr、V、Mg、Zn中属于体心立方晶格的有__________ ,属于面心立方晶格的有__________ ,属于密排六方晶格的有__________ 。