设二阶控制系统的单位阶跃响应曲线如图所示

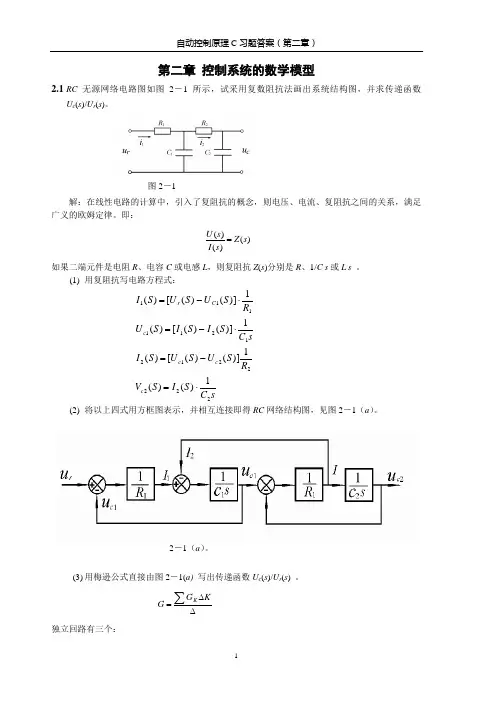
1习题1-1 试列举几个日常生活中的开环和闭环控制系统的例子，并说明其工作原理。

1-2 根据题1-1图所示的电动机速度控制系统工作原理图：（1）将a ，b 与c ，d 用线连接成负反馈系统；（2）画出系统方框图。

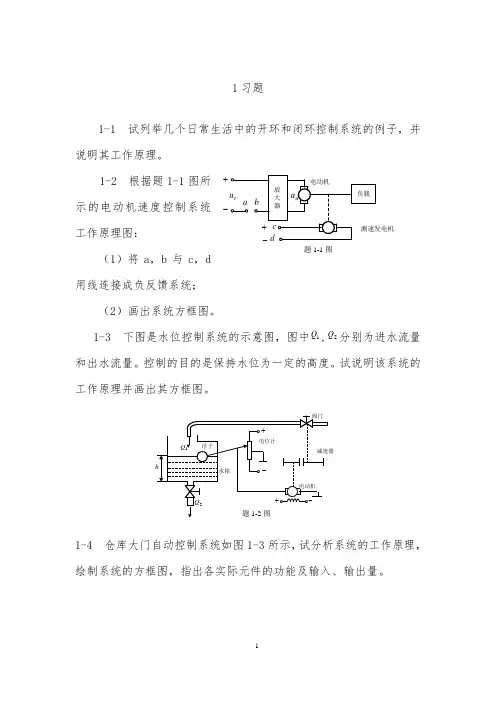
1-3 下图是水位控制系统的示意图，图中1Q ,2Q 分别为进水流量和出水流量。

控制的目的是保持水位为一定的高度。

试说明该系统的工作原理并画出其方框图。

1-4 仓库大门自动控制系统如图1-3所示，试分析系统的工作原理，绘制系统的方框图，指出各实际元件的功能及输入、输出量。

2习题2-1 求下列函数的拉氏变换。

（1）t t t f 4cos 4sin )(+= （2）t e t t f 43)(+= （3）t te t f --=1)( （4）()cos3t f t e t -=2-2求下列函数的拉氏反变换。

（1）)3)(2(1)(+++=s s s s F（2）()()()2114F s s s =++（3）()225sF s s s =-+（4）()221225s F s s s +=++(5) )3()1(2)(2=++=s s s s s G (6) ))()(()()(c s b s a s d s s G ++++=(7) 152122)(2+++=s s s s G2-3 解微分方程()()()22681d y t dy t y t dt dt++=，初始条件：(0)1y =，'(0)0y = 。

2-4 试证明图2-75所示电气系统与机械系统具有相同的传递函数。

图2-75 题2-4 图2-5 试分别写出图2-76中各有源网络的传递函数。

（1） （2）图2-76 题2-5图2-6系统的方框图如图2-77所示，试求该系统的输入输出传递函数。

图2-77 题2-6图2-7 系统的方框图如图2-78所示，试用梅逊公式求传递函数。

图2-78 题2-7图2-8 已知系统结构如图2-79所示。

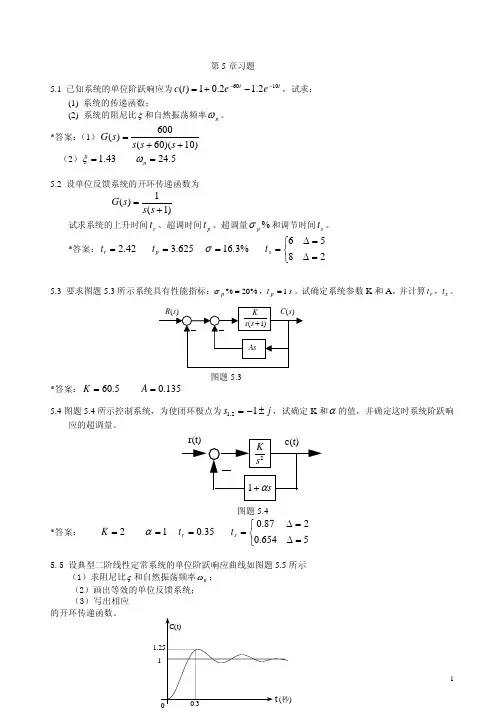
第5章习题5.1 已知系统的单位阶跃响应为t te et c 10602.12.01)(−−−+=，试求：(1) 系统的传递函数；(2) 系统的阻尼比ξ和自然振荡频率n ω。

*答案：（1）)10)(60(600)(++=s s s s G（2）43.1=ξ 5.24=n ω5.2 设单位反馈系统的开环传递函数为)1(1)(+=s s s G试求系统的上升时间r t 、超调时间p t 、超调量%p σ和调节时间s t 。

*答案：42.2=r t 625.3=p t%3.16=σ ⎩⎨⎧=∆=∆=2856s t5.3 要求图题5.3所示系统具有性能指标：%20%=p σ，s t p 1=。

试确定系统参数K 和A ，并计算r t ，s t 。

图题5.3*答案：5.60=K 135.0=A5.4图题5.4所示控制系统，为使闭环极点为s j1=−±，试确定K 和α的值，并确定这时系统阶跃响应的超调量。

*答案： 2=K1=α 35.0=r t ⎩⎨=∆=5654.0s t5.5 设典型二阶线性定常系统的单位阶跃响应曲线如图题5.5所示 （1）求阻尼比ς和自然振荡频率n ω；（2）画出等效的单位反馈系统； （3）写出相应的开环传递函数。

)10(100)(+=S S s G 图题5.5*答案（1）4.0=ζ 4.11=n ω(3)9.12)s(s 129.96)(+=s G5.6图题5.6所示采样控制系统，已知图中线性网络部分的单位阶跃响应为1−−e t，采样周期为T ，求系统在输入单位阶跃信号时的输出响应y nT ()。

零阶保持器线性网络uy T图题5.6*答案：nTenT y −=1)(5.7 试求下列状态方程的解，设初始状态为)0(x 。

x x ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡−−−=300020001& 答案：)0()(32x e e e t x t tt⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=−−−5.8 求下列状态方程在单位阶跃输入作用下的响应。

3-1设温度计需要在一分钟内指示出响应值的98%，并且假设温度计为一阶系统，求时间常数T 。

如果将温度计放在澡盆内，澡盆的温度以10C/min 的速度线性变化。

求温度计的误差。

解：c(t)=c(∞)98%t=4T=1 min r(t)=10te(t)=r(t)-c(t)c(t)=10(t-T+e )-t/T =10(T-e )-t/T =10T =2.5T=0.253-2电路系统如图所示，其中F C k R k R μ5.2,200,20110=Ω=Ω=。

设系统初始状态为零，试求：系统的单位阶跃响应8)()(1=t u t u c c 以及时的1t 值；解:R 1Cs+1R 1/R 0G (s )= u c (t)=K(1–e t T -)KTs +1=T=R 1C=0.5 K=R 1/R 0=10=10(1–e -2t )8=10(1–e -2t)0.8=1–e-2te -2t =0.2 t=0.8g(t)=e -t/T T Kt 1=0.8=4u c (t)=K(t-T+T e -t/T )=4R(s)=1s 2R(s)=1R(s)=1s 3T 2=K(s s+1/T+T s 2-1s 3-T 2)=1.2Ts 1s 3K +1U c (s)= -0.5t+0.25-0.25e -2t )12t 2u c (t)=10(3-3已知单位反馈系统的开环传递函数为)5(4)(+=s s s G 试求该系统的单位阶跃响应。

解:C(s)=s 2+5s+4R(s)4s(s+1)(s+4)C(s)=4R(s)=s1s+41+1/3s =4/3s +1-c(t)=1+ 4e 13-4t -t 3-e3-4已知单位负反馈系统的开环传递函数为 )1(1)(+=s s s G 试求该系统的上升时间r t 。

、峰值时间p t 、超调量%σ和调整时间s t 。

1s(s+1)G(s)=t p =d ωπ 3.140.866= =3.63t s = ζ3ωn=6t s = ζ4ωn =8解:C(s)=s 2+s+1R(s)12= 1ωn 2ωn ζ=1ζ=0.5=1ωn =0.866d ω= ωn 2 ζ1-=60o -1ζ=tg β21-ζt r =d ωπβ-= 3.14-3.14/30.866=2.42σ%=100%e -ζζπ1-2=16%e -1.83-6已知系统的单位阶跃响应为t te et c 10602.12.01)(---+= ，试求：（1）系统的闭环传递函数；（2）系统的阻尼比ζ和无阻尼自然震荡频率n ω；解:s+60+C(s)=0.21s 1.2s +10-s(s+60)(s+10)=600=s 2+70s+600C(s)R(s)600R(s)=s 12=600ωn2ωn ζ=70ζ=1.43=24.5ωn3-7设二阶控制系统的单位阶跃响应曲线如图所示，如果该系统为单位负反馈系统，试确定其开环传递函数。

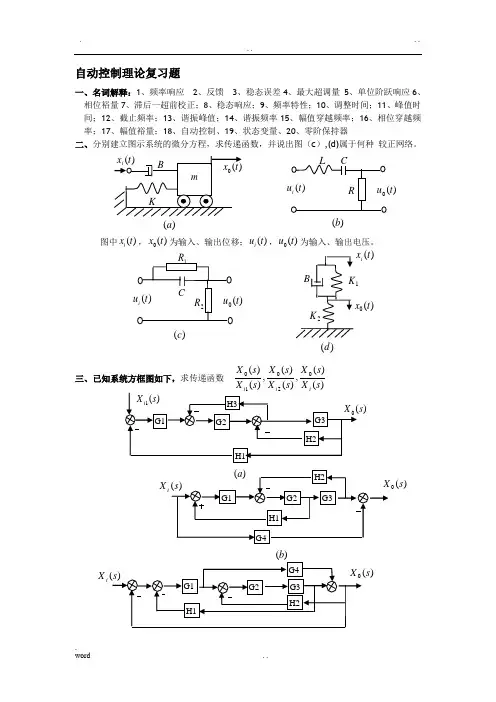
自动控制理论复习题一、名词解释：1、频率响应 2、反馈 3、稳态误差4、最大超调量 5、单位阶跃响应6、相位裕量7、滞后一超前校正；8、稳态响应；9、频率特性；10、调整时间；11、峰值时间；12、截止频率；13、谐振峰值；14、谐振频率15、幅值穿越频率；16、相位穿越频率；17、幅值裕量；18、自动控制、19、状态变量、20、零阶保持器二、分别建立图示系统的微分方程，求传递函数，并说出图（c ）,(d)属于何种 较正网络。

图中)(t x i ，)(0t x 为输入、输出位移；)(t u i ，)(0t u 为输入、输出电压。

三、已知系统方框图如下，求传递函数)(,)(,)(000s X s X s X)(a )(b )t )t )(c )(t x i 1)(0t x )(d )(0s )(b X i )s X i )s四、已知系统的开环的幅相特性（Nyguist ）如图所示，图中P 为开环传递函数G(s)H(s)五、计算 1、设某二阶系统的单位阶跃响应曲线如图所示，如果该系统为单位反馈型式，试确定其开环传递函数。

2、某系统如图所示，n p t 调整时间 s t 。

（设误差带宽度取±2％ ）)(c )(a))(a )(b ))六、已知系统的开环传递函数)()(s H s G 的幅频特性曲线如图示，且)()(s H s G 为最小相位系统。

试求)()(s H s G = ？七、某系统的开环传递函数为)12()1()()(-+=s s sK s H s G ，试画出其乃奎斯特图，并说明当K取何值时系统稳定？八、已知系统闭环传递函数为))()(01221101a s a s a s a s a a s a s X s X n n n n i +++⋅⋅⋅+++=-- 试证明系统对速度输入的稳态误差为零。

十、判断正误1、各项时域指标（最大超调量，调整时间等）是在斜坡信号作用下定义的。

2、对于结构不稳定系统，可以通过改变某些系统结构参数而使其稳定。

第三章例3-1 系统的结构图如图3-1所示。

已知传递函数 )12.0/(10)(+=s s G 。

今欲采用加负反馈的办法，将过渡过程时间t s减小为原来的0.1倍，并保证总放大系数不变。

试确定参数K h 和K 0的数值。

解 首先求出系统的传递函数φ（s ），并整理为标准式，然后与指标、参数的条件对照。

一阶系统的过渡过程时间t s 与其时间常数成正比。

根据要求，总传递函数应为)110/2.0(10)(+=s s φ即HH K s K s G K s G K s R s C 1012.010)(1)()()(00++=+= )()11012.0(101100s s K K K HHφ=+++=比较系数得⎪⎩⎪⎨⎧=+=+1010110101100H HK K K 解之得9.0=H K 、100=K解毕。

例3-10 某系统在输入信号r (t )=(1+t )1(t )作用下，测得输出响应为：t e t t c 109.0)9.0()(--+= （t ≥0）已知初始条件为零，试求系统的传递函数)(s φ。

解 因为22111)(ss s s s R +=+=)10()1(10109.09.01)]([)(22++=+-+==s s s s s s t c L s C 故系统传递函数为11.01)()()(+==s s R s C s φ 解毕。

例3-3 设控制系统如图3-2所示。

试分析参数b 的取值对系统阶跃响应动态性能的影响。

解 由图得闭环传递函数为1)()(++=s bK T Ks φ系统是一阶的。

动态性能指标为)(3)(2.2)(69.0bK T t bK T t bK T t s r d +=+=+= 因此，b 的取值大将会使阶跃响应的延迟时间、上升时间和调节时间都加长。

解毕。

例 3-12 设二阶控制系统的单位阶跃响应曲线如图3-34所示。

试确定系统的传递函数。

解 首先明显看出，在单位阶跃作用下响应的稳态值为3，故此系统的增益不是1，而是3。

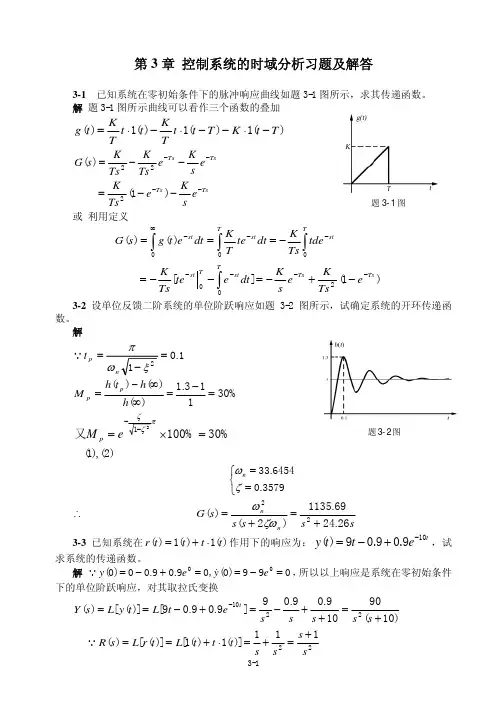
《自控理论》复习题1设二阶控制系统的单位阶跃响应曲线如图所示，若该系统为单位反馈控制系统， 试确定其单位传递函数。

解：由图知，该系统为欠阻尼二阶系统，从图中直接得出%30%=σ s t p 1.0=根据公式3.0%21==--ζπζσe解得 358.0)(ln )(ln 222=+=σπσζ 1.012=-=ζωπn p t 1265.331-=-=s t p n ζπω于是开环传递函数为)1.24(3.1132)2()(2+=+=s s s s s G n ζωω2设电子心率起搏器系统如图所示，其中模仿心脏的传递函数相当于一纯积分器。

要求： 若5.0=ζ对于最佳响应，问起搏器的增益K 应为多大？解：系统的开环传递函数为：)105.0()(+=s s Ks G所以闭环传递函数 Ks s KK s s K s 202020)105.0()(2++=++=φ5.0,202,202===ζζωωn n K解之得：K=20 20=n ω3已知反馈系统的开环传递函数为)110)(15(10)()(++=s s s H s G 试用奈氏判据判断系统的闭环稳定性。

解 系统开环频率特性为1800)()(010)0()0()110)(15(10)()(-∠=∞∞∠=++=j H j G j H j G j j j H j G ωωωω由于Im[)()(ωωj H j G ]<0 ω∀，故幅相曲线与负实轴没有交点，)(ωϕ从 0递减至 180-。

作幅相曲线。

开环系统的所有极点都在s 的左半面，P=0。

而由开环幅相曲线可知，开环幅相曲线逆时针包围（-1，j0）点的圈熟数N=0。

根据奈氏判据，闭环极点位于s 的右半面的个数Z=P-2N=0系统闭环稳定。

上述结果推广到一般情况)1)(1()()(11++=s T s T Ks H s G 对于所有的K ，1T ，2T ，其幅相曲线和图4设反馈控制系统中，1)(,)5)(2(*)(2=++=s H s s s K s G 要求：（1）概略绘制系统根轨迹图，判断系统的稳定性。

⼤连理⼯⾃动控制原理考研试卷99-05⼤连理⼯⼤学⼀九九九年硕⼠⽣⼊学考试《⾃动控制原理（含20%现代）》试题⼀、（10分）试建⽴图⼀所⽰校正环节的动态结构图，并指出这是⼀个什么样的校正环节。

⼆、（10分）给定系统的动态结构图如图⼆所⽰。

试求传递函数)()(s R s C ， )()(s R s E 。

三、（10分）请解释对于图三所⽰的两个系统，是否可以通过改变K 值（K>0）使系统稳定。

四、（10分）已知单位反馈系统的开环传递函数为试绘制K<<0 →∞的根轨迹图。

五、（15分）已知系统的开环传递函数为G(s)H(s)=)110)(1()11.0(+-+s s s s K1. 试绘制K=1时的对数幅频、相频特性的渐近线；2. 应⽤Nyguist 判据分析系统的稳定性，并说明改变K 值是否可以改变系统的稳定性。

六、（6分）简单说明PID 调节器各部分的作⽤。

答： P 作⽤：I 作⽤：D 作⽤：七、（9分）设有两个⾮线性系统，它们的⾮线性部分⼀样，线性部分分别如下：1． G(s)=)11.0(2+s s2. G(s)=)1(2+s s试问：当⽤描述函数法分析时，哪个系统分析的准确度⾼？为什么？⼋、（10分）给定系统如图四所⽰。

试求在单位阶跃输⼊时，系统输出的Z 变换Y(z).九、（20分）设系统的状态空间表达式为1．试求状态转移矩阵；2．为保证系统状态的能观性，a 应取何值？ 3．试求状态空间表达式的能观规范形；4．⽤李亚普诺夫第⼆⽅法判断系统的稳定性。

⼤连理⼯⼤学⼆OOO 年硕⼠⽣⼊学考试《⾃动控制原理（含20%现代）》试题⼀、（20分）（本题仅限于单考⽣完成，单考⽣还需在以下各题中选做80分的考题，统考⽣不做此题） 1．给定系统的开环传递函数为试判别K 取值时系统稳定。

2．已知某⼀闭环系统有⼀对主导极点，由于这对主导极点距离S 平⾯的虚轴太近，使得系统的阶跃响应较差。

试问系统响应较差表现在哪⽅⾯？欲改善系统性能应采取什么措施？⼆、（10分）试求图⼀所⽰系统的微分⽅程。

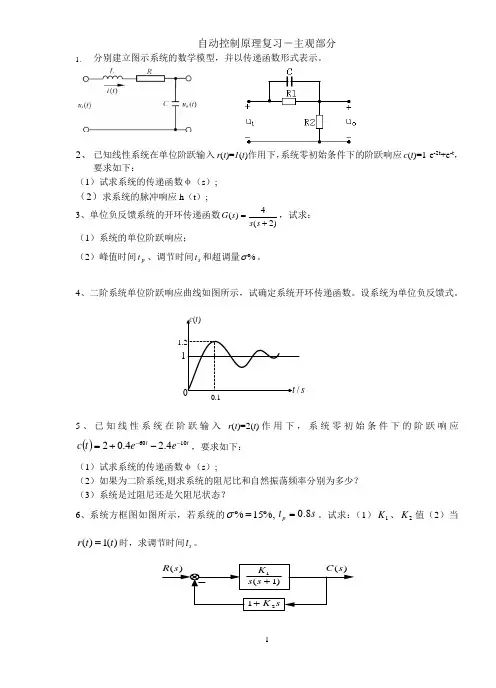
自动控制原理复习－主观部分1、分别建立图示系统的数学模型，并以传递函数形式表示。

2、已知线性系统在单位阶跃输入r(t)=1(t)作用下，系统零初始条件下的阶跃响应c(t)=1-e-2t+e-t，要求如下：（1）试求系统的传递函数φ（s）;（2）求系统的脉冲响应h（t）;3、单位负反馈系统的开环传递函数)2(4)(+=sssG，试求：（1）系统的单位阶跃响应；（2）峰值时间pt、调节时间s t和超调量%σ。

4、二阶系统单位阶跃响应曲线如图所示，试确定系统开环传递函数。

设系统为单位负反馈式。

5、已知线性系统在阶跃输入r(t)=2(t)作用下，系统零初始条件下的阶跃响应()tt eet c10604.24.02---+=，要求如下：（1）试求系统的传递函数φ（s）;（2）如果为二阶系统,则求系统的阻尼比和自然振荡频率分别为多少？（3）系统是过阻尼还是欠阻尼状态？6、系统方框图如图所示，若系统的%,15%=σstp8.0=。

试求：（1）1K、2K值（2）当)(1)(tt r=时，求调节时间st。

)1(1+ssKsK21+)(sR)(sCst/)(t c2.17、已知单位反馈系统的开环传递函数为()()()10141121022+++=s s s s s G ，输入为()()221t t t t r ++= 试求P K 、V K 和a K ．和ss e 。

如果()()()12120++=s s s G 时重新计算。

8、已知单位反馈系统的开环传递函数)5)(11.0(100)++=s s s G （（1）要求计算r (t )分别为1（t ），t 和t 2/2时，系统的静态误差系数（2）2/)(1)2t t t t r ++=（时系统的稳态误差。

9、如果已知单位反馈系统的开环传递函数)2)(11.0(100)++=s s s G （（1）要求计算r (t )分别为2，2t 和t 2/2时，系统的静态误差系数（2）输入信号为2/22)(2t t t r ++=时,求系统的稳态误差。

习题3-1.选择题：（1）已知单位负反馈闭环系统是稳定的，其开环传递函数为：)1(2)s )(2+++=s s s s G （，系统对单位斜坡的稳态误差是：a.0.5 b.1 3-2 已知系统脉冲响应t e t k 25.10125.0)(-=试求系统闭环传递函数)(s Φ。

解Φ()(./(.)s t s ==+001251253-3 一阶系统结构图如图3-45所示。

要求系统闭环增益2=ΦK ，调节时间4.0≤s t s ，试确定参数21,K K 的值。

图3.38 题3-3图解 由结构图写出闭环系统传递函数111)(212211211+=+=+=ΦK K sK K K s K sK K s K s令闭环增益212==ΦK K ， 得：5.02=K 令调节时间4.03321≤==K K T t s ，得：151≥K 。

3-4 设二阶控制系统的单位阶跃响应曲线如图 3.39 所示。

如果该系统为单位反馈控制系统，试确定其开环传递函数。

图3.39 题3-4图 解：由图2.8知，开环传递函数为3-5 设角速度指示随动统结构图如图3-40所示。

若要求系统单位阶跃响应无超调，且调节时间尽可能短，问开环增益K 应取何值，调节时间s t 是多少？图3-40 题3-5图解：依题意应取 1=ξ，这时可设闭环极点为02,11T -=λ。

写出系统闭环传递函数Ks s Ks 101010)(2++=Φ 闭环特征多项式20022021211010)(⎪⎪⎭⎫ ⎝⎛++=⎪⎪⎭⎫ ⎝⎛+=++=T s T s T s K s s s D 比较系数有 ⎪⎪⎩⎪⎪⎨⎧=⎪⎪⎭⎫ ⎝⎛=K T T 101102200 联立求解得 ⎩⎨⎧==5.22.00K T 因此有 159.075.40''<''==T t s3-6 图3.41所示为某控制系统结构图，是选择参数K 1和K 2，使系统的ωn =6，ξ=1.3-7 已知系统的特征方程，试判别系统的稳定性，并确定在右半s 平面根的个数及纯虚根。

东北农业大学网络教育学院自动控制原理作业题作业题（一）一、控制系统如图所示。

简述该系统的工作原理，说明该系统的给定值、被控制量和干扰量，并画出该系统的方块图。

图1-7发电机-电动机调速系统减速器负载Θr给定值被控量Wm+E -EΘrWm发电机-电动机调速系统二、求有源网络的传递函数。

三、单位反馈控制系统的开环传递函数为)1)(1()(2+++=cs bs as s Ks G ， 求：1）位置误差系数，速度误差系数和加速度误差系数；2）当参考输入为2)(1t t t ，，时，系统的稳态误差。

四、已知某一控制系统如图所示，其中)(s G c 为PID 控制器，它的传递函数为s K sK K s G d ip c ++=)(，要求校正后系统的闭环极点为1010j ±-和-100，确定PID 控制器的参数d i p K K K 和,。

五、已知某一单位反馈控制系统如图所示。

设计一串联校正装置)(s G c ，使校正后的系统同时满足下列性能指标要求： 跟踪输入221)(t t r =时的稳态误差为0.1；相位裕度为︒=45γ六、已知负反馈控制系统的开环传递函数为)2)(1()()(++=s s s ks H s G试绘制控制系统的根轨迹，并依此分析系统的稳定性，计算ξ=0.5时系统的动态性能。

作业题（二）一、控制系统如图所示，输入信号为t t r =)(。

要求系统输出响应的稳态误差为0，试确定K d 的值。

二、已知单位负反馈控制系统如图所示，试回答：1）G(s)=1时，闭环系统是否稳定？2）ss K s G p )1()(+=时，闭环系统的稳定条件是什么？三、单位反馈控制系统，若要求：（1）跟踪单位斜坡输入时系统的稳态误差为2（2）设该系统为三阶，其中一对复数闭环极点为1±j 求满足上述要求的开环传递函数。

四、系统方块图如图所示。

请画出信号流图，并利用梅逊公式求取传递函数C (s )/R (s )ABE+_+_+-11C s21R 21C s11R ()R s ()C s C D五、已知单位负反馈控制系统的开环传递函数为)15.0()()(+=s s Ks H s G应用根轨迹法分析开环放大倍数K 对系统的影响，计算K=5时系统的性能。

习题3-1.选择题：（1）已知单位负反馈闭环系统是稳定的，其开环传递函数为：)1(2)s )(2+++=s s s s G （，系统对单位斜坡的稳态误差是： 3-2 已知系统脉冲响应t e t k 25.10125.0)(-=试求系统闭环传递函数)(s Φ。

解 Φ()()./(.)s L k t s ==+001251253-3 一阶系统结构图如图3-45所示。

要求系统闭环增益2=ΦK ，调节时间4.0≤s t s ，试确定参数21,K K 的值。

…图 题3-3图解 由结构图写出闭环系统传递函数111)(212211211+=+=+=ΦK K sK K K s K sK K s K s 令闭环增益212==ΦK K ， 得：5.02=K 令调节时间4.03321≤==K K T t s ，得：151≥K 。

3-4 设二阶控制系统的单位阶跃响应曲线如图 所示。

如果该系统为单位反馈控制系统，试确定其开环传递函数。

图 题3-4图 解：由图知，`开环传递函数为3-5 设角速度指示随动统结构图如图3-40所示。

若要求系统单位阶跃响应无超调，且调节时间尽可能短，问开环增益K 应取何值，调节时间s t 是多少图3-40 题3-5图*解：依题意应取 1=ξ，这时可设闭环极点为02,11T -=λ。

写出系统闭环传递函数Ks s Ks 101010)(2++=Φ闭环特征多项式20022021211010)(⎪⎪⎭⎫⎝⎛++=⎪⎪⎭⎫⎝⎛+=++=T s T s T s K s s s D比较系数有 ⎪⎪⎩⎪⎪⎨⎧=⎪⎪⎭⎫ ⎝⎛=K T T 101102200 联立求解得 ⎩⎨⎧==5.22.00K T 因此有 159.075.40''<''==T t s；3-6 图所示为某控制系统结构图，是选择参数K 1和K 2，使系统的ωn =6，ξ=1. 【3-7 已知系统的特征方程，试判别系统的稳定性，并确定在右半s 平面根的个数及纯虚根。

选择题.1. 某环节的传递函数为G(s)=e-2s，它是( )。

A.比例环节B.延时环节C.惯性环节2. 系统的输出信号对控制作用的影响（）。

A. 开环有B. 闭环有C. 都有3. 若F(s)=421s+，则Lim f tt→0()=( )。

A. 4B. 2C. 04. 放大环节对数幅频特性为位于横轴上方与角频率ω无关且平行于横轴的直线，则其放大倍数K（）。

A. K 〉10B. K 〉1C. K 〉05. 对于系统的抗干扰能力（）。

A. 闭环强B. 开环强C. 两者一样6. 积分环节的频率特性与（）重合。

A. 负虚轴B.正虚轴C. 虚轴7. 放大环节对数幅频特性为位于横轴上方与角频率ω无关且平行于横轴的直线，则其放大倍数K（）。

A. K =1B. K 〉1C. K < 18. 传递函数是复变量s的有理真分式函数，分子的阶数m( )分母的阶数n 且所有系数均为实数。

A. 大于或等于B. 大于C. 小于或等于9. 线性系统稳定的充分必要条件是它的所有特征根具有（）的实数部分。

A. 负B. 正C. 零10. 系统的输出信号对控制作用的影响（）。

A. 开环有B. 闭环有C. 都有11.对于欠阻尼二阶系统,下列描述正确的的是（）。

A. 当ξ保持不变时，ωn 越大，系统的超调量σP越大B. 当ωn 不变时，阻尼比ξ越大，系统的调整时间ts越大C. 当ωn不变时，阻尼比ξ越大，系统的超调量σ越小12. 设单位反馈系统开环传递函数为G(s)=1/Ts,输入信号为r(t)=3t，则系统稳态误差ess等于（）。

A. TB. 3TC. 6T13. 惯性环节对数幅频特性曲线高频段的渐近线斜率为（）dB/dec。

A. 20B. -40C. -2014. 振荡环节对数幅频特性曲线高频段的渐近线斜率为（）dB/dec。

A. 20B. -40C. -2015. 下列校正环节的相位特征分别归类为相位超前校正的是（）。

A.P调节器B. PD调节器C. PID调节器16 当系统稳态性能不佳时，一般可采用以下措施改善（）。

试题编号：重庆邮电大学2009学年2学期《自动控制原理》试卷（期中）（A 卷）（闭卷）一、简答题（本大题共5小题，每小题4分，共20分） 1． 传递函数定义及其主要性质。

答：线性定常系统在零初始条件下，输出量的拉氏变换与输入量的拉氏变换之比，称为传递函数。

（2分）主要性质：(每回答正确2个1分，全部正确2分)1）传递函数只适用于线性定常系统：由于传递函数是基于拉氏变换，将原来的线性常系数微分方程从时域变换到复域，故只适用于线性定常系统。

2）传递函数是在零初始条件下定义的。

如果系统为非零初始条件，非零初始值V(s)，则系统新的输入、输出关系为：Y(s)=G(s).U(s)+ V(s)3)传递函数只表示了系统的端口关系，不明显表示系统内部部件的信息。

因此对于同一个物理系统，如果描述的端口不同，其传递函数也可能不同；而不同的物理系统，其传递函数可能相同。

4)传递函数是复变量S 的有理真分式函数，分子多项式的次数n 低于或等于分母多项的次数m ，所有系数均为实数。

2． 线性控制系统的稳定性定义。

答：如果线性控制系统在初始扰动的影响下，其动态过程随时间的推移逐渐衰减并趋于零或原平衡点，则称系统渐进稳定，简称稳定（3分），反之，如果在初始扰动下，系统的动态过程随时间的推移而发散，则不稳定。

（1分）3． 闭环系统的零、极点位置对于时间响应性能的超调量、调节时间的有何影响？ 答：（1）超调量主要取决于闭环复数主导极点的衰减率21//ξξωσ-=d ，与其他闭环零、极点接近坐标原点的程度有关；（2分）（2）条件时间主要取决于靠近虚轴的闭环复数极点的实部绝对值ξωσ=，如果实数极点距离虚轴最近，并且它附近没有实数零点，则调节时间主要取决于该实数极点的模值。

（2分）4． 对于一个给定的开环增益为o k 最小相位系统，说明采用频率方法和根轨迹法判断稳定性的统一性。

答：频率法判断系统稳定性时，当o k 较小时，其副相曲线在)(ωj Go 平面不包围（-1，j0）这点，系统稳定，随着o k 的增加，副相曲线包围（-1，j0）这点，系统不稳定。

⾃动控制原理答案黄坚习题详解汇总第⼆章⾃动控制系统的数学模型习题2-1 试建⽴图⽰电路的动态微分⽅程。

解：（a ）解法⼀：直接列微分⽅程组法-==+O i C O C C u u u R u R u dt du C 21i i O O u CR dt du u R CR R R dt du 121211+=++? 解法⼆：应⽤复数阻抗概念求)()(11)(11s U s I Cs R Cs R s U O i ++= （1） 2)()(R s U s I O = （2）联⽴式（1）、（2），可解得： Cs R R R R Cs R R s U s U i o 2 12112)1()()(+++= 微分⽅程为: i ioo u CR dt du u R CR R R dt du 121211+=++ （b ）解法⼀：直接列微分⽅程组法++=+===COC i O L C O L L L u R u dt du C R u u u u R u i dt di L u)(212 (a) (b) + u C -io o o u R u R R dt du C R R L dt u d LC R 22121221)()(=++++?解法⼆：应⽤复数阻抗概念求++=+=)(]1)()([)()()()(2122s U sC s U R s U R s U Ls R R s U s U CC O i OC)()()()()()(2212121s U R s U R R s sU C R R L s U LCs R io o o =++++? 拉⽒反变换可得系统微分⽅程：io o o u R u R R dt du C R R L dt u d LC R 22121221)()(=++++2-7 证明图⽰的机械系统(a)和电⽹络系统(b)是相似系统（即有相同形式的数学模型）。

解：(a)取A 、B 两点分别进⾏受⼒分析。

1、设二阶控制系统的单位阶跃响应曲线如图所示，若该系统为单位反馈控制系统，
试确定其单位传递函数。

(20%)
2、已知某系统结构图如下，求其闭环传递函数C（S）/R（S）。

(10%)
3、已知单位反馈系统，开环传函为G（S）=K/[S（TS+1）]，要求单位阶跃函数
作用时，超调量为16%，调节时间为7，求K，T。

(10%)
4、已知单位反馈系统，开环传函为G（S）=k(S+1)/[S(S+1/2)2]，试绘制k从零趋
近于无穷大时的根轨迹。

(10%)
5、已知最小相位系统开环频率特性的伯德图，（1）求开环增益K。

（2）求穿越频
率wc。

（3）写出开环传递函数。

（4）求相角裕度。

（5）求幅值裕度。

（6）判断闭环系统的稳定性。

(15%)
6、求使图示系统稳定的K值的范围。

(10%)
7、已知线性元件的频率特性及非线性元件描述函数有关的曲线，两者串联起来构
成一单位反馈系统图示，判断系统是否存在自振。

(5%)
8、试小结用频率法进行超前校正的主要步骤。

(10%)
9、某离散系统的闭环脉冲传递函数为G（z）=(3.68z+2.64)/(z2+2.31z+3),判断该系
统的稳定性。

（10%）。

1.设二阶控制系统的单位阶跃响应曲线如图所示，若该系统为单位反馈控制系统， 试确定其单位传递函数。

解：由图知，该系统为欠阻尼二阶系统，从图中直接得出%30%=σ s t p 1.0=根据公式3.0%21==--ζπζσe1.012=-=ζωπn p t解得 358.0)(ln )(ln 222=+=σπσζ 1265.331-=-=s t p n ζπω于是开环传递函数为 )1.24(3.1132)2()(2+=+=s s s s s G n ζωω2.已知控制系统结构如图所示，（1） 当b=0时，试确定单位阶跃输入时系统的阻尼系数、自然频率、最大超调量以及单位斜坡输入所引起的稳态误差。

（2） 确定系统阻尼比为0.8时的速度反馈常数b 的值，并确定在单位阶跃输入下系统的最大超调量和单位斜坡输入所引起的稳态误差。

（3） 怎样使上一问的阻尼比保持0.8不变而使其稳态误差等于第一问的稳态误差值。

（1） 当b=0时，开环传递函数为)4(16)(+=s s s G闭环传递函数16416)(2++=s s s φ 75.15.3%,3.16%,2124,41621========∴--n s n n t e ζωσωζωζπζ当r(t)=t 时，25.01==K e ss （2） 当b 不为0时， 4,16)164(16)()164(16)(2=+++=⇒++=n s b s s b s s s G ωφ 令 15.022/121648.0=⇒+=+==b b b n ωζ 094.15.3%,52.1%21====∴--n s t e ζωσζπζ 当r(t)=t 时4.01==K e ss （3） 使用比例加微分串联校正可以达到目的，如图所示，这时在原闭环系统上加入一零点。

3.如图所示的控制系统结构图，误差E(s)在输入端定义，扰动输入n(t)=2 X 1(t).(1) 试求K=40时，系统在扰动输入下的稳态输出和稳态误差。