七年级数学下册 5.1 轴对称 轴对称中的作图题素材 (新版)湘教版

轴对称的性质及其应用轴对称的性质有二:(1)对应点所连的线段被对称轴垂直平分，对应线段相等,对应角相等;(2)两个图形关于某直线对称，如果它们的对应线段(或延长线）相交，那么交点在对称轴上,下面例谈轴对称轴性质的应用：一、补画图形为轴对称图形例1 如图1是由三个小正方形组成的图形,请你在图中补画一个小正方形，使补画后的图形为轴对称图形（尽可能多画几个图）分析:利用性质（1)作图。

解：所作图有下面几种图点评:本类型题可先作出对称轴，然后由轴对称的性质（1）补全图.二、设计路程最短问题例2 如图2，李庄M计划向两旁的交叉公路l1、l2旁设两上供货点，为使每次向两个供货点供货所走的路程最短,问供货点应设在什么地方？图分析：要让所走路程最短，可以尝试利用轴对称性质，分别作点M关于直线l1、l2的对称点M1、M2；连结M1M2分别交直线l1、l2于点A、B。

解:如图2，作M 关于l 1、l 2的对称点M 1、M 2，连M 1M 2交l 1、l 2于A 、B ，则A 、B 为两个供货点，因为MA+AB+BM=MM 1+AB+BM 2,所以沿着MA 、AB 、BM 供货,路程最短。

点评:本类型是由轴对称的性质（1）作点关于直线（对称轴）的对称点，然后解决问题。

三、求角度例3 如图3，已知△ABC 中，∠A=40°，AB=AC ，MN 是△DAB 的对称轴，交AB 于M ，AC 于D ，求∠DBC 的度数。

分析：利用等腰三角形和轴对称的性质解题。

解：因为∠A=40°,AB=AC，所以∠C=∠ABC=240180︒-︒=70°。

因为MN 是AB 的对称轴，由性质（1）知∠DAM=∠DBM ,所以∠DBM=40°,∠DBC=∠ABC -∠ABD=70°—40°=30°.四、折纸问题例4 如图4所示，把一张长方形纸片ABCD 沿EF 折叠后,点D 、C 分别落在点D′、C′的位置上,D′E 与BC 相交于点G,若∠CFC′=110°，求∠AEG 和∠FGD′的度数.图N图P分析：折纸问题是一种轴对称问题，折痕是对称轴，本题可利用轴对称性质(2）解决问题。

《轴对称的性质》典型例题例1 把下面的图补充完整．（1）如图甲是轴对称图形的一部分，其中l 是对称轴，请把另一部分画出来．（2）如图乙，是轴对称中的一个图形，其中l 是对称轴，请把另一个画出来．例2 如图所示，填空:(1)线段AB 的对应线段是__________（2）点C 的对应点是__________（3)ABC ∠的对应角是_________（4）连接BE ，则BE 被直线_____m例3 如图，在ABC ∆中，AD AC AB ,=平分BAC ∠,点P 在DA 的延长线上，你能利用轴对称的性质证明PB PC =吗？例4作出下列图形的对称轴或者对称图形图1 图2例5分析下列图形中,哪些是轴对称图形？如果是轴对称图形,作出对称轴．(1）线段；（2）角；（3）任意三角形;（4）等腰三角形参考答案例1 作法：（1）①过A 、B 两点分别作直线l 的垂线，交l 于E 、F 两点；②截取FB B F EA A E ='=',；③连结D B A C ''、、，就是所求作图形．（2）类似于(1）可以作出（2）来．说明：我们作图的依据就是轴对称（或轴对称图形)的对称轴，垂直平分它们对应点连成的线段．例2 分析：依据轴对称或轴对称图形的性质可以得到解：分别是(1）AE （2）D (3)AED ∠ （4）垂直平分例3 分析:轴对称性质可以证明线段相等解：因为AC AB =DAC BAD ∠=∠AD AD =所以BAD ∆≌CAD ∆所以AD 垂直平分BC点P 在DA 的延长线上所以PA 、PB 关于PD 对称所以PB PC =本题的其他解法略例4 分析：在图1中给出对称轴,可以根据对称轴的性质，对应点连线被对称轴垂直平分画出另一部分，在图2中，根据轴对称的性质，很容易画出对称轴．解:如图1′,2′图1′ 图2′就是要求做的对称图形OEF直线m就是所求做的对称轴．例5分析：线段、角、等腰直角三角形是轴对称图形．解：线段的对称轴是线段AB所在的直线和它的垂直平分线．（如图1)角的对称轴是角的平分线所在的直线；（如图2）等腰直角三角形的对称轴是底边的垂直平分线．（如图3）图1 图2 图3尊敬的读者：本文由我和我的同事在百忙中收集整编出来，本文档在发布之前我们对内容进行仔细校对，但是难免会有不尽如人意之处，如有疏漏之处请指正，希望本文能为您解开疑惑,引发思考。

第5章轴对称与旋转
5．1 轴对称
5．1.1 轴对称图形
基础题
知识点1 轴对称图形
1．(郴州中考)下列图案是轴对称图形的是(A)
2．(衡阳中考)下列图案中，不是轴对称图形的是(A)
知识点2 对称轴
3．(山西中考)如图，正方形地砖的图案是轴对称图形，该图形的对称轴有(C)
A．1条
B．2条
C．4条
D．8条
4．下图中的五角星有几条对称轴？请作出这些对称轴．
解：有5条对称轴．如图所示．
5．下面的图形是轴对称图形吗？如果是，画出它的对称轴．
解：略．
中档题
6．(西宁中考)在一些汉字的美术字中，有的是轴对称图形．下面四个美术字中可以看作轴对称图形的是(D)
7．(青海中考)以下图形中对称轴的数量小于3的是(D)
8．下列四句话中的文字有三句具有对称规律，其中没有这种规律的一句是(B)
A．上海自来水来自海上
B．有志者事竟成
C．清水池里池水清
D．蜜蜂酿蜂蜜
9．如图，在3×3的正方形网格中，已有两个小正方形被涂黑，再将图中剩余的编号为1－7的小正方形中任意一个涂黑，则所得图案是一个轴对称图形的编号有2，3，4，5，7．
10．如图，从我们今天这节课学习的知识来考虑，哪一个与其他三个不同？请指出这个图形，并简述你的理由．
解：图形②.理由是：只有图形②不是轴对称图形．
综合题
11．如图，等边三角形中，已有两个小等边三角形被涂黑，再将图中其余小等边三角形涂黑一个，使整个被涂黑的图案构成一个轴对称图形，作出所有的图形．
解：如图所示，方法有3种．。

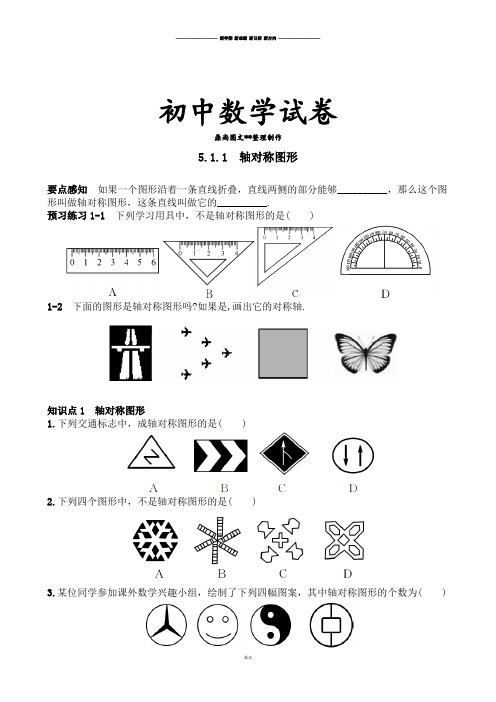
初中数学试卷鼎尚图文**整理制作5.1.1 轴对称图形要点感知如果一个图形沿着一条直线折叠，直线两侧的部分能够__________，那么这个图形叫做轴对称图形，这条直线叫做它的__________.预习练习1-1 下列学习用具中，不是轴对称图形的是( )1-2下面的图形是轴对称图形吗?如果是,画出它的对称轴.知识点1 轴对称图形1.下列交通标志中，成轴对称图形的是( )2.下列四个图形中，不是轴对称图形的是( )3.某位同学参加课外数学兴趣小组，绘制了下列四幅图案，其中轴对称图形的个数为( )A．1个 B．2个 C．3个 D．4个4.下列说法中错误的是( )A.教室里的黑板是轴对称图形B.扑克牌中的梅花图案是轴对称图形C.五星红旗的五角星图案不是轴对称图形D.英文字母印刷体大写“W”是轴对称图形知识点2 对称轴5.如图，正方形地砖的图案是轴对称图形，该图形的对称轴有( )A.1条B.2条C.4条D.8条6.下列“数字”图形中，有且仅有一条对称轴的是( )7.下列关于轴对称图形的对称轴的说法中正确的是( )A.轴对称图形的对称轴只能是一条B.轴对称图形的对称轴一定是线段C.轴对称图形的对称轴可以有多条D.轴对称图形的对称轴一定是射线8.下图中的五角星有几条对称轴？请作出这些对称轴.9.下列图形中，不是轴对称图形的是( )10.永州的文化底蕴深厚，永州人民的生活健康向上，如瑶族长鼓舞，东安武术，宁远举重等，下面的四幅简笔画是从永州的文化活动中抽象出来的，其中是轴对称图形的是( )11.下列四句话中的文字有三句具有对称规律，其中没有这种规律的一句是( )A.上海自来水来自海上B.有志者事竟成C.清水池里池水清D.蜜蜂酿蜂蜜12.正方形的对称轴的条数为( )A．1 B．2 C．3 D．4 13.下列四个图形：其中是轴对称图形，且对称轴的条数为2的图形的个数是( )A．1 B．2 C．3 D．414.如图，正三角形网格中，已有两个小正三角形被涂黑，再将图中其余小正三角形涂黑一个，使整个被涂黑的图案构成一个轴对称图形的方法有__________种.15.如图，从我们今天这节课学习的知识来考虑，哪一个与其他三个不同？请指出这个图形，并简述你的理由.16.分别找出具有一条对称轴、两条对称轴、三条对称轴、四条对称轴的几何图形，并画出来(包括对称轴).17.我们把形如abba的四位数称为“对称数”，如1 991、2 002等，试问在1 000～2 000之间有几个“对称数”？18.请在下面这一组图形符号中找出它们所蕴含的内在规律，然后在横线上的空白处填上恰当的图案.19.一天，小明发现如果将4棵树栽于正方形的四个顶点上，如图(1)所示，恰好构成一个对称图形.你还能找到其他两种栽树的方法，也使其组成一个轴对称图形吗？请在图（2）、（3）上表示出来.如果是栽5棵树，又如何呢？6棵、7棵呢？请分别在图（4）、（5）、（6）上表示出来.参考答案要点感知互相重合对称轴预习练习1-1 C1-2略.1.B2.B3.C4.C5.C6.A7.C8.有5条对称轴.图略.9.C 10.C 11.B 12.D 13.C 14.315.图形②.理由是：图形②不是轴对称图形.16.答案不唯一，图略.17.有1 001，1 111，1 221，1 331，…，1 991，共10个.18.每个图形是由各数字和它的轴对称数字组成的轴对称图形.图略.19.答案不唯一，如图所示.。

轴对称中的作图题由于与轴对称有关的作图题，能有效的考查同学们的动手操作能力和空间想象能力，一直是考试的热点，下面就这方面的问题选取数例加以归析，供同学们参考。

一、画轴对称例1、如图，已知△ABC和直线MN，画出△EFG，使△EFG与△ABC关于直线MN对称。

分析：只需分别作△ABC的三个顶点A、B、C的对称点E、F、G，然后顺次连结E、F、G即可。

解：方法一：作AO⊥MN，垂足为O，在AO的延长线上截取OE=OA，点E就是点A关于直线MN的对称点，同法画点B、C的对称点F、G，然后顺次连结E、F、G得△EFG。

则△EFG就是所求。

方法二：也可以利用全等知识进行作图，即先出A、E的对称点E、G，然后分别以E、G 为圆心，AB、CB为半径作弧，两弧交于点F。

则△EFG就是所求。

二、确定对称点例2、如图，四边形ABCD和四边形EFGH关于直线MN对称，连接AC与BD，设它们交于点P，怎样找出点P关于MN的对称点Q？分析：找点P关于对称轴的对称点Q，有多种方法。

关键是要充分利用轴对称的性质。

解：方法一：沿直线MN对折，在点P扎孔找到对称点Q；方法二：连接FH或EG，过点P作MN的垂线，交FH于点Q，点Q即为所求；方法三：连接HG，EG交于点Q，Q就是点P关于直线MN的对称点方法四：作点P关于直线MN的对称点Q，作PO⊥MN，垂足为O，在PO的延长线上截取OQ=OP，点Q就是点P关于直线MN的对称点。

方法五：连接FH，在FH上分别截取FQ=BP或HQ=DP，得到点Q，则点Q即为所求；三、确定对称轴例3、如图，△EFG与△ABC关于某直线成轴对称，请用不同的方法确定对称轴。

分析：确定对称轴的关键是利用对称轴是对称点连线的垂直平分线和对应边（或延长线的交点）在对称轴上。

解：方法一：连接对称点C、G与对称点A、E，再取CG、AE的中点M、N，直线MN就是所求的对称轴；方法二：连接对称点C、G，再作CG的中垂线MN，直线MN就是所求的对称轴；方法三：连接对称点C、G，再分别延长BC、FG交于M，过M作CG的垂线MN，直线MN 就是所求的对称轴。

《轴对称》典型例题例1 指出下列图形中的轴对称图形例2 指出下列图形中的轴对称图形，并指出轴对称图形的对称轴．(1)正方形；(2)长方形；(3)圆；(4)平行四边形．例3 画出下列图形的对称轴。

例4 指出下边哪组图形是轴对称的，并指出对称轴．(1)任意两个半径相等的圆；(2)正方形的一条对角线把一个正方形分成的两个三角形；(3)长方形的一条对角线把长方形分成的两个三角形；(4)两个全等的三角形．(1) (2) (3) (4)(5) (6) (7) (8)例5 找出下面的轴对称图形，并说出它们各有几条对称轴．例6 下列图形中，不是轴对称图形的是( )(A)有两个角相等的三角形(B)有一个内角是︒45的直角三角形(C)有一个内角是︒30，另一个内角为︒120的三角形(D)有一个角是︒30的直角三角形例7 观察中(1)～(5)，它们是不是轴对称图形?有什么共同特点?例8 请分别画出下图中3个图形的对称轴．例9 如图，(1)正三角形，(2)正四边形，(3)正五边形，(4)正六边形，(5)正八边形，(6)正九边形都是轴对称图形，数一数它们的对称轴的条数．观察后分析：正多边形对称轴的条数与边数"有什么关系?根据你的分析结果回答，正十边形，正十六边形，正二十九边形分别有几条对称轴?正五十边形呢?正一百边形呢?参考答案例1分析：正确理解轴对称图形概念．解：轴对称图形是(2)(3)(4)(6)(7)(8)例2 分析：判断一个图形是否是轴对称图形，关键是能否找到一条直线使该图的两部分沿这条直线对折后完全重合．解：(1)、(2)、(3)都是轴对称图形，(4)不是轴对称图形．正方形的对称轴是两条对边中点所在的直线和正方形对角线所在的直线；长方形的对称轴是两条对边中点所在的直线；圆的对称轴是任意一条直径所在的直线．说明：对称轴是一条直线，不是线段．例3分析：依据定义可以画出，但可能是多条．解：如图例4 分析：判断两个图形是否是轴对称，关键是能否找到一条直线使这两个图形沿这条直线对折后能够重合．解：(1)和(2)每组的两个图形都是轴对称的．(3)和(4)每组的两个图形不是轴对称的．(1)的对称轴是连结两个圆心的线段的垂直平分线；(2)的对称轴就是原正方形分成两三角形时的这条对角线所在的直线．说明：对称轴是直线而非线段．例5分析：本题主要考查识别轴对称图形的能力．根据轴对称图形的概念来认真识别．但要注意．图(9)(10)这两个图也有“对称”性，但它们没有对称轴．不能把它们误认为是轴对称图形．解：根据图形可知：(1)是轴对称图形，它有3条对称轴；(2)是轴对称图形，它有5条对称轴；(3)是轴对称图形．它有4条对称轴.(4)是轴对称图形．它有1条对称轴；(5)是轴对称图形，它有2条对称轴；(6)不是轴对称图形；(7)是轴对称图形，它有1条对称轴；(8)是轴对称图形，它有1条对称轴；(9)(10)虽然有“对称”性，但都不是轴对称图形．例6 分析：在(A)中，有两个角相等的三角形一定是等腰三角形，而等腰三角形一定是轴对称图形，它的对称轴为底边上的高(或底边上的中线或顶角的平分线). 而(B)和(C)中的两个三角形同样也是等腰三角形，所以也是轴对称图形. 那么(D)中三角形的三个内角各不相等，不是等腰三角形，所以(D)不是轴对称图形.解：选(D)说明：在三角形中，只有等腰三角形才是轴对称图形，而不是等腰三角形的三角形就一定不是轴对称图形.例7分析：本题主要考查两个图形成轴对称图形的理解．可以利用轴对称的概念加以判断，但不能把两个图形成轴对称与一个图形是轴对称图形的概念相混淆．解：它们都是轴对称图形，每一组中都有两个图形．可以沿某一条直线对折使两个图形能完全重合在一起，所以每幅图中的两个图形成轴对称．轴对称图形是一个图形．可以有一条或许多条对称轴．(1)～(5)两个图形成轴对称，一般来说只有一条对称轴．例8分析：找对称轴从不同角度观察，全面分析．解：(1)有6条对称轴；(2)有5条对称轴；(3)有6条对称轴．画图略．例9分析：正多边形并不都是轴对称图形．但是，是轴对称图形的正多边形的对称轴的条数与其边数有着密切的联系，请仔细找出它们之间的规律．解：正三角形有3条对称轴，正四边形有4条对称轴，正五边形有5条对称轴，正六边形就有6条对称轴，正八边形有8条对称轴，正九边形有9条对称轴．正多边形对称轴的条数与边数n之间的关系是：边数是n，对称轴的条数是n条．所以正十边形有10条对称轴，正十六边形有16条对称轴，正二十九边形就有29条对称轴，正五十边形就有50条对称轴，正一百边形就有100条对称轴．。