五校2018_2019学年高一数学上学期第一次联考试题

江苏省盱眙中学、泗洪中学2018～2019学年度第一学期第一次月检测高一数学试题一、选择题：本大题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.【2016北京理科1】已知集合，，则A. B.C. D.2.已知集合A=，B=，则A. A B=B. A BC. A BD. A B=R3.函数，则= （）A. 1B. -1C. 2018D. -20184.已知全集,集合,集合,则集合（）A. B. C. D.5.函数的单调递增区间是（）A. B. C. D.6.已知函数，则函数的值域为（）A. B. C. D.7.已知函数分别由下表给出则不等式的解集为（）.A. B. C. D.8.已知函数且.则（）A. B. C. D.二、填空题：本题共6小题，每小题5分，共30分。

9.已知集合,,则集合=______．10.若，则=___________．11.已知若B是A的子集，则实数m的取值范围为___．12.函数的值域为_______．13.已知，则不等式的解集是______．14.若函数在区间上单调递减，在上单调递增，则实数的取值范围是_________．三、解答题：共80分，解答时应写出文字说明、证明过程或演算步骤15.已知集合，求：（1）；（2）16.已知函数的定义域为集合，函数的值域为集合．（1）求，；（2）设集合，若，求实数的取值范围．17.已知函数（1）若，求的定义域；（2）若，证明：函数在区间（0,2）上是减函数.18.如图，有一块长方形的绿地ABCD，经测量百米，百米，，拟过线段BC上一点E 设计一条直路EF（点F在四边形ABCD的边上，不计路的宽度），EF将绿地分成两部分，且右边面积是左边面积的3倍，设百米，百米．学_科_网...（1）当点F与点D重合时，试确定点E的位置；（2）当点F在DA上时，求路EF的长度y取值范围．19.已知函数.（1）若在区间上不单调，求的取值范围；（2）证明：函数图像与直线恒有交点；（3）若，求函数在的最大值。

2018~2019学年名校联盟高一第一次联考数 学一、选择题1.已知集合2{|21}A y y x x ==+-，则R C A =（ ）A.(,2)-∞-B.(,2]-∞-C.[2,)-+∞D.(2,)-+∞答案：A解答：由2{|(1)2}[2,)A y y x ==+-=-+∞，(,2)R C A =-∞-.2.函数02(1)()1x f x x -=++ ）A.(1,2]B.(,2]-∞C.(,1)-∞D.(,1)(1,2]-∞答案：D解答：由题意有1020x x -≠⎧⎨-≥⎩，得2x ≤且1x ≠.3.已知函数322,1(),1x x f x x ax x⎧+<⎪=⎨-≥⎪⎩，若[(0)]2f f =-，则实数a =（）A.2B.3C.4D.5答案：B解答：由[(0)](2)422f f f a ==-=-，解得3a =.4.下列函数中与函数||y x =相等的函数为（ ）A.2y =B.y =C.y =D.2x y x =答案：C解答：因为2(0)y x x ==≥，y x ==，y x ==，2(0)x y x x x ==≠，所以y x ==.5.若2{1,22}a a a ∈-+，则实数a 的值为（ ）A.1B.2C.0D.1或2答案：B解答：当1a =时，则2221a a -+=违背了集合的互异性，故1a ≠，必有222a a a -+=，解得：1a =(舍去)或2a =，故实数a 的值为2.6.函数42()2f x x x =-的值域为（ ）A.[0,)+∞B.(,0]-∞C.[1,)-+∞D.(,1]-∞-答案：C解答：由22()(1)11f x x =--≥-，故函数()f x 的值域为[1,)-+∞. 7.函数21()||f x x x =+的图象为（） A.B.C.D.答案：D解答：因为()()2211()f x f x x x x x===-+-+-，所以()f x 在其定义域R 上为偶函数，即排除A 、B ，又因为()1102f =>，故选D. 8.已知集合2{|}1A x Z Z x =∈∈-，则集合A 的真子集的个数为（ ） A.13B.14C.15D.16 答案：C解答：当且仅当11x -=±或2±时，21Z x ∈-，解得1x =-或0或2或3，则{1,0,2,3}A =-， ∵集合A 有四个元素，∴集合A 的真子集的个数为421-=15.9.若2(1)f x x x -=-，则(1)f x +=（ ）A.232x x ++B.221x x --C.22x x +D.241x x ++答案：A解答：由22(1)[(2)1](2)(2)32f x f x x x x x +=+-=+-+=++.10.在边长为2的菱形ABCD 中，60ABC ∠=︒，动点P 由点C 开始沿菱形边逆时针运动到点B （不包括B 、C 两点），若(06)CP x x =<<，PBC ∆的面积为y ，则y 关于x 的函数关系式为（ ）A.,024),46x y x x x <<=≤≤⎨-<<B.1,02241(6),462x x y x x x ⎧<<⎪⎪⎪=≤≤⎨⎪⎪-<<⎪⎩C.,0241(6),462x x y x x x ⎧<<⎪=≤≤⎪-<<⎩D.,024),46x x y x x x <<=≤≤-<<⎩答案：D解答：①当02x <<时，122y x =⨯=； ②当24x ≤≤时，11222ABCD y S ==⨯= ③当46x <<时，12))2y x x =⨯-=-； 故y 关于x的函数关系式为,024),46x x y x x x <<=≤≤-<<⎩.11.已知函数2,1()23,1ax a x f x ax ax a x +≥⎧=⎨-+-+<⎩，若函数()f x 的值域为R ，则实数a 的取值范围是（ ） A.3(0,]2B.3(1,]2C.[2,)+∞D.[3,)+∞答案：A解答：由2,1()(1)3,1ax a x f x a x x +≥⎧=⎨--+<⎩，①当0a =时，0,1()3,1x f x x ≥⎧=⎨<⎩与()f x 的值域为R 矛盾； ②当0a <时，1x ≥时，有()2f x ax a a =+≤0<，而二次函数2(1)3y a x =--+开口向上，()3f x >，此时函数()f x 的值域不可能为R ； ③当0a >，1x ≥时，()2f x a ≥，当0a >，1x <时，()3f x <，若函数()f x 的值域为R ，只需23a ≤，可得302a <≤，由上知实数a 的取值范围是302a <≤. 12.已知定义在R 上的函数21,0()1,0x f x x x ⎧≠⎪=⎨⎪=⎩，若关于x 的方程2[()]()0f x bf x c ++=有5个不同的实数解，分别为1x ，2x ，3x ，4x ，5x ，且满足12345x x x x x <<<<，则 15324(2)f x x x x x ++--=（ ） A.14B.1C.18D.19答案：B解答：易知函数()f x 为偶函数，若方程2[()]()0f x bf x c ++=有5个不同的实数解， 则方程20t bt c ++=有两个不相等的实数根.显然1x 与5x ，2x 与4x 关于原点对称，30x =， 则15324(2)(0)1f x x x x x f ++--==.二、填空题13.若{|122}A x x =-≤-≤，{|3}B x x =>，则AB = .答案： {|34}x x <≤解答：由{|14}A x x =≤≤，则{|34}AB x x =<≤. 14.函数12y x =-的单调减区间为 . 答案： (,2)-∞，(2,)+∞解答： 函数12y x =-可看作1y x=向右平移2个单位得到， 因为1y x=在(,0)-∞和(0,)+∞单调递减， 所以12y x =-在(,2)-∞和(2,)+∞单调递减.15.已知函数()f x ax =的最小值为34，则实数a = . 答案：1解答：t =，则22()(1)(0)y f x a t t at t a t ==+-=-+≥，若0a ≤时，()f x 不存在最小值.当0a >时，12t a =时，()f x 取得最小值，所以213424a a a a -+=， 24310a a --=，1a =.16.定义域为[2,2]-的减函数()f x 是奇函数，若(2)1f -=，则221()t at a f x -++≤对所有的11t -≤≤，及22x -≤≤都成立的实数a 的取值范围为 .答案： (,3]-∞-解答：由题意有(2)(2)1f f =--=-，又因为()f x 在[2,2]-上单调递减，所以()()21f x f ≥=-，故当11t -≤≤时，2211t at a -++≤-，即2220t at a -++≤，令2()22g t t at a =-++，只需(1)330(1)30g a g a -=+≤⎧⎨=+≤⎩， 解得：3a ≤-.三、解答题17.已知集合{|13}A x a x a =-<<+，{|21}B x x =-≤≤.（1）当0a =时，求A B ； （2）若()B AB ⊆，求实数a 的取值范围. 答案：（1）{|23}A B x x =-≤<；（2）(2,1)--.解答：（1）当0a =时，有{|13}A x x =-<<，则{|23}A B x x =-≤<，（2）由()B AB ⊆知B A ⊆， 故有1231a a -<-⎧⎨+>⎩，解得：21a -<<-，故实数a 的取值范围为(2,1)--.18.已知函数2()f x =（1）求函数()f x 的定义域；（2）画出函数()f x 的图象.（1）{|1}x x ≠±；（2）略.解答：（1）由221()||1x f x x -==-，令||10x -≠可得1x ≠±， 故函数()f x 的定义域为{|1}x x ≠±.（2）由，故函数()f x 的图象为19.如图所示，动物园要建造一面靠墙的3间面积相同的矩形熊猫居室，如果可供建造围墙的材料总长为48m ，那么宽x （单位：m ）为多少，才能使所建造的每间熊猫居室面积最大？每间熊猫居室的最大面积是多少？答案：宽6x m =时，每间熊猫居室面积最大，最大值为248m .解答： 由题意知每间熊猫居室的面积1(484)3S x x =-. 又0448x <<，∴012x <<. 224416(6)4833S x x x =-=--+. ∴6x =时，max 48S =.即宽6x m =时，每间熊猫居室面积最大，最大值为248m .20.若函数2()22f x x ax a =-+的定义域和值域均为[1,1]-，求实数a 的值.当1a =2()22f x x ax a =-+的定义域和值域均为[1,1]-. 解答：由二次函数()f x 的对称轴为x a =，①当1a ≥，min ()(1)11f x f ==≠-（舍去），②当1a ≤-时，min max ()(1)411()(1)1f x f a f x f =-=+=-⎧⎨==⎩，解得12a =-（不合题意舍去）， ③当11a -<<时，2min ()()21f x f a a a ==-=-，解得：1a =1a =+合题意舍去），∵11a -<=0<，∴1()(1)(1)1f a f f -=<-<=，则当1a =2()22f x x ax a =-+的定义域和值域均为[1,1]-.21.已知函数2()m f x x n =+的图象过点(0,1)，1(1,)2-. （1）求m ，n 的值，并判断函数()f x 的奇偶性；（2）证明函数()f x 在[0,)+∞上是减函数；（3）若(3)(2)f a f a ->，求实数a 的取值范围.答案：（1）略；（2）略；（3）(,3)(1,)-∞-+∞.解答： （1）由(0)1f =得1m n=， 由1(1)12m f n -==+，联立解得1m n ==. ∴21()1f x x =+，定义域为R . ∵2211()()()11f x f x x x -===-++，∴()f x 是偶函数. 证明：（2）设120x x ≤<，则222121211222222212121211(1)(1)()()()()011(1)(1)(1)(1)x x x x x x f x f x x x x x x x ---+--=-==>++++++， ∴12()()f x f x >，∴()f x 在[0,)+∞上是减函数.（3）由（1）（2）可知，为偶函数，且在上是减函数，在(,0]-∞上为增函数，所以⇔32a a -<，整理得：2230a a +->，所以(3)(1)0a a +->，即1a >或.即时，实数a 的取值范围是(,3)(1,)-∞-+∞. 22.已知二次函数2()(0,,)f x ax bx c a b R c R =++≠∈∈，且函数图象过点(1,0).（1）若函数()f x 图象的对称轴方程为14x =，方程()530f x x ++=有两个相等的实数根， 求函数()f x 的解析式；（2）令函数()()3g x f x bx =-，若1x ，2x 为方程()0g x =的两个实数根，求21||x x -的最小值.答案：（1）2()21f x x x =--或2502525()999f x x x =--； （2）略.解答： （1）由题意有0124a b c b a ++=⎧⎪⎨-=⎪⎩，得2a b c b =-⎧⎨=⎩，则2()2f x bx bx b =-++. 方程()530f x x ++=可化为：22(5)(3)0bx b x b -++++=， 2(5)8(3)0b b b ∆=+++=，解得：1b =-或259-， 故函数()f x 的解析式为2()21f x x x =--或2502525()999f x x x =--. （2）由（1）知，c a b =--，方程()0g x =可化为220ax bx c -+=， 有12122b x x a cx x a ⎧+=⎪⎪⎨⎪=⎪⎩，且2440b ac ∆=->.21()1f x x =+[0,)+∞(3)(2)f a f a ->3a <-(3)(2)f a f a ->21||x x -=====≥. 当21||x x -取最小值时，2a b =-，c b =，22248120b b b ∆=+=>， 此时方程有两个解，符合题意.。

注意事项：1）、开始答卷前，考生务必将自己的姓名、准考证号填写清楚，并贴好条形码。

请认真核准条形码上的准考证号、姓名。

2）、将选择题用2B 铅笔把答题卡上对应题目的答案标号涂黑，非选择题用0.5毫米黑色墨水签字笔将答案答在答题卡上对应的答题区域内，在试卷上作答无效。

3）、考生必须保持答题卡的整洁。

第 I 卷 （选择题共60分）一、 选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

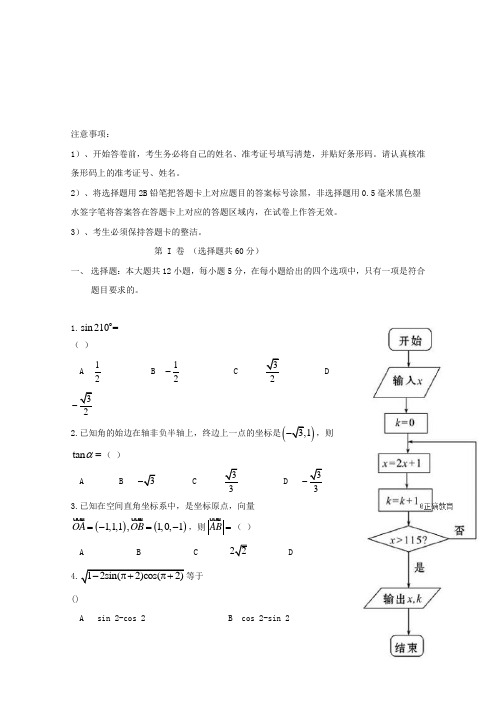
1.sin 210=（ ）A 12B 12-2.已知角的始边在轴非负半轴上，终边上一点的坐标是()，则tan α=（ ）A B 3 D 3- 3.已知在空间直角坐标系中，是坐标原点，向量()()1,1,1,1,0,1OA OB =-=-，则AB =（ ）A B C()A sin 2-cos 2B cos 2-sin 2C ±(sin 2-cos 2)D sin 2+cos 25. 有3个兴趣小组，甲、乙两位同学各自参加其中一个小组，每位同学参加各个小组的可能性相同，则这两位同学参加同一个兴趣小组的概率为 ( ) A 13B 12C 23D 346. 某中学采用系统抽样方法，从该校高一年级全体800名学生中抽50名学生做牙齿健康检查．现将800名学生从1到800进行编号．已知从33～48这16个数中取的数是39，则在第1小组1～16中随机抽到的数是 ( )A 5B 7C 11D 137. 按如图所示程序框图运算，若输出2k =,则输入的的取值范围是 ( )A (28,+∞)B (-∞,57］C (28,57］D ［28,57)8. 已知一个小虫在边长为的正三角形内部爬行，到各个顶点的距离不小于时为安全区域，则小虫在安全区域内爬行的概率是 （ ）A 16-B 6C 16π-D 6π 9. 已知点M 是直线3420x y +-=上的动点，点N 为圆()()22111x y +++= 上的动点，则|MN|的最小值是 ( ) 9413A B 1 C D 55510.函数()()sin 0,2f x A x B πωϕωϕ⎛⎫=++>< ⎪⎝⎭的图象如下， 则()()()()301220182S f f f f =++++-等于 ( )A 0B 504C 1 009D 2 01810. 已知向量(2sin ,m B =，2cos 2,2cos 12B n B ⎛⎫=- ⎪⎝⎭， 且∥，则锐角B 的值为 ( )A B C D 12643ππππ。

2018～2019学年度第一学期期中联考高一数学试卷本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．第Ⅰ卷注意事项：1．答第Ⅰ卷前，考生务必将自己的姓名、考生号涂写在答题卡上。

2．选出答案后，用铅笔把答题卡上对应的题目的答案标号涂黑，如需改动，用橡皮擦干净后，再填涂。

其他答案，写在答题卡上，不能答在试卷上。

一、选择题：（本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的） 1．集合{1,2}的子集有 （ ） A ．2个B ．3个C ．4个D ．5个2． 设集合{}|43A x x =-<<，{}|2B x x =≤，则A ∪B =（ ） A ．(4,3)- B ．(4,2]- C ．(,2]-∞ D ．(,3)-∞3．已知()5412-+=-x x x f ，则()x f 的表达式是（ ）A ．x x 62+B ．782++x xC ．322-+x xD ．1062-+x x4．下列对应关系：（ ）①{1,4,9},{3,2,1,1,2,3},A B ==---f ：x x →的平方根 ②,,A R B R ==f ：x x →的倒数③,,A R B R ==f ：22x x →-④{}{}1,0,1,1,0,1,A B f =-=-：A 中的数平方.其中是A 到B 的映射的是（ ） A ．①③ B ．②④ C ．③④ D ．②③ 5、下列四个图像中，是函数图像的是 （ ）A 、（3）、（4）B 、（1）C 、（1）、（2）、（3）D 、（1）、（3）、（4）6、下列各组函数是同一函数的是 （ ）①()f x =与()g x =；②()f x x =与()g x =；③0()f x x =与01()g x x=；④2()21f x x x =--与2()21g t t t =--。

A 、①② B 、①③ C 、②④ D 、①④7.已知函数212x y x⎧+=⎨-⎩ (0)(0)x x ≤>，使函数值为5的x 的值是（ ）A ．-2B ．2或52-C ． 2或-2D ．2或-2或52-8、函数y =（ ）A 、[]5,1--B 、(,5][2,)-∞-+∞C 、[]5,2-- D 、(,2][2,)-∞-+∞ 9．若R y x ∈,，且)()()(y f x f y x f +=+，则 （ ）A ． 0)0(=f 且)(x f 为奇函数B ．0)0(=f 且)(x f 为偶函数C ．)(x f 为增函数且为奇函数D ．)(x f 为增函数且为偶函数10.下列四个说法:①方程x 2＋2x －7＝0的两根之和为－2，两根之积为－7；②方程x 2－2x＋7＝0的两根之和为－2，两根之积为7；③方程3 x 2－7＝0的两根之和为0，两根之积为73-；④方程3 x 2＋2x ＝0的两根之和为－2，两根之积为0．其中正确说法的个数是 （ ）（A ）1个 （B ）2个 （C ）3个 （D ）4个 11．已知集合A={x|x>1},={x|x>}B a -，若B A ⊆，则有（ ） A ．1a <- B ．1a >- C ． 1a ≤- D ．1a ≥-12、若对于任意实数x 总有()()f x f x -=且()f x 在区间(,1]-∞-上是增函数则 （ ） A 、3()2f -＜(1)f -＜(2)f B 、(2)f ＜3()2f -＜(1)f - C 、(1)f -＜3()2f -＜(2)f D 、(2)f ＜(1)f -＜3()2f -第Ⅱ卷二、填空题：（本大题共4个小题，每小题5分，共20分．请将答案填在答题卡上） （13）若2a =5b =10，则a 1+b1=_______． （14）若函数y=f (x )的定义域是[0，2]，则函数g (x )的定义域是_______．（15）已知a ，b 为常数，若f (x )=x 2+4x +3，f (ax +b )=x 2+10x +24，则5a –b=_______．（16）已知函数()()2211,22x a x x f x x ⎧⎪=⎨⎛⎫⎪ ⎪⎝⎭⎩－，≥，－＜，满足对任意的实数x 1≠x 2，都有f (x 1)－f (x 2)x 1－x 2＜0成立，则实数a 的取值范围为______________.三、解答题：（本大题共5个小题，共60分．解答应写出文字说明，证明过程或演算步骤） （17）（本小题满分10分）计算：120333113864π---+（）（）（）；（Ⅱ）7log 23log lg25lg47++．（18）（本小题满分12分）已知全集U=R ，集合A={x |–7≤2x –1≤7}，B={x |m –1≤x ≤3m –2}． （Ⅰ）当m=3时，求A ∩B 与()U AB ð；（Ⅱ）若A ∩B=B ，求实数m 的取值范围．（19）（本小题满分12分）已知函数f (x )是定义在R 上的奇函数，当x ＞0时，()(1)f x x x =-+． （Ⅰ）求函数f (x )的解析式；（Ⅱ）求关于m 的不等式f (1–m )+ f (1–m 2)＜0的解集．（20）（本小题满分12分）已知定义域为R 的函数()122x x bf x a++=+－ 是奇函数．（Ⅰ）求a ，b 的值；（Ⅱ）若对任意的t ∈R ，不等式f (t 2－2t )＋f (2t 2－k )<0恒成立，求k 的取值范围．(21) （12分）某租赁公司拥有汽车100辆，当每辆车的月租金为3000元时，可全部租出，当每辆车的月租金每增加50元时，未租出的车将会增加一辆，租出的车每辆每月需维护费150元，未租出的车每辆每月需要维护费50元.（1）当每辆车的月租金定为3600元时，能租出多少辆车？（2）当每辆车的月租金定为多少元时，租赁公司的月收益最大？最大月收益是多少？（22）（本小题满分12分）已知函数f (x )=ax 2+bx+c ，且(1)2af =-，3a ＞2c ＞2b ． （Ⅰ）求证：a ＞0且－3＜b a ＜34－； （Ⅱ）求证：函数f (x )在区间（0，2）内至少有一个零点； （Ⅲ）设x 1，x 2是函数f (x )的两个零点，求|x 1–x 2|的范围．高一数学试卷参考答案一，选择题。

五校联盟18-19年度第一学期期中考试高一数学试卷一.选择题1.下列集合中表示同一集合的是（）A.：:•4—YO.N -B. 了—也.二广「厂”C. : -- D：/•：・：.:・： :D. - . ：..：：.■'12：【答案】B【解析】A选项点集中元素点的坐标不同，C选项中前一个是点集，后一个是数集，D选项中前一个是数集,后一个是点集，故选B2.如图所示，U是全集，A,B是U的子集，则阴影部分所表示的集合是（）A. B. C.二. j D. Ai JM【答案】C【解析】试题分析：由图象可知阴影部分是集合B与集合A在全集U中的补集的公共元素，因此答案选C.考点：集合的运算3.下列哪组中的两个函数是同一函数（）A. y = &与”•B. y =--^与y=x+1 x- 1C. f（x）= IM与u（t）=（树D. y=x 与或x）=猊【答案】D【解析】【分析】首先利用同一函数的定义，对各个选项逐个分析，分别从定义域、值域和对应法则几个角度去区分，从而确定出正确结果.【详解】对于A , V =-^ = |xLy = ^? = x,两个函数的值域不同，所以不是同一函数;对于B,函数_!_ = *十I)与y =x+ I的定义域不同，所以不是同一函数；x-1对于C, f(x) = |刈与虱t) = f价的定义域不相同，所以不是同一函数；对于D, g(x) = J^ = x,与y=x是同一"函数；故选D.【点睛】该题考查的是有关选择同一函数的问题，涉及到的知识点有同一函数的定义，以及相关式子的化简公式，必须保证三要素都是完全一样的，才能保证是同一函数^,, lg(x । 1),4.函数Rx)=卧，’的定义域是() x-1A. B. I L 一C. ।। , - - 'D. I - - . I- -【答案】C【解析】试题分析：分母不等于零，对数真数大于零，所以t1,解得十⑹.[#一1 丰U考点：定义域.5.函数f(x)一上一的图象关于( )xA.原点对称B.x轴对称C.y轴对称D.直线丫=工对称【答案】A【解析】【分析】利用奇偶性的定义，判断函数为奇函数，故图像关于原点对称^【详解】函数的定义域为,即[-依0)口(。

一、选择题(本大题共12小题，每小题5分，共60分．在下列各题的四个选项中，只有一个选项是符合题目要求的)1．设集合U ＝{1,2,3,4,5}，∁U A ＝{1,3,5}，则A 等于( )A ．UB ．{1,2,4}C ．{2,4}D ．{2,3,4} 2．函数f (x )＝x ＋1＋4x 的定义域是( )A ．[－1,0)∪(0，＋∞)B ．[－1，＋∞)C ．(0，＋∞)D ．(1，＋∞)3．下列函数中，既是偶函数又在(0，3)上是递减的函数是( )A ．y ＝x 3B ．y ＝－x 2＋1C ．y ＝|x |＋1D ．y ＝x 4．已知函数f (x )＝2x 2＋2kx －8在[－5，－1]上单调递减，则实数k 的取值范围是( )A ．(－∞，2]B ．[2，＋∞)C ．(－∞，1]D ．[1，＋∞)5．下列各函数中，值域为(0，＋∞)的是( )A ．113+=x y B ．x y 21-= C ．352++=x x y D ． 22x y -=6．设f(x)＝2x ＋3，g(x ＋2)＝f(x)，则g(x)等于( )A ．2x ＋1B ．2x ＋7C ．2x －3D ．2x －17．当α∈⎭⎬⎫⎩⎨⎧-3,2,1,21,1时，函数y ＝x α的值域为R 的α值有( )A ．1个B ．2个C ．3个D ．4个8．如果函数f(x)＝x 2＋bx ＋c 对任意实数t ，都有f(2＋t)＝f(2－t)，则( )A ．f(2)<f(1)<f(4)B ．f(1)<f(2)<f(4)C ．f(2)<f(4)<f(1)D ．f(4)<f(2)<f(1)9．定义在R 上的偶函数f (x )在区间[－2，－1]上是增函数，将f (x )的图像沿x 轴向右平移两个单位，得到函数g (x )的图像，则g (x )在下列区间一定是减函数的是( )A ．[3,4]B ．[1,2]C ．[2,3]D ．[－1,0] 10．函数y ＝x 2＋2x －3的单调递减区间是( )A ．[1，＋∞)B ．(－∞，-3]C ．(－∞，-3]⋃[1，＋∞)D ．(－∞，＋∞)11．已知函数f (x )＝ax 3－bx －1(ab ≠0)的最大值为M ，最小值为N ，则M ＋N 等于( )A ．－2B ．－1C ．0D ．112．已知函数f (x )＝⎩⎨⎧x 2－2x ＋2(x <1)，－x －1(x ≥1)若f (2－x )>f (x )，则x 的取值范围是( )A ．(－1，＋∞)B ．(－∞，－1)C ．(1，＋∞)D ．(－∞，1) 二、填空题（本大题共4小题，每小题5分，共20分．把答案填在题中横线上） 13．函数f (x )＝31+-x a 的图像一定过定点P ，则P 点的坐标是________．14．若函数f (x )的定义域是[0，1]，则函数F(x)=)31()2(++x f x f 的定义域为 .15．计算：0175.0231)21(3256)61(027.0+-+-----= .16．已知函数f (x )＝x 21＋x 2，那么f (1)＋f (2)＋f (12)＋f (3)＋f (13)＋f (4)＋f (14)＝________. 三、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤） 17.(10分)已知函数12)(2-+-=ax x x f ，若)(x f 在[－1，1]上的最大值为)(a g ，求)(a g 的解析式.18. (12分)设 A={x|2x 2+ax+2=0}, B={x|x 2+3x+2a=0}, A ∩B={2}. (1)求a 的值及 A ,B ;(2)设全集I=A ∪B ,求(∁I A )∪(∁I B ); (3)写出(∁I A )∪(∁I B )的所有子集.19.(12分)已知函数)(x f 是定义在R 上的奇函数，且当0>x 时，x x f )21()(=.(1)求函数)(x f 的解析式；(2)画出函数)(x f 的图象，根据图象写出该函数的单调区间． 20.(12分)已知幂函数)(x f y =的图像经过点)2,2(． (1)求)(x f y =的解析式；(2)判断)(x f y =在其定义域上的单调性，并加以证明． 21．(12分)某租赁公司拥有汽车100辆．当每辆车的月租金为3000元时，可全部租出．当每辆车的月租金每增加50元时，未租出的车将会增加一辆．租出的车每辆每月需要维护费150元，未租出的车每辆每月需要维护费50元．（Ⅰ）当每辆车的月租金定为4000元时，能租出多少辆车？（Ⅱ）当每辆车的月租金定为多少元时，租赁公司的月收益最大？最大月收益是多少？22. (12分)已知)(x f 对任意的实数n m ,都有1)()()(-+=+n f m f n m f ,且当0>x 时,有1)(>x f .(1)求)0(f ;(2)求证:)(x f 在R 上为增函数;(3)若2)1(=f 且3)()23(2<-+-a a f a f ,求实数a 的取值范围.参考答案一、选择题(本大题共12小题，每小题5分，共60分．在下列各题的四个选项中，只有一个选项是符合题目要求的) 1．答案：C 解析：A ＝{2,4}． 2．答案：A 解析：x ＋1≥0且x ≠0. 3．答案：B解析： A 中y ＝x 3为奇函数，不是偶函数；D 中y ＝x 不具奇偶性；C 中y ＝|x |＋1在(0，3)上为增函数，故选B.4．答案：A 解析：∵x ＝－b 2a ＝－k 2，∴－k2≥－1，k ≤2.. 5. 答案 D解析：A 中，因为11+x ∈(－∞，0)∪(0，＋∞)，所以y ＝3的值域是(0,1)∪(1，＋∞)．B 中，因为1－2x ≥0，所以2x ≤1，x ≤0，x y 21-=的定义域是(－∞，0]，所以0<2x ≤1，所以0≤1－2x <1，所以x y 21-=的值域是[0,1)．C 中，y ＝x 2＋5x ＋3＝413)25(2-+x 的值域是),413[+∞-.D 中，22x y -=的值域为(0，＋∞)． 6．答案：D解析：g(x ＋2)＝2x ＋3，令x ＋2＝t ，则x ＝t －2，所以g(t)＝2(t －2)＋3＝2t －1，即g(x)＝2x －1. 7．答案：B解析：α＝1或α＝3. 8．答案：A解析：由f(2＋t)＝f(2－t)知二次函数图像的对称轴为直线x ＝2. 9．答案：A解析：∵f (x )为偶函数且在[－2，－1]上是增函数，∴f (x )在[1,2]上是减函数．将f (x )的图像沿x 轴向右平移两个单位，得g (x )在[3,4]上是减函数．故选A. 10．答案：B解析：由x 2＋2x －3≥0，得x ≥1或x ≤－3，所以函数减区间为(－∞，－3]．故选B 11．答案：A解析：∵y ＝f(x)＋1是奇函数，最大值为M ＋1，最小值为N ＋1，(M ＋1)＋(N ＋1)＝0，∴M ＋N ＝－2. 12．答案：C解析：由题意知f(x)在R 上是减函数，∴2－x<x ，∴x>1.二、填空题（本大题共4小题，每小题5分，共20分．把答案填在题中横线上） 13．答案: (1,4)解析:由于函数y ＝a x 恒过(0,1)，而y ＝a x －1＋3的图像可看作由y ＝a x 的图像向右平移1个单位，再向上平移3个单位得到的，则P 点坐标为(1,4)．14．答案： ⎥⎦⎤⎢⎣⎡210，解析：由⎩⎨⎧0≤2x ≤1，0≤x ＋13≤1，得⎩⎪⎨⎪⎧0≤x ≤12，－13≤x ≤23，所以x ∈⎣⎢⎡⎦⎥⎤0，12. 15．答案：32解析：原式＝131)2(36])103[(438313+-+--＝1312363106+-+-＝32.16．答案：72解析：观察x 取值的规律，自变量取x 和取1x时函数值和为1.三、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤） 17.(10分)解：f (x )＝－(x －a )2＋a 2－1， ------------------2分(1)当a ≤－1时，f (x )在[－1，1]上是减少的，所以f (x )max ＝f (－1)＝－2a －2. ------------------4分 (2)当－1<a <1时，f (x )在[－1，a ]上是增加的，在(a ，1]上是减少的， 所以f (x )max ＝f (a )＝a 2－1. ------------------6分 (3)当a ≥1时，f (x )在[－1，1]上是增加的，所以f (x )max ＝f (1)＝2a －2， ------------------8分所以⎪⎪⎪⎩⎪⎪⎪⎨⎧≥-<<---≤--=,1,22,11,1,1,22)(2a a a a a a a g ------------------10分18. (12分)解:(1)∵A ∩B={2},∴8+2a+2=0,∴a=-5, ------------------2分∴A=⎭⎬⎫⎩⎨⎧221， ,B={}25-，. ------------------4分 (2)∵I=⎭⎬⎫⎩⎨⎧2215-，，,∴(∁I A )∪(∁I B )= ⎭⎬⎫⎩⎨⎧215-，. ------------------8分(3)由(2)知(∁I A )∪(∁I B )的所有子集有φ,⎭⎬⎫⎩⎨⎧21,{}5-,⎭⎬⎫⎩⎨⎧215-，.----------------12分] 19.(12分)解：(1)因为)(x f 是R 上的奇函数，所以f(0)＝0. ------------------2分当x<0时，－x>0，,2)21()()(x x x f x f ---=-=--= -----------------4分所以⎪⎪⎩⎪⎪⎨⎧>=<-=0,)21(,00,0,2)(x x x x f x x------------------6分(2)函数图象如图所示，------------------10分通过函数的图象可以知道，f (x )的单调递减区间是(－∞，0)，(0，＋∞)．----12分20.(12分)解：(1)设a x x f =)(，将)2,2(代入得， 2＝2α，所以α＝12.-----------------2分所以x x f =)((x ≥0)． -----------------4分(2) x x f =)(在定义域),0[+∞上为增函数． -----------------5分证明：任取 ),0[,21+∞∈x x 且,21x x <则 -----------------6分21212121212121))(()()(x x x x x x x x x x x x x f x f +-=++-=-=-.-------8分),0[,21+∞∈x x 且,21x x < ,021<-∴x x 021>+x x ，所以)()(21x f x f <∴． -----------------10分即幂函数x x f =)(在),0[+∞上为增函数． -----------------12分 21．(12分)解：（Ⅰ）当每辆车的月租金定为4000元时，未租出的车辆数为205030004000=-，100﹣20=80，所以这时租出了80辆车． -----------------6分（Ⅱ）设每辆车的月租金定为x 元，则租赁公司的月收益为50503000)150(503000-100)(⨯----=x x x x f ）（, -----------------8分 整理得307050)4050(501-)(2+-=x x f -----------------10分所以，当4050=x 时，)(x f 最大，最大值为307050)4050(=f ，即当每辆车的月租金定为4050元时，租赁公司的月收益最大，最大月收益为307050元． -----------------12分 22. (12分)(1)解:令1)0(,1)0(2)0(,0=∴-====f f f n m 则. -----------------2分 (2)证明:任取 R x x ∈21,且,21x x <则1)(,01212>->-x x f x x . -----------------4分1)()()(-+=+n f m f n m f ,)(1)(11)()(])[()(111121122x f x f x f x x f x x x f x f =-+>-+-=+-=∴)()(12x f x f >∴， -----------------6分)(x f ∴在R 上为增函数. -----------------7分(3)解: 3)()23(2<-+-a a f a f ,即21-)()23(2<-+-a a f a f , -------8分2)23(2<-+-∴a a a f .2)1(=f ,)1()24(2f a a f <--∴ 又)(x f 在R 上为增函数,1242<--∴a a ,即0342>+-a a -----------------10分13<>a a 或解得故实数a 的取值范围为),3()1,(+∞⋃-∞. -----------------12分。

五校联盟18-19年度第一学期期中考试高一数学试卷时间:120分钟满分:150分一．选择题1．下列各组集合中，表示同一集合的是（ ）A ．M={（3，2）}，N={（2，3）}B ．M={3，2}，N={2，3}C ．M={（x ，y ）|x +y=1}，N={y |x +y=1}D ．M={1，2}，N={（1，2）}2、如下图所示，是全集，，是的子集，则阴影部分所表示的集合是( )A .B .C .D .3．下列哪组中的两个函数是同一函数（ ）A ．y =√x 2与y=√x 33B ．y =x 2−1x−1与y=x+1C ． f(x)=|x |与g(t)=(√t)2D ．y=x 与g(x)=334．函数的定义域是( )A ． (－1，＋∞)B ． [－1，＋∞)C ． (－1,1)∪(1，＋∞)D ． [－1,1)∪(1，＋∞) 5、函数的图象关于( )A. 原点对称B. 轴对称C.轴对称D.直线对称6、已知时，函数和的图象只可能是( )A. B. C. D.7、设，，，则，，的大小关系是( )A.B.C.D.8．已知函数121,(2)()(3),(2)x f x f x x x ⎧⎪+≥=⎨+<⎪⎩，则f （1）- f （9）=（ ）A ．﹣1B ．﹣2C ．6D ．79．已知幂函数f(x)=x α的图象过(4,2)，若()3f m =，则log 33m 值为（ ）A ． 1B ． √3C ． 3D ． 910．已知函数()()1g x f x x =--，其中()g x 是偶函数，且()21f =，则()2f -=（ ）．A. 1-B. 1C. 3-D. 311．若函数()(),1{231,1x a x f x a x x >=-+≤是R 上的减函数，则实数a 的取值范围是（ ） A ． 2,13⎛⎫⎪⎝⎭ B ． 3,14⎡⎫⎪⎢⎣⎭ C ． 2,3⎛⎫+∞ ⎪⎝⎭ D ． 23,34⎛⎤⎥⎝⎦12. 已知函数)(x f 是定义在R 上的偶函数，且在区间),0[+∞上是单调递增，若实数a 满足313(log )(log )2(1)f a f a f +≤，则a 的取值范围是（ ）.(0,3]A 1.(0,]3B .[1,3]C 1.[,3]3D二 .填空题：13、函数恒过定点__________．14．已知函数21,()2,x x f x x x ⎧+=⎨-⎩≤0>0若f (x )＝10，则x 的值是________15.已知2log 3x =，则44=22x xx x ----__________________________.16．已知函数若函数y=f （x ）的图象与y=k 的图象有三个不同的公共点，这三个公共点的横坐标分别为a ，b ，c ，且a ＜b ＜c ，则c ab -的取值范围是______________．三．解答题17．（本题满分12分）（1）设全集{}1,2,3,4,5,6U =，A,B 都是U 的子集，{}1,2A =，{}()4,6U A B =I ? 写出所有符合题意的集合B 。

2018-2019学年安徽省安庆市五校联盟高一上学期期中联考数学试卷★祝考试顺利★注意事项：1、答题前，请先将自己的姓名、准考证号用0.5毫米黑色签字笔填写在试题卷和答题卡上的相应位置，并将准考证号条形码粘贴在答题卡上的指定位置。

用2B铅笔将答题卡上试卷类型A后的方框涂黑。

2、选择题的作答：每个小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。

写在试题卷、草稿纸和答题卡上的非选择题答题区域的答案一律无效。

3、主观题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域的答案一律无效。

如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。

不按以上要求作答无效。

4、选考题的作答：先把所选题目的题号在答题卡上指定的位置用2B铅笔涂黑。

答案用0.5毫米黑色签字笔写在答题卡上对应的答题区域内，写在试题卷、草稿纸和答题卡上的非选修题答题区域的答案一律无效。

5、保持卡面清洁，不折叠，不破损，不得使用涂改液、胶带纸、修正带等。

6、考试结束后，请将本试题卷、答题卡、草稿纸一并依序排列上交。

一．选择题1.下列集合中表示同一集合的是（）A. B.C. D.【答案】B【解析】A选项点集中元素点的坐标不同，C选项中前一个是点集，后一个是数集，D选项中前一个是数集，后一个是点集，故选B2.如图所示，是全集，是的子集，则阴影部分所表示的集合是（）A. B. C. D.【答案】C【解析】试题分析：由图象可知阴影部分是集合B与集合A在全集U中的补集的公共元素，因此答案选C.考点：集合的运算3.下列哪组中的两个函数是同一函数（）A. 与B. 与y=x+1C. 与D. y=x与【答案】D【解析】【分析】首先利用同一函数的定义，对各个选项逐个分析，分别从定义域、值域和对应法则几个角度去区分，从而确定出正确结果.【详解】对于A，，两个函数的值域不同，所以不是同一函数；对于B，函数与的定义域不同，所以不是同一函数；对于C，与的定义域不相同，所以不是同一函数；对于D，，与是同一函数；故选D.【点睛】该题考查的是有关选择同一函数的问题，涉及到的知识点有同一函数的定义，以及相关式子的化简公式，必须保证三要素都是完全一样的，才能保证是同一函数.4.函数的定义域是（）A. B.C. D.【答案】C【解析】试题分析：分母不等于零，对数真数大于零，所以，解得.考点：定义域.5.函数的图象关于( )A. 原点对称C. 轴对称D. 直线对称【答案】A【解析】【分析】利用奇偶性的定义，判断函数为奇函数，故图像关于原点对称.【详解】函数的定义域为，即.，所以函数为奇函数，图像关于原点对称，故选A.【点睛】本小题主要考查函数的奇偶性.务必记住，要判断一个函数是奇函数还是偶函数，需要先求函数的定义域.属于基础题.6.当时，函数和的图象只能是A.B.C.D.【答案】B【解析】略7.设，，，则的大小关系是( )A.C.D.【答案】A【解析】【分析】先得到最小的，然后利用，求得的大小关系.【详解】由于，而，所以，故选A.【点睛】本小题主要考查利用指数函数、对数函数、幂函数的性质比较大小.属于基础题.8.已知函数，则f（1）- f（9）=（）A. ﹣1B. ﹣2C. 6D. 7【答案】A【解析】【分析】利用分段函数，分别求出和的值，然后作差得到结果.【详解】依题意得，，所以，故选.【点睛】本小题主要考查利用分段函数求函数值，只需要将自变量代入对应的函数段，来求得相应的函数值.属于基础题.9.已知幂函数的图象过，若，则值为（）A. 1B.C. 3D. 9【答案】B【解析】【分析】由函数的图象过点，先求出幂函数，再由，能求出的值，最后求的值.【详解】∵幂函数幂函数的图象过，，解得．则故选：B．【点睛】本题考查幂函数的解析式的求法及应用，考查对数恒等式的应用，解题时要认真审题，注意待定系数法的灵活运用，是基础题．10.已知函数，其中是偶函数，且，则（）．A. B. C. D.【答案】C【解析】【分析】先将代入，求得的值.然后利用奇偶性，求得的值.【详解】，由于函数为偶函数，故，. 【点睛】本小题主要考查函数的奇偶性，考查利用函数的奇偶性来求函数值，属于基础题.注意偶函数的定义.11.若函数是上的减函数，则实数的取值范围是（）A. B. C. D.【答案】D【解析】∵函数是上的减函数∴∴故选D点睛：本题考查分段函数的单调性，解决本题的关键是熟悉指数函数，一次函数的单调性，确定了两端函数在区间上单调以外，仍需考虑分界点两侧的单调性，需要列出分界点出的不等关系.12.已知函数是定义在R上的偶函数，且在区间上是单调递增，若实数a满足，则a的取值范围是（）A. B. C. D.【答案】D【解析】【分析】根据函数为偶函数可知，函数在上递减，在上递增.利用对数运算，将题目所给不等式转化为，即，由此解得的取值范围.【详解】由于函数为偶函数，且在上递增，属于函数在上递减.原不等式等价于，即，即，所以，，解得.【点睛】本小题考查函数的奇偶性与函数的单调性，考查利用函数的奇偶性来求解不等式.如果一个函数为奇函数，那么它的图像关于原点对称，在轴两侧的单调性是相同的，如果一个函数为偶函数，则图像关于轴对称，在轴两侧的单调性是相反的本小题属于中档题.二 .填空题13.函数恒过定点__________．【答案】【解析】试题分析：定点．考点：函数的定点．14.已知函数,若=10，则=________。