土地耕地需求量预测
- 格式：doc
- 大小：659.38 KB
- 文档页数：24
下载文档原格式
合集下载
土地需求量预测
第一节
概 述
影响土地需求量的因素
1、以人口发展为中心的社会发展对土地的需求 是影响土地需求量的重要因素； 2、以国民经济发展为中心的国民经济各部门的 发展对土地的需求是影响土地需求量的重要因素； 3、规划地区土地资源自身的特点决定的土地条 件也是影响土地利用需求量的一个因素。
第一节
概 述
二、土地需求预测的内容
( E P) 1 S (1 ) LF D
其中：S E P L F D – – – – – – 规划目标年耕地需求量（公顷）； 规划目标年粮食需求量（公斤）； 规划目标年粮食调出量（公斤）； 规划目标年粮食播面单产（公斤/公顷） 规划目标年耕地复种指数 规划目标年粮经比。
规划年期 2010 2020 耕地总需求量（公顷） 97132.93 97638.29
1）基础数据预测：包括人口预测、消费水平预测、 作物产量预测、城市化水平预测； 2）农业用地预测：包括耕地、园地、牧草地、林地 及水产养殖用地预测。农业用地需求量取决于人 口发展规模、消费水平变化及经济发展对农产品 的需求量。 3）建设用地预测：按用地类型分为城乡居民点用地、 工业用地、矿山用地、交通运输用地、水利用地、 风景旅游用地、军事用地等。
2、粮食需求总量预测
本地区人口粮食需求量 = 总人口 * 粮食消费水平 注意区分：粮食自给类型、城乡粮食消费类型对粮食需 求量计算的影响。 粮食需求总量=本地区人口粮食需求量+商品粮调出量 结合人口预测结果，计算得到2010年粮食需求总量为 803637吨，2020年为922659吨。
3. 主要粮食播面单产水平预测
（二）城镇和农村居民点用地需求预测
第五节 土地供需平衡
土地供需分析：是指在土地供给量和土地需求量预 测和估算的基础上加以比较，借以评价供需关系， 引导土地供需平衡的过程。
耕地需求预测相关方法
浅析耕地需求预测的相关方法[摘要] 目前,我国正处于工业化、城镇化快速发展的阶段,建设用地供需矛盾突出,耕地保护面临严峻的形势。
耕地需求预测为耕地保护提供了科学、合理、实用的预测数据。
本文对趋势分析法、指数平滑法、回归分析法、马尔柯夫链预测法、灰色模型五种预测模型从不同角度进行了分析。
[关键词] 耕地需求预测模型目前,我国正处于工业化、城镇化快速发展的阶段,建设用地供需矛盾突出,农用地特别是耕地保护面临严峻的形势。
土地利用总体规划规定了土地用途,严格限制农用地转为建设用地,控制用地总量,对耕地实行特别保护。
对耕地进行保护,多大面积的耕地保有量是合理的,这是一个重要的问题。
针对我国人口、地形、社会发展等现实情况,我们将耕地控制在怎样一个范围内,既不阻碍经济发展又能保障粮食安全,这是一个亟待解决的问题。
对耕地数量的预测是建立在科学、合理、实用的基础上的,因此我们引入了耕地需求预测模型。
经济预测的方法多种多样,耕地需求量预测模型的选择,要根据耕地的特殊性,及相关数据的采集情况来选择适用的模型。
现在主要介绍以下几种模型:趋势分析法、指数平滑法、回归分析法、马尔柯夫链预测法、灰色模型法。
趋势分析法又称时间序列预测法,是将历史资料和数据按时间顺序排列成一系列,根据时间时间顺序所反映的经济现象的发展过程、方向和趋势,将时间顺序外推或延伸,以预测经济现象未来可能达到的水平。
它是迄今为止研究最多,也较为常用的一种定量预测方法。
时间序列的趋势有确定性和非确定性两种,前者分为线性趋势模型和非线性趋势模型。
其中非线性趋势预测通常可以认为是由于某种固定因素作用同一方向所形成,主要有有多项式趋势模型、指数趋势模型、龚伯茨模型等几种形式。
趋势分析是一种确定的外推,在处理历史资料,拟合曲线,得到模拟曲线的过程都不考虑随机误差。
指数平滑是加权移动平均法的进一步发展和完善,它是由美国经济学家布朗于1959年在《库存管理的统计预测》一书中首先提出来的。
第5章 土地需求量预测
第五章 土地需求量预测
【内容提要】土地需求量预测是确定各部门未来用地 数量，为合理配置和调整土地利用结构提供依据， 也是土地供需平衡的主要内容。本章主要介绍各部 门用地预测的程序和方法，土地供需问题分析的基 本原理。 【重点内容】掌握部门用地预测的程序和方法，土地 供需平衡分析的基本原理。 【教学要求】理解和掌握土地需求量预测的基本原理 ，能够通过土地供需平衡分析找出供需问题。
2004
2810.26
506.94
5543.58
湖南省粮食单产水平预测
年份 单产（千克/公 顷）
集约程度 高集约 低集约
2010
7080.00 6487.95
2020
7780.00 7075.02
4、粮作比
湖南省1997—2004年粮作比 年份 1997 1998 1999 63.97 2000 62.86 2001 60.55 2002 59.73 2003 58.59 2004 62.06
（二）土地利用目标的内容（在定性的基础上，通 过具体的量化指标来实现） 1、总目标:定性描述，主要依据国家土地利用政策 、法律和上级土地利用总体规划的要求，结合本地 区国民经济和社会发展规划、土地资源状况综合确 定。 2、具体目标（强制性控制和指标性目标）： （1）耕地保护方面。 （2）建设用地方面。分总量控制和各项建设用地分 项控制目标。 （3）土地生态方面。 （4）土地利用效率方面。
规划 目标 年
粮食需 求 （万吨 ）
复种 指数
粮作 单产 比 （千克/公顷） （%）
2010
2896.1
2.30 56.58
高集 约
低集 约 高集 约 低集 约
【内容提要】土地需求量预测是确定各部门未来用地 数量，为合理配置和调整土地利用结构提供依据， 也是土地供需平衡的主要内容。本章主要介绍各部 门用地预测的程序和方法，土地供需问题分析的基 本原理。 【重点内容】掌握部门用地预测的程序和方法，土地 供需平衡分析的基本原理。 【教学要求】理解和掌握土地需求量预测的基本原理 ，能够通过土地供需平衡分析找出供需问题。
2004
2810.26
506.94
5543.58
湖南省粮食单产水平预测
年份 单产（千克/公 顷）
集约程度 高集约 低集约
2010
7080.00 6487.95
2020
7780.00 7075.02
4、粮作比
湖南省1997—2004年粮作比 年份 1997 1998 1999 63.97 2000 62.86 2001 60.55 2002 59.73 2003 58.59 2004 62.06
（二）土地利用目标的内容（在定性的基础上，通 过具体的量化指标来实现） 1、总目标:定性描述，主要依据国家土地利用政策 、法律和上级土地利用总体规划的要求，结合本地 区国民经济和社会发展规划、土地资源状况综合确 定。 2、具体目标（强制性控制和指标性目标）： （1）耕地保护方面。 （2）建设用地方面。分总量控制和各项建设用地分 项控制目标。 （3）土地生态方面。 （4）土地利用效率方面。
规划 目标 年
粮食需 求 （万吨 ）
复种 指数
粮作 单产 比 （千克/公顷） （%）
2010
2896.1
2.30 56.58
高集 约
低集 约 高集 约 低集 约
土地利用规划中耕地需求量预测方法探讨
情 况 来 看 ， 革 开 放 以 后 ， 区 之 间 和 人 均 之 间 的 差 改 地
定 的数 学方法 进 行科 学 的加 工 整 理 ， 以 揭示 有 关 借 变 量之 间 的规 律性 联 系 ， 于预 测 和 推 测 未来 发 展 用 变化情 况 的一 类 预测方 法 。 依 照 预测 选 择 基础 数 据 的不 同 ， 以将其 方 法 可 分 为直 接预测 法 和间接 预测 法 。 直 接预 测 法 是指 依 据所 要 达 到 的 目标 ， 选 择 在 的既定 目标上 ， 以历 史发 展 的信息 数据 为基 础 ， 用 使
思路 如下 ：
（ ） 口预 测 一 人
候 、 灌 条件 、 物 品种 、 排 作 生产 和经 营水 平 等 因 素 。 依据 预测 区域多 年来农作 物单产 水平可 以运用 回归 分析 法 、 指数 平滑 法 、 色预测法 等方法 预测农作 物 灰 在规划 目标 年的产量 水平 。
中 图 分类 号 ： ３ １ Ｆ ０ 文献标识码 ： Ａ 文 章 编 号 ： ６ ２ ３ ９ ２ ｌ ） ２— ０ ５—０ １ ７ —５ ７ （ ０ ０ ０ ０ ０ ６
土 地 资 源 是 一 种 数 量 有 限 的 自然 资 源 ， 会 发 社
不 同的 预测模 型 ， 预测 目标 的发 展情 况进 行预测 ， 对
物产 量 的预测水平 ， 同时 考 虑 到复 种 指数 等 因素 条 件下 就可 以得到 在粮食 安全战 略的基础 上对耕地 的 需求 量 。 根据农作 物产 品需求 量和农 作物耕 地单产预 测
ＤＣ Ａ— ＤＴＣ／ Ｉ （ ＭＣ ・ ＰＯＧ ・ＧＰＡＰ）
制定 政策 ， 择 人 口的 最佳 发 展 方 案 ， 出改 进 措 选 提 施， 以使人 口的发 展更 加 适应 物 质 资料 生 产 发展 的
定 的数 学方法 进 行科 学 的加 工 整 理 ， 以 揭示 有 关 借 变 量之 间 的规 律性 联 系 ， 于预 测 和 推 测 未来 发 展 用 变化情 况 的一 类 预测方 法 。 依 照 预测 选 择 基础 数 据 的不 同 ， 以将其 方 法 可 分 为直 接预测 法 和间接 预测 法 。 直 接预 测 法 是指 依 据所 要 达 到 的 目标 ， 选 择 在 的既定 目标上 ， 以历 史发 展 的信息 数据 为基 础 ， 用 使
思路 如下 ：
（ ） 口预 测 一 人
候 、 灌 条件 、 物 品种 、 排 作 生产 和经 营水 平 等 因 素 。 依据 预测 区域多 年来农作 物单产 水平可 以运用 回归 分析 法 、 指数 平滑 法 、 色预测法 等方法 预测农作 物 灰 在规划 目标 年的产量 水平 。
中 图 分类 号 ： ３ １ Ｆ ０ 文献标识码 ： Ａ 文 章 编 号 ： ６ ２ ３ ９ ２ ｌ ） ２— ０ ５—０ １ ７ —５ ７ （ ０ ０ ０ ０ ０ ６
土 地 资 源 是 一 种 数 量 有 限 的 自然 资 源 ， 会 发 社
不 同的 预测模 型 ， 预测 目标 的发 展情 况进 行预测 ， 对
物产 量 的预测水平 ， 同时 考 虑 到复 种 指数 等 因素 条 件下 就可 以得到 在粮食 安全战 略的基础 上对耕地 的 需求 量 。 根据农作 物产 品需求 量和农 作物耕 地单产预 测
ＤＣ Ａ— ＤＴＣ／ Ｉ （ ＭＣ ・ ＰＯＧ ・ＧＰＡＰ）
制定 政策 ， 择 人 口的 最佳 发 展 方 案 ， 出改 进 措 选 提 施， 以使人 口的发 展更 加 适应 物 质 资料 生 产 发展 的
第09章 土地需求量预测
9
一、粮食需求量预测思路
（3）居民收入水平的提高 随着居民收入水平的提高，食物消费支出构成会发 生变化，据有关研究表明，人均GDP每增10个百分点将 增加间接粮食消费4300万t。
（4）食物消费结构的变化 1994年城镇居民按收入等级中最高收入组的动物性 食物消费量分别相应高于平均值5.llkg、l.59kg、 3.82kg、1.60kg。由于中国人口饮食习惯，其膳食结构 仍将以植物性食物为主，动物性食物为辅，并将逐步、 适当增加动物性食物消费。
18
一、耕地需求量
2．人工饲料地面积 5）确定饲料作物种植面积（S1） 式中：A为复种指数。 6）确定饲料作物轮作地净面积（S2） 式中：S2为饲料作物轮作地净面积（hm2）；S1为饲料 作物种植面积（hm2）；n为饲料作物轮作中田区总数；n 为饲料作物所占田区数。 7）确定饲料作物轮作地毛面积（S3） S3=S2（1+K） 式中：K为道路、沟渠、林带面积占饲料作物轮作净面 19 积比重，一般取K=2％～3％。
第九章 土地需求量预测
第一节 土地需求概念 第二节 粮食需求量预测 第三节 农业用地需求量预测 第四节 建设用地需求量预测 第五节 生态用地需求量预测 第六节 土地需求量定量预测方法 第七节 土地供需平衡分析
1
第一节 土地需求概念
一、土地需求
二、影响土地需求的因素 三、土地需求预测
7
一、粮食需求量预测思路
（1）人口增长 据有关部门研究，21世纪的前10年，年平均增加人 口在1000万左右。据此预测，2010年我国人口可达14亿 （13.94亿～14.3亿）、2020年达到15亿（14.7亿～15.4 亿）、2030年达到16亿（15.3亿～16.3亿）。2050年达 到16亿，此后可能实现人口的零增长或负增长。 2008年《国家粮食安全中长期规划纲要(2008～2020)》 认为，2007年我国“人均占有量380公斤，人均消费量 388公斤”。每增加1亿人增加口粮3880万t。预测中人均 粮食占有量参数2010年为395kg，2030年保持400kg，认 为基本可以满足消费。
土地需求量预测方法与内容
进行总人口预测时，除预测户籍人口外，还应预测城市范 围内暂住人口数量，暂住人口预测方法与总人口机械增长预测 方法相同。经济发达地区还应考虑人口流动因素。
9
3.6.2 人口预测
2）城乡人口预测
城镇人口是指城市、建制镇建成区范围内常住人口。乡村人口 是指村庄、集镇常住人口。流动人口一般不计入城镇与乡村人口， 但在确定建设用地规模时应予以考虑。
新建城镇的规划人均建设用地指标宜在第Ⅲ级内确定，当城镇的
18 发展用地偏紧时，可在第Ⅱ级内确定。
19
20
1）城镇：用地定额指标概算 法
按上述公式分段或逐年确定K值计算。 ──因建设重大项目引起人口变动的，可按劳动力带眷系数法，
即根据新建工业项目的职工数及带眷情况计算人口机械增长。
7
8
受资源、生态条件严重制约的，应按环境容量法确定适宜的人 口规模。
式中：PMAX ──城市的极限人口；PIMAX──自然资源、生态条件供给能 力和某项基础设施支持能力的最大值。
2）城镇人口预测
13
3.6.2 人口预测
2）城镇人口预测
(3) Logistic模型
逻辑斯谛曲线能够比较适合地反映国家或区域城镇人口的增殖规律，那么如 何运用这曲线进行城镇人口的发展预测呢？
这一规律的描述，即城镇人口发展预测模型，后来由比利时数学家维哈尔斯 特（Verhulst）归纳提炼成一般的数学表达式。
土地需求量预测方法和内容
1
3.6.1 概述
1）预测的程序
确定预测目的 —→ 制定预测计划 —→ 收集基础资料 —→ 检验现有资料 —→ 实施预测过程 —→ 分析预测误差。
2）预测的方法
据不完全统计，世界上至今所采用的预测方法达150多种，其中 常用方法15—20种。大致可分为三类：1、定性预测。2、定量预测。 3、综合预测。
9
3.6.2 人口预测
2）城乡人口预测
城镇人口是指城市、建制镇建成区范围内常住人口。乡村人口 是指村庄、集镇常住人口。流动人口一般不计入城镇与乡村人口， 但在确定建设用地规模时应予以考虑。
新建城镇的规划人均建设用地指标宜在第Ⅲ级内确定，当城镇的
18 发展用地偏紧时，可在第Ⅱ级内确定。
19
20
1）城镇：用地定额指标概算 法
按上述公式分段或逐年确定K值计算。 ──因建设重大项目引起人口变动的，可按劳动力带眷系数法，
即根据新建工业项目的职工数及带眷情况计算人口机械增长。
7
8
受资源、生态条件严重制约的，应按环境容量法确定适宜的人 口规模。
式中：PMAX ──城市的极限人口；PIMAX──自然资源、生态条件供给能 力和某项基础设施支持能力的最大值。
2）城镇人口预测
13
3.6.2 人口预测
2）城镇人口预测
(3) Logistic模型
逻辑斯谛曲线能够比较适合地反映国家或区域城镇人口的增殖规律，那么如 何运用这曲线进行城镇人口的发展预测呢？
这一规律的描述，即城镇人口发展预测模型，后来由比利时数学家维哈尔斯 特（Verhulst）归纳提炼成一般的数学表达式。
土地需求量预测方法和内容
1
3.6.1 概述
1）预测的程序
确定预测目的 —→ 制定预测计划 —→ 收集基础资料 —→ 检验现有资料 —→ 实施预测过程 —→ 分析预测误差。
2）预测的方法
据不完全统计，世界上至今所采用的预测方法达150多种，其中 常用方法15—20种。大致可分为三类：1、定性预测。2、定量预测。 3、综合预测。
耕地需求量的预测方法
耕地需求量的预测方法一、规划目标年粮食总需求量预测1、根据消费水平设计、人口预测结果、工业发展水平确定规划目标年各类粮食的需求量 i Q =∑=nj j q 1 式中：i Q ——规划目标年某种粮食的总需求量（包括小麦、玉米、大豆、稻谷等） j q ——规划目标年i 种粮食j 种用途的需求量（包括：口粮、工业用粮、饲料用粮、种子粮、储备粮等）2、根据规划目标年各类粮食的需求量，确定规划目标年粮食的总需求量∑==mi i Q Q 1 式中：Q ——规划目标年粮食的总需求量；m ——粮食品种；i Q ——规划目标年某种粮食的总需求量二、计算粮食作物播种面积需求量1、根据历年粮食作物播种面积单产的统计资料，利用回归分析方法预测规划目标年的粮食作物播种面积单产y2、计算粮食作物播种面积需求量播S =yQ 式中： 播S ——规划目标年粮食作物播种面积需求量；Q ——规划目标年粮食的总需求量；y ——规划目标年的粮食作物播种面积单产三、规划目标年粮食作物耕地面积预测1、根据历年粮食作物复种指数统计资料，利用回归分析方法预测规划目标年的粮食作物复种指数p2、计算规划目标年粮食作物耕地面积 S=p 播S 式中：S ——规划目标年粮食作物耕地面积需求量；播S ——规划目标年粮食作物播种面积需求量；p ——规划目标年粮食作物复种指数（p =100 粮食作物耕地面积粮食作物播种面积% 四、规划目标年耕地需求量预测 1、根据历年经济作物所种总耕地面积的比例统计资料，利用回归分析方法预测规划目标年的经济作物所占比例g2、计算耕地的总需求量总S =g-1S 式中： 总S ——耕地的总需求量；S ——规划目标年粮食作物耕地面积需求量；g ——预测规划目标年的经济作物所占比例。
10第十章土地需求量预测
Z=H(1+k) 式中：Z—规划期农村居民点新增用地面积
K—道路、建筑等占地系数（一般取0.3-0.6）
3.两区累加法 先分别计算生活区和生产区的占地面积， 然后累计加总，即可得到居民点用地面积，其公式为：
M=M1+M2 =(m1+m2+m3+m4)xk+SΣPi
式中：M—居民点用地面积n i=1 M1—生活区用地面积 M2—生产区用地面积 m1—居住建筑面积 m2—公共建筑面积 m3—自留地面积 m4—生活区内不宜利用的土地面积 Pi—各种生产建筑物面积 k—系数，k=1.2-1.3 S—系数，S=10-15
1.蔬菜地面积需求量：
（1）确定蔬菜内部需要量（v）
（2）确定蔬菜的商品率（p）
（3）确定蔬菜作物总产量（w）
w v
1 p
_
（4）确定蔬菜作物加权平均单产（ Y F）
具体确定方法如下： ①确定各类蔬菜作物的种植结构（F） ②确定各类蔬菜作物平均先进单产：即根据地区平均单产（Y地区） 和高产单位的平均单产（Y单位）相加取半，即
（二）水利工程用地需求量 1.渠道工程用地面积依据其长度和宽度来计算。
QVC Ri
式中Q—渠道设计流量（立方米/秒）；
ωR——水过力水半断径面积（平R方米）(m)
λ（m)—湿周
i—渠道比降 c—糙率系数 V—流速
C
1
1
R6
n
2.水库用地预测
(1)库容简易测算法 水库工程用地可依据水位—库容关系曲线估算
（7）确定蔬菜轮作地毛面积（S3） S3=S2（1+K1+K2）
式中K1—蔬菜轮作地上林带、道路、沟渠用地占蔬菜轮作地净 面积的比重， K1=5%~7%；K2—温床、温室占地面积占蔬菜轮 作地净面积的比重，K2=2%~3%
耕地需求量预测方法探讨——以河南省南阳市为例
耕地 指标是 土地 利用 总体 规划 调整 指标 中最重 要 的指 标 ｌ上 轮土 地利 用 总体 规 划 （９７ ２ １ ） 耕地 指 标 预 】 １ ， １９ ～００年 在
测上 多是一 种静 态 的 、 制性 规划 模式 ， 控 未考 虑各 地非 均 衡
的方 法 主要采 用趋 势 预测法 与灰 色 预测 法 。其 中趋势 预测 法是 指规 划 区域 、单 位 的耕地 面 积或 建设 用地 面 积 的变 化 是在 时间 序列 七 展开 的 ， 着时 间 的推 移 ， 以得 到一 系列 随 可 依 赖 于 时间 的数 据 ， ｔ， ， ）即假 定 变量 的 过去 变 动 趋势 外 ，
留法的 耕地 需求 量预 测方 法。 关键 词 耕 地 需求 量 ； 粮食 需 求 ； 学模 型 ； 留法 数 预 中图分类 号 Ｆ ０ 文献标 识码 Ａ ３１ 文章 编号
Ｏ １— ６ １ ２ ０ ）０ ５ １— ３ ５ ７ ６ １ （ ０ ６ ２ — ３ ９ ０
Ｓｔ ｄｙｏ ｔ ｅＰｒ ｄｉｔｏｎＭ ｅ ｈ ｄ ｆＣｕｌｉａｔｄ Ｌａ ｍ ａｎ ｕ ｎ ｈ ｅ ｃｉ ｔ ｏ ｏ ｔｖ ｅ ｎｄ Ｄｅ ｄ
模 型是 通过 时序 数据 累加 的生 成模 块 建立起 来 ，滤 去原 始 序 列 中可能 混入 的随机 量 ，从上 下 波动 的 时间 序列 中寻 找 某种 隐 含 的规 律性 。两 种方 法 的 区别在 于趋 势 预测法 适 合 于散 点 图呈直 线分 布 的数据 ，而 灰 色预 测法适 用 样本 数 量
延 到 未来 ， 从而 得 到预测期 的变 量数 值 。而灰 色 系统 预测
发展 的个性 化要 求 ，降 低 了预测 的 准确性 与 用地 指标 调整 的可信 度 。 因此新一 轮 的土地 规划修 编 中 ， 对南 阳市 耕地 在 供给量 进行 系统 分析 的基础 上 ， 用粮 食需求 预测 法 、 采 数学 模型法 与预 留法进 行耕 地需 求量 预测 。通 过对 比发 现基 于
实验4 土地需求量预测
实验4 土地需求量预测实验学时：4学时实验类型：综合实验要求：选修1实验目的1）学习土地利用需求量预测的原则、内容等基本知识，了解土地需求量预测的意义，掌握土地需求量预测的步骤和方法；2）了解耕地需求预测的重要性和作用，掌握利用粮食安全法和人均耕地法预测耕地的需求量；3）了解建设用地需求预测的重要性和作用，掌握利用人均定额法、双因素预测法、GM （1，1）模型法等预测城镇建设用地和农村居民点用地的需求量。
2 基本理论2.1 相关定义土地需求量预测是在全面考虑生产与生活需要，分析社会经济条件优势，协调主导产业与基础产业关系基础上，根据土地生产率与人口增长等方面因素，对规划区范围内，各业用地面积在规划期内增减进行的测算。
借此掌握未来规划年度各类用地需求量和土地利用结构的变化趋势，为有计划、因地制宜的安排农业和非农业用地、加强土地利用科学管理和宏观控制、协调产业用地矛盾以及编制土地利用总体规划提供依据。
土地需求量预测包括农业用地和建设用地需求量预测。
农业用地需求量预测具体包括耕地、园地、林地、牧草地和水产用地需求量预测；建设用地需求量预测具体包括各类建设用地,如城乡居民点用地、独立工矿用地、交通运输用地、水利工程用地和特殊用地需求量预测。
土地需求量与人口规模、消费水平、经济发展水平、城镇化水平和作物产量等因素有着密切的联系。
相关土地需求量预测方法和分析参见附录3。
2.2 预测依据1）国家重点建设项目和基础设施建设项目用地规模预测的依据；2）城镇村及工矿建设用地、交通用地、水利建设等用地规模预测的依据。
包括规划区域经济社会发展规划、城镇建设总体规划、总人口和城市化发展预测、人均建设用地定额以及各类专项规划等；3）耕地、园地、林地和水产养殖用地的需求量预测依据。
包括区域国民经济发展战略目标的要求、非农建设占用耕地应补充的数量级土地适宜性评价结果等。
2.3 预测内容1）基础数据预测包括人口规模、消费水平、经济发展水平、城市化水平和作物单产等。
第五章 土地需求量预测
人口统计学法
具体做法： 1.将现有的人口按性别和年龄分组，确定各年龄
组的出生率、死亡率； 2.根据本地区经济活动的历史和未来趋势确定人
口的迁移率； 3.求一个周期内的人口变化，它等于各年龄组的
人口数量乘以个年龄组的比率求和； 4.把每一组人口推向年龄较大的一个周期，如此
反复地推到任意远的未来。
劳动平衡法
基础资料 观念 数据
定性分析推理
定量数学模型
提出预测课题 工作组织 工作方法 预测期限 预测范围
预测范围
综合分析 定性 定量
预测范围
决策
部门规划预测法 二、数学模型预测法
（一）总人口预测 1.自然增长法 2.回归分析法 3.人口统计学法
（二）城镇人口预测 1.劳动平衡法 2.城镇／乡村增长差法 3.劳动力转移法
N——规划人口数；
J2——人均用地定额。
农村个人建房系数法
首先根据规划期间需建房户数推算农民建房需新增用地面积：
H=(N/P+F0)×n/2×d×e 式中：H—规划期农村个人建房户需占用土地面积；
N—规划目标年农村人口数；
P—户均人口数； n—规划年限；
F0—规划期农村总户数； d—规划期间建房户所占比例；
（三）农业人口预测
自然增长法
计算公式： P=B(1+Y)n±ΔG 或 P=B(1+K)n
式中：P——规划期末的人口总数 B——基期的人口数 Y——规划期间人口自然增长率 K——规划期间人口年平均增长率 n——规划期到基期相隔的年数 g——人口机械增长数
回归分析法
计算公式： P＝b0＋bt
式中：P——预测人口数； t——年代序号数； b0和b——两个待定参数。
基于粮食安全策略的耕地需求量预测研究——以湖北省为例
ＤＥ ＮＧ ｎ —ｉ Ｙｉｇｌ ｎ，Ｕ Ｕ Ｙａ － ｎ ，Ｌ Ｕ ｏｌ ｎ ｆ ｇ Ｉ Ｙａ —ｉ ａ ｎ
（ ｏｌ ｆ ｅｏｒｅａｄＥ ｖｒ ｍ ｎ ，ｉ ｃ ， ｈｎＵ ｉ ｒｉ ， ｈｎ４ ０ ７ ，Ｃ ｉａ ￣ｈｏ ｓｕｃ ｎ ｎｉ ｎ ｅｔ ｃ ｎ ｅ Ｗｕａ ｎ ｅｓｙ Ｗｕａ ３０ ９ ｈｎ ） ｏＲ ｏ Ｓｅ ｖ ｔ
ｔｅ ｇ ｏ ｓａ ａ ｌ ａ ｄ ｓ ｃ ｓｒ ｇ ｅ ｓｖ ｎ ｌｓｓａ ｄ ｇｅ ｙ ｔｍ． Ｂ ｔ ｈ ｔ ｏ ｓ ａ ａ ｅ ｎ ｔ ｅ ｈ ｓ ｒｃ ｄ ｔ Ｈ ｔ ｅ ｃ ｍｍｏ ．Ａｓ ｈ ｓ ｒ ｂ ｅｌ ｎ ｕ ｈ ａ ｅ ｓ ｉｅ ａ ａｙ ｉ ｎ ｒ ｙ ｓ ｓｅ ｒ ｒ ｕ ｅ ｍｅ ｈ ｒ ｂ ｄ ｏ ｈ ｉｔ ｉ ａａ Ｏ ｈ ｏ ｔ ｄ ｅ ｓ ｏ ｎ
的耕 地需求 量 。
１ １ 人 口预测 ．
首先对待预测区域人 口规模 进行预测 ， 可采用 自然
增长 牢法 、 和生育 率法 等方 法 。 总 １２ 基 于粮食 安全 策略下 的粮食 总供 给量 预测 ． 基于粮 食安全 策略 下 的粮 食 总 供 给量 预 测 主要 从 方 面考 虑 ， 先是满 足 区域 内人 口的 粮食 自给率 ， 首 其次 是 考虑 区域粮 食外调 状况 ， 次 是饲料 粮需求 总 量预测 。 再
加 的 各 种 可 能性 ， 最终 确 定 耕 地 需 求 的 合 理 规 模 。
关键词 ： 粮食安全 ； 耕地 需求量 ； 预测 中图分 类号 ： Ｏ ｓ— ３ 文献标识 码 ： Ａ
文章编号 ：６２— ８ ７ ２０ ） １ ０ ２ ０ １７ ５６ （０ ６ ０ — ０ ７— ３
Ｒｅ ｅ ｒ ｈ ｏ ｈ ｅ ｉｔｏ ｆＧ ｒ ｓ ａ ｌ ｓ ａ ｃ ｎ ｔ ｅ Ｐｒ ｄ ｃｉ ｎ ｏ ｏ ｓＡｒ ｂ ｅ Ｌａ ｄ Ｂａ ｅ ｎ Ｆｏ ｄ－ａ ｅ ｙ ｎ ｓ ｄ ｏ ｏ ｓｆｔ
（ ｏｌ ｆ ｅｏｒｅａｄＥ ｖｒ ｍ ｎ ，ｉ ｃ ， ｈｎＵ ｉ ｒｉ ， ｈｎ４ ０ ７ ，Ｃ ｉａ ￣ｈｏ ｓｕｃ ｎ ｎｉ ｎ ｅｔ ｃ ｎ ｅ Ｗｕａ ｎ ｅｓｙ Ｗｕａ ３０ ９ ｈｎ ） ｏＲ ｏ Ｓｅ ｖ ｔ
ｔｅ ｇ ｏ ｓａ ａ ｌ ａ ｄ ｓ ｃ ｓｒ ｇ ｅ ｓｖ ｎ ｌｓｓａ ｄ ｇｅ ｙ ｔｍ． Ｂ ｔ ｈ ｔ ｏ ｓ ａ ａ ｅ ｎ ｔ ｅ ｈ ｓ ｒｃ ｄ ｔ Ｈ ｔ ｅ ｃ ｍｍｏ ．Ａｓ ｈ ｓ ｒ ｂ ｅｌ ｎ ｕ ｈ ａ ｅ ｓ ｉｅ ａ ａｙ ｉ ｎ ｒ ｙ ｓ ｓｅ ｒ ｒ ｕ ｅ ｍｅ ｈ ｒ ｂ ｄ ｏ ｈ ｉｔ ｉ ａａ Ｏ ｈ ｏ ｔ ｄ ｅ ｓ ｏ ｎ
的耕 地需求 量 。
１ １ 人 口预测 ．
首先对待预测区域人 口规模 进行预测 ， 可采用 自然
增长 牢法 、 和生育 率法 等方 法 。 总 １２ 基 于粮食 安全 策略下 的粮食 总供 给量 预测 ． 基于粮 食安全 策略 下 的粮 食 总 供 给量 预 测 主要 从 方 面考 虑 ， 先是满 足 区域 内人 口的 粮食 自给率 ， 首 其次 是 考虑 区域粮 食外调 状况 ， 次 是饲料 粮需求 总 量预测 。 再
加 的 各 种 可 能性 ， 最终 确 定 耕 地 需 求 的 合 理 规 模 。
关键词 ： 粮食安全 ； 耕地 需求量 ； 预测 中图分 类号 ： Ｏ ｓ— ３ 文献标识 码 ： Ａ
文章编号 ：６２— ８ ７ ２０ ） １ ０ ２ ０ １７ ５６ （０ ６ ０ — ０ ７— ３
Ｒｅ ｅ ｒ ｈ ｏ ｈ ｅ ｉｔｏ ｆＧ ｒ ｓ ａ ｌ ｓ ａ ｃ ｎ ｔ ｅ Ｐｒ ｄ ｃｉ ｎ ｏ ｏ ｓＡｒ ｂ ｅ Ｌａ ｄ Ｂａ ｅ ｎ Ｆｏ ｄ－ａ ｅ ｙ ｎ ｓ ｄ ｏ ｏ ｓｆｔ
第五章 土地需求量预测
一、耕地需求量预测
7．耕地需求量的确定 根据近年来该市各类农产品自给率变化情况，综合考虑 到该地区的耕地资源禀赋及社会经济发展趋势，确定规划目 标年粮食自给率为60%，油料作物自给率为100%，蔬菜自给 率为150%，瓜果类自给率为120%，其他农作物不考虑自给 率。根据以上对各类作物需求预测及其自给率的确定，按下 式： 耕地需求量=∑（各类作物种植面积需求量×各类作物自 给率+其他农作物种植面积）/耕地复种指数 计算可以得出该市耕地需求量。
一、耕地需求量预测
1．粮食作物播种面积预测 粮食单产的预测直接决定着粮食作物用地需求量的多少， 所以粮食单产的预测在慎重的基础上力求准确。FAO有一种 计算作物光温生产潜力的理论方法。即利用辐射数据，计算某 种标准作物可能的潜在产量；通过这种方法求得的作物潜在产 量，是在理想条件仅受光温和作物品种影响的理论潜力，它是 裸露于自然气温下作物生产力的上限。该计算结果，即作物潜 在产量可以作为评价区域土地生产潜力和不同时期作物单产水 平高低的重要依据。 根据以往的粮食作物单产资料，应用农业生态区域法 （AEZ）计算粮食作物气候生产潜力，通过产潜比增长公式 法计算各年粮食单产。
第四节土地供需平衡分析二土地供需平衡协调土地现状态势土地开发潜力供给制约和引导需求耕地总量动态平衡和重点建设项目用地国民经济发展态势规划方案优选协调供需平衡土地总供给量土地总需求量随着经济的发展及人口的增加建设用地规模逐渐增加进而带来耕地逐渐减少和生态环境的逐渐恶化在可持续发展观与建立和谐社会目标的追求下建设用地的扩张应该保证不会威胁粮食安全及破坏生态环境因此建设用地的供给能力受到粮食安全和生态安全的制约
第二节
建设用地需求量预测
一、总规模预测① 拉动建设用地规模增加的因素不仅仅是人口数量一个 因素，而是多个因素共同作用的结果。从系统工程的角度出 发，可以构建“压力-状态-响应”(PSR)模型来分析。经济 发展、人口增加是建设用地扩展的目标驱动力。在该驱动力 作用下，土地利用现状发生响应性变化，这种变化是基于建 设用地存量的基础上，使建设用地规模不断扩展。
土地利用现状及土地利用预测方法[汇总]
![土地利用现状及土地利用预测方法[汇总]](https://img.taocdn.com/s1/m/5f2b55200a4c2e3f5727a5e9856a561252d3211a.png)
一、土地利用现状分析的内容（一）、社会经济发展情况（二）、土地利用历史变化趋势（三）、土地利用现状结构与布局（四）、土地开发利用程度与效益（五）、土地利用存在问题及开发利用潜力二、要求1、收集有关资料。
2、核实各类土地面积。
3、注意与有关专题研究的内容相协调、相衔接。
主要分析方法有动态分析法、对比分析法。
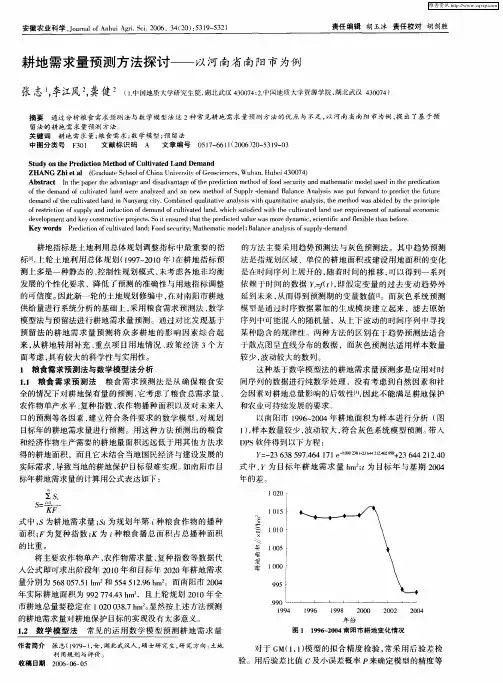
一、土地利用结构布局案例：根据1996 年土地利用变更调查数据汇总, 全省（广东省）土地总面积1797.52 万公顷, 其中,已利用土地1671.22 万公顷, 土地利用率为92.97%。
土地利用现状如下：1. 农用地全省耕地、园地、林地、牧草地、水面等农用地面积共1527.40 万公顷, 占全省土地总面积84.97%。
①耕地。
含灌溉水田、旱地和菜地等, 共327.22 万公顷, 占全省土地总面积的18.20%。
其中, 灌溉水田223.90 万公顷, 占耕地面积的68.42% ; 旱地86.51 万公顷, 占26.44% ; 菜地3.71 万公顷, 占1.14% ; 其它13.1 万公顷, 占4.0%。
②园地。
包括果园、桑园、茶园、热作园等, 共78.96 万公顷, 占土地总面积的439% 。
园地中以果园和热作园为主, 其中果园57.09 万公顷, 占园地面积的72.30% , 全省各地均有分布。
热作园11.47 万公顷, 占园地面积的14.53%, 主要分布在粤西的湛江和茂名两市。
桑园主要分布在西江和北江流域茶园主要在山区。
③林地。
林地是本省面积最大的用地类型, 主要分布在丘陵山区。
林业部门统计面积为1083.6 万公顷, 土地利用变更调查数据为1032.3 万公顷。
全省森林覆盖率为56.3%。
④专用牧草地。
共 2.83 万公顷, 占土地总面积的0.16%。
⑤水面。
包括淡水产养殖、水库、河流、湖泊、坑塘水面等共86.09 万公顷, 占土地总面积的 4.79%。
2. 建设用地全省居民点及工矿用地、交通用地、水利水工用地共143.82 万公顷, 占全省土地总面积的8.00%。
第二章各类用地需求量预测P56-92
（2）计算规划年有关指标：
• 土地垦殖率；土地利用率；林地覆盖率；水面利用率；土 地建设利用率；土地农业利用率；基本农田面积；土地复 种指数。
表1 各类用地综合平衡表
单位：公顷
土地利用类型
期内减少
基期面积
牧 利
草 农用 村用 工矿
地地地
用地 用地 域 用地
三级地类面积比重和分布； 产草量、载畜量等。
• 居民点及工矿用地
居民点及工矿用地面积占辖区总土地面 积百分比；
二级地类的面积、比重和分布； 居民点分布形式，按城市和乡镇分别计
算人均用地面积等。
• 交通用地
交通用地面积及占辖区总土地面积百分 比；
二级地类面积、比重及分布；
现有交通网对经济发展的适应程度等。
• 土地利用历史变化分析 进行历史性的纵向分析，并探讨这
些变化的内外原因、变化规律及变化 的合理性。
通过分析从时间的纵向角度反映土 地结构变化的趋势。
• 土地利用结构分析
着重阐述和分析土地利用的地类数 量、结构及特点。（全国有8个一级
类(新3个)，79个二级类（新15个）；
通过与同类地区和发达地区的横向 比较，分析各类用地面积及结构形成
方法
• 静态分析法、动态变化分析法、对比分析法、 指标分析法、图上分析法
一、静态分析法
是分析对象在某一时期或时刻的 状况与特点。主要用于对基期年 土地利用结构与布局进行分析。
• 耕地
辖区耕地面积及其在全县土地总面积 中所占的百分比；
二级地类面积及在耕地中的比重； 高、中、低产田的百分比； 辖区人均耕地面积及耕地地域分布利
第二节
土地需求量预测
一、内容
• 包括农业用地和建设用地两个方面： 其中：①农业用地：
• 土地垦殖率；土地利用率；林地覆盖率；水面利用率；土 地建设利用率；土地农业利用率；基本农田面积；土地复 种指数。
表1 各类用地综合平衡表
单位：公顷
土地利用类型
期内减少
基期面积
牧 利
草 农用 村用 工矿
地地地
用地 用地 域 用地
三级地类面积比重和分布； 产草量、载畜量等。
• 居民点及工矿用地
居民点及工矿用地面积占辖区总土地面 积百分比；
二级地类的面积、比重和分布； 居民点分布形式，按城市和乡镇分别计
算人均用地面积等。
• 交通用地
交通用地面积及占辖区总土地面积百分 比；
二级地类面积、比重及分布；
现有交通网对经济发展的适应程度等。
• 土地利用历史变化分析 进行历史性的纵向分析，并探讨这
些变化的内外原因、变化规律及变化 的合理性。
通过分析从时间的纵向角度反映土 地结构变化的趋势。
• 土地利用结构分析
着重阐述和分析土地利用的地类数 量、结构及特点。（全国有8个一级
类(新3个)，79个二级类（新15个）；
通过与同类地区和发达地区的横向 比较，分析各类用地面积及结构形成
方法
• 静态分析法、动态变化分析法、对比分析法、 指标分析法、图上分析法
一、静态分析法
是分析对象在某一时期或时刻的 状况与特点。主要用于对基期年 土地利用结构与布局进行分析。
• 耕地
辖区耕地面积及其在全县土地总面积 中所占的百分比；
二级地类面积及在耕地中的比重； 高、中、低产田的百分比； 辖区人均耕地面积及耕地地域分布利
第二节
土地需求量预测
一、内容
• 包括农业用地和建设用地两个方面： 其中：①农业用地：
5第五章土地需求量预测
总人口 7544400 7566400 7617400 7668000 7740300 7790700 7845592 7892563 7939533 7967668 7988883
?
（三）劳动平衡法
• 1、前提条件：各种人口资料齐全。有具体的国民经济发
展计划。
• 2、适用范围：城市和城镇居民点人口预测。 • 3、计算公式：
规划区域供应给人类利用的各类土地类型的数量 之和。包括土地的自然供给和土地的经济供给
3、土地需求
人类从事生产与消费活动对土地的需要
4、土地供需分析
是在土地供给量和土地需求量预测和估算的基 础上加以比较，依据土地供给和土地需求量两 者之间的数量比较借以评价供不应求、供过于 求和供需平衡状况。
End
A—昼夜平均交通量（辆/昼夜） N—公路年平均货运强度（t） d—汽车运输天数（d） p—每辆汽车载重量（t）
第四节 土地供需平衡分析
土地供需平衡分析目的在于了解土地供需方面 存在的问题，寻求协调土地供需的途径和方法。 一、基本概念
1、土地供给
自然界赋予人类社会生产和生活利用的土地数量和 质量
2、土地供给量
1、前提条件 预测精度要求高；历史数据充分。 2、适用范围：总人口预测、城镇人口预测。 3、具体方法 （1）根据人口统计资料，将人口数和年代数
在直角坐标系中绘出散点图；
年份 1993年 1994年 2019年 2019年 2019年 2019年 2019年 2000年 2019年 2019年 2019年 2019年
• 解：
• 1990-2019年人口年均增长率：K=0.016
• P(2000年)=110×(1+0.016) 4 =117.21万人
土地耕地需求量预测
.《土地利用规划学》耕地需求量预测-----------基于回归分析法学院：资源与环境学院班级：2013009姓名：x学号：201300926指导老师：x目录一、趋势外推预测法： (2)1. 绘制时间序列散点图： (2)2. 由最小二乘法求参数： (2)3.进行耕地预测： (4)二、回归预测法： (4)（一）回归分析概述： (4)（二）一元线性回归： (4)1.绘制散点图： (4)2.最小二乘法估计参数： (5)3.回归方程及回归系数的检验： (6)1）拟合优度检验（R2） (6)2）相关系数显著性检验： (8)3）回归方程的显著性检验（F 检验） (9)4. 利用回归模型进行预测： (9) (10)（三）多元线性回归分析：1.建立回归模型： (10)2.最小二乘法估计参数： (11)3.多元线性回归模型的统计检验 (13)(1)拟合优度检验（可决系数与调整的可决系数） (13)(2) 方程的显著性检验(F检验) (15)(3) 变量的显著性检验（t检验） (16)三、总结： (18)耕地需求量预测根据下表进行该地2016年耕地需求量预测方法一：仅根据耕地面积变化趋势进行分析方法二：对耕地面积和人口做回归分析方法三：将耕地面积与人口、粮食产量及化肥施用量做回归分析（本方法不用计算耕地需求量，只列出方程并检验即可）以上三种方法在EXCEL或MATLAB软件中完成，要求步骤完整，排版清晰。
表1：基本资料一、趋势外推预测法：概念：规划区域或单位的耕地面积或建设用地面积的变化是在时间序列上展开的。
随着时间的推移，可以得到一系列依赖于时间的数据Y t=f(t)。
已时间为参数的数列称之为时间序列。
若假定变量的过去变动趋势外延到未来，从而得到预测值期的变量数值，这就是趋势预测法。
1.绘制时间序列散点图：由图可以看出：该地区历年耕地面积变化趋势呈递减趋势且年变化增减幅度大致相等，所以拟合方程为直线方程y=a+bx。
土地需求量预测(1)
4.预测耕地需求量（G） G=∑Ci/（Yi*f）（i=1，2，……m）
可编辑ppt
9
案例：严志强.广西耕地资源可持续利用
与粮食安全问题研究.热带地理,2002（2）
预测广西2010年P=5500万人，J=450500kg（小康水平400-600kg）
则 粮食需求量C=P*J=2475-2750万t
求量(X1)和商品率(f)：X=X1/(1-f)
2、确定放牧牲畜标准头数(N) 将畜产品需求量换算成标准牲畜单
位，再按放牧牲畜占牲畜总头数的比例， 计算放牧牲畜的标准头数。
可编辑ppt
14
3、确定牧草地的载畜量(m)
牧草地的载畜量一般根据牧草地 单位面积产草量（p）、草地利用率 (k)、放牧天数(n)和牲畜日粮(j)计 算，用公式表示：m= p·k/（n·j）
5、汇总形成综合材料
根据调整和补充的部门用地 预测及用地计划，进行汇总，经 过综合平衡，形成土地需求量预 测的综合材料。
可编辑ppt
5
四、土地需求量预测应收集的资料
1、人口资料 2、社会经济资料 3、土地利用现状及历史动态变化资料 4、有关规划、区划及专题研究成果资料
可编辑ppt
6
第五章 土地需求量预测
可编辑ppt
2
二、土地需求量预测的任务
土地需求量预测的任务就是根据规 划区域的社会、经济发展和土地资源条 件，研究分析远景土地利用总的趋势， 对各业用地面积在规划期内的增减变化 情况及对总用地规模进行测算。掌握规 划年度各类用地需求量和土地利用结构 的变化趋势，从而为土地利用总体规划 有计划安排各项用地提供科学的依据。
调入-) 其中：Xi=P*Ji 式中：P-规划期总人口
Ji-规划期计划第i种农产品人均占有量
可编辑ppt
9
案例：严志强.广西耕地资源可持续利用
与粮食安全问题研究.热带地理,2002（2）
预测广西2010年P=5500万人，J=450500kg（小康水平400-600kg）
则 粮食需求量C=P*J=2475-2750万t
求量(X1)和商品率(f)：X=X1/(1-f)
2、确定放牧牲畜标准头数(N) 将畜产品需求量换算成标准牲畜单
位，再按放牧牲畜占牲畜总头数的比例， 计算放牧牲畜的标准头数。
可编辑ppt
14
3、确定牧草地的载畜量(m)
牧草地的载畜量一般根据牧草地 单位面积产草量（p）、草地利用率 (k)、放牧天数(n)和牲畜日粮(j)计 算，用公式表示：m= p·k/（n·j）
5、汇总形成综合材料
根据调整和补充的部门用地 预测及用地计划，进行汇总，经 过综合平衡，形成土地需求量预 测的综合材料。
可编辑ppt
5
四、土地需求量预测应收集的资料
1、人口资料 2、社会经济资料 3、土地利用现状及历史动态变化资料 4、有关规划、区划及专题研究成果资料
可编辑ppt
6
第五章 土地需求量预测
可编辑ppt
2
二、土地需求量预测的任务
土地需求量预测的任务就是根据规 划区域的社会、经济发展和土地资源条 件，研究分析远景土地利用总的趋势， 对各业用地面积在规划期内的增减变化 情况及对总用地规模进行测算。掌握规 划年度各类用地需求量和土地利用结构 的变化趋势，从而为土地利用总体规划 有计划安排各项用地提供科学的依据。
调入-) 其中：Xi=P*Ji 式中：P-规划期总人口
Ji-规划期计划第i种农产品人均占有量
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
《土地利用规划学》耕地需求量预测-----------基于回归分析法学院：资源与环境学院班级：2013009姓名：x学号：201300926指导老师：x目录一、趋势外推预测法： (2)1. 绘制时间序列散点图： (2)2. 由最小二乘法求参数： (3)3.进行耕地预测： (5)二、回归预测法： (5)（一）回归分析概述： (5)（二）一元线性回归： (5)1.绘制散点图： (5)2.最小二乘法估计参数： (6)3.回归方程及回归系数的检验： (8)1）拟合优度检验（R2） (8)2）相关系数显著性检验： (9)3）回归方程的显著性检验（F 检验） (10)4. 利用回归模型进行预测： (11)（三）多元线性回归分析： (12)1.建立回归模型： (12)2.最小二乘法估计参数： (13)3.多元线性回归模型的统计检验 (16)(1)拟合优度检验（可决系数与调整的可决系数） (16)(2) 方程的显著性检验(F检验) (17)(3) 变量的显著性检验（t检验） (18)三、总结： (20)耕地需求量预测根据下表进行该地2016年耕地需求量预测方法一：仅根据耕地面积变化趋势进行分析方法二：对耕地面积和人口做回归分析方法三：将耕地面积与人口、粮食产量及化肥施用量做回归分析（本方法不用计算耕地需求量，只列出方程并检验即可）以上三种方法在EXCEL或MATLAB软件中完成，要求步骤完整，排版清晰。
表1：基本资料一、趋势外推预测法：概念：规划区域或单位的耕地面积或建设用地面积的变化是在时间序列上展开的。
随着时间的推移，可以得到一系列依赖于时间的数据Y t=f(t)。
已时间为参数的数列称之为时间序列。
若假定变量的过去变动趋势外延到未来，从而得到预测值期的变量数值，这就是趋势预测法。
1.绘制时间序列散点图：由图可以看出：该地区历年耕地面积变化趋势呈递减趋势且年变化增减幅度大致相等，所以拟合方程为直线方程y=a+bx 。
2.由最小二乘法求参数：◎由最小二乘法原理导出方程组：y na b xx y a x b xiiiiii∑∑∑∑∑=+=+2◎联解上面方程可得参数a 和b()()()b x y nx y xnx a y nbxnii iiiiii=--=-∑∑∑∑∑∑∑1122◎计算附表如下：年份x该地市耕地面积（ha ）y x2xy19912847513964081 5669392411992 283422 3968064 564576624 1993 282474 3972049 562970682 1994 279647 3976036 557616118 1995 278546 3980025 555699270 1996 278936 3984016 556756256 1997 275374 3988009 549921878 1998 272198 3992004 543851604 1999 260484 3996001 520707516 2000 257416 4000000 514832000 2001 256471 4004001 513198471 2002 255503 4008004 511517006 2003 255910 4012009 512587730 2004 254872 4016016 510763488 2005 253690 4020025 508648450 2006 251479 4024036 504466874 2007 252465 4028049 506697255 2008 250175 4032064 502351400 2009 244610 4036081 491421490 2010 243540 4040100 489515400 2011 241587 4044121 485831457 2012 240116 4048144 483113392求和 44033 5753666 88132935 1.151E+10根据公式1可得：⎩⎨⎧==-2234.784734441b a →x y 78.22344734441-= ◎进行耕地预测：根据方程2016年的耕地面积为ha)（229126201678.22344734441=⨯-=y二、回归预测法： （一）回归分析概述：回归分析是借助数学模型对客观世界所存在的事物间的不确定关系的一种数量化描写，即通过一个或几个变量的变化去解释另一变量的变化。
它的目的是在于对相关随机变量进行估计、预测和控制，确定变这些量之间数量关系的可能形式，并用一个数学模型来表示。
◎回归分析的分类：⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧非线性回归线性回归按方程式特征分类多元回归简单回归按自变量个数分类回归分析 （二）一元线性回归： 1.绘制散点图：◎由图我们可以看出：随着该地区人口的增加，耕地面积变化趋势呈递减趋势，且增加幅度大致相等，所以拟以直线方程y=a+bx 。
2.最小二乘法估计参数：◎最小二乘法原理是要使残差平方和为最小，即：()()Q y yy a bx i i ni i i n=-=--==∑∑ 1212◎要使Q 最小，可由极值原理得:()()∂∂∂∂Qa y a bx Qb y a bx x i i i i i =---==---=∑∑2020◎所以可以导出方程组：y na b xx y a x b xiiiiii∑∑∑∑∑=+=+2◎两个方程联立求解可得回归方程的参数：()()()b x y nx y xnx a y nbxnii iiiiii=--=-∑∑∑∑∑∑∑1122◎根据公式求出方程：y = -460.71x + 492931◎用excel高级分析进行回归分析可得如下几表：表（1）回归统计表回归统计Multiple R0.97407693R Square0.94882587Adjusted R Square 0.94626716标准误差3460.07955观测值22表（2）方差分析表方差分析df SS MS FSignificanceF回归分析 1 4.44E+09 4.44E+09 370.8225 2.22E-14 残差20 2.39E+08 11972150总计21 4.68E+09表（3）回归参数表回归参数表Coefficients标准误差 t StatP-valueLower95%Upper95%下限95.0%上限95.0%Intercept 492931.47 12039.25 40.94371 9.19E-21 467818 518044.9 467818 518044.9 X Variable1-460.70827 23.92451 -19.2568 2.22E-14 -510.614 -410.803 -510.614 -410.8033.回归方程及回归系数的检验：1）拟合优度检验（R 2）◎拟合优度检验是对样本回归直线与样本观测值之间拟合程度的检验。
◎度量拟合优度的指标：可决系数R 2由图可知：∑∑∑===-+-=-ni in i i ni i y y y y y y 121212)ˆ()ˆ()( 即： 总离差平方和 = 回归平方和 + 残差（剩余）平方和◎如果实际观测点离样本回归线越近，则回归平方和在总平方和i中占的比重越大，因此拟合优度等于回归平方和/Y 的总离差：9488.0)ˆ()ˆ(222=--==∑∑iii Y Y Y Y R 总离差平方和回归平方和称R 2为可决系数。
可决系数的取值范围：[0，1] ,R2越接近1，说明实际观测点离样本线越近，拟合优度越高。
R 2≥0.8说明拟合得很好。
8.09488.02≥=R所以该回归方程拟合程度很好.◎此外拟合优度测定还可用标准误差来估计1()ˆ2e ---=∑k n yy S iiSe表示根据所建立的回归方程，用自变量来预测因变量时，平均预测误差的大小；故S e 越小越好，越小说明波动性越小。
2）相关系数显著性检验： （1）提出假设;0:0=b H（2）根据公式计算R 的值得9741.0)()())((12121=-⋅---=∑∑∑===ni i ni ini i iy y x xy y x xR（3）查R 表得临界值423.0)2( =-n R α相关系数显著性检验表（4）若)2(->n R R α则应该拒绝原假设，否则接受。
◎这里显然R=0.9741>0.423，所以拒绝原假设，相关系数具有很高显著性，即两者具有很强线性相关性。
3）回归方程的显著性检验（F 检验）（1）提出假设：H 0：b=0 （2）在H 0成立时，统计量F 为：)2,1(~)2()ˆ()ˆ(1212，----=∑∑==n F n yyy y F ni i i ni i由给定的显著水平α，查F 分布表得临界值λ； ◎查表可得35.4=λ （3）根据公式计算F 的值8225.370)2()ˆ()ˆ(1212=---=∑∑==n yy y yF ni ii ni i（4）比较λ与F 的值，若λ>F ，则否定H 0，即认为x 、Y 之间存在线性相关关系；若不能否定H0，则没有理由认为x 、Y 之间存在线性相关关系.◎这里显然F=370.8225远大于λ=4.35，所以否定原假设，说明回归方程具有很高显著性，x 、Y 之间存在很强的线性相关关系。
4.利用回归模型进行预测：1.利用趋势外推法确定2016年的人口数量求得拟合方程为：y = 4.8312x - 9167.3所以可得2016年的人口为：（万人）5729167.3-20164.8312≈⨯=y2.根据耕地与人口的回归方程可得： 2016年的耕地面积为：a)229404.9(h 492931 + 572-460.71=⨯=y（三）多元线性回归分析： 1.建立回归模型：假设随机变量y 与p 个自变量之间存在着线性相关关系，假定回归方程如下：)......,(21n x x x f y =2.最小二乘法估计参数：建立多元线性回归方程，实际上是对多元线性模型进行估计，寻求估计参数的过程。
与一元线性回归分析相同，其基本思想是根据最小二乘原理，求解使全部观测值与回归值的残差平方和达到最小值。
由于残差平方和是的非负二次式，所以它的最小值一定存在。
根据极值原理，当Q取得极值时，应满足由上式，即满足上式称为正规方程组。
它可以化为以下形式◎利用克拉默法则进行求解：对于n 个变量、n 个方程的线性方程组11112211211222221122n n n n n n nn n na x a x a xb a x a x a x b a x a x a x b +++=⎧⎪+++=⎪⎨⎪⎪+++=⎩如果它的系数行列式0D ≠，则该方程组有唯一解, 1,2,,j j D x j nD== nmn na a a a D ...............1111=其中j D （1,2,,j n =）是将行列式D 中第j 列的元素换成 方程组右端的常数项所得到的n 阶行列式，即111,111,111,1,1j j nj n n j nn j nna ab a a D a a b a a -+-+=所以： D D 00=β D D 11=β D D 22=β DD 33=β根据克拉默法则可得多元回归方程为：32100.221992.26318.30821.609781x x x y +--=◎用excel高级分析里面的回归分析对本题进行计算可得如下几表：回归统计Multiple R 0.980033844R Square 0.960466335Adjusted R Square 0.953877391标准误差3205.701822观测值22方差分析df SS MS FSignificanceF回归分析 3 4.49E+09 1.5E+09 145.7694 8.16E-13 残差18 1.85E+08 10276524总计21 4.68E+09回归参数表Coefficients 标准误差t Stat P-valueLower95% Upper95%下限95.0%上限95.0%Intercept609781.213456203.33 10.84956 2.51E-09 491702.4 727860 491702.4 727860 X Variable -308.176370138.0734 -2.23197 0.038565 -598.258 -18.0949 -598.258 -18.0949x yβα+=ˆ1 2X Variable 2-263.9174591134.17-1.96704 0.064788 -545.798 17.96333 -545.798 17.96333X Variable 32218.9995382129.259 1.042147 0.31114-2254.41 6692.406 -2254.41 6692.4063.多元线性回归模型的统计检验(1)拟合优度检验（可决系数与调整的可决系数）◎总离差平方和的分解(同一元线性回归分析）由图可知：∑∑∑===-+-=-ni in i i ni i y y y y y y 121212)ˆ()ˆ()( 即： 总离差平方和 = 回归平方和 + 残差（剩余）平方和oyiy ix yy i -i i yy ˆ-y yi -ˆY◎可决系数：TSSRSSTSSESS R -==12该统计量越接近于1，模型的拟合优度越高。