控制测量学水准网按条件平差算例(新)

r nt
3
4
L1
p1 0 0
5 6
记：观测值
L n1
L2
相应权阵
p
nn
0
p2
0
7 8
Ln
0
0
pn
9
10
4 /7
v1
平差值改正数
V
n1
v2
vn
平差值
Lˆ
n1
Lˆ1 Lˆ2
Lˆn
L1
L2
Ln
v1 v2
vn
4
控制网平差
1 2 3 4 5 6 7 8 9
10
13 /7 4
2）平差值函数的权倒数
设有平差值函数为 f Lˆ1, Lˆ2,, Lˆn
它的权函数式为：
d
(
Lˆ1
)dLˆ1
(
Lˆ2
)dLˆ2
(
Lˆn
)dLˆn
f1dLˆ1 f2dLˆ2 fndLˆn
令
f T f1, f2, fn
则 d f T dLˆ
9
2） 改正数条件方程
10
以 Lˆi L（i v=i 1、i 2、… ）代入n (1)得纯量形式为：
5 /7 4
a1v1 a2v2 anvn wa 0
b1v1 b2v2 bnvn wb 0
r1v1 r2v2 rnvn wr 0
（2）
1 2 3 4 5 6 7 8 9
控制网平差
第九章 控制网平差
1
2
3 4 5
[本章提要] 9.1 条件平差数学模型和公式
6
9.2 水准网按条件平差算例
7 8
9.3 附合导线按条件平差算例

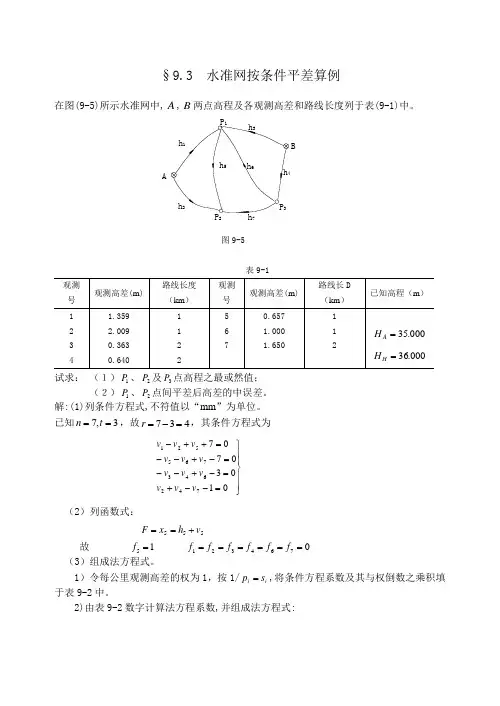
在图 表9-1试求： （１）1P 、2P 及3P 点高程之最或然值； （２）1P 、2P 点间平差后高差的中误差。

解:(1)列条件方程式,不符值以“mm ”为单位。

已知3,7==t n ，故437=-=r ，其条件方程式为⎪⎪⎭⎪⎪⎬⎫=--+=-+--=-+--=++-01030707742643765521v v v v v v v v v v v v（2）列函数式：555v h x F +==故 15=f 0764321======f f f f f f（3）组成法方程式。

1）令每公里观测高差的权为1，按1/i i s p =,将条件方程系数及其与权倒数之乘积填于表9-2中。

2)由表9-2数字计算法方程系数,并组成法方程式:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----------5221251021411013⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡d c b a k k k k +⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---1377=0 表9-2 条件方程系数表（4）法方程式的解算。

1）解算法方程式在表9-3中进行。

2）[]pvv 计算之检核。

[][]wk pvv -= []467.35=-wk由表9-3中解得[]47.35-=pvv ，两者完全一致，证明表中解算无误。

（5）计算观测值改正数及平差值见表9-4。

（6）计算321,,P P P 点高程最或然值。

359.3611=+=x H H A P m 012.3722=+=x H H A P m表9-4 改正数与平差值计算表（7）精度评定。

1）单位权（每公里观测高差）中误差2）21,P P 点间平差后高差中误差mm 0.3447.35±=±=μmmP m FF 2.252.00.31±=±=±=μ。

2.2 数据存储方案设计
这里的数据存储是指数据在内存中的存储。
测量平差程序中用到的数据较多，一般先将磁盘
中的数据读到内存中，按照不同的类别有序地放
在变量或数组中，然后再进行平差计算，最后将 计算结果写到磁盘文件中。
三、水准网平差界面设计
要整洁、简练、实用、方便有关数据的输入 或输出，必要的话要考虑和用户的交互，尽量不 要画蛇添足。
第三章
水准网平差程序设计
本章难点： 1、近似高程计算 2、最短路线的计算
3、误差方程及法方程的构建
4、直接计算出法方程的系数矩阵BTPB和常 数矩阵BTPL
一、水准网间接平差算法概述
该课程中所采用的平差模型为间接平差，即所 选的独立参数的个数等于必要观测数，这样可以 将每个观测值表示成这t个参数的函数，组成观测 方程。 L B X d 间接平差的函数模型： n ,1 n ,t t ,1 n ,1 0 平差时一般对所选参数取近似值 X X x 代入上式 并令 l L ( BX 0 d ) L L0
1）基本信息部分：该部分仅占一行，其内容为
已知点数N1，未知点数N2，高差观测值个数NS。
2）已知点高程信息：该部分占N1行，每行格式为
已知点编号，该点的高程（单位：米）。 注意：在给控制点编号时，先给待定点编号，然后 给已知点编号。编号从1开始顺序编号。 3）高差观测值信息：该部分占NS行，每行格式为 测段编号，测段起点编号，测段终点编号，测段观 测高差（单位：米），测段长度（单位：千米）。 4）点名信息：该部分占N（N=N1+N2）行，每行 格式为 水准点编号，该点名称 其中点名长度不超过8个字符，即4个汉字。但最好 用字符串命名。
式中，正负号取决于高差起始点到终点的方向与 推算路线是否一致。

§ 9.3 水准网按条件平差算例在图(9-5)所示水准网中，A,B两点高程及各观测高差和路线长度列于表(9-1)中。

•.一h s/ I \ ：'1 h5 「6A丈' \ 』4\ \ I\ \ x J、\rh2、丿P sJL ___ ■--P2 h7图9-5试求：(1) R、P2及P s点高程之最或然值；(2) P i、F2点间平差后高差的中误差。

解：(1)列条件方程式，不符值以“ mm”为单位。

已知n =7,t =3，故r =7 -3 =4，其条件方程式为w -V2 +V5 +7 =0-V5 -V6 ■ V7 _ 7 = 0 _V3 1V4 ■ V6 - 3 = 0 IV2 ■ V4 -V7 -1 = 0 I(2)列函数式：F = x5 = h5 V5故f5 -1 f^f^f^f^f^f^0(3 )组成法方程式。

1) 令每公里观测高差的权为1,按1/ P i =s，将条件方程系数及其与权倒数之乘积填于表9-2中。

2) 由表9-2数字计算法方程系数，并组成法方程式：表9-2条件方程系数表观测号 abcdsfF s1 111 2-113-1-1-1 4-1151-111 6-110 0 71-1z1-1-11" jg*1观测号%/P%dP %fP %1 1 1112 1-113 2-2-2-24 2-225 11-1116 1-11722-2z1-311（4）法方程式的解算。

1 ）解算法方程式在表 9-3中进行。

2） Ipvv 计算之检核。

pvv ] = -Wk I -Wk I-35.467由表9-3中解得Pvvl--35.47，两者完全一致，证明表中解算无误。

（5） 计算观测值改正数及平差值见表 9-4。

（6） 计算R,P 2,P 3点高程最或然值。

H P l= H A X ! =36.359 mH p 2 =H A x 2 =37.012 m-1 0 -14 -1 -2 -15 -2 -2 -2 5_7 -7 —3=0k a k b k cR 36 =H B+X4 =35.360 m5 4A(7) 精度评定。

i
i
i
h h V 改厕厕短的改正数， 代入上式，得：
i
i
i
V1 V2 V3 V4 W 0
W H A h1 h2 h3 h4 H B
1.附合水准路线的条件数和条件方程式组成
观测值5个，待定水准点2 个，所以条件有3个，可 以列出3个条件方程：
h1
H B h1 h2 H A 0
V 1 V 3 V 2 W a 0 V 2 V 4 V 6 W b 0 V 4 V 5 V 3 W c 0
(二)观测值权的确定：
1.各水准路线都进行了往返观测，每公里水准路线的观测中误差为 ，
则m：i
R mi2
1 4n
n i
2 i
i
式中，为测往返测高程不符值，以mm为单位；R为测段长度，以km为单位；n
H A h2 h3 h5 H D 0
H B h1 h3 h4 H C 0
一般以1个已知点为起点，其它已知点为终点，所构成的附合 水准路线为已知点数减1，这样可以列出的条件方程式为已知 水准点个数减1.
2.闭合水准路线的条件数和条件方程式的组成
从一个水准点出发，经过若干水准测段，又回到该 水准点，这样的水准路线称为闭合水准路线。
V 1 V 7 V 8 W b 0
V 2 V 8 V 7 W c 0
V 3 V 5 V 8 W d 0
V 4 V 6 V 5 W e 0
2.闭合水准路线的条件数和条件方程式的组 成
图(c)是四边形状水准网，网中有4个待定点，没有已知点， 在平差计算时，只能确定个待定水准点之间的相互关系，如 果确定一个水准点的高程，就可以确定其他点的高程。因此， 该网的必要观测是3个，观测值总数是6个，又3个多余观测， 可以列出3个条件方程。为了让所列立的条件方程式互相独 立，没个条件方程都要求有一个其他方程没有用到的观测值， 即：

目录目录 (1)观测误差 (2)摘要： (2)关键词： (2)引言 (3)1水准测量 (4)1.1水准测量的原理 .............................................................................. •1.2水准网...................................................................................... •2条件平差 .. (6)2.1 衡量精度的指标 (6)2.2条件平差的原理 .............................................................................. •3水准网的平差 .. (14)3.1必要观测与多余观测 (14)3.2条件方程 (14)3.3条件平差法方程式 (14)3.4条件平差的精度评定 (15)3.5水准网的条件平差 (18)致谢 (20)参考文献 (21)观测误差由观测者、外界环境引起的偶然误差学生：xxx 指导教师：xxx摘要:对一系列带有偶然误差的观测值，采用合理的的方法消除它们间的不符值，得出未知量的最可靠值；以及评定测量成果的精度。

关键词:偶然误差；观测值；精度引言测量工作中，要确定地面点的空间位置，就必须进行高程测量，确定地面点的高程。

几何水准测量是高程测量中最基本、最精密的一种方法。

通过测量仪器，工具等任何手段获得的以数字形式表示的空间信息，即观测量。

然而，测量是一个有变化的过程，受仪器、观测值、外界环境因素的影响，观测的结果与客观上存在的一个能反映其真正大小的数值，即真值（理论值），有一定的差异。

可以说在测量中产生误差是不可避免的。

所以，观测值不能准确得到，在测量上称这种差异为观测误差。

根据其对观测结果影响的性质，可将误差分为系统误差和偶然误差两种。

目录目录 (1)观测误差 (2)摘要: (2)关键词: (2)引言 (3)1水准测量 (4)1.1水准测量的原理 (4)1.2水准网 (5)2条件平差 (6)2.1衡量精度的指标 (6)2.2条件平差的原理 (8)3水准网的平差 (14)3.1必要观测与多余观测 (14)3.2条件方程 (14)3.3条件平差法方程式 (14)3.4条件平差的精度评定 (15)3.5水准网的条件平差 (18)致 (21)参考文献 (21)观测误差—由观测者、外界环境引起的偶然误差学生： xxx 指导教师：xxx摘要:对一系列带有偶然误差的观测值，采用合理的的方法消除它们间的不符值，得出未知量的最可靠值；以及评定测量成果的精度。

关键词:偶然误差；观测值；精度引言测量工作中，要确定地面点的空间位置，就必须进行高程测量，确定地面点的高程。

几何水准测量是高程测量中最基本、最精密的一种方法。

通过测量仪器，工具等任何手段获得的以数字形式表示的空间信息，即观测量。

然而，测量是一个有变化的过程，受仪器、观测值、外界环境因素的影响，观测的结果与客观上存在的一个能反映其真正大小的数值，即真值（理论值），有一定的差异。

可以说在测量中产生误差是不可避免的。

所以，观测值不能准确得到，在测量上称这种差异为观测误差。

根据其对观测结果影响的性质，可将误差分为系统误差和偶然误差两种。

前者可以通过在观测过程中采取一定的措施和在观测结果中加入改正数，消除或减弱它的影响，使其达到忽略不计的程度。

但是，观测结果中，不可避免地包含了后者，它是不可消除的，但可以选择较好的观测条件或采用适当的数据处理方法减弱它。

现在我们要讨论的就是采用适当的数据处理方法来减弱其对水准测量中的影响。

1 水准测量1.1水准测量的原理1.1.1 水准测量的基本原理水准测量是利用水准仪提供的水平视线在水准尺上读数，直接测定店面上两点的高差，然后根据已知点高程及测得的高差来推算待定点的高程。

-0.8206
+58.00
+17.00
-1.8889
-5.00
-1.22
+0.1414
+3.00
+6.45
-0.8206
+58.00
35.45
+1
-0.1111
-1
-0.78
+0.0911
0
0
0
0
-0.18
+6
-0.6667
+4
+5.34
-0.6239
+5
+7.86
-1.0000
0
+6
-0.6667
1.114
1.142
0.078
0.099
1.216
5
5
5
2
2
2
图9-10
（2）列误差方程，得
式中
mm mm
mm mm
mm mm
（3）组成法方程，将误差方程系数、常数项以及权填入表9-10。
表9-10
编号
（mm）
-1.0918
0.9074
0.1794
1
2
3
4
5
6
-1
0
-1
+1
0
0
+1
-1
0
0
+1
0
0
+1
+4
+5.33
-0.6238
+5
+7.86
-1.0000
0
-0.18
-1
+0.1111

§9.1 条件平差原理在条件观测平差中，以n 个观测值的平差值1ˆ⨯n L作为未知数，列出v 个未知数的条件式，在min =PV V T 情况下，用条件极值的方法求出一组v 值，进而求出平差值。

9.1.1基础方程和它的解设某平差问题，有n 个带有相互独立的正态随机误差的观测值 ，其相应的权阵为 ， 它是对角阵，改正数为 ，平差值为 。

当有r 个多余观测时，则平差值 应满足r 个平差值条件方程为：⎪⎪⎭⎪⎪⎬⎫=++++=++++=++++0ˆˆˆ0ˆˆˆ0ˆˆˆ221122112211οοοr L r L r L r b L b L b L b a L a L a L a n n n n n n （9-1） 式中i a 、i b 、…i r （i =1、2、…n ）——为条件方程的系数；0a 、0b 、…0r ——为条件方程的常项数以ii i v L L +=ˆ（i =1、2、…n ）代入(9-1)得条件方程（9-2）式中a w 、b w 、……r w 为条件方程的闭合差，或称为条件方程的不符值，即（9-3） 令⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⨯n n n n r r r r b b b a a a A212121⎪⎪⎭⎪⎪⎬⎫++⋅⋅⋅++=++⋅⋅⋅++=++++=022110221102211r L r L r L r w b L b L b L b w a L a L a L a w n n n n n b n n a ⎪⎪⎭⎪⎪⎬⎫=++⋅⋅⋅++=++⋅⋅⋅++=++⋅⋅⋅++000221122112211r n n b n n a n n w v r v r v r w v b v b v b w v a v a v a ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⨯n n L L L L 211⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⨯n n L L L L ˆˆˆˆ211⎪⎪⎪⎪⎫ ⎛=⨯b a r w w W 1⎪⎪⎪⎪⎫ ⎛=⨯n v v V 211⎪⎪⎪⎫⎛=⨯οοb a A o r 11⨯n L nn P ⨯1⨯n V 1ˆ⨯n L 1ˆ⨯n L⎪⎪⎪⎫⎛=⨯n n p p P 000021则(9-1)及（9-2）上两式的矩阵表达式为0ˆ0=+A LA （9-4） 0=+W AV （9-5）上改正数条件方程式中V 的解不是唯一的解，根据最小二乘原理，在V 的无穷多组解中，取PV V T = 最小的一组解是唯一的，V 的这一组解，可用拉格朗日乘数法解出。

一、水准网条件平差示例 范例：有一水准网（如图8-3所示），已知点A ，B 的高程为: HA=50.000m ， HB=40.000 m ，观测高差及路线长度见表8-1。

试用条件平差求:(1) 各观测高差的平差值；(2) 平差后P 1到P 2点间高差的中误差。

图8-3【解】1）、求条件方程个数；由图易知：n=7，t=3，条件式r=4。

故应列4个平差值条件方程，三个闭合环，一个附和路线2）、列平差值条件方程； 所列4个平差值条件方程为：⎪⎪⎭⎪⎪⎬⎫=-+-=--=-+=+-0ˆˆ0ˆˆˆ0ˆˆˆ0ˆˆˆ31643765521BA H H h h h h h h h h h h h 3)、转换成改正数条件方程；以ii i V L L +=ˆ代入上式可得： ⎪⎪⎭⎪⎪⎬⎫=-+-+-=--+--=-++-+=+-++-00003131643643765765521521B A H H h h v v h h h v v v h h h v v v h h h v v v 化简可得：⎪⎪⎭⎪⎪⎬⎫=--=+--=+-+=++-0403070731643765521mm mm mm mm v v v v v v v v v v v 可知条件方程系数阵为：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-----000101010110011100000010011⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=2101001000210000210000010000001称对P ⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=2010010002000020000010000001称对Q ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-----=320125100141101300100110001101001100000110010002010102200211000000100114)、组成法方程； 先求权阵P ；以1km 观测高差为单位权观测高差，则： 11=P ，12=P ，213=P ，214=P ，15=P ，16=P ，217=P ，而各观测高差两两相互独立，所以权阵为：，则协因数阵为：则，法方程的系数阵Naa 为：⎥⎥⎦⎤⎢⎢⎣⎡-----⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-----==-=00010101011001110000001001120100100020000200000100000010001010101100111000000100111TT AQA T A AP aa N 称对所以，法方程为：043773212510014110134321=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----k k k k 5）、解算法方程，求出联系数K⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡34831.213483.002247.177528.2437758427.025843.012360.023596.025843.032584.011236.012360.012360.011236.031461.014607.023596.012360.014608.046067.04377320125100141101314321k k k k 6）、求V 及高差平差值Lˆ 所以4210.212.118.3213.0214.418.214.0ˆ22222220⨯+⨯-+⨯-+⨯-+⨯-+⨯+⨯-==）（）（）（）（）（r PV V T σ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡-----=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-------⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡==045.2157.1798.3270.0427.4775.2427.034831.213483.002247.177528.2002001100011020022000001100134831.213483.002247.177528.200001010101100111000000100112010010002000020000010000001m m T K T QA V 称对mmmm v v v v v v v h h h h h h h h h h h h h h L ⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----+⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=5020.108548.56472.45007.143556.200028.153556.100.22.18.33.04.48.24.0500.10856.5651.4501.14360.20000.15356.10ˆˆˆˆˆˆˆˆ7654321765432176543217）、精度评定1）、单位权方差估值计算mm 98.24605.35±==2）、建立所求精度的平差值函数的算式，并按误差传播律求平差值函数的精度 依题意列平差值函数为： 5ˆh =ϕ 则:[]Tf 0010000=[][][][]51687.048313.01)16853.3146.0(1001111236.001124.016853.03146.0100110011111ˆˆ=-=+-=⨯---=-=-=--TTT T T aaaa N AQf N QA f Qf fQ ϕϕ所以：mm Q 14.251687.098.2ˆˆ0ˆ±=⨯==ϕϕϕσσ【答】：各观测高差的平差值为：}{m m m m m m m5020.108548.56472.45007.143556.200028.153556.10平差后P1到P2点间高差的中误差为：±2.14mm987654321ACPB 图8-11二、测角网条件平差 范例：有一测角网（如图8-11所示），A 、B 、C 三点为已知三角点，P 为待定点。

水准平差实例实例1 符合水准路线平差（单一水准路线）实例2 三角高程平差实例3 水准网平差（多条水准路线）实例1、符合水准路线平差这是一条符合水准的测量数据和简图，A和B是已知高程点，2、3和4是待测的高程点。

测站点高差(米) 距离（米）高程(米)A -50.440 1474.4440 96.06202 3.252 1424.71703 -0.908 1749.32204 40.218 1950.4120B 88.1830水准原始数据表水准路线图（模拟）图中h为高差。

在平差易中输入以上数据，如下图“水准数据输入”所示：水准数据输入在测站信息区中输入A、B、2、3和4号测站点，其中A、B为已知高程点，其属性为01，其高程如“水准原始数据表”；2、3、4点为待测高程点，其属性为00，其它信息为空。

因为没有平面坐标数据，故在平差易软件中没有网图显示。

根据控制网的类型选择数据输入格式，此控制网为水准网，选择水准格式，如下图“选择格式”所示：选择格式注意：1、在“计算方案”中要选择“一般水准”，而不是“三角高程”。

“一般水准”所需要输入的观测数据为：观测边长和高差。

“三角高程”所需要输入的观测数据为：观测边长、垂直角、站标高、仪器高。

2、在一般水准的观测数据中输入了测段高差就必须要输入相对应的观测边长，否则平差计算时该测段的权为零，因此导致计算结果错误。

在观测信息区中输入每一组水准观测数据测段A点至2号点的观测数据输入（观测边长为平距）如下图“A－>2观测数据”所示：A－>2观测数据测段2号点至3号点的观测数据输入如下图“2－>3观测数据”所示：2－>3观测数据测段3号点至4号点的观测数据输入如下图“3－>4观测数据”所示：3－>4观测数据测段4号点至B点的观测数据输入如下图“4－>B观测数据”所示：4－>B观测数据以上数据输入完后，点击菜单“文件\另存为”，将输入的数据保存为平差易数据格式文件（格式内容详见附录A）：[STATION]A,01,,,96.062000B,01,,,88.1830002,003,004,00[OBSER]A,2,,1474.444000,-50.44002,3,,1424.717000,3.25203,4,,1749.322000,-0.90804,B,,1950.412000,40.2180平差计算选择菜单“平差->闭合差计算”，计算该水准路线的高差闭合差。

基础方程组中方程数是n+r个，而未知数是r个联系数、n个 改正数，与方程数相同，所以方程取得唯一解。改正数方程 确定了解满足最小二乘条件，而条件方程确定所得解能消除 不符值。 注意： r×n n×1 r×1 n×1 没有唯一解是不可改变的，上述唯 一解是在附加条件情况下的唯一解。
A V +W = 0
改正数方程代入条件方程，得：
r × n n× n n×r r ×1
A Q AT K + W = 0
r ×1
K 若令 N aa = AQAT ⇒ N aa r ×1+ W1 = 0 r×
r ×r
注：公式称法方程。其中系数阵是一对称方阵，给出 注： 下标aa是为了和以后要介绍的其它平差方法的法方程 系数阵有所区别。
三角形
t = 2 *3 − 4 = 2 r = 3− 2 =1
大地四边形
中心多边形
扇形
t = 2*4 − 4 = 4 r = 8−4 = 4
t = 2 * 7 − 4 = 10 r = 18 −10 = 8 =k +2
t = 2 *5 − 4 = 6 r = 11 − 6 = 5 = k +1
A
2 1 3
aa ab ar k a + k b + ... + k r + wa = 0 p p p ab bb br p k a + p k b + ... + p k r + wb = 0 （4－1－15） . ar br rr p k a + p k b + ... + p k rr + wr = 0

function tiaojian%条件方程的组成A=[1 -1 0 0 1 0 0;0 0 1 -1 1 0 0;0 0 1 0 0 1 1;0 1 0 -1 0 0 0];W=[7 8 6 -3]';%协因数阵的组成Q=diag([1.1 1.7 2.3 2.7 2.4 1.4 2.6]);P=inv(Q);%法方程组成Naa=A*Q*A';%求解联系数K和改正数K=-inv(Naa)*W;V=Q*A'*K;%计算观测值的平差值h=[1.359 2.009 0.363 1.012 0.657 0.238 -0.595]';adjh=h+V/1000;%精度评定VTPV=V'*P*V;r=4;var0=sqrt(VTPV/r);%计算单位权方差%评定观测值平差值函数的精度fs=[0 0 0 0 1 0 0]';%函数的系数Qss=fs'*Q*fs-(A*Q*fs)'*inv(Naa)*A*Q*fs;%观测值平差值函数的协因数varS=Qss*var0;%观测值平差值函数的方差%写输出结果文件fid=fopen('C:\Documents and Settings\陈岑\桌面\tiaojian.dat','w+'); fprintf(fid,'%s\n\n ',' ######水准网平差算例######'); fprintf(fid,'%s ','观测值改正数');fprintf(fid,'\n');for i=1:7fprintf(fid,' %s%1.0f ','V',i);fprintf(fid,'%15.3f\n',V(i));endfprintf(fid,'\n');fprintf(fid,'%s\n','观测值平差值');for i=1:7fprintf(fid,' %s%1.0f ','h',i);fprintf(fid,'%15.3f',h(i));fprintf(fid,'\n');endfprintf(fid,'\n');fprintf(fid,'%s ','单位权中误差');fprintf(fid,'\n');fprintf(fid,' %s %3.2f ','m0=',var0);fprintf(fid,'\n');fclose(fid);######水准网平差算例######观测值改正数V1 -0.243V2 2.855V3 -4.243V4 -0.145V5 -3.902V6 -0.615V7 -1.142观测值平差值h1 1.359h2 2.009h3 0.363h4 1.012h5 0.657h6 0.238h7 -0.595单位权中误差m0= 2.22-------------------------------------------------------------------------------------- 间接平差（水准网）function [B,l,P,h]=Finput%误差方程的组成B=[1 0;0 1;1 0;0 1;-1 1;-1 0];l=[0 0 4 3 7 2]';%协因数阵Q的组成Q=diag([1.1 1.7 2.3 2.7 2.4 4.0]);P=inv(Q);%观测值h=[1.359 2.009 0.363 1.012 0.657 -0.357]';function jianjie1[B,l,P,h]=Finput;%fafangchengdezuchengNbb=B'*P*B;% adjx Vadjx=inv(Nbb)*B'*P*l;V=B*adjx-l;%计算观测值的平差值adjh=h+V/1000;%精度评定VTPV=V'*P*V;r=4;var0=sqrt(VTPV/r);%计算单位权方差%写输出结果文件fid=fopen('C:\Documents and Settings\陈岑\桌面\jianjie1.dat','w+'); fprintf(fid,'%s\n\n ',' ######水准网间接平差算例######'); fprintf(fid,'%s ','观测值改正数');fprintf(fid,'\n');for i=1:6fprintf(fid,' %s%1.0f ','V',i);fprintf(fid,'%15.3f\n',V(i));endfprintf(fid,'\n');fprintf(fid,'%s\n','观测值平差值');for i=1:6fprintf(fid,' %s%1.0f ','adjh',i);fprintf(fid,'%15.3f',adjh(i));fprintf(fid,'\n');endfprintf(fid,'\n');fprintf(fid,'%s ','单位权中误差');fprintf(fid,'\n');fprintf(fid,' %s %3.2f ','m0=',var0);fprintf(fid,'\n');fclose(fid);######水准网间接平差算例######观测值改正数V1 -0.243V2 2.855V3 -4.243V4 -0.145V5 -3.902V6 -1.757观测值平差值adjh1 1.359 adjh2 2.012 adjh3 0.359 adjh4 1.012 adjh5 0.653 adjh6 -0.359单位权中误差m0= 2.22。

1.单位权中误差的计算公式：
m0 ˆ0
PVV
r
2.每km高差中误差：
m m0
C
3.最弱点的高程中误差
最弱点是指误差最大的待定水准点，一般为离开已知水准点 最远的点。首先要列出最弱点的权函数式：
V F f 1V1 f 2V 2 f nV n
利用m f
1
m0式P计f 算最弱点高程中误差。
V 1 V 7 V 8 W b 0
V 2 V 8 V 7 W c 0
V 3 V 5 V 8 W d 0
V 4 V 6 V 5 W e 0
2.闭合水准路线的条件数和条件方程式的组 成
图(c)是四边形状水准网，网中有4个待定点，没有已知点， 在平差计算时，只能确定个待定水准点之间的相互关系，如 果确定一个水准点的高程，就可以确定其他点的高程。因此， 该网的必要观测是3个，观测值总数是6个，又3个多余观测， 可以列出3个条件方程。为了让所列立的条件方程式互相独 立，没个条件方程都要求有一个其他方程没有用到的观测值， 即：
在水准网中，把3条或3条以 上水准路线的交点称为结点。 两条水准路线的交点称为节点。
（一）按间接平差法对结点进行平差
1.误差方程式的列立
不考虑水准路线中的节点，将水准路线的高差作为独立观测 值，取结点的近似高程改正数为未知数，列立每条水准路线 高差观测值的误差方程。
如图，路线高差观测值以表示，已知
（一）按间接平差法对结点进行平差
3.法方程式的解算 法方程式系数阵的逆阵为：
Q
N Q QQ 1
11
XX
21
31
Q 12
Q 22
Q 32
Q
13
Q Q23

附合导线按条件平差算例9.4.1附合导线的条件平差方程式如图9-6所示，符合在已知),(A A y x A ，),(C C y x C 之间的单一符合导线有n 条AB α与CDα是已知方位角。

设观测角为β、β、… …、β，测角中误差为 ，观测边长为s 、s 、… …、s ，故t1为v 1=ii BACD 011=+∑+=a i n i v ω （9-2）式中a ω—方位角条件的不符值，按180)1(ˆ11+-∑+-=+=n in i CD BAaβααω （9-3）若导线的A 点与C 点重合，则形成一闭合导线，由此坐标方位角条件就成了多边形的图形闭合条件。

2、纵、横坐标条件 设以1ˆx ∆、2ˆx ∆、…、n x ˆ∆表示图中各导线边的纵坐标增量之平差值；1ˆy∆、2y ∆、…、n yˆ∆表示图中各导线边的横坐标增量之平差值；由图可写出以坐标增量平差值表示的纵、横坐标条件。

⎪⎪⎭⎪⎪⎬⎫∑+∆∑+=∆∑+=∑+∆∑+=∆∑+=∆∆yi n i n A i n A C xi n i n A i nA C v y y yy y v x x xx x 111111ˆˆ （9-4）σ令⎪⎪⎭⎪⎪⎬⎫--∆∑=--∆∑=)()(11A Ci nyA C i nx y y y x x x ωω （9-5）则⎪⎪⎭⎪⎪⎬⎫=+∑=+∑∆∆0011yyi nx xi nv v ωω （9-6） 以微分量代替改正数，则有)()()(211n xi nx d x d x d v ∆++∆+∆=∑∆{}ρα1231211)()()(cos v y y y y y y v v n Csi i nxin-'++-+--∑=∑∆将上式代入式9-6得纵坐标条件式，且同理已可得横坐标的条件式即⎪⎪⎭⎪⎪⎬⎫=+-'∑+∑=+-'∑-∑====0)(1sin 0)(1cos 1111y i i Cni sii n i x i i Cni si i n i v x x v v y y v ωραωρα （9-7）上式就是单一符合导线的纵、横坐标条件方程x ω、y ω为条件式的不符值，按⎪⎪⎭⎪⎪⎬⎫-'=-∆∑+=-'=-∆∑+=C CCi nA yC CC i nA x y y y y y x x x x x 11ωω （9-8）式中i x 、i y 是由观测值计算的各导线点的近似坐标。

内蒙古科技大学本科生毕业设计说明书（毕业论文）题目：水准网条件平差程序设计学生姓名：学号：1072143138专业：测绘工程班级：测绘10-1班指导教师：水准网条件平差程序设计摘要近年来，随着我国经济的快速发展，国家大力于投资各种铁路建设和公路建设，测绘工程的运用也越来越突出。

以水准网布设的高程控制网在各类工程中随处可见。

但观测到的数据存在着各种各样的误差，这就需要我们通过简易平差或严密平差来对数据进行处理，从而使数据能够达到工程的预期精度。

本文主要研究如何解决绘图软件行业标准的网络数据处理问题。

从水准网的结构，平差基本原理、调整模型，基本方程及其解，并对法方程组成，求解，平差值的计算及其精度评定作了介绍。

和Visual ，利用C语言是程序设计的相干事情。

在今后的测量工作中，可结合实际平差方案进行平差计算。

关键词：平差模型；精度评定；程序设计Leveling Network Adjustment Program DesignAbstractIn recent years, with China's rapid economic development, the state vigorously investment in all kinds of railway construction and road construction, the use of mapping project is also more and more prominent. In order to control the network level network in various engineering in everywhere. But the observed data exist various error, this needs us through simple adjustment or rigorous adjustment for data processing, so that data to achieve the desired precision engineering.This paper mainly studies how to solve the problem of mapping software industry standard network data processing. From the structure adjustment of leveling network, the basic principle, adjustment model, basic equation and its solution, and the composition of the solution of equations, adjustment calculation and precision evaluation, gross error elimination are introduced as well. And the use of Visual programming software, using C programming language is related to program design. The measurement work in the future, can be combined with the actual adjustment adjustment calculation.Key words: adjustment model；the accuracy assessment；program design目录摘要 (I)Abstract.......................................................................................................................... I I 第一章绪论 (1) (1) (2) (2)第二章条件平差数学模型 (3)条件平差模型 (3) (6) (8) (11) (13) (17)第三章水准网的设计 (18) (18) (18) (19) (19) (20)第四章C语言介绍 (21) (21) (22) (22)第五章程序设计 (24)水准网条件平差和测角网条件平差实例 (24) (24) (27) (32)参考文献 (57)附录A：外文文献 (57)附录B：中文译文 (69)致谢 (74)第一章绪论施工测量工作是非常基本的，重要环节。

内蒙古科技大学本科生毕业设计说明书（毕业论文）题目：水准网条件平差程序设计学生姓名：学号：1072143138专业：测绘工程班级：测绘10-1班指导教师：水准网条件平差程序设计摘要近年来，随着我国经济的快速发展，国家大力于投资各种铁路建设和公路建设，测绘工程的运用也越来越突出。

以水准网布设的高程控制网在各类工程中随处可见。

但观测到的数据存在着各种各样的误差，这就需要我们通过简易平差或严密平差来对数据进行处理，从而使数据能够达到工程的预期精度。

本文主要研究如何解决绘图软件行业标准的网络数据处理问题。

从水准网的结构，平差基本原理、调整模型，基本方程及其解，并对法方程组成，求解，平差值的计算及其精度评定作了介绍。

和Visual ，利用C语言是程序设计的相干事情。

在今后的测量工作中，可结合实际平差方案进行平差计算。

关键词：平差模型；精度评定；程序设计Leveling Network Adjustment Program DesignAbstractIn recent years, with China's rapid economic development, the state vigorously investment in all kinds of railway construction and road construction, the use of mapping project is also more and more prominent. In order to control the network level network in various engineering in everywhere. But the observed data exist various error, this needs us through simple adjustment or rigorous adjustment for data processing, so that data to achieve the desired precision engineering.This paper mainly studies how to solve the problem of mapping software industry standard network data processing. From the structure adjustment of leveling network, the basic principle, adjustment model, basic equation and its solution, and the composition of the solution of equations, adjustment calculation and precision evaluation, gross error elimination are introduced as well. And the use of Visual programming software, using C programming language is related to program design. The measurement work in the future, can be combined with the actual adjustment adjustment calculation.Key words: adjustment model；the accuracy assessment；program design目录摘要 (I)Abstract.......................................................................................................................... I I 第一章绪论 (1) (1) (2) (2)第二章条件平差数学模型 (3)条件平差模型 (3) (6) (8) (11) (13) (17)第三章水准网的设计 (18) (18) (18) (19) (19) (20)第四章C语言介绍 (21) (21) (22) (22)第五章程序设计 (24)水准网条件平差和测角网条件平差实例 (24) (24) (27) (32)参考文献 (57)附录A：外文文献 (57)附录B：中文译文 (69)致谢 (74)第一章绪论施工测量工作是非常基本的，重要环节。