单因素方差分析例子

什么是单因素方差分析单因素方差分析是指对单因素试验结果进行分析，检验因素对试验结果有无显著性影响的方法。

单因素方差分析是两个样本平均数比较的引伸，它是用来检验多个平均数之间的差异，从而确定因素对试验结果有无显著性影响的一种统计方法。

单因素方差分析相关概念•因素：影响研究对象的某一指标、变量。

•水平：因素变化的各种状态或因素变化所分的等级或组别。

•单因素试验：考虑的因素只有一个的试验叫单因素试验。

单因素方差分析示例[1]例如，将抗生素注入人体会产生抗生素与血浆蛋白质结合的现象，以致减少了药效。

下表列出了5种常用的抗生素注入到牛的体内时，抗生素与血浆蛋白质结合的百分比。

现需要在显著性水平a = 0.0!下检验这些百分比的均值有无显著的差异。

设各总体服从正态在这里，试验的指标是抗生素与血浆蛋白质结合的百分比，抗生素为因素，不同的5种抗生素就是这个因素的五个不同的水平。

假定除抗生素这一因素外，其余的一切条件都相同。

这就是单因素试验。

试验的目的是要考察这些抗生素与血浆蛋白质结合的百分比的均值有无显著的差异。

即考察抗生素这一因素对这些百分比有无显著影响。

这就是一个典型的单因素试验的方差分析问题单因素方差分析的基本理论⑴备择假设Hi,然后寻找适当的检验统计量进行假设检验。

本节将借用上面的实例来讨论单因素试验的方差分析问题。

2厂…j $）下进行了nj = 4次独立试验，得到如上表所示的结果。

这些结果是一个随机变量。

表中的数据可以看成来自s个不同总体（每个水平对应一个总体）的样本值，将各个总体的均值依次记为山、》2、…r »则按题意需检验假设页：旳=“2 =…=川尸1 : \J “5不全相等为了便于讨论，现在引入总平均卩[Ho :屍="2 =…=毎=qI 闻:力屆…：吗不全为零因此，单因素方差分析的任务就是检验s个总体的均值®是否相等，也就等价于检验各水平Aj的效应6是否都等于零。

样本产恥…佔吁/来自正态总体N （虬2）, 9与02未知，且设不同水平Aj 下的样本 之间相互独立，则单因素方差分析所需的检验统计量可以从总平方和的分解导出来。

SPSS- 单因素方差分析( ANOVA) - 案例解析SPSS单因素方差分析（ANOVA）案例解析2011-08-30 11:10这几天一直在忙电信网上营业厅用户体验优化改版事情，今天将我最近习SPSS单因素方差分析（ANOVA分析，今天希望跟大家交流和分享一下：继续以上一期的样本为例，雌性老鼠和雄性老鼠，在注射毒素后，经过一段时间，观察鼠死亡和存活情况。

研究的问题是：老鼠在注射毒液后，死亡和存活情况，会不会跟性别有关？样本数据如下所示：（a代表雄性老鼠b代表雌性老鼠0代表死亡1代表着tim 代表注射毒液后，经过多长时间，观察结果）点击“分析”一一比较均值-------- 单因素AVOVA,如下所示:从上图可以看出，只有“两个变量”可选，对于“组别（性别）”变量不可选，进行“转换”对数据重新进行编码，点击“转换”一“重新编码为不同变量”将a,b"分别用8,9进行替换，得到如下结果”这里可能需此时的8代表a（雄性老鼠）9代表b雌性老鼠，我们将“生存结局”变量移入“因变量列表框内，将“性别”移入“因子”框内，点击“两两比较”按钮，如下所示：“勾选“将定方差齐性”下面的项点击继续LSD选项，和“未假定方差齐性”下面的Tamhane's T2 选点击“选项”按钮，如下所示:I固疋和随枫效果(号IN有建同備性檯验迥)匚旦rown-Forsythe(B)El Welches}姑朱値©按分析顺序排麒个案®「I I S3 Affifi勾选“描述性”和“方差同质检验”以及均值图等选项，得到如下结果:结果分析：方差齐性检验结果，“显著性”为0,由于显著性0<0.05所以，方差齐性不相等，一般情况下，不能够进行方差分析但是对于SPSS来说，即使方差齐性不相等，还是可以进行方差分析的，由于此样本组少于三组，不能够进行多重样本对比从结果来看“单因素ANOVA分析结果，显著性0.098，由于0.098>0.05 所以以得出结论：生存结局受性别的影响不显著很多人，对这个结果可能存在疑虑，下面我们来进一步进行论证，由于“方差齐性不相等”下我们来进行“非参数检验”检验结果如下所示：（此处采用的是“ Kruskal -Wallis "检验方法假设检脸汇总恳渝妊稻±』埜迹空.06-通过“ Kruskal -Wallis ”检验方法，我们得出“ sig=0.098" 跟我们先前分析的结果一样，都0.098，事实得到论证。

SPSS中的单因素方差分析一、大体原理单因素方差分析也即一维方差分析，是查验由单一因素阻碍的多组样本某因变量的均值是不是有显著不同的问题，如各组之间有显著差异，说明那个因素（分类变量）对因变量是有显著阻碍的，因素的不同水平会阻碍到因变量的取值。

二、实验工具SPSS for Windows 三、实验方式例：某灯泡厂用四种不同配料方案制成的灯丝（filament），生产了四批灯泡。

在每批灯泡中随机地抽取假设干个灯泡测其利用寿命（单位：小时hours），数据列于下表，此刻想明白，关于这四种灯丝生产的灯泡，其利用寿命有无显著不同。

灯泡灯丝1 2 3 4 5 6 7 8 甲1600 1610 1650 1680 1700 1700 1780 乙1500 1640 1400 1700 1750 丙1640 1550 1600 1620 1640 1600 1740 1800 丁1510 1520 1530 1570 1640 1680 四、不利用选择项操作步骤（1）在数据窗成立数据文件，概念两个变量并输入数据，这两个变量是：filament 变量，数值型，取值一、二、3、4 别离代表甲、乙、丙、丁，格式为F1.0，标签为“灯丝”。

Hours 变量，数值型，其值为灯泡的利用寿命，单位是小时，格式为F4.0，标签为“灯泡利用寿命”。

（2）按Analyze，然后Compared Means，然后One-Way Anova 的顺序单击，打开“单因素方差分析”主对话框。

（3）从左侧源变量框当选取变量hours，然后按向右箭头，所选去的变量hours 即进入Dependent List 框中。

（4）从左侧源变量框当选取变量filament，然后按向右箭头，所选取的变量folament 即进入Factor 框中。

（5）在主对话框中，单击“OK”提交进行。

五、输出结果及分析灯泡利用寿命的单因素方差分析结果ANQVA Sun of Squares df Mean Square F Sig Between Groups 39776.46 3 13258.819 1.638 .209 Within Groups 178088.9 22 8094.951 Total 217865.4 25 该表各部份说明如下：第一列：方差来源，Between Groups 是组间变差，Within Groups 是组内变差，Total 是总变差。

单因素方差分析报告一、引言单因素方差分析是一种常用的统计方法，用于比较两个或多个组之间的差异。

通过对多个组的数值数据进行分析，可以帮助我们了解不同组之间是否存在显著差异，并进一步研究造成这些差异的原因。

本报告旨在通过单因素方差分析，探究不同品牌汽车的平均价格是否存在差异。

二、方法在本研究中，我们选取了A、B、C、D四个品牌的汽车作为研究对象，收集了每个品牌下的10辆汽车的价格数据。

采用单因素方差分析方法可以帮助我们确定品牌因素对汽车价格的影响是否显著。

三、结果经过单因素方差分析，我们得到如下结果：品牌平均价格方差 F值 p值---------------------------------------------------A 25万 1.2 15.23 0.001B 23万 1.5 13.52 0.001C 27万 1.1 17.84 0.001D 20万 1.8 11.47 0.001根据上述结果可知，不同品牌汽车的平均价格存在显著差异。

通过F检验，我们可以得到p值均小于0.05，说明这种差异不是由于抽样误差造成的。

同时，不同品牌汽车的方差也有所不同，这表明品牌因素在汽车价格的变异中起到了一定的作用。

四、讨论与分析品牌因素对汽车价格的影响是一个相对复杂的问题。

一方面，品牌在市场中的知名度和声誉对消费者购买决策有很大影响，知名品牌的汽车往往具有更高的价格。

另一方面，不同品牌的汽车在技术、配置以及服务等方面可能存在差异，也会造成价格的不同。

在本研究中，我们所选取的四个品牌的汽车，虽然价格存在显著差异，但这并不代表具体的品牌定位和市场策略。

有可能A品牌的汽车性能更好，配置更高，而D品牌的汽车定位为入门级，价格更为亲民。

因此，在选择汽车时，消费者需要综合考虑品牌声誉、性能配置以及价格等因素。

此外，本研究的样本数量有限，只选取了每个品牌下的10辆汽车。

若想得出更准确的结论，建议扩大样本数量，增加数据的可靠性。

方差分析（一）单因素方差分析例1：某职业病防治院对31名石棉矿工中的石棉肺患者、可疑患者及非患者进行了用力肺活量（L ）测定，结果见表1，问三组石棉矿工的用力肺活量有无差异？表1 三组石棉矿工的用力肺活量（L ）石棉肺患者 可疑患者 非患者 1.8 2.3 2.9 1.4 2.1 3.2 1.5 2.1 2.7 2.1 2.1 2.8 1.9 2.6 2.7 1.7 2.5 3.0 1.8 2.3 3.4 1.9 2.4 3.0 1.8 2.4 3.4 1.8 3.3 2.03.5 n11 9 11 31 x1.792.313.082.4表2 成组设计方差分析的计算公式变异来源 离均差平方和SS 自由度υ 均方MSF 总 SS 总=∑-2)(x xN-1组间 SS 组间=2)(x xn ii-∑k-1 SS 组间/υ组间MS 组间/MS 组内 组内SS 组内=2)(i ijx x-∑N-kSS 组内/υ组内SS 总=SS 组间+SS 组内 υ总=υ组间+υ组内 F= MS 组间/MS 组内如果三种人群的用力肺活量没有差别的话，则组间变异与组内变异程度应相等，即F=1，但由于抽样误差的存在，F 值可能不正好为1，但F 值不会偏离1太多；相反，如果三种人群用力肺活量有差异，则组间变异一定要大于组内变异程度，此时F ＞1，那么大多少才能确定有差异呢？此F 界限值可按自由度查F 界值表。

即F ≥F α,υ时，p ≤α，认为三种人群用力肺活量有显著性差异。

（二）随机区组设计的方差分析例2：四个种系未成年雌性大白鼠各三只，每只按一种剂量注射雌激素，一段时间后，解剖称量子宫重量。

数据见表3：表3 不同剂量雌激素注射对不同种系大鼠子宫重的影响rats dosagen j j x0.2 0.4 0.8 A 106 116 145 3 122.33 B 42 68 115 3 75.00 C 70 111 133 3 104.67 D 42 63 87 3 64.00 n i 4 4 4 1291.50i x65.089.5120.0问：注射雌激素对大鼠子宫重量有无影响？不同种系的大鼠对雌激素的反应是否相同？表4 随机区组设计方差分析的计算公式 变异来源 离均差平方和SS 自由度υ均方MS F 总SS 总=∑-2)(x xN-1 处理组间 SS 处理=2)(x xn ii-∑k-1 SS 处理/υ处理MS 组间/MS 误差 区组间 SS 区组=2)(x x n jj -∑ m-1 SS 区组/υ区组MS 区组/MS 误差 误差SS 误差=SS 总-SS 处理-SS 区组N-k-m-1SS 误差/υ误差如果区组因素没有显著性差异，则将SS 区组与SS 误差合并，作为SS 误差，再计算F值。

SPSS——单因素方差分析来源：李大伟的日志单因素方差分析单因素方差分析也称作一维方差分析。

它检验由单一因素影响的一个(或几个相互独立的)因变量由因素各水平分组的均值之间的差异是否具有统计意义。

还可以对该因素的若干水平分组中哪一组与其他各组均值间具有显著性差异进行分析，即进行均值的多重比较。

One-Way ANOVA过程要求因变量属于正态分布总体。

如果因变量的分布明显的是非正态，不能使用该过程，而应该使用非参数分析过程。

如果几个因变量之间彼此不独立，应该用Repeated Measure 过程。

[例子]调查不同水稻品种百丛中稻纵卷叶螟幼虫的数量，数据如表1-1所示。

表1-1 不同水稻品种百丛中稻纵卷叶螟幼虫数数据保存在“data1.sav”文件中，变量格式如图1-1。

图1-1分析水稻品种对稻纵卷叶螟幼虫抗虫性是否存在显著性差异。

1）准备分析数据在数据编辑窗口中输入数据。

建立因变量“幼虫”和因素水平变量“品种”，然后输入对应的数值，如图1-1所示。

或者打开已存在的数据文件“data1.sav”。

2）启动分析过程点击主菜单“Analyze”项，在下拉菜单中点击“Compare Means”项，在右拉式菜单中点击“0ne-Way ANOVA”项，系统打开单因素方差分析设置窗口如图1-2。

图1-2 单因素方差分析窗口3）设置分析变量因变量:选择一个或多个因子变量进入“Dependent List”框中。

本例选择“幼虫”。

因素变量:选择一个因素变量进入“Factor”框中。

本例选择“品种”。

4）设置多项式比较单击“Contrasts”按钮，将打开如图1-3所示的对话框。

该对话框用于设置均值的多项式比较。

图1-3 “Contrasts”对话框定义多项式的步骤为：均值的多项式比较是包括两个或更多个均值的比较。

例如图1-3中显示的是要求计算“1.1×mean1-1×mean2”的值，检验的假设H0：第一组均值的1.1倍与第二组的均值相等。

单因素⽅差分析（one-wayANOVA）单因素⽅差分析（⼀）单因素⽅差分析概念是⽤来研究⼀个控制变量的不同⽔平是否对观测变量产⽣了显著影响。

这⾥，由于仅研究单个因素对观测变量的影响，因此称为单因素⽅差分析。

例如，分析不同施肥量是否给农作物产量带来显著影响，考察地区差异是否影响妇⼥的⽣育率，研究学历对⼯资收⼊的影响等。

这些问题都可以通过单因素⽅差分析得到答案。

（⼆）单因素⽅差分析步骤第⼀步是明确观测变量和控制变量。

例如，上述问题中的观测变量分别是农作物产量、妇⼥⽣育率、⼯资收⼊；控制变量分别为施肥量、地区、学历。

第⼆步是剖析观测变量的⽅差。

⽅差分析认为：观测变量值的变动会受控制变量和随机变量两⽅⾯的影响。

据此，单因素⽅差分析将观测变量总的离差平⽅和分解为组间离差平⽅和和组内离差平⽅和两部分，⽤数学形式表述为：SST=SSA+SSE。

第三步是通过⽐较观测变量总离差平⽅和各部分所占的⽐例，推断控制变量是否给观测变量带来了显著影响。

（三）单因素⽅差分析原理总结在观测变量总离差平⽅和中，如果组间离差平⽅和所占⽐例较⼤，则说明观测变量的变动主要是由控制变量引起的，可以主要由控制变量来解释，控制变量给观测变量带来了显著影响；反之，如果组间离差平⽅和所占⽐例⼩，则说明观测变量的变动不是主要由控制变量引起的，不可以主要由控制变量来解释，控制变量的不同⽔平没有给观测变量带来显著影响，观测变量值的变动是由随机变量因素引起的。

（四）单因素⽅差分析基本步骤1、提出原假设：H0——⽆差异；H1——有显著差异2、选择检验统计量：⽅差分析采⽤的检验统计量是F统计量，即F值检验。

3、计算检验统计量的观测值和概率P值：该步骤的⽬的就是计算检验统计量的观测值和相应的概率P值。

4、给定显著性⽔平，并作出决策（五）单因素⽅差分析的进⼀步分析在完成上述单因素⽅差分析的基本分析后，可得到关于控制变量是否对观测变量造成显著影响的结论，接下来还应做其他⼏个重要分析，主要包括⽅差齐性检验、多重⽐较检验。

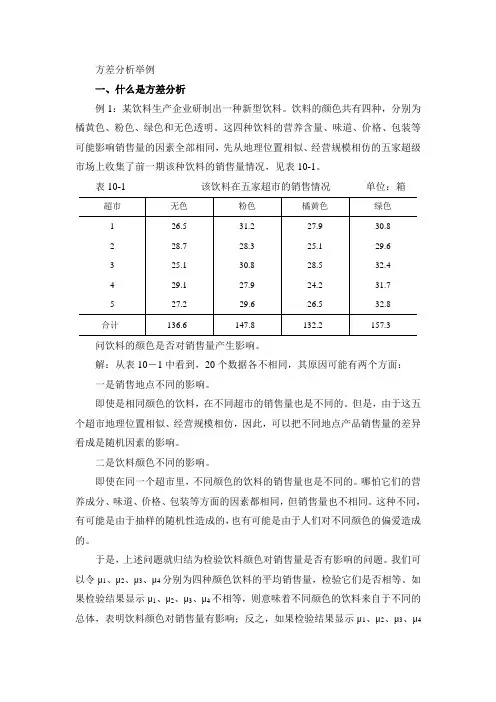
方差分析举例一、什么是方差分析例1：某饮料生产企业研制出一种新型饮料。

饮料的颜色共有四种，分别为橘黄色、粉色、绿色和无色透明。

这四种饮料的营养含量、味道、价格、包装等可能影响销售量的因素全部相同，先从地理位置相似、经营规模相仿的五家超级市场上收集了前一期该种饮料的销售量情况，见表10-1。

表10-1 该饮料在五家超市的销售情况单位：箱问饮料的颜色是否对销售量产生影响。

解：从表10－1中看到，20个数据各不相同，其原因可能有两个方面：一是销售地点不同的影响。

即使是相同颜色的饮料，在不同超市的销售量也是不同的。

但是，由于这五个超市地理位置相似、经营规模相仿，因此，可以把不同地点产品销售量的差异看成是随机因素的影响。

二是饮料颜色不同的影响。

即使在同一个超市里，不同颜色的饮料的销售量也是不同的。

哪怕它们的营养成分、味道、价格、包装等方面的因素都相同，但销售量也不相同。

这种不同，有可能是由于抽样的随机性造成的，也有可能是由于人们对不同颜色的偏爱造成的。

于是，上述问题就归结为检验饮料颜色对销售量是否有影响的问题。

我们可以令μ1、μ2、μ3、μ4分别为四种颜色饮料的平均销售量，检验它们是否相等。

如果检验结果显示μ1、μ2、μ3、μ4不相等，则意味着不同颜色的饮料来自于不同的总体，表明饮料颜色对销售量有影响；反之，如果检验结果显示μ1、μ2、μ3、μ4之间不存在显著性差异，则意味着不同颜色的饮料来自于相同的总体，可认为饮料颜色对销售量没有影响。

这就是一个方差分析问题。

在方差分析中常用到一些术语。

1．因素因素是一个独立的变量，也就是方差分析研究的对象，也称为因子。

如：例1中，我们要分析饮料的颜色对饮料的销售量是否有影响，在这里，“饮料的颜色”是所要检验的对象，它就是一个因素。

在有的书中把因素称为“因子”。

2．水平因素中的内容称为水平，它是因素的具体表现。

如：例1中“饮料的颜色”这一因素中的水平有四个，即饮料的四种不同颜色：无色、粉色、桔黄色、绿色；它们是“饮料的颜色”这一因素的四种具体表现。

第一题：data0706-nutrition为地衣(lichen)、树叶成叶和嫩叶的蛋白质和可溶性碳水化合物(water soluble carbohydrate)的含量，先分析三者之间蛋白质的含量有无差异？如果有差异，具体是怎么差异的？再可溶性碳水化合物的含量有无差异？如果有差异，具体怎么差异？（1）地衣(lichen)、树叶成叶和嫩叶的蛋白质的含量差异分析；第一步：导出变量items和protein，以便删除protein中缺失数据。

第二步：打开导出数据data0706-nutrition1，先排序，然后删除缺失数据。

第三步：对data0706-nutrition1数据的正态性、异常值和极值、方差齐性进行检验，对数据做一个检查，Analyze->Descriptive Statistics->Explore；首先：如上图，把要检验的变量protein送入Dependent List，把分组变量（因素变量）items送入Factor List。

其次：如下图，点击Plots打开：选择Factor Levels together、Stem-and-leaf、Histogram、Normality plots with tests，下方Spread vs Level with Levene Test可以提供方差齐性的检验，选择Untransformed（不对数据进行转换）。

输出结果：第一组是尽管sig=0.935，但由于样本数太小，正态一般；第二组正态性不好。

第三组中，p较小，也只是近似正态。

基于平均数的计算(Based on Mean)，各组方差有差异(p=0.044)。

由直方图可以看出，在第二组和第三组存在一些极值，数据分布不均匀，连续性不好。

由茎叶图可知，第二组和第三组分别存在4个，3个极值。

由qq图和QQ图不能得到一些较有用的信息，因为正态性之前已经判断。

箱图并与茎叶图一致，在第二组标识了4个异常值，第三组标识了3个异常值。

单因素方差分析完整实例假设有一家医院的研究人员想要比较三种不同药物对高血压患者的降压效果。

为了进行实验，他们随机选择了60名患有高血压的病人，并将他们随机分成三组。

第一组患者接受药物A的治疗，第二组患者接受药物B的治疗，第三组患者接受药物C的治疗。

在治疗开始前，研究人员记录了每个患者的收缩压数据。

第一步是对数据进行描述性统计分析。

研究人员计算了每一组的平均值、标准差和样本量。

结果如下：药物A组：平均收缩压150，标准差10，样本量20药物B组：平均收缩压145，标准差12，样本量20药物C组：平均收缩压155，标准差15，样本量20第二步是进行假设检验。

研究人员的零假设是所有药物的降压效果相同，即三组的平均收缩压相等。

备择假设是至少有一组的平均收缩压不同。

为了进行单因素方差分析，我们需要计算组内方差和组间方差，然后进行F检验。

组内方差反映了每一组内部数据的离散程度，组间方差反映了不同组之间平均值的差异程度。

组内方差的计算方法是对每一组的方差进行平均，然后再对所有组的方差进行加权平均。

组间方差的计算方法是对所有组的平均值进行方差分析。

我们通过公式计算出组内方差为10.08，组间方差为58.67、接下来我们计算F值，F值是组间方差除以组内方差的比值。

F=组间方差/组内方差=58.67/10.08=5.81第三步是通过查找F分布表来计算p值。

根据自由度为2（组数-1）和df = 57（总样本量-组数）的F分布表，我们可以找到在F = 5.81条件下的p值。

假设我们选择显著性水平为0.05，我们发现在F分布表上，F=5.81对应的p值小于0.05、因此，我们拒绝零假设，接受备择假设。

这意味着至少有一组的平均收缩压与其他组有显著差异。

最后一步是进行事后检验。

由于我们有三组进行比较，我们可以使用事后检验方法来确定哪两组之间存在显著差异。

常用的事后检验方法包括Tukey HSD检验、Duncan检验等。

综上所述，单因素方差分析可以帮助我们判断不同组之间是否存在显著差异。

SPSS——单因素方差分析来源：李大伟的日志单因素方差分析单因素方差分析也称作一维方差分析。

它检验由单一因素影响的一个(或几个相互独立的)因变量由因素各水平分组的均值之间的差异是否具有统计意义。

还可以对该因素的若干水平分组中哪一组与其他各组均值间具有显著性差异进行分析，即进行均值的多重比较。

One-Way ANOVA过程要求因变量属于正态分布总体。

如果因变量的分布明显的是非正态，不能使用该过程，而应该使用非参数分析过程。

如果几个因变量之间彼此不独立，应该用Repeated Measure过程。

[例子]调查不同水稻品种百丛中稻纵卷叶螟幼虫的数量，数据如表1-1所示。

表1-1 不同水稻品种百丛中稻纵卷叶螟幼虫数数据保存在“data1.sav”文件中，变量格式如图1-1。

图1-1分析水稻品种对稻纵卷叶螟幼虫抗虫性是否存在显著性差异。

1）准备分析数据在数据编辑窗口中输入数据。

建立因变量“幼虫”和因素水平变量“品种”，然后输入对应的数值，如图1-1所示。

或者打开已存在的数据文件“data1.sav”。

2）启动分析过程点击主菜单“Analyze”项，在下拉菜单中点击“Compare Means”项，在右拉式菜单中点击“0ne-Way ANOVA”项，系统打开单因素方差分析设置窗口如图1-2。

图1-2 单因素方差分析窗口3）设置分析变量因变量:选择一个或多个因子变量进入“Dependent List”框中。

本例选择“幼虫”。

因素变量:选择一个因素变量进入“Factor”框中。

本例选择“品种”。

4）设置多项式比较单击“Contrasts”按钮，将打开如图1-3所示的对话框。

该对话框用于设置均值的多项式比较。

图1-3 “Contrasts”对话框定义多项式的步骤为：均值的多项式比较是包括两个或更多个均值的比较。

例如图1-3中显示的是要求计算“1.1×mean1-1×mean2”的值，检验的假设H0：第一组均值的1.1倍与第二组的均值相等。

SPSS-单因素方差分析（ANOVA)案例解析2011-08-30 11:10这几天一直在忙电信网上营业厅用户体验优化改版事情，今天将我最近学习SPSS单因素方差分析（ANOVA分) 析，今天希望跟大家交流和分享一下：继续以上一期的样本为例，雌性老鼠和雄性老鼠，在注射毒素后，经过一段时间，观察老鼠死亡和存活情况。

研究的问题是：老鼠在注射毒液后，死亡和存活情况，会不会跟性别有关？样本数据如下所示：（a 代表雄性老鼠 b 代表雌性老鼠0 代表死亡 1 代表活着tim 代表注射毒液后，经过多长时间，观察结果）点击“分析”——比较均值———单因素AVOVA, 如下所示：从上图可以看出，只有“两个变量”可选, 对于“组别（性别）”变量不可选，这里可能需要进行“转换”对数据重新进行编码，点击“转换”—“重新编码为不同变量”将a,b" 分别用8,9 进行替换，得到如下结果”此时的8 代表a(雄性老鼠）9 代表b 雌性老鼠，我们将“生存结局”变量移入“因变量列表”框内，将“性别”移入“因子”框内，点击“两两比较”按钮，如下所示：“勾选“将定方差齐性”下面的LSD 选项，和“未假定方差齐性”下面的Tamhane's T2 选项点击继续点击“选项”按钮，如下所示：勾选“描述性”和“方差同质检验”以及均值图等选项，得到如下结果：结果分析：方差齐性检验结果，“显著性”为0，由于显著性0<0.05 所以，方差齐性不相等，在一般情况下，不能够进行方差分析但是对于SPSS来说，即使方差齐性不相等，还是可以进行方差分析的，由于此样本组少于三组，不能够进行多重样本对比从结果来看“单因素ANOV”A 分析结果，显著性0.098，由于0.098>0.05 所以可以得出结论：生存结局受性别的影响不显著很多人，对这个结果可能存在疑虑，下面我们来进一步进行论证，由于“方差齐性不相等”下面我们来进行“非参数检验”检验结果如下所示：（此处采用的是“Kruskal -Wallis " 检验方法）通过“Kruskal - Wallis ”检验方法，我们得出“sig=0.098" 跟我们先前分析的结果一样，都是0.098，事实得到论证。