第15讲 乘法公式的综合运用(学生版)
- 格式:pdf
- 大小:151.46 KB
- 文档页数:4

乘法公式应用综合在咱们的数学世界里,乘法公式那可真是个神奇的存在!就像一把万能钥匙,能帮咱们打开好多难题的锁。
先来说说完全平方公式吧,(a ± b)² = a² ± 2ab + b²,这玩意儿可太有用啦!我记得有一次,我去逛菜市场,看到一个卖水果的摊位。
摊主正在算着成本和利润。
他说一箱苹果进价是 a 元,他打算每箱加价 b 元出售。
那按照完全平方公式,他每箱的利润就是 (a + b)² - a² = 2ab +b²。
这可让他一下子就清楚了自己能赚多少钱。
还有平方差公式 (a + b)(a - b) = a² - b²,也是解决问题的好帮手。
比如在装修房子的时候,要计算房间地面的面积。
如果房间的长是 (a + b) 米,宽是 (a - b) 米,那么地面的面积就是 a² - b²平方米。
乘法公式在代数运算中更是大显身手。
比如化简式子 (x + 2y)² - (x - 2y)²,咱们就可以直接套用公式。
先把前面的 (x + 2y)²展开得到 x² +4xy + 4y²,后面的 (x - 2y)²展开得到 x² - 4xy + 4y²,然后一减,4xy 就抵消掉了,剩下 8xy 。
是不是很简单?再看这道题:已知 a + b = 5 ,ab = 3 ,求 a² + b²的值。
这时候咱们就可以用完全平方公式啦,(a + b)² = a² + 2ab + b²,变形一下,a² + b² = (a + b)² - 2ab ,把数值带进去,5² - 2×3 = 19 。
乘法公式在几何图形中也有出色的表现。
比如说一个正方形的边长增加了 x ,那它的面积增加多少呢?原来正方形的边长是 a ,面积就是 a²。

平方差公式一、内容和内容解析【内容】八年级上册第15章第2节乘法公式---平方差公式【内容解析】整式乘法的平方差公式是把特殊形式的多项式相乘写成公式的形式,既为符合公式特征的整式乘法运算带来简便;又为后续学习用公式法分解因式奠定基础;同时平方差公式将在九年级“一元二次方程”中有广泛地应用。
“平方差公式”又是初中阶段的第一个公式,无论是公式的探究过程,还是结构特征的剖析都是学习其它公式的基础。
所以“平方差公式”是一个重要公式。
基于上述分析,确定本节的教学重点是;理解并掌握平方差公式及其结构特征;会运用此公式进行计算。
二、目标和目标解析【目标】1、了解平方差公式产生的背景,理解平方差公式的意义,掌握平方差公式的结构特征,并能灵活运用平方差公式解决问题。
2、经历平方差公式产生的过程,体验知识的产生与发展,积累数学活动的经验,感受利用归纳、转化、数形结合等数学思想与方法解决数学问题的策略。
3、在探索平方差公式的过程中,培养学生观察、归纳、概括的能力,同时在解决问题过程中学会与他人合作交流。
在公式的学习及运用中积累解题的经验、体会成功的喜悦,增强学生学数学、用数学的兴趣,【目标解析】1、了解平方差公式产生的背景,理解平方差公式的意义,掌握平方差公式的结构特征,并能灵活运用平方差公式解决问题。
让学生经历特例—归纳—猜想—验证—用数学符号表示,这一数学活动过程,进一步发展学生的符号感、推理能力、归纳能力,让学生能清楚地知道公式中a 、b 各代表什么,并在运用中与平方差公式的结构特征联系起来分析解答题目。
2、在探索平方差公式的过程中,培养学生观察、归纳、概括的能力,体会数形结合、转化等思想。
让学生能够认识到从具体到抽象,从特殊到一般,找寻规律,自我归纳,建立解决同类问题的模型,并能了解公式的几何意义及运用转化的思想解决数学问题。
3、通过探索新知,应用新知这一过程,创设自主探究与合作交流的学习气氛。
体验知识的产生与发展,积累数学活动的经验,在公式的学习及运用中积累解题的经验、体会成功的喜悦,增强学生学数学、用数学的兴趣,三、教学问题诊断分析学生的认知基础:第一、七年级学生已有用字母表示数的基础。

乘法公式的用法1、套用 : 这是最初的公式运用阶段,在这个环节中,应弄清乘法公式的来龙去脉,准确地掌握其特征,为辨认和运用公式打下基础,同时能提高学生的观察能力。
例 1. 计算:解:原式2、连用 : 连续使用同一公式或连用两个以上公式解题。
例 2.计算:解:原式例 3.计算:解:原式3、逆用 : 学习公式不能只会正向运用,有时还需要将公式左、右两边交换位置,得出公式的逆向形式,并运用其解决问题。
例4.计算:解:原式5、变用: 题目变形后运用公式解题。
例 5.计算:解:原式6、活用:把公式本身适当变形后再用于解题。
这里以完全平方公式为例,经过变形或重新组合,可得如下几个比较有用的派生公式:灵活运用这些公式,往往可以处理一些特殊的计算问题,培养综合运用知识的能力。
例 6. 已知,求的值。
解:例 7. 计算:解:原式例 8. 已知实数 x 、 y 、 z 满足,那么()解:由两个完全平方公式得:从而学习乘法公式应注意的问题注意掌握公式的特征,认清公式中的“两数”.例1、计算 (-2 x 2 -5)(2 x 2 -5)分析:本题两个因式中“ -5 ”相同,“ 2 x 2 ”符号相反,因而“ -5 ”是公式 ( a + b )( a - b )= a 2 - b 2 中的 a ,而“ 2 x 2 ”则是公式中的 b .解:原式 =(-5-2 x 2 )(-5+2 x 2 )=(-5) 2 -(2 x 2 ) 2 =25-4 x 4 .例2、计算 (- a 2 +4 b ) 2分析:运用公式 ( a + b ) 2 = a 2 +2 ab + b 2 时,“ - a 2 ”就是公式中的 a ,“ 4 b ”就是公式中的 b ;若将题目变形为 (4 b - a 2 ) 2 时,则“ 4 b ”是公式中的 a ,而“ a 2 ”就是公式中的 b .(解略)注意为使用公式创造条件例 3 计算 (2 x + y - z +5)(2 x - y + z +5) .分析:粗看不能运用公式计算,但注意观察,两个因式中的“ 2 x ”、“ 5 ”两项同号,“ y ”、“ z ”两项异号,因而,可运用添括号的技巧使原式变形为符合平方差公式的形式.解:原式 = 〔 (2 x +5)+( y - z ) 〕〔 (2 x +5)-( y - z ) 〕=(2 x +5) 2 -( y - z ) 2=4 x 2 +20 x +25- y +2 yz - z 2 .例 4 计算 ( a -1) 2 ( a 2 + a +1) 2 ( a 6 + a 3 +1) 2分析:若先用完全平方公式展开,运算十分繁冗,但注意逆用幂的运算法则,则可利用乘法公式,使运算简便.解:原式 =[( a -1)( a 2 + a +1)( a 6 + a 3 +1)] 2=[( a 3 -1)( a 6 + a 3 +1)] 2=( a 9 -1) 2 = a 18 -2 a 9 +1例 5 计算 (2+1)(2 2 +1)(2 4 +1)(2 8 +1) .分析:此题乍看无公式可用,“硬乘”太繁,但若添上一项( 2-1 ),则可运用公式,使问题化繁为简.解:原式 =(2-1)(2+1)(2 2 +1)(2 4 +1)(2 8 +1)=(2 2 -1)(2 2 +1)(2 4 +1)(2 8 +1)=(2 4 -1)(2 4 +1)(2 8 +1)= ( 2 8 -1 )( 2 8 +1 )=2 16 -1(三)、注意公式的推广计算多项式的平方,由 ( a + b ) 2 = a 2 +2 ab + b 2 ,可推广得到: ( a + b + c ) 2 = a 2 + b 2 + c 2 +2 ab + 2 ac +2 bc .可叙述为:多项式的平方,等于各项的平方和,加上每两项乘积的 2 倍.例 6 计算 (2 x + y -3) 2解:原式 =(2 x ) 2 + y 2 +(-3) 2 +2 · 2 x · y +2 · 2 x (-3)+2 · y (-3)=4 x 2 + y 2 +9+4 xy -12 x -6 y .(四)、注意公式的变换,灵活运用变形公式例 7 (1) 已知 x + y =10 , x 3 + y 3 =100 ,求 x 2 + y 2 的值;(2) 已知: x +2 y =7 , xy =6 ,求 ( x -2 y ) 2 的值.分析:粗看似乎无从下手,但注意到乘法公式的下列变形: x 2 + y 2 =( x + y ) 2 -2 xy , x 3 + y 3 =( x + y ) 3 -3 xy ( x + y ) , ( x + y ) 2 -( x - y ) 2 =4 xy ,问题则十分简单.解: (1) ∵ x 3 + y 3 =( x + y ) 3 -3 xy ( x + y ) ,将已知条件代入得 100=10 3 -3 xy · 10 ,∴ xy =30 故 x 2 + y 2 =( x + y ) 2 -2 xy =10 2 -2 × 30=40 .(2)( x -2 y ) 2 =( x +2 y ) 2 -8 xy =7 2 -8 × 6=1 .例 8 计算 ( a + b + c ) 2 +( a + b - c ) 2 +( a - b + c )+( b - a + c ) 2 .分析:直接展开,运算较繁,但注意到由和及差的完全平方公式可变换出 ( a + b ) 2 +( a - b ) 2 =2( a 2 + b 2 ) ,因而问题容易解决.解:原式 =[( a + b )+ c ] 2 +[( a + b )- c ] 2 +[ c +( a - b )] 2 +[ c -( a - b )] 2=2[( a + b ) 2 + c 2 ]+2[ c 2 +( a - b ) 2 ]=2[( a + b ) 2 +( a - b ) 2 ]+ 4 c 2= 4 a 2 +4 b 2 + 4 c 2(五)、注意乘法公式的逆运用例 9 计算 ( a -2 b + 3 c ) 2 -( a +2 b -3 c ) 2 .分析:若按完全平方公式展开,再相减,运算繁杂,但逆用平方差公式,则能使运算简便得多.解:原式 =[( a -2 b + 3 c )+( a +2 b -3 c )][( a -2 b + 3 c )-( a +2 b -3 c )]= 2 a (-4 b + 6 c )=-8 ab + 12 ac .例 10 计算 ( 2 a +3 b ) 2 -2( 2 a +3 b )(5 b -4 a )+( 4 a -5 b ) 2分析:此题可以利用乘法公式和多项式的乘法展开后计算,但逆用完全平方公式,则运算更为简便.解:原式 =( 2 a +3 b ) 2 +2( 2 a +3 b )( 4 a -5 b )+( 4 a -5 b ) 2=[( 2 a +3 b )+( 4 a -5 b )] 2=( 6 a -2 b ) 2 = 36 a 2 -24 ab +4 b 2 .四、怎样熟练运用公式:(一)、明确公式的结构特征这是正确运用公式的前提,如平方差公式的结构特征是:符号左边是两个二项式相乘,且在这四项中有两项完全相同,另两项是互为相反数;等号右边是乘式中两项的平方差,且是相同项的平方减去相反项的平方.明确了公式的结构特征就能在各种情况下正确运用公式.(二)、理解字母的广泛含义乘法公式中的字母 a 、 b 可以是具体的数,也可以是单项式或多项式.理解了字母含义的广泛性,就能在更广泛的范围内正确运用公式.如计算( x +2 y - 3 z ) 2 ,若视 x +2 y 为公式中的 a , 3 z 为 b ,则就可用( a - b ) 2 = a 2 - 2 ab + b 2 来解了。

专题复习:乘法公式知识点归纳及典例+练习题一、知识概述 1、平方差公式 由多项式乘法得到 (a+b)(a-b) =a -b . 即两个数的和与这两个数的差的积,等于它们的平方差. 2、平方差公式的特征 ①左边是两个二项式相乘,并且这两个二项式中有一项完全相同,另一项互为相反数; ②右边是乘式中两项的平方差(相同项的平方减去相反项的平方); ③公式中的 a 和 b 可以是具体数,也可以是单项式或多项式; ④对于形如两数和与这两数差相乘的形式,就可以运用上述公式来计算. 3、完全平方公式 由多项式乘法得到(a±b) =a ±2ab+b2 2 2 2 2即两数和(或差)的平方,等于它们的平方和,加(或减)它们的积的 2 倍. 推广形式:(a+b+c) =a +b +c +2ab+2bc+2ca 4、完全平方公式的特征 (a+b) =a +2ab+b 与(a-b) =a -2ab+b 都叫做完全平方公式,为了区别,我们把前者叫做两数 和的完全平方公式,后者叫做两数差的完全平方公式. ①两公式的左边:都是一个二项式的完全平方,二者仅有一个符号不同;右边:都是二次三项式,其 中有两项是公式左边两项中每一项的平方,中间是左边二项式中两项乘积的 2 倍,两者也仅有一个符号不 同. ②公式中的 a、b 可以是数,也可以是单项式或多项式. ③对于形如两数和(或差)的平方的乘法,都可以运用上述公式计算. 5、乘法公式的主要变式 (1)a -b =(a+b)(a-b); (2)(a+b) -(a-b) =4ab; (3)(a+b) +(a-b) =2(a +b ); (4)a +b =(a+b) -2ab=(a-b) +2ab (5)a +b =(a+b) -3ab(a+b). 熟悉这些变形公式,明确它们间联系,综合运用,常可简化解题过程. 注意:(1)公式中的 a,b 既可以表示单项式,也可以表示多项式. (2)乘法公式既可以单独使用,也可以同时使用. (3)这些公式既可以正用,也可以逆用,因此在解题时应灵活地运用公式,以计算简捷为宜.3 3 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2二、典型例题讲解 例 1、计算: (1)(3a+2b)(2b-3a); (2)(x-2y)(-x-2y);(3) (4)(a+b+c)(a-b-c). 解:;(1)原式=(2b+3a)(2b-3a) =(2b) -(3a) =4b -9a2 2 2 2(2)原式=(-2y+x)(-2y-x) =(-2y) -x =4y -x2 2 2 2(3)原式=== (4)原式=[a+(b+c)][a-(b+c)] =a -(b+c)2 2 2 2=a -(b +2bc+c ) =a -b -2bc-c 例 2、计算: (1)2004 -19962 2 2 2 2 22(2)(x-y+z) -(x+y-z)2(3)(2x+y-3)(2x-y-3). 解:(1)2004 -1996 =(2004+1996)(2004-1996) =4000×8=32000 (2)(x-y+z) -(x+y-z)2 2 2 2=[(x-y+z)+(x+y-z)][ (x-y+z)-(x+y-z)]=2x(-2y+2z)=-4xy+4xz (3)(2x+y-3)(2x-y-3)=[(2x-3)+y][(2x-3)-y] =(2x-3) -y =4x -12x+9-y =4x -y -12x+9; 例 3、计算: (1)(3x+4y) ; (3)(2a-b) ;2 2 2 2 2 2 2 2 2(2)(-3+2a) ; (4)(-3a-2b)22解:(1)原式=(3x) +2·3x·4y+(4y) =9x +24xy+16y2 2 22(2)原式=(-3) +2·(-3)·2a+4a =4a -12a+922(3)原式=(2a) +2·2a·(-b)+(-b) =4a -4ab+b2 222(4)原式=[-(3a+2b)] =(3a+2b)2 22=(3a) +2·(3a)·2b+(2b) =9a +12ab+4b2 22例 4、已知 m+n=4, mn=-12,求(1);(2);(3).解:(1);(2);(3)2.例 5、多项式 9x +1 加上一个单项式后,使它能够成为一个整式的完全平方,那么加上的单项式可以是 ________(填上一个你认为正确的即可). 分析: 解答时,很多学生只习惯于课本上的完全平方的顺序,认为只有添加中间(两项的乘积的 2 倍)项,即 9x +1+6x=(3x+1) 或 9x -6x+1=(3x-1) ;但只要从多方面考虑,还会得出2 2 2 2,9x +1-1=9x =(3x) , 9x +1-9x =12, 所以添加的单项式可以是 6x,22222-6x,,-1,-9x .2答案:±6x 或 例 6、计算:或-1 或-9x2,并说明结果与 y 的取值是否有关. 解:从上述结果可以看出,结果中不含 y 的项,因此结果与 y 的取值无关. 点评: (1)利用平方差公式计算的关键是弄清具体题目中,哪一项是公式中的 a,哪一项是公式中的 b; (2)通常在各因式中, 相同项在前, 相反项在后, 但有时位置会发生变化, 因此要归纳总结公式的变化, 使之更准确的灵活运用公式. ①位置变化:(b+a)(-b+a)=(a+b)(a-b)=a -b ; ②符号变化:(-a-b)(a-b)=(-b-a)(-b+a)=(-b) -a =b -a ; ③系数变化:(3a+2b)(3a-2b)=(3a) -(2b) =9a -4b ; ④指数变化:(a +b )(a -b )=(a ) -(b ) =a -b ; ⑤连用公式变化:(a-b)(a+b)(a +b )(a +b ) =(a -b )(a +b )(a +b )=(a -b )(a +b ) =a -b ; ⑥逆用公式变化:(a-b+c) -(a-b-c)2 2 8 8 2 2 2 2 4 4 4 4 4 4 2 2 4 4 3 3 3 3 3 2 3 2 6 6 2 2 2 2 2 2 2 2 2 2=[(a-b+c)+(a-b-c)][(a-b+c)-(a-b-c)] =4c(a-b). 例 7、已知 .求 分析:的值.若直接代入求解则十分繁杂。
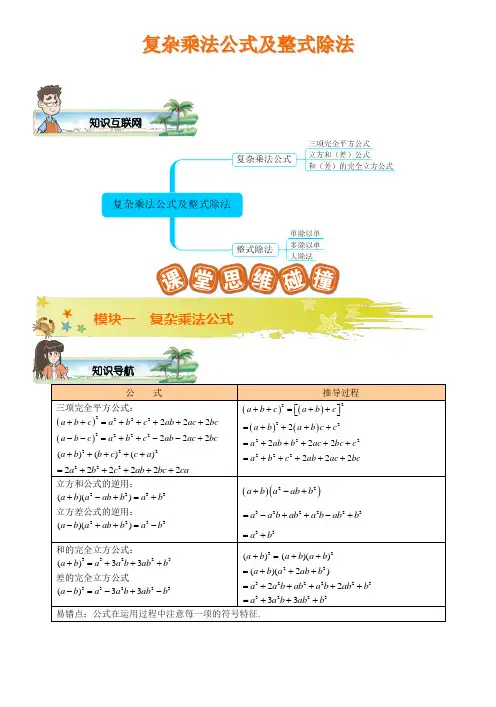
复杂乘法公式及整式除法公 式推导过程三项完全平方公式:()2222222a b c a b c ab ac bc ++=+++++()2222222a b c a b c ab ac bc --=++--+222()()()a b b c c a +++++ 222222222a b c ab bc ca =+++++()()()()22222222222222222a b c a b c a b a b c c a ab b ac bc ca b c ab ac bc++=++⎡⎤⎣⎦=++++=+++++=+++++立方和公式的逆用:2233()()a b a ab b a b +-+=+ 立方差公式的逆用:2233()()a b a ab b a b -++=- ()()22a b a ab b +-+322223a a b ab a b ab b =-++-+ 33a b =+和的完全立方公式:33223()33a b a a b ab b +=+++ 差的完全立方公式33223()33a b a a b ab b -=-+-3()a b +=2()()a b a b ++ 22()(2)a b a ab b =+++32222322a a b ab a b ab b =+++++ 322333a a b ab b =+++易错点:公式在运用过程中注意每一项的符号特征.模块一 复杂乘法公式知识导航知识互联网【例1】 利用三项完全平方公式计算:⑴ 2(3)x y ++=;⑵ 2122x y z ⎛⎫--= ⎪⎝⎭ .【例1】 利用立方和(差)公式的逆用填空:⑴ 2(2)(24)x x x +-+= ;⑵ 33(25)()8125a b a b +=+;⑶ 2(21)(421)x x x -++= ;⑷ 3311()32278a b a b ⎛⎫-=- ⎪⎝⎭; ⑸ ()()()4222416x x x x -+++= .【例2】 利用完全立方公式计算:⑴ 3(2)x +⑵ 3(32)x y + ⑶ 3(45)a b -【例3】 ⑴ 已知3a b +=且2ab =,则33a b +的值为 .⑵ 已知1a b -=-且225a b +=,则33a b -的值为 . ⑶ 已知:1x y +=,则333x y xy ++= .能力提升模块二 整式除法基本运算夯实基础定 义示例剖析⑴ 单项式除以单项式: 把系数与同底数幂分别相除作为商的因式,对于只在被除式里含有的字母,则连同它的指数作为商的一个因式. 523122a a x x x ÷=÷=,2623ab ab b ÷=⑵ 多项式除以单项式:先把这个多项式的每一项除以这个单项式,再把所得的商相加.()423264232x x x x x x +-÷=+- ()22232321a b ab ab ab ab b -+÷=-+易错点:多项式除以单项式,商的每一项的符号易错.【例4】 ⑴ 计算:224(6)=x y xy ÷- ;⑵ 计算:322223=533y y y y ⎛⎫-+÷ ⎪⎝⎭ ;⑶ 计算:()()23422261222xy x y x y xy -+÷-= ; ⑷ 计算:()()()()343827x y x y x y x y -+÷+-=⎡⎤⎣⎦ ;⑸ 计算:()23293n m m a b ab ++÷-(m 、n 是正整数).【例5】 ⑴已知:42==mnmna a a a a a ÷, ,求2m n -的值。



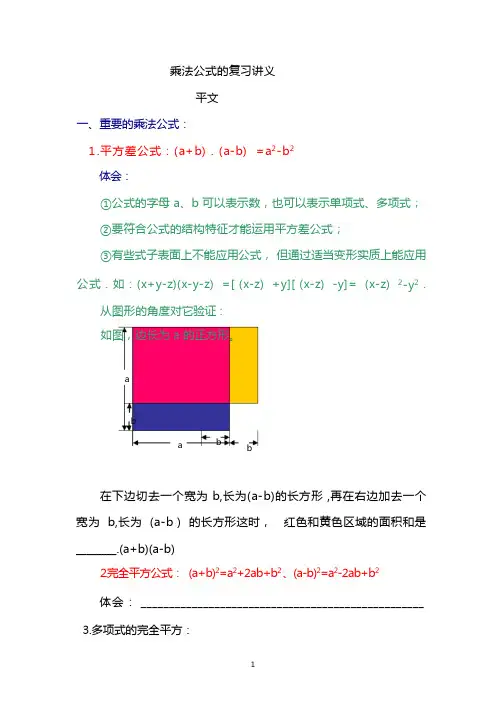
乘法公式的复习讲义平文一、重要的乘法公式:1.平方差公式:(a+b).(a-b) =a2-b2体会:①公式的字母 a、b 可以表示数,也可以表示单项式、多项式;②要符合公式的结构特征才能运用平方差公式;③有些式子表面上不能应用公式,但通过适当变形实质上能应用公式.如:(x+y-z)(x-y-z) =[ (x-z) +y][ (x-z) -y]= (x-z) 2-y2.从图形的角度对它验证 :如图,边长为 a 的正方形。
aba b b在下边切去一个宽为 b,长为(a-b)的长方形 ,再在右边加去一个宽为 b,长为 (a-b ) 的长方形这时,红色和黄色区域的面积和是________.(a+b)(a-b)2.完全平方公式: (a+b)2=a2+2ab+b2 、(a-b)2=a2-2ab+b2体会: __________________________________________________ 3.多项式的完全平方:(a+b+c)2=a2+b2+c2+2ab+2bc+2ac、(a-b-c)2=a2+b2+c2-2ab+2bc-2ac思考: (a+b-c)2=_______________(a-b+c)2=_______________体会: __________________________________________________ ___________________________________________.4.两个一次二项式相乘: (x+a) . (x+b) =x2+(a+b)x+ab.体会: a、b 可以是正数也可以是负数。
5.补充几个乘法公式:①立方差公式:(a-b)(a2+ab+b2)=a3-b3② 立方和公式:(a+b)(a2-ab+b2)=a3+b3体会规律: _____________________________________6. 由平方差、立方和(差)公式引伸的公式 :(a+b) (a3-a2b+ab2-b3)=a4-b4;(a+b)(a4-a3b+a2b2-ab3+b4)=a5+b5;(a+b)(a5-a4b+a3b2-a2b3+ab4-b5)=a6-b6 …………注意观察左边第二个因式的项数、指数、系数、符号的规律在正整数指数的条件下,可归纳如下:设 n 为正整数(a+b)(a2n-1-a2n-2b+a2n-3b2 -…+ab2n-2-b2n-1)=a2n-b2n(a+b)(a2n-a2n-1b+a2n-2b2 -…-ab2n-1+b2n)=a2n+1+b2n+1类似地:(a-b) (a n-1+a n-2b+a n-3b2+…+ab n-2+b n-1)=a n-b n 二、例题分析:题型 1 :平方差公式的应用:(1) 公式中的字母 a、b 可以表示数,也可以是表示数的单项式、多项式即整式.(2)要符合公式的结构特征才能运用平方差公式.(3)有些多项式与多项式的乘法表面上不能应用公式,但通过加法或乘法的交换律、结合律适当变形实质上能应用公式.例 1.计算(3x-1)(3x+1)(9x2+1)例 2.计算(2x-1)2(1+2x)2- (2x+3) 2(2x-3)2例 3.计算(x2-x+2)(x2-x-2)变式 1:计算(x+y+z)(x+y-z)变式 2:已知 z2=x2+y2 ,化简(x+y+z)(x-y+z)(-x+y+z)(x+y-z).变式 3:计算(a- 2b+c)(a+2b-c)-(a+2b+c) 2变式 4: (a+b+c)(a+b-c)(a-b+c)(-a+b+c)例4. 计算(1)899×901+1 (2) 1232-122×118变式 1:计算: 1002-992+982-972+ …+42-32+22-1例 5:计算: (2+1) (22+1) (24+1) (28+1) (216+1) (232+1)++变式:计算:+例 6.探索题:(x-1)(x+1)=x 2 1(x-1) (x 2+x+1)=x 3-1(x-1)(x 3+x 2+x+1)=x 4-1(x-1)(x 4+x 3+x 2+x+1)=x 5-1……试求 26+25+24+23+22+2+1 的值,判断 22005+22004+22003+ …+2+1 的末位数。

2024北师大版数学七年级下册1.6.3《乘法公式综合运用》教案3一. 教材分析《乘法公式综合运用》是北师大版数学七年级下册1.6.3的教学内容。
这部分内容是在学生掌握了平方差公式、完全平方公式等乘法公式的基础上进行学习的。
通过这部分的学习,学生能够灵活运用乘法公式解决实际问题,提高他们的解决问题的能力。
二. 学情分析面对七年级的学生,他们在之前的学习中已经掌握了平方差公式、完全平方公式等乘法公式。
但是,他们在运用这些公式解决实际问题时,往往会存在理解不深、运用不灵活的情况。
因此,在教学这部分内容时,需要引导学生深入理解乘法公式的内涵,提高他们解决问题的能力。
三. 教学目标1.知识与技能:使学生掌握乘法公式的运用方法,能够灵活解决实际问题。
2.过程与方法:通过自主学习、合作交流,培养学生解决问题的能力。
3.情感态度与价值观:激发学生学习数学的兴趣,培养他们积极思考、勇于探索的精神。
四. 教学重难点1.重点:乘法公式的运用。
2.难点:灵活运用乘法公式解决实际问题。
五. 教学方法采用自主学习、合作交流、教师引导相结合的教学方法,让学生在探究中掌握知识,提高解决问题的能力。
六. 教学准备1.准备相关的乘法公式的资料,以便在教学中进行查阅。
2.准备一些实际问题,让学生进行练习。
七. 教学过程1.导入(5分钟)教师通过提问的方式,引导学生回顾之前学过的平方差公式、完全平方公式等乘法公式,为新课的学习做好铺垫。
2.呈现(10分钟)教师通过展示一些实际问题,让学生尝试运用乘法公式进行解决。
学生在解决问题的过程中,教师给予适当的引导和提示。
3.操练(10分钟)学生分组进行练习,教师给出一些运用乘法公式的问题,学生通过合作交流,共同解决问题。
4.巩固(5分钟)教师挑选一些学生解决的实际问题,让学生上台进行讲解,以此巩固乘法公式的运用。
5.拓展(5分钟)教师提出一些拓展问题,引导学生深入思考,提高他们解决问题的能力。

乘法公式的综合应用乘法公式是数学中常见的一个工具,它可以在各种实际问题中得到广泛的应用。
本文将介绍乘法公式的几个重要应用,包括比例关系、面积和体积计算、概率问题等。
第一部分:比例关系的应用乘法公式在比例关系的建立和求解中起着关键作用。
比例关系是两个或多个量之间的等比关系,常用形式为a:b=c:d。
乘法公式可以用来求解未知量或进行比较。
例子1:若一辆汽车每小时行驶60公里,则2小时行驶的里程是多少?解:根据题意可知,汽车的行驶速度为60公里/小时,行驶时间为2小时。
我们可以用乘法公式来求解问题。
令行驶里程为x公里,则60公里/小时乘以2小时等于x公里,即60*2=x。
通过计算可得,x=120公里。
例子2:一桶水中液位每分钟下降0.5厘米,若桶里的水先后下降了10厘米和15厘米,则这两段时间的时间差是多少?解:设时间差为t分钟,根据题意可得水面下降的速度为0.5厘米/分钟。
利用乘法公式,可以得到0.5厘米/分钟乘以t分钟等于水位下降的总高度,即0.5t=25、通过计算可得,t=50分钟。
第二部分:面积和体积的计算乘法公式在计算面积和体积时也起到重要的作用。
对于不规则图形和立体图形,乘法公式可以通过将各个边长或高度相乘得到最终的结果。
例子3:一个长方形花坛的长为5米,宽为3米,求其面积是多少?解:面积可以通过将长和宽相乘得到,即5米*3米=15平方米。
因此,该花坛的面积为15平方米。
例子4:一个正方体的边长为2厘米,求其体积是多少?解:体积可以通过将边长相乘三次得到,即2厘米*2厘米*2厘米=8立方厘米。
因此,该正方体的体积为8立方厘米。
第三部分:概率问题乘法公式在概率问题中也发挥着重要的作用。
通过乘法公式,可以计算得到事件发生的概率。
例子5:有一个有15个白色球和10个红色球的箱子,从箱子中随机抽取两个球,不放回。
求抽出两个白色球的概率。
解:首先计算抽出第一个白色球的概率,为15/25;然后计算抽出第二个白色球的概率,为14/24、通过乘法公式,可以得到两个白色球同时被抽出的概率为(15/25)*(14/24)=7/20。
专题 乘法公式-重难点题型【知识点1 乘法公式】平方差公式:(a +b )(a -b )=a 2-b 2。
两个数的和与这两个数的差的积,等于这两个数的平方差。
这个公式叫做平方差公式。
完全平方公式:(a +b )2=a 2+2ab +b 2,(a -b )2=a 2-2ab +b 2。
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们积的2倍。
这两个公式叫做完全平方公式。
【题型1 乘法公式的基本运算】【例1】(2021•锦江区校级开学)下列运算正确的是( )A .(x +y )(﹣y +x )=x 2﹣y 2B .(﹣x +y )2=﹣x 2+2xy +y 2C .(﹣x ﹣y )2=﹣x 2﹣2xy ﹣y 2D .(x +y )(y ﹣x )=x 2﹣y 2【变式1-1】(2021春•龙岗区校级期中)下列关系式中,正确的是( )A .(a ﹣b )2=a 2﹣b 2B .(a +b )(﹣a ﹣b )=a 2﹣b 2C .(a +b )2=a 2+b 2D .(﹣a ﹣b )2=a 2+2ab +b 2【变式1-2】(2021春•舞钢市期末)下列乘法运算中,不能用平方差公式计算的是( )A .(m +1)(﹣1+m )B .(2a +3b ﹣5c )(2a ﹣3b ﹣5c )C .2021×2019D .(x ﹣3y )(3y ﹣x ) 【变式1-3】(2021春•龙岗区校级月考)下列各式,能用平方差公式计算的是( )A .(2a +b )(2b ﹣a )B .(﹣a ﹣2b )(﹣a +2b )C .(2a ﹣3b )(﹣2a +3b )D .(13a +1)(−13a −1) 【题型2 完全平方公式(求系数的值)】【例2】(2021春•仪征市期中)若多项式4x 2﹣mx +9是完全平方式,则m 的值是( )A .6B .12C .±12D .±6 【变式2-1】(2021春•南山区校级期中)如果x 2+8x +m 2是一个完全平方式,那么m 的值是( )A .4B .16C .±4D .±16【变式2-2】(2021春•新城区校级期末)已知:(x ﹣my )2=x 2+kxy +4y 2(m 、k 为常数),则常数k 的值为 .【变式2-3】(2021春•邗江区期中)若x 2﹣2(m ﹣1)x +4是一个完全平方式,则m = .【题型3 完全平方公式的几何背景】【例3】(2021春•兴宾区期末)有A ,B 两个正方形,按图甲所示将B 放在A 的内部,按图乙所示将A ,B 并列放置构造新的正方形.若图甲和图乙中阴影部分的面积分别为3和16,则正方形A ,B 的面积之和为( )A.13B.19C.11D.21【变式3-1】(2021春•芝罘区期末)用4块完全相同的长方形拼成如图所示的正方形,用不同的方法计算图中阴影部分的面积,可得到一个关于a,b的等式为()A.4a(a+b)=4a2+4ab B.(a+b)(a﹣b)=a2﹣b2C.(a+b)2=a2+2ab+b2D.(a+b)2﹣(a﹣b)2=4ab【变式3-2】(2021春•岚山区期末)现有四个大小相同的长方形,可拼成如图1和图2所示的图形,在拼图2时,中间留下了一个边长为4的小正方形,则每个小长方形的面积是()A.3B.6C.12D.18【变式3-3】(2021春•深圳期中)有两个正方形A,B.现将B放在A的内部得图甲,将A,B并列放置后,构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为1和12,若三个正方形A和两个正方形B,如图丙摆放,则阴影部分的面积为()A.28B.29C.30D.31【题型4 平方差公式的几何背景】【例4】(2021•庐江县开学)如图1,在边长为a的正方形中剪去一个边长为b(b<a)的小正方形,把剩下部分拼成一个梯形(如图2),利用这两个图形的面积,可以验证的等式是()A.a2+b2=(a+b)(a﹣b)B.(a﹣b)2=a2﹣2ab+b2C.(a+b)2=a2+2ab+b2D.a2﹣b2=(a+b)(a﹣b)【变式4-1】(2021春•博山区期末)如图1,将一个大长方形沿虚线剪开,得到两个长方形,再将这两个长方形拼成图2所示图形,正好是边长为x的大正方形剪去一个边长为1的小正方形(阴影部分).这两个图能解释下列哪个等式()A.(x﹣1)2=x2﹣2x+1B.(x+1)(x﹣1)=x2﹣1C.(x+1)2=x2+2x+1D.x(x﹣1)=x2﹣x【变式4-2】(2021春•洪江市期末)如图(1),从边长为a的大正方形的四个角中挖去四个边长为b的小正方形后,将剩余的部分剪拼成一个长方形,如图(2),通过计算阴影部分的面积可以得到()A.(a﹣2b)2=a2﹣4ab+b2B.(a+2b)2=a2+4ab+b2C.(a﹣2b)(a+2b)=a2﹣4b2D.(a+b)2=a2+2ab+b2【变式4-3】(2020春•阳谷县期末)如图1,将边长为a的大正方形剪去一个边长为b的小正方形,再沿图中的虚线剪开,然后按图2所示进行拼接,请根据图形的面积写出一个含字母a,b的等式.【题型5 乘法公式(求代数式的值)】【例5(2021春•邗江区校级期末)若xy=﹣1,且x﹣y=3.(1)求(x﹣2)(y+2)的值;(2)求x2﹣xy+y2的值.【变式5-1】(2021•宁波模拟)已知(2x+y)2=58,(2x﹣y)2=18,则xy=.【变式5-2】(2021春•驿城区期末)已知a ﹣b =9,ab =﹣14,则a 2+b 2的值为 .【变式5-3】(2021春•聊城期末)已知:a ﹣b =6,a 2+b 2=20,求下列代数式的值:(1)ab ;(2)﹣a 3b ﹣2a 2b 2﹣ab 3.【题型6 乘法公式的综合运算】【例6】(2020秋•东湖区期末)实践与探索如图1,边长为a 的大正方形有一个边长为b 的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示).(1)上述操作能验证的等式是 ;(请选择正确的一个)A .a 2﹣b 2=(a +b )(a ﹣b )B .a 2﹣2ab +b 2=(a ﹣b )2C .a 2+ab =a (a +b )(2)请应用这个公式完成下列各题:①已知4a 2﹣b 2=24,2a +b =6,则2a ﹣b = .①计算:1002﹣992+982﹣972+…+42﹣32+22﹣12.【变式6-1】(2021•滦南县二模)【阅读理解】我们知道:(a +b )2=a 2+2ab +b 2①,(a ﹣b )2=a 2﹣2ab +b 2①,①﹣①得:(a +b )2﹣(a ﹣b )2=4ab ,所以ab =(a+b)24−(a−b)24=(a+b 2)2−(a−b 2)2. 利用上面乘法公式的变形有时能进行简化计算.例:51×49=(51+492)2−(51−492)2=502−12=2500﹣1=2499. 【发现运用】根据阅读解答问题 (1)填空:102×98= (102+982) 2﹣ (102−982) 2;(2)请运用你发现的规律计算:19.2×20.8.【变式6-2】(2021春•平顶山期末)我们将(a+b)2=a2+2ab+b2进行变形,如:a2+b2=(a+b)2﹣2ab,ab= (a+b)2−(a2+b2)2等.根据以上变形解决下列问题:(1)已知a2+b2=8,(a+b)2=48,则ab=.(2)已知,若x满足(25﹣x)(x﹣10)=﹣15,求(25﹣x)2+(x﹣10)2的值.(3)如图,四边形ABED是梯形,DA①AB,EB①AB,AD=AC,BE=BC,连接CD,CE,若AC•BC=10,则图中阴影部分的面积为.【变式6-3】(2021春•滨江区校级期末)数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b,宽为a的长方形.并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.(1)请用两种不同的方法求图2大正方形的面积:方法1:;方法2:;(2)观察图2,请你写出代数式:(a+b)2,a2+b2,ab之间的等量关系;(3)根据(2)题中的等量关系,解决如下问题:①已知:a+b=5,(a﹣b)2=13,求ab的值;①已知(2021﹣a)2+(a﹣2020)2=5,求(2021﹣a)(a﹣2020)的值.。
八年级数学上册乘法公式的综合应用与拓展 (学生版)•、基本公式1. 平方差公式:(a+b)(a-b)=a 2-b 22例:计算 1999 -2000 X 199822 22. 完全平方公式(a+b) =a +2ab+b (a-b)例:运用公式简便计算3. 完全平方公式a+b(或a-b)、ab 、a 2+b 2这三者任意知道两项就可以求出第三项(a+b)2、(a-b) 2、ab 这三者任意知道两项就可以求出第三项① a 2 b 2 = (a b)2 - 2aba 2b 2 = (a-b) 2+2ab2 2 2 2② (a-b) =(a+b) -4ab(a+b) =(a-b) +4ab(2)完全平方公式变用 2:两个完全平方公式之和的整合2 2 2 2(a+b) + (a-b) =2 (a+b)例1 •已知a b 2 , ab =1,求a 2 b 2的值。
2例 2.已知 a • b = 8 , ab = 2,求(a - b)的值。
例3.已知a - b = 4, ab = 5,求a 2 b 2的值。
2 2例 4 .已知 m +n =7, mn= —18,求 m — mr+ n 的值.例 5 (3)已知:x+2y=7 , xy=6,求(x-2y)2 的值.例6.已知a +丄=5,求(1) a 2+W , (2) (a —丄)2的值.a a a(1)完全平方公式变用 1:利用已知的两项求第三项2 2 2=a -2ab+b (1) 1032(2) 19821 1例7.已知x -― =3,求x4■ ~4的值。
x x3=a -b二、公式的灵活运用1. 对公式的基本变用 _ 2 2(1)位置变化,x y -y x =x_y(2 )符号变化,(彳勺片—x j_y 2= x 2-y 22. 整体思想的应用(1 )应用整体思想,首先要能识别公式中的“两数”2 2例1计算(-a +4b )分析:运用公式(a +b )2=a 2+2ab +b 2时, ______ 就是公式中的a, _____ 就是公式中的b ;若将题目变形为(4b -a 2)2时,则 ________ 是公式中的a ,而 _______ 就是公式中的b .(解略)练习 1•计算:5x 23y 25x 2-3y 2练习2•计算: x -y z x -y —z 练习 3.计算:Ixy z m Jlxy- z m 1练习 4.计算:x ■ y -2z x y 6z(2 )应用应用整体思想,其次能正确选取负号和减号 例计算:(-2 x 2-5)(2 x 2-5)分析:本题两个因式中“-5 ”相同,“2x 2”符号相反,因而 ______ 是公式(a +b )( a -b )= a 2-b 2中的a,而 _____ 则是公式中的b .解:原式=(3 )应用整体思想,要善于分组加括号例&解下列各式(1) (2) (3) 已知 a 24b 2=i3, ab=6,求(a^bj ,(a_b j 的值。
第一讲:乘法例1:解答:56×4=例2:解答:3×42= 把42分拆成40和2例3:解答:4×329=例4:有9箱货物(重量如下所示),你能想个好办法计算出结果吗?123kg 124kg 125kg133kg 134kg 135kg143kg 144kg 145kg例5:计算:73÷5 (被除数可以分拆成除数5的倍数50和23)73÷5=14…3 50÷5=1023÷5=4 (3)例6:王华在数学考试时,把一个数除以3错算成了乘3,结果得225,正确答案应该是多少?练习:1.用数卡①②③④⑤⑥⑦⑧⑨摆数(1)任选其中6张数卡,摆出2个三位数,使它们的差最大(2)任选其中6张数卡,摆出2个三位数,使它们的差最小(3)你发现了什么特征吗?2.小华在练习英文打字,5分钟打了450个字母,他平均每分钟打几个字母,照这样计算,10分钟能打多少个字母?(用两种方法解)3.☆7 7×△___________2 4 9 3☆,△各是多少?4.在□里填上适当的数(1)□□□(2)□□ 7× 8 ×□__________ ___________5 2 3 2 2 7 8 5(3) 45÷□=□...3 (4) 51÷□=□ (3)5.从4-9这六个数中选出不同的数字填入□中,使得到的商最接近200。
□□□÷□6.在□中填上合适的数7.一个数与自己本身相乘相除,所得的积与商相乘结果为100,这个数是多少?第二讲:运算定律二、例题例3 4821-998 例4 4×125×25×8例5 125×(8+10)例6 9123-(123+88)例7 124×83+83×176例8 9999×1001例9 136--(36--18)例10 269+(31—17)练习:1、2105-769-2312、585-438+15-623、32×125×73+732+2684、425-2217-7835、38+137+62+12636、(1528+2899)+20727、1245-135-65 8、2132-(632+83)9、7755-(2187+755) 10、3065-738-106511、1883-398 12、(13×125)×(3×8)第三讲:乘法应用题知识要点:理解1.求几个相同数的和的问题可用乘法计算。
北师大版数学七年级下册1.6.3《乘法公式综合运用》说课稿3一. 教材分析《北师大版数学七年级下册1.6.3《乘法公式综合运用》》这一节的内容是在学生已经掌握了有理数的乘法、平方差公式和完全平方公式的基础上进行讲解的。
通过这一节的内容,学生能够进一步理解和掌握乘法公式的运用,提高解决实际问题的能力。
二. 学情分析学生在学习这一节内容时,已经有了一定的数学基础,对于有理数的乘法和平方差公式、完全平方公式已经有了一定的了解。
但是,学生在运用乘法公式解决实际问题方面还存在一些困难,需要通过本节课的学习来进行巩固和提高。
三. 说教学目标1.知识与技能目标:学生能够理解和掌握乘法公式的运用,能够运用乘法公式解决实际问题。
2.过程与方法目标:通过学生的自主探究和合作交流,培养学生的解决问题的能力。
3.情感态度与价值观目标:激发学生学习数学的兴趣,培养学生的自信心和自主学习能力。
四. 说教学重难点1.教学重点:学生能够理解和掌握乘法公式的运用。
2.教学难点:学生能够灵活运用乘法公式解决实际问题。
五. 说教学方法与手段在本节课的教学中,我将采用问题驱动的教学方法,引导学生通过自主探究和合作交流来解决问题。
同时,我也会运用多媒体教学手段,如PPT等,来进行辅助教学,提高学生的学习兴趣和效果。
六. 说教学过程1.导入新课:通过一个实际问题的引入,激发学生的学习兴趣,引出本节课的内容。
2.自主探究:学生通过自主学习,理解乘法公式的运用,并能够解决一些简单的问题。
3.合作交流:学生分组讨论,共同解决一些复杂的问题,培养学生的合作交流能力。
4.总结提高:学生进行总结,教师进行点评,加强对乘法公式的理解和运用。
5.巩固练习:学生进行练习,巩固所学知识,提高解决问题的能力。
七. 说板书设计板书设计要简洁明了,能够突出本节课的重点内容。
可以设计一些乘法公式的示例,以及解决实际问题的步骤,帮助学生理解和掌握。
八. 说教学评价教学评价可以通过学生的课堂表现、练习成绩和课后反馈来进行。