课后习题 机械原理第十章作业答案 王德伦版

习题解答第一章绪论1-1 答：1 ）机构是实现传递机械运动和动力的构件组合体。

如齿轮机构、连杆机构、凸轮机构、螺旋机构等。

2 ）机器是在组成它的实物间进行确定的相对运动时，完成能量转换或做功的多件实物的组合体。

如电动机、内燃机、起重机、汽车等。

3 ）机械是机器和机构的总称。

4 ）a. 同一台机器可由一个或多个机构组成。

b. 同一个机构可以派生出多种性能、用途、外型完全不同的机器。

c. 机构可以独立存在并加以应用。

1-2 答：机构和机器，二者都是人为的实物组合体，各实物之间都具有确定的相对运动。

但后者可以实现能量的转换而前者不具备此作用。

1-3 答：1 ）机构的分析：包括结构分析、运动分析、动力学分析。

2 ）机构的综合：包括常用机构设计、传动系统设计。

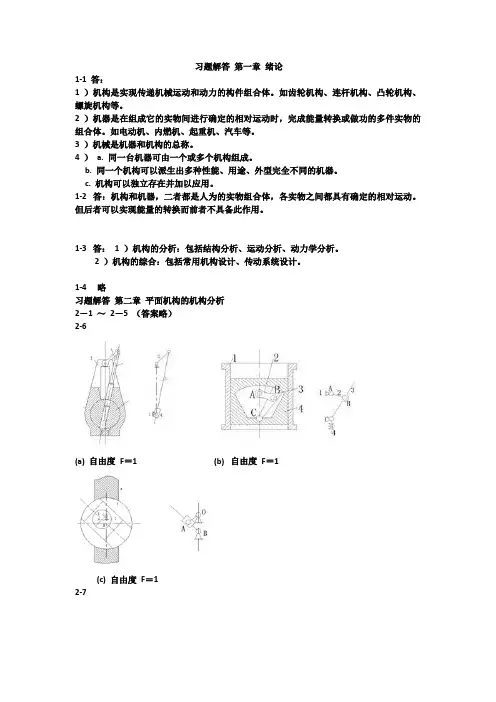
1-4 略习题解答第二章平面机构的机构分析2－1 ～2－5 （答案略）2-6(a) 自由度F＝1 (b) 自由度F＝1(c) 自由度F＝12-7题2 －7 图F ＝3 × 7 －2 × 9 －2 ＝12 -8a) n ＝7 ＝10 ＝0 F ＝3×7－2×10 ＝1b) B 局部自由度n ＝3 ＝3 ＝2 F＝3×3 －2×3－2＝1c) B 、D 局部自由度n ＝3 ＝3 ＝2 F＝3×3 －2×3－2 ＝1d) D( 或C) 处为虚约束n ＝3 ＝4 F＝3×3 －2×4＝1e) n ＝5 ＝7 F＝3×5－2×7＝1f) A 、B 、C 、E 复合铰链n ＝7 ＝10 F ＝3×7－2×10 ＝1g) A 处为复合铰链n ＝10 ＝14 F ＝3×10 －2×14＝2h) B 局部自由度n ＝8 ＝11 ＝1 F ＝3×8－2×11－1 ＝1i) B 、J 虚约束C 处局部自由度n ＝6 ＝8 ＝1 F ＝3×6 －2×8－1＝1j) BB' 处虚约束A 、C 、D 复合铰链n ＝7 ＝10 F ＝3×7－2×10＝1 k) C 、D 处复合铰链n＝5 ＝6 ＝2F ＝3×5－2×6－2 ＝1l) n ＝8 ＝11 F ＝3×8－2×11 ＝2m) B 局部自由度I 虚约束4 杆和DG 虚约束n ＝6 ＝8 ＝1 F ＝3×6－2×8－1 ＝12-9a) n ＝3 ＝4 ＝1 F ＝3 × 3 －2 × 8 －1 ＝0 不能动。

第二章2-1 何谓构件何谓运动副及运动副元素运动副是如何进行分类的答：参考教材5~7页;2-2 机构运动简图有何用处它能表示出原机构哪些方面的特征答：机构运动简图可以表示机构的组成和运动传递情况,可进行运动分析,也可用来进行动力分析;2-3 机构具有确定运动的条件是什么当机构的原动件数少于或多于机构的自由度时,机构的运动将发生什么情况答：参考教材12~13页;2-5 在计算平面机构的自由度时,应注意哪些事项答：参考教材15~17页;2-6 在图2-22所示的机构中,在铰链C、B、D处,被连接的两构件上连接点的轨迹都是重合的,那么能说该机构有三个虚约束吗为什么答：不能,因为在铰链C、B、D中任何一处,被连接的两构件上连接点的轨迹重合是由于其他两处的作用,所以只能算一处;2-7 何谓机构的组成原理何谓基本杆组它具有什么特性如何确定基本杆组的级别及机构的级别答：参考教材18~19页;2-8 为何要对平面高副机构进行“高副低代"“高副低代”应满足的条件是什么答：参考教材20~21页;2-11 如图所示为一简易冲床的初拟设计方案;设计者的思路是：动力由齿轮1输入,使轴 A连续回转；而固装在轴A上的凸轮2与杠杆3组成的凸轮机构将使冲头上下运动以达到冲压目的;试绘出其机构运动简图,分析其是否能实现设计意图并提出修改方案;解：1取比例尺绘制机构运动简图;2分析其是否可实现设计意图;F=3n- 2P l +P h –p’ -F’=3×3-2×4+1-0-0=0此简易冲床不能运动,无法实现设计意图;3修改方案;为了使此机构运动,应增加一个自由度;办法是：增加一个活动构件,一个低副;修改方案很多,现提供两种;※2-13图示为一新型偏心轮滑阎式真空泵;其偏心轮1绕固定轴心A转动,与外环2固连在一起的滑阀3在可绕固定轴心C转动的圆柱4中滑动;当偏心轮按图示方向连续回转时可将设备中的空气吸入,并将空气从阀5中排出,从而形成真空;1试绘制其机构运动简图；2计算其自由度;解：1取比例尺作机构运动简图如图所示;2 F=3n-2p1+p h-p’-F’=3×4-2×4+0-0-1=12-14 解：1绘制机构运动简图1）绘制机构运动简图F=3n-2P l +P h –p’-F’=3×5-2×7+0-0-0=12）弯曲90o 时的机构运动简图※2-15试绘制所示仿人手型机械手的食指机构的机构运动简图以手掌8作为相对固定的机架,井计算自由度;解：1取比倒尺肌作机构运动简图；2计算自由度1⨯=-F210⨯73=2-17 计算如图所示各机构的自由度;aF=3n- 2P l +P h–p’-F’=3×4-2×5+1 -0-0=1A处为复合铰链bF=3n-2P l +P h–p’-F’=3×7-2×8+2-0-2=12、4处存在局部自由度cp’= 2P l ’+P h ’-3n’=2×10+0-3×6=2,F=3n-2P l +P h–p’-F’=3×11-2×17+0-2-0=1C、F、K 处存在复合铰链,重复部分引入虚约束※2-21图示为一收放式折叠支架机构;该支架中的件1和5分别用木螺钉连接于固定台板1’和括动台板5’上．两者在D处铰接,使活动台板能相对于固定台极转动;又通过件1,2,3,4组成的铰链四杆机构及连杆3上E点处的销子与件5上的连杆曲线槽组成的销槽连接使活动台板实现收放动作;在图示位置时,虽在活动台板上放有较重的重物．活动台板也不会自动收起,必须沿箭头方向推动件2,使铰链B,D重合时．活动台板才可收起如图中双点划线所示;现已知机构尺寸l AB=l AD=90 mm；l BC=l CD=25 mm,其余尺寸见图;试绘制该机构的运动简图,并计算其自由度;解：F=3n-2p1+p b-p’-F’=3×5-2×6+1-0-1=12-23 图示为一内燃机的机构简图,试计算其自由度,并分析组成此机构的基本杆组;有如在该机构中改选EG为原动件,试问组成此机构的基本杆组是否与前有所不同;解：1计算自由度F=3n-2P l +P h–p’-F’=3×7-2×10+0-0-0=12拆组3EG 为原动件,拆组2-24 试计算如图所示平面高副机构的自由度,并在高副低代后分析组成该机构的基本杆组;1、解：1计算自由度F=3n-2P l +P h –p ’-F ’=3×5-2×6+1-0-1=12从结构上去除局部自由度、虚约束、多余的移动副、转动副如图2所示 3高副低代如图3所示 4拆组如图4所示 2、解：1计算自由度F=3n-2P l +P h –p ’-F ’=3×-2×9+1-0-1=12从结构上去除局部自由度、虚约束、多余的移动副、转动副如图b 所示 3高副低代如图c 所示 4拆组如图d 所示第三章3—1 何谓速度瞬心相对瞬心与绝对瞬心有何异同点 答：参考教材30~31页;3—2 何谓三心定理何种情况下的瞬心需用三心定理来确定 答：参考教材31页;※3-3机构中,设已知构件的尺寸及点B 的速度v B 即速度矢量pb,试作出各机构在图示位置时的速度多边形;※3-4 试判断在图示的两机构中．B 点足否都存在哥氏加速度又在何位置哥氏加速度为零怍出相应的III 级组II 级组II 级组II 级组机构位置图;并思考下列问题;1什么条件下存在氏加速度2根椐上一条．请检查一下所有哥氏加速度为零的位置是否已全部找出;3图 a 中,a kB2B3=2ω2v B2B3对吗为什么;解：1图 a 存在哥氏加速度,图 b 不存在;2由于a kB2B3==2ω2v B2B3故ω3,v B2B3中只要有一项为零,则哥氏加速度为零;图 a 中B 点到达最高和最低点时构件1,3．4重合,此时v B2B3=0,当构件1与构件3相互垂直．即_f=；点到达最左及最右位置时ω2=ω3=0．故在此四个位置无哥氏加速度;图 b 中无论在什么位置都有ω2=ω3=0,故该机构在任何位置哥矢加速度都为零; 3对;因为ω3≡ω2;3-5 在图示的曲柄滑块机构中,已知mm l mm l mm l mm l DE BD A AB 40,50,100,30C ====,曲柄以等角速度s rad /101=ω回转,试用图解法求机构在︒=451ϕ位置时,点D 、E 的速度和加速度以及构件2的角速度和角加速度;解：1以选定的比例尺l μ作机构运动简图（2）速度分析AB)(m/s 3.01⊥==AB B l v ωBCBCv v v v v C C C B C B C //32322⊥∨∨+=+=？方向：？0？大小：？根据速度影像原理,作BC BD bc bd //2=求得点d,连接pd;根据速度影像原理,作BDE bde ∆≈∆求得点e,连接pe,由图可知)(/r 2/m/s,175.0m/s,173.0,m/s 23.0223232顺时针s ad l bc c c v pe v pd v BC v v C C v E v D ========μωμμμ （3）加速度分析A)(B m/s 3221→==AB B l a ω根据速度影像原理作BC BD c b d b /''/''2=求得点'd ,连接''d p ;根据速度影像原理,作BDE e d b ∆≈'''∆求得点e ',连接e p '',由图可知)(/36.8//,m/s 8.2'',m/s 64.2''2'2'22222顺时针s rad l c n l a e p a d p a BC a BC B C a E a D =======μαμμτ 3-6 在图示机构中,设已知各构件的尺寸,原动件1以等角速度1ω顺时针方向转动,试用图解法求机构在图示位置时构件3上C 点速度和加速度比例尺任选;abc3-7 在图示机构中,已知mm l mm l mm l mm l mm l BC CD EF A AE 50,75,35,40,70B =====,曲柄以等角速度s rad /101=ω回转,试用图解法求机构在︒=501ϕ位置时,C 点的速度c v 和加速度c a ; 解：1以选定的比例尺l μ作机构运动简图;速度分析m/s 72.0m/s,4.01111====AF F AB B l v l v ωω AFAF EFv v v v F F F F F //15145⊥⊥∨+==方向：大小：v d 用速度影响法求2速度分析CD ED v v v CDD C ⊥⊥∨+=方向：大小： BC AB v v v CBB C ⊥⊥∨+=方向：大小：3加速度分析)(m/s 2.7A),(B m/s 42211221A F l a l a AF F AB B →==→==ωω AFA F v a a a a a F F rF F k F F F F F ///21511515145→→∨++==方向：大小：ω EFEF l a a a a a EFEF n E F E F F ⊥→++==方向：大小：2444450ωτa d 用加速度影像法求CD D C l a a a a CDCDnCD D C ⊥→∨∨++=方向：大小：23ωτ CBB C l a a a a CB CBnCB B C ⊥→∨∨++=方向：大小：22ωτ 2m/s 3''=⋅=a C c p a μ3-8 在图示凸轮机构中,已知凸轮1以等角速度s rad /101=ω转动,凸轮为一偏心圆,其半径︒====90,50,15,251B ϕmm l mm l mm R AD A ;试用图解法求构件2的角速度2ω和角加速度2α; 解：1以选定的比例尺l μ作机构运动简图;2速度分析：将机构进行高副低代,其替代机构如图b 所示;m/s 15.0141===AB B B l v v ωCDAB BD v v v B B B B //4242⊥⊥∨+=方向：大小：？？)(/3.2//222逆时针s rad l pb l v BD v BD B ===μω3加速度分析A)m/s(B 5.12141→===AB B B l a a ω其中,）（顺时针222222222242242rad/s 9.143/''/,m/s 286.0,m/s 746.02=======BD a BD D B BD n D B B B k B B l b n l a l a v a μαωωτ 3-11 试求图示机构在图示位置时的全部瞬心; 解：a 总瞬心数：4×3/2=6对P 13：P 12、P 23、P 13在同一直线上, P 14、P 34、P 13在同一直线上 对P 24:P 23、P 34、P 24在同一直线上,P 12、P 14、P 24在同一直线上 d 总瞬心数：4×3/2=6对P 13：P 12、P 23、P 13在同一直线上, P 14、P 34、P 13在同一直线上 对P 24:P 23、P 34、P 24在同一直线上,P 12、P 14、P 24在同一直线上※3-12 标出图示的齿轮一连杆组合机构中所有瞬心,并用瞬心法求齿轮1与齿轮3的传动比ω1/ω3; 解：1瞬新的数目：K=NN-1/2=66-1/2=152)为求ω1/ω3需求3个瞬心P 16、P 36、P 13的位置,3)ω1/ω3= P 36P 13/P 16P 13=DK/AK,由构件1、3在K 点的速度方向相同,可知ω3与ω1同向;3-13 在图示四杆机构中,s rad mm l mm l CD AB /10,90,602===ω,试用瞬心法求：1当︒=165ϕ时点C 的速度C v ；当︒=165ϕ时构件3的BC 线上或其延长线上速度最小的一点E 的位置及其速度大小；3当0=C v 时ϕ角之值有两解;解：1以选定的比例尺l μ作机构运动简图（2）因P 24为构件2、4的顺心,则m/s 4.0rad/s 5.4424242242424=⋅==⋅=⋅=CD C D P A P l v DP AP l l ωωωω，对P 24:P 23、P 34、P 24在同一直线上,P 12、P 14、P 24在同一直线上（3）因构件3的BC 线上速度最小的点到绝对瞬心P 13的距离最近,故从P 13作BC 线的垂线交于E 点; 对P 13：P 12、P 23、P 13在同一直线上, P 14、P 34、P 13在同一直线上,故m/s 357.0131321313133313=⋅⋅=⋅⋅⋅=⋅⋅=⋅=E P B P l E P u B P v E P l v ABl l B l E P E ωμμωω（4）若0=C v ,则04=ω,DP AP l l DP A P 24242242424⋅=⋅=ωωω若024=A P ,则P 24与P 12重合,对P 24:P 23、P 34、P 24在同一直线上,P 12、P 14、P 24在同一直线上 若024=A P ,则A 、B 、C 三点共线;︒=⋅-++︒=︒=⋅-+=6.226)2arccos(1804.26)2arccos(22222221212211ADAC D C AD AC AD AC D C AD AC ϕϕ， ※3-15 在图示的牛头刨机构中,l AB =200 mnl,l CD =960 mm,l DE =160 mm, h=800mm,h 1=360mm,h 2=120mm;设曲柄以等角速度ω1=5 rad ／s ．逆时针方向回转．试以图解法求机构在φ1=135o 位置时．刨头点的速度v C ;sm AP v v P P P l p c l /24.1,,)2(151********===μωμ出瞬心利用顺心多边形依次定所示作机构运动简图，如图（1）以:解。

机械原理课后全部习题答案目录第1章绪论 (1)第2章平面机构的结构分析 (3)第3章平面连杆机构 (8)第4章凸轮机构及其设计 (15)第5章齿轮机构 (19)第6章轮系及其设计 (26)第8章机械运动力学方程 (32)第9章平面机构的平衡 (39)第一章绪论一、补充题1、复习思考题1)、机器应具有什么特征？机器通常由哪三部分组成？各部分的功能是什么？2）、机器与机构有什么异同点？3）、什么叫构件？什么叫零件？什么叫通用零件和专用零件？试各举二个实例。

4）、设计机器时应满足哪些基本要求？试选取一台机器，分析设计时应满足的基本要求。

2、填空题1)、机器或机构，都是由组合而成的。

2）、机器或机构的之间，具有确定的相对运动。

3）、机器可以用来人的劳动，完成有用的。

4）、组成机构、并且相互间能作的物体，叫做构件。

5）、从运动的角度看，机构的主要功用在于运动或运动的形式。

6）、构件是机器的单元。

零件是机器的单元。

7）、机器的工作部分须完成机器的动作，且处于整个传动的。

8）、机器的传动部分是把原动部分的运动和功率传递给工作部分的。

9）、构件之间具有的相对运动，并能完成的机械功或实现能量转换的的组合，叫机器。

3、判断题1)、构件都是可动的。

（）2）、机器的传动部分都是机构。

（）3）、互相之间能作相对运动的物件是构件。

（）4）、只从运动方面讲，机构是具有确定相对运动构件的组合。

（）5）、机构的作用，只是传递或转换运动的形式。

（）6）、机器是构件之间具有确定的相对运动，并能完成有用的机械功或实现能量转换的构件的组合。

（）7）、机构中的主动件和被动件，都是构件。

（）2 填空题答案1）、构件2）、构件3）、代替机械功4）、相对运动5）、传递转换6）、运动制造7）、预定终端8）、中间环节9）、确定有用构件3判断题答案1）、√2）、√3）、√4）、√5）、×6）、√7）、√第二章 机构的结构分析2-7 是试指出图2-26中直接接触的构件所构成的运动副的名称。

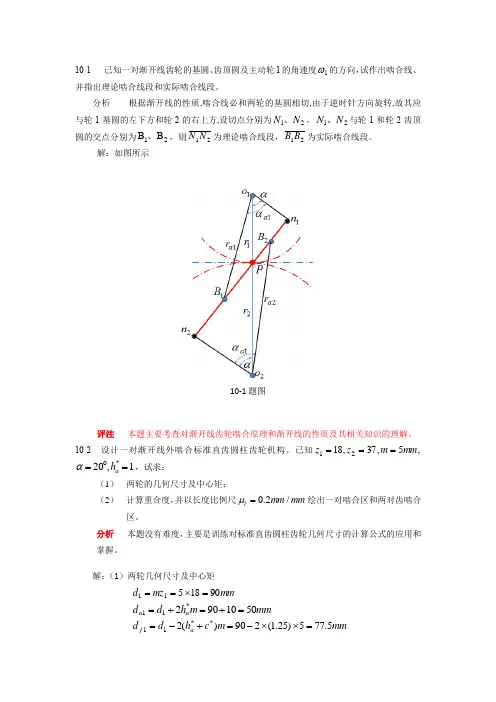
10-1 已知一对渐开线齿轮的基圆、齿顶圆及主动轮1的角速度1ω的方向，试作出啮合线、并指出理论啮合线段和实际啮合线段。

分析根据渐开线的性质,啮合线必和两轮的基圆相切,由于逆时针方向旋转,故其应与轮1基圆的左下方和轮2的右上方,设切点分别为21N N 、，21N N 、与轮1和轮2齿顶圆的交点分别为21B B 、，则21N N 为理论啮合线段，21B B 为实际啮合线段。

解：如图所示10-1题图评注本题主要考查对渐开线齿轮啮合原理和渐开线的性质及其相关知识的理解。

10-2 设计一对渐开线外啮合标准直齿圆柱齿轮机构。

已知,5,37,1821mm m z z ===1,20*==a h α，试求：（1） 两轮的几何尺寸及中心矩；（2） 计算重合度，并以长度比例尺mm mm l /2.0=μ绘出一对啮合区和两对齿啮合区。

分析本题没有难度，主要是训练对标准直齿圆柱齿轮几何尺寸的计算公式的应用和掌握。

解：（1）两轮几何尺寸及中心矩mm mz d 9018511=⨯==mm m h d d a a 5010902*11=+=+=mm m c h d d a f 5.775)25.1(290)(2**11=⨯⨯-=+-=mm d d b 572.849397.09020cos 011=⨯== mm me e s s 854.722121=====πmm mz d 18537522=⨯==mm m h d d a a 195101852*22=+=+=mm m c h d d a f 5.1725)25.1(2185)(2**22=⨯⨯-=+-=mm d d b 854.1739397.018520cos 022=⨯==mm z z m a 5.137)3718(25)(221=+=+= （3） 计算重合度01111125.325020cos 45arccos cos arccos ==== a a b a r r r r αα 02222294.265.9720cos 5.92arccos cos arccos ====a ab a r r r r αα )]tan (tan )tan (tan [212211ααααπε'--'-=a a a z z 51.1)]20tan 94.26(tan 37)20tan 25.32(tan 18[21=-+-= πmm m p b 764.1420cos 5cos === παπmm p B B b a 741.23761.1461.121=⨯==ε一对齿啮合和两对齿啮合区如图所示。

第十章 齿轮机构及其设计习题10-21解：1) 因为7692.06550cos ===K b K r r α， 故压力角452439715.3900'''==K α展角：1375.06932.08307.0tan =-=-==K K K K inv αααθ曲率半径：mm r K b K 535.418307.050tan =⨯==αρ2) 087273.050==K θ，根据渐开线函数表，有 图10-21 ()25434087223.0087273.0087223.0087925.0455*******'''=---+'=K α mm r r K b K 860.6082155.050cos ===α习题10-23 解：分度圆半径：mm mz r 3923262=⨯== 齿顶圆半径：mm mh r r a a 42339*=+=+=基圆半径：mm r r b 648.3620cos 39cos 0=⨯==α 齿廓在齿顶处压力角：0241.2942648.36arccos arccos ===a b a r r α 齿廓在分度圆处曲率半径：mm r 339.1320sin 39sin 0=⨯==αρ齿廓在齿顶处曲率半径：mm tg tg r a b a 516.20241.29648.360=⨯==αρ习题10-25解：基圆节距mm L L p b 914.5512.27426.3356=-=-= 模数mm p m b 003.220cos 1415.3914.5cos 0=⨯==απ 取标准模数mm m 2=。

习题10-26解：中心距()()()5059157001221121112=+⨯=+=⇒+=i m a z mz i a大齿轮齿数：9055091122=⨯==z i z 小、大齿圆分度圆直径为 mm mz d 25055011=⨯==，mm mz d 45059022=⨯==小、大齿轮齿顶圆直径为()mm h z m d aa 2605522*11=⨯=+=，()mm h z m d a a 4605922*22=⨯=+= 小、大齿轮基圆直径为mm d d b 923.23420cos 250cos 01===α，mm d d b 862.42220cos 450cos 02===α 分度圆上齿厚及齿槽宽mm m p s e 854.72514159.322=⨯====π习题10-27 解：齿根圆直径与基圆直径重合时，有()**02220cos c h z m mz a --= 齿数为()46.41229397.015.220cos 122**0**=--=-=-+=c h z m c h z a a 当齿数大于41齿时，齿根圆直径大于基圆直径。

《机械原理》习题解答机械工程学院目录第1章绪论 (1)第2章平面机构的结构分析 (3)第3章平面连杆机构 (8)第4章凸轮机构及其设计 (15)第5章齿轮机构 (19)第6章轮系及其设计 (26)第8章机械运动力学方程 (32)第9章平面机构的平衡 (39)第一章绪论一、补充题1、复习思考题1)、机器应具有什么特征？机器通常由哪三部分组成？各部分的功能是什么？2）、机器与机构有什么异同点？3）、什么叫构件？什么叫零件？什么叫通用零件和专用零件？试各举二个实例。

4）、设计机器时应满足哪些基本要求？试选取一台机器，分析设计时应满足的基本要求。

2、填空题1)、机器或机构，都是由组合而成的。

2）、机器或机构的之间，具有确定的相对运动。

3）、机器可以用来人的劳动，完成有用的。

4）、组成机构、并且相互间能作的物体，叫做构件。

5）、从运动的角度看，机构的主要功用在于运动或运动的形式。

6）、构件是机器的单元。

零件是机器的单元。

7）、机器的工作部分须完成机器的动作，且处于整个传动的。

8）、机器的传动部分是把原动部分的运动和功率传递给工作部分的。

9）、构件之间具有的相对运动，并能完成的机械功或实现能量转换的的组合，叫机器。

3、判断题1)、构件都是可动的。

（）2）、机器的传动部分都是机构。

（）3）、互相之间能作相对运动的物件是构件。

（）4）、只从运动方面讲，机构是具有确定相对运动构件的组合。

（）5）、机构的作用，只是传递或转换运动的形式。

（）6）、机器是构件之间具有确定的相对运动，并能完成有用的机械功或实现能量转换的构件的组合。

（）7）、机构中的主动件和被动件，都是构件。

（）2 填空题答案1）、构件2）、构件3）、代替机械功4）、相对运动5）、传递转换6）、运动制造7）、预定终端8）、中间环节9）、确定有用构件3判断题答案1）、√2）、√3）、√4）、√5）、×6）、√7）、√第二章 机构的结构分析2-7 是试指出图2-26中直接接触的构件所构成的运动副的名称。

WE CAN DO BETTER.质心位于1s ，1S B l =17.5mm ，连杆质量为 4.53572kg,质心位于2s ，2S B l =145.6mm,转速为200r/min ，滑块质量为2.267985kg ，设曲柄为水平位置为初始位置，题10-2图试计算：1） t=1s 时滑块的速度和加速度，并比较精确解与级数展开的近似解的计算结果； 2） t=1s 机构的总惯性力；3） 在曲柄相反的方向上，距A 为r 处（自行给定）进行离心惯性力平衡所需的质量； 4） 尝试用曲柄附加质量完全平衡滑块的水平惯性力和综合考虑水平和垂直惯性力过平衡方法，计算机构的惯性力，并与没有平衡的机构惯性力进行比较。

（1）转速为200r/min ，即（10/3）r/s ，所以t=1s 时曲柄与水平方向夹角为120°其中X-Y 为定坐标系，X ’-Y ’是动坐标系；V 为实际速度，Va 为滑块的铰接点在动坐标系下的速度，Vq 为牵连速度AC q d V ⋅=ωγcot ⋅=q V V︒=+60βα︒=+90βγBCAB l l ︒⋅=60sin sin β︒-⋅=60cos cos AC BC AC l l d β0.362052928得出V=2.202583BC an l V a 2'=136.3746462642γsin qa v v ==7.8962325366ACq l a ⋅=2ω158.8141850421q na a a -=βcos '0=16.80285881369 得出0a =16.80285881369 级数展开方法：根据滑块的位移公式：()()2sin 1cos ⎥⎦⎤⎢⎣⎡-+=t l l l t l x BC AB BC AB ωω将滑块的位移公式中的根式使用级数展开为2462462461()sin ()sin ()sin 2816AB AB AB BC BC BCl l l t t t l l l ωωω=-+-+⋅⋅⋅ 从第二项以后各项的值很小可忽略，误差不足1%，从而可以得出滑块位移的近似表达式222cos (1sin )2ABAB BC BC l x l t l t l ωω≈+-对上式求一阶微分得tl l t l v BCABAB ωωωω2sin 2sin 2⋅⋅-⋅⋅-≈=2.3228216031对上式求二阶微分得222cos cos 2ABc AB BCl a l t tl ωωωω≈--=45.1528403912 （2）其中AB F 是杆AB 的惯性力；q F BC 是杆BC 的牵连惯性力，t F BC 是BC 杆相对惯性力的切矢量，n F BC 是BC 杆相对惯性力的法矢量；C F 是C 滑块的惯性力。