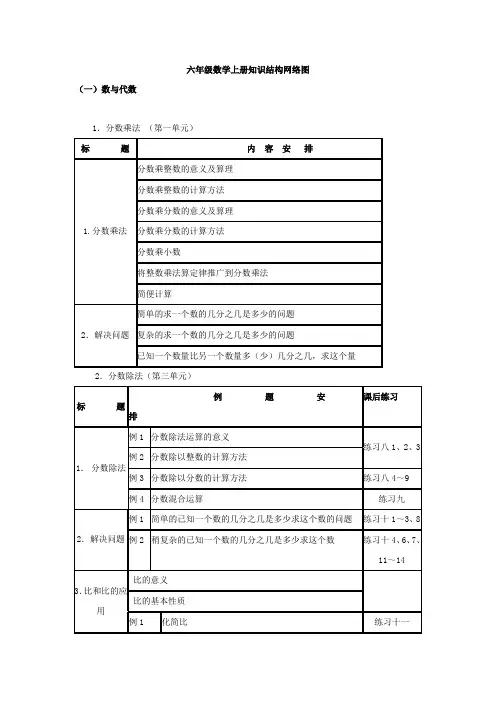
小学六年级 分数乘法 思维导图

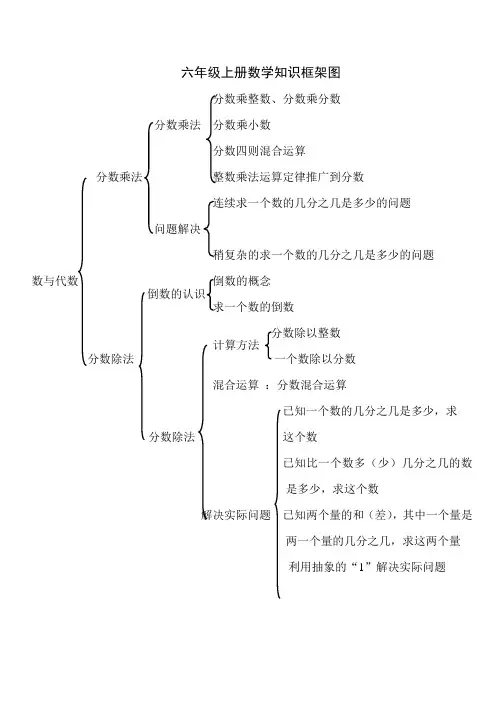
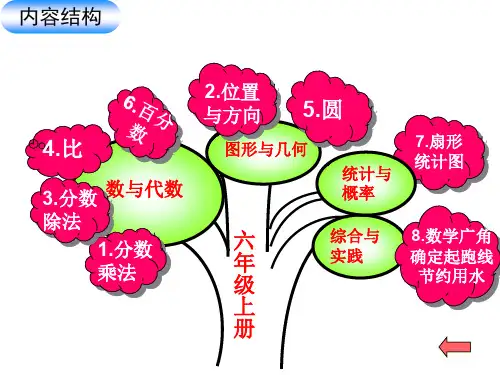
六年级上册数学知识框架图
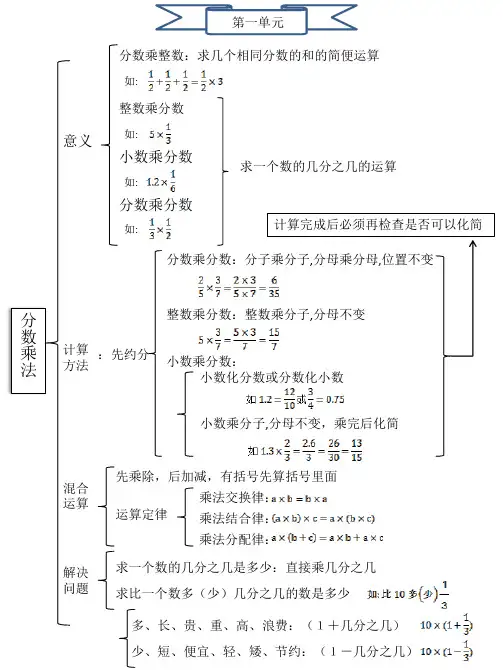
分数乘整数、分数乘分数 分数乘法 分数乘小数
分数四则混合运算
分数乘法 整数乘法运算定律推广到分数
连续求一个数的几分之几是多少的问题
问题解决
稍复杂的求一个数的几分之几是多少的问题 数与代数 倒数的概念
求一个数的倒数
分数除以整数 分数除法 一个数除以分数
混合运算 ：分数混合运算
已知一个数的几分之几是多少，求
分数除法 这个数
已知比一个数多（少）几分之几的数
是多少，求这个数
解决实际问题 已知两个量的和（差），其中一个量是
两一个量的几分之几，求这两个量
利用抽象的“1”解决实际问题
倒数的认识
计算方法
比的意义：求比值
比的基本性质比的基本性质
比
化简比
比的应用：按比分配
数与代数百分数的意义和读、写法
求百分率
百分数和分数、小数的互化
百分数求一个数的百分之几是多少
求一个数比另一个多（或少）百分之几
用百分数解决问题
求比一个数多（或少）百分之几的数是多少
根据平面示意图，用方向和距离描述某个点的位置位置与方向根据方向和距离的描述，在图上确定某个点的位置
描述简单的路线图
空间与几何圆的认识
圆的周长
圆基本应用
圆的面积圆环面积
解决实际问题
扇形
扇形统计图的认识统计与概率扇形统计图
选择合适的统计图
确定起跑线
综合实践活动
节约用水
数学广角数与形（找规律）。

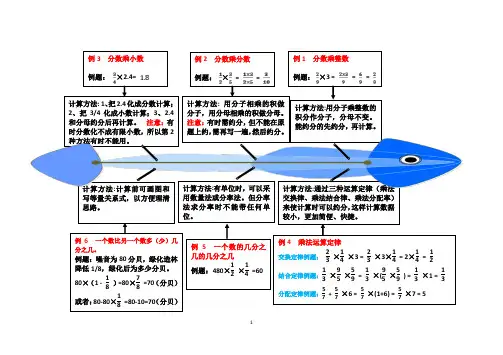
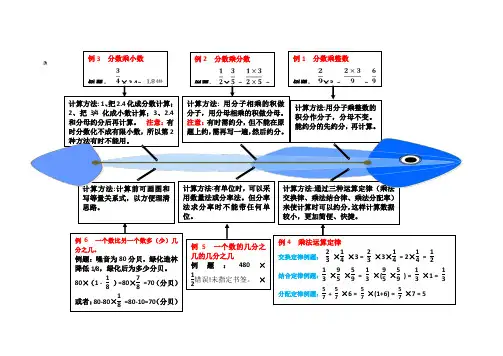
1计算方法:通过三种运算定律（乘法交换律、乘法结合律、乘法分配率）来使计算时可以约分，这样计算数据较小，更加简便、快捷。

计算方法:计算前可画图和写等量关系式，以方便理清思路。

例1 分数乘整数 例题： ×3 == =计算方法:用分子乘整数的积分作分子，分母不变。

能约分的先约分，再计算。

例2 分数乘分数 例题： × ==计算方法: 用分子相乘的积做分子，用分母相乘的积做分母。

注意：有时需约分，但不能在原题上约，需再写一遍，然后约分。

例3 分数乘小数 例题： ×2.4=计算方法: 1、把2.4化成分数计算；2、把3/4化成小数计算；3、2.4和分母约分后再计算。

注意：有时分数化不成有限小数，所以第2种方法有时不能用。

例4 乘法运算定律交换定律例题： 23 ×14 ×3 = 23 ×3×14 = 2×14 = 12结合定律例题：13 ×95 ×59 = 13 ×(95 ×59 ) = 13 ×1 = 13分配定律例题：57 + 57 ×6 = 57 ×(1+6) = 57 ×7 = 5计算方法:有单位时，可以采用数量法或分率法。

但分率法求分率时不能带任何单位。

例 5 一个数的几分之几的几分之几例题：480×12 ×14 =60例6 一个数比另一个数多（少）几分之几。

例题：噪音为80分贝，绿化造林降低1/8，绿化后为多少分贝。

80×（1 - 18 ）=80×78 =70（分贝）或者：80-80×18 =80-10=70（分贝）。

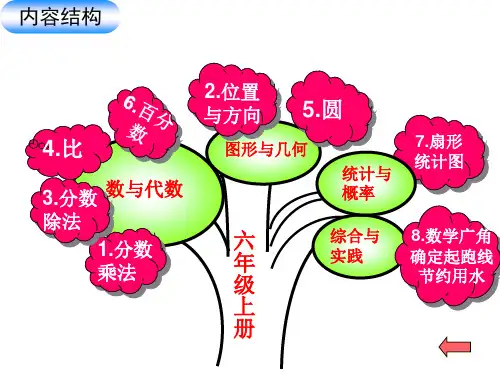
小学六年级数学上册1-4单元期中知识点总结，附思维导图！第一单元分数乘法一、分数乘法的意义1、分数乘整数：分数乘整数的意义与整数乘法的意义相同，就是求几个相同加数和的简便运算。

二、分数乘法的计算法则1、整数和分数相乘：整数和分子相乘的积作分子，分母不变。

2、分数和分数相乘：分子相乘的积作分子，分母相乘的积作分母。

3、注意：能约分的先约分，然后再乘，得数必须是最简分数。

当带分数进行乘法计算时，要先把带分数化成假分数再进行计算。

三、分数大小的比较一个数（0除外）乘大于1的数，积大于原来的数。

一个数（0除外）乘小于1的数（0除外），积小于原来的数。

一个数（0除外）乘1，积等于原来的数。

四、分数混合运算1、分数混合运算顺序：(与整数相同)，先乘、除后加、减，有括号的先算括号里面的。

2、整数乘法运算定律：乘法交换律：a×b=b×a乘法结合律：(a×b)×c=a×(b×c)乘法分配律：a×(b±c)=a×b±a×c五、解决实际问题1、分数应用题一般解题步骤（1）找出含有分率的关键句。

（2）找出单位“1”的量（3）根据线段图写出等量关系式：单位“1”的量×对应分率=对应量。

（4）根据已知条件和问题列式解答。

2、解题技巧（1）已知单位“1”的量，求它的几分之几是多少，用单位“1”的量与分数相乘。

（乘法）（2）找单位“1”：“的”前或“比”后，“的”字相当于“×”，“是”、“占”字相当于“＝”（3）求一个数的几倍：一个数×几倍；求一个数的几分之几是多少：一个数×分数。

（4）写数量关系式技巧：①“的”相当于“×”，“占”、“是”、“比”相当于“= ”②分率前是“的”：单位“1”的量×分率=分率对应量分率前是“多或少”的意思：单位“1”的量×（1±分率）=分率对应量第二单元位置与方向一、确定物体位置的方法：先确定中心或观测点，然后确定方向，再以比例尺来确定距离；最后在具体位置标出名称。

计算方法:通过三种运算定律（乘法交换律、乘法结合律、乘法分配率）来使计算时可以约分，这样计算数据较小，更加简便、快捷。

计算方法:计算前可画图和写等量关系式，以方便理清思路。

例1 分数乘整数 例题： ×3 ==计算方法:用分子乘整数的积分作分子，分母不变。

能约分的先约分，再计算。

例2 分数乘分数例题： × ==计算方法: 用分子相乘的积做分子，用分母相乘的积做分母。

注意：有时需约分，但不能在原题上约，需再写一遍，然后约分。

例3 分数乘小数例题： ×2.4=错计算方法: 1、把2.4化成分数计算； 2、把3/4化成小数计算；3、2.4和分母约分后再计算。

注意：有时分数化不成有限小数，所以第2种方法有时不能用。

例4 乘法运算定律交换定律例题： 23 ×14 ×3 = 23 ×3×14 = 2×14 = 12结合定律例题：13 ×95 ×59 = 13 ×(95 ×59 ) = 13 ×1 = 13分配定律例题：57 + 57 ×6 = 57 ×(1+6) = 57 ×7 = 5计算方法:有单位时，可以采用数量法或分率法。

但分率法求分率时不能带任何单位。

例 5 一个数的几分之几的几分之几例题：480×12错误!未指定书签。

×例6 一个数比另一个数多（少）几分之几。

例题：噪音为80分贝，绿化造林降低1/8，绿化后为多少分贝。

80×（1 - 18 ）=80×78 =70（分贝）或者：80-80×18 =80-10=70（分贝）。

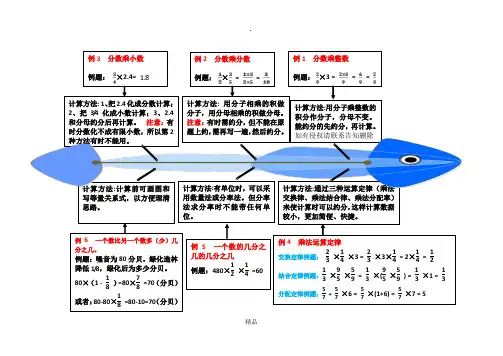
.精品 计算方法:通过三种运算定律（乘法交换律、乘法结合律、乘法分配率）来使计算时可以约分，这样计算数据较小，更加简便、快捷。

计算方法:计算前可画图和写等量关系式，以方便理清思路。

例1 分数乘整数 例题： ×3 = = = 计算方法:用分子乘整数的积分作分子，分母不变。

能约分的先约分，再计算。

如有侵权请联系告知删除例2 分数乘分数 例题： × = = 计算方法: 用分子相乘的积做分子，用分母相乘的积做分母。

注意：有时需约分，但不能在原题上约，需再写一遍，然后约分。

例3 分数乘小数例题： ×2.4= 计算方法: 1、把2.4化成分数计算；2、把3/4化成小数计算；3、2.4和分母约分后再计算。

注意：有时分数化不成有限小数，所以第2种方法有时不能用。

例4 乘法运算定律 交换定律例题： 23 ×14 ×3 = 23 ×3×14 = 2×14 = 12 结合定律例题：13 ×95 ×59 = 13 ×(95 ×59 ) = 13 ×1 = 13 分配定律例题：57 + 57 ×6 = 57 ×(1+6) = 57 ×7 = 5计算方法:有单位时，可以采用数量法或分率法。

但分率法求分率时不能带任何单位。

例 5 一个数的几分之几的几分之几 例题：480×12 ×14 =60 例6 一个数比另一个数多（少）几分之几。

例题：噪音为80分贝，绿化造林降低1/8，绿化后为多少分贝。

80×（1 - 18 ）=80×78 =70（分贝）或者：80-80×18 =80-10=70（分贝）。

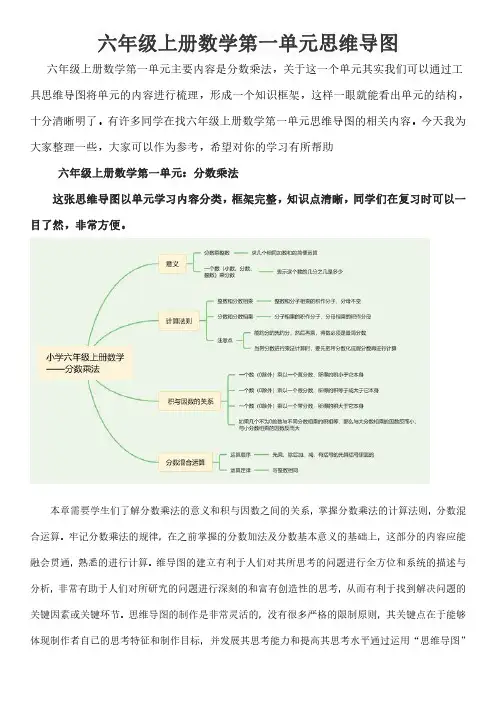
六年级上册数学第一单元思维导图六年级上册数学第一单元主要内容是分数乘法，关于这一个单元其实我们可以通过工具思维导图将单元的内容进行梳理，形成一个知识框架，这样一眼就能看出单元的结构，十分清晰明了。

有许多同学在找六年级上册数学第一单元思维导图的相关内容。

今天我为大家整理一些，大家可以作为参考，希望对你的学习有所帮助
六年级上册数学第一单元：分数乘法
这张思维导图以单元学习内容分类，框架完整，知识点清晰，同学们在复习时可以一目了然，非常方便。

本章需要学生们了解分数乘法的意义和积与因数之间的关系，掌握分数乘法的计算法则，分数混合运算。

牢记分数乘法的规律，在之前掌握的分数加法及分数基本意义的基础上，这部分的内容应能融会贯通，熟悉的进行计算。

维导图的建立有利于人们对其所思考的问题进行全方位和系统的描述与分析，非常有助于人们对所研究的问题进行深刻的和富有创造性的思考，从而有利于找到解决问题的关键因素或关键环节。

思维导图的制作是非常灵活的，没有很多严格的限制原则，其关键点在于能够体现制作者自己的思考特征和制作目标，并发展其思考能力和提高其思考水平通过运用“思维导图”
的方法可以大大提高人的思考能力。

为了方便大家参考，下面时一些优秀同学的这思维导图，我进行的收集，仅供同学们参考。