八年级数学每日一练 一

1、下列图形中，是轴对称图形的有( )A. 1个B. 2个C. 3个D. 4个2、如图，直线AC是四边形ABCD的对称轴.若AC=10 cm，BD=8 cm，则阴影部分的面积为 .3、如图，∠MON内有一点P，点P关于OM的对称点是G，点P关于ON的对称点是H，GH分别交OM，ON于点A，B. 若∠MON=35°，则∠GOH的度数为( ) A. 60° B. 70° C. 80° D. 90°2题3题4、如图，在△ABC中，AC＞AB，D是BA延长线上一点，E是∠CAD的平分线上一点，EB=EC，过点E作EF⊥AC于点F，EG⊥AD于点G.(1)求证：△EGB≌△EFC；(2)若AB=3，AC=5，求AF的长.1、若点A(-2，3)关于y轴的对称点为点B，点B向下平移4个单位长度得到点C，则点C的坐标为 .2、如图，AF=AB，∠F AB=60°，AE=AC，∠EAC=60°，CF和BE交于点O.下列结论：①CF=BE；②∠AMO=∠ANO；③OA平分∠FOE；④∠COB=120°.其中正确的是 (填序号).3、如图，BD平分∠ABC，DE⊥AB于点E，△ABC的面积为90，AB=18,BC=12，求DE 的长为 .1. 已知△ABC的三边长分别为3，5，7，△DEF的三边长分别为3，3x-2，2x-1，则当x= 时，这两个三角形全等.2、如图，AB=AD，BC=DC，∠B=30°，∠BAD=46°，则∠ACD的度数为( )A. 120°B. 125°C. 127°D. 104°3. 如图，O是直线BC上一点，∠AOB=30°，OP平分∠AOC，PM∥BC交AO于点M，MP=8，PD⊥OC于点D，则PD的长为 .4. 如图，在Rt△ABC中，∠ACB=90°，AC=BC，直线l经过顶点C，AD⊥l于点D，BE⊥l 于点E.若BE=3，DE=5，求AD的长.1、如图，在△ABC中，∠C=90°，∠B=30°，AD是△ABC的角平分线，DE⊥AB，垂足为E，DE=1，则BC的长为( )A. 3B. 2C. 3D. 3+22、如图，在△ABC中，AD平分∠BAC，BD⊥AD于点D，DE∥AC交AB于点E.若AB=8，则DE的长为3、已知A(a，-5)，B(2，b).若A，B两点关于x轴对称，则a= ，b= ；若A，B两点关于y轴对称，则a= ，b= .1题2题4、如图∠BAC=∠BDC=90°AB=AC求证：∠ADB=45°1、如图，点A，C，B，D在同一条直线上，且AC=BD，AM=CN，BM=DN.若∠NEB=110°，则∠N的度数为( )2、如图，点C，E分别为△ABD边BD，AB上的点，且AE=AD，CE=CD，∠D=70°，∠ECD=150°，求∠B的度数为 .3、如图，AD=AE，BE=CD，∠1=∠2=110°，∠BAE=60°，则∠CAE的度数为 .1题2题3题4、如图，点D，B分别是线段AE，CF上的一点，且AD=BC，AB=DC，连接EF.求证：(1)∠A=∠C；(2)∠E=∠F.1、如图，点D是BC上一点，AB=AD，BC=DE，AC=AE，若∠BAD=40°，则∠CDE的度数为2. 如图，AB=AC,AD=AE,∠BAC=∠DAE，B,D,E三点共线.若∠1=25°，∠2=30°，则∠3的度数为 .3、如图，在△ABC中，AB=10，BC=9，AC=6,AD平分∠BAC交BC于点D，点E在AB 上，且AE=AC，则△BDE的周长为 .1题2题3题4、如图，在△ABC中，AC=BC，点D是AB上的一点，AE⊥CD于点E.若CE=BF，AE=EF+BF，试判断AC与BC的位置关系，并说明理由.1. 如图，BD=CF，FD⊥BC于点D，DE⊥AB于点E，BE=CD. 若∠AFD=132°，则∠EDF的度数为 .2、如图，MN∥PQ，AB⊥PQ，点A，D在直线MN上，点B，C在直线PQ上，点E在AB上，AD+BC=7，AD=EB，DE=EC，则AB的长为 .3、如图，在△ABC中，AB=AC,AB＞BC，点D在边BC上，CD=2BD，点E，F在线段AD上，∠1=∠2=∠BAC. 若△ABC的面积为15，则△ACF与△BDE的面积之和为 .1题2题3题4、如图，在△ABC中，AB=BC，∠ABC=90°，点D为AB延长线上一点，点E在BC上，且BE=BD，连接AE，DE，DC.（1）求证：△ABE≌△CBD（2）若∠CAE=30°，求∠BDC的度数。

1．已知，如图，△ABC中，AB＝AC，∠A＝120°，BC＝18cm，AB的垂直平分线交BC于点M，交AB于点E，AC的垂直平分线交BC于点N，交AB于点F，则MN的长为（）A．18cm B．12cm C．6cm D．3cm2．如图，在等腰△ABC中，CA＝CB，∠C＝50°，DE⊥AC，FD⊥AB，则∠EDF＝．3．如图，AB＝AC，AE＝ED＝DB＝BC，求∠A的度数．1．如图，P为△ABC内一点，过点P的线段MN分别交AB、BC于点M、N，且M、N分别在P A、PC的中垂线上．若∠ABC＝80°，则∠APC的度数为（）A．120°B．125°C．130°D．135°2．如图，DE是△ABC的边AB的垂直平分线，垂足为点D，DE交AC于点E，且AC＝7，△BEC的周长为11，则BC的长为．3．计算：△ABC在平面直角坐标系xOy中的位置如图所示．（1）作△ABC关于y轴成轴对称的△A1B1C1，并写出A1、B1、C1的坐标；（2）在y轴上有一点P，使P A+PB的值最小，请在坐标系中标出点P的位置．1．已知等腰三角形一腰上的高线与另一腰的夹角为60°，那么这个等腰三角形的顶角等于（）A．15°或75°B．30°C．150°D．150°或30°2．如图，∠AOB＝30°，M、N分别是射线OA、OB上的动点，OP平分∠AOB，且OP＝6cm，则△PMN的周长的最小值为cm．3．如图，在△ABC中，∠BAC＝∠ACB，点D是BC边上一点，且满足∠B＝∠1，CE平分∠ACB交AD于点E．（1）若∠ADC＝80°，求∠2的度数；（2）过点E作EF∥AB，交BD于点F，请说明∠FEC＝3∠3．八年级上册数学每日一练171．如图，在△ABC中，∠B＝∠C，点D在BC边上，点E在AC上，∠ADE＝∠AED，若∠BAD＝40°，则∠CDE的度数为（）A．10°B．15°C．20°D．25°2．如图，已知△ABC与△ABD关于AB所在的直线对称，延长AD交CB的延长线于点E，若AC+BC＝AE，且∠C＝40°，则∠E的度数为．3．如图，在△ABC中，∠BAC＝105°，MP垂直平分AB，分别交AB、BC于点M、P，NQ垂直平分AC，分别交AC．BC于点N、Q，连接AP、AQ，求∠P AQ的度数．八年级上册数学每日一练181．如图，在△ABC中，AB＝AC，点D为AB边上一点，且AD＝CD＝BC，则∠A的度数为（）A．38°B．36°C．32°D．30°2．如图，在△ABC中，DE垂直平分AC，交AC边于点E，交BC边于点D，若AE＝3，△ABD的周长为14，则△ABC的周长为．3．如图，BD是△ABC的角平分线，DE∥BC，交AB于点E．（1）求证：∠EBD＝∠EDB．（2）当AB＝AC时，请判断CD与ED的大小关系，并说明理由．八年级上册数学每日一练191．如图，∠AOB＝30°，点P是∠AOB内的定点且OP＝4，若点M，N分别是射线OA，OB上异于点O的动点，则△PMN周长的最小值是（）A．B．C．4D．82．若等腰三角形一腰上的中线将它的周长分成了15cm和18cm两部分，则它的腰长为cm．3．如果等腰三角形的一个内角等于40°，则它两底角的平分线所夹的钝角为．4．如图，在△ABC中，边AB的垂直平分线OM与边AC的垂直平分线ON交于点O，这两条垂直平分线分别交BC于点D、E．已知△ADE的周长为13cm．分别连接OA、OB、OC，若△OBC的周长为27cm，则OA的长为cm．5．下列说法正确的个数有（）①有两组边对应相等，一组角对应相等的两个三角形全等；②垂直于同一条直线的两直线平行；③三角形的中线把三角形的面积平分；④等腰三角形高所在的直线是对称轴．A．1个B．2个C．3个D．4个八年级上册数学每日一练201．如图，在△ABC中，边AB，AC的垂直平分线交于点P，连接AP，BP，CP，若∠BAC ＝50°，则∠BPC＝°．2．如图，在Rt△ABC中，∠B＝90°，AC＝60cm，∠A＝60°，点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（0＜t≤15）．过点D作DF⊥BC于点F，连接DE，EF．（1）求证：AE＝DF；（2）当t为何值时，△DEF为直角三角形？请说明理由．。

每日一练（一） 1. 分式的混合运算． （1）222()ababba； （2）22122aaaa；

（3）22211444aaaaa； （4）4222abaababaab； （5）222244(4)2xxyyxyxy； （6）1abb； （7）22433842xxyxyy； （8）22164244244aaaaaaa； （9）2222222xyxyxxyyxyxy； （10）22266(3)443xxxxxxx； （11）22142aaa； （12）211xxx； （13）211393aaaaa； （14）222211xxxxx； （15）22

2xyx

xyxy． 每日一练（二） 1. 分式的混合运算． （1）2211xxxxx；

（2）22226923xyxxyyyxyxyxy； （3）22221212432xxxxxxxx； （4）4224222162+816421xxxxxxxxxx； （5）2221111xxx； （6）4122aaa； （7）224114422aaaaaa； （8）22225baabaabab； （9）2222142442aaaaaaaaa． 每日一练（三） 1. 先化简，再求值． （1）22(2)(69)6xxxxx，其中x=1；

（2）22224481668xxxxxxx，其中x=1； （3）3134222xxxxx，其中x=-1； （4）222211432aaaaaaaaa，其中a=3． 2. 已知2xy，求222xyyxyxyxy的值． 3. 已知15mn，求2224224nmmnmnnmnm的值． 4. 已知12xx，求221xx，441xx的值． 每日一练（四） 1. 解下列分式方程． （1）211323xxx； （2）21233yyy；

第1题图 2八年级数学每日一题〔亲爱的同学们，每天练一练，越来越聪明〕班级：姓名：1. (1) 如图1,在正方形ABCD 中,点E ,F 分别在边BC ,CD 上,AE ,BF 交于点O ,∠AOF ＝90°.求证：BE ＝CF .(2) 如图2,在正方形ABCD 中,点E ,H ,F ,G 分别在边AB ,BC ,CD ,DA 上,EF ,GH 交于点O ,∠FOH ＝90°, EF ＝4.求GH 的长.(3) 点E ,H ,F ,G 分别在矩形ABCD 的边AB ,BC ,CD ,DA 上，EF ,GH 交于点O , ∠FOH ＝90°,EF ＝4. 直接写出以下两题之答案：①如图3,矩形ABCD 由2个全等的正方形组成,那么 GH=___________；②如图4,矩形ABCD 由n 个全等的正方形组成,那么 GH=___________；(用n 的代数式表示).第1题图1EDCBAO2.如图，在ABC △中，D 是BC 边上的一点，E 是AD 的中点，过点A 作BC 的平行线交BE 的延长线于F ，且AF DC =，连接CF ．(1)试说明：D 是BC 的中点；(2)假设AB ＝13，BC ＝10，AD=12,试猜想四边形ADCF 的形状，并说明理由．3.〔结果中保存π〕〔1〕操作：如图1，在线段AB 所在的直线上取一点O 〔O 点在线段外〕，将线段AB 绕点O 旋转一周，所得到的图形是个圆环〔如图2〕，此圆环的面积就是线段AB 所扫过的面积，AB=2，OA=1，那么线段AB 扫过的面积为 ．BA FCED〔2〕如图3，在Rt △ABC 中，∠C =90°，∠B=30°，AC=2，假设将△AB C 绕点A 旋转一周，那么边．BC ．．扫过的图形为 ，面积为 ． 〔3〕假设将图3中的Rt △ABC 绕点C 旋转一周，那么边．A ．B ．扫过的图形是什么？面积为多少？4.如图，等腰梯形ABCD 中，AD ∥BC ，AB=CD ，AD=10cm ，BC=30cm ，动点P 从点A 开场沿AD 边向点D 以每秒1cm 的速度运动，同时动点Q 从点C 开场沿CB 边向点B 以每秒3cm 的速度运动，当其中一点到达端点时，另一点也随之停顿运动，设运动时间是为t 秒． 〔1〕t 为何值时，四边形ABQP 是平行四边形？〔2〕四边形ABQP 能成为等腰梯形吗？假如能，求出t 的值；假如不能，请说明理由．图1图2图3B A O30CBA2OF E D CBA5.如图，四边形ABCD 中，AB=CD ，M 、N 分别是AD 、BC 的中点，延长BA 、NM 、CD 分别交于点E 、F 。

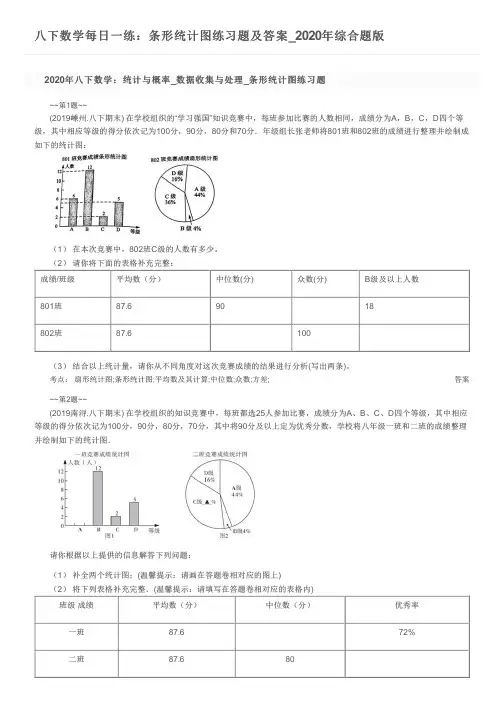
八下数学每日一练：条形统计图练习题及答案_2020年综合题版答案2020年八下数学：统计与概率_数据收集与处理_条形统计图练习题~~第1题~~(2019嵊州.八下期末)在学校组织的“学习强国”知识竞赛中，每班参加比赛的人数相同，成绩分为A ，B ，C ，D 四个等级，其中相应等级的得分依次记为100分，90分，80分和70分．年级组长张老师将801班和802班的成绩进行整理并绘制成如下的统计图：（1） 在本次竞赛中，802班C 级的人数有多少。

（2） 请你将下面的表格补充完整：成绩/班级平均数（分）中位数(分)众数(分)B 级及以上人数801班87.69018802班87.6100（3） 结合以上统计量，请你从不同角度对这次竞赛成绩的结果进行分析(写出两条)。

考点： 扇形统计图;条形统计图;平均数及其计算;中位数;众数;方差;~~第2题~~(2019南浔.八下期末) 在学校组织的知识竞赛中，每班都选25人参加比赛，成绩分为A 、B 、C 、D 四个等级，其中相应等级的得分依次记为100分，90分，80分，70分，其中将90分及以上定为优秀分数，学校将八年级一班和二班的成绩整理并绘制如下的统计图．请你根据以上提供的信息解答下列问题：（1） 补全两个统计图；(温馨提示：请画在答题卷相对应的图上)（2） 将下列表格补充完整．(温馨提示：请填写在答题卷相对应的表格内)班级 成绩平均数（分）中位数（分）优秀率一班87.672%二班87.680答案答案答案（3） 从以上信息进行分析，你认为哪个班更优秀?并说明理由．考点： 扇形统计图;条形统计图;~~第3题~~(2019扬州.八下期末) 某中学现有学生740人，学校为了进一步丰富学生课余生活，拟调整兴趣活动小组，为此进行了一次抽样调查，根据采集到的数据绘制的统计图（不完整）如下：请你根据图中提供的信息，完成下列问题：（1） 图1中，“电脑”部分所对应的圆心角为（2） 在图2中，将“体育”部分的图形补充完整；（3） 爱好“书画”的人数占被调查人数的百分比（4） 估计这个八年级现有学生中，有多少人爱好书画？考点： 用样本估计总体;扇形统计图;条形统计图;~~第4题~~(2019商水.八下期末) 某中学七、八年级各选派10名选手参加知识竞赛，计分采用10分制，选手得分均为整数，成绩达到6分或6分以上为合格，达到9分或10分为优秀，这次竞赛后，七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下，其中七年级代表队得6分、10分的选手人数分别为a 、b.队别平均分中位数方差合格率优秀率七年级6.7m 3.4190%n 八年级7.17.5 1.6980%10%（1） 请依据图表中的数据，求a 、b 的值；（2） 直接写出表中的m 、n 的值；（3） 有人说七年级的合格率、优秀率均高于八年级；所以七年级队成绩比八年级队好，但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由。

初二数学每日练习题1. 计算下列有理数的乘法：(1) \(-3 \times 4\)(2) \(\frac{1}{2} \times \frac{3}{4}\)(3) \(-\frac{2}{3} \times \frac{5}{6}\)2. 解下列一元一次方程：(1) \(2x + 3 = 7\)(2) \(-4y + 6 = -10\)(3) \(5z - 8 = 12\)3. 将下列各数化为最简分数：(1) \(\frac{12}{18}\)(2) \(\frac{-15}{-25}\)(3) \(\frac{24}{36}\)4. 计算下列多项式乘以单项式的结果：(1) \(3x^2 \times 2x\)(2) \(-5ab \times 4b\)(3) \(7m^3 \times (-2m)\)5. 找出下列各组数的最小公倍数：(1) 6 和 8(2) 15 和 20(3) 24 和 366. 判断下列各组角的类型：(1) \(30^\circ\) 和 \(60^\circ\)(2) \(45^\circ\) 和 \(135^\circ\)(3) \(120^\circ\) 和 \(60^\circ\)7. 计算下列平行四边形的面积：(1) 底为 5 厘米，高为 3 厘米(2) 底为 8 厘米，高为 4 厘米(3) 底为 10 厘米，高为 2 厘米8. 完成下列几何图形的全等证明：(1) 证明 \(\triangle ABC \cong \triangle DEF\)，已知 \(AB = DE\)，\(BC = EF\)，\(AC = DF\)(2) 证明 \(\triangle GHI \cong \triangle JKL\)，已知 \(GH = JK\)，\(HI = KL\)，\(\angle G = \angle J\)9. 计算下列各组数据的平均数：(1) 5, 7, 9(2) 2, 4, 6, 8(3) 10, 15, 20, 2510. 解下列不等式，并找出解集：(1) \(x + 3 > 5\)(2) \(2y - 4 \leq 6\)(3) \(-3z + 6 \geq -9\)。

10月17日 每日一练一、基础过关1、如图，△ABC ≌△BAD ，点A 和点B ，点C 和点 D 是对应点，如果AB=8cm ，BD=7cm ，AD=6cm ，那么BC 的长是（） A.5cmB.6cmC.7cmD.8cm【解答】∵△ABC ≌△BAD ，AD=6cm ，∴BC=AD=6（cm ），故选：B 。

【点评】本题考查的是全等三角形的性质，掌握全等三角形的对应边相等是解题的关键2、如图，△AOB ≌△COD ，∠B=29°，∠C=90°，则∠COD 的度数是________。

解答：∵△AOB ≌△COD ，∠B=29°，∴∠D=∠B=29°， ∵∠C=90°，∴∠COD=180°-∠C-∠D=180°-90°-29°=61°【点评】本题考查了全等三角形的性质和三角形的内角和定理，能根据全等三角形的性质求出∠D 的度数是解此题的关键。

二、能力提升3、如图，CE=CA ，ED=CB ，CD=AB ，求证：△ABC ≌△CDE 。

【解答】证明：在△ABC 和△CDE 中，⎪⎩⎪⎨⎧===)()()(已知已知已知CD AB ED CB CE AC ，∴△ABC ≌△CDE （SSS ）【点评】本题考查了全等三角形的证明（SSS ），熟练掌握SSS 的符号语言是解题的关键。

4、如图，已知点D 是△ABC 边BC 延长线上一点，DF 交AC 于点E ，∠A=35°，∠ACD=83°. （1）求∠B 的度数；（2）若∠D=42°，求∠AFE 的度数。

【解答】（1）∵∠ACD 是△ABC 的一个外角，∠A=35°，∠ACD=83°， ∴∠B=∠ACD-∠A=48°。

（2）∵∠AFE 是△BDF 的一个外角，∠B=48°，∠D=42°， ∴∠AFE=∠B+∠D=48°+42°=90°【点评】本题考查的是三角形外角性质，掌握三角形的一个外角等于和他不相邻的两个内角的和是解题的关键三、思维拓展5、如图，DE ⊥AB 于E ，DF ⊥AC 于F ，若BD=CD ，BE=CF 。

1. |−1|+√8−(12)0−2√2．2.a 2;2a:1a 2;1÷a;1a 2:a −3．3.2a 2;2a a 2;1÷(1−1a:1)4. 2x 3−8x 2+8x5. 9x 2−y 2+2y −16. (x −1+3x:1x:1)÷x 2:6x:9x:1，其中x =√3−3．7.x 2x;1=1+22x;1．8. √9−(−1)2024−√273+|1−√2|9. (a −2a;1a )÷1;a 2a 2:a ．10. a −1+2a;4a 2;4÷2a:2a:2．11. (x 2+2)2−6(x 2+2)+912. 4x 3−16x 2y +16xy 213. 人们把√5;12这个数叫做黄金分割数，著名数学家华罗庚优选法中就应用了黄金分割数．设a =√5;12，b =√5:12，求下面的值： (1)直接写出a +b 和ab 的值：a +b =______，ab =______；(2)求s =11:a +11:b 的值．14. 2x:1=x x:1+1；15. −22+(π−3)0+(13);2；16. (1−2a:1)⋅a 2;1a 2;2a:117. (x 2;2x x 2;4x:4+1)÷x 2;1x 2:x ．18. −2x 3y 2+28x 2y −4xy ；19. (x 2+y 2)2−4x 2y 2．20. 先化简，再求值：x 2:x x 2;2x:1÷(2x;1−1x )，请你从−1≤x <3的范围内选取一个你喜欢的整数作为x 的值．21. 6x 2;3x −3x =2x;3．22.√12+(−1)2024+√27−(√2−1)0；23.(xx2;9−1x:3)÷33;x24.x2;4x:4x:1÷(x:4x:1−x)+125.(a+1)2−32；26.(2a−3b)(7x+y)+(x−5y)(2a−3b)．27.先化简、再求值：(1x;1+x;3x2;1)÷xx:1，其中x从0，1，2，3中取一个你认为合适的数代入求值．28.2x;3−3x;2=0；29. (√48−√27)÷√3+√6×2√13．30.x 2:2x:1x ÷(x −1x )．31. (2x:1x:2−1)÷x 2;2x:1x 2;4．32. x 2+4y −4−y 2．33. m 2(a −b )+n 2(b −a )34. 先化简：(x −1−3x:1)÷x 2:4x:4x:1，再从−2,−1,−6中选择一个合适的数作为x 代入求值．35. 2x;2=1x ；36. −√273+(−12);1+(π−3.14)0；37. (x +2−x 2x;2)÷x 2:2x x 2;438. 3x x;2−x 2;1x 2;4x:4⋅3x;6x:1．39. 3a 3−12ab 2；40. 2mx 2−4mx +2m ；41. 先化简：(1+1x:1)÷x 2;42x:2，再从−2，−1，1，2中选一个合适的把一代入数作为x 的值代入求值．42. x:2x;2−16x 2;4=1．43.−3;1×√27+|1−√3|+(−1)2023；44.x2x;1−1x;1；45.(1b −1a)⋅aba2;b2=1a:b．46.a2(x−y)+b2(y−x)；47.x4−2x2+1．48.先化简，再求值：x2;4x:4x2;4÷x2;2xx:2，其中x=13．49.3x:2=1x:1；50. √83−|2√2−5|+(−12);2.51. (a:2a;2−4a 2;4)÷a:4a;2．52. (1−3x:1)÷x 2;4x:4x:1．53. −3x 3+6x 2y 2−3xy 354. 2a (a −b )+8a 3(b −a )55. 先化简再求值：(1x;1−1)÷x;2x 2;2x:1，其中x 是不等式组{x −3(x −2)≥24x −2<5x −1 的一个整数解．56. x x;2−1=8x 2;457. (−12);2+|√3−2|+√273−(3−π)0．58. x:1x 2:4x:4⋅(x −1−3x:1)．59. x:1x;1−x 2;2x x 2;1÷x 2;x;2x 2:2x:160. (a −2b )2−4a 261. (x 2+2x )2+2(x 2+2x )+162. 先化简(1+1x;2)÷x 2;2x:1x 2;4，然后从−1，1，−2，2中选取一个合适的数作为x 的值代入求值．63.x x;3−1=18x 2;9．64. (−2);1+(3.14−π)0+(−23)200×(−112)20165. (3a a;1−a a:1)÷a a 2;1．66. (1−2x )÷x 2;4x:4x 2;4−x:4x:2．67. x 3−4x 2+4x68. 3m (2x −y )2−3mn 269. (x −1+3x:1x:1)÷x 2:6x:9x:1，其中x =√2−1．70. 5x;4x;2=4x:103x;6−1．。

每日一题初中数学【每日一题】（第1期）1、如图，/ B0C=9，点A在0B上，且0A=1,按下列要求画图：以A为圆心，1为半径向右画弧交0C于点A,得第1条线段AA i;再以A i为圆心，1为半径向右画弧交0B于点A2, 得第2条线段A1A2；再以A为圆心，1为半径向右画弧交0C于点A,得第3条线段心… 这样画下去，直到得第n 条线段，之后就不能再画出符合要求的线段了，则n= _______解析；由题意知；A0 - A^A^A = jfj4, - - t则ZAOA Y =20心厶］OA.= “卫具…’、:Z5OC = 9°.-.^^=18°, = 27% AA3A.B = 36= = 45°9 妝Y 90°解得n<10TH为整数，初中数学【每日一题】（第2期）2、已知：如图，△ ABC是边长3cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB BC方向匀速移动，它们的速度都是1cm/s，当P到达点B时，P、Q两点停止运动.设点P的运动时间为t（s），当t为_____________________ 时，△ PBQ是直角三角答案：n=9形.* 匚答案：t=1秒或t=2秒解析：棍据题盍；“朮■叫硕AABC 中,AABO眈叫ZB=60° ,.'.BP= (3-t ) cm△PBQ 中* EPW-右6Q=tj若△PBQ是宜甬三角形」则ZBQR-50-1或ZBPQ=«〔1)当ZBOP^SO* 吋，理=¥»PPt = -(3-d；2解得：t=l(2)当ZBPQ-90* 吋丁BP = -BO解得：t=2二当日秒或"秒吋，APBQ是直角三角形初中数学【每日一题】(第3期)水滴石穿!3、如图，等腰△ ABC中，AB=AC / DBC=15 , AB的垂直平分线MN交AC于点D,则/ A 的度数是°.【解析】试题分析：设/ A=x°,根据MN为中垂线可得：/ ABD=/ A=x°,则/ ABC=(x+15) °，根据AB=AC可得：/ C=Z ABC=(x+15) °，则根据厶ABC的内角和定理可得：x+x+15+x+15=180 °，解得：x=50 ° .初中数学【每日一题】(第4期)锲而不舍，金石可镂！如图，在△ ABC中，/ ABC与/ ACB的平分线相交于点0,过点0作DE// BC,分别交AB AC于点D E,若AB=6, AC=5则厶ADE的周长是答案：50°答案：11【解析】试题分析：根据题意可得：△ BDO^A COE是等腰三角形，OD=BD OE=EC则厶ADE的周长=AD+DE+AE=AD+DO+OE+AE=AD+BD+AE+CE=AB+AC=6+5=11.考点：（1）、角平分线的性质；（2）、等腰三角形的性质•初中数学【每日一题】（第5期）小水长流，贝U能穿石！如图所示，三角形ABC的面积为1 . AP垂直/ B的平分线BP于点P.则三角形PBC的面积是____________________ .【解析】试题分析：过点P作PEL BP,垂足为P,交BC于点E,由角平分线的定义可知/ ABP=/ EBP 结合BP=BP以及/ APB=/ EPB=90 即可证出厶ABP^A EBP（ASA，进而可得出AP=EP根据三角形的面积即可得出，再根据— art1故答案为：-考点：等腰三角形的判定与性质；角平分线的定义；三角形的面积；全等三角形的判定与性质.初中数学【每日一题】（第6期）立志不坚，终不济事！如图，△ ABC是等腰直角三角形，延长BC至E使BE=BA过点B作BD1AE于点(1)求证：BF=2AD(2)若CE龙，求AC的长试题解析：(1)证明：•「△ ABC是等腰直角三角形,••• AC=BC/ FCB" ECA=90 ,••• ACL BE, BD L AE,•••/ CBF+Z CFB=90，/ DAF+Z AFD=90 ,vZ CFB Z AFD•••/ CBF Z CAEAC^BC^CBF=ZCAE在厶BCF与△ ACE中, ，•••△ BCF^A ACE••• AE=BFv BE=BA BD L AE,••• AD=ED 即AE=2AD••• BF=2AD(2)由(1)知厶BCF^A ACE••• CF=CE血,•••在Rt△ CEF中, EF=JH+E=2,v BD L AE, AD=ED•AF=FE=2•AC=AF+CF=2+ .考点：全等三角形的判定与性质；勾股定理初中数学【每日一题】（第7期）已知，如图，△ ABC是等边三角形，AE=CD BQLAD 于Q, BE 交AD 于点P ,初中数学【每日一题】（第8期）如图，/ MON=90 , △ ABC 的顶点 A B 分别在OM ON 上，当A 点从0点出发沿着 0M 向 右运动时，同时点 B 在ON 上运动，连结 0C.若AC=4, BC=3 AB=5贝U 0C 的长度的最大【解析】30度角的直角三角形.考点：全等三角形的判定与性质；等边三角形的性质；含试题分析：取AB中点E,连接OE CE在直角三角形AOB中，OE= AB,利用勾股定理的逆定理可得△ ACB是直角三角形，所以CE= AB,利用OE+C匡OC所以OC的最大值为OE+CE即OC的最大值=AB=5考点：勾股定理的逆定理初中数学【每日一题】（第9期）精诚所至，金石为开！著名画家达芬奇不仅画艺超群，同时还是一个数学家、发明家•他曾经设计过一种圆规如图所示，有两个互相垂直的滑槽（滑槽宽度忽略不计），一根没有弹性的木棒的两端A、B 能在滑槽内自由滑动，将笔插入位于木棒中点P处的小孔中，随着木棒的滑动就可以画出一个圆来•若AB=20cm则画出的圆的半径为_______________________ cm试题解析：连接OP•••△ AOB是直角三角形，P为斜边AB的中点,丄••• OP^ AB■/ AB=20cmOP=i0cm考点：直角三角形斜边上的中线.初中数学【每日一题】（第10期）最可怕的是比你优秀的人还比你努力！如图，在△ ABC中，AB=AC点E为BC边上一动点（不与点B、C重合），过点E 作射线EF交AC于点F,使/ AEF=/ B.£C-(1)判断/ BAE与/ CEF的大小关系，并说明理由；(2)请你探索：当△ AEF为直角三角形时，求/ AEF与/ BAE的数量关系.【解析】(1)/ BAE/ FEC理由如下：•••/ B+/ BAE/ AEC / AEF=/ B，•••/ BAE/ FEC(2)如图1,当/AFE=90 时，•••/ B+/ BAE/ AEF/ CEF/ B=/ AEF=/ C,•••/ BAE/ CEF•••/ C+/ CEF=90，•••/ BAE/ AEF=90，即/ AEF与/ BAE的数量关系是互余；如图2，当/ EAF=90时，•••/ B+/ BAE/ AEF/ 1，/ B=/ AEF=/ C,•••/ BAE/ 1，vZ C+Z 1+Z AEF=90 ,••• 2Z AEF+Z 1=90°,即2Z AEF与Z BAE的数量关系是互余.A【点评】此题考查了等腰三角形的性质以及外角的性质，此题难度适中，注意掌握分类讨论思想的应用.初中数学【每日一题】（第11期）耐心是一切聪明才智的基础！如图，△ ABC的三边AB BC CA长分别是20、30、40,其三条角平分线将△ ABC分成三个三角形，则*心：*曲：鼻「削）等于试题分析：由角平分线的性质可得，点O到三角形三边的距离相等，即三个三角形的AB BC CA的高相等，禾I」用面积公式即可求解.过点O作ODL AC于D, OELAB于E，OF L BC于F，v O是三角形三条角平分线的交点，二OD=OE=OF v AB=20 BC=30 AC=4Q .•声^： $皿：'s =2: 3: 4. 故答案为：2：3：4.考点：角平分线的性质；三角形的面积.初中数学【每日一题】（第12期）如图，已知/ AOB=60，点P在0A上，OP=8点M N在边0B上，PM=PN若MN=2 贝U 0M=________________ .解：过P作PCL MN•/ PM=PN••• C为MN中点.WC = SC = = I°■在Rt△ OPC中，/ AOB=60，•••/ OPC=30，• 2OC=OP=，OC=4初中数学【每日一题】（第13期）能坚持别人不能坚持的,才能拥有别人不能拥有的如图，Rt△ ABC中，/ ACB=90 , CD是斜边AB上的高，角平分线AE交CD于H, EF丄AB于F,下列结论：①/ ACD M B;②CH=CE=EF③AC=AF④ CH=HD其中正确的结论为（）A.①②④B.①②③C.②③D.①③•••/ B和/ ACD都是/ CAB的余角，•••/ ACD M B,故①正确;v CDL AB, EF丄AB••• EF// CD，•••/ AEF=/ CHE•••/ CEH/ CHE••• CH=CE=EF故②正确；v角平分线AE交CD于H,•••/ CAE/ BAE•••△ ACE^A AFE（AAS ,••• AC=AF故③正确；CH=CE=E^HD故④错误.故：正确答案选B初中数学【每日一题】（第14期）如图，在△ ABC中, AC=BC / C=90 , D是AB的中点，DEI DF,点E, F 分别如图，连接CDv BC=AC / BCA=90•••△ ABC是等腰直角三角形v D为AB中点• BD=CD=AD CD平分/ BCA CDL AB•••/ A+Z ACD=/ ACD+Z FCD=90•••/ A=Z FCDvZ CDF Z CDE=90 Z CDE Z ADE=90•Z ADE玄CDF在厶ADE和厶CFD中vZ A=Z FCD AD=CD Z ADE Z CDF•△ADE^A CFD( ASA初中数学【每日一题】（第15期）耐心和恒心总会得到报酬的。