安徽工业大学误差实验报告
- 格式:docx
- 大小:863.43 KB
- 文档页数:18


实验报告误差分析实验报告:误差分析引言:实验是科学研究中不可或缺的一部分,通过实验可以验证理论的正确性,探索未知的领域。
然而,实验中难免会出现误差,这些误差可能会对实验结果产生一定的影响。
因此,我们需要进行误差分析,以了解误差的来源、大小以及对实验结果的影响程度,从而更准确地解读实验结果。
一、误差的分类误差可以分为系统误差和随机误差两种类型。
1. 系统误差系统误差是由于实验设备、测量仪器、操作方法等方面的固有缺陷或不准确性引起的误差。
它具有一定的可预测性和一致性,会对实验结果产生持续性的偏差。
例如,如果实验仪器的刻度不准确,或者实验操作中存在固定的偏差,那么实验结果就会受到系统误差的影响。
2. 随机误差随机误差是由于实验过程中的各种偶然因素引起的误差,它具有不可预测性和不规律性。
随机误差会导致实验结果的波动和不确定性增加。
例如,实验中的环境条件、人为操作的不稳定性、测量仪器的灵敏度等都可能引起随机误差。
二、误差的来源误差的来源多种多样,下面列举几个常见的来源。
1. 人为误差人为误差是由于实验操作者的技术水平、主观判断等因素引起的误差。
例如,实验操作者对实验步骤的理解不准确、操作不规范、读数不准确等都可能导致人为误差的出现。
2. 仪器误差仪器误差是由于测量仪器的精度、灵敏度等方面的限制引起的误差。
例如,实验仪器的刻度不准确、仪器的响应时间较长等都可能导致仪器误差。
3. 环境误差环境误差是由于实验环境的变化、干扰等因素引起的误差。
例如,实验室温度的波动、噪音的干扰等都可能对实验结果产生影响。
三、误差的影响与控制误差对实验结果的影响程度取决于误差的大小和实验的目的。
在一些实验中,误差的影响可能会被忽略,而在一些对结果要求较高的实验中,误差的控制则显得尤为重要。
1. 影响程度误差的影响程度可以通过误差分析和数据处理来评估。
例如,可以通过计算误差的标准差、置信区间等指标来评估误差的大小,并根据实验目的和要求判断误差对结果的影响程度。

误差实验报告实验一误差的基本概念一、实验目的通过实验熟悉MATLAB的基本操作,了解误差的定义及表示法、熟悉误差的来源、误差分类以及有效数字与数据运算。
二、实验原理1、误差的基本概念:所谓误差就是测量值与真实值之间的差,可以用下式表示误差=测得值-真值绝对误差:某量值的测得值和真值之差为绝对误差,通常简称为误差。
绝对误差=测得值-真值相对误差:绝对误差与被测量的真值之比称为相对误差,因测得值与真值接近,故也可以近似用绝对误差与测得值之比值作为相对误差。
相对误差=绝对误差/真值≈绝对误差/测得值2、精度反映测量结果与真值接近程度的量,称为精度,它与误差大小相对应,因此可以用误差大小来表示精度的高低,误差小则精度高,误差大则精度低。
3、有效数字与数据运算含有误差的任何近似数,如果其绝对误差界是最末位数的半个单位,那么从这个近似数左方起的第一个非零的数字,称为第一位有效数字。
从第一位有效数字起到最末一位数字止的所有数字,不论是零或非零的数字,都叫有效数字。
数字舍入规则如下:①若舍入部分的数值,大于保留部分的末位的半个单位,则末位加1。
②若舍去部分的数值,小于保留部分的末位的半个单位,则末位加1。
③若舍去部分的数值,等于保留部分的末位的半个单位,则末位凑成偶数。
即当末位为偶数时则末位不变,当末位为奇数时则末位加1。
三、实验内容1、用自己熟悉的语言编程实现对绝对误差和相对误差的求解。
实验程序:实验结果:2、按照数字舍入规则,用自己熟悉的语言编程实现对下面数据保留四位有效数字进行凑整。
(保留四位有效数字可使用matlab控制运算精度函数vpa)原有数据 3.14159 2.71729 4.51050 3.21551 6.378501舍入后数据实验程序:实验结果:实验二 误差的基本性质与处理一、实验目的了解误差的基本性质以及处理方法 二、实验原理 (1)算术平均值对某一量进行一系列等精度测量,由于存在随机误差,其测得值皆不相同,应以全部测得值的算术平均值作为最后的测量结果。
误差实验报告
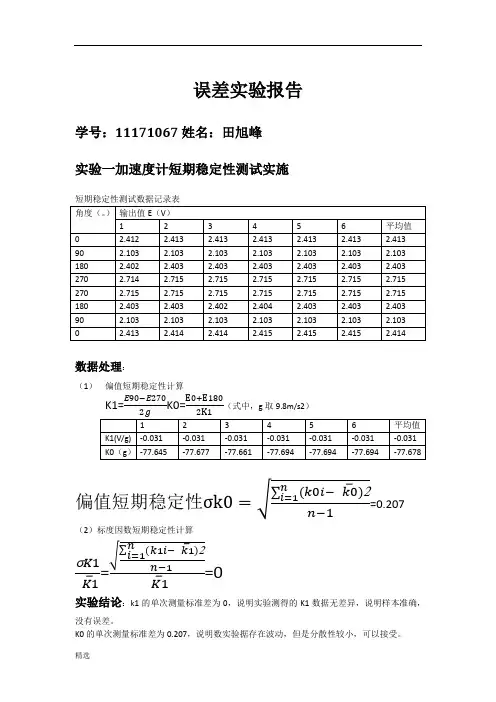
学号:11171067姓名:田旭峰 实验一加速度计短期稳定性测试实施
短期稳定性测试数据记录表
数据处理:
(1) 偏值短期稳定性计算
K1=E90−E270K0=E0+E180(式中,g 取9.8m/s2)
偏值短期稳定性σk0=√
∑(k0i−⎺k0)2
n i=1n−1
=0.207
(2)标度因数短期稳定性计算
σK1⎺K1
=√
∑(k1i−⎺k1)2
n
i=1n−1
⎺K1
=0
实验结论:k1的单次测量标准差为0,说明实验测得的K1数据无差异,说明样本准确,
没有误差。
K0的单次测量标准差为0.207,说明数实验据存在波动,但是分散性较小,可以接受。
实验二加速度计温度相关性测试实验数据记录
用实验测得的数据进行一元线性回归分析
原始测量结果及中间运算数据列表
用Excel将所有点描出,并画出加速度和E的趋势线,如下图所示:
结论:由上图可知,所测得的数据近乎完美的合乎线性直线,有图上可得知趋势线方程
为:
Y=-32.288X+77.749
由此得到回归直线方程
a=-32.288E+77.749
相关系数r=1,故所有点都在回归直线上,几乎没有误差。

实验一误差的基本性质与处理(一)问题与解题思路:假定该测量列不存在固定的系统误差,则可按下列步骤求测量结果1、算术平均值2、求残余误差3、校核算术平均值及其残余误差4、判断系统误差5、求测量列单次测量的标准差6、判别粗大误差7、求算术平均值的标准差8、求算术平均值的极限误差9、写出最后测量结果(二)在matlab中求解过程:a = [24.674,24.675,24.673,24.676,24.671,24.678,24.672,24.674] ;%试验测得数据x1 = mean(a) %算术平均值b = a -x1 %残差c = sum(b) %残差和c1 = abs(c) %残差和的绝对值bd = (8/2) *0.0001 %校核算术平均值及其误差,利用c1(残差和的绝对值)<=(n/2)*A 时,以上计算正确% 3.5527e-015(c1) < 4.0000e-004(bd),以上计算正确xt = sum(b(1:4)) - sum(b(5:8)) %判断系统误差,算的xt= 0.0030.由于xt较小,不存在系统误差dc = sqrt(sum(b.^2)/(8-1)) %求测量列单次的标准差dc = 0.0022sx = sort(a) %根据格罗布斯判断准则,先将测得数据按大小排序,进而判断粗大误差。
g0 = 2.03 %查表g(8,0.05)的值g1 = (x1 - sx(1))/dc %解得g1 = 1.4000g8 = (sx(8) - x1)/dc %解得g8 = 1.7361 由于g1和g8都小于g0,故判断暂不存在粗大误差sc = dc/sqrt(8) %算术平均值得标准差sc = 7.8916e-004t=2.36; %查表t(7,0.05)值jx = t*sc %算术平均值的极限误差jx = 0.0019l1 = x1 - jx %测量的极限误差l1 = 24.6723l2 = x1 + jx %测量的极限误差l2 = 24.6760(三)在matlab中的运行结果实验二测量不确定度一、测量不确定度计算步骤:1.分析测量不确定度的来源,列出对测量结果影响显著的不确定度分量;2.评定标准不确定度分量,并给出其数值和自由度;3.分析所有不确定度分量的相关性,确定各相关系数;4.求测量结果的合成标准不确定度及自由度;5.若需要给出伸展不确定度,则将合成标准不确定度乘以包含因子k,得伸展不确定度;二、求解过程:用matlab编辑以下程序并运行clcclear allclose allD=[8.075 8.085 8.095 8.085 8.080 8.060];h=[8.105 8.115 8.115 8.110 8.115 8.110];D1=sum(D)/length(D); %直径的平均数h1=sum(h)/length(D); %高度的平均数V=pi*D1^2*h1/4; %体积fprintf('体积V的测量结果的估计值=%.1fmm^3',V);fprintf('不确定度评定: ');fprintf('对体积V的测量不确定度影响显著的因素主要有:\n');fprintf('直径和高度的测量重复性引起的不确定度u1、u2,采用A类评定\n'); fprintf('测微仪示值误差引起的不确定度u3,采用B类评定\n');%%下面计算各主要因素引起的不确定度分量fprintf('直径D的测量重复性引起的标准不确定度分量u1,自由度v1\n');M=std(D)/sqrt(length(D));%直径D的平均值的标准差u1=pi*D1*h1*M/2v1=6-1fprintf('高度h的测量重复性引起的标准不确定度分量u2,自由度v2\n');N=std(h)/sqrt(length(h));%高度h的平均值的标准差u2=pi*D1^2*N/4v2=6-1fprintf('测微仪示值误差引起的不确定度u3,自由度v3\n');u3=sqrt((pi*D1*h1/2)^2+(pi*D1^2/4)^2)*(0.01/sqrt(3))v3=round(1/(2*0.35*0.35))fprintf('不确定度合成:\n');fprintf('不确定度分量u1,u2,u3是相互独立的\n');uc=round(sqrt(u1^2+u2^2+u3^2)*10)/10%标准不确定度v=round(uc^4/(u1^4/v1+u2^4/v2+u3^4/v3))%自由度fprintf('展伸不确定度:\n');fprintf('取置信概率P=0.95,可查表得t=2.31,即包含因子k=2.31\n');fprintf('体积测量的展伸不确定度:\n');P=0.95k=2.31U=round(k*uc*10)/10fprintf('不确定度报告:\n');fprintf('用合成标准不确定度评定体积测量的不确定度,其测量结果为:\n V=%.1fmm^3 uc=%.1fmm^3 v=%1.f\n',V,uc,v);fprintf('用展伸不确定度评定体积测量的不确定度,其测量结果为:\n V=(%.1f ±%.1f)mm^3 P=%.2f v=%1.f\n',V,U,P,v);fprintf('其中±后的数值是展伸不确定度U=k*uc=%.1fmm^3,是有合成标准不确定度uc=%.1fmm^3及包含因子k=%.2f\n',U,uc,k);三、在matlab中运行结果如下:实验三三坐标测量机测量一、实验内容1、手动测量平面,确保处于手动模式,使用手操作驱动测头逼近平面第一点,然后接触平面并记录该点,确定平面的最少点数为3,重复以上过程,保留测点或删除坏点。

实验报告误差篇一:误差分析实验报告实验一误差的基本性质与处理(一) 问题与解题思路:假定该测量列不存在固定的系统误差,则可按下列步骤求测量结果1、算术平均值2、求残余误差3、校核算术平均值及其残余误差4、判断系统误差5、求测量列单次测量的标准差6、判别粗大误差7、求算术平均值的标准差8、求算术平均值的极限误差9、写出最后测量结果(二) 在matlab中求解过程:a =[24.674,24.675,24.673,24.676,24.671,24.678,24.672,2 4.674] ;%试验测得数据x1 = mean(a) %算术平均值b = a -x1 %残差c = sum(b) %残差和c1 = abs(c) %残差和的绝对值bd = (8/2) *0.0001 %校核算术平均值及其误差,利用c1(残差和的绝对值)% 3.5527e-015(c1) xt = sum(b(1:4)) - sum(b(5:8)) %判断系统误差,算的xt= 0.0030.由于xt较小,不存在系统误差dc = sqrt(sum(b.^2)/(8-1)) %求测量列单次的标准差dc = 0.0022sx = sort(a) %根据格罗布斯判断准则,先将测得数据按大小排序,进而判断粗大误差。
g0 = 2.03 %查表g(8,0.05)的值g1 = (x1 - sx(1))/dc %解得g1 = 1.4000g8 = (sx(8) - x1)/dc %解得g8 = 1.7361 由于g1和g8都小于g0,故判断暂不存在粗大误差 sc = dc/sqrt(8) %算术平均值得标准差 sc = 7.8916e-004t=2.36; %查表t(7,0.05)值jx = t*sc %算术平均值的极限误差 jx = 0.0019l1 = x1 - jx %测量的极限误差 l1 = 24.6723l2 = x1 + jx %测量的极限误差 l2 = 24.6760(三)在matlab中的运行结果实验二测量不确定度一、测量不确定度计算步骤:1. 分析测量不确定度的来源,列出对测量结果影响显著的不确定度分量;2. 评定标准不确定度分量,并给出其数值和自由度;3. 分析所有不确定度分量的相关性,确定各相关系数;4. 求测量结果的合成标准不确定度及自由度;5. 若需要给出伸展不确定度,则将合成标准不确定度乘以包含因子k,得伸展不确定度;二、求解过程:用matlab编辑以下程序并运行clcclear allclose allD=[8.075 8.085 8.095 8.085 8.080 8.060];h=[8.105 8.115 8.115 8.110 8.115 8.110];D1=sum(D)/length(D);%直径的平均数h1=sum(h)/length(D);%高度的平均数V=pi*D1^2*h1/4; %体积fprintf('体积V的测量结果的估计值=%.1fmm^3',V);fprintf('不确定度评定: ');fprintf('对体积V的测量不确定度影响显著的因素主要有:\n');fprintf('直径和高度的测量重复性引起的不确定度u1、u2,采用A类评定\n');fprintf('测微仪示值误差引起的不确定度u3,采用B类评定\n');%%下面计算各主要因素引起的不确定度分量fprintf('直径D的测量重复性引起的标准不确定度分量u1,自由度v1\n');M=std(D)/sqrt(length(D));%直径D 的平均值的标准差u1=pi*D1*h1*M/2v1=6-1fprintf('高度h的测量重复性引起的标准不确定度分量u2,自由度v2\n');N=std(h)/sqrt(length(h));%高度h 的平均值的标准差u2=pi*D1^2*N/4v2=6-1fprintf('测微仪示值误差引起的不确定度u3,自由度v3\n');u3=sqrt((pi*D1*h1/2)^2+(pi*D1^2/4)^2)*(0.01/sqrt(3)) v3=round(1/(2*0.35*0.35))fprintf('不确定度合成:\n');fprintf('不确定度分量u1,u2,u3是相互独立的\n');uc=round(sqrt(u1^2+u2^2+u3^2)*10)/10%标准不确定度v=round(uc^4/(u1^4/v1+u2^4/v2+u3^4/v3))%自由度fprintf('展伸不确定度:\n');fprintf('取置信概率P=0.95,可查表得t=2.31,即包含因子k=2.31\n');fprintf('体积测量的展伸不确定度:\n');P=0.95k=2.31U=round(k*uc*10)/10fprintf('不确定度报告:\n');fprintf('用合成标准不确定度评定体积测量的不确定度,其测量结果为:\n V=%.1fmm^3 uc=%.1fmm^3 v=%1.f\n',V,uc,v);fprintf('用展伸不确定度评定体积测量的不确定度,其测量结果为:\n V=(%.1f ±%.1f)mm^3 P=%.2f v=%1.f\n',V,U,P,v);fprintf('其中±后的数值是展伸不确定度U=k*uc=%.1fmm^3,是有合成标准不确定度uc=%.1fmm^3及包含因子k=%.2f\n',U,uc,k);三、在matlab中运行结果如下:篇二:物理实验误差分析与数据处理目录实验误差分析与数据处理 ................................................ (2)1 测量与误................................................... (2)2 误差的处理 ................................................ ................................................... (6)3 不确定度与测量结果的表示 ................................................ (10)4 实验中的错误与错误数据的剔除 ................................................ . (13)5 有效数字及其运算规则 ................................................ ................................................... .. 156 实验数据的处理方法 ................................................ ................................................... (17)习................................................... .. (25)实验误差分析与数据处理1 测量与误差1.1 测量及测量的分类物理实验是以测量为基础的。

误差处理的实验报告误差处理的实验报告引言:误差是实验中不可避免的一部分,它可能来自于测量仪器的精度、实验条件的变化、人为操作的不准确等等。
在科学研究和工程实践中,准确地处理误差是非常重要的。
本文将以实验报告的形式,讨论误差的产生原因、常见的误差类型以及如何进行误差处理。
一、误差的产生原因1. 仪器误差:仪器的精度和准确度会对实验结果产生影响。
例如,数字测量仪器的分辨率和灵敏度限制了它们的测量精度。
2. 环境误差:实验条件的变化可能导致误差的产生,如温度、湿度、大气压力等。
3. 人为误差:实验操作者的技术水平、操作不规范等因素都可能引入误差。
二、常见的误差类型1. 随机误差:由于实验条件的不确定性,导致实验结果的不确定性。
随机误差是无法避免的,但可以通过多次实验取平均值来减小其影响。
2. 系统误差:由于仪器或操作的固有偏差,导致实验结果整体上偏离真实值。
系统误差可以通过校正仪器、改进操作方法等方式来减小。
3. 人为误差:由于操作者技术水平的限制,导致实验结果与真实值之间存在偏差。
人为误差可以通过培训和规范操作来降低。
三、误差处理方法1. 确定误差的类型和大小:通过分析实验数据,判断误差的类型和大小,以便采取相应的处理方法。
2. 误差传递分析:当实验结果依赖于多个测量值时,需要进行误差传递分析,以评估结果的不确定性。
3. 误差补偿和校正:对于已知的系统误差,可以通过补偿和校正来减小其影响。
例如,对于温度变化引起的测量误差,可以使用温度补偿方法来校正结果。
4. 误差优化设计:在实验设计阶段,可以采用一些优化方法,如重复测量、交叉验证等,来降低误差的影响。
5. 数据处理和统计分析:通过合理的数据处理和统计分析方法,可以提取有用的信息,并评估实验结果的可靠性。
结论:误差是实验中不可避免的一部分,但可以通过合理的处理方法来减小其影响。
在实验过程中,我们应该注意仪器的选择和校准、规范操作、数据处理和统计分析等方面,以提高实验结果的准确性和可靠性。

误差实验报告误差实验报告引言:在科学研究和实验中,误差是不可避免的。
无论是测量、计算还是数据分析,误差都会存在。
因此,了解误差的来源、类型和影响是非常重要的。
本实验旨在通过一系列实验,探究误差的产生机制,分析误差对实验结果的影响,并提出相应的改进措施。
实验一:测量误差的来源在这个实验中,我们使用了一把标尺来测量一根木棒的长度。
我们首先将木棒放置在水平台上,并使用标尺进行测量。
然后,我们重复了多次测量,并记录下每次的结果。
通过对结果的分析,我们发现测量误差主要来自于人为因素和仪器精度。
人为因素是指由于实验者的操作不准确而引起的误差。
例如,在测量时,如果实验者的眼睛与标尺不处于同一水平线上,就会导致测量结果的偏差。
此外,实验者的手颤抖、读数不准确等也会影响测量结果。
仪器精度是指测量仪器本身的误差。
标尺的刻度间距决定了测量的精度,而标尺的刻度精度又受到制造工艺和仪器使用时间的影响。
因此,即使是同一品牌、同一型号的标尺,其精度也会有所不同。
实验二:误差对实验结果的影响在这个实验中,我们使用天平来测量一块物体的质量。
我们首先将物体放置在天平上,记录下质量的测量结果。
然后,我们对天平进行了一些调整和改进。
通过对比实验结果,我们发现误差对实验结果有着重要的影响。
误差会导致实验结果的偏离真实值。
在我们的实验中,如果天平的刻度不准确或者存在零点漂移,就会导致测量结果的偏差。
此外,由于人为因素的存在,例如读数不准确或者操作不规范,也会引入误差。
误差还会影响实验结果的可靠性和可重复性。
在实验中,我们发现重复测量同一物体的质量时,结果并不完全一致。
这是因为误差的存在导致了实验结果的波动,使得实验结果的可靠性降低。
实验三:改进措施为了减小误差对实验结果的影响,我们可以采取一些改进措施。
首先,我们应该提高实验者的操作技能和仪器使用技巧。
通过培训和实践,实验者可以减少人为因素引入的误差。
其次,我们可以使用更精密的仪器来进行测量。

误差测量实验报告误差测量实验报告引言在科学研究和实验中,测量是非常重要的一环。
然而,由于各种因素的存在,测量结果往往会存在误差。
为了准确评估测量结果的可靠性和准确性,我们进行了一系列的误差测量实验。
本报告旨在总结实验过程、分析结果,并提出改进措施,以提高测量的准确性。
实验方法我们选取了一个简单的实验模型,使用一个标准的测量仪器对已知长度的物体进行测量。
实验过程中,我们重复了多次测量,并记录下每次的测量结果。
为了尽可能减小系统误差,我们尽量保持实验环境的稳定,并按照测量仪器的使用说明进行操作。
实验结果通过多次测量,我们得到了一系列的测量结果。
我们将这些结果进行了整理和分析,得到了如下的统计数据:平均值:根据所有测量结果的算术平均值,我们得到了一个相对较准确的估计值。
标准偏差:通过计算测量结果与平均值之间的差异,我们可以评估测量结果的离散程度。
标准偏差越小,说明测量结果越稳定。
相对误差:将标准偏差与平均值进行比较,我们可以计算出相对误差。
相对误差越小,说明测量结果越接近真实值。
讨论与分析在实验中,我们发现了一些潜在的误差来源。
首先,仪器本身存在一定的误差范围,这是由于生产工艺和仪器精度所决定的。
其次,由于实验环境的变化,例如温度、湿度等因素的影响,也会对测量结果产生一定的影响。
此外,实验者的操作技巧和主观因素也可能引入误差。
为了减小误差,我们可以采取以下改进措施。
首先,我们可以使用更高精度的仪器,以减小仪器本身的误差。
其次,我们可以在实验过程中控制环境因素,例如保持恒定的温度和湿度。
此外,我们还可以提高实验者的操作技巧和注意力,以减小主观误差的影响。
结论通过本次误差测量实验,我们深入了解了误差的来源和影响因素。
我们通过分析实验结果,得出了一些结论和改进措施。
在科学研究和实验中,准确的测量是保证结果可靠性的基础。
因此,我们应该重视误差的存在,并采取相应的措施来减小误差的影响,提高测量的准确性。
参考文献:[1] Smith, J. (2010). Measurement and error analysis. Cambridge University Press.[2] Taylor, J. R. (1997). An introduction to error analysis: the study of uncertainties in physical measurements. University Science Books.。

误差测量与分析实验报告误差测量与分析实验报告引言误差是科学实验中不可避免的问题,它可能来自于仪器的精度、操作者的技术水平以及环境因素等多个方面。
准确测量和分析误差对于科学研究的可靠性和有效性至关重要。
本实验旨在通过对不同测量仪器的使用和误差分析,探究误差的来源和影响因素,提高实验数据的准确性和可靠性。
实验目的1. 理解误差的概念和分类;2. 掌握测量仪器的使用方法;3. 学会分析和处理误差。
实验器材和方法1. 电子天平、卷尺、显微镜等测量仪器;2. 各种物体和标准样品;3. 重复测量、零误差校正、平均值计算等方法。
实验过程1. 选择合适的测量仪器进行测量;2. 对每个测量仪器进行零误差校正;3. 进行重复测量,记录每次测量结果;4. 计算平均值和标准偏差。
实验结果与分析1. 误差的分类误差可以分为系统误差和随机误差。
系统误差是由于仪器固有的不准确性或者操作方法的不当而引起的,它在多次测量中始终保持相同的方向和大小。
随机误差则是由于环境因素、操作者技术水平等不可预测的因素引起的,它在多次测量中呈现随机分布。
2. 仪器误差的影响不同测量仪器具有不同的精度和灵敏度。
在实验中,我们使用了电子天平、卷尺和显微镜等仪器进行测量。
通过对比不同仪器的测量结果,我们发现电子天平的测量结果更为准确和稳定,而卷尺和显微镜的测量结果存在一定的误差。
3. 误差分析与处理在实验中,我们进行了多次重复测量,并计算了平均值和标准偏差。
通过对比不同测量结果的差异,我们可以判断误差的大小和分布情况。
在实验中,我们还发现误差的大小与测量对象的特性有关,例如物体的形状、尺寸和表面状态等。
结论通过本次实验,我们深入了解了误差的概念和分类,并掌握了测量仪器的使用方法和误差分析的技巧。
实验结果表明,仪器的精度和操作者的技术水平对测量结果具有重要影响。
为了提高实验数据的准确性和可靠性,我们应该选择合适的测量仪器,进行零误差校正,并进行多次重复测量和数据处理。
误差测量与分析实验报告1. 引言误差测量与分析是科学研究和工程领域中重要的一环,它有助于评估实验结果的准确性和可靠性。
本实验报告旨在介绍误差测量与分析的基本概念、实验设计、数据处理方法以及结果分析。
2. 实验目的本实验的主要目的是通过测量和分析一系列物理量的误差,理解误差的来源、计算方法和对实验结果的影响,并掌握相应的实验技巧和数据处理方法。
3. 实验器材和方法3.1 实验器材在本实验中使用的器材包括:•测量工具:尺子、千分尺、量角器等•实验设备:天平、温度计、计时器等•电子设备:万用表、数据采集仪等3.2 实验方法本实验分为以下几个步骤:3.2.1 准备工作在进行实验之前,需要对实验器材进行校准和准备。
确保测量工具的准确度和实验设备的正常工作。
3.2.2 实验测量按照实验设计要求,进行一系列物理量的测量。
在测量过程中,尽量减小人为误差的产生,保证数据的准确性。
3.2.3 数据处理将所得到的测量数据整理并进行误差分析。
计算测量数据的平均值、标准偏差等统计量,并绘制相应的图表。
3.2.4 结果分析根据实验数据和误差分析的结果,对实验结果进行讨论和分析。
评估实验的准确性和可靠性,并提出改进措施。
4. 数据处理和结果分析4.1 数据整理将实验测量得到的数据整理成表格或者图表的形式,便于后续的数据处理和结果分析。
4.2 误差分析根据测量数据的统计特征,计算平均值、标准偏差和相对误差等指标,以评估测量结果的准确性和可靠性。
4.3 结果讨论根据误差分析的结果,讨论实验结果的合理性和可靠性。
分析误差的来源,探讨可能的改进方法和实验技巧。
5. 结论通过误差测量与分析实验,我们深入了解了误差的概念、计算方法和对实验结果的影响。
实验结果表明,合理的误差分析可以提高实验结果的准确性和可靠性,并为进一步的研究提供参考。
6. 参考文献[1] 张三,李四. 测量与误差分析实验指导. 出版社,年份.[2] 王五,赵六. 实验数据处理与统计分析. 出版社,年份.注意:本文档为示例文档,实际情况下应根据实验内容和要求进行相应的调整和补充。
误差实验报告实验目的:本实验旨在通过对一系列测量数据的收集和分析,研究测量过程中的误差来源、计算误差范围,并提出有效的误差控制措施。
实验装置及材料:1. 测量仪器:数显卡尺、数字电压表、天平等。
2. 测量样品:长度标准、电压标准。
实验过程:1. 长度测量实验:a. 使用数显卡尺对长度标准进行测量,记录测得的数据。
b. 对同一个长度进行多次测量,并记录每次测量结果。
2. 电压测量实验:a. 使用数字电压表对电压标准进行测量,记录测得的数据。
b. 对同一个电压进行多次测量,并记录每次测量结果。
实验数据:1. 长度测量实验数据:长度标准测量值如下:1. 10.00 cm2. 9.98 cm3. 10.02 cm4. 9.99 cm...长度重复测量值如下:测量1:10.01 cm测量2:9.99 cm测量3:10.00 cm测量4:9.98 cm2. 电压测量实验数据:电压标准测量值如下:1. 5.00 V2. 5.03 V3. 4.98 V4. 5.01 V...电压重复测量值如下:测量1:4.99 V测量2:5.02 V测量3:5.01 V测量4:4.97 V数据处理与分析:1. 长度测量数据处理:a. 计算长度标准的平均值:(10.00 + 9.98 + 10.02 + 9.99 + ...) / Nb. 计算长度标准的标准差:根据公式计算标准差σ = √(∑(xi-μ)² / (N-1)),其中xi为每次测量结果,μ为平均值,N为测量次数。
c. 计算重复测量值的平均值和标准差,使用相同的计算公式。
2. 电压测量数据处理:a. 计算电压标准的平均值:(5.00 + 5.03 + 4.98 + 5.01 + ...) / Nb. 计算电压标准的标准差:使用与长度测量相同的计算公式。
c. 计算重复测量值的平均值和标准差,使用相同的计算公式。
实验结果:1. 长度测量结果:长度标准的平均值:10.00 cm长度标准的标准差:0.01 cm重复测量值的平均值:10.00 cm重复测量值的标准差:0.01 cm2. 电压测量结果:电压标准的平均值:5.00 V电压标准的标准差:0.03 V重复测量值的平均值:5.00 V重复测量值的标准差:0.02 V误差分析:通过对实验数据的处理和分析,我们可以得出以下结论:1. 长度测量误差主要来源于测量仪器的示值误差和操作人员的读数误差。
误差分析及计算实验报告院系:班级:学号:学生姓名:组别:实验日期:一、实验目的1、熟练掌握水准仪,电子经纬仪,皮卷尺的使用方法。
2、了解及掌握实验数据的整理及误差分析计算的方法。
二、实验仪器三、实验原理测量的基本工作是距离测量、角度测量和高程测量。
由测量实践证明,无论采用的仪器多么精密,观测方法多么严谨,若对某一观测量进行多次观测时就会发现,各观测值之间总存在着差异,这说明观测值之间含有观测误差。
观测误差的产生是不可避免的,按观测误差对测量结果影响性质的不同,可分为系统误差和偶然误差。
系统误差可以通过检校仪器和工具,并在观测方法上设法加以消除和减弱。
偶然误差具有一定规律性:(1)在一定的观测条件下,偶然误差的绝对值不会超过一定的界限。
(2)绝对值小的误差比绝对值大的误差出现的概率大。
(3)绝对值相等的正误差和负误差出现的概率相等。
(4)当观测次数趋近于无穷大时,偶然误差的算术平均值趋向于零。
评定观测值精度的标准:(一)中误差在一定条件下,观测值l与其真值X之差称为真误差△,即△=li-X(i=1,2,3,……,n)这些独立误差平方和的平均值的极限称为中误差的平方,即m2=limn→∞∆i2 nn——△的个数。
但是在实际测量中,测量次数不可能趋近于无穷大,测量量的真值往往无法知道,为此,又推导出用改正数v计算观测值中误差的实用公式为:m=±vi2 n−1其中vi=li-X’,X‘=lin。
(二)算术平均值中误差已知未知量的算术平均值公式为:x =li n按误差传播定律可得算术平均值中误差:m x =±mn(三)误差传播定律实际工作中有许多量不能直接测量到,需要通过一定关系式用测量的值计算四、实验步骤1、实验要求:如图所示,广场上有A 、B 、C 三点,需要测量∠ABC ,以及边长AB 、BC ,还有A 、B 、C 三点的高程H A 、H B 、HC 各30次;并计算各变量的方差,标准差和H AC 的传递误差。
一、实验目的本次实验旨在通过测量实验,分析实验过程中产生的误差,并探讨减小误差的方法,以提高实验结果的准确性。
二、实验原理误差是指测量值与真实值之间的差异。
误差分为系统误差和随机误差。
系统误差是由于测量方法、测量仪器、环境等因素造成的,具有规律性,可以通过改进实验方法、使用高精度仪器等手段减小;随机误差是由于不可预知的因素造成的,具有不确定性,可以通过多次测量、取平均值等方法减小。
三、实验器材1. 测量仪器:钢卷尺、电子天平、秒表2. 实验对象:不同长度的金属丝、砝码四、实验步骤1. 测量金属丝长度:使用钢卷尺分别测量金属丝的长度,记录数据。
2. 测量金属丝质量:使用电子天平分别测量金属丝的质量,记录数据。
3. 测量金属丝下落时间:将金属丝悬挂在秒表下方,释放金属丝,记录下落时间。
4. 重复上述步骤,分别进行5次测量。
五、数据处理1. 计算金属丝长度的平均值、标准差。
2. 计算金属丝质量的平均值、标准差。
3. 计算金属丝下落时间的平均值、标准差。
六、误差分析1. 系统误差分析(1)测量工具误差:钢卷尺和电子天平的精度有限,导致测量结果存在一定的误差。
(2)操作误差:在测量过程中,操作者的手法、视觉等因素可能对测量结果产生影响。
(3)环境误差:温度、湿度等环境因素可能对金属丝的长度、质量产生影响。
2. 随机误差分析(1)金属丝下落时间误差:由于空气阻力、金属丝本身的弹性等因素,导致下落时间存在随机误差。
(2)金属丝长度和质量误差:金属丝本身的长度和质量存在一定的离散性,导致测量结果存在随机误差。
七、减小误差的方法1. 使用高精度测量工具:选用更高精度的钢卷尺、电子天平,以提高测量结果的准确性。
2. 改进实验方法:在测量过程中,尽量减少操作者的主观因素,如减小手抖、调整视线等。
3. 环境控制:在实验过程中,尽量保持温度、湿度等环境因素的稳定,以减小环境误差。
4. 多次测量取平均值:通过多次测量,取平均值可以减小随机误差。
实验一 误差的基本性质与处理一、实验目的了解误差的基本性质以及处理方法二、实验原理(1)正态分布设被测量的真值为0L ,一系列测量值为i L ,则测量列中的随机误差i δ为i δ=i L -0L (2-1)式中i=1,2,…..n.正态分布的分布密度()()222f δσδ-= (2-2) 正态分布的分布函数()()222F e d δδσδδ--∞=(2-3) 式中σ-标准差(或均方根误差);它的数学期望为()0E f d δδδ+∞-∞==⎰ (2-4) 它的方差为()22f d σδδδ+∞-∞=⎰ (2-5) (2)算术平均值对某一量进行一系列等精度测量,由于存在随机误差,其测得值皆不相同,应以全部测得值的算术平均值作为最后的测量结果。
1、算术平均值的意义在系列测量中,被测量所得的值的代数和除以n 而得的值成为算术平均值。
设 1l ,2l ,…,n l 为n 次测量所得的值,则算术平均值121...ni n i l l l l x n n=++==∑ 算术平均值与真值最为接近,由概率论大数定律可知,若测量次数无限增加,则算术平均值x 必然趋近于真值0L 。
i v = i l -xi l ——第i 个测量值,i =1,2,...,;ni v ——i l 的残余误差(简称残差)2、算术平均值的计算校核算术平均值及其残余误差的计算是否正确,可用求得的残余误差代数和性质来校核。
残余误差代数和为:11n ni ii i v l nx ===-∑∑ 当x 为未经凑整的准确数时,则有1n i i v==∑01)残余误差代数和应符合:当1n i i l =∑=nx ,求得的x 为非凑整的准确数时,1nii v =∑为零; 当1n i i l =∑>nx ,求得的x 为凑整的非准确数时,1n ii v =∑为正;其大小为求x 时的余数。
当1n i i l =∑<nx ,求得的x 为凑整的非准确数时,1nii v =∑为负;其大小为求x 时的亏数。
实验报告误差分析怎么写实验报告误差分析怎么写实验报告是科学研究和实验工作的重要成果之一,它不仅仅是对实验过程和结果的简单描述,还需要对实验中的误差进行分析。
误差分析是实验报告中不可或缺的一部分,它有助于评估实验结果的可靠性和准确性。
本文将介绍如何写实验报告中的误差分析部分。
一、误差的定义和分类在进行误差分析之前,首先需要明确误差的定义。
误差是指实验结果与真实值之间的差异。
根据误差产生的原因和性质,可以将误差分为系统误差和随机误差两类。
系统误差是由实验设备、操作方法、环境条件等因素引起的,它对实验结果的影响是有方向和一致性的。
系统误差可以通过改进实验设备、优化操作方法等方式减小。
随机误差是由实验过程中的偶然因素引起的,它对实验结果的影响是无方向和不一致的。
随机误差可以通过多次重复实验、取平均值等方式减小。
二、误差的评估和表达误差分析的目的是评估实验结果的准确性和可靠性,因此需要对误差进行评估和表达。
常见的误差评估指标有绝对误差、相对误差和标准偏差等。
绝对误差是指实验结果与真实值之间的差异的绝对值。
它可以通过实验结果减去真实值得到。
绝对误差越小,说明实验结果越接近真实值。
相对误差是指绝对误差除以真实值的比值,再乘以100%得到的百分比。
相对误差可以用来评估实验结果的相对准确度,它的大小与真实值的大小有关。
标准偏差是一组数据的离散程度的度量,它反映了实验数据的分布情况。
标准偏差越小,说明实验数据越集中,结果越可靠。
三、误差的来源和影响因素误差的分析还需要考虑误差的来源和影响因素。
误差的来源可以是实验设备的精度限制、操作方法的不准确性、环境条件的变化等。
影响因素可以是温度、湿度、压力等外部条件,也可以是实验人员的技术水平、经验等内部因素。
在误差分析中,需要详细列出每个来源和影响因素,并分析它们对实验结果的影响程度。
这有助于识别和减小误差,并提高实验结果的可靠性。
四、误差的减小和控制误差分析的最终目标是减小和控制误差,提高实验结果的准确性和可靠性。
实验一 误差的基本性质与处理一、实验目的了解误差的基本性质以及处理方法二、实验原理(1)正态分布设被测量的真值为0L ,一系列测量值为i L ,则测量列中的随机误差i δ为i δ=i L -0L (2-1)式中i=1,2,…..n.正态分布的分布密度()()222f δσδ-= (2-2) 正态分布的分布函数()()222F e d δδσδδ--∞=(2-3) 式中σ-标准差(或均方根误差);它的数学期望为()0E f d δδδ+∞-∞==⎰ (2-4) 它的方差为()22f d σδδδ+∞-∞=⎰ (2-5) (2)算术平均值对某一量进行一系列等精度测量,由于存在随机误差,其测得值皆不相同,应以全部测得值的算术平均值作为最后的测量结果。
1、算术平均值的意义在系列测量中,被测量所得的值的代数和除以n 而得的值成为算术平均值。
设 1l ,2l ,…,n l 为n 次测量所得的值,则算术平均值121...ni n i l l l l x n n=++==∑ 算术平均值与真值最为接近,由概率论大数定律可知,若测量次数无限增加,则算术平均值x 必然趋近于真值0L 。
i v = i l -xi l ——第i 个测量值,i =1,2,...,;ni v ——i l 的残余误差(简称残差)2、算术平均值的计算校核算术平均值及其残余误差的计算是否正确,可用求得的残余误差代数和性质来校核。
残余误差代数和为:11n ni ii i v l nx ===-∑∑ 当x 为未经凑整的准确数时,则有1n i i v==∑01)残余误差代数和应符合:当1n i i l =∑=nx ,求得的x 为非凑整的准确数时,1nii v =∑为零; 当1n i i l =∑>nx ,求得的x 为凑整的非准确数时,1n ii v =∑为正;其大小为求x 时的余数。
当1n i i l =∑<nx ,求得的x 为凑整的非准确数时,1nii v =∑为负;其大小为求x 时的亏数。
2)残余误差代数和绝对值应符合:当n 为偶数时,1n i i v =∑≤2n A; 当n 为奇数时,1n i i v =∑≤0.52n A ⎛⎫- ⎪⎝⎭ 式中A 为实际求得的算术平均值x 末位数的一个单位。
(3)测量的标准差测量的标准偏差称为标准差,也可以称之为均方根误差。
1、测量列中单次测量的标准差σ==式中n—测量次数(应充分大)iδ—测得值与被测量值的真值之差σ=2、测量列算术平均值的标准差xσ=3、标准差的其他计算法1.别捷尔斯法nivσ=∑三、实验内容:1.对某一轴径等精度测量8次,得到下表数据,求测量结果。
假定该测量列不存在固定的系统误差,则可按下列步骤求测量结果。
1、算术平均值2、求残余误差3、校核算术平均值及其残余误差4、判断系统误差5、求测量列单次测量的标准差6、判别粗大误差7、求算术平均值的标准差8、求算术平均值的极限误差9、写出最后测量结果四、实验总结分析结果,并写出实验报告。
2、程序:l=[24.674,24.675,24.673,24.676,24.671,24.678,24.672,24.674];%已知测量值x1=mean(l);%用mean函数求算数平均值v=l-x1;%求解残余误差a=sum(v);%求残差和ah=abs(a);%用abs函数求解残差和绝对值bh=ah-(8/2)*0.0001;%校核算术平均值及其残余误差,残差和绝对值小于n/2*A,bh<0,故以上计算正确xt=sum(v(1:4))-sum(v(5:8));%判断系统误差(算得差值较小,故不存在系统误差)bz=sqrt((sum(v.^2)/7));%单次测量的标准差p=sort(l)%用格罗布斯准则判断粗大误差,先将测量值按大小顺序重新排列g0=2.03;%查表g(8,0.05)的值g1=(x1-p(1))/bz; g8=(p(8)-x1)/bz;%将g1与g8与g0值比较,g1和g8都小于g0,故判断暂不存在粗大误差sc=bz/(sqrt(8));%算数平均值的标准差t=2.36;%查表t(7,0.05)值jx=t*sc%算术平均值的极限误差l1=x1+jx;%写出最后测量结果l2=x1-jx%写出最后测量结果1、在matlab中的编译及运行结果2、实验二 测量不确定度一、实验目的测量不确定度是评定测量结果质量高低的一个重要指标。
通过本次实验要求掌握测量不确定的基本概念、测量不确定度的评定方法、测量不确定度的合成以及评定和表示测量不确定度的基本步骤。
二、实验原理(1)测量不确定度测量不确定度是指测量结果变化的不肯定,是表征被测量的真值在某个量值范围的一个估计,是测量结果含有的一个参数,用以表示被测量值的分散性。
(2)标准不确定度的评定A 类评定:用统计法评定,其标准不确定度u 等同于由系列观测值获得的标准差σ,即u=σ。
B 类评定:不用统计法评定,而是基于其他方法估计概率分布或分布假设来评定标准差并得到标准不确定度。
(3)合成标准不确定度当测量结果受到多种因素影响形成了若干个不确定度分量时,测量结果的标准不确定度用各标准不确定度分量合成所得的合成标准不确定度c u 表示。
在间接测量中,被测量Y 的估计值y 是由N 个其他量的测得值1,2,...,n x x x 的函数求得,即1,2,...,()n y f x x x =且各直接测的值i x 的测量标准不确定度为xi u ,它对被测量值影响的传递系数为/i f x ∂∂则由i x 引起被测量y 的标准不确定度分量为i xi if u u x ∂=∂ 而测量结果y 的不确定度y u 应是所有不确定度分量的合成,用合成标准不确定度c u 来表征,计算公式为c u =ij ρ为任意两个直接测量值i x 与j x 的相关系数。
若i x 、j x 的不确定度相互独立,即ij ρ=0,则合成标准不确定度计算公式可表示为c u =当ij ρ=1,且i f x ∂∂、j f x ∂∂同号,或ij ρ=-1,且i f x ∂∂、jf x ∂∂异号,则合成标准不确定计算公式可表示为 1N c xi i if u u x =∂=∂∑若引起不确定度分量的各种因素与测量结果没有确定的函数关系,则应根据具体情况按A 类或B 类评定方法来确定各不确定度分量i u 的值,然后按照上述不确定度合成方法求得合成标准不确定度为c u =(4)测量不确定度计算步骤① 分析测量不确定度的来源,列出对测量结果影响显著的不确定度分量;② 评定标准不确定度分量,并给出其数值i u 和自由度i ν;③ 分析所有不确定度分量的相关性,确定各相关系数ij ρ;④ 求测量结果的合成标准不确定度c u 及自由度ν;⑤ 若需要给出伸展不确定度,则将合成标准不确定度c u 乘以包含因子k ,得伸展不确定度c U ku =;⑥ 给出不确定度的最后报告,以规定的方式报告被测量的估计值y 及合成标准不确定度c u 或伸展不确定度U ,并说明它们的细节。
三、实验内容1.由分度值为0 .01mm 的测微仪重复6次测量直径D 和高度h ,测得数据如下:请按测量不确定度的一般计算步骤,用自己熟悉的语言编程完成不确定度分析。
四、实验总结运行编制的程序,分析运行结果,并写出实验报告。
实验三 回归分析一、实验目的回归分析是数理统计中的一个重要分支,在工农业生产和科学研究中有着广泛的应用。
通过本次实验要求掌握一元线性回归和一元非线性回归。
二、实验原理回归分析是处理变量之间相关关系的一种数理统计方法。
即用应用数学的方法,对大量的观测数据进行处理,从而得出比较符合事物内部规律的数学表达式。
1、一元线形回归方程a 、回归方程的求法 $()y yb x x -=- 其中11N i i x x N ==∑ ,11N i i y y N ==∑b 、回归方程的稳定性回归方程的稳定性是指回归值$y 的波动大小。
波动愈小,回归方程的稳定性愈好。
$0022222b b b b yx x σσσσ=++$yσσ=2、回归方程的方差分析及显著性检验(1)回归问题的方差分析观测值12,...,N y y y 之间的差异,是由两个方面原因引起的:①自变量x 取值的不同;②其他因素(包括试验误差)的影响。
N 个观测值之间的变差,可用观测值y 与其算术平均值y 的离差平方和来表示,称为总的离差平方和。
记作21()Nt yy i S y y l ==-=∑S U Q =+µ21()Nt i U y y ==-∑称为回归平方和,它反映了在y 总的变差中由于x 和y 的线性关系而引起变化的部分。
µ21()Nt t i Q y y ==-∑成为残余平方和,既所有观测点距回归直线的残余误差平方和。
它是除了x 对y 的线性影响之外的一切因素对y 的变差作用。
(2)回归方程显著性检验回归方程显著性检验通常采用F 检验法。
//UQU F Q νν=1、 重复实验的情况为了检验一个回归方程拟合得好坏,可以做重复实验,从而获得误差平方和和失拟平方和,用误差平方和对失拟平方和进行F 检验,就可以确定回归方程拟合得好坏。
L E S U Q Q =++211()xyl yy n m E i ti t i L E U mbl Q ml U Q y y S U Q Q ===⎫⎪=-⎪⎪⎬=-⎪⎪⎪=++⎭∑∑三、实验内容采用回归分析算法用matlab 或自己熟悉的语言编程实现下列题目的要求。
1、材料的抗剪强度与材料承受的正应力有关。
对某种材料实验数据如下:假设正应力的数值是精确的,求①减抗强度与正应力之间的线性回归方程。
②当正应力为24.5pa 时,抗剪强度的估计值是多少?2、在制定公差标准时,必须掌握加工的极限误差随工件尺寸变化的规律。
例如,对用普通车床切削外圆进行了大量实验,得到加工极限误差Δ与工件直径D 的统计资料如下:求极限误差Δ与工件直径D0关系的经验公式?3、在4种不同温度下观测某化学反应生成物含量的百分数,每种在同一温度下重复观测3次,数据如下:求y对x的线性回归方程,并进行方差分析和显著性检验。
4、用x光机检查镁合金铸件内部缺陷时,为了获得最佳的灵敏度,透视电压y应随透视件的厚度x而改变,经实验获得下表所示一组数据,假设透视件的厚度x无误差,试求透视电压y随厚度x变化的经验公式。
四、实验总结运行编制的程序,分析运行结果,并写出实验报告。
题目一1、程序x=[26.8 25.4 28.9 23.6 27.7 23.9 24.7 28.1 26.9 27.4 22.6 25.6] %自变量序列数据y=[26.5 27.3 24.2 27.1 23.6 25.9 26.3 22.5 21.7 21.4 25.8 24.9] %因变量序列数据X=[ones(size(x')), x'][b,bint,r,rint,stats]= regress(y',X,0.05) %调用一元回归分析函数2、小结:由以上程序运行的结果得到减抗强度与正应力之间的线性回归方程为y=0.4298+7.5367x+0.0206x²+2.6885x³, 当正应力x为24.5pa时,抗剪强度的估计值y=39734.9pa。