下载文档原格式
手把手教你应用赤平投影（CAD图解）来庆超一、序言岩质边坡稳定性分析方法有许多，但无论是平面滑动的单一楔形断面滑体、单滑块和多滑块分析法，还是楔体滑动的仿平面分析法、楔体分割法、立体分析法、霍克分析法以及《岩土工程勘察规范》（GB50021－94）推荐法等，在计算边坡稳定性系数时，需要知道滑体控制平面（包括结构面和坡面、坡顶面）或直线（包括平面的法线）的地质产状，以及平面与平面、直线与直线、直线与平面间夹角等。
其中平面和直线的产状可以通过现场测量获取，除此之外的几何参数，在没有发明极射赤平投影之前，都是用计算法求得，不仅它们的计算公式复杂，而且计算过程繁琐，也很容易出错。
如果采用极射赤平投影求解边坡稳定性分析所需的几何参数，那就可以简化这些几何参数的计算过程，而且一般情况下只需要在现场测量出各个控制平面的地质产状即可。
二、极射赤平投影的基本原理（一）投影要素极射赤平投影（以下简称赤平投影）以圆球作为投影工具，其进行投影的各个组成部分称为投影要素，包括：1.投影球（也称投射球）：以任意长为半径的球。
2.球面：投影球的表面称为球面。
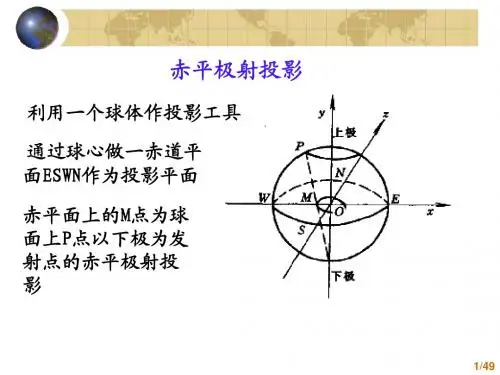
3.赤平面（也称赤平投影面）：过投影球球心的水平面。
4.大圆：通过球心的平面与球面相交而成的圆，统称为大圆（如图一（a）中ASBN、PSFN、NESW），所有大圆的直径相等，且都等于投影球的直径。
当平面直立时，与球面相交成的大圆称为直立大圆（如图一（a）中PSFN）；当平面水平时，与球面相交成的大圆称为赤平大圆或基圆（如图一（a）中NESW）；当平面倾斜时，与球面相交成的大圆称为倾斜大圆（如图一（a）中ASBN）。
5.小圆：不过球心的平面与球面相而成的圆，统称为小圆（如图一（b）、（c）中AB、CD、FG、PACB）。
当平面直立时，与球面相交成的小圆称为直立小圆（如图一（b）中DC）；当平面水平时，与球面相交成的小圆称为水平小圆（如图一（b）中AB）；当平面倾斜时，与球面相交成的小圆称为倾斜小圆（如图一（b）中FG或图一（c）中PACB）。
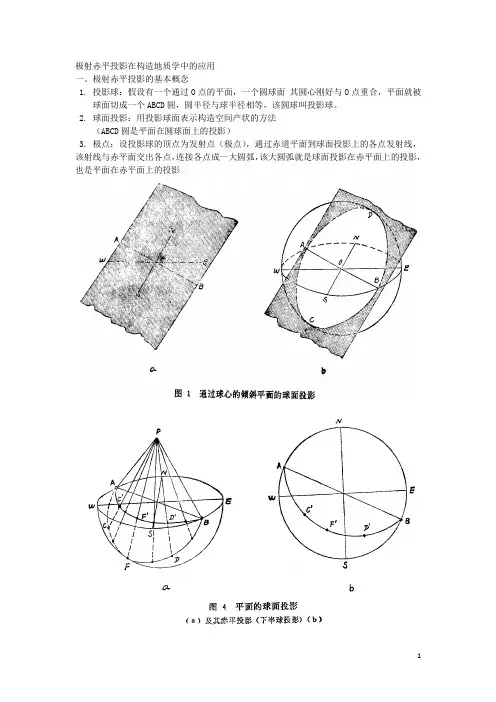
极射赤平投影在构造地质学中的应用一、极射赤平投影的基本概念1. 投影球：假设有一个通过O点的平面，一个圆球面其圆心刚好与O点重合，平面就被球面切成一个ABCD圆，圆半径与球半径相等，该圆球叫投影球。
2. 球面投影：用投影球面表示构造空间产状的方法（ABCD圆是平面在圆球面上的投影）3. 极点：设投影球的顶点为发射点（极点），通过赤道平面到球面投影上的各点发射线，该射线与赤平面交出各点，连接各点成一大圆弧，该大圆弧就是球面投影在赤平面上的投影，也是平面在赤平面上的投影4. 赤平投影：以圆球面上的一个极点为发射点，将球面投影投到赤道平面上的一种投影（下半球投影）特点：（1）可将物体在三度空间的特征表现在平面上（2）能定量表现构造的产状要素（3）不涉及构造的具体位置、大小、距离二、极射赤平投影的基本原理1. 空间上任一通过球心的平面，球面投影为一直径等于投影球直径的大圆，其赤平投影：（1）水平平面：赤平投影是赤平大圆周（2）直立平面：赤平投影是赤平大圆的一条直径，其方位就是直立平面的走向（3）倾斜平面：赤平投影为一弦等于投影球半径的大圆弧2. 空间上任一不通过球心的平面，球面投影为一直径小于投影球直径的小圆，其赤平投影：（1）水平平面：赤平投影小圆与赤平大圆同心（2）直立平面、倾斜平面均为圆心在外的小圆弧3. 空间任一条直线（过圆心）的球面投影是两个点，赤平投影：（1）直立直线：赤平投影在圆心，两点重合为一点（2）水平直线：赤平投影为两个点，在赤平大圆周上（3）倾斜直线：赤平投影为一个点三、吴氏网的成图原理1. 吴氏网的组成(1)基圆：赤平大圆，一周360°(2)经线：一系列走向SN的经向大圆弧(3)纬线：一系列走向EW的纬向小圆弧标准的吴氏网基圆直径为 20cm，网格的纵横角距为2º2. 成图原理：(1) 经向大圆弧：A. 一系列通过圆心，走向 SN，分别倾向 E、 W，倾角0º-90º的许多平面的投影大圆组成B. 这些大圆弧与EW直径的交点到直径端点的角距，是其所代表的各平面的倾角值，由圆周到圆心0º-90º(2)纬向小圆弧：A. 由一系列走向 EW ，不过圆心（只有一个过圆心）的直立的小圆投影而成B. 由圆周到圆心9º—90º(3)各经纬弧的交点：是一系列不同倾伏方向，不同倾伏角直线的赤平投影四、平面和直线的赤平投影1. 准备工作2. 平面的赤平投影3. 平面法线的赤平投影(1)法线垂直平面，交角90°(2)倾（伏）向相反，二者关系明确4. 直线的赤平投影五、褶皱要素的赤平投影轴面、枢纽的赤平投影赤平投影赤平投影英文：stereographic projection释文：把面和线投影在投影球的赤道平面上,在构造地质学中用以解决地质构造的角度和方位问题。
⼿把⼿教你应⽤⾚平投影（CAD图解）⼿把⼿教你应⽤⾚平投影（CAD图解）来庆超⼀、序⾔岩质边坡稳定性分析⽅法有许多，但⽆论是平⾯滑动的单⼀楔形断⾯滑体、单滑块和多滑块分析法，还是楔体滑动的仿平⾯分析法、楔体分割法、⽴体分析法、霍克分析法以及《岩⼟⼯程勘察规范》（GB50021－94）推荐法等，在计算边坡稳定性系数时，需要知道滑体控制平⾯（包括结构⾯和坡⾯、坡顶⾯）或直线（包括平⾯的法线）的地质产状，以及平⾯与平⾯、直线与直线、直线与平⾯间夹⾓等。
其中平⾯和直线的产状可以通过现场测量获取，除此之外的⼏何参数，在没有发明极射⾚平投影之前，都是⽤计算法求得，不仅它们的计算公式复杂，⽽且计算过程繁琐，也很容易出错。
如果采⽤极射⾚平投影求解边坡稳定性分析所需的⼏何参数，那就可以简化这些⼏何参数的计算过程，⽽且⼀般情况下只需要在现场测量出各个控制平⾯的地质产状即可。
⼆、极射⾚平投影的基本原理（⼀）投影要素极射⾚平投影（以下简称⾚平投影）以圆球作为投影⼯具，其进⾏投影的各个组成部分称为投影要素，包括：1.投影球（也称投射球）：以任意长为半径的球。
2.球⾯：投影球的表⾯称为球⾯。
3.⾚平⾯（也称⾚平投影⾯）：过投影球球⼼的⽔平⾯。
4.⼤圆：通过球⼼的平⾯与球⾯相交⽽成的圆，统称为⼤圆（如图⼀（a）中ASBN、PSFN、NESW），所有⼤圆的直径相等，且都等于投影球的直径。
当平⾯直⽴时，与球⾯相交成的⼤圆称为直⽴⼤圆（如图⼀（a）中PSFN）；当平⾯⽔平时，与球⾯相交成的⼤圆称为⾚平⼤圆或基圆（如图⼀（a）中NESW）；当平⾯倾斜时，与球⾯相交成的⼤圆称为倾斜⼤圆（如图⼀（a）中ASBN）。
5.⼩圆：不过球⼼的平⾯与球⾯相⽽成的圆，统称为⼩圆（如图⼀（b）、（c）中AB、CD、FG、PACB）。
当平⾯直⽴时，与球⾯相交成的⼩圆称为直⽴⼩圆（如图⼀（b）中DC）；当平⾯⽔平时，与球⾯相交成的⼩圆称为⽔平⼩圆（如图⼀（b）中AB）；当平⾯倾斜时，与球⾯相交成的⼩圆称为倾斜⼩圆（如图⼀（b）中FG或图⼀（c）中PACB）。
手把手教你应用赤平投影（CAＤ图解）来庆超一、序言岩质边坡稳定性分析方法有许多，但无论是平面滑动的单一楔形断面滑体、单滑块和多滑块分析法，还是楔体滑动的仿平面分析法、楔体分割法、立体分析法、霍克分析法以及《岩土工程勘察规范》（GB5002１－94)推荐法等，在计算边坡稳定性系数时,需要知道滑体控制平面（包括结构面和坡面、坡顶面)或直线（包括平面的法线）的地质产状,以及平面与平面、直线与直线、直线与平面间夹角等.其中平面和直线的产状可以通过现场测量获取,除此之外的几何参数,在没有发明极射赤平投影之前，都是用计算法求得，不仅它们的计算公式复杂,而且计算过程繁琐，也很容易出错。
如果采用极射赤平投影求解边坡稳定性分析所需的几何参数，那就可以简化这些几何参数的计算过程，而且一般情况下只需要在现场测量出各个控制平面的地质产状即可。
二、极射赤平投影的基本原理（一）投影要素极射赤平投影(以下简称赤平投影）以圆球作为投影工具，其进行投影的各个组成部分称为投影要素，包括：1。
投影球（也称投射球)：以任意长为半径的球。
２.球面:投影球的表面称为球面.３.赤平面（也称赤平投影面）：过投影球球心的水平面。
4.大圆：通过球心的平面与球面相交而成的圆,统称为大圆（如图一（a）中ＡSBN、PSFN、NESＷ)，所有大圆的直径相等,且都等于投影球的直径。
当平面直立时，与球面相交成的大圆称为直立大圆（如图一(a)中PSＦN);当平面水平时，与球面相交成的大圆称为赤平大圆或基圆（如图一(a)中NESW）;当平面倾斜时，与球面相交成的大圆称为倾斜大圆（如图一（a)中ASBN).５．小圆：不过球心的平面与球面相而成的圆，统称为小圆（如图一(b)、(c）中AＢ、CD、FＧ、PAＣＢ)。
当平面直立时,与球面相交成的小圆称为直立小圆（如图一（b)中ＤＣ）；当平面水平时,与球面相交成的小圆称为水平小圆（如图一(b）中AB)；当平面倾斜时，与球面相交成的小圆称为倾斜小圆(如图一（b）中ＦG或图一（ｃ）中PAＣＢ）。
极射赤平投影CAD图解一、序言岩质边坡稳定性分析方法有许多，但无论是平面滑动的单一楔形断面滑体、单滑块和多滑块分析法，还是楔体滑动的仿平面分析法、楔体分割法、立体分析法、霍克分析法以及《岩土工程勘察规范》（GB50021－94）推荐法等，在计算边坡稳定性系数时，需要知道滑体控制平面（包括结构面和坡面、坡顶面）或直线（包括平面的法线）的地质产状，以及平面与平面、直线与直线、直线与平面间夹角等。
其中平面和直线的产状可以通过现场测量获取，除此之外的几何参数，在没有发明极射赤平投影之前，都是用计算法求得，不仅它们的计算公式复杂，而且计算过程繁琐，也很容易出错。
如果采用极射赤平投影求解边坡稳定性分析所需的几何参数，那就可以简化这些几何参数的计算过程，而且一般情况下只需要在现场测量出各个控制平面的地质产状即可。
二、极射赤平投影的基本原理（一）投影要素极射赤平投影（以下简称赤平投影）以圆球作为投影工具，其进行投影的各个组成部分称为投影要素，包括：1.投影球（也称投射球）：以任意长为半径的球。
2.球面：投影球的表面称为球面。
3.赤平面（也称赤平投影面）：过投影球球心的水平面。
4.大圆：通过球心的平面与球面相交而成的圆，统称为大圆（如图一（a）中ASBN、PSFN、NESW），所有大圆的直径相等，且都等于投影球的直径。
当平面直立时，与球面相交成的大圆称为直立大圆（如图一（a）中PSFN）；当平面水平时，与球面相交成的大圆称为赤平大圆或基圆（如图一（a）中NESW）；当平面倾斜时，与球面相交成的大圆称为倾斜大圆（如图一（a）中ASBN）。
5.小圆：不过球心的平面与球面相而成的圆，统称为小圆（如图一（b）、（c）中AB、CD、FG、PACB）。
当平面直立时，与球面相交成的小圆称为直立小圆（如图一（b）中DC）；当平面水平时，与球面相交成的小圆称为水平小圆（如图一（b）中AB）；当平面倾斜时，与球面相交成的小圆称为倾斜小圆（如图一（b）中FG或图一（c）中PACB）。
6.极射点：投影球上两极的发射点（如图一），分上极射点（P）和下极射点（F）。
由上极射点（P）把下半球的几何要素投影到赤平面上的投影称为下半球投影；由下极射点（F）把上半球的几何要素投影到赤平面上的投影称为上半球设影。
一般采用下半球投影。
7.极点：通过球心的直线与球面的交点称为极点，一条直线有两个极点。
铅直线交球面上、下两个点（也就是极射点）；水平直线交基圆上两点；倾斜直线交球面上两点（如图五中A、B）。
（二）平面的赤平投影平面与球面相交成大圆或小圆，我们把大圆或小圆上各点和上极射点（P）的连线与赤平面相交各点连线称为相应平面的赤平投影。
1.过球心平面的赤平投影随平面的倾斜而变化：倾斜平面的赤平投影为大圆弧（如图二中的NB′S）；直立平面的赤平投影是基圆的一条直径（如图一（a）中的NS）；水平面的赤平投影就是基圆（如图一中的NESW）。
2.不过球心平面的赤平投影也随平面倾斜而变化：直立平面的赤平投影是基圆内的一条圆弧（如图三KD′H）；倾斜平面的赤平投影有以下三种情况：⑴当倾斜小圆在赤平面以下时，投影是一个圆，且全部在基圆之内（如图三FG）；⑵当倾斜小圆全部位于上半球时，投影也是一个圆，但全部在基圆之外；⑶当倾斜小圆一部分在上半球，另一部分在下半球时，赤平面以下部分的投影在基圆之内，以上部分的投影在基圆之外。
当球面小圆通过上极射点时，其赤平投影为一条直线（如图一（c）中PACB 的投影为AB）；水平小圆的赤平投影在基圆内（如图四中A′B′），A′B′是一个与基圆同心的圆。
（三）直线的赤平投影直线AB的投影点就是其极点A、B和极射点P的连线与赤平面的交点A′、B′。
铅直线的投影点位于基圆中心；过球心的水平直线的投影点就是基圆上两个极点，两点间距离等于基圆直径；倾斜直线的投影点有两个，一点在基圆内，另一个在基圆外，两点呈对蹼点，在赤平投影图上两点的角距相差180°（如图五）。
（四）吴氏网及其CAD制作目前广泛使用的极射赤平投影有等角距投影网和等面积投影网。
等角距投影网是由吴尔福发明的，简称吴氏网；等面积投影网是由施密特发明的，简称施氏网。
两者的主要区别在于：球面上大小相等的小圆在吴氏网上的投影仍然是圆，投影圆的直径角距相等，但由于在赤平面上所处位置不同，投影圆的大小不等，其直径随着投影圆圆心与基圆圆心的距离增大而增大。
而在施氏网上的投影则呈四级曲线，不成圆，但四级曲线所构成的图形面积是相等的，且等于球面小圆面积的一半。
使用吴氏网求解面、线间的角距关系时，旋转操作显示其优越性，不仅作图方便，而且较为精确。
而使用施氏网时，可以作出面、线的极点图或等密度图，能够真实反映球面上极点分布的疏密，有助于对面、线群进行统计分析，但其存在作图麻烦等缺点。
1.吴氏网的结构及成图原理吴氏网（图六）由基圆、南北经向大圆弧（NGS）、东西纬向小圆弧（ACB）等经纬线组成。
标准吴氏网的基圆直径为20cm，经、纬线间的角距为2°。
(1)基圆，由指北方向（N）为0°,顺时针方向刻出360°，这些刻度起着量度方位角的作用；(2)经向大圆弧是由一系列通过球心，走向南北，分别向西和向东倾斜，倾角由0°到90°（角距间隔为2°）的许多赤平投影大圆弧所组成。
这些大圆弧与东西直径线EW的交点到端点（E点和W 点）的距离分别代表各平面的倾角。
如图六中GW表示的大圆弧NGS所代表的平面向西倾斜，倾角为30°。
(3)纬向线是由一系列走向东西的直立平面的赤平投影小圆弧所组成。
这些小圆弧离基圆的圆心O愈远，其所代表的球面小圆的半径角距就愈小，反之离圆心O愈近，则半径角距就愈大。
相邻纬向小圆弧间的角距也是2°，它分割南北直径线的距离，与经向大圆弧分割东西径线的距离是相等的。
如图六所示，ED＝SH＝WG＝NF，角距都为30°。
2.吴氏网的CAD图解绘制吴氏网，其实质就是在赤平大圆上画出经向大圆弧和纬向小圆弧。
那么这些大圆弧和小圆弧都是怎样是绘制出来的呢？在没有CAD制图系统软件以前，人们通过平面几何关系利用圆规、直尺等原始工具绘制，其绘制过程很复杂。
而在CAD制图系统软件下，绘制大圆弧和小圆弧是非常简的，下面就介绍它们的原理和绘制过程。
(1)绘制大圆弧的原理与步骤要绘制大圆弧，应至少知道大圆弧上的三个点N、S、B′（如图二所示），其中N、S点是每条大圆弧都必须经过的，是已知点。
现在只要能确定经向大圆弧与东西径线EW的交点B′，问题就迎刃而解。
①计算OB′长度根据倾斜平面的倾角、基圆的直径，可按下式计算点O与点B′之间的距离（公式一）式中R——基圆的半径；α——大圆弧所代表平面的倾角（°）。
②以基圆的圆心为圆心，OB′长为半径画一个圆，该圆与基圆的东西径向线EW交于B′点。
③过N、S、B′三个点画一个圆，并剪掉基圆外部分，大圆弧也就绘制完成。
(2)绘制小圆弧的原理与步骤要绘制半径角距为的小圆弧，同样也应至少知道小圆弧上的三个点（如图六所示的A、C、B 三个点）。
根据吴氏网的结构与原理，可以通过CAD制图确定A、C、B三个点的位置。
①确定点C，首先用公式一计算点O与点C间距离，但其中为小圆弧的半径角距；然后以基圆的圆心为圆心，OC长为半径画圆，该圆与基圆的南北径向线NS交于C点。
②以基圆的圆心为基点，将南北径线ON分别逆时针和顺时针旋转角度，得两条直线，分别与基圆交于A、B点。
③过A、C、B三个点画一个圆，并剪掉基圆外部分，小圆弧也就绘制完成。
三、赤平投影网CAD图解的应用利用传统标准吴氏网对平面、直线进行投影时，一般步骤是：把透明纸（或透明胶片等）蒙在吴氏网上，画基圆及“十”字网心，并用针固定于网心上，使透明纸能够绕网心旋转。
然后在透明纸上标出E、S、W、N，以正北（N）为0°，顺时针数到360°。
东西直径EW确定倾角，一般是圆周为0°，至圆心为90°。
这样做具有以下缺点：一是较麻烦，二是当旋转透明纸时，容易从针孔处发生破裂而移位；三就是准确性不高；四是效率低。
如果用CAD制图，则可避免上述不足，且使作图更简化，用不着吴氏网中的那么多的经、纬线，只需要画出基圆及其南北径线和东西径线。
1.平面赤平投影的CAD图解（如图七）例1：一平面产状126°∠30°，绘制其赤平投影图。
(1)绘制一直径为20cm的基圆，同时画出铅直和水平两条直径，并标出E、S、W、N。
后面的例子均需要这一步，画法与之相同，所以不再重复。
(2)平面的倾向是126°，则其走向为36°。
将南北径线绕基圆的圆心O顺时针旋转36°到达AB 位置，与基圆交于A、B两点，则AB就是平面的走向线。
(3)以基圆的圆心O为基点，将射线ON顺时针旋转126°到达OD位置，与基圆相交于点D，则OD即为该平面的倾向线。
(4)用公式一计算线段OC长度。
以基圆的圆心O为圆心，OC为半径画圆，交OD于C点。
(5)采用三点法，即过A、C、B三点画圆，并切掉基圆外部分，所得大圆弧ACB即为该平面的赤平投影。
2.直线赤平投影的CAD图解（如图八）例2：一直线产状330°∠40°，绘制其赤平投影图。
(1)将ON绕圆心O顺时针旋转330°后到达OA位置，与基圆交于点A，则OA即为该直线的倾伏向。
(2)用公式一计算OA′值。
以基圆的圆心O为圆心，OA′为半径画圆，交OA于A′点，则点A′即为该直线的赤平投影。
3.平面法线赤平投影的CAD图解（如图九）例3：一平面产状为105°∠40°，绘制其法线的赤平投影。
(1)按例1所述方法，绘制产状为105°∠40°平面的赤平投影大圆弧NB′S。
(2)平面法线的倾角与平面的倾角之和等于90°，因此平面法线的倾角为50°。
用公式一计算OA′。
以基圆的圆心O为圆心，OA′为半径画圆，交B′O的延长线于A′点，则A′点为该平面法线的赤面投影，也称其为平面的极点。
由于平面法线倾向与平面倾向相反，相差180°，平面法线的倾角与平面的倾角之和等于90°，因此也可根据平面法线产状与平面产状间的这种关系，首先计算法线的产状为285°∠50°，然后再按例2方法绘制法线的赤平投影。
4.相交两条直线所构成平面的产状例4：已知两直线180°∠20°和90°∠32.3°相交，用赤平投影法求解这两条直线所构成平面的产状（如图十（a）、（b））。
(1)为很好地利用CAD制图解决这个问题，引入两条直线倾角与平面倾角间的关系式：tan2βsin2γ=tan2α1+tanα2-2tanα1tanα2cosγ （公式二）式中β——两条相交直线所构成平面的倾角（°）；α1、α2——分别为两条直线的倾伏角（°）；γ——两条直线倾向夹角（°）。
