岩石地球化学计算

岩石化学的表达形式-1
1. 过去，氧化物重量百分数（wt%） 2. 现在，氧化物质量百分数（wB%）
岩石化学以氧化物形式表达是人为的，实际
上组成岩石的矿物成分并非以氧化物形式结合 中。硅酸盐熔体的近代物理和测试研究表明， 不存在氧化物，但已形成习惯，且易于组合在 造岩矿物，故仍以氧化物形式表达。
化学成分是岩石的主要成分的一种表现形式。岩石化 学成分研究的范围日益广泛，其重要性也与日俱增。
岩石化学基本概念-2
1946年，扎瓦里茨基定义：“从广义来解释， 岩石化学应该包括当研究岩石的化学性质时， 我们所碰到的一切化学问题”
1956年，契特维里科夫认为：“查明各个岩石 及天然组合（岩系）中的全部化学联系属于岩 石化学的研究领域，岩石化学的任务不仅在于 研究岩石及其共生组合的化学亲合性，而且还 要发现岩石组分和矿物成分中的规律性，并且 查明它们在矿物成分上的发生的变化规律”
19世纪以来，随着硅酸盐物理化学和结晶化学 的发展，把氧化物进行合理的归并，换算成少 数几个参数或换算成标准矿物成分，因而出现 了不同类型的计算方法。 CIPW法（ 1900 ）、尼格里法（1919）、扎瓦 里茨基法（1933）巴尔特法（1948）…
岩石化学发展简史-2
20世纪50年代到21世纪初，发展迅速。 1. 矿床的火山成因说受到极大重视，岩石化学走
关于烧失量
当样品加热到灼烧温度（一般为1000℃ ）时， CO2 、 H2O+ 、 F、Cl、S、有机质等这些组分 分解放出，样品重量的变化 。是灼烧过程中 各种化学反应所引起的重量增加或减少的代数 和。大多是变轻（只有FeO很高时灼烧变重）。
重量增加或减少是很复杂的，很难明确确定， 测烧失量就没有意义，因此在计算时应剔出。

岩石化学计算方法讲解之四——CIPW标准矿物计算法（一）方法的任务和原理本方法为美国岩石学家克劳斯（Cross）、伊丁斯（Iddings）、皮尔逊（Pirsson）和华盛顿（Washington）四人，于本世纪初（1903年）所创立，后又经A·约翰森、凯尔西等多人修改。

方法的基本任务和内容是根据岩石化学全分析数据，按照各组分间组成矿物的一般规律，将其换算为理论上所应出现的各种矿物成分。

并进而根据矿物成分进行岩石的定量矿物分类。

因此法在计算中，仅只考虑各组分间的化学组合关系和矿物的简单化学成分，而对其形成的物理化学条件和各种矿物实际的复杂成分考虑不多，故所计算出的矿物多与岩石中实际存在的矿物成分有较大出入，故将所计算出的矿物称为“标准矿物”（或“虚拟成分”）。

“标准矿物”成分的计算，主要的依据是其通用的化学分子式中各种组分的数量关系。

CIPW将“标准”矿物划分为硅铝质（SAL）和铁镁质（FEM）两组，即：矿物代号矿物名称分子式SAL组 Q 石英SiO2C 刚玉Al2O3E 锆石ErO2·SiO2or正长石K2O·Al2O3·6SiO2Ab钠长石Na2O·Al2O3·6SiO2An钙长石CaO·Al2O3·2SiO2Lc白榴石K2O·Al2O3·4SiO2Ne 霞石Na2O·Al2O3·2SiO2Kp钾霞石K2O·Al2O3·2SiO2NL石盐NaClTh 无水芒硝Na2SO4Nc钠碳酸盐Na2CO3FEM组Ac 锥辉石Na2O·FeO3·4SiO2Ns 钠硅酸盐Na2O·SiO2Ks 钾硅酸盐K2O·SiO2Di 透辉石CaO·（Mg,Fe）O·2SiO2Wo 硅灭石CaO·SiO2Hy 紫苏辉石（Mg,Fe）O·SiO2En 顽大辉石MgO·SiO2Fs 斜铁辉石FeO·SiO2Ol 橄榄石2（Mg·Fe）O·SiO2Fo 镁橄榄石2MgO·SiO2Fa 铁橄榄石2FeO·SiO2Cs 钙硅酸盐2CaO·SiO2Mt 磁铁矿FeO·Fe2O3Cm 铬铁矿FeO·Cr2O3Hm 赤铁矿Fe2O3ILm 钛铁矿FeO·TiO2TPn 榍石CaO·TiO2·SiO2Pf 钙钛矿CaO·TiO2Ru 金红石TiO2Ap 砱灰石3（3CaO,P2O5）·CaF2F 萤石CaF2Py 黄铁矿FeS2Cc方介石CaO·CO3 标准矿物成分计算的基本原则和程序也是本书第一节所述的那些，这里再着重说明如下几点：1、除可做为常量组分的类质同象混入物以外的所有微量组分，均同相应的组分组成各种副矿物，如石盐（HL—Nacl）、黄铁矿（Pr—FeS2）、砱灰石（Ap—3（3CaO·P2O5）·CaF2）、铬铁矿（Cm—FeO·Cr2O3）、钛铁矿（ILm —FeO·TiO2）……等。

岩石化学计算方法讲解之五——尼格里标准分子计算法（一）方法的任务鉴于CIPW法在计算岩石的矿物成分时，仅仅考虑到各种组分间的化学组合关系，而很少考虑岩石的成因条件，因而所计算出来的矿物成分往往同岩石中实际存在的矿物组成有较大的误差。

为此，尼格里1937年提出了他所创立的标准分子计算法。

其主要任务是将岩石的化学分析结果，尽可能计算成为符合岩石实际存在的矿物成分，这样就不仅可以将岩石的化学分析同显微镜下的研究紧密结合起来，而且由于此法可以计算出反映岩石不同成因条件（岩浆、交代、变质）的不同的矿物组成方案，通过对这些方案的分析和比较，或者根据所计算中的矿物组合做出的物理化学图解，可以得出有关岩石成因和演变的某些有重要意义的认识和结论（鉴于该法的许多用途大体与CIPW法相近，故此处对这方面不再具体介绍）。

（二）方法的原理1、概述：该法所依据的基本原理，不仅是岩石化学组分间的化学组合关系，而且考虑到不同成因条件下矿物形成的特点和规律。

由于同样的化学组分在不同的成因条件下，可以形成不同的矿物组合方案的可能性。

而为了寻求同岩石实际矿物组成相符合的矿物方案，往往需要在计算中把一种矿物方案换算成另一种方案。

为了给此种转变矿物方案的工作提供便利的基础和条件，尼格里提出了原始分子和矿物标准分子的概念。

整个计算方法是先把组成岩石的各种氧化物计算为原始分子，然后再进一步根据岩石的实际情况把原始分子换算为标准矿物分子。

2、原始分子及其组成：所谓原始分子（或称基本分子），即是由各氧化物按一定组合规律和量比关系而组成的原子团。

它并非是岩石中实际存在的矿物，而仅仅是人为设置的一个“建造单元”，是为了供进一步计算的一些原子团，是组成各种矿物的基础。

为了实现既便于把原始分子换算为标准矿物，又便于把计算出的一种矿物方案转变成另一种矿物方案，尼格里巧妙地把各种原始分子（包括以后的标准矿物分子）的当量，设计为等于其化学式的分子量被其化学式中的正价数目而除所得的分子量。

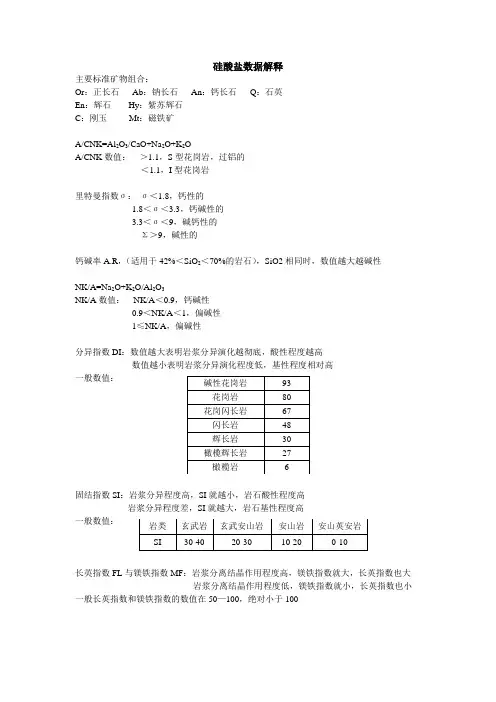
主要标准矿物组合：Or ：正长石 Ab ：钠长石 An ：钙长石 Q ：石英En ：辉石 Hy ：紫苏辉石C ：刚玉 Mt ：磁铁矿A/CNK=Al 2O 3/CaO+Na 2O+K 2OA/CNK 数值： ＞1.1，S 型花岗岩，过铝的＜1.1，I 型花岗岩里特曼指数σ： σ＜1.8，钙性的1.8＜σ＜3.3，钙碱性的3.3＜σ＜9，碱钙性的Σ＞9，碱性的钙碱率A.R ，（适用于42%＜SiO 2＜70%的岩石），SiO2相同时，数值越大越碱性NK/A=Na 2O+K 2O/Al 2O 3NK/A 数值： NK/A ＜0.9，钙碱性0.9＜NK/A ＜1，偏碱性1≤NK/A ，偏碱性分异指数DI ：数值越大表明岩浆分异演化越彻底，酸性程度越高数值越小表明岩浆分异演化程度低，基性程度相对高一般数值：固结指数SI ：岩浆分异程度高，SI 就越小，岩石酸性程度高岩浆分异程度差，SI 就越大，岩石基性程度高一般数值：长英指数FL 与镁铁指数MF ：岩浆分离结晶作用程度高，镁铁指数就大，长英指数也大 岩浆分离结晶作用程度低，镁铁指数就小，长英指数也小 一般长英指数和镁铁指数的数值在50—100，绝对小于100稀土重量ΣREE：一般几百都是偏低，上千就高。

轻重稀土比值ΣCe/ΣY：一次热事件的早期单元，比值较大，轻稀土越富集随着岩浆演化到晚期单元，比值减小，(La/Yb)N：(Ce/Yb)N：反映轻稀土的分馏程度，比值越大，轻稀土分馏越明显，富集程度越高。

数值一般和1比较(Sm/Eu)N：反映重稀土的分馏程度，比值越小，重稀土分馏越明显，富集程度越高。

数值一般和1比较元素铕值δEu：：δEu＞0.7，基性岩浆分异的花岗岩，成因与板块有关0.3＜δEu＜0.7，分布最广泛，地壳经不同程度的部分熔融形成δEu＜0.3，岩浆演化晚期的偏碱性花岗岩，一个超单元的最后一、二个单元，由完全的分异结晶作用形成δEu一般都是亏损微量元素数据解释元素含量数值对比，和地壳丰度值特征参数：Nb*，Sr*，P*，Ti*，Zr*，数值小于1就亏损，大于1，就富集，与投图一致。

2. 地球化学区别于地球科学的其他学科
——着重于研究地质作用中的化学运动形式及其规律, 以区 别于构造地质学和古生物学； ——地球化学以观察原子为出发点，研究原子活动的整个历 史，包括元素富集与分散、固结形式及流体状态迁移等， 重视研究微量元素及同位素，以此区别于矿物学、岩石学 及矿床学的研究内容。地球化学基本原理具有更为普遍、 更为深刻的意义。 ——地球化学是地球物质科学（material science of the earth） 中研究物质成分的主干学科，又兼具分支学科和基础理论 学科的双重特点。
其他早期教材：
戚长谋等, 地球化学通论.1994, 地质出版社. 涂光炽等, 地球化学.1984, 上海科技出版社. 布朗洛,A.H., 地球化学(中译本), 1982,地质出版社. 戈尔德斯密特, V.M.,地球化学(中译本), 1954,科学出版社.
地球化学英文主要参考书
Fancis Albarede, Geochemistry: An introducion. 2003, Cambridge University Press. Faure, G. Principles and Applications of Geochemistry. (2nd.). 1998, Prentice Hall. Ottonello, G. Principles of Geochemistry. 1997, Columbia University Press.
例如：元素Ni在橄榄岩/玄 武岩之间如何分配？在辉 石/斜长石之间如何分配？
二、地球化学研究的基本问题
2. 研究元素的共生组合和赋存形式
共生组合——前者指无成因含义，后者有成因含义。具有共 同或相似迁移历史和分配规律的元素常在特定的地质体中形 成有规律的组合，称为元素共生组合，如Cu、Pb、Zn 在热 液矿床中形成共生组合，Cr、Ni、Co和铂族元素在基性超 基性岩中形成共生组合。 赋存形式(存在形式,赋存状态):指元素在地质体中以什么形 式存在，常见形式例如:化合物(氧化物,硫化物,硅酸盐,碳 酸盐等等)、类质同像混入物、机械混入物、包裹体及吸附 物等等。

岩石化学计算方法基础知识讲解岩石化学计算方法基础知识讲解岩石化学是研究岩石化学特征及其应用的学科。

是岩石学的一个分支，又称化学岩石学。

岩石化学主要应用于结晶岩（火成岩、变质岩）的研究，其中又以火成岩研究为主，应用最为广泛的则为结晶程度差的火山岩。

以下是店铺为大家整理的岩石化学计算方法基础知识讲解相关内容，仅供参考，希望能够帮助大家。

1、岩石类型（或岩石系列）用以说明岩石主要化学组分之间的含量关系。

岩石类型（或系列）不同，不仅其化学组成上有重大差异，而且更表现在其矿物组成上具有明显的不同特点。

同时其岩石化学的计算程序和结果也各有差异。

因此在计算中，应首先根据各组分之间含量上的相互关系确定岩石所属的类型（或系列）。

在岩石化学计算中，一般是将岩浆岩划分如下四个类型（或系列）。

(1) 正常类型，也称为钙硷系列。

指岩石中Al的含量能全部和K、Na及部分Ca组成长石类矿物，而多余的Ca则参加到暗色矿物中去。

因而岩石中既可有钾长石、钠长石及斜长石，也可以有单斜石和角闪石的存在，其表达方式因计算方法不同而有所不同，但基本意义是相同的。

即：查氏公式：K+NaAl）（2）硷极度过饱和：指岩石中K、Na含量不仅使全部的Al消耗殆尽而组成硷性长石，同时也能使全部Fe3+和Fe2+，Mg2+、Mn2+等消耗完而组成霓石类矿物，并且还有剩余。

少数情况下出现霞石等硅不饱和矿物。

表达式：查氏公式：K+Na;Al+Fe2++Mn2+ 尼氏公式：AlK;Fe3++Fe2++Mn2+2、分子数与原子数岩石化学全分析结果，都是用重量百分含量表达的，但岩石化学在把各种元素或其氧化物按其组成矿物的规律进行换算时，是根据各矿物分子式中各元素的原子或氧化物的分子之间的量比关系进行的。

故在计算时，都要根据某一方法的需要，将化学分析结果的氧化物重量百分含量换算为原子数或分子数。

例如：SiO2的重量百分含量为50%，其分子量为60.08，则分子数为50/6008=0.833，为消除小数点，均将计算结果乘以1000，故SiO2的分子数为0.833×1000=833。

岩石化学计算方法基础知识讲解之一——岩浆岩的化学组成及主要造岩矿物的化学特征许多地质工作者反映，对岩石化学计算方法的道理不好理解。

其原因主要是许多讲述这些方法的文献没有对其有关原理没有说明。

为此在讲述各种计算方法之前，有必要说明一下有关的道理和依据，弄清楚这些道理就很容易理解和掌握各种计算方法了。

因为岩石化学计算方法主要是用于解决和说明岩浆岩的化学及有关特征的，因而这里在论述有关内容时均以岩浆岩为主，只有在涉及其它类型岩石时，再做具体的说明。

众所周知，岩浆岩主要是由硅酸盐熔浆经冷却结晶作用所形成的。

组成硅酸盐熔浆的主要化学成份是：SiO2、TiO2、Al2O3、Fe2O3、FeO、MnO、MgO、CaO、Na2O、K2O、H2O等。

这些组分在结晶作用中，按照其各自的晶体化学特征互相结合组成各种造岩矿物。

已知岩浆岩的主要造岩矿物可分如下两大类：1、暗色矿物：以铁镁硅酸盐为主，包括杆栏石、辉石、角闪石、霓石等。

2、浅色矿物：以钾、钠、钙的铝硅酸盐为主。

主要有钾长石，斜长石、石英、霞石、白榴石等。

所有矿物尽管各方面都有很多特点和性质，彼此也有很多差别，但在大多数情况下之所以做为一种矿物存在的最本质的因素则是其化学成分。

正是这一内在的因素，决定了各种矿物间许多的不同特点和性质，现将各主要造岩矿物化学组成上的特点分述于后：1、暗色（铁镁）矿物（1）杆栏石：属岛状硅酸盐，为一类质同象系列矿物的总称。

其化学通式为（Mg,Fe）2SiO4。

其中铁镁可以任意比例混合形成相对应的各种杆栏石。

如图4所示（所标的百分数为镁杆栏石的含量）Mg2SiO4 镁杆栏石贵杆栏石镁铁杆栏石铁镁杆栏石铁杆栏石Fe2SiO4100% 90 70 50 10 0图4：杆栏石的种属划分杆栏石在化学组成上的特点是：（i）为含铁、镁组分的简单硅酸盐；（ii）其中的金属离子（Mg,Fe）与硅离子之比例关系为2：1。

即每一个硅离子需要两个Mg或Fe或（Mg+Fe）离子相匹配。

岩石化学计算方法基础知识讲解之一——岩浆岩的化学组成及主要造岩矿物的化学特征许多地质工作者反映，对岩石化学计算方法的道理不好理解。

其原因主要是许多讲述这些方法的文献没有对其有关原理没有说明。

为此在讲述各种计算方法之前，有必要说明一下有关的道理和依据，弄清楚这些道理就很容易理解和掌握各种计算方法了。

因为岩石化学计算方法主要是用于解决和说明岩浆岩的化学及有关特征的，因而这里在论述有关内容时均以岩浆岩为主，只有在涉及其它类型岩石时，再做具体的说明。

众所周知，岩浆岩主要是由硅酸盐熔浆经冷却结晶作用所形成的。

组成硅酸盐熔浆的主要化学成份是：SiO2、TiO2、Al2O3、Fe2O3、FeO、MnO、MgO、CaO、Na2O、K2O、H2O等。

这些组分在结晶作用中，按照其各自的晶体化学特征互相结合组成各种造岩矿物。

已知岩浆岩的主要造岩矿物可分如下两大类：1、暗色矿物：以铁镁硅酸盐为主，包括杆栏石、辉石、角闪石、霓石等。

2、浅色矿物：以钾、钠、钙的铝硅酸盐为主。

主要有钾长石，斜长石、石英、霞石、白榴石等。

所有矿物尽管各方面都有很多特点和性质，彼此也有很多差别，但在大多数情况下之所以做为一种矿物存在的最本质的因素则是其化学成分。

正是这一内在的因素，决定了各种矿物间许多的不同特点和性质，现将各主要造岩矿物化学组成上的特点分述于后：1、暗色（铁镁）矿物（1）杆栏石：属岛状硅酸盐，为一类质同象系列矿物的总称。

其化学通式为（Mg,Fe）2SiO4。

其中铁镁可以任意比例混合形成相对应的各种杆栏石。

如图4所示（所标的百分数为镁杆栏石的含量）Mg2SiO4 镁杆栏石贵杆栏石镁铁杆栏石铁镁杆栏石铁杆栏石Fe2SiO4100% 90 70 50 10 0图4：杆栏石的种属划分杆栏石在化学组成上的特点是：（i）为含铁、镁组分的简单硅酸盐；（ii）其中的金属离子（Mg,Fe）与硅离子之比例关系为2：1。

即每一个硅离子需要两个Mg或Fe或（Mg+Fe）离子相匹配。

亚碱性系列再分：钙碱性与拉斑玄武岩-4
③较方便的可用 FeO*/MgO与 SiO2、FeO*关 系图（图8） FeO*= FeO+0.9 Fe2O3。
图8 FeO*/MgO与SiO2、FeO*关系图 （A.Miyashiro，1974）
亚碱性系列再分：钙碱性与拉斑玄武岩-4
FeO'－FeO'/MgO变异图
Sub-Ab Ab B as -T rach-Neph
0 35
45
55
65
75
40 .001
0.01
0.1
1
10
SiO2
Zr/TiO2 *0.000 1
利用Minpet模板图判别岩类-2
5
Com/Pant Phonolite
2 1
Alkali Rhyolite Phonolite
1
Rhyolite
酸度、碱度、系列及类型图解-1

据SiO2可划分酸度，据SiO2及K2O+Na2O 可确定δ﹛δ=（K2O+Na2O）2/（SiO2-43） ﹜值，碱度及系列。由SiO2及K2O+Na2O 含量，从图上即可简便的同确定火山岩类 的酸度、碱度、系列、岩石组合、类型及 名称。
酸度、碱度、系列及类型图解-2
Cpx2+0.014× Opx× Ol－0.011 × Ol2)=32.264。 以标准矿物Opx、Ol值代入方程式，如计算值等号 右边列出的数值小，为碱性系列；如计算值比等 号右边值列出值大，则为亚碱性系列。图中曲线 判别率较好，其可靠性可达96％。??
玄武岩类系列参考图解判别
16 14 12 10
区分碱、亚碱性两个系列-2
②较可靠的是Ol′-Ne′Q′图 Ol′、Ne′、Q′ 为阳离子标准矿物计算值 Ol′=Ol+3/4Hy， Q′= Q+2/5Ab+1/4Hy Ne′= Ne+3/5Ab。 由于标准矿物计算用全岩 化学成分，因此精度较 大。

邵跃等人在狮子山地区开展矽卡岩型铜矿床原生晕的研究发 现（图），铜、银、钼三个元素在剖面上具有垂直分带现象。
• 银异常主要分布在 沿矿带轴向的前上 方（前缘），矿带 尾部异常收敛；
• 钼异常主要分布在 沿矿带轴向的后下 方（尾部），矿带 前缘无异常出现；
• 铜异常虽然在矿带 前后均有异常出现， 但在矿带前缘比矿 带尾部异常强。
（2）平均异常强度 （ C）—异常范围里元素含量
的平均值：
C C
NT
（3）
（4）异常的连续性（t） 矿体中包含夹石一样，原生晕中也经常包含一些 正常含量点，从而产生异常的不连续性。
异常点数 总点数
（5）异常的均匀性 :相邻两点地球化学指标差值大小的 度量
（6）异常渐变性:含量变化梯度小，渐变性好；梯度大， 渐变性差
第四章 岩石地球化学测量
一、热液矿床原生晕的形成及影响因素 二、热液矿床原生晕的组分特征 三、热液矿床原生晕的形态特征与内部结构 四、热液矿床原生晕的分带特征 五、分散矿化原生晕与多建造晕 （复合晕） 六、岩浆矿床 七、沉积-层状矿床 八、岩石地球化学找矿的应用
一、热液矿床原生晕的形成及影响
主要内容：
MLij(标) 第i中段第j个元素的标准线金属量
m
M Lij（标）
第i中段j个元素的标准线金属量之和
j 1
标准化系数
M Dij
Lij(标) m
MLij（标）
j1
根据分带指数，分带序列由上到下初步确定为：
（As、Sb）—Pb —（Cu、Bi）—Mo
由分带指数初步确定的分带序列为：
（As、Sb）—Pb —（Cu、Bi）—Mo
• 为了取得可以互相对比的资料，1965年，谢 学锦、邵跃将地球化学异常分成内带、中带、 外带三个浓度带。并视浓度变化的陡度，以异 常下限值的1倍、2倍、4倍三个数值来划分外、 中、内带，称三级浓度带。

量,mg/g;
S2— 300—600℃ 时 检 测 到 的 单 位 质 量 储 层 岩 石 中 烃 类 含 量,mg/g;
S11— 90—200℃ 时 检 测 到 的 单 位 质 量 储 层 岩 石 中 烃 类 含
量,mg/g; 汽油峰
2020/8/1
（三）录井参数及意义
• 储集层岩石热解录井分析参数的含义
应用效果
2020/8/1
1958.50-1985.30m分析样品91块，计算地化 轻重指数比：1.1，判断原油性质接近重稠 油；计算Pg＝3.94 mg/g,根据原油性质结合 上述图版判断含油气丰度较低；其主要峰形 特征为可溶烃峰（S1）值和热解烃峰（S2） 值较低，S2的峰形低扩，说明重质的成分 C33以后均匀分布，分析为残余油，后对 1958.09－2006.69 m试油： 12mm油嘴，油 花，水104方，为含油水层，原油密度：
取分析样品（生油岩和储油岩），置入特制裂解炉中对样 品进行程序升温，使岩石样品中的烃类和干酪根（生油母质） 在不同温度范围内挥发和裂解，通过载气的吹洗使其与岩石样
品实现物理分离，由载气携带直接进入氢焰离子化检测器（FID
）进行定量检测，检测结果经气电转换将烃类浓度的变化转变 成相应的电信号的变化，经放大进入计算机进行运算处理，得
到烃类各组分含量S0、 S1、 S2、 S4和裂解烃峰顶温度Tmax。
一个分析流程大致需要12－13min。
2020/8/1
仪器的分析流程
2020/8/1
数据处理方法
面积积分定量法
根据分析样品的出峰面积大小确定物质的含量， 而出峰的面积采用定基线、定时间窗口的方法进行 积分，在相同操作条件下，用已知参数的标准物质 响应值标定未知参数分析样品的含烃量，即外标法。

岩石化学计算方法讲解之六——吴利仁超基性岩石化学计算方法（一）方法的原理鉴于超基性岩在理论上和实际应用中均有着重要的意义，在化学和矿物组成上也有着一定的特殊性，因而许多研究者，如苏联的索博列夫、我国的王恒升、白文吉、吴利仁、肖序常、高纪璞、李军等地质学者，都提出了专门用于超基性岩的岩石化学计算方法。

这里我们仅将吴利仁的计算方法予以介绍。

其它方法读者可参考有关文献。

吴氏关于超基性岩的岩石化学计算方法的基础是查瓦里茨基计算法，即在查法的基础上，结合超基性岩的岩石化学特点加以修改和补充而成。

他对查法的主要改动是：1、超基性岩中K、Na含量甚微，但它们对超基性岩浆的来源和含矿性有着重要的指示作用，因而不可忽略，仍需予以表示。

为此对超基性岩的主要特征数值仍沿用s、a、b、c等四个。

但因a、c值均很小，若仍按查氏法那样在T形图上投影，则将使全部投影点集中于Sb轴两侧的附近处，使其难以分辩。

为此，吴氏在做投影图时将主要数值从四个减少为三个，即将a和c或a和c值予以合并，做为一个数值表示。

也即是超基性岩的主要数值为s、b和（a+c）或（a+c），且s+b+（a+c）或（a+c）=100。

2、对补充数值，除仍保留了查氏的Q值外，其余根据超基性岩本身的特点予以改动，即：（1）鉴于超基性岩中的镁铁的相对含量，即所称的镁铁比值（m/f），不仅是划分超基性岩的类型和探讨岩浆来源的重要依据，而且也是其含矿性的主要标志。

为此，将其做为超基性岩的一个重要补充数值。

且在计算m/f时，根据Ni2+常同Mg2+、Mn2+常同Fe2+成类质同象混入的实际情况，分别将Ni2+合并到Mg2+中，将Mn2+合并到Fe2+中。

则m/f的计算公式为：++++++++=23222/MnFe Fe Ni Mg f m 根据m/f 值，吴利仁将我国的超基性岩划分为如下三类，即： 岩石类型 m/f 镁质超基性岩 >7-6.5 铁质超基性岩 2-6.5 富铁质超基性岩 0.5-2实践证明，工业铬铁矿床均产于镁质超基性岩中，而铁质超基性岩则与硫化铜镍矿床有密切联系，富铁质超基性岩与钒钛磁铁矿物及碳酸盐矿床（烧绿石）有密切关系。

玄武岩的TiO2-Y/Nb判别图解
玄武岩的P2O5-Zr判别图解
玄武岩的TiO2-Zr/(P2O5×104)判别图解
玄武岩Nb/Y-Zr/（P2O5×104)判别图解
2.三角图解
AI为板内碱性玄武岩；AII为板内碱性玄武岩与板内拉斑玄武岩；B为E型MORB；C为 板内拉斑玄武岩与火山弧玄武岩；D为N型MORB与火山弧玄武岩
砂岩判别函数图解
判别别函1 0.0447SiO 0.140MgO 0.195CaO 0.719Na 2 0.972TiO 2 0.008Al 2 O3 0.267Fe 2 O3 0.208FeO 3.028MnO 2 O 0.032K 2 O 7.510P 2 O5 0.303
玄武岩的La/10-Y/15-Nb/8三角判别图解
花岗岩Hf-Rb/10-Ta×3判别图解
花岗岩Hf-Rb/30-Ta×3判别图解
1.2.2 微量元素地球化学
ΣREE LREE/HREE δEu （La/Sm）N （La/Yb）N （Gd/Yb）N δCe 总分配系数D
CL 1 C0 D (1 D)F CL 1 C0 D (1 P)F
WPG
qz alkali syenite
ORG
alk . gr
granite
granodiorite
qz syenite
qz qz monzosy. monzon.
e alit ton
qz diorite
Alkali feldspar
COLG
Plagioclase feldspar
玄武岩TiO2－K2O－P2O5判别图解
火成岩类R1-R2因子判别图
R1 4Si 11(Na K) 2(Fe T i)

粗面英安岩
响岩质 碱玄岩
(Q ＞ 20% ) 粗安岩
7
( O l＜ 1 0 % ) 玄 武 碧玄岩 粗面粗安岩
玄武岩 5
流纹岩
3
玄武岩
玄武 安山岩
安山岩
英安岩
1
37 41 45 49 53
超基性
基性
45
52
57 61 65 69
中性
酸性
63
73 77 W t%
二、火成岩类型的划分
（3） SiO2—K2O
四、火成岩系列的划分
3个主要系列：碱性系列、钙碱性系列和拉斑玄武岩系列 （1）碱性和亚碱性系列的划分
➢ SiO2－（Na2O+K2O）变异图：适用于侵入岩和火山岩
Alkali vs. Silica diagram for Hawaiian volcanics: Seems to be two distinct groupings: alkaline and subalkaline
Pla板te块M边a缘rgin
Ser系ies 列 Con汇v聚er的gent Di离ve散rg的ent
Alkaline
yes
Tholeiitic
yes
yes
Calc-alkaline yes
W板ith块in内P部late
O大ce洋a的nic Co大nt陆in的ental
yes
yes
yes
yes
七、火成岩形成构造环境的判别
四、火成岩系列的划分
（3）其它的划分方法
五、岩浆演化－ Harker图解
问题的提出：在一个地区常出现一组密切共生、成分变化大的火成岩－－ 那么这些岩石间的成因关系如何？演化方式如何？

岩石化学计算方法基础知识讲解之二——岩石中主要化学组分的性状及组成矿物的一般规律组成硅酸卤盐岩石的主要氧化物有：SiO2、Al2O3、Fe2O3、FeO、MgO、CaO、Na2O、K2O等八种，这也是造岩矿物的主要成分。

根据大量的实际资料和有关的物理化学实验，它们组成矿物的主要规律是：SiO2：在岩浆岩中含量为24-80%，在岩浆结晶过程中，SiO2首先同各种金属元素组成各种饱和的硅酸盐矿物，其中镁铁硅酸盐有辉石、角闪石、铝硅酸盐为斜长石，钾长石。

在形成饱和矿物后，若SiO2仍有剩余，则以游离的SiO2即石英出现，当SiO2不足时，即不能和全部金属离子形成硅饱和矿物，而只能形成硅不饱和矿物。

其中镁铁硅酸盐为杆栏石，铝硅酸盐为白榴石和霞石。

因此，在一般情况下，硅不饱和矿物（杆栏石、白榴石、霞石等）在岩石中是不能同石英共生的，但在喷出岩中因来不及反应，也可以出现这种共生。

Al2O3：在火成岩中平均含量15.5%，变动在0-20%之间，极少数情况可达28%。

Al首先可以取代硅，即占据硅氧四面体中硅的位置，但此时由于Al3+代替了Si4+，则周围的氧有1/4电价未满足，这就要求有一个较大的一价或二价阳离子进入格架中，以平衡此1/4电价。

这些大的阳离子需要被8个或更多的氧离子所包围，此种离子只能是半径小，配位数为8或8以上的K、Na、Ca，而不能是半径小于6次配位的Mg、Fe离子。

由此则形成了一方面是K、Na、Ca的铝硅酸盐（长石类）；另一方面则是Mg、Fe的简单硅酸盐（辉石、角闪石）两个系统，从而构成了浅、暗两大矿物系列。

但当岩石中的Al量在使全部K、Na、Ca组成长石后，仍有剩余时，剩余的Al也参加到暗色矿物中，首先代替6次配位的Mg2+、Fe2+，但因这样替换造成原子价不平衡，因此也就必须同时代替4次配位的Si4+，结果就使(MgFe)2[Si2O6]分子中混入了Al2[Si2O6]分子。

形成普通辉石、角闪石类矿物。

FeO*(TFeO)=FeO＋0.8998Fe2O3 在使用TAS分类图时，首先要检查一下 要进行分类的岩石是否为“高镁”火山岩； 谨慎使用那些风化、蚀变、变质、变形 或者经历过重结晶作用的岩石化学分析数 据，但对于许多低级变质火山岩，要求烧 失量应小于5％；
（一）利用常量元素开展岩石的分类 岩石的分类通常是基于主量元素成分，单它 们的具体命名要根据矿物组成。但是对火山岩而 言，岩石的具体命名也主要依据化学成分。 图1是Le Maitre et al (1989)提出的全碱 （Na2O+K2O）—SiO2的TAS分类图。 Wilson (1989)利用Cox et al (1979)的TAS图解 对侵入岩也进行了分区和命名（图2）。
如果岩石中含有较多的含水矿物，如黑云母，角闪石
或白云母，特别是蚀变强烈的岩石（含大量粘土矿物和
碳酸盐矿物），则岩石的总量将会低于99%，这时往往 用烧失量(LOI)或直接分析H2O+、H2Oˉ、F和CO2的含 量来补充。
在运用已有的常量元素时，应注意下列 几点：
测试样品必须是未蚀变的新鲜岩石，其 检验的标准是岩石中H2O＋＜2％，CO2＜
0.5％；否则不能使用，只有高镁火山熔 岩（苦橄岩、科马提岩、麦美奇岩、玻古 安山岩）例外；
使用原始数据进行各种分类图表和化学 参数计算前，必须先去除H2O或烧失量， 重新计算为干成分的100%标准化时的主元 素质量百分数后，才能使用；
在计算CIPW标准矿物含量时，如果是全 铁含量，应找一个有效的方法将全铁分成 FeO和Fe2O3；一般采用：
1、用Muller等方法时，计算镁值（耐火度） （Mg# =MgO*100/ (MgO+FeO＊)(摩尔比)， FeO＊＝FeO+0.899Fe2O3。

岩石地球化学计算1. TFe2O3=FeO+0.9Fe2O3FeOT(wt.%)=FeO(wt.%)+Fe2O3(wt.%)*0.8998=FeO(wt.%)+Fe2O3(wt.%)*(71.844/(159.6882/2))2. LOI 烧失量3. Mg#=100*(MgO/40.3044)/(MgO/40.3044+FeOT/71.844)FeOm71.85 ；MgOm40.31上述是分别测试分析了FeO和Fe2O3的计算方法，如果是测试的全铁，也可以近似计算。

通常说的高Mg，是指岩石具有较高的MgO含量，如火山岩中的高镁安山岩（通常情况下，异常高的MgO含量指示着可能有地幔物质参与，如俯冲带地幔楔或者软流圈熔体上涌等等）。

Mg#（镁指数）也可以定量的表示岩石中的Mg含量高低。

Mg#通常用于镁铁质岩石，可以粗略指示地幔岩石的部分熔融程度，高Mg#的地幔橄榄岩可能经历了更高程度的部分熔融，常在92-93左右，而原始地幔会相对富集，Mg#较低，在88-89左右。

4. 里特曼组合指数δ或里特曼指数δ=（K2O+Na2O）2/（SiO2-43）（wt%）δ<3.3 者称为钙碱性岩，δ=3.3-9 者为碱性岩，δ>9 者为过碱性岩。

5.A/NK = Al2O3/102/(Na2O/62+K2O/94)6.A/CNK = Al2O3/102/(CaO/56+Na2O/62+K2O/94)7.全碱ALK = Na2O+K2O8.AKI = (Na2O/62+K2O/94)/Al2O3*1029.AR = (Al2O3+CaO+Na2O+K2O)/(Al2O3+CaO-Na2O-K2O)10.固结指数(SI) =MgO×100/(MgO+FeO+F2O3+Na2O+K2O) (Wt%)11.阳离子R1-R2图（岩石氧化物wt%总量不用换算成100%）R1=（4Si-11(Na+K)-2(Fe+Ti)*1000R2=（6Ca+2Mg+Al）*100012.(La/Sm)N对δEu的双变量斜边图解认识Eu异常。