自相关过程的改进型EWMA控制图
- 格式:pdf
- 大小:654.63 KB
- 文档页数:7
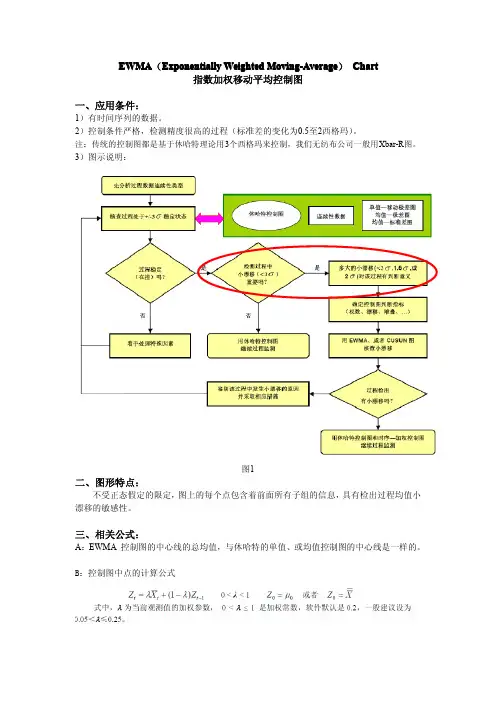
EWMA(Exponentially Weighted Moving-Average)Chart指数加权移动平均控制图一、应用条件:1)有时间序列的数据。
2)控制条件严格,检测精度很高的过程(标准差的变化为0.5至2西格玛)。
注:传统的控制图都是基于休哈特理论用3个西格玛来控制,我们无纺布公司一般用Xbar-R图。
3)图示说明:图1二、图形特点:不受正态假定的限定,图上的每个点包含着前面所有子组的信息,具有检出过程均值小漂移的敏感性。
三、相关公式:A:EWMA控制图的中心线的总均值,与休哈特的单值、或均值控制图的中心线是一样的。
B:控制图中点的计算公式注:从公式中可以看出每个点包含着前面所有子组的信息。
C:控制限的计算公式五:举例说明以某精密标准件的厚度为例,用Xbar-R图控制,没有异常,如图2图2但是用EWMA控制图来控制却有异常:图3可以从上控制线的数据来说明,Xbar-R的UCL值是3.178;而EWMA的UCL值是3.07596。
而他们的中心线都是一致的3.0385。
六:目前我司应用的控制图(以亲水产品的回渗为例):图4七、个人总结:没必要在无纺布领域应用EWMA控制图,因为休哈特理论是从电子和机加工行业延伸出来的,这种行业基本上是标准模具控制,加工条件相对稳定,才用3个西格玛进行控制。
而我们的无纺布这种流程性材料工艺本身决定随机因素影响较大,用0.5-2个西格玛来控制,基本上是不可行,可以说是作茧自缚。
克重还勉强可以控制(取样数据较多的情况下),如强力、伸长率、亲水性能就更难控制。
如果客户问及,我们可以说无纺布领域的物理性能控制用3西格玛就已经足以严格。
如果要用EWMA控制图,我们可以用minitab来做相应的分析用如图5。
图5。

基于批均值的自相关过程EWMA控制图
王彩玲;师义民
【期刊名称】《沈阳师范大学学报(自然科学版)》
【年(卷),期】2010(28)3
【摘要】给出基于批均值构造新过程的方法,证明了新过程仍然是平稳过程.针对q 阶滑动平均过程(MA(q))给出了新过程的标准差截断公式,利用该公式构建修正EWMA控制图,并通过随机模拟给出平均运行批长.并将此控制图与利用新过程标准差构建的EWMA控制图和批均值控制图进行了比较,控制图和平均运行批长均表明利用标准差截断公式构建的修正EWMA控制图不仅优于批均值控制图,而且具有和利用新过程标准差构建的EWMA控制图相同的控制性能.由于新过程包括了原过程的几乎全部信息,所以在新过程的基础上设计的修正EWMA控制图能够完全反映原过程的生产情况.而修正EWMA控制图构造简单,易于实施,因此对现代生产过程具有很强的可行性和很高的利用价值.
【总页数】4页(P387-390)
【作者】王彩玲;师义民
【作者单位】中国人民解放军理工大学指挥自动化学院,江苏南京,210007;西北工业大学应用数学系,陕西西安,710072
【正文语种】中文
【中图分类】O213.1
【相关文献】
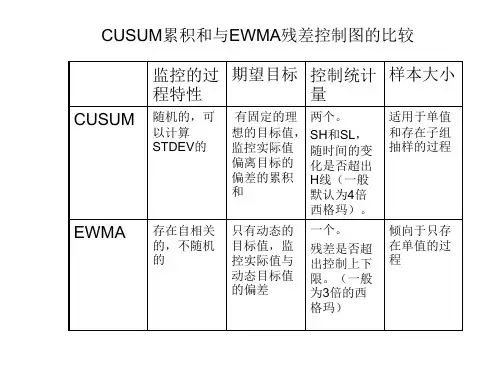
1.自相关过程的批滑动均值EWMA控制图 [J], 王彩玲;师义民
2.平稳自相关过程的EWMA控制图 [J], 王海宇;徐济超;杨剑锋;常广庶
3.自相关计数过程单侧EWMA控制图的构建 [J], 张敏;聂国华;何桢
4.自相关过程的改进型EWMA控制图 [J], 张志雷
5.自相关过程的EWMA残差控制图的设计与性能评价 [J], 尚云艳;郭鹏江;夏志明因版权原因,仅展示原文概要,查看原文内容请购买。

控制图(control charts)又名:统计过程控制( statistical process control)方法演变:EQ \o(\s\up5(-),\s\do2(x))计量值控制图:⎺X-R控制图(又名均值极差控制图),⎺X-s控制图,单值控制图(又名X 控制图,X-R控制图,IX-MR控制图,XmR控制图,移动极差控制图),移动均值-移动极差控制图(又名MA-MR控制图),目标偏差控制图(又名差异控制图、偏差控制图、名义值偏差控制图),CUSUM(又名累计和控制图),EWMA(又名指数加权移动平均控制图),多元控制图(又名Hotelling T2控制图)。
计数值控制图:p控制图(又名不良品率控制图),np控制图,c控制图(又名缺陷数控制图),u控制图。
两种数据都适用的控制图:短期过程控制图(又名稳定控制图或者Z控制图),组控制图(又名多属性值控制图)。
概述控制图是一种对过程变异进行分析和控制的图形工具。
数据按时间顺序绘制在图上,控制图一般有一条代表均值的中心线,一条上控制限位于中心线上方,一条下控制限位于中心线下方,这些线是根据过程数据确定的。
通过当前数据和由历史数据计算所得的控制限的比较,我们可以判定当前过程变异是稳定的(受控制)还是不稳定的(不受控制,受到某个特定因素的干扰)。
控制图分为很多种,不同的过程、不同的数据,我们采用不同的控制图。
计量值数据的控制图经常是成对应用,其中常绘制在上方的一张控制图监测均值,或者说过程数据的分布中心,而绘制在下方的一张控制图监测极差,或者说分布的波动程度。
如果借助于练习打靶的例子来说明,那么均值就是靶子上射击集中的地方,极差是射击点的离散程度。
计量值数据要成对使用控制图,计数值数据则通常只使用一张控制图就足够了。
适用场合·当你希望控制当前过程,问题出现时能察觉并能对其采取补救措施时;·当你希望对过程输出的变化范围进行预测时:·当你判断一个过程是否稳定(处于统计受控状态)时;·当你分析过程变异来源是随机性(偶然事件)还是非随机性(过程本身固有)时;·当你决定怎样完成一个质量改进项目时——防止特殊问题的出现,或对过程进行基础性的改变。


SPC中的EWMA指数加权移动平均控制图========================================================== 本文由QuAInS[注1]根据Douglas Montgomery[注2]相关专注整理而成==========================================================在统计过程控制SPC中,指数加权移动平均(EWMA: Exponentially Weighted Moving Average)控制图常用来侦测流程的微小偏移,作用与累积和控制图(CUSUM:Cumulative Sum)类似,但设置和操作通常要容易一些。
EWMA有时也称为几何移动平均(GMA: Geometric Moving Average),在时间序列建模和预测领域应用十分广泛。
指数加权移动平均控制图由Roberts在1959年提出,后来被广泛使用。
其定义公式为:, 其中常数λ的取值范围为0<λ≤1,z i是EWMA统计量,即所有之前样本均值的加权平均值,。
该公式的初始值z0(当i=1时)取流程的目标值(即在z0=μ0),有时也用初始数据的均值作为初始值,即z0=XBar。
由于EWMA是所有之前和当前样本的加权平均,因此对数据的正态性假设很不敏感,因此,用于单个观测值是十分理想的。
如果观测值x i是独立的随机变量,方差为σ2,那么z i的方差为因此,EWMA控制图的纵轴是z i,横轴是样本序号或时间,中心线和控制限的计算公式为:注意到上述公式中的(1-λ)2i部分,当i逐渐增大时,(1-λ)2i将很快收敛到0,因此当i增大时,UCL和LCL将稳定到下面两个值:,但当i比较小时,强烈建议使用精确公式,这样十分有助于提高此时EWMA控制图的作用以侦测流程的偏移。
以下是一个EWMA控制图的示例:如何决定公式中L和λ的值EWMA控制图对于侦测流程的微小偏移十分有用。

多变量 EWMA 控制图
EWMA 控制图的多变量形式。
使用多变量 EWMA 控制图可以在指数加权控制图中同时监控两个或多个相关过程特征。
例如,使用多变量 EWMA 控制图可以监控塑料注模过程中的温度和压力。
每个多变量 EWMA 点都结合了来自与用户定义的加权因子组合的所有以前子组或观测值的信息。
多变量 EWMA 控制图可以帮助您较其他多变量控制图(如 T 方控制图)更快地检测出较小的过程偏差。
多变量 EWMA 控制图的另一个优点是,当计算中增加了一个小值或大值时,它们不会受到很大影响。
而且,您还可以将多变量 EWMA 控制图自定义为能检测过程中任意大小的偏差。
因此,它们经常用于监控受控过程,以检测出背离目标的较小偏差。
例如,下面的多变量 EWMA 控制图就是上述塑料注模示例的图示:
多变量 EWMA 控制图
控制上限之上没有点,因此可以认为变异是稳定的。
但是,有几个点比其余的点位置高,可以对这几个点进行分析。
图中的点可以基于子组,也可以基于单个观测值。
当数据在子组中时,计算每个子组中所有观测值的均值。
然后根据这些均值得出指数加权移动平均值。
如果有单个观测值,则根据单个观测值得出指数加权移动平均值。

SPC中的EWMA指数加权移动平均控制图========================================================== 本文由QuAInS[注1]根据Douglas Montgomery[注2]相关专注整理而成==========================================================在统计过程控制SPC中,指数加权移动平均(EWMA: Exponentially Weighted Moving Average)控制图常用来侦测流程的微小偏移,作用与累积和控制图(CUSUM:Cumulative Sum)类似,但设置和操作通常要容易一些。
EWMA有时也称为几何移动平均(GMA: Geometric Moving Average),在时间序列建模和预测领域应用十分广泛。
指数加权移动平均控制图由Roberts在1959年提出,后来被广泛使用。
其定义公式为:, 其中常数λ的取值范围为0<λ≤1,z i是EWMA统计量,即所有之前样本均值的加权平均值,。
该公式的初始值z0(当i=1时)取流程的目标值(即在z0=μ0),有时也用初始数据的均值作为初始值,即z0=XBar。
由于EWMA是所有之前和当前样本的加权平均,因此对数据的正态性假设很不敏感,因此,用于单个观测值是十分理想的。
如果观测值x i是独立的随机变量,方差为σ2,那么z i的方差为因此,EWMA控制图的纵轴是z i,横轴是样本序号或时间,中心线和控制限的计算公式为:注意到上述公式中的(1-λ)2i部分,当i逐渐增大时,(1-λ)2i将很快收敛到0,因此当i增大时,UCL和LCL将稳定到下面两个值:,但当i比较小时,强烈建议使用精确公式,这样十分有助于提高此时EWMA控制图的作用以侦测流程的偏移。
以下是一个EWMA控制图的示例:如何决定公式中L和λ的值EWMA控制图对于侦测流程的微小偏移十分有用。



EWMA 控制图
一种类型的时间加权控制图,图中标绘了指数加权移动平均值。
每个 EWMA 点都根据用户定义的加权因子结合了来自之前所有子组或观测值的信息。
EWMA 控制图的优点是,当较小值或较大值进入计算时不会严重影响到这些控制图。
通过更改使用的权重以及控制限制的 s 数量,可以构建控制图,该图可以检测过程中几乎任何大小的偏移。
因此,它们经常用于监控受控过程,以检测出背离目标的较小偏差。
例如,一家离心机转子生产商想要跟踪一周内生产的所有转子的直径。
直径与目标值必须非常接近,因为即使很小的偏差都会导致问题的出现。
以下 EWMA 控制图产生的结果如下:
EWMA 控制图
点似乎在中心线附近随机变化,而且在控制限制范围内。
未显示出任何趋势或模式。
转子直径的变异性似乎是稳定的。
图中的点可以基于子组,也可以基于单个观测值。
当数据在子组中时,计算每个子组中所有观测值的均值。
然后根据这些均值得出指数加权移动平均值。
如果有单个观测值,则根据单个观测值得出指数加权移动平均值。
EWMA(Exponentially Weighted Moving-Average)Chart指数加权移动平均控制图一、应用条件:1)有时间序列的数据。
2)控制条件严格,检测精度很高的过程(标准差的变化为0.5至2西格玛)。
注:传统的控制图都是基于休哈特理论用3个西格玛来控制,我们无纺布公司一般用Xbar-R图。
3)图示说明:图1二、图形特点:不受正态假定的限定,图上的每个点包含着前面所有子组的信息,具有检出过程均值小漂移的敏感性。
三、相关公式:A:EWMA控制图的中心线的总均值,与休哈特的单值、或均值控制图的中心线是一样的。
B:控制图中点的计算公式注:从公式中可以看出每个点包含着前面所有子组的信息。
C:控制限的计算公式五:举例说明以某精密标准件的厚度为例,用Xbar-R图控制,没有异常,如图2图2但是用EWMA控制图来控制却有异常:图3可以从上控制线的数据来说明,Xbar-R的UCL值是3.178;而EWMA的UCL值是3.07596。
而他们的中心线都是一致的3.0385。
六:目前我司应用的控制图(以亲水产品的回渗为例):图4七、个人总结:没必要在无纺布领域应用EWMA控制图,因为休哈特理论是从电子和机加工行业延伸出来的,这种行业基本上是标准模具控制,加工条件相对稳定,才用3个西格玛进行控制。
而我们的无纺布这种流程性材料工艺本身决定随机因素影响较大,用0.5-2个西格玛来控制,基本上是不可行,可以说是作茧自缚。
克重还勉强可以控制(取样数据较多的情况下),如强力、伸长率、亲水性能就更难控制。
如果客户问及,我们可以说无纺布领域的物理性能控制用3西格玛就已经足以严格。
如果要用EWMA控制图,我们可以用minitab来做相应的分析用如图5。
图5。