DFP变尺度法例题终结版

点云对齐杨成林∗2009年5月31日进行数据采集时，由于受到测量设备和坏境的限制，物体表面完整测量数据的获得往往需要通过多次测量完成。

由于每次测量得到的点云数据往往只覆盖物体部分表面，并且可能出现平移错位和旋转错位，因此为了得到物体完整表面的点云数据，需要对这些局部点云数据进行对齐。

点云的对齐所用的方法可分为两种，一种是依靠测量设备进行对齐，另一种则是根据测量后的数据处理对齐。

第一种方法通过特定的设备测量待测工件或测量传感器在多次测量中的位姿。

通过测得的位姿来对齐多次测量数据。

这一方法快速方便，不需后续处理，不过需要额外的设备，而且不能完全满足测量视角的要求。

第二种方法利用测量得到的数据进行对齐，不受设备的约束，测量视角的选择可以更加自由，不过有时计算量很大，而且会因为局部最优等问题得不到正确的对齐。

本文主要讨论后一种对齐方式。

1ICP方法对于两个点集:作为对齐基准的点集P={p1,p2,...,p n}和待对齐的点集X={x1,x2,...,x m}，两个点云的对齐是使以下目标函数的值最小f(R,t)=mi=1||Rx i+t−y i||22(1)其中R和t分别是旋转矩阵和平移向量，而y i是点x i经过变换后的对应点。

此公式中，对应点可以有多种定义方法，比如规定y i为点x i在P中的最近点。

点云对齐问题的难点在于：y i是R和t的函数，事先无法确定，而∗*****************1且对应点的求取通常是计算量很大的工作。

在对应点是最近点的情况，原始的方法计算复杂度为O(mn)，常用的改进方法kd-tree方法计算复杂度在最好的情况下为O(m log n)。

在点集中点数很多的情况下，计算上的消耗是很大的，所以目标函数求值是计算量很大的工作。

虽然对于一般的最优化问题，减少目标函数的计算次数也是一个重要的目标，但在点云对齐问题中，减少目标函数的计算显得尤为重要。

为了解决这一问题，对齐问题的处理通常分为初始对齐和精确对齐两步。

第四章
第四章
无约束优化问题标准形式：
无约束优化问题标准形式：
§
§
§
§
§
§
图最速下降法的收敛过程
αα
2
2
例4－1 求目标函数
取初始点
[2,2]
=
x
例4－2 求目标函数解取初始点[2,2]
=x
算出一维搜索最佳步长
§
例4－3 用梯度法求下面无约束优化问题：
例4－3 用梯度法求下面无约束优化问题：
例4－3 用梯度法求下面无约束优化问题：
例4－3 用梯度法求下面无约束优化问题：
例4－3 用梯度法求下面无约束优化问题：
梯度法的特点
x
给定0,ε
一般迭代式：
§4.3
§4.3
§4.3
§4.3
α0
d 0
x
x 1
x*
1
α1d 1
1()
f −∇x d 1
4-4 共轭方向法
假设目标函数f (x ) 在极值点附近的二次近似函数为
沿某个下降方向
如果能够选定这样的搜索方向，那么对于二
α
0d0
x0x1x*
1
α
1
d1
1
()
f
−∇x d
1。

X ( k 1) X ( k ) ( k ) [ H ( X ( k ) )]1f ( X ( k ) )
式中，步长因子 ( k ) 又称阻尼因子。
（2-46）
阻尼（修正）牛顿法特点：
（1）阻尼牛顿法保持了牛顿法收敛快的特点，且对
初始点无特别要求。虽然计算量多了一些，但实用性更好
4.4.2 牛顿法
S
(k )
[ H ( X
(k )
)] f ( X
1
(k )
)
(2-45)
4.4.2 牛顿法
X ( k 1) X ( k ) [ H ( X ( k ) )]1 f ( X ( k ) )
S ( k ) [ H ( X ( k ) )]1 f ( X ( k ) )
迭代开始（k＝0）规定： A( 0) I 。 利用上式求得的校正矩代入式(2-54)，可得到变尺度矩阵的DFP递推 公式 ：
A( k 1)
(k) X A g g A A( k ) (k ) T (k ) (k ) T (k) (k ) X g g A g
4.4.2 牛顿法
上式就是原始牛顿法的迭代公式。
由上式 (2-44)(可知， 牛顿法的搜索方向 ( k 1) k) ( k ) 1 (k ) 为
X
X
[H ( X
)] f ( X
(k ) 1
)
S
(k )
[ H ( X
)] f ( X
(k )
)
(2-45)
牛顿法的迭代步长恒取1
4.4.2 牛顿法
X ( k 1) X ( k ) ( k ) [ H ( X ( k ) )]1f ( X ( k ) )

5）检查迭代次数，若k=n(完成一轮迭代仍未能满足精度要求)，则令 = 进行下一轮迭代计算；若k n,则进行下一步；
6）构造新的迭代方向
五、DFP法的特点
1）DFP法具有牛顿法的二阶收敛速度，因变尺度矩阵 最终逼近 。
2）对任意给定的初始点 ，都具有最速下降方向 =-▽f( )。这是由于初始变尺度矩阵 =I(单位阵)，所以搜索方向 =- ▽f( )=-▽f( )。
3）每次搜产生的方向都是共轭的。
4）计算公式具有递推性，便于迭代。只要给出 ， ，即可往下计算。
5）计算方便，无需计算二阶导数矩阵及其逆矩阵。
六、BFGS法
本章学习要点
1）首先要抓住并理解各种优化方法的基本思想、具体的迭代步骤，读懂计算程序框图；其次是较复杂的数学推导。对于工程技术人员来说，主要是应用。因此，对每种优化方法书中都有较简单的数学模型的例题，用手算的迭代过程，读者将例题与计算程序框图结合起来，认真地阅读理解。有条件最好再上机运算，在实践中进一步理解每种优化方法的迭代逻辑。
一、基本思想
二、构造变尺度矩阵 的基本要求
三、校正矩阵 de推导
四、变尺度法的迭代步骤
1）给定初始点 、收敛精度ε和维数n;
2）置k=0, = =I（n×n阶单位阵），计算梯度 =▽f( ),搜索方向 =- ▽f( )=- ；
3）进行一维搜索求最优步长因子，迭代点：
minf( + = +
4）收敛精度判断
第七节
变尺度法是在克服了梯度法收敛速度慢和牛顿法计算量、存储量大的特点基础上而发展起来的，被公认为是求解无约束优化问题最有效的算法之一，现已在工程优化设计中得到了广泛的应用。变尺度法的种类较多，这里只介绍其中最常用的两种方法：DFP法和BFGS法。DFP变尺度法先由戴维顿（Davidon）于1959年提出，后经费莱彻（Fletcher）和鲍威尔（Powell）于1963年改进而来，故又称DFP法。

2.6、DFP变尺度法：变尺度法是Davidon 由于1959年提出后又经Fletcher和Powell加以 发展和完善了后的一种变尺度法，故称DFP变 尺度法
1、基本思想： 变尺度法是克服了梯度法收敛慢和牛顿法计 算量大的缺点而发展起来的，是求解无约束问题 最有效的算法，在工程优化设计中得到了广泛的 应用。 利用牛顿法的迭代公式，然后并不是直接 计算 [ H ( x )] 而是 用一个对称正定矩阵 G( x )近似 (k ) 地代替 [ H ( x )] , G( x ) 在迭代过程中不断改进。
⑥检查迭代次数若 若 k n 则转(7)
( k 1)
k n
置
( k 1)
x
x
则转(2)
(k )
⑦计算
f ( x
( k 1)
)g
(k )
( k 1)
g
g
(k )
g
(k )
(k )
x
x
x
E
(k )
G
(k )
E
(k )
G
( k 1)
然后 置 k 1 k转(3) G
说明: 已有文献证明：对于二次函数 f ( x)DFP 变尺度法所构成的搜索方向 S S S S 为一组关于海色矩阵共轭的矢量。所以DFP变 尺度法属于共轭方向法，具有二次收敛性,在任 意情况下，这样方法对于二次目标函数都将在 几步内搜索到目标函数的最优点，而是最后的 构造矩阵必等于海色矩阵.
0 1
计算 x
点的导数值
S
( 0)
( 0)
g
( 0)
f ( x
( 0)
8(8 5) 24 ) 2(9 6) 6

( j)
H k +1 Ap
( j)
( j)
= H k Ap
(k )
( j)
+
p p p p( j )
(k )
( k )T
Ap
(k )
( j)
( k )T
q
−
Hkq q q
( k ) ( k )T ( k )T
H k q( k )
=p
−
Hkq
( Ap
(k ) T (k )
)
q
( k )T
Hkq
= p( j )
(k ) ( k )T (k )
∆x ∆x H k ∆g ∆g H k H k +1 = H k + ( k ) T ( k ) − ( k )T (k ) ∆x ∆g ∆g H k ∆g
(k ) ( k )T (k ) ( k )T
p p H k q q H k (k ) H k +1q = H k + ( k )T ( k ) − ( k )T q (k ) p q q Hkq ( k ) ( k )T ( k ) ( k ) ( k )T (k ) p p q Hkq q Hkq (k ) =H k q + − =p ( k ) ( k )T ( k ) ( k )T (k ) p q q Hkq
( i )T
p
( k )T
Ap
( j)
= λk d
( k )T
Ap
( j)
= −λk ( H k g k ) Ap
T
( j)
T T T = −λk g k H k Ap ( j ) = −λk g k p ( j ) = −λk λ j g k d ( j ) = 0.

A1=A0+△A0 推广到一般的k+1次构造矩阵
Ak+1=Ak+△Ak
矩阵序列的 基本迭代式
△Ak称为校正矩阵
拟牛顿条件
设F（x）为一般形式n阶的目标函数，并具有连续的一、二 阶偏导。在点 处的二次泰勒近似展开
该近似二次函数的梯度是
沿g(k)方向一维搜索，
求最优步长(k)。
x(k+1)= x(k)- (k) g(k)
出口
例 8-4 用最速下降法求解下列问题
min f (x) 2x12 x22 ，
给 定 初 始 点 x(1) (1, 1)T , 1 ．
10
解 目 标 函 数 f (x) 的 梯 度 及 x(1) 处 的 最 速 下 降 方 向 为
f(xk+1)
>
阻尼牛顿法
对原始牛顿法的改进
为解决原始牛顿法的不足，加入搜索步长(k)
因此，迭代公式变为：
x (k+1) = x (k) - (k) Hk-1gk 这就是阻尼牛顿法的迭代公式，最优步长(k)也称
为阻尼因子，是沿牛顿方向一维搜索得到的最优步 长。
牛顿法算法步骤
⑴任选初始点 ，给定精度ε，置k←0 ⑵计算 点的梯度矢量及其模
(x)=
x (k)
gk+
Hkx=0
得 x (k+1) = x (k) - Hk-1gk
即牛顿法迭代公式，方向- Hk-1gk称为牛顿方向
三、原始牛顿法的特点
若用原始牛顿法求某二次目标函数的最优解，则 构造的逼近函数与原目标函数是完全相同的二次式， 其等值线完全重合，故从任一点出发，一定可以一次 达到目标函数的极小点。
二、 确k定的方确法定自学，不作要求。记住

1.Fibonacci法—理想方法，不常用。
2.黄金分割法（0.618法）
原理：提高搜索效率：1）每次只插一个值，利用一个前次的插值；2）每次的缩短率λ相同。左右对称。
程序：p52
（四）插值方法
1.抛物线法
原理：任意插3点：
算得： ； ；
要求：
设函数 用经过3点的抛物线 代替，有
解线代数方程
解得：
程序框图p57
网格法 ，缩小区间，继续搜索。
Monte Carlo方法 ， ，随机数。
比较各次得到的 得解
遗传算法(专题)
（二）区间消去法（凸函数）
1.搜索区间的确定：高—低--高（ ）则区间内有极值。
2.区间消去法原理：在区间[a, b]内插两个点a1, b1保留有极值点区间，消去多余区间。
缩短率：
（三）0.618法
可行方向—约束允许的、函数减小的方向。（图）约束边界的切线与函数等高线的切线方向形成的区域。
数学模型
用内点法或混合法，取 ，
直接方法
（一）随机方向法
1.在可行域产生一个初始点 ，因 （约束），则
--（0，1）的随机数。
2.找k个随机方向，每个方向有n个方向余弦，要产生kn个随机数 ， ， ，随机方向的单位向量为
3.取一试验步长 ，计算每个方向的最优点
4.找出可行域中的最好点 得搜索方向 。以 为起点， 为搜索方向得 。最优点必须在可行域内或边界上，为此要逐步增加步长。
得
穷举下去得递推公式
3.算例
p73
4.框图p72
5.特点
作业：1. 2.
（六）变尺度法
1.引言
坐标变换
二次函数
令 为尺度变换矩阵

f (x*) 0, 2 f x 正定，则 x 为 f (x) 的严格局部极小
点。
如果 2 f x 负定，则 x 为 f (x) 的严格局部极大点。
无约束优化的最优性条件----凸优化的一阶条件
定理(一阶充要条件)
设 f : Rn R 是凸函数且在 x 处连续可微，则 x 为 f (x)的全局极小点的充要条件是 f (x*) 0.
f (x p) f (x)+f (x)T p o( )
P是什么方向时，函数值 f (x p) 下降最快？也就是
p是什么方向时，f (x)T p 取得最小值？
f (x)T p f (x) p cos(f (x), p)
当 cos(f (x), p) 1 时，f (x)T p 最小，最小值为
令 f x 0, 即：
利用一阶条件 求驻点
利用二阶条件 判断驻点是否 是极小点
x12 1 0
x22
2x2
0
得到驻点： 1 1 1 1
x1
0 ,
x2
2 ,
x3
0
,
x4
2
.
无约束优化的最优性条件
函数 f x 的Hesse阵：
2
f
x
2x1
0
0
2
x2
2
利用二阶条件 判断驻点是否 是极小点
2 0
0 2
的行列式小于0；
x1, x4是鞍点；
2
f
x2
2 0
0
2
是正定矩阵；
x2 是极小点；
2
f
x3
2 0
0 2
是负定矩阵；
x3 是极大点。
• 对某些较简单的函数，这样做有时是可行的；

(0)
) = (4,100) , P
T
(0)
= − H ( X (0) )∇f ( X (0) ) = (−4, −100)T
_
1.求迭代点X (1) , 令ϕ0 α）=f ( X (0) + α 0 P (0) )得ϕ0 α 0）的最小值点α 0 = 0.02 （ （
= X
(1) (0)
+ α 0 P ( 0 ) = (2, 2) T + 0.02( − 4, − 100) T = (1.92, 0) T
表2 DFP变尺度法结果表
K αK
0 1 2 0.02 0.5
X1
2 1.92 0
X2 2 0 0.0015 5
∂ X K ∂X 1
_
∇f (X
_ K
_ K
f (X )
4 3.84 0
100 0
100.2 3.84
104 3.686
0.0775 0.07 75
6.006×10−5
下一个搜索方向：P = − H( X )∇f ( X ) = [ −3.84, −0.0031]
(1) (1) (1)
_
T
2.求迭代点 X ，令 ϕ1 = f ( X (1) + ∂1 P (1) )
(2)
得 ϕ(∂1) 的最小值点∂ 1
1
=0.5
T
[ 0, − 0 .0 0 1 5 5 ] T (2) ∇f ( X ) = [ 0, −0.0775]
∆X(0) (∆X(0) )T H(X(0) )∆g(0) (∆g(0) )T H(X(0) ) H(X(0) ) = H(X(0) ) + − − (0) (0) (∆g )∆X (∆g(0) )T H(X(0) )∆g(0)

for(j=0;j<n;j++)
{
h[i][j]=0;
if(j==i) h[i][j]=1;
}
g1=g2; k=-1;
}else{
int j;
double a1=0,a2=0;
for(i=0;i<n;i++){
dg[i]=g2[i]-g1[i];
dx[i]=xk1[i]-xk[i];
}
for(i=0;i<n;i++){
if(ia==1) { aa=a[1]; *ft=f[1]; break; }
d=(pow(a[0],2)-pow(a[2],2))*(a[0]-a[1])-(pow(a[0],2)-pow(a[1],2))*(a[0]-a[2]);
if(fabs(d)==0) break;
c=((f[0]-f[2])*(a[0]-a[1])-(f[0]-f[1])*(a[0]-a[2]))/d;
ib=0;
if(ia==1) { xx=xk; break; }
ib=0;
for(i=0;i<n;i++) s[i]=0;
for(i=0;i<n;i++)
for(j=0;j<n;j++)
s[i]+= -h[i][j]*g1[j];
aa=lagrange(xk,ft,s);
xk1=iterate(xk,aa,s);
a[1]=(a[0]+a[2])/2;
f[1]=func(xk,a[1],s);
}
}else{
if(*ft>f[1]) {a[0]=aa;f[0]=*ft;}

【MATLAB与机械设计】多维优化之DFP变尺度法1.程序框图其中E矩阵的求解公式为：2.MATLAB可执⾏程序function [k,x_min,f_min]= variable_metric_algorithm(f,x,exp)%% 程序说明%{该程序应⽤于多维⽆条件优化问题中的变尺度法变量说明：输⼊值部分f为⽬标函数，对于⽬标函数中⾃由变量的个数没有要求x为初值矩阵，要求在调⽤函数是必须为⼀⾏n列的形式，否则会导致后期维度出现错误exp为精度返回值部分k为迭代次数x_min为函数的局部极⼩值数列f_min为函数的局部极⼩值调⽤⽅法：clcclearsyms x1 x2%所有的⾃由变量且必须由x1,x2,x3……表⽰x=[0,0];f=x1^2+x2^2-x1*x2-10*x1-4*x2+60;exp=0.01;[k,x_min,f_min]=variable_metric_algorithm(f,x,exp)%}%% 确定维度x_size=size(x,2);x_i= sym(zeros(1,x_size));%class(x_i)for i=1:x_sizesyms(['x' num2str(i)]);x_i(1,i)=['x' num2str(i)];end%% 迭代主题grad_f=gradient(f,x_i);H=eye(x_size);fz_d=-subs(grad_f,x_i,x);fz_d=double(fz_d);g0=fz_d;k=0;while 1s=-H*g0;syms as=s';f_b=subs(f,x_i,x+a.*s);f_bd=diff(f_b,a);a=solve(f_bd==0,a);a=double(a);x_1=x+a*s;fz_d1=-subs(grad_f,x_i,x_1);fz_d1=double(fz_d1);fz_dm1=norm(fz_d1);g1=fz_d1;if fz_dm1<=expx_min=x_1;f_min=subs(f,x_i,x_min);k=k;break;elseif k==x_sizefz_d=-subs(grad_f,x_i,x_1);fz_d=double(fz_d);k=0;H=eye(x_size);elsedeta_x=x_1-x;deta_f_d=fz_d1-fz_d;A=(deta_x')*(deta_x);sub_A=(deta_x)*deta_f_d;B=H*deta_f_d*(deta_f_d')*H; sub_B=(deta_f_d')*H*deta_f_d; E=A./sub_A-B./sub_B;H=H+E;k=k+1;endx=x_1;g0=g1;endendend。

step4. 若 || f ( xk1) || ,停止，x* xk1 ;
否则，令 k : k 1, 转step 2 。
14
➢算法框图
给定初始点x0和精度 || f ( x0 ) ||
停止，输出x1
否
是
| x1 x0 |
是 停止，输出x0
否 否
2 f (x0) 0
计算x1
x0
f ( x0 ) 2 f (x0)
1
13 62
x2
x1
1d 1
(
36 , 31
8 31
)T
7
三、最速下降法的特点
1.性质. 设 f ( x) 有一阶连续偏导数，若 步长 满足 k
f ( xk d k ) min f ( xk d k )
k
则有 f ( xk d k )T d k 0。 k
证明：令 ( ) f ( xk d k )，所以
5
一、梯度法（最速下降法）：
1. 搜索方向：d k f ( xk ) ,也称为最速下降方向；
2. 搜 索 步 长: k 取 最 优 步 长, 即 满 足
f (xk
kd k )
min
f
(xk
d k ) 。
二、梯度法算法步骤：
1. 给定初始点 x1 Rn ,允许误差 0, 令k 1。
2. 计算搜索方向 d k f ( xk ) ;
Step3. 令 xk 1 xk kd k , 其中tk : f ( xk kd k ) min f ( xk d k )。
24
Step 4. 判断 xk 1 是否满足终止准则： yes: 计算 stop, 则x* : xk1
No : 转 step 5 。

变尺度法 (拟牛顿法)
一.尺度矩阵的引入
尺度变化可以降低函数的偏心程度（通过放大或者缩小各个坐标）
若f (x) 1 xT Gx bT x c，G是对称正定阵，则G与单位阵E合同，故存在一个 2
可逆矩阵Q, 使得QT GQ=E,即函数偏心程度为0 QT Q=G 1 xTGx 1 xTQTGQx
满足上述方程的解很多，我们可以如下确定一组解：
kukukT yk sk k vk vkT yk H k yk
这样，我们可以取：
uk sk ,
kukukT yk sk ,
vk H k yk , k vk vkT yk H k yk ;
8
即：
uk sk , vk Hk yk ,
计算H
，令
k
k

k
1，转step
3.
10
四、变尺度法算法框图：
k k1
给定x0 , H 0
, k 0
d k -H kf (xk )
一维搜索得 k xk 1 xk k d k
修正Hk
N
产生H k 1
xk1 xk
Stop y xk1 解
11
4
(1)d k


H
k
gk为下降方向，则d
k
与梯度方向成钝角，即gT k
d
k

0

gT k
H
k
gk

0,
gT k
H
k
gk

0
H k 对称正定
（3）
f
(x)

1 2
xT Gx

bT
x

)
Step4: 令 k
k 1,
返回Step2.
注: 第一步迭代与最速下降法相同.
三. 对称秩2算法（DFP校正公式）
设校正矩阵的形式为:
H k H k 1 k uk uk
T
Page 10
k vk vk
T
( II )
其中 k 0, uk = uk 1 , uk 2 , , ukn 0
x
k 1
x k d .
k k
Page 13
Step3: 计算
k 1 x
k 1
x
k 1
k
k 1 f ( x
) f ( x )
k T
H k 1 H k d
k 1
k 1 k 1 k 1 k 1
T k 1
)
H k k 1 k 1 H k
2
0 4 , 10 1
0 8
2 x1 f x , 8 x2
0
2 f x 0
2 2 0 0 f ( x ) , d f ( x ) 8 8
f
T
H1 H 0
1 1
T
T
1 1

H 0 1 1 H 0
T
1 H 0 1 Page 16
T
又
0.26154 1 x x 1.04 x
1
f x
0
0.52308 8.36923
1 0 0
Page 15
f
x 1.47692,
1
0.36923 ,

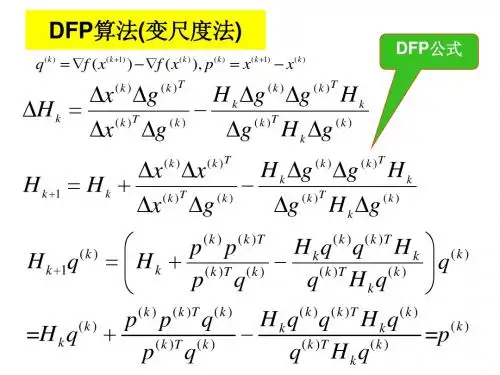
dfp变尺度法
DFP变尺度法（Davidon-Fletcher-Powell变尺度法）是一种拟牛顿优化算法，用于求解无约束极值问题它综合了梯度法和牛顿法的优点，具有较快的收敛速度和较广的应用范围DFP算法在优化领域中被认为是一种高效的方法，尤其在处理高维问题时具有显著优势。

DFP变尺度法的基本思想是在每次迭代中，用一组线性方程组来近似表示目标函数的Hessian矩阵这样，我们可以用较少的计算代价获得牛顿法类似的收敛速度变尺度法的关键在于选择合适的尺度矩阵，以保证算法的收敛性和稳定性。

DFP算法的步骤如下。

1.初始化：选择一个初始点x0.
2.计算目标函数的梯度g（x）。

f(x)=f(x0)+γ(x-x0).
其中，γ为尺度因子
3.计算Hessian矩阵的近似值H
H=I-γ²g²(x).
4.更新搜索方向。

s=-Hg(x).
5.更新x。

x=x0+αs.
其中，α为线搜索参数。

6.重复步骤2-5，直到满足终止条件（如收敛或达到迭代次数限制）。

DFP变尺度法在实际应用中通常与一维搜索技术和黄金分割法相结合，以提高收敛速度和稳定性此外，还可以根据问题特点对算法进行适当调整，如引入局部搜索、调整线搜索策略等，以适应不同问题的需求总之，DFP变尺度法是一种高效、实用的优化算法，在许多领域都得到了广泛应用。

小值，计算将失败。 如图所示为一个三维优化问题的示例，设第一环中
各1矢=0量，必则在新该生平方面向内与，e使2 、搜e索3共局面限，于随二后维的空各间环，方不向能组得中到，
最优解。
x3S1x1 1=0Fra bibliotek2e2
x2
3e3
鲍威尔基本算法的退化
二、鲍威尔修正算法
在某环已经取得的n+1各方向中，选取n个线性无关 的并且共轭程度尽可能高的方向作为下一环的基本方向组
组矢量式，中，1(Sk) 1、(k)、2S(k2)(k、) 、• ••••、• 、nS(k)n为(k)为个第方k向环的基最本优方步向长。 表次示搜为索若将S在2在(第k) 降、k环维S的3的(k优)空、化间•搜进• 索•行、过，程S无n中(k法)的出得线现到性n1组维(k)合空=0，间，以的则后函方的数向各极Sk
故得最优解
梯度法
优化设计是追求目标函数值最小，因此，自然可以设想 从某点出发，其搜索方向取该点的负梯度方向，使函数值在 该点附近下降最快。这种方法也称为最速下降法。
一、基本原理
梯度法的迭代公式为：
x(k+1)=x(k)-(k)g(k) 其中g(k)是函数F(x)在迭代点x(k)处的梯度f(x(k)) ， (k)一
对于n维优化问题，如果只利用函数值求最优值的解法，称 为直接搜索法；
解析法的收敛速率较高，直接法的可靠性较高。
本章介绍的坐标轮换法和鲍威尔法属于直接法；梯度法、 共轭梯度法、牛顿法和变尺度法属于解析法
无约束优化方法算法的基本过程是:
从选定的某初始点x(k)出发，沿着以一定规律产生的 搜索方向S(k) ,取适当的步长a(k) ,逐次搜寻函数值下降的 新迭代点x(k+1),使之逐步逼近最优点x* 。可以把初始点 x(k) 、搜索方向S(k) 、迭代步长a(k) 称为优化方法算法的 三要素。其中以搜索方向S(k)更为突出和重要，它从根本 上决定着一个算法的成败、收敛速率的快慢等。所以， 一个算法的搜索方向成为该优化方法的基本标志，分析、 确定搜索方向S(k)是研究优化方法的最根本的任务之一。