三重积分在球坐标系下的计算

三重积分球面坐标fai三重积分是数学中的一种重要的积分方法，它可以用来求解三维空间中的各种物理量，如质量、体积、电荷等。

而球面坐标系是三维空间中的一种常用坐标系，它可以用来描述球面上的点的位置。

本文将以三重积分球面坐标为标题，介绍三重积分在球面坐标系下的应用。

我们来看一下球面坐标系的定义。

球面坐标系是由一个半径为r的球面和两个角度θ和φ组成的坐标系。

其中，θ表示点与正z轴的夹角，φ表示点在xy平面上的投影与正x轴的夹角。

因此，一个点在球面坐标系下的坐标可以表示为(r,θ,φ)。

接下来，我们来看一下如何在球面坐标系下进行三重积分。

假设我们要求解一个球面上的某个物理量f(r,θ,φ)，那么它的三重积分可以表示为：∭f(r,θ,φ)drdθdφ其中，积分区域为整个球面，即r从0到R，θ从0到π，φ从0到2π。

在球面坐标系下，积分元素可以表示为：dV=r²sinθdrdθdφ因此，上述三重积分可以进一步化简为：∭f(r,θ,φ)drdθdφ=∫₀²π∫₀ᴨ∫₀ᴿf(r,θ,φ)r²sinθdrdθdφ这个式子看起来比较复杂，但实际上它的计算方法与直角坐标系下的三重积分类似。

我们可以先对r进行积分，然后对θ进行积分，最后对φ进行积分。

在计算过程中，需要注意一些特殊情况，如当θ=0或π时，sinθ=0，此时积分元素为0，需要特殊处理。

三重积分在球面坐标系下的应用非常广泛，例如可以用来求解球体的体积、质量、重心等物理量。

此外，它还可以用来求解球面上的电荷分布、电势等问题。

在实际应用中，我们可以利用计算机软件进行计算，大大提高了计算效率和精度。

三重积分球面坐标是数学中的一个重要概念，它可以用来描述三维空间中的各种物理量，并且在实际应用中具有广泛的应用价值。

希望本文能够对读者理解和掌握三重积分球面坐标的相关知识有所帮助。

三重积分的计算方法三重积分是多元函数积分的一种形式，它在数学和物理学中都有着广泛的应用。

在实际问题中，我们经常需要计算三维空间中某个区域内的函数取值总和，而三重积分就是用来描述这种情况的工具。

在本文中，我们将介绍三重积分的计算方法，包括直角坐标系下的三重积分和柱坐标系、球坐标系下的三重积分计算方法。

首先，我们来看直角坐标系下的三重积分计算方法。

设函数为f(x, y, z)，积分区域为V，那么三重积分的计算公式为：∫∫∫V f(x, y, z) dV。

其中，dV表示微元体积。

在直角坐标系下，微元体积可以表示为dV = dx dy dz，因此三重积分可以表示为：∫∫∫V f(x, y, z) dx dy dz。

这样，我们就可以按照一定的积分顺序，依次对x、y、z进行积分，从而计算出三重积分的值。

在实际计算中，我们需要根据具体的问题选择合适的积分顺序，以简化计算过程。

接下来，我们来看柱坐标系下的三重积分计算方法。

在柱坐标系下，积分区域V可以用柱坐标表示，即V={(ρ, φ, z) | (ρ, φ, z) ∈ D, α ≤ ρ ≤ β, α1 ≤ φ ≤ β1, γ1 ≤ z ≤γ2}。

这时，三重积分的计算公式变为：∫∫∫V f(ρ, φ, z) ρ dρ dφ dz。

在柱坐标系下，微元体积可以表示为dV = ρ dρ dφ dz，因此三重积分可以表示为：∫∫∫V f(ρ, φ, z) ρ dρ dφ dz。

通过将函数用柱坐标表示，并按照一定的积分顺序，依次对ρ、φ、z进行积分，我们也可以计算出三重积分的值。

最后，我们来看球坐标系下的三重积分计算方法。

在球坐标系下，积分区域V可以用球坐标表示，即V={(r, θ, φ) | (r, θ, φ) ∈ D, α ≤ r ≤ β, α1 ≤ θ ≤ β1, α2 ≤ φ ≤β2}。

这时，三重积分的计算公式变为：∫∫∫V f(r, θ, φ) r^2 sinφ dr dθ dφ。

球面坐标是三维空间中描述点的位置的一种方法，它使用了半径 r、极角θ 和方位角φ，球面坐标经常用于计算球面上的函数值，尤其在物理学和工程学领域。

在球面坐标系中进行三重积分计算时，我们需要了解如何将三维空间内的函数表示为球面坐标系内的函数，以及如何对球面坐标系内的函数进行积分。

在本文中，我们将介绍如何计算三重积分的 f本人。

第一步，将三维空间内的函数表示为球面坐标系内的函数。

球坐标系中一个点的坐标可由三个参数来确定，即 r、θ 和φ。

函数在球面坐标系内的表示通常需要将其转换成球面坐标系内的 r、θ 和φ 的函数。

这通常需要进行一些代数运算和三角函数的转换。

对于一个常见的球面坐标系内的函数f(r, θ, φ)，我们需要将其转换成球坐标系内的 r、θ 和φ 的函数f(r(θ, φ), θ, φ)。

第二步，确定积分的上下限。

在三重积分中，确定积分的上下限是十分重要的。

在球面坐标系内进行三重积分时，确定 r、θ 和φ 的取值范围是需要考虑的问题。

通常情况下，r 的取值范围是[0, ∞)，θ 的取值范围是[0, π]，φ 的取值范围是[0, 2π]。

但在具体问题中，可能会有不同的取值范围。

第三步，进行积分运算。

在确定了函数在球面坐标系内的表示和积分的上下限之后，我们可以开始进行积分运算。

按照球面坐标系内的积分公式和上下限进行积分运算，得到所需的三重积分的值。

通过以上三步，我们可以计算出三重积分的 f本人。

需要注意的是，在实际问题中，对于复杂的函数和积分上下限的确定可能需要更多的代数运算和数学技巧。

因此在进行具体计算时，需要仔细分析问题，理清思路，确保计算的准确性。

球面坐标系计算三重积分的 f本人需要将函数表示为球面坐标系内的函数，确定积分的上下限，进行积分运算。

在实际问题中可能需要更多的数学技巧和分析能力，但掌握了基本的方法和步骤，我们就可以顺利地解决球面坐标系的三重积分计算问题。

在进行球面坐标系内的三重积分计算时，除了上文提到的三个基本步骤外，还有一些注意事项和常见问题需要我们在实际计算中加以重视和解决。

三重积分的计算方法三重积分是微积分中的重要内容，它在物理学、工程学、经济学等领域都有着广泛的应用。

在实际问题中，我们常常需要对三维空间中的某些物理量进行积分运算，而三重积分就是用来描述这种三维空间中的积分运算的工具。

下面，我们将介绍三重积分的计算方法。

首先，我们来看三重积分的定义。

对于空间中的一个有界闭区域V，如果函数f(x, y, z)在V上有定义且在V上可积，那么三重积分∬∬∬_{V}f(x,y,z)dxdydz的计算方法如下：1. 将积分区域V投影到xy平面上，得到投影区域D。

2. 在D上选择一个合适的坐标系，通常选择直角坐标系或极坐标系。

3. 再在D上选择一个曲线坐标系，通常选择柱坐标系或球坐标系。

4. 根据选择的坐标系，写出积分的累次积分式。

5. 按照累次积分的顺序依次进行积分运算。

在实际计算中，我们通常会遇到一些复杂的积分问题，下面我们来看一些常见的计算方法。

首先是直角坐标系下的三重积分计算。

在直角坐标系下，积分区域V可以用不等式形式表示，利用三次积分的性质，可以将三重积分化为三个一重积分的累次积分。

这样就可以分别对x、y、z进行积分，从而简化计算。

其次是极坐标系下的三重积分计算。

在极坐标系下，积分区域V通常是某个平面区域在z轴上的投影区域，利用极坐标系的性质，可以将三重积分化为一个二重积分和一个一重积分的累次积分。

这样就可以利用极坐标系的简洁性，简化计算过程。

最后是球坐标系下的三重积分计算。

在球坐标系下，积分区域V通常是一个球体或球体的一部分，利用球坐标系的性质，可以将三重积分化为一个球面上的二重积分和一个一重积分的累次积分。

这样就可以利用球坐标系的简洁性，简化计算过程。

总之，三重积分的计算方法是多样的，我们可以根据具体的问题选择合适的坐标系和积分顺序，从而简化计算过程。

在实际问题中，我们需要灵活运用不同的计算方法，以便高效地解决问题。

希望本文对读者有所帮助，谢谢阅读！。

球面坐标计算三重积分公式dv球面坐标是三维坐标系中的一种坐标系统，由径向距离r、极角θ和方位角φ组成。

它常用于描述球对称的物体的性质和为球对称的场提供方便的数学表达方式。

球面坐标系下的三重积分可以用于求解球对称体的体积、质心、转动惯量等问题。

球面坐标系下的三重积分公式可以通过坐标变换和雅可比行列式的性质来推导得到。

三重积分公式可以分为直角坐标系到球面坐标系的转换和球面坐标系到直角坐标系的转换两部分。

首先来推导直角坐标系到球面坐标系的转换。

假设有一个在直角坐标系下的积分体元dV，在球面坐标系下的体元为dV =r^2sinθdrdθdφ。

其中，r为球面到原点的距离，θ为球面与正半轴的夹角，φ为球面上的方位角。

则有：∫∫∫f(x, y, z)dV = ∫∫∫f(rsinθcosφ, rsinθsinφ, rcosθ) r^2sinθdrdθdφ其中，f(x, y, z)是在直角坐标系下的函数，f(rsinθcosφ,rsinθsinφ, rcosθ)是在球面坐标系下的函数。

接下来推导球面坐标系到直角坐标系的转换。

由于球面坐标系的坐标轴不是直角坐标系的坐标轴，为了将球面坐标系下的函数转换为直角坐标系下的函数，需要用雅可比行列式进行修正。

则有：∫∫∫f(r, θ, φ)dV = ∫∫∫f(x, y, z) Jdxdydz其中，f(r, θ, φ)是在球面坐标系下的函数，f(x, y, z)是在直角坐标系下的函数。

J为雅可比行列式，可以通过求偏导数来计算：J = ∂(x, y, z)/∂(r, θ, φ)将J乘以直角坐标系下的积分体元dxdydz，则有：∫∫∫f(r, θ, φ)dV = ∫∫∫f(x, y, z) |J|dxdydz其中，|J|为雅可比行列式的绝对值。

这样就得到了球面坐标系下的三重积分公式。

通过适当的变换和雅可比行列式的计算，可以将球面坐标系下的函数转换为直角坐标系下的函数进行计算。

在实际问题中，可以使用数值方法，如数值积分或计算机模拟，来近似计算球面坐标系下的三重积分。

三重积分的计算方法三重积分是数学中的重要概念，用于计算三维空间中的体积、质量、重心等物理量。

在本文中，我们将介绍三重积分的计算方法，并提供一些实例来帮助读者更好地理解。

一、直角坐标系下的三重积分在直角坐标系下，三重积分的计算方法可以通过迭代法实现。

首先，我们需要确定被积函数的积分区域。

假设被积函数为f(x, y, z)，积分区域为V。

我们可以将V分割成若干个小立方体，每个小立方体的体积为ΔV。

将V分割成小立方体后，我们需要选择一个小立方体，并在其中选择一个点(x,y,z)作为积分点。

然后，我们将小立方体的体积ΔV乘以被积函数在积分点的值f(x,y,z)，得到积分项f(x,y,z)ΔV。

最后，将所有积分项相加并取极限，即可求得三重积分的值。

这个计算过程可以表达为以下公式：∭V f(x,y,z) dV = lim ΔV→0 ∑ ∑ ∑ f(x,y,z)ΔV其中，ΔV表示小立方体的体积，Σ表示对整个区域V内的小立方体进行求和。

举例来说，如果我们要计算函数f(x,y,z) = x^2 + 2y^2 + 3z^2在立方体V: 0≤x≤1，0≤y≤2，0≤z≤3上的三重积分，那么我们可以将V分割成许多小立方体，并选择一个小立方体上的点(x,y,z)作为积分点。

然后，将小立方体体积ΔV乘以函数值f(x,y,z)，并对所有小立方体进行求和，最后取极限即可得到结果。

二、柱坐标系和球坐标系下的三重积分在某些情况下，采用直角坐标系计算三重积分可能会比较复杂。

此时，我们可以选择转换到柱坐标系或球坐标系下进行计算，以简化问题。

在柱坐标系下，我们将积分区域V进行柱坐标变换，得到新的积分区域。

具体的变换公式可以参考相关数学教材。

然后，按照直角坐标系下的计算方法进行计算。

在球坐标系下的计算方法与柱坐标系类似，先进行球坐标变换，然后按照直角坐标系下的计算方法进行计算。

三、应用举例现在，让我们通过一个应用举例来更好地理解三重积分的计算方法。

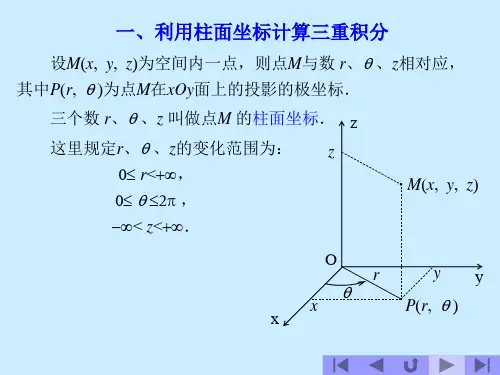
利用球面坐标计算三重积分设M（x，y，z）为空间内一点，则点M也可用这样三个有次序的数r，φ，θ来确定，其中r为原点O与点M间的距离，φ为有向线段与z轴正向所夹的角，θ为从正z轴来看自x轴按逆时针方向转到有向线段的角，这里P为点M在xOy面上的投影。

这样的三个数r，φ，θ叫做点M的球面坐标，这里r，φ，θ的变化范围为0 ≤ r < +∞,0 ≤φ≤π,0 ≤θ≤ 2π.r = 常数，即以原点为心的球面；φ= 常数，即以原点为顶点、z轴为轴的圆锥面；θ = 常数，即过z轴的半平面。

点M的直角坐标与球面坐标的关系为（3）为了把三重积分中的变量从直角坐标变换为球面坐标，用三组坐标面r = 常数，φ=常数，θ= 常数把积分区域Ω分成许多小闭区域。

考虑由r，φ，θ各取得微小增量dr，dφ，dθ所成的六面体的体积。

不计高阶无穷小，可把这个六面体看作长方体，其经线方向的长为rd φ，纬线方向的宽为r sinφdθ，向径方向的高为dr，于是得dv = r 2 sinφdrdφdθ，这就是球面坐标系中的体积元素。

再注意到关系式（3），就有,（4）其中F（r，φ，θ）= f（r sinφcosθ，r sinφsinθ，r cosφ）。

（4）式就是把三重积分的变量从直角坐标变换为球面坐标的公式。

要计算变量变换为球面坐标后的三重积分，可把它化为对r对φ及对θ的三次积分。

若积分区域Ω的边界曲面是一个包围原点在内的闭曲面，其球面坐标方程为r = r（φ，θ），则。

当积分区域Ω为球面r = a所围成时，则。

特别地，当F（r，φ，θ）= 1时，由上式即得球的体积，这是我们所熟知的。

例2 求半径为a的球面与半顶角为α的内接锥面所围成的立体的体积。

解设球面通过原点O，球心在z轴上，又内接锥面的顶点在原点O，其轴与z轴重合，则球面方程为r = 2acosφ，锥面方程为φ=α。

因为立体所占有的空间闭区域Ω可用不等式0≤r≤2acosφ, 0≤φ≤α, 0≤θ≤2π来表示，所以在三重积分的应用中也可采用元素法。

二重积分与三重积分的计算方法二重积分是求解平面上一块区域上的一些函数的积分，而三重积分是求解空间中一个区域上的一些函数的积分。

二重积分的计算方法包括直角坐标系下的直角坐标法和极坐标法，而三重积分的计算方法则包括直角坐标系下的直角坐标法和柱坐标法、球坐标法。

一、二重积分的计算方法：1.直角坐标法：设区域D在xoy平面上，函数f(x, y)在D上有定义且连续，直角坐标法的二重积分计算公式为：∬f(x, y)dσ = ∫∫f(x, y)dxdy其中积分区域D的边界可以由不等式关系来描述。

2.极坐标法：当函数f(x,y)在此区域上具有简单的表示形式f(r,θ)时，采用极坐标法可以简化计算。

极坐标法的二重积分计算公式为：∬f(x, y)dσ = ∫∫f(rcosθ, rsinθ)rdrdθ其中积分区域D的边界可以由不等式关系来描述。

二、三重积分的计算方法：1.直角坐标法：设区域V在xyz空间中，函数f(x, y, z)在V上有定义且连续，直角坐标法的三重积分计算公式为：∭f(x, y, z)dV = ∫∫∫f(x, y, z)dxdydz其中积分区域V的边界可以由不等式关系来描述。

2.柱坐标法：当函数f(x,y,z)在此区域上具有简单的表示形式f(ρ,θ,z)时，采用柱坐标法可以简化计算。

柱坐标法的三重积分计算公式为：∭f(x, y, z)dV = ∫∫∫f(ρcosθ, ρsinθ, z)ρdρdθdz其中积分区域V的边界可以由不等式关系来描述。

3.球坐标法：当函数f(x,y,z)在此区域上具有简单的表示形式f(ρ,θ,φ)时，采用球坐标法可以简化计算。

球坐标法的三重积分计算公式为：∭f(x, y, z)dV = ∫∫∫f(ρsinφcosθ, ρsinφsinθ,ρcosφ)ρ²sinφdρdθdφ其中积分区域V的边界可以由不等式关系来描述。

以上是二重积分和三重积分的计算方法的基本原理和公式，具体应用中还需要根据具体的题目和区域形状选择合适的计算方法。

三重积分计算详解例题当我们进行三重积分计算时，通常会遇到一个三维空间中的函数，我们希望求解该函数在某个特定区域上的体积、质量、质心等物理量。

下面我将以一个具体的例题来详细解释三重积分的计算过程。

假设我们要计算函数f(x, y, z) = x^2 + y^2 + z^2在球体x^2 + y^2 + z^2 <= 1上的体积。

首先，我们需要确定积分的顺序，由于球体的形状对称性较好，我们选择球坐标系进行积分。

球坐标系下，积分区域为0 ≤ r ≤ 1, 0 ≤ θ ≤ π, 0 ≤ φ ≤ 2π。

接下来，我们可以按照r、θ、φ的顺序进行积分。

首先对r进行积分，然后是θ，最后是φ。

具体的计算过程如下：∫∫∫(球体内部) x^2 + y^2 + z^2 dV = ∫[0, 2π] ∫[0, π] ∫[0, 1] (r^2) r^2 sin(θ) dr dθ dφ。

其中，dV = r^2 sin(θ) dr dθ dφ是球坐标系下的体积元素。

对r进行积分后得到，∫[0, 2π] ∫[0, π] ∫[0, 1] r^4sin(θ) dr dθ dφ = 2π ∫[0, π] sin(θ) dθ ∫[0, 1]r^4 dr.继续计算可得，2π (-cos(π) + cos(0)) (1/5) = 2π (2) (1/5) = 4π/5。

因此，函数f(x, y, z) = x^2 + y^2 + z^2在球体x^2 + y^2+ z^2 <= 1上的体积为4π/5。

这就是对三重积分计算的详细解释。

在实际应用中，我们可以根据具体情况选择合适的坐标系和积分顺序，通过逐步积分来求解体积、质心等物理量。

希望这个例题能够帮助你更好地理解三重积分的计算过程。