07第七章 理想流体动力学
- 格式:ppt
- 大小:1.59 MB
- 文档页数:3

第七章不可压缩流体动力学基础在询面的章节中,我们学习了理想流体和粘性流体的流动分析,按照水力学的 观点,求得平均量。
但是,很多问题需要求得更加详细的信息,如流速、压强等 流动参数在二个或三个坐标轴方向上的分布情况。
本章的容介绍流体运动的基本 规律、基本方程、定解条件和解决流体问题的基本方法。
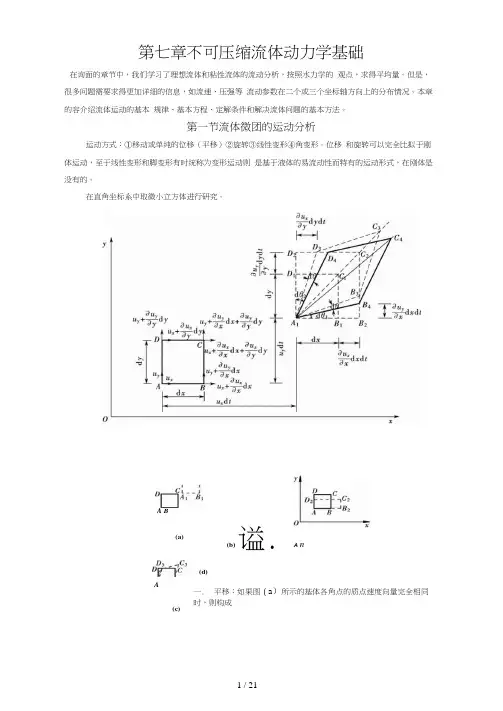
第一节流体微团的运动分析运动方式:①移动或单纯的位移(平移)②旋转③线性变形④角变形。
位移 和旋转可以完全比拟于刚体运动,至于线性变形和脚变形有时统称为变形运动则 是基于液体的易流动性而特有的运动形式,在刚体是没有的。
在直角坐标系中取微小立方体进行研究。
(b)谥.A n(d)一. 平移:如果图(a )所示的基体各角点的质点速度向量完全相同时,则构成(c)A B(a)A了液体基体的单纯位移,其移动速度为心、®、“,。
基体在运动中可能沿直线也 可能沿曲线运动,但其方位与形状都和原来一样(立方基体各边的长度保持不 变)。
二、 线变形:从图(b )中可以看出,由于沿y 轴的速度分量,B 点和C 点都比 A 点和D 点大了竺如 而比就代表〃y = l 时液体基体运动时,在单位时间沿勿dyy 轴方向的伸长率。
du x °"、. du : dxdydz三、 角变形(角变形速度)—BIA ■ dp -------------------------------- Jda-0 = dp + 00 =J"些+些k dz. dx四、旋转(旋转角速度)1O = —0 =—21勿du vdx—dx角变形:血 A那么,代入欧拉加速度表达式,得:du r du Tdu r八 八5=说=古叫 云+"卑+"0+-叭巴加、6仇 du Ya v = ----- = — + u v ---------- + U.0, +ii t a ). -iLCoydt dt dy “'2 …加.du diL q 。


第四章 流体的积分关系式及其应用众所周知,一个固体质点在保守力场中运动时,质点的动能和势能之和保持不变,这就是经典物理中的机械能守恒定律。
从数学的观点看,机械能守恒是动量方程的一次积分,称为能量积分。
有了能量积分方程,我们在处理保守场中的动力学问题时,就可通过该方程将始、末两态直接联系起来,而不必考虑中间过程的细节。
在流体力学中也有类似的积分。
前面一章建立了控制流体流动的微分方程组,原则上利用该方程组可以求解满足Stokes 假设的Newton 流体的任意流动问题。
对于理想流体流动问题,可以直接积分微分方程,得到积分方程。
利用积分方程求解流动问题显然更为简便,因而这些积分方程得到广泛应用。
什么样的流体是理想流体呢?当流体发生剪切变形时总会伴有粘性应力。
粘性应力不仅与流体的粘性性质(以粘性系数表征)有关,还依赖于速度梯度,对于低粘(μ小)流体的流动,如果速度的空间变化不太急剧,粘性应力就比较小。
如果粘性应力对所研究的流动问题影响较小,可以忽略流体的粘性,认为流体是无粘的,即理想流体。
一般常见的流体,如空气和水,粘性系数很小,在自然界和工程中遇到的这些流体的大多数流动,粘性的影响都可以忽略,都可以近似看作理想流体流动。
在流体力学发展的历史上,无粘流理论是流体力学中历史悠久,发展完善,成果辉煌,应用广泛的一个分支领域。
§4.1理想流体运动方程的进一步化简理想流体满足Euler 方程:dV pF dt ρ∇=-, (4-1)或者改写成兰姆—葛罗米柯形式2rot 2VV p V V F t ρ⎛⎫∂∇+∇+⨯=-⎪∂⎝⎭。
(4-2)若体力有势F π=-∇,(4-3)其中π代表体力势,即单位质量流体的势能。
如果体力仅为重力,取z 轴沿g -方向,并取0z =为零势能面,则gz π=。
若流体密度是常量或仅为压强的函数,则称流体是正压流体。
若流体正压,)(p ρρ=,此时可定义压力函数()dpP p ρ=⎰(4-4-1)或()dpdP p ρ=。


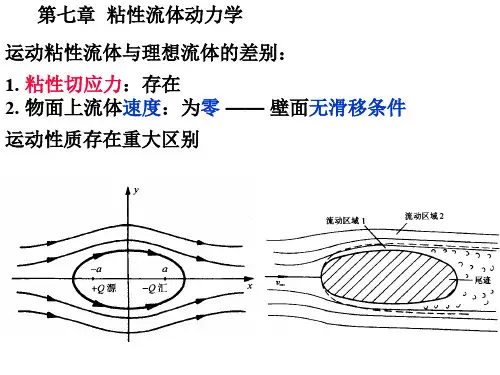
第七章 粘性流体动力学基础实际流体都具有粘性,而在研究粘性较小的流体的某些流动现象时,可将有粘性的实际流体近似地按无粘性的理想流体处理。
例如,粘性小的流体在大雷诺数情况下,其流速和压强分布等均与理想流体理论十分接近。
但在研究粘性小的流体的另一些问题时,与实际情况不符,如按照理想流体理论得到绕流物体的阻力为零。
产生矛盾的主要原因是未考虑实际流体所具有的粘性对流动的影响。
本章,首先建立具有粘性的实际流体运动微分方程,并介绍该方程的在特定条件下的求解。
由于固体边界对流体与固体的相互作用有重要的影响,本章后面主要介绍边界层的一些基本概念、基本原理和基本的分析方法。
§7.1 纳维—斯托克斯方程7.1.1 粘性流体的应力实际流体具有粘性,运动时会产生切应力,它的力学性质不同于理想流体,在作用面上的表面应力既有压应力,也有切应力。
在流场中任取一点M ,过该点作一垂直于z 轴的水平面,如图7-1 所示。
过M 点作用于水平面上的表面应力p n 在x 、y 、z 轴上的分量为一个垂直于水平面的压应力p zz 和两个与水平面相切的切应力τzx 、τzy 。
压应力和切应力的下标中第一个字母表示作用面的法线方向,第二个字母表示应力的作用方向。
显然,通过M 点在三个相互垂直的作用面上的表面应力共有九个分量,其中三个是压应力p xx 、p yy 、p zz ,六个是切应力τxy 、τxz 、τyx 、τyz 、τzx 、τzy ,将应力分量写成矩阵形式:图7-1 作用于水平面的表面应力⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧ττττττzz zyzxyz yy yxxz xy xx p p p (7-1) 九个应力分量中,由于τxy =τyx 、τyz =τzy 、τzx =τxz ,粘性流体中任意一点的应力分量只有6个独立分量,即τxy 、τyz 、τzx 、p xx 、p yy 、p zz 。
7.1.2 应力形式的运动方程在粘性流体的流场中,取一以点M 为中心的微元直角六面体,其边长分别为dx 、dy 、 dz 。



流体动力学方程
《流体动力学方程》
一、定义
流体动力学方程又称为气体动力学方程。
它描述了理想流体在特定条件下的流动规律。
它是一组称为Navier-Stokes方程的微分方程,用来描述流体的压力、速度、温度和其他物理量之间的关系。
二、表达式
Navier-Stokes方程又称为流体动力学方程,包括控制方程和物理方程两部分。
控制方程:
u/t + (u)u = -P + μ2u
其中,u为物质的速度,t为时间,P为压强,μ为粘性系数。
物理方程:
u/t + (u)u = -P + c(T) + 2u
其中,t为时间,P为压强,T为温度,C为热扩散系数。
三、应用
1、气体动力学:流体动力学研究的最重要应用之一就是对于气
体动力学的研究,包括非定常气流、边界层气流、喷气发动机气流等。
2、水力机械:流体动力学方程在水力机械方面也有重要应用,
它可以用来研究水力机械系统中的液体流动特性。
3、流体动力:流体动力学方程可用于研究流体中的动力学特性,从而求解流体在某种特定条件下的动力学参数。