相似三角形的判定(3)

《相似三角形（3）》教学设计教学评价评价量规：随堂提问、动手实践、操作演练、练习反馈；评价策略：坚持“及时评价与激励评价相结合，定量化评价与定性化评价相统一”的原则，最大限度地做到面向全体学生，充分关注学生的个性差异，将学生自评、生生互评和教师概括引领、激励式点评有机结合，既有即兴评价，又有概要性评价；既有学生的自评，又有师生、生生之间的互评，力求在评价中帮助学生认识自我、建立自信，使其逐步养成独立思考、自主探索、合作交流的学习习惯。

教学流程活动流程活动内容及目的活动一创设情境，导入新课（3——5分钟）学生借助已有的知识和经验感知和体会数学的应用价值。

活动二演示操作，形成假设（10——15分钟）探究实践，总结发现自己观察到的结论。

并加以推理证明。

活动三验证假设，获得定论（10——15分钟）将自己发现的结论加以证明。

类比活动2探究结论，运用所学勾股定理加以证明。

活动四运用新知，解决问题（3——5分钟）应用所学知识来解决实际问题活动五回顾总结，推荐作业（3——5分钟）通过归纳、作业，巩固自己所学知识，形成技能技巧。

教学程序问题与情境师生互动媒体使用与设计意图活动1：创设情境导入新课问题：（1）我们已学习过哪些判定三角形相似的方法？（2）如图，△ABC中，点D在AB上，如果AC2=AD•AB，那么△ACD与△ABC相似吗？说说你的理由．(3)观察两副三角尺，同样角度的两个三角尺的三个内角有什么关系？这两个三角形相似吗？如果两个三角形有两组对应角相等，它们相似吗？——引出课题．教师通过提出问题，引导学生复习学过的知识，在此基础上激发学生学习新知的欲望。

学生思考回答，同时教师将学生的回答整理板书到黑板上。

本次活动教师应重点关注：学生能否熟练回答三角形相似的判定定理，相似三角形的判定方法和性质是否熟练。

用已学的知识能否顺利完成练习。

【媒体使用】播放图片，依次出示相关内容。

【设计意图】复习旧知，承前启后；通过本环节的复习和情景创设，让学生达到复习旧知，为新课做好铺垫的目的。

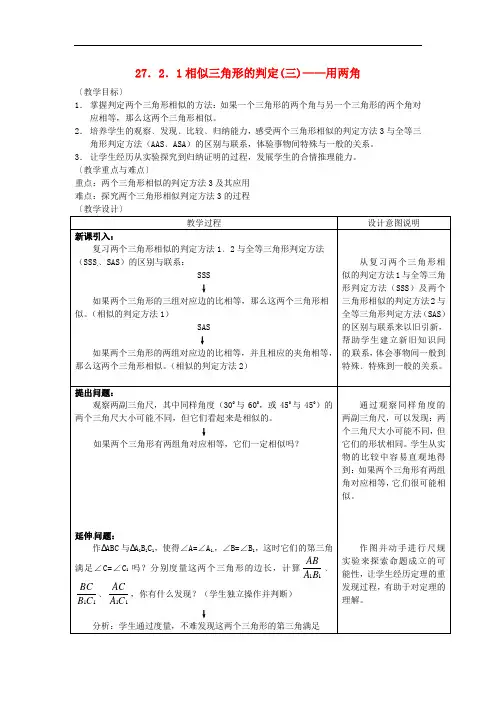
27．2．1相似三角形的判定(三)——用两角〔教学目标〕1． 掌握判定两个三角形相似的方法：如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似。

2． 培养学生的观察﹑发现﹑比较﹑归纳能力，感受两个三角形相似的判定方法3与全等三角形判定方法（AAS ﹑ASA ）的区别与联系，体验事物间特殊与一般的关系。

3． 让学生经历从实验探究到归纳证明的过程，发展学生的合情推理能力。

〔教学重点与难点〕重点：两个三角形相似的判定方法3及其应用 难点：探究两个三角形相似判定方法3的过程 〔教学设计〕教学过程设计意图说明新课引入：复习两个三角形相似的判定方法1﹑2与全等三角形判定方法（SSS ﹑SAS ）的区别与联系：SSS ↓如果两个三角形的三组对应边的比相等，那么这两个三角形相似。

（相似的判定方法1）SAS ↓如果两个三角形的两组对应边的比相等，并且相应的夹角相等，那么这两个三角形相似。

（相似的判定方法2）从复习两个三角形相似的判定方法1与全等三角形判定方法（SSS ）及两个三角形相似的判定方法2与全等三角形判定方法（SAS ）的区别与联系来以旧引新，帮助学生建立新旧知识间的联系，体会事物间一般到特殊﹑特殊到一般的关系。

提出问题：观察两副三角尺，其中同样角度（300与600，或450与450）的两个三角尺大小可能不同，但它们看起来是相似的。

↓如果两个三角形有两组角对应相等，它们一定相似吗？延伸问题：作∆ABC 与∆A 1B 1C 1，使得∠A=∠A 1，∠B=∠B 1，这时它们的第三角满足∠C=∠C 1吗？分别度量这两个三角形的边长，计算11ABA B ﹑11BC B C ﹑11ACA C ，你有什么发现？（学生独立操作并判断） ↓分析：学生通过度量，不难发现这两个三角形的第三角满足通过观察同样角度的两副三角尺，可以发现：两个三角尺大小可能不同，但它们的形状相同。

学生从实物的比较中容易直观地得到：如果两个三角形有两组角对应相等，它们很可能相似。

求证（ ） 求证（2）AC2=AD · AB
CD2=AD · DB
D
例3、如图所示，在△ABC中D为AC边上一 、如图所示， 中 为 边上一 点，若∠DBC= ∠A, 的长。 求DC的长。 的长
D
BC =
C
6,
AC=3,
A
B
A
已知：如图所示，Rt⊿ABC与Rt⊿A′B′C′中 已知：如图所示，Rt⊿ABC与Rt⊿A′B′C′中， ∠C=∠C′=90°， C=∠C′=90° = 求证： 求证： Rt⊿ABC∽Rt⊿A′B′C′
知识顾
我们学习了哪些判定三角形相似的方法，请你 我们学习了哪些判定三角形相似的方法， A D 用几何语言叙述。 用几何语言叙述。
A D B E C B （3）∵ ） C
AB DE
E
= AC DF
F
= BC EF
∴△ABC∽△DEF ∽ （2）∵DE∥BC ） ∥ ∴△ADE∽△ABC ∽
（4） ∵ ）
A A'
B
C
B'
C'
判定定理3 如果一个三角形的两个角 判定定理3：如果一个三角形的两个角与另一个三角 两个角与另一个三角
两个角对应相等 相似。 形的两个角对应相等，那么这两个三角形相似 形的两个角对应相等，那么这两个三角形相似。
可以简单说成：两角对应相等 两三角形相似 相似。 可以简单说成：两角对应相等，两三角形相似。 对应相等，
A B E F G C D
1.已知 如图 ∠ACB=90°,AD=DB,DE⊥AB 已知:如图 已知 如图, ° ⊥ 的延长线于F,试说明 于D交AC于E,交BC的延长线于 试说明 交 于 交 的延长线于 试说明: DC2=DE·DF (2)CD2=CE . CA

例2 如图，在 Rt△ABC 与 Rt△ ABC 中，
B AC 1 ∠C =∠C ′= 90°，且 A AB AC 2 求证：△ ABC∽△ABC.
还可以根据相似三角形 的判定定理2，来证明这两 个直角三角形相似.
练习 1.如图,O为△ABC内一点，D、E、F
分别是OA、OB、OC中点. 求证：△ABC∽△DEF.
= 4 BC 2 =(2 BC )2. 由此得出，BC = 2BC .
BC 1 AB AC . 从而 BC 2 AB AC
因此△ AB C ∽△ABC.
(三边对应成比例的两个三角形相似)
说一说
在例2的证明中，还可以根据哪个判定定理说明 △ ABC ∽ △ABC ？
AD AE DE AB AC BC AD AB A B AE DE AB AC BC A ' B ' A ' C ' BC AB AC BC ∴ AE= A'C', DE= B'C',
A
A'
D B' C' B E
C
∴△A'B'C' ≌ △ADE ∴ △A'B'C' ∽ △ABC
证明： E O
A D F
B
C
D, E , F 分别为OA,OB,OC的中点， 1 1 1 DE = AB , EF BC , DF AC . 2 2 2 DE EF DF 1 . AB BC AC 2 △ABC∽△DEF.
练习
AB AC BC 2.如图， = = , AD AE DE
AB AC 1 ∠C =∠C ′= 90°，且 AB AC 2

九 年 级 数 相学 下 似）
相似三角形判定（3） --定理(两角相等)
(
⒌
学习目标
(1)掌握“两角对应相等，两个三角形相似”的判定． (2)知道“斜边的比等于一组直角边比的两个直角三角形 相似”的判定.
阅读指导 阅读课本P45-48练习前的内容.完成
（1）学习P46探究4，①画出符合要求的两个三角形， ②观察这两个三角形是否相似， ③自己完成证明过程. （2）学习P46例1，体会定理运用的推理过程和书写格式. （3）学习P47思考，①这样两个三角形是否相似？ ②体会分析证明过程.
回顾
三角形相似的判定：
对应角相等，对应边成比例 相似三边形.
判定定理0：平行于三角形一边的直线截得的三角形与
原三角形相似.
判定定理1：三边对应成比例,两三角形相似. 判定定理2：两边对应成比例夹角相等,两三角形相似.
问题1 画△ABC,使∠A=45°,∠B=60°; 再画△A’B’C’,使∠A’=45°,∠B’=60°. 这两个三角形相似吗？为什么？
（2）图2中AB∥CD∥EF，找出图中所有的相似三角形。 答：相似三角形有 △AOB∽△FOE∽△DOC。
A A E G C C 图 1 图 2 O E F D B D F B
（3）在△ ABC和△A’B’C’中，如果∠A ＝80°，∠ C＝ 60°，∠ A’ ＝80°，∠B’＝40°，那么这两个三角形是否相似？为什么？ ∠B=180 °－（∠A+∠C)=180 °－（80 °+60 °)=40 °
检测二
1.找出图中所有的相似三角形. 2.证明：相似三角形对应高的 比等于相似比. 并证明你的结论. C C’
C
A
D
B

相似三角形的判定（三）知识点回顾：1.关于三角形的判定方法(1)定义法：对应角相等、对应边成比例(2)预备定理：平行于三角形一边的直线和它两边(或两边延长线)相交，所构成的三角形和原三角形相似.(3)判定定理1.两角对应相等两三角形相似(4)判定定理2.两边对应成比例且夹角相等，两三角形相似(5)判定定理3.三边对应成比例的两三角形相似(6)直角三角形判定的方法①以上各种判定方法均适用②如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和直角对应成比例，那么这两个直角三角形相似③直角三角形被斜边上的高分成的两个直角三角形和原三角形相似2、判定定理的适用范围(1)已知有一角相等时，可选择判定定理1与判定定理2.(2)有两边对应成比例时，可选择判定定理2与判定定理3.(3)直角三角形判定先考虑判定直角三角形相似的方法.还可以考虑一般三角形相似的方法说明：一般不用定义来判定三角形的相似.3、三角形相似的基本图形：①平行型：如图1，“A”型即公共角对的边平行，“×”型即对顶角对的边平行，都可推出两个三角形相似；②相交线型：如图2，公共角对的边不平行，即相交或延长线相交或对顶角所对边延长相交.图中几种情况只要配上一对角相等，或夹公共角（或对顶角）的两边成比例，就可以判定两个三角形相似.例题讲解 课前练习1.在图3中，若DE ∥BC ，DB ∶DA=9∶4，则ΔABC 与ΔADE 的相似比是______.2.如图4, 在梯形ABCD 中，EF 交DB 、DC 于E 、F,则图中的相似三角形共有_____对；若AE ∶EF=4∶3则ΔAFD 与ΔGFC 的相似比是______.3.如图5，当∠ADC=∠____时，ΔABC ∽ΔACD ；当AD 2=_________时，ΔABC ∽ΔACD.4. ΔABC 的三边长为3、4、5,ΔA /B /C /的最短边为5,若ΔABC ∽ΔA /B /C /,则ΔA /B /C /的面积为____.例1、如图：点G 在平行四边形ABCD 的边DC 的延长线上,AG 交BC 、BD 于点E 、F ，则△AGD ∽ ∽ 。

和HFCD，矩形对角线AC的长是 ；
挑战自我
三个边长为a的正方形ABEG、GEFH
和HFCD，矩形对角线AC的长是 ；
已知：如图,四边形ABEG 、GEFH 、
HFCD都是边长为a的正方形. 求证：△AEF∽△CEA.
证法1：∵正方形ABEG的边长为a，
证法1：∵正方形ABEG的边长为a， ∴AE= a.
AE∶EF= a∶a= ,
EC∶EA=2a∶
a=
,
证法2:根据题意，可得 AE= a ，AF= a , AC= a.
在△AEF和△CEA中，
AE∶EF= a∶a= ,
EC∶EA=2a∶
CA∶AF = a∶
a=
a=
,
,
证法2:根据题意，可得 AE= a ，AF= a , AC= a.
在△AEF和△CEA中，
∴
∴DE=B´C´,EA= C´A´. ∴ △ADE≌△A´B´C´.
证明:在△ABC的边AB 上截取AD= A´B´,过点 D作DE∥BC交AC于点E. 这样, △ADE∽△ABC. ∵ AD= A´B´， ∴ 又
∴
∴DE=B´C´,EA= C´A´. ∴ △ADE≌△A´B´C´. ∴ △A´B´C´∽△ABC.
∴ △AEF∽△CEA.
证法2:根据题意，可得 AE= a ，AF= a , AC= a.
证法2:根据题意，可得 AE= a ，AF= a , AC= a.
在△AEF和△CEA中，
AE∶EF= a∶a= ,
证法2:根据题意，可得 AE= a ，AF= a , AC= a.
在△AEF和△CEA中，
解：∵
2)AB=5厘米， BC=6厘米， AC=8厘米， A´B´=10 厘米 , B´C´=12 厘米 , A´C´ =16厘米.

0
已知： 如图， 已知 ： 如图 ， 在 △ ABC中 ， ∠ ACB=90° ， 中 ° CD⊥AB于D. ⊥ 于 求证： 求证：△ABC∽△CBD∽△ACD. C
A
D
B
结论： 结论：
直角三角形被斜边上的高分成的两个直 角三角形和原三角形相似. 角三角形和原三角形相似.
C
A
D
B
C
A
D
B
∵在△ABC中，∠ACB=90°， 中 ° CD⊥AB于D, ⊥ 于 ∴△ABC∽△CBD∽△ACD. ∽ ∽
0
B
C
3.如图， △ABC中，∠ACB=90°， CD⊥AB于 如图， 如图 中 ° ⊥ 于
于点E, 点D, DE⊥AC于点 ⊥ 于点
C
AD CE 求证： 求证： = AC BD
A
E
D
B
4.在Rt△ABC中，CD是斜边 上的高，点F是 △ 是斜边AB上的高 中 是斜边 上的高， 是 CD上一点，BE⊥AF交AF的延长线于点 ， 上一点， ⊥ 交 的延长线于点 的延长线于点E， 上一点 C 2 E 求证： 求证： AD = CDi AC
相似三角形的判定（ 相似三角形的判定（三）
猜想：两个角对应相等的两个三角形相似. 猜想：两个角对应相等的两个三角形相似.
已知：如图， 已知：如图，在△ABC和△A´B´C ´ 和 中，∠A=∠A´ ，∠B=∠B´ . ∠ ∠ 求证：△ABC∽△A´B´C´. 求证： ∽
A A'
B
C B'
C'
相似三角形判定定理3 相似三角形判定定理3： 如果一个三角形的两个角与另一个三角形的两个 如果一个三角形的两个角与另一个三角形的两个 两个角与另一个三角形的 对应相等，那么这两个三角形相似 相似. 角对应相等，那么这两个三角形相似. 简单说成：两角对应相等 两三角形相似 相似. 简单说成：两角对应相等，两三角形相似. 对应相等，

(三边对应成比例的两个三角形相似.)
例4 在△ABC和△A′B′C′中，已知： AB＝6cm，BC＝
8cm，AC＝10cm，A′B′＝18cm，B′C′＝24cm，A′C′＝
30cm．试证明△ABC与△A′B′C′相似．
证明
∵
AB 6 1 A′B′＝18 ＝ 3
BC 8 1
，
B′C′＝ 24 ＝ 3
AC 10 1 依据下列各组条件，A′证C′明＝△30A＝ BC3和△A′B′C′相似
∴
AB BC AC A′B′＝ B′C′＝ A′C′
AB＝10cm，B∴C＝△8cAmB，CA∽C△＝A1′6Bc′Cm′（,A′如B′果＝一16个cm三，角
B′C′＝25.6cm，形A的′C三′ =条1边2.8和c另m 一个三角形的三条边
对应成比例，那么这两个三角形相
似）．
生活中的三角形
如图，AB是斜靠在墙上的长梯，梯脚B距墙1.6 米，梯子上一点D距离墙1.4米，BD长为0.55米， 则梯子的长为——————
A
D
E
B
C
习题24.3
4． 依据下列各组条件，判断△ABC和△A′B′C′是不是相似， 如果相似，请给出证明过程． （1） ∠A＝70°，∠B＝46°，∠A′＝70°，∠C′＝64°； （2） AB＝10厘米，BC＝12厘米，AC＝15厘米，A′B′＝150 厘米，B′C′＝180厘米，A′C′＝225厘米； （3） ∠B=35°，BC=10，BC上的高AD=7，∠B′=35°， B′C′=5，B′C′上的高A′D′=3．5．
一、复习提问
我们已经有哪些判别两三角形相似的方法？
（1）相似三角形的定义 （2）两角对应相等的两个三角形相似。 （3）两角对应成比例且夹角相等的两个三角形相似。

2.提供更多实际情境题目，让学生在解决问题的过程中加深对定理的理解和应用。
3.增加课堂互动，鼓励学生提问和分享解题思路，以提高他们的逻辑思维和表达能力。
4.对于学习困难的学生，制定个性化的辅导计划，确保他们能够跟上课程进度。
-针对难点，教师应采用以下教学方法：
-使用动态几何软件或实物模型，帮助学生直观感受相似三角形的形成过程。
-设计阶梯式问题，引导学生逐步理解判定定理3的每个要素。
-通过小组讨论和同伴互助，让学生在互动中解决难点问题。
-提供多层次的练习题，让学生在不同的难度级别上反复练习，逐步突破难点。
四、教学流程
（一）导入新课（用时5分钟）
然而，我也意识到教学过程中存在的一些不足。例如，对于一些理解能力较弱的学生，我可能需要提供更多的个别辅导和额外的练习机会。此外，我也应该考虑引入更多的直观教具或多媒体资源，来帮助那些对几何图形感知能力较弱的学生。
在未来的教学中，我计划在以下几个方面进行改进：
1.强化学生对定理条件的记忆，通过反复练习和复习，确保他们能够熟练掌握。
3.成果展示：每个小组将向全班展示他们的讨论成果和实验操作的结果。
（四）学生小组讨论（用时10分钟）
1.讨论主题：学生将围绕“相似三角形判定定理3在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法，并与其他小组成员进行交流。
2.引导与启发：在讨论过程中，我将作为一个引导者，帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
-着重讲解如何从给定的信息中识别出符合判定定理3的条件，并运用这一条件判断三角形是否相似。
-通过典型例题和练习题，强化学生对定理3的记忆和应用能力。
-举例：给定三角形ABC和三角形DEF，如果∠A=∠D，∠B=∠E，且AB/DE=AC/DF，则证明三角形ABC与三角形DEF相似。

证明：连接AC、BD．
∵ ∠A和∠D都是 弧BC所对的圆周角，
A ∴ ∠A＝∠D
同理 ∠C＝∠B ∴ △PAC∽△PDB
D P O·
B
PA PC
C
PD PB
即 PA·PB＝PC·PD
典例：
例3、 如图，Rt△ABC中，CD是斜边上的高，
△ACD和△CBD都和△ABC相似吗？证明你的结
论．
C
12
∵∠ADE=∠B, ∠B=∠B'
A
∴∠ADE=∠B'
A'
又∵∠A=∠A',AD=A'B'
∴△ADE≌△A'B'C'
D
∴△A'B'C'∽△ABC
B
E
C B'
C'
相似三角形的判定
如果一个三角形的两个角与另一个三角形的两 个角对应相等，那么这两个三角形相似． (简 称：两角）：
A′ 符号语言：
A
在△A´B´C´和△ABC中，
3、(简称：三边）：如果两个三角形的三组对应边 的比相等，那么这两个三角形相似.
4、(简称：两边夹角）：如果两个三角形的两组对 应边的比相等，并且相应的夹角相等，那么这两个 三角形相似. 5、(简称：两角）：如果一个三角形的两个角与 另一个三角形的两个角对应相等，那么这两个三 角形相似．
A
DB
练习：
1、如果两个等腰三角形有一对底角对应相等那么它 们是否一定相似?有一对顶角对应相等呢?
2、有一个角等于300的两个等腰三角形是否相似? 等于1200呢?
练习：
3、 已知:如图,∠ABD=∠C AD=2 AC=8， 求AB 长.

知识与技能：1.初步掌握“三组对应边的比相等的两个三角形相似”的判定方法。
2. 能够运用三角形相似的条件解决简单的问题。
过程与方法：经历两个三角形相似的探索过程，体验用类比、实验操作、分析归纳得出数学结论的过程
情感、态度与价值观：通过画图、度量等操作，培养学生获得数学猜想的经验，激发学生探索知识的兴趣，体验数学活动充满着探索性和创造性．
又∵A’B’:AB=B’C’:BC=A’C’:CA
∴DE:BC=B’C’:BC,EA:CA=A’C’:CA.
因此DE=B’C’,EA=A’C’.
∴△ADE≌△A’B’C’
∴△ABC∽△A’B’C’
【活动三】知识应用
例1：在△ABC和△A′B′C′中，已知：
(1)AB＝6 cm，BC＝8 cm，AC＝10 cm，
思想小结：
类比思想 、分类讨论思想
师：提出问题：这节ຫໍສະໝຸດ 你有什么收获？生：1、相似三角形的判定（3）
2、灵活使用三角形的判定（3）说明两个三角形相似
3、类比思想 分类讨论思想
【活动六】作业
1.整理三角形相似的判定方法。
2.课堂作业：习题23.2第3 、14题
3.基础训练：基础练习23.2（四）
师：不经历风雨，怎么见彩虹
生：计算，看边是不是对应成比例
师：分析，看看两个三角形是否相似
生：∴ΔABC∽ΔADE
∴∠BAC=∠DAE
∴∠BAC━∠DAC=∠DAE━∠DAC
即∠BAD=∠CAE
师：分析，看看两个三角形是否相似
生：答案是2:1
【活动四】课堂巩固练习
练习：要画两个相似的三角形,其中一个三角形的三边的长分别为8、10、12,另一个三角形的一边长为4。求另一个三角形的其余两边的长。你画的三角形唯一吗?

2、判断图中△AEB和△FEC是否相似？ AE 54 解： ∵ = =1.5 FE 36
B
45
1
BE 45 ＝ ＝1.5 CE 30
E 36
2
F
A
54
30 C
AE BE ∴ ＝ FE CE
∵∠1＝∠2 ∴△AEB∽△FEC
3.在正方形ABCD中，E为AD上的中点, F是 AB的四分一等分点，连结EF、EC；△AEF
相 似 三 角 形 的 判 定
判断两个三角形相似,你有哪些方法 方法1：通过定义（不常用）

三个角对应相等 三边对应成比例
方法2：通过平行线。 方法3：三边对应成比例。
如果有一点E在边AC上，那么点E应该在什么
位置才能使△ADE∽△ABC相似呢？ 此时， C AD 1 AE 1 ？ =？ AB 3 AC 3
∴△ABC∽△ A ' B ' C '
B′
(两边对应成比例且夹角 C′ 相等，两三角形相似)
想一想：如果对应相等的角不是两条对应 边的夹角，那么两个三角形是否相似呢？
C A
D
F
B E
1、已知△ABC和 △A’B’C’,根据下列条件 判断它们是否相似.
（1）∠A=120°,AB=7cm,AC=14cm, ∠A`=120°,A`B`=3cm,A`C`=6cm; (2) ∠A＝45°，AB=12cm， AC=15cm ∠A’＝45°，A’B’＝16cm，A’C’＝20cm
B D A
E
A = A
如果一个三角形的两条 边与另一个三角形的两 条边对应成比例，并且 夹角相等，那么这两个 三角形一定相似吗？
• 已知:如图△ABC和△A`B`C`中,∠A＝∠A` , ∠A` ,A`B`:AB=A`C`:AC. • 求证:△ABC∽△A`B`C` 证明:在△ABC的边AB、AC(或它们的延长线) 上分别截取AD=A`B`,AE=A`C`,连结DE. ∠A=∠A`, 这样,△ADE≌△A`B`C`.

27.2.1 相似三角形的判定（3）（导学案）班级：姓名：学号一、学习目标1、掌握相似三角形的判定方法3的内容，并会运用判定方法3解决简单的问题。

2、经历两个三角形相似的探索过程，体验用类比、实验操作、分析归纳得出数学结论的过程；通过画图、度量等操作，培养同学们获得数学猜想的经验，激发同学们探索知识的兴趣，体验数学活动充满着探索性和创造性．3、能够运用三角形相似的条件解决简单的问题．二、重、难点重点：经历探索相似三角形的判定方法3的学习过程；能说出相似三角形的判定方法3 并会简单应用。

难点：运用相似三角形的判定方法3解决实际问题。

三、自主学习（Ⅰ）复习回顾1、相似三角形的预备定理2、相似三角形的判定定理13、相似三角形的判定定理24、思考是否还有类似判定定理1和2的判定三角形相似的方法？5、两个三角形的三边长分别为2、3、4和4、6、X，求X为多少时这两个三角形相似？（Ⅱ）自主探究（阅读书本P44—45）阅读书本的探究3并对照之前的学习相识的方法来得出相识判定3相识判定3：数学符号语言：例1、完成书本例题1例2、如图，△ABC中，点D在AB上，如果AC2=AD•AB，那么△ACD与△ABC相似吗？说说你的理由．例3、已知：如图，在四边形ABCD 中，∠B=∠ACD ，AB=6，BC=4，AC=5，CD=217，求AD 的长．（Ⅲ）自我尝试1、如果在△ABC 中∠B=30°，AB=5㎝，AC=4㎝，在△A ’B ’C ’中，∠B ’=30°A ’B ’=10㎝，A ’C ’=8㎝，这两个三角形一定相似吗？试着画一画、看一看？2、完成书本P45的练习1、2、33、如图，AB •AC=AD •AE ，且∠1=∠2，求证：△ABC ∽△AED ．4、已知：如图，P 为△ABC 中线AD 上的一点，且BD 2=PD •AD ，求证：△ADC ∽△CDP ．5、四、自学小结通过本节课的自学我掌握了： 还存在哪些困惑：五、课堂小结知识点：1、相识三角形的判定3“两边对应相等，并且两对应边的夹角也相等，两三角形相识”2、会应用所学的相识来判定三角形相识数学思想：从特殊到一般、类比、转化等思想五、作业设计（1）课堂作业（2）课后作业。

如果有一点E在边 上 那么点E应该在什么 如果有一点 在边AC上，那么点 应该在什么 在边 位置才能使△ 相似呢？ 位置才能使△ADE∽△ABC相似呢？ 此时， ∽ 相似呢 ， 1 AD 1 AE C =？ =？ ？ 3 AB 3 AC
B D A
E
∠A = ∠A
如果一个三角形的两条 边与另一个三角形的两 条边对应成比例， 条边对应成比例，并且 夹角相等， 夹角相等，那么这两个 三角形一定相似吗 一定相似吗？ 三角形一定相似吗？
解:(2)
AB 12 3 Q = = A′B′ 16 4
AC 15 3 = = ， A′C ′ 20 4
AB AC ∴ = . A′B′ A′C ′
又∠A=∠A′,
∴∆ABC∽∆Α′Β′C ′
（3）课本 45练习 （1）2（1) ）课本P 练习1（ ） （
2、判断图中△AEB 和△FEC是否相似？ 、判断图中△ 是否相似？
相 似 三 角 形 的 判 定
( ) 三
复习回顾: 复习回顾
判断两个三角形相似, 判断两个三角形相似,你有哪些方法 方法1：通过定义（不常用） 方法 ：通过定义（不常用）
{
三个角对应相等 三边对应成比例
方法2：通过平行线。 方法 ：通过平行线。 方法3：三边对应成比例。 方法 ：三边对应成比例。
观察思考: 观察思考
证明： ∠BAD = ∠CAE Q
∴ ∠BAD + ∠DAC = ∠CAE + ∠DAC
即∠BAC = ∠EAD AB AC Q = AE AD ∴ ∆ABC ∽ ∆AED
A B C D E
4.在正方形 在正方形ABCD中，E为AD上的中点 F是 上的中点, 在正方形 中 为 上的中点 是 AB的四分一等分点，连结EF、EC；△AEF 的四分一等分点，连结 、 ； 的四分一等分点 是否相似?说明理由 与△DCE是否相似 说明理由 是否相似 说明理由.

谢谢！
6．已知平行四边形 ABCD，AE 与 BC 延长线相交于 E，与 CD 相交于 F.求证：△AFD∽△EAB.
证明：∵四边形 ABCD 是平行四边形 ∴AD∥BE，∠D＝∠B ∴∠DAF＝∠2＝∠3. 求证：△ABC∽△ADE.
解：∵∠1＝∠3 ∴∠1＋∠DAC＝∠3＋∠DAC ∴∠BAC＝∠DAE ∵∠2＝∠3， 又∵AC 与 ED 相交，设交于 F ∴∠CFD＝∠AFE
2．如图，D 为⊙O 上一点，点 C 在直径 BA 的延长线上，且∠CDA ＝∠CBD. (1)求证：CD 是⊙O 的切线； (2)过点 B 作⊙O 的切线交 CD 的延长线于点 E，BC＝6，ABDD＝ 23.求 BE 的长．
(1)证明：如图所示，连接 OD， 答案图
∵OB＝OD，∴∠OBD＝∠BDO. ∵∠CDA＝∠CBD，∴∠CDA＝∠ODB. 又 AB 是⊙O 的直径，∴∠ADO＋∠ODB＝90°.∴∠ADO＋∠ CDA＝90°， 即∠CDO＝90°.∴CD 是⊙O 的切线．
5．(2015·贵州)如图，在△ACB 中，∠ACB＝90°，点 O 是 AC 边上的一点，以 O 为圆心，OC 为半径的圆与 AB 相切于点 D，连接 OD. 求证：△ADO∽△ACB.
证明：∵OC 为半径的圆与 AB 相切于点 D ∴DO⊥AB ∴∠ODA＝90° ∴∠ACB＝∠ODA＝90° 又∵∠A＝∠A ∴△ADO∽△ACB
(2)解：∵∠C＝∠C，∠CDA＝∠CBD，∴ △CAD∽△CDB. ∴CBCD＝BADD＝32.∵BC＝6，∴CD＝4. ∵CE、BE 是⊙O 的切线，∴BE＝DE，BE⊥BC. ∴BE2＋BC2＝EC2，即(4＋BE)2＝62＋BE2 解得 BE＝52.
3．(2016·武汉)Rt△ACB 中，∠ACB＝90°，CD 为 AB 边上的中线， MN⊥CD 于 G，MN 分别交 AC、CB 于 M、N. (1)如图 1，求证：△CMN∽△CBA； (2)如图 1，若MNGG＝196，AB＝10，求 AC 的值； (3)如图 2，CE⊥AB 于 E，CE 交 MN 于 F 点，若 CF＝EF，求 证：AE·BE＝4NF2.