阿贝成像原理和空间频率的测量

实验二阿贝成像原理和空间滤波实验1. 引言阿贝所提出的显微镜成像的原理以及随后的阿一波特实验在傅里叶光学早期发展历史上具有重要的地位。

这些实验简单而且漂亮，对相干光成像的机理、对频谱的分析和综合的原理做出了深刻的解释。

同时，这种用简单模板做滤波的方法，直到今天，在图像处理中仍然有广泛的应用价值。

1.1实验目的和意义1 ).加强对傅里叶光学中有关空间频率、空间频谱和空间滤波等概念的理解。

2 ).用一个带有蓝天白云还有城楼的光栅进行空间滤波和图像再现，熟悉空间滤波的光路及空间滤波的原理。

2. 系统概述2. 1系统原理二维傅里叶变换).1设有一个空间二维函数，其二维傅里叶变换为)yg(x, dxdyfy)i2x(f,y)g (x,y)exp xg( (1F) f,)G(f yxyx -1f,fG(f,f)的又是式中，而分别为x,y方向的空间频率，其量纲为L)y,g(x yxyx逆傅里叶变换，即),fG(f -1dfdf(fx fyfG(f,)exp)i2 F ) 2 ( y),(gx yx yyyxxx 式(2)表示任意一个空金函数，可以表示为无穷多个基元函数)x,y(g dfy)df2(fx fpexi的基元的线性叠加，是相应于空间频率为ff,)G(ff, yxyxyyxx函数的权重，称为的空间频率。

)(f,fG )y,x(g yx当是一个空间周期性函数时，其空间频率是不连续的离散函数。

)x,yg(2).光学傅里叶变换理论证明，如果在焦距为F的会聚透镜的前焦面上放一振幅透过率为g(x,y)的图象作为物，并以波长为入的单色平.面焦镜后象图，则在透面波垂照明的傅，()上的振幅分布就是y X),yg(x标与坐，变换其中里叶f,f),fG(f yxyx 的关系为,y x''yx 3 ()f f, 1图• Yx FF ，由此可见，复杂的二维傅里1面称为频谱面(或傅氏面) 故一，见图y x 叶变换可以用一透镜来实现，称为光学傅里叶变换，频谱面上的光强分布则为2..，称为频谱，也就是物的夫琅禾费衍射图。

实验二 阿贝成像原理和空间滤波实验1． 引言阿贝所提出的显微镜成像的原理以及随后的阿—波特实验在傅里叶光学早期发展历史上具有重要的地位。

这些实验简单而且漂亮，对相干光成像的机理、对频谱的分析和综合的原理做出了深刻的解释。

同时，这种用简单模板做滤波的方法，直到今天，在图像处理中仍然有广泛的应用价值。

1．1 实验目的和意义1）.加强对傅里叶光学中有关空间频率、空间频谱和空间滤波等概念的理解。

2）.用一个带有蓝天白云还有城楼的光栅进行空间滤波和图像再现，熟悉空间滤波的光路及空间滤波的原理。

2． 系统概述2．1 系统原理1）.二维傅里叶变换设有一个空间二维函数),(y x g ，其二维傅里叶变换为=),(y x f f G F [][]d xdy y f x f i y x g y x g y x ⎰⎰∞∞-+-=)(2exp ),(),(π （1）式中y x f f ,分别为x,y 方向的空间频率，其量纲为L -1，而),(y x g 又是),(y x f f G 的逆傅里叶变换，即=),(y x g F -1[]=),(y x f f G []y x y x y x df df y f x f i f f G ⎰⎰∞∞-+)(2exp ),(π （2） 式（2）表示任意一个空金函数),(y x g ，可以表示为无穷多个基元函数[])(2ex p y f x f i y x +π的线性叠加，),(y x f f G y x df df 是相应于空间频率为y x f f ,的基元函数的权重，),(y x f f G 称为),(y x g 的空间频率。

当),(y x g 是一个空间周期性函数时，其空间频率是不连续的离散函数。

2）.光学傅里叶变换理论证明，如果在焦距为F 的会聚透镜的前焦面上放一振幅透过率为),(y x g 的图象作为物，并以波长为λ的单色平面波垂照明图象，则在透镜后焦面（x ',y '）上的振幅分布就是),(y x g 的傅里叶变换),(y x f f G ，其中y x f f ,与坐标x ',y '的关系为Fy f F x f Y x λλ','== （3） 图 1 故x '—y '面称为频谱面（或傅氏面），见图1，由此可见，复杂的二维傅里叶变换可以用一透镜来实现，称为光学傅里叶变换，频谱面上的光强分布则为2),(y x f f G ，称为频谱，也就是物的夫琅禾费衍射图。

实验6-3 阿贝成像与空间滤波实验【实验目的】1、 通过实验了解空间频率、空间频谱的概念以及傅里叶光学的基本思想。

2、 了解阿贝成像的原理，理解透镜成像的物理过程。

3、 了解如何通过空间滤波的方法，实现对图象的改造。

【实验原理】1、傅里叶光学变换设有一个空间二维函数()y x g ,，其二维傅里叶变换为：()()[]()()[]dxdy y f x f i y x g y x g F f f G y x y x +-==⎰⎰∞π2exp ,,, （6-3-1）式中x f 、y f 分别为x 、y 方向的空间频率，()y x g ,是()y x f f G ,的逆傅里叶变换，即：()[]()()[]y x y x yx y x df df y f x f i f f G f f G F y x g +==⎰⎰∞-π2exp ,,),(1 (6-3-2)该式表示：任意一个空间函数()y x g ,可表示为无穷多个基元函数()[]y f x f i y x +π2exp 的线性叠加。

()y x y x df df f f G ,是相应于空间频率为x f 、y f 的基元函数的权重，()y x f f G ,称为()y x g ,的空间频谱。

理论上可以证明，对在焦距为f 的会聚透镜的前焦面上放一振幅透过率为()y x g ,的图像作为物，并用波长为λ的单色平面波垂直照明，则在透镜后焦面()y x '',上的复振幅分布就是()y x g ,的傅里叶变换()y x f f G ,，其中空间频率x f 、y f 与坐标x '、y '的关系为： ⎪⎪⎩⎪⎪⎨⎧'='=f y f f x f y x λλ （6-3-3） 故()y x '',面称为频谱面（或傅氏面），由此可见，复杂的二维傅里叶变换可以用一透镜来实现，称为光学傅里叶变换，频谱面上的光强分布，也就是物的夫琅禾费衍射图。

阿贝成像原理和空间滤波一、实验目的1．透镜的傅里叶变换作用；2．空间频谱面的位置及空间频谱的观察；3. 孔径对成像质量的影响；4．验证阿贝成像原理，强化空间滤波概念的理解。

二、实验原理1．阿贝成像原理1873年，阿贝(Abbe)在研究显微镜成像原理时提出了一个相干成像的新原理，这个原理为当今正在兴起的光学信息处理奠定了基础。

如图1-1所示，用一束平行光照明物体，按照传统的成像原理，物体上任一点都成了一次波源，辐射球面波，经透镜的会聚作用，各个发散的球面波转变为会聚的球面波，球面波的中心就是物体上某一点的像。

一个复杂的物体可以看成是无数个亮度不同的点构成，所有这些点经透镜的作用在像平面上形成像点，像点重新叠加构成物体的像。

这种传统的成像原理着眼于点的对应，物像之间是点点对应关系。

阿贝成像原理认为，透镜的成像过程可以分成两步：第一步是通过物的衍射光在透镜后焦面(即频谱面)上形成空间频谱，这是衍射所引起的“分频”作用；第二步是代表不同空间频率的各光束在像平面上相干叠加而形成物体的像，这是干涉所引起的“合成”作用。

成像过程的这两步本质上就是两次傅里叶变换。

如果这两次傅里叶变换是完全理想的，即信息没有任何损失，则像和物应完全相似。

如果在频谱面上设置各种空间滤波器，挡去频谱某一些空间频率成份，则将会使像发生变化。

空间滤波就是在光学系统的频谱面上放置各空间滤波器，去掉(或选择通过)某些空间频率或者改变它们的振幅和相位，使二维物体像按照要求得到改善。

这也是相干光学处理的实质所在。

以图l-l 为例，平面物体的图像可由一个二维函数g(x,y)描述，则其空间频谱G(fx ，fy)即为g(x ，y)的傅里叶变换：2(,)(,)(,)x y i f x f y x y G f f g x y e dxdy π∞-∞-=⎰⎰ （1-1）图1-1 阿贝成像原理设,x y ''为透镜后焦面上任一点的位置坐标，则式中为x x f F λ'=，y y f F λ'= （1-2）方向的空间频率，量纲为L-1, F 为透镜焦距，λ为入射平行光波波长。

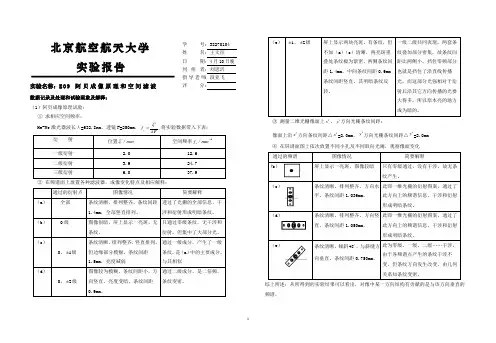
北京航空航天大学实验报告实验名称：E 09 阿贝成像原理和空间滤波数据记录及处理和试验现象及解释： （1）阿贝成像原理试验： ① 求相应空间频率：He-Ne 激光器波长λ=632.8nm ，透镜F=250mm ，x fξ'=,将实验数据带入下表：② 在频谱面上放置各种滤波器，成像变化特点及相应解释：③ 测量二维光栅像面上x '，y '方向光栅条纹间距：像面上沿x '方向条纹间距△x '=2.0mm ，y '方向光栅条纹间距△y '=2.0mm ④ 在屏谱面图上依次放置不同小孔及不同取向光阑，观察像面变化 综上所述：从所得到的实验结果可以看出，对像中某一方向结构有贡献的是与该方向垂直的频谱。

学号：38270104 姓名：王文征 日期：4月10日晚同组者：刘思沂指导老师：段亚飞评分：（2）高低通滤波：①将物面换上3号样品，则在像面上出现带网格的“光”字。

②用白屏观察焦面上物的空间频谱。

光栅为一周期性函数，其频谱是有规律排列的分立点阵。

而字迹不是周期性函数，它的频谱是连续的，一般不易看清。

由于光字笔画较粗，空间低频成分较多，因此频谱面的光轴附近只有光字信息而没有网格信息，由于仅保留了离轴较近的低频成份，因而图像细结构消失。

③将3号滤波器（φ=1mm 的圆孔光阑）放在后焦面的光轴上，出现“光”字，网格信息消失，亮度较暗。

换上4号滤波器（φ=0.4mm的圆孔光阑）,光字更暗。

④将频谱面上光阑作一平移，使不在光轴上的一衍射点通过光阑，发现越偏离光轴图像越暗。

换上4号样品，使之成像。

然后在后焦面上放上5号滤波器，发现未放之前出现红色十字，放上5号滤波器后“十”字中间变暗，四周轮廓也较为清晰，它阻挡低频分量而允许高频成份通过，可以实现图像的衬度反转或边缘增强，所以图像轮廓明显。

（3）θ调制试验：衍射频上花、叶、背景的光栅走向蓝（背景）红（花）绿（叶）利用阿贝成像实验中的结论，对像中某一方向结构有贡献的是与该方向垂直的频谱。

实验一 阿贝成像原理和空间滤波一、实验目的1．了解透镜孔径对成像的影响和两种简单的空间滤波。

2．掌握在相干光条件下调节多透镜系统的共轴。

3．验证和演示阿贝成像原理，加深对傅里叶光学中空间频谱和空间滤波概念的理解。

4．初步了解简单的空间滤波在光信息处理中的实际应用。

二、实验原理1．阿贝成像原理1873年，阿贝(Abbe)在研究显微镜成像原理时提出了一个相干成像的新原理，这个原理为当今正在兴起的光学信息处理奠定了基础。

如图1-1所示，用一束平行光照明物体，按照传统的成像原理，物体上任一点都成了一次波源，辐射球面波，经透镜的会聚作用，各个发散的球面波转变为会聚的球面波，球面波的中心就是物体上某一点的像。

一个复杂的物体可以看成是无数个亮度不同的点构成，所有这些点经透镜的作用在像平面上形成像点，像点重新叠加构成物体的像。

这种传统的成像原理着眼于点的对应，物像之间是点点对应关系。

阿贝成像原理认为，透镜的成像过程可以分成两步：第一步是通过物的衍射光在透镜后焦面(即频谱面)上形成空间频谱，这是衍射所引起的“分频”作用；第二步是代表不同空间频率的各光束在像平面上相干叠加而形成物体的像，这是干涉所引起的“合成”作用。

成像过程的这两步本质上就是两次傅里叶变换。

如果这两次傅里叶变换是完全理想的，即信息没有任何损失，则像和物应完全相似。

如果在频谱面上设置各种空间滤波器，挡去频谱某一些空间频率成份，则将会使像发生变化。

空间滤波就是在光学系统的频谱面上放置各空间滤波器，去掉(或选择通过)某些空间频率或者改变它们的振幅和相位，使二维物体像按照要求得到改善。

这也是相干光学处理的实质所在。

以图l-l 为例，平面物体的图像可由一个二维函数g(x,y)描述，则其空间频谱G(f x ，f y )即为g(x ，y)的傅里叶变换：2(,)(,)(,)x y i f x f y x y G f f g x y edxdy π∞-∞-=⎰⎰ （1-1）图1-1 阿贝成像原理设,x y ''为透镜后焦面上任一点的位置坐标，则式中为x x f F λ'=，y y f Fλ'= （1-2） 方向的空间频率，量纲为L -1, F 为透镜焦距，λ为入射平行光波波长。

实验二阿贝成像原理和空间滤波实验1．引言阿贝所提出的显微镜成像的原理以及随后的阿—波特实验在傅里叶光学早期发展历史上具有重要的地位。

这些实验简单而且漂亮，对相干光成像的机理、对频谱的分析和综合的原理做出了深刻的解释。

同时，这种用简单模板做滤波的方法，直到今天，在图像处理中仍然有广泛的应用价值。

1．1实验目的和意义1）.加强对傅里叶光学中有关空间频率、空间频谱和空间滤波等概念的理解。

2）.用一个带有蓝天白云还有城楼的光栅进行空间滤波和图像再现，熟悉空间滤波的光路及空间滤波的原理。

2．系统概述2．1 系统原理二维傅里叶变换）.1设有一个空间二维函数，其二维傅里叶变换为)yg(x,??????dxdyfy)i2x(f,y)g?(x,y)exp??xg(（1F）???f,)G(f yxyx??-1f,fG(f,f)的又是式中，而分别为x,y方向的空间频率，其量纲为L)y,g(x yxyx逆傅里叶变换，即 ??????),fG(f?-1dfdf(fx?fyfG(f,)exp)i2?? F）2 （?y),(gx yx yyyxxx??式（2）表示任意一个空金函数，可以表示为无穷多个基元函数)x,y(g???dfy)df2(fx?fpexi的基元的线性叠加，是相应于空间频率为ff,)G(ff,yxyxyyxx函数的权重，称为的空间频率。

)(f,fG)y,x(g yx当是一个空间周期性函数时，其空间频率是不连续的离散函数。

)x,yg(2）.光学傅里叶变换理论证明，如果在焦距为F的会聚透镜的前焦面上放一振幅透过率为g(x,y)的图象作为物，并以波长为λ的单色平面焦镜后象图，则在透面波垂照明??的傅,（）上的振幅分布就是y x),yg(x标与坐，变换其中里叶f,f),fG(f yxyx??的关系为,y x''yx 3 （）?f?f, 1 图Yx??FF??，由此可见，复杂的二维傅里1面称为频谱面（或傅氏面）故—，见图y x叶变换可以用一透镜来实现，称为光学傅里叶变换，频谱面上的光强分布则为2，称为频谱，也就是物的夫琅禾费衍射图。

实验二阿贝成像原理和空间滤波实验1. 引言阿贝所提出的显微镜成像的原理以及随后的阿一波特实验在傅里叶光学早期发展历史上具有重要的地位。

这些实验简单而且漂亮，对相干光成像的机理、对频谱的分析和综合的原理做出了深刻的解释。

同时，这种用简单模板做滤波的方法，直到今天，在图像处理中仍然有广泛的应用价值。

1. 1实验目的和意义1).加强对傅里叶光学中有关空间频率、空间频谱和空间滤波等概念的理解。

2).用一个带有蓝天白云还有城楼的光栅进行空间滤波和图像再现，熟悉空间滤波的光路及空间滤波的原理。

2. 系统概述2. 1系统原理1).二维傅里叶变换设有一个空间二维函数g(x, y)，其二维傅里叶变换为G(f x, f y) =F g(x, y) 1二g(x, y)expLi2二(f x X f y y)dxdy (1)a式中f x, f y分别为x,y方向的空间频率，其量纲为L-1，而g(x,y)又是G(f x，f y)的逆傅里叶变换，即g(x, y) = F-1G(f x，f y)L G(f x, f y)exp【2二(f x X f y y)df x df y (2)-^O式(2)表示任意一个空金函数g(x, y)，可以表示为无穷多个基元函数expi2二(f x x • f y y) 的线性叠加，G(f x, f y) df x df y是相应于空间频率为f x, f y的基元函数的权重，G(f x, f y)称为g(x, y)的空间频率。

当g(x, y)是一个空间周期性函数时，其空间频率是不连续的离散函数2) .光学傅里叶变换理论证明，如果在焦距为 F 的会聚透镜的前焦面上放一振幅透过率为g (x, y)的图象作为物，并以波长为 入的单色平 面波垂照明图象，则在透镜后焦面(x , y ') 上的振幅分布就是g(x,y)的傅 里叶变换G(f x ，f y )，其中f x ，f y 与坐标 x , y 的关系为 故x — y •面称为频谱面(或傅氏面)，见图1，由此可见，复杂的二维傅里 叶变换可以用一透镜来实现，称为光学傅里叶变换，频谱面上的光强分布则为2G(f X ,f y )，称为频谱，也就是物的夫琅禾费衍射图。

光信息专业实验指导材料（试用）实验1－1 阿贝成像原理与空间滤波[实验目的]1、了解阿贝成像原理，并进行实验验证；2、加深对空间频谱和空间滤波概念的理解；3、利用空间滤波技术消除图像噪声；4、了解透镜的傅里叶变换作用。

[实验仪器]实验室提供：半导体激光器（带二维调节架），光具座导轨（1000mm ），滑块，傅里叶透镜（φ80，f 190），准直透镜（φ55，f 50），扩束镜（带二维调节架），放大镜，干板架，正交光栅2枚（空间频率分别为25 lp/mm 和100 lp/mm ）,“光”字屏，毛玻璃屏，白屏，小孔屏，滤波器组件（带二维调节架），手电筒。

[实验原理]一、阿贝成像理论1873年阿贝首次提出了一个与几何光学传统成像理论完全不同的概念，它认为相干照明下透镜成像过程可分作两步：首先，物光波经透镜，在透镜后焦面上形成频谱，该频谱称为第一次衍射像；然后频谱成为新的次波源，由它发出的次波在像平面上干涉而形成物体的像，该像称为第二次衍射像。

上述过程即为“阿贝成像理论”。

根据这一理论，像的结构完全依赖于频谱的结构。

图1是上述成像过程的示意图。

设相干平行光照射复振幅为),(00y x g 的物面，由傅里叶光学可知，经透镜L 的傅里叶变换，在其后焦面（频谱平面）上可得到物的频谱，其数学表述为：物平面 频谱平面 像平面图1 阿贝成像理论示意图()()()[]0000002j exp ,,dy dx vy ux πy x g v u G +-=⎰⎰∞∞- （1）式中u ，v 为空间频率。

透镜L 则称为傅里叶变换透镜。

由频谱面到像平面，光波完成了一次夫朗和费衍射过程，相当于频谱又经过一次傅里叶变换，在像平面上综合成物体的像。

()()()[]dudv y v x u πu,v G y x g '+'=''⎰⎰∞∞-2j exp ,' （2）由（1）、（2）式可见，物面与像面的复振幅之比是一个常数，所以像与物几何相似。

阿贝成像原理与空间滤波实验内容：l．光路调节本实验基本光路图如图1所示，其中透镜L 1 (焦距f 1)、L 2 (焦距f 2)组成倒装置望远镜系统将激光扩展成具有较大截面的平行光束，L(焦距为f)则为成像透镜。

调节步骤如下：图1 空间滤波实验光路(1) 调节激光管的仰角及转角，使光束平行于光学平台水平面。

(2) 放上L 1和L 2，使产生一扩束的平行光并调节它们共轴。

怎样检验 L 2出来的光是否平行光?如L 1的焦距为 mm，L 2焦距为 mm，，则扩束多少倍? (3)放上物(带光栅的“光”字)及透镜L，调节它们共轴，调节L 位置，使大于4 m 距离的屏幕上得到清晰的图像。

固定物及透镜L 位置(调节成像时，可在物面前暂放一毛玻璃，以便在扩展光源照明下，找到成像的精确位置。

)(4)确定频谱面位置去掉物，用毛玻璃在L 后焦面附近移动，当毛玻璃散射产生的散斑达到最大线度时，毛玻璃上光点最小，此毛玻璃所在平面就是频谱面。

然后将滤波器支架放在此平而上。

2．阿贝成像原理实验(1) 在物平面放上一维光栅，像平面上看到沿铅垂方向的光栅条纹。

频谱面上出现0，±1，±2，±3，… ，一排清晰衍射光点，如图2中A 所示。

测量l，2，3级衍射点与光轴(0级衍射)的距离x′，由式(3)求出相应空间频率f x，并求光栅的基频。

图2 频谱面及光阑A.频谱面上的衍射光斑B.只通过0级C.只通过0级和±1级D.遮挡±1级E.遮挡0级(2)在傅氏面上放上可调狭缝及其他附加光阑，按图2中A，B，C，D，E 分别通过一定的空间频率成分，按表l 依次记录像面上成像的特点及条纹间距，特别注意观察D 和E 两条件下图像的差异，并对图像变化作出适当的解释。

表1像面成像特点条件 通过的衍射点 图像情况 简要解释 A 全部 B 0级 C 0，±1级 D 0，±2级 E ±1，±2级衍射次级位置 x′/mm间频空率 f x /mm -11 2 3(3)取下物向上的一维光栅，换上一个二维正交光栅则在频谱而上吖看到二维离散的光点阵(即止交光栅的频谱)，像而上可以看到放大了的止交光栅的像测出像面上的网格间距。

阿贝成像原理和空间滤波[引言]傅立叶光学是近代光学的一个分支，它是用空间频谱的语言分析光信息。

1874年阿贝（E.Abbe）提出了二次衍射成像原理，这一原理是建立在傅里叶光学基础上的信息光学理论，阿贝——波特（Porter）实验是阿贝成像理论的有力证明。

阿贝成像原理所揭示的物体成像过程中频谱的分解与综合，使得人们可以通过物理手段在谱面上改变物体频谱的组成和分布，从而达到处理和改造图像的目的，这就是空间滤波。

阿贝成像理论空间滤波的目的是通过有意识的改变像的频谱，使像产生所希望的变换，将 调制与空间滤波结合，像面各相应部分可呈现不同颜色。

本实验形象地说明了傅立叶光学的应用。

通过本实验可以把透镜成像与干涉、衍射联系起来，初步了解透镜的傅里叶变换性质，从而有助于对现代光学信息处理中的用光学方法实现对输入信息的各种变换或处理这一手段的理解。

[实验目的]1．通过本实验，掌握阿贝成像原理，了解阿贝-波特实验。

2．加深对傅里叶光学中空间频率、空间频谱等概念的理解。

3．掌握空间滤波的方法。

[基本原理]1．阿贝成像原理阿贝研究显微镜成像时，提出了一种不同于几何光学的新观点，即将物像看成是不同空间频率的集合，在相干平行光照明下，显微镜物镜的成像过程分两步完成：①入射光经过物的衍射在物镜的后焦面上形成夫琅禾费衍射图样(初级衍射图或称频谱图)；②各初级衍射图样作为新的子波源发出的球面波在像平面上相干叠加成像。

（如图一所示）将显微镜的成像过程看成是上述两步成像的过程，是波动光学的观点，后图一阿贝成像原理光路图来人们称其为阿贝成像原理。

阿贝成像原理不仅用傅里叶变换阐述了显微镜成像的机理，更重要的是首次引入频谱的概念，启发人们用改造频谱的手段来改造信息。

2．空间频谱任何一个物理真实的物平面上的空间分布函数),(y x g 可以表示成无穷多个基元函数)](2ex p[y f x f i y x +π的线性叠加，即y x y x y x f f y f x f i f f G y x g d d )](2exp[),(),(+=⎰⎰∞+∞-π （1）式中，x f 、y f 是基元函数的参量，称为该基元函数的空间频率，),(y x f f G 是该基元函数的权重，称为),(y x g 的空间频谱。

阿贝成像空间频率的值阿贝成像空间频率的值指的是在光学成像中，通过阿贝准则来描述图像的空间频率。

阿贝准则是描述光学系统分辨率的基本原理，它规定了光学系统能够分辨两个物体的最小距离。

阿贝成像空间频率的值是用来衡量图像中最小可分辨细节的频率。

阿贝成像空间频率的值与光学系统的参数有关，主要包括光源的波长、透镜的孔径和物体的距离等。

在实际应用中，我们常常使用空间频率的倒数来表示分辨率，即空间频率的倒数越大，表示分辨率越高。

在光学成像中，空间频率的值越高，表示图像中的细节越丰富，分辨率越高。

例如，在显微镜中观察细胞的结构，如果空间频率的值足够高，我们可以清晰地看到细胞核、细胞质和细胞膜等细节。

而如果空间频率的值较低，我们只能看到模糊的图像，无法分辨细胞的具体结构。

阿贝成像空间频率的值还与光学系统的分辨能力有关。

分辨能力是指光学系统能够分辨两个相邻物体的能力，通常用最小可分辨角来表示。

最小可分辨角越小，表示分辨能力越高，能够分辨的细节越小。

而最小可分辨角与空间频率的值成反比，即最小可分辨角越小，空间频率的值越高。

在实际应用中，我们常常通过控制光源的波长、透镜的孔径和物体的距离等参数来调节阿贝成像空间频率的值。

例如，在显微镜中，我们可以使用不同波长的光源来观察样品，通过改变波长可以改变阿贝成像空间频率的值，从而实现不同空间分辨率下的观察。

阿贝成像空间频率的值是衡量光学系统分辨率的重要指标，它与光学系统的参数密切相关，决定了我们能够观察到的图像中的细节丰富程度。

在实际应用中，我们可以通过调节光源的波长、透镜的孔径和物体的距离等参数来控制阿贝成像空间频率的值，从而实现不同分辨率下的图像观察。