椭圆的定义及性质(课堂PPT)
- 格式:ppt
- 大小:997.50 KB
- 文档页数:2






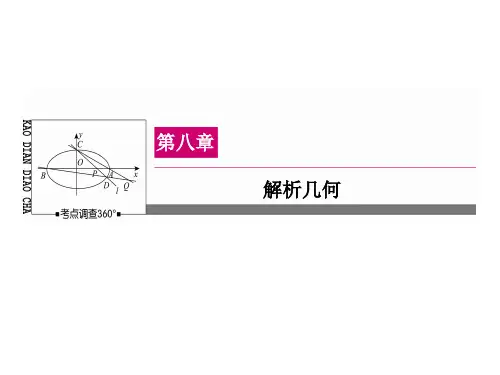



第九讲椭圆的定义与性质高考要求⑴了解圆锥曲线的实际背景,了解圆锥曲线在刻画现实世界和解决实际问题中的作用.⑵掌握椭圆、抛物线的定义、几何图形、标准方程及简单性质.⑶了解双曲线的定义、几何图形和标准方程,知道它的简单几何性质.⑷了解圆锥曲线的简单应用.⑸理解数形结合的思想.⑹了解方程的曲线与曲线的方程的对应关系.知识精讲(一)知识内容1.椭圆的定义:平面内与两个定点的距离之和等于常数(大于)的点的轨迹(或集合)叫做椭圆.这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距.2.椭圆的标准方程:①,焦点是,,且.②,焦点是,,且.3.椭圆的几何性质(用标准方程研究):⑴范围:,;⑵对称性:以轴、轴为对称轴,以坐标原点为对称中心,椭圆的对称中心又叫做椭圆的中心;⑶椭圆的顶点:椭圆与它的对称轴的四个交点,如图中的;⑷长轴与短轴:焦点所在的对称轴上,两个顶点间的线段称为椭圆的长轴,如图中线段的;另一对顶点间的线段叫做椭圆的短轴,如图中的线段.⑸椭圆的离心率:,焦距与长轴长之比,,越趋近于,椭圆越扁;反之,越趋近于,椭圆越趋近于圆.(二)典例分析【例1】⑴经过点,的椭圆的标准方程是;⑵焦点的坐标分别为和,且过点的椭圆的方程.⑶已知椭圆的中心在原点,且经过点,,求椭圆的标准方程.【变式1】设是两个定点,且,动点到点的距离是,线段的垂直平分线交于点,求动点的轨迹方程.【例2】⑴椭圆和一定具有()A.相同的离心率 B.相同的焦点C.相同的顶点 D.相同的长轴长⑵已知椭圆的中心在原点,长轴长为,离心率为,则椭圆的方程是____________.⑶若椭圆的离心率为,则.【变式2】⑴点为椭圆上一点,以点以及焦点,为顶点的三角形的面积为,则点的坐标是____ __.⑵已知,是椭圆的两个焦点,过且与椭圆长轴垂直的直线交椭圆于两点,若是正三角形,则这个椭圆的离心率是_________.⑶(08江苏)在平面直角坐标系中,设椭圆的焦距为,以点为圆心,为半径作圆.若过点作圆的两条切线互相垂直,则椭圆的离心率为.【例3】⑴已知,,是椭圆上一点,则的最大值为________.⑵(2009上海)已知、是椭圆的两个焦点,为椭圆上一点,且.若的面积为,则.【变式3】(2006四川)如图,把椭圆的长轴分成等份,过每个分点作轴的垂线交椭圆的上半部分于七个点,是椭圆的左焦点,则.【例4】已知点是椭圆上到直线:的距离最小的点,则点的坐标为_________.【变式4】设为椭圆短轴上的一个端点,为椭圆上的一个动点,求的最大值【例5】椭圆的左、右焦点分别为、,点为其上的动点,当为钝角时,点横坐标的取值范围是_______.【变式5】设椭圆:的左右焦点分别为,若椭圆上存在一点,使,试求该椭圆的离心率的取值范围.【例6】解方程:.【例7】椭圆的弦被点所平分,求此弦所在的直线方程.【例8】椭圆中心是坐标原点,焦点在轴上,,过椭圆左焦点的直线交椭圆于、两点,,且,求此椭圆的方程.【例9】如图,椭圆上的点与椭圆右焦点的连线与轴垂直,且(是坐标原点)与椭圆长轴和短轴端点的连线平行.⑴求椭圆的离心率;⑵是椭圆的左焦点,是椭圆上的任一点,证明:;⑶过且与垂直的直线交椭圆于、,若的面积是,求此时椭圆的方程及的长.【例10】(2007广东高考)在平面直角坐标系中,已知圆心在第二象限、半径为的圆与直线相切于坐标原点.椭圆与圆的一个交点到椭圆两焦点的距离之和为.⑴求圆的方程;⑵试探究圆上是否存在异于原点的点,使到椭圆右焦点的距离等于线段的长.若存在,请求出点的坐标;若不存在,请说明理由.【例11】(2008朝阳高三期末)设动点的坐标为(),且动点到定点,的距离之和为.⑴求动点的轨迹的方程;⑵过点作直线与曲线交于、两点,若(为坐标原点),是否存在直线,使得四边形为矩形,若存在,求出直线的方程,若不存在,请说明理由.【例12】过椭圆:上一点引圆:的两条切线、,切点为、,直线与轴、轴分别相交于、两点⑴设,且,求直线的方程;⑵若椭圆的短轴长为,且,求此椭圆的方程;⑶试问椭圆上是否存在满足的点,说明理由.【变式6】已知均在椭圆上,直线、分别过椭圆的左右焦点、,当时,有.⑴求椭圆的方程;⑵设是椭圆上的任一点,为圆的任一条直径,求的最大值.家庭作业习题1. (08浙江)已知、为椭圆的两个焦点,过的直线交椭圆于、两点,若,则=________.习题2. 若椭圆的离心率为,则的值等于.习题3. 设为椭圆的两个焦点,在椭圆上,已知是一个直角三角形的三个顶点,且,求的值.习题4. 设椭圆:的左焦点为,上顶点为,过点作垂直于的直线交椭圆于另外一点,交轴正半轴于点,且⑴求椭圆的离心率;⑵若过、、三点的圆恰好与直线:相切,求椭圆的方程.月测备选习题1. 已知椭圆的左、右焦点分别为、,且,点在椭圆上,,,则椭圆的离心率()A. B. C. D.习题2. (2009丰台区一模)在平面直角坐标系中,已知顶点和,顶点在椭圆上,则.习题3. 已知椭圆上一点,、为椭圆的两个焦点,且,求椭圆的方程.习题4. 已知是椭圆:的左、右焦点,点在椭圆上,线段与轴的交点满足.⑴求椭圆的方程.⑵椭圆上任一动点关于直线的对称点为,求的取值范围.。