泰勒公式展开常用

高中泰勒公式展开式大全
高中数学中，泰勒公式是一种重要的数学工具，用于将一个函数在某一点附近展开成无限项的幂级数。

它在数学分析、微积分等领域有着广泛的应用。

下面将为大家介绍一些常见的高中泰勒公式的展开式。

1. 正弦函数展开式：
正弦函数的泰勒展开式可以写成：
sin(x) = x - (x^3)/3! + (x^5)/5! - (x^7)/7! + ...
2. 余弦函数展开式：
余弦函数的泰勒展开式可以写成：
cos(x) = 1 - (x^2)/2! + (x^4)/4! - (x^6)/6! + ...
3. 自然指数函数展开式：
自然指数函数的泰勒展开式可以写成：
e^x = 1 + x + (x^2)/2! + (x^3)/3! + ...
4. 对数函数展开式：
对数函数的泰勒展开式可以写成：
ln(1+x) = x - (x^2)/2 + (x^3)/3 - (x^4)/4 + ...
这些展开式在高中数学中经常用到，可以用来近似计算复杂的函数值。

通常情况下，展开式的前几项会给出较为准确的结果，而随着项数的增加，近似的精度也会提高。

需要注意的是，泰勒展开式只在展开点附近有效，当离展开点越远，近似的精度就会变得越低。

因此，在实际应用中，需要根据具体问题选择合适的展开点和合适的项数，以得到满意的近似结果。

以上是一些常见的高中泰勒公式的展开式，通过学习和理解这些展开式，可以帮助我们更好地理解和应用数学知识，提高解决问题的能力。

泰勒公式展开常用【原创版】目录1.泰勒公式的定义和基本概念2.泰勒公式的展开形式3.泰勒公式的应用领域4.泰勒公式的优点和局限性正文泰勒公式是微积分学中的一种重要公式，它用于描述一个可微函数在某一点附近的近似值。

泰勒公式可以将函数展开为一个无穷级数，该级数的每一项都与该点的各阶导数有关。

一、泰勒公式的定义和基本概念泰勒公式的定义如下：设函数 f(x) 在点 a 附近可微，如果在点 a 的邻域内，f(x) 可以展开为：f(x) = f(a) + f"(a)(x-a) + f""(a)(x-a)^2/2! + f"""(a)(x-a)^3/3! +...+ f^n(a)(x-a)^n/n! + Rn(x)其中，f"(a)、f""(a)、f"""(a) 等表示函数 f(x) 在点 a 的各阶导数，n! 表示 n 的阶乘，Rn(x) 表示泰勒公式的余项。

二、泰勒公式的展开形式泰勒公式的展开形式可以分为两部分：一部分是级数前面的各项，它们是函数 f(x) 在点 a 的各阶导数乘以 (x-a) 的相应次方；另一部分是余项 Rn(x)，它表示函数 f(x) 在点 a 附近与级数前面的各项的误差。

三、泰勒公式的应用领域泰勒公式在数学和物理等领域具有广泛的应用。

在近似计算中，泰勒公式可以用来估算函数在某一点附近的值，这对于许多实际问题具有重要意义。

此外，泰勒级数还可以用于求解微分方程、研究函数的性质等。

四、泰勒公式的优点和局限性泰勒公式的优点在于它可以将复杂的函数在某一点附近近似为简单的多项式，从而简化问题。

同时，泰勒公式可以描述函数在邻域内的行为，为我们提供了函数的局部性质。

然而，泰勒公式也存在局限性。

首先，泰勒公式的展开需要知道函数在点 a 的各阶导数，这对于某些函数可能难以求得。

其次，泰勒公式的余项 Rn(x) 可能较大，导致近似结果的误差较大。

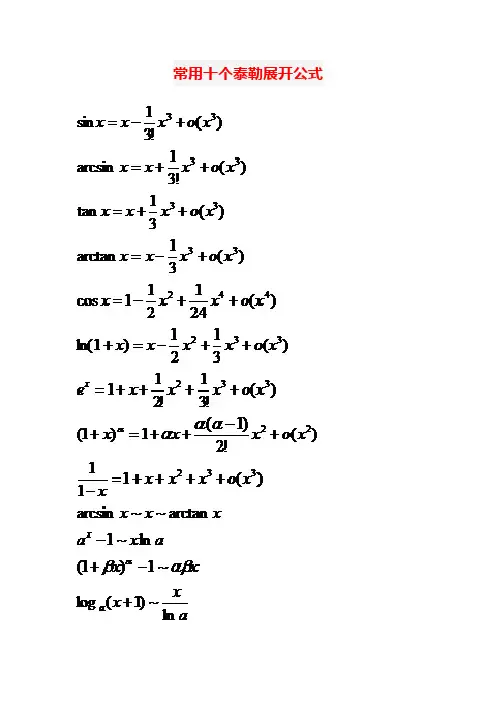
常用十个泰勒展开公式比较通俗地讲解一下泰勒公式是什么。

泰勒公式，也称泰勒展开式。

是用一个函数在某点的信息，描述其附近取值的公式。

如果函数足够平滑，在已知函数在某一点的各阶导数值的情况下，泰勒公式可以利用这些导数值来做系数，构建一个多项式近似函数，求得在这一点的邻域中的值所以泰勒公式是做什么用的？简单来讲就是用一个多项式函数去逼近一个给定的函数(即尽量使多项式函数图像拟合给定的函数图像)，注意，逼近的时候一定是从函数图像上的某个点展开。

如果一个非常复杂函数，想求其某点的值，直接求无法实现，这时候可以使用泰勒公式去近似的求该值，这是泰勒公式的应用之一。

泰勒公式在机器学习中主要应用于梯度迭代。

******************************************************************* ******************************************************************************************************************************** ************************************************************* 1. 问题的提出多项式是最简单的一类初等函数。

关于多项式，由于它本身的运算仅是有限项加减法和乘法，所以在数值计算方面，多项式是人们乐于使用的工具。

因此我们经常用多项式来近似表达函数。

这也是为什么泰勒公式选择多项式函数去近似表达给定的函数。

******************************************************************* ******************************************************************************************************************************* ************************************************************2. 近似计算举例初等数学已经了解到一些函数如：的一些重要性质，但是初等数学不曾回答怎样来计算它们，以f(x) = 的近似计算为例：①. 一次（线性）逼近利用微分近似计算公式f(x) f() + ()(x - ) (该式由导数/微分的极限表达公式转换得到)，对 = 0 附近的 f(x) 的线性逼近为：f(x) f(0) + (0) x , 所以 f(x) = 1，所以f(x) 在 = 0 附近的线性逼近函数(x) = 1，如下图：线性逼近优点：形式简单，计算方便；缺点：离原点O越远，近似度越差。

8个泰勒公式总结1. 一阶泰勒公式一阶泰勒公式是数学中用来近似计算函数值的重要公式。

它基于函数在某一点的导数，可以将函数在该点附近的近似值表示为一个线性函数。

一阶泰勒公式可以表示为：f(x) ≈ f(a) + f'(a)(x-a)其中，f(x)是函数在点x处的值，f(a)是函数在点a处的值，f'(a)是函数在点a处的导数。

2. 二阶泰勒公式二阶泰勒公式是泰勒公式的推广，可以更精确地近似计算函数值。

它基于函数在某一点的导数和二阶导数，可以将函数在该点附近的近似值表示为一个二次函数。

二阶泰勒公式可以表示为：f(x) ≈ f(a) + f'(a)(x-a) + (1/2)f''(a)(x-a)^2其中，f(x)是函数在点x处的值，f(a)是函数在点a处的值，f'(a)是函数在点a处的一阶导数，f''(a)是函数在点a处的二阶导数。

3. 多项式泰勒公式多项式泰勒公式是泰勒公式的另一种表现形式。

它通过将函数展开成一系列幂函数的和，来近似计算函数值。

多项式泰勒公式可以表示为：f(x) ≈ f(a) + f'(a)(x-a) + (1/2)f''(a)(x-a)^2 + ... + (1/n!)f^(n)(a) (x-a)^n其中，f(x)是函数在点x处的值，f(a)是函数在点a处的值，f'(a)是函数在点a处的一阶导数，f''(a)是函数在点a处的二阶导数，f^(n)(a)是函数在点a处的n阶导数，n!表示n的阶乘。

4. 常用的泰勒公式展开函数在实际计算中，有一些常见的函数的泰勒公式展开式被广泛使用。

这些函数包括正弦函数、余弦函数、指数函数等。

正弦函数的泰勒公式展开式为：sin(x) ≈ x - (1/3!)x^3 + (1/5!)x^5 - (1/7!)x^7 + ...余弦函数的泰勒公式展开式为：cos(x) ≈ 1 - (1/2!)x^2 + (1/4!)x^4 - (1/6!)x^6 + ...以及指数函数的泰勒公式展开式为：e^x ≈ 1 + x + (1/2!)x^2 + (1/3!)x^3 + ...5. 泰勒级数泰勒级数是指将一个函数展开成一系列幂函数的和的无穷级数。

十个常用泰勒公式展开常用泰勒公式是在微积分中常用的一种展开函数的方法，可以将一个复杂的函数表示为一系列简单的多项式函数的和。

这些多项式函数的系数与原函数在某个点的导数有关，通过计算这些导数可以得到展开式的各项系数。

以下是十个常用的泰勒公式展开。

1. 正弦函数展开：正弦函数的泰勒展开式为：sin(x) = x - (x^3)/3! + (x^5)/5! - (x^7)/7! + ...2. 余弦函数展开：余弦函数的泰勒展开式为：cos(x) = 1 - (x^2)/2! + (x^4)/4! - (x^6)/6! + ...3. 自然指数函数展开：自然指数函数的泰勒展开式为：e^x = 1 + x + (x^2)/2! + (x^3)/3! + ...4. 对数函数展开：对数函数的泰勒展开式为：ln(1+x) = x - (x^2)/2 + (x^3)/3 - (x^4)/4 + ...5. 幂函数展开：幂函数的泰勒展开式为：(x+a)^n = a^n + n*a^(n-1)*x + (n*(n-1)*a^(n-2)*x^2)/2! + ...6. 反正弦函数展开：反正弦函数的泰勒展开式为：arcsin(x) = x + (x^3)/6 + (3*x^5)/40 + ...7. 反余弦函数展开：反余弦函数的泰勒展开式为：arccos(x) = π/2 - arcsin(x) = π/2 - x - (x^3)/6 - (3*x^5)/40 - ...8. 反正切函数展开：反正切函数的泰勒展开式为：arctan(x) = x - (x^3)/3 + (x^5)/5 - (x^7)/7 + ...9. 双曲正弦函数展开：双曲正弦函数的泰勒展开式为：sinh(x) = x + (x^3)/3! + (x^5)/5! + (x^7)/7! + ...10. 双曲余弦函数展开：双曲余弦函数的泰勒展开式为：cosh(x) = 1 + (x^2)/2! + (x^4)/4! + (x^6)/6! + ...以上是十个常用的泰勒公式展开。

泰勒公式展开常用摘要：一、泰勒公式简介1.泰勒公式定义2.泰勒公式的意义和应用二、泰勒公式展开的常用方法1.多项式展开2.级数展开三、泰勒公式展开的应用实例1.函数逼近2.数值积分四、泰勒公式展开的局限性及改进1.泰勒级数的收敛性2.泰勒级数的改进方法正文：泰勒公式是一种在给定点附近近似计算函数值的方法，广泛应用于数值分析、函数逼近等领域。

本文将介绍泰勒公式展开的常用方法、应用实例以及局限性及改进方法。

一、泰勒公式简介泰勒公式（Taylor formula）是一种用多项式来近似表示函数的方法。

给定一个函数f(x)，如果我们可以找到一个多项式P(x)，使得当x 趋近于某个点a 时，f(x) 与P(x) 的差值趋近于0，那么这个多项式P(x) 就是函数f(x) 在点a 处的泰勒多项式。

泰勒公式可以表示为：f(x) ≈ f(a) + f"(a)(x-a) + f""(a)(x-a)^2/2! + ...+ f^n(a)(x-a)^n/n!其中，f"(a)、f""(a) 等表示函数f(x) 在点a 处的各阶导数值。

二、泰勒公式展开的常用方法泰勒公式展开通常有两种方法：多项式展开和级数展开。

1.多项式展开多项式展开是利用泰勒公式中各阶导数值来构造一个多项式，从而逼近给定函数。

常用的多项式展开方法有Legendre 多项式、Chebyshev 多项式、Fourier 多项式等。

2.级数展开级数展开是将泰勒公式中的无穷级数展开，通过截断求和来近似计算函数值。

常用的级数展开方法有Cochran-Maclaurin 公式、Machin-like 公式等。

三、泰勒公式展开的应用实例1.函数逼近泰勒公式可以用来逼近任意给定的函数。

例如，在数值分析中，我们可以用泰勒公式来近似计算复杂数学模型中的函数值，从而降低计算复杂度。

2.数值积分泰勒公式可以用来改进数值积分方法，例如高斯积分公式、辛普森公式等。

8个泰勒公式常用公式泰勒公式是一种在微积分中非常重要的工具，它可以利用函数在其中一点的导数来近似地表示函数在该点附近的取值。

在数学和物理等领域，泰勒公式广泛应用于函数的近似计算和数值求解等问题。

下面我们介绍一些常用的泰勒公式及其应用。

1.一阶泰勒公式一阶泰勒公式也称为泰勒展开式，用于近似地表示函数在其中一点附近的取值。

设函数$f(x)$在$x=a$处可导，则函数$f(x)$在$x=a$处的一阶泰勒公式为$$f(x)\approx f(a)+f'(a)(x-a)$$其中$f'(a)$表示函数$f(x)$在$x=a$处的导数。

一阶泰勒公式常用于近似计算和数值求解等问题中。

2.二阶泰勒公式二阶泰勒公式是泰勒展开式的推广，用于更精确地近似表示函数在其中一点附近的取值。

设函数$f(x)$在$x=a$处二阶可导，则函数$f(x)$在$x=a$处的二阶泰勒公式为$$f(x)\approx f(a)+f'(a)(x-a)+\frac{f''(a)}{2!}(x-a)^2$$其中$f''(a)$表示函数$f(x)$在$x=a$处的二阶导数。

二阶泰勒公式在高精度数值求解和近似计算等问题中广泛应用。

3.泰勒级数泰勒级数是将一个函数在其中一点处展开成无穷级数的形式，用于表示函数在该点附近的取值。

设函数$f(x)$在$x=a$处具有无限阶导数，则函数$f(x)$在$x=a$处的泰勒级数为$$f(x)=f(a)+f'(a)(x-a)+\frac{f''(a)}{2!}(x-a)^2+\frac{f'''(a)}{3!}(x-a)^3+...$$泰勒级数是一种非常重要的数学工具，能够用无穷阶导数展开的形式表示函数，具有广泛的应用价值。

4.泰勒多项式泰勒多项式是将函数在其中一点处展开成有限项多项式的形式，用于近似地表示函数在该点附近的取值。

泰勒展开常用公式【原创实用版】目录1.泰勒公式的定义与意义2.泰勒公式的常用展开形式3.泰勒公式的应用领域正文泰勒公式是微积分学中的一种重要公式，它可以用来描述一个可微函数在某一点附近的近似值。

泰勒公式在数学、物理等学科中有着广泛的应用。

一、泰勒公式的定义与意义泰勒公式是指，如果一个函数 f(x) 在 x=a 处可微，那么在 a 附近的某个点 x=a+h，函数 f(x) 可以展开成以下形式：f(x) = f(a) + f"(a)h + f""(a)h^2/2! + f"""(a)h^3/3! +...+ f^n(a)h^n/n! + Rn(h)其中，f"(a)、f""(a)、f"""(a) 等表示函数 f(x) 在点 a 处的各阶导数，n! 表示 n 的阶乘，Rn(h) 表示泰勒公式的余项。

二、泰勒公式的常用展开形式泰勒公式的展开形式取决于函数的阶数 n，一般情况下，我们使用前n+1 项来近似表示函数。

根据展开的项数，泰勒公式的常用形式有以下几种：1.泰勒展开一级形式（展开到一次项）f(x) ≈ f(a) + f"(a)(x-a)2.泰勒展开二级形式（展开到二次项）f(x) ≈ f(a) + f"(a)(x-a) + f""(a)(x-a)^2/2!3.泰勒展开三级形式（展开到三次项）f(x) ≈ f(a) + f"(a)(x-a) + f""(a)(x-a)^2/2! +f"""(a)(x-a)^3/3!以此类推，可以得到泰勒展开的 n 级形式。

三、泰勒公式的应用领域泰勒公式在数学和自然科学等领域有着广泛的应用，主要包括以下几个方面：1.近似计算：泰勒公式可以用来近似计算函数在某一点附近的值，这对于求解实际问题具有重要意义。

泰勒展开常用公式【最新版】目录1.泰勒公式的定义与意义2.泰勒公式的常用展开形式3.泰勒公式的应用实例正文1.泰勒公式的定义与意义泰勒公式，以英国数学家布鲁克·泰勒（Brook Taylor）的名字命名，是一种用于描述一个可微函数在某一点附近的近似值的数学公式。

泰勒公式可以将函数在某一点展开成无穷级数，该级数的每一项都与该点的各阶导数有关。

泰勒公式在数学、物理等科学领域具有重要的应用价值。

2.泰勒公式的常用展开形式泰勒公式的常用展开形式如下：f(x) ≈ f(a) + f"(a)(x-a) + (f""(a)(x-a)^2)/2! +...+(f^n(a)(x-a)^n)/n! + Rn(x)其中，f(x) 是要展开的函数，a 是函数的某一点，f"(a)、f""(a) 等分别表示函数在点 a 处的一阶导数、二阶导数等，n! 表示 n 的阶乘，Rn(x) 是泰勒公式的余项。

3.泰勒公式的应用实例泰勒公式在许多科学领域都有广泛应用，例如在数值分析、近似计算、泛函分析等方面都有重要作用。

下面我们通过一个具体的应用实例来说明泰勒公式的使用。

假设我们要计算函数 f(x) = e^x 在点 a = 0 处的近似值，我们可以利用泰勒公式进行展开：f(x) ≈ f(0) + f"(0)(x-0) + (f""(0)(x-0)^2)/2! +...由于 f(0) = 1，f"(0) = 1，f""(0) = 1，我们可以将这些值代入公式中，得到：e^x ≈ 1 + x + (x^2)/2! +...通过泰勒公式，我们可以将复杂的指数函数 e^x 展开成多项式，从而简化计算。

当然，实际应用中，我们通常只需要取展开式的前几项，就可以获得较好的近似结果。

总之，泰勒公式是一种重要的数学工具，它为我们提供了一种在特定点附近近似计算函数值的方法。

【泰勒展开】常见泰勒公式大全几个常见的泰勒公式(x\rightarrow0) ：sinx = x -\frac{x^3}{6} +o(x^3)\qquad \qquad \quad \ \ arcsinx=x+\frac{x^3}{6}+o(x^3)cosx=1-\frac{x^2}{2}+\frac{x^4}{24}+o(x^4)\qquad \quad arccosx=? [1]tanx = x +\frac{x^3}{3}+o(x^3)\qquad \qquad \quad \ arctanx=x-\frac{x^3}{3}+o(x^3)e^x = 1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+o(x^3) \qquad ln(1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}+o(x^3)(1+x)^{\alpha}=1+\alpha x+\frac{\alpha(\alpha-1)}{2}x^2+o(x^2)另外\begin{align} &对于 (1+x)^{\alpha}=1+\alphax+\frac{\alpha(\alpha-1)}{2}x^2+o(x^2) \\&\text{当}\alpha =\frac{1}{2}\text{，则}\sqrt{1+x}=1+\frac{1}{2}x-\frac{1}{8}x^2+o\left( x^2 \right) \\ &\text{当}\alpha =\frac{1}{3}\text{，则}\sqrt[3]{1+x}=1+\frac{1}{3}x-\frac{1}{9}x^2+o\left( x^2 \right) \end{align}习题中常见(x \rightarrow 0) ：\begin{align} tanx - sinx &= \frac{1}{2}x^3+o(x^3)\\ x - sinx &= \frac{1}{6}x^3+o(x^3)\\ arcsinx - x &=\frac{1}{6}x^3+o(x^3)\\ tanx - x &=\frac{1}{3}x^3+o(x^3)\\ x-arctanx&=\frac{1}{3}x^3+o(x^3) \end{align}即有\begin{align*} tanx - sinx &\sim \frac{1}{2}x^3\\ x - sinx &\sim \frac{1}{6}x^3\\ arcsinx - x &\sim\frac{1}{6}x^3\\ tanx - x &\sim \frac{1}{3}x^3\\ x-arctanx &\sim\frac{1}{3}x^3 \end{align*}还可以得到(x\rightarrow0) ：\begin{align} x-\ln \left( 1+x \right) \,&\sim\frac{x^2}{2} \\ e^x-1-x\,&\sim \frac{x^2}{2} \\ 1-\cos ^ax\ &\sim \frac{ax^2}{2} \\ f\left( x \right)^{g\left( x \right)}-1 &\sim g\left( x \right)\left[ f\left( x \right) -1 \right] \qquad \left( 当f\left( x \right) \rightarrow 1\text{且}f\left( x\right) ^{g\left( x \right)}\rightarrow 1 \right)\end{align}注：上述四结论来自：有时还会用到\left( 1+x \right) ^{\frac{1}{x}}=e-\frac{e}{2}x+\frac{11e}{24}{x^2}+o\left( x^2 \right) [2]一般地\begin{align} e^{x}&=\sum_{n=0}^{\infty}\frac{x^{n}}{n!} =1+x+\frac{x^{2}}{2 !}+\cdots+\frac{x^{n}}{n!} x^{n}+\cdots \\ \ sinx&=\sum_{n=0}^{\infty} \frac{(-1)^{n}}{(2 n+1) !} x^{2 n+1}=x-\frac{x^{3}}{3 !} +\frac{x^{5}}{5!} -\cdots+\frac{(-1)^{n}}{(2 n+1) !} x^{2 n+1}+\cdots\\ \ cos x&=\sum_{n=0}^{\infty} \frac{(-1)^{n}}{(2 n) !}x^{2 n}=1-\frac{x^{2}}{2!} +\frac{x^{4}}{4!} -\cdots+\frac{(-1)^{n}}{(2n)!} x^{2n}+\cdots \\ \ ln(1+x)&=\sum_{n=0}^{\infty} \frac{(-1)^{n}}{n+1}x^{n+1}=x-\frac{1}{2} x^{2}+\frac{1}{3} x^{3}-\cdots+\frac{(-1)^{n}}{n+1} x^{n+1}+\cdots, x \in(-1,1] \\ \frac{1}{1-x}&=\sum_{n=0}^{\infty}x^{n}=1+x+x^{2}+x^{3}+\cdots+x^{n}+\cdots, x \in(-1,1) \\ \frac{1}{1+x} &= \sum_{n = 0}^{\infty}(-1)^{n} x^{n} = 1-x+x^{2}-x^{3}+\cdots+(-1)^{n} x^{n}+\cdots, x\in(-1,1) \\ (1+x)^{\alpha} &= 1+\sum_{n = 1}^{\infty} \frac{\alpha(\alpha-1) \cdots(\alpha-n+1)}{n !} x^{n} = 1+\alpha x+\frac{\alpha(\alpha-1)}{2 !}x^{2}+\cdots+\frac{\alpha(\alpha-1) \ldots(\alpha-n+1)}{n !} x^{n}+\cdots, x \in(-1,1) \\ \arctan x &=\sum_{n = 0}^{\infty} \frac{(-1)^{n}}{2 n+1} x^{2\pi+1} = x-\frac{1}{3} x^{3}+\frac{1}{5}x^{5}+\cdots+\frac{(-1)^{n}}{2 n+1} x^{2 n+1}+\cdots, x \in[-1,1] \\ \end{align}{\LARGE \begin{align} \arcsin x &= \sum_{n =0}^{\infty} \frac{(2 n!)x^{2n+1}}{4^{n}(n !)^{2}(2n+1)} = x+\frac{1}{6} x^{3}+\frac{3}{40}x^{5}+\frac{5}{112} x^{7}+\frac{35}{1152}x^{2}+\cdots+\frac{(2 n) !}{4^{n}(n !)^{2}(2 n+1)}x^{2 n+1}+\cdots, x \in(-1,1) \\ \tan x &= \sum_{n = 1}^{\infty} \frac{B_{2n}4^{n}(4^{n}-1)}{(2 n) !} x^{2n-1} = x+\frac{1}{3} x^{3}+\frac{2}{15}x^{5}+\frac{17}{315} x^{7}+\frac{62}{2835}x^{9}+\frac{1382}{155925} x^{11}+\frac{21844}{6081075} x^{13}+\frac{929569}{} x^{15}+\cdots ,x \in(-1,1) \\ \sec x &= \sum_{\pi = 0}^{\infty} \frac{(-1)^{n}E_{2n} x^{2 n}}{(2 n) !} = 1+\frac{1}{2} x^{2}+\frac{5}{24} x^{4}+\frac{61}{720} x^{6}+\cdots, x \in\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\\ \csc x &=\sum_{n = 0}^{\infty} \frac{(-1)^{n+1} 2\left(2^{2\mathrm{n}-1}-1\right) B_{2n}}{(2 n) !} x^{2 x-1} =\frac{1}{x}+\frac{1}{6} x+\frac{7}{360}x^{3}+\frac{31}{15120} x^{5}+\frac{127}{604800}x^{7}+\frac{73}{3421440} x^{2}+\frac{1414477}{}x^{11}+\cdots, x \in(0, \pi)\\ \cot x &= \sum_{n =0}^{\infty} \frac{(-1)^{n} 2^{2n} B_{2n}}{(2 n) !}x^{2 n-1} = \frac{1}{x}-\frac{1}{3} x-\frac{1}{45}x^{3}-\frac{2}{945} x^{5}-\cdots, x \in(0, \pi)\end{align}}相关链接：1.^利用arccosx = pi/2 - arcsinx即可得出。