独立性检验的基本思想及其初步应用导学案

独立性检验的基本思想及初步应用教案第一章：独立性检验简介1.1 学习目标：（1）理解独立性检验的定义及作用；（2）了解独立性检验在实际应用中的重要性；（3）掌握独立性检验的基本步骤。

1.2 教学内容：（1）独立性检验的定义；（2）独立性检验的实际应用案例；（3）独立性检验的基本步骤。

1.3 教学活动：（1）介绍独立性检验的概念；（2）通过实际案例让学生了解独立性检验的应用；（3）引导学生掌握独立性检验的基本步骤。

第二章：卡方检验2.1 学习目标：（1）理解卡方检验的原理；（2）掌握卡方检验的计算方法；（3）学会判断卡方检验的结果。

2.2 教学内容：（1）卡方检验的原理；（2）卡方检验的计算方法；（3）卡方检验的结果判断。

2.3 教学活动：（1）讲解卡方检验的原理；（2）通过示例让学生掌握卡方检验的计算方法；（3）引导学生学会判断卡方检验的结果。

第三章：列联表与独立性检验3.1 学习目标：（1）了解列联表的概念；（2）掌握列联表的绘制方法；（3）学会利用列联表进行独立性检验。

3.2 教学内容：（1）列联表的概念；（2）列联表的绘制方法；（3）利用列联表进行独立性检验。

3.3 教学活动：（1）介绍列联表的概念；（2）通过示例让学生掌握列联表的绘制方法；（3）引导学生学会利用列联表进行独立性检验。

第四章：独立性检验的应用4.1 学习目标：（1）学会运用独立性检验解决实际问题；（2）掌握独立性检验在调查分析中的作用；（3）了解独立性检验在实际应用中的局限性。

4.2 教学内容：（1）独立性检验在实际问题中的应用；（2）独立性检验在调查分析中的作用；（3）独立性检验的局限性。

4.3 教学活动：（1）讲解独立性检验在实际问题中的应用；（2）通过案例分析让学生了解独立性检验在调查分析中的作用；（3）引导学生认识独立性检验的局限性。

第五章：练习与拓展5.1 学习目标：（1）巩固所学独立性检验知识；（2）提高运用独立性检验解决实际问题的能力；（3）培养学生的创新意识和拓展能力。

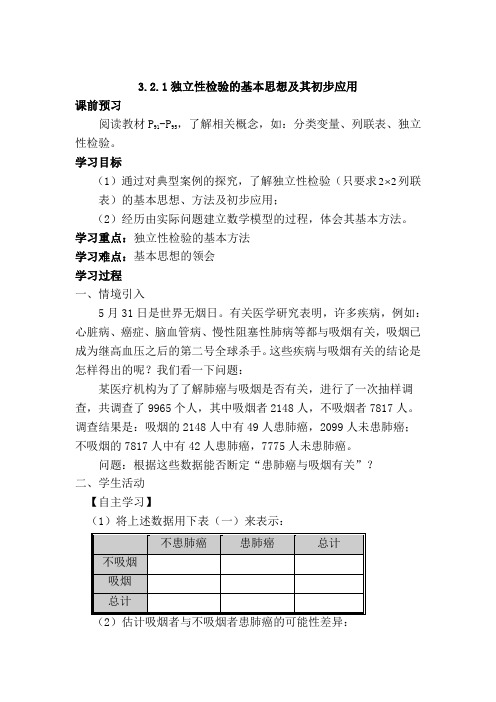
3.2.1独立性检验的基本思想及其初步应用课前预习阅读教材P91-P95，了解相关概念，如：分类变量、列联表、独立性检验。

学习目标（1）通过对典型案例的探究，了解独立性检验（只要求22 列联表）的基本思想、方法及初步应用；（2）经历由实际问题建立数学模型的过程，体会其基本方法。

学习重点：独立性检验的基本方法学习难点：基本思想的领会学习过程一、情境引入5月31日是世界无烟日。

有关医学研究表明，许多疾病，例如：心脏病、癌症、脑血管病、慢性阻塞性肺病等都与吸烟有关，吸烟已成为继高血压之后的第二号全球杀手。

这些疾病与吸烟有关的结论是怎样得出的呢？我们看一下问题：某医疗机构为了了解肺癌与吸烟是否有关，进行了一次抽样调查，共调查了9965个人，其中吸烟者2148人，不吸烟者7817人。

调查结果是：吸烟的2148人中有49人患肺癌，2099人未患肺癌；不吸烟的7817人中有42人患肺癌，7775人未患肺癌。

问题：根据这些数据能否断定“患肺癌与吸烟有关”？二、学生活动【自主学习】（1）将上述数据用下表（一）来表示：在不吸烟者中患肺癌的人约占多大比例？ ； 在吸烟的人中患肺癌的人约占多大比例？ 。

问题：由上述结论能否得出患肺癌与吸烟有关？把握有多大？ 【合作探究】1、观察、分析样本数据的列联表和柱形图、条形图，你能得出什么结论？2、该结论能否推广到总体呢？3、假设0H ：患肺癌与吸烟没有关系。

则两事件发生的概率有何关系？何结论？4、构造随机变量22()()()()()n ad bc Ka b c d a c b d -=++++（其中n a b c d =+++），结合3中结论，若0H 成立，则K 2应该很 (大、小)根据表(一)中的数据，利用4中公式，计算出K 2的观测值，该值说明什么？（统计学中有明确的结论，在0H 成立的情况下，P(K 2≥6.635)≈0.01。

）5、结合表（二）和三维柱形图、二维条形图如何判断两个分类变量是否有关系？利用独立性检验呢？二者谁更精确？ 【当堂检测】在某医院，因为患心脏病而住院的665名男性病人中，有214人秃顶；而另外772名不是因为患心脏病而住院的男性病人中有175名秃顶. 分别利用图形和独立性检验方法判断秃顶与患心脏病是否有关系？。

第一章 统计案例第二节 独立性检验的基本思想及初步应用（第1课时）一、学习目标1.了解两个分类变量的列联表,并用二维条形图表示,会计算K 2的观测值.2.了解独立性检验的思想,并会用独立性检验思想对两个变量之间是否有关联进行检验.3.通过实例说明独立性检验的方法和步骤,会根据22⨯列联表求统计量2K ,体会独立性检验的作用.【重点、难点】用独立性检验思想对两个变量之间是否有关联进行检验;根据22⨯列联表求统计量2K .二、学习过程复习引入：经常上网会影响学习吗?下表为教育部对1000名中学生进行调查的结果.经常上网影响学习吗?如何判断?经常上网 不经常上网总计 不及格 80 120 200及格 120 680 800总计 200 800 1000问题1:(1)通过上述数据经常上网的人成绩及格的比例为 ,不经常上网的人成绩及格的比例为 ,这个数据可以初步判断经常上网对学习成绩是有影响的,但这种说法的把握性有多大,还需要进行独立性检验才知道.(2)独立性检验的概念用统计量K 2的大小来研究两个变量是否有关系的方法,称为独立性检验.问题2:两个分类变量A 和B 的2×2列联表一般地,假设有两个分类变量A 和B ,它们的可能取值分别为{A 1,A 2}和{B 1,B 2}, 其样本频数列联表(称为2×2列联表)为:B AB 1 B 2 总计 A 1 a bA 2 c d总计问题3:统计量K 2的计算公式是怎样的?若有如下列联表所示的抽样数据:类1 类2 总计类 A a b a+b类 B c d c+d总计 a+cb+d a+b+c+d则K 2= (其中n=a+b+c+d ).问题4:根据K 2判断两变量是否有关联当K 2≤2.706时, 充分的证据判定变量A 、B 有关联,可以认为变量A 、B 是 关联的;当K 2>2.706时,有 的把握判定变量A 、B 有关联;当K 2>3.841时,有 的把握判定变量A 、B 有关联;当K 2>6.635时,有 的把握判定变量A 、B 有关联.答案：问题1:(1)60% 85% ；问题2:a+b c+d a+c b+d a+b+c+d问题3:错误!未找到引用源。

1．1 独立性检验【课标要求】1．了解独立性检验的意义、理解2×2列联表．2．会用χ2判断事件A与B之间的关系．3．掌握独立性检验的基本步骤．4．通过典型案例，掌握独立性检验的基本思想．【核心扫描】1．用χ2判断事件A与B之间的关系．(重点)2．独立性检验的基本思想及方法．(难点)自学导引1．2×2列联表与卡方统计量(1)一般地，对于两个研究对象Ⅰ和Ⅱ，Ⅰ有两类取值类A和类B，Ⅱ也有两类取值类1和类2，可以得下联表所示的抽样数据：将形如此表的表格称为2×2列联表．(2)卡方统计量χ2＝，其中n＝a＋b＋c＋d为样本容量．2．独立性检验利用χ2统计量来研究两类对象是否有关系的方法称为独立性检验．3．独立性检验的基本步骤(1)提出假设H0：Ⅰ与Ⅱ没有关系；(2)根据2×2列联表与公式χ2＝(n＝a＋b＋c＋d)，计算χ2的值；(3)查对临界值(如表)，作出判断．试一试：结合反证法与独立性检验原理的关系，说明独立性检验．提示独立性检验类似于数学中的反证法，要确认“两个变量有关系”这一结论成立的可信度，首先假设结论不成立，在假设下，我们构造的统计量χ2应该很小．如果由观测数据计算得到的χ2值很大，则在一定程度上说明假设不合理，再根据不合理的程度与临界值的关系作出判断．想一想：当χ2>6.635时，我们应当拒绝统计假设，还是接受统计假设．这种估计出错的可能性有多大？提示拒绝统计假设，由P(χ2>6.635)＝0.01，即这种估计出错的可能性为1%.名师点睛1．独立性检验(1)利用随机变量χ2＝，(其中n＝a＋b＋c＋d为样本容量)，来确定在多大程度上可以认为“两个分类变量有关系”的方法称为两个分类变量的独立性检验．(2)独立性检验的基本思想类似于反证法．要确认“两个分类变量有关系”这一结论成立的可信程度，首先假设该结论不成立，即假设结论“两个分类变量没有关系”成立，在该假设下构造的随机变量χ2应该很小．如果由观测数据计算得到的χ2的观测值很大，则在一定程度上说明假设不合理．根据随机变量χ2的含义，可以通过概率P(χ2≥x0)的大小来评价该假设不合理的程度有多大，从而说明这“两个分类变量有关系”这一结论成立的可信程度有多大．如P(χ2≥6.635)≈0.01，由实际计算得χ2>6.635说明假设不合理的程度约为99%，即两个分类变量有关系这一结论成立的可信程度为99%.2．利用χ2的值判定两个研究对象Ⅰ和Ⅱ之间的关系(1)若χ2＞10.828，则有99.9%的把握认为“Ⅰ与Ⅱ有关系”；(2)若χ2＞6.635，则有99%的把握认为“Ⅰ与Ⅱ有关系”；(3)若χ2＞2.706，则有90%的把握认为“Ⅰ与Ⅱ有关系”；(4)若χ2≤2.706，则认为没有充分的证据显示“Ⅰ与Ⅱ有关系”，但也不能作出结论“H0成立”，即不能认为Ⅰ与Ⅱ没有关系.题型一利用χ2判定两个变量间的关系【例1】某电视台联合相关报社对“男女同龄退休”这一公众关注的问题进行了民意调查，数据如下表所示：根据表中数据，能否在犯错误的概率不超过0.001的前提下认为对这一问题的看法与性别有关系？(P(χ2≥10.828)≈0.001)[思路探索] 属于计算χ2，并用临界值表作出判断．解提出假设H0：对这一问题的看法与性别无关．由列联表中的数据，可以得到：χ2＝≈125.161>10.828.又P(χ2>10.828)≈0.001.故在犯错误的概率不超过0.001的前提下认为对“男女同龄退休”这一问题的看法与性别有关．规律方法根据假设检验的思想，比较计算出的χ2与临界值的大小，选择接受假设还是拒绝假设．【训练1】为了研究色盲与性别的关系，调查了1 000人，调查结果如下表所示：根据上述数据试问色盲与性别是否是相互独立的？解提出假设H0：色盲与性别没有关系．由已知条件可得下表依据公式得χ2＝≈27.139.当H0成立时，χ2≥10.828的概率约为0.001，因为χ2≈27.139>10.828，所以我们有99.9%的把握认为色盲与性别是有关的．题型二独立性检验的基本思想【例2】某教育机构为了研究人具有大学专科以上学历(包括大学专科)和对待教育改革态度的关系，随机抽取392名成年人进行调查，所得数据如下表所示：对于教育机构的研究项目，根据上述数据能得出什么结论？[思路探索] 计算χ2的值，作出判断．解提出假设H0：具有大学专科以上学历和对待教育改革的态度无关．由公式得：χ2＝≈1.78.因为1.78<2.706.所以我们没有理由说人具有大学专科以上学历(包括大学专科)和对待教育改革的态度有关．规律方法提出假设，计算χ2的值，结合临界值得出结论．【训练2】某大型企业人力资源部为了研究企业员工工作积极性和对待企业改革态度的关系，随机抽取了189名员工进行调查，所得数据如下表所示：对于人力资源部的研究项目，根据上述数据能得出什么结论？解提出假设H0：工作积极性与是否积极支持企业改革无关．χ2＝≈10.759.当H0成立时，χ2＞6.635的概率约为0.010，因为10.759>6.635，所以有99%的把握说：抽样员工对待企业改革的态度与工作积极性是有关的，可以认为企业的全体员工对待企业改革的态度与其工作积极性是有关的．题型三独立性检验综合应用【例3】(14分)某中学举办安全法规知识竞赛，从参赛的高一、高二学生中各抽出100人的成绩作为样本．对高一年级的100名学生的成绩进行统计，并按[40,50)，[50,60)，[60,70)，[70,80)，[80,90)，[90,100]分组，得到成绩分布的频率分布直方图(如图)．(1)若规定60分以上(包括60分)为合格，计算高一年级这次知识竞赛的合格率；(2)统计方法中，同一组数据常用该组区间的中点值作为代表，据此，估计高一年级这次知识竞赛的学生的平均成绩；(3)若高二年级这次知识竞赛的合格率为60%，由以上统计数据填写下面2×2列联表，并问是否有99%的把握认为“这次知识竞赛的成绩与年级有关系”？参考数据与公式：由列联表中数据计算χ2的公式χ2＝临界值表审题指导本题综合考查了频率分布直方图的识图、应用、统计量的计算，2×2列联表及独立性检验知识．【解题流程】―→―→―→―→―→[规范解答] (1)高一合格率为0．02×10＋0.03×10＋0.02×10＋0.01×10＝0.8＝80%.(2分)(2)高一样本的平均数为45×＋55×＋65×＋75×＋85×＋95×＝72，据此，可以估计高一年级这次知识竞赛的学生的平均成绩为72分．(7分)(3)(12分)χ2＝≈9.5>6.635.所以有99%的把握认为“这次知识竞赛的成绩与年级有关系”．(14分)【题后反思】统计的基本思维模式是归纳，通过部分数据的性质来推测全部数据的性质，从数据上体现的只是统计关系，而不是因果关系．【训练3】某企业有两个分厂生产某种零件，按规定内径尺寸(单位：mm)的值落在[29.94,30.06)的零件为优质品．从两个分厂生产的零件中各抽出了500件，量其内径尺寸，得结果如下表：甲厂：乙厂：(1)试分别估计两个分厂生产零件的优质品率；(2)由以上统计数据填下面2×2列联表，并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”.附：χ2＝，【解析】(1)甲厂抽查的产品中有360件优质品，从而甲厂生产的零件的优质品率估计为＝72%；乙厂抽查的产品中有320件优质品，从而乙厂生产的零件的优质品率估计为＝64%. (2)χ2＝≈7.35>6.635，所以有99%的把握认为两个分厂生产的零件的质量有差异．误区警示不理解χ2的意义，得出的结论出现错误【示例】吃零食是中学生中普遍存在的现象，吃零食对中学生的身体发育有诸多不利的影响，下面给出了性别与吃零食的2×2列联表：试推断，男生与女生，谁更喜欢吃零食．[错解] 由公式χ2＝≈4.722>3.841.所以说女生更喜欢吃零食，一个人吃零食与性别有关．我们由χ2的值判断A与B是否有关系，只是统计上的结论，具体到每个个体则不一定成立．[正解] 由公式χ2＝≈4.722>3.841.所以有95%的把握认为吃零食与性别有关，但具体到每一个人则不能说吃零食与性别有关，也可能与其他因素有关．统计量χ2的值说明变量有关的可信度，与所给统计数据也有关系．所得结论也只是统计上的结论，不能具体到个体.。

第三章 统计案例3.2独立性检验的基本思想及其初步应用一、学习目标1、了解独立性检验的基本思想、方法及初步应用。

了解独立性检验的常用方法：等高条形图及2k 统计量法。

2、了解实际推断原理和假设检验的基本思想、方法及初步应用。

3、能运用自己所学知识对具体案例进行检验。

【重点、难点】重点：1、了解独立性检验的基本思想、方法及初步应用。

了解独立性检验的常用方法：等高条形图及2k 统计量法。

2、了解实际推断原理和假设检验的基本思想、方法及初步应用。

3、能运用自己所学知识对具体案例进行检验。

难点：1、实际推断原理和假设检验的基本思想、方法及初步应用。

2、解决独立性检验与其它知识（如概率）等的综合应用题。

二、学习过程 【导入新课】1.与列联表相关的概念(1)分类变量：变量的不同“___”表示个体所属的_________，像这样的变量称为分类变量. (2)列联表：①列出的_____分类变量的_______，称为列联表.②一般地，假设有两个分类变量X 和Y ，它们的取值分别为 {}{}2121,,y y x x 和其样本频数列联表(称为2×2列联表)为：2.等高条形图等高条形图与表格相比，图形更能直观地反映出两个分类变量间是否 _________，常用等高条形图展示列表数据的_________. 3．独立性检验的基本思想(1)定义：利用随机变量__来判断“两个分类变量_______”的方法称为独立性检验.(2)公式：=2k ____________________，其中=n ________.(3)独立性检验的具体做法：①根据实际问题的需要确定容许推断“两个分类变量有关系”犯错误概率的上界α，然后k.查表确定_______k的_______k.②利用公式计算随机变量2③如果_____，就推断“X与Y有关系”，这种推断犯错误的概率不超过α；否则，就认为在_____________不超过α的前提下不能推断“X与Y有关系”，或者在样本数据中_________________支持结论“X与Y有关系”.典型例题类型一利用等高条形图判断两个分类变量是否相关例1.下列关于等高条形图的叙述正确的是( )A.从等高条形图中可以精确地判断两个分类变量是否有关系B.从等高条形图中可以看出两个变量频数的相对大小C.从等高条形图可以粗略地看出两个分类变量是否有关系D.以上说法都不对例2、为了解铅中毒病人与尿棕色素为阳性是否有关系，分别对病人组和对照组的尿液作尿棕色素定性检查，结果如下：病人与尿棕色素为阳性是否有关系？类型二独立性检验的基本思想例3、为了探究学生选报文、理科是否与对外语的兴趣有关，某同学调查了361名高二在校学生，调查结果如下：理科对外语有兴趣的有138人，无兴趣的有98人，文科对外语有兴趣的有73人，无兴趣的有52人.能否在犯错误的概率不超过0.1的前提下，认为“学生选报文、理科与对外语的兴趣有关”？类型三独立性检验的综合应用例4、某高校共有学生15 000人，其中男生10 500人，女生4 500人，为调查该校学生每周平均体育运动时间的情况，采用分层抽样的方法，收集300位学生每周平均体育运动时间的样本数据(单位：小时).(1)应收集多少位女生的样本数据？(2)根据这300个样本数据，得到学生每周平均体育运动时间的频率分布直方图(如图所示)，其中样本数据的分组区间为：［0，2］，(2，4］，(4，6］，(6，8］，(8，10］，(10，12］.估计该校学生每周平均体育运动时间超过4小时的概率.(3)在样本数据中，有60位女生的每周平均体育运动时间超过4小时.请完成每周平均体育运动时间与性别的列联表，并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.附：变式拓展1、在调查的480名男人中有38名患有色盲，520名女人中有6名患有色盲，分别利用图形和独立性检验的方法来判断色盲与性别是否有关？你所得到的结论在什么范围内有效？2、在一次重要会议上，为了搞好对外宣传工作，会务组选聘了16名男记者和14名女记者担任对外翻译工作，调查发现，男、女记者中分别有10人和6人会俄语.根据以上数据完成以下2×2列联表：会俄语不会俄语总计男女总计30并回答能否在犯错误的概率不超过0.10的前提下认为性别与会俄语有关？3、某中学将100名高一新生分成水平相同的甲、乙两个“平行班”，每班50人．陈老师采用A，B两种不同的教学方式分别在甲、乙两个班级进行教改实验．为了解教学效果，期末考试后，陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计，作出茎叶图如图．记成绩不低于90分者为“成绩优秀”．(1)在乙班样本的20个个体中，从不低于86分的成绩中随机抽取2个，求抽出的两个均“成绩优秀”的概率；(2)由以上统计数据作出列联表，并判断能否在犯错误的概率不超过0.1的前提下认为：“成绩优秀”与教学方式有关．三、学习反思1.判断两个分类变量是否有关系的两种常用方法(1)利用数形结合思想，借助等高条形图来判断两个分类变量是否相关是判断变量相关的常见方法.(2)一般地，在等高条形图中，b a a + 与 dc c+ 相差越大，两个分类变量有关系的可能性就越大.2、独立性检验的步骤：第一步，确定分类变量，获取样本频数，得到列联表.第二步，根据实际问题的需要确定容许推断“两个分类变量有关系”犯错误概率的上界α，然后查表确定临界值0k .第三步，利用公式()()()()d b c a d c b a bc ad n k ++++-=22)( 计算随机变量2k 的观测值k .第四步，作出判断.如果0k k >，就推断“X 与Y 有关系”这种推断犯错误的概率不超过α，否则就认为在犯错误的概率不超过α的前提下不能推断“X 与Y 的关系”，或者在样本数据中没有发现足够证据支持结论“X 与Y 有关系”.四、随堂检测1、某地区甲校高二年级有1 100人，乙校高二年级有900人，为了统计两个学校高二年级在学业水平考试中的数学学科成绩，采用分层抽样的方法在两校共抽取了200名学生的数学成绩，如下表：(已知本次测试合格线是50分，两校合格率均为100%) 甲校高二年级数学成绩：(1)计算x，y的值，并分别估计以上两所学校数学成绩的平均分(精确到1分).(2)若数学成绩不低于80分为优秀，低于80分为非优秀，根据以上统计数据写下面2×2列联表，并回答能否在犯错误的概率不超过0.05的前提下认为“两个学校的数学成绩有差异？”。

2017级人教版数学选修1-1 编号：5 编制时间： 2019.1.11 编制人：
第一章统计案例
1.2.1 独立性检验的基本思想及其初步应用
【学习目标】
通过探究“秃顶是否与患心脏病有关系”引出独立性检验的问题，并借助样本数据的列联表、柱形图和条形图展示患心脏病的秃顶比例比患其它病的秃顶比例高，让学生亲身体验独立性检验的实施步骤与必要性
【重点难点】
重点：独立性检验的实施步骤
难点; 独立性检验的实施步骤
【预习案】
1. 独立性检验的原理：
2. 独立性检验的步骤
【探究案】
例1 在某医院，因为患心脏病而住院的665名男性病人中，有214人秃顶；而另外772名不是因为患心脏病而住院的男性病人中有175名秃顶. 分别利用图形和独立性检验方法判断秃顶与患心脏病是否有关系？你所得的结论在什么范围内有效？
例2为考察高中生的性别与是否喜欢数学课程之间的关系，在某城市的某校高
1。

独立性检验的基本思想及初步应用教学目标：1. 了解独立性检验的基本思想及其在实际问题中的应用。

2. 学会使用假设检验方法判断两个分类变量之间是否具有独立性。

3. 掌握利用独立性检验解决实际问题的基本步骤。

教学内容：第一章：独立性检验的基本思想1.1 独立性检验的定义1.2 独立性检验的基本原理1.3 独立性检验的应用场景第二章：列联表与卡方检验2.1 列联表的定义及制作2.2 卡方检验的原理及计算2.3 卡方检验的判断标准第三章：假设检验方法3.1 假设检验的定义及类型3.2 独立性检验的假设条件3.3 独立性检验的步骤及注意事项第四章：实际问题中的应用4.1 案例一：产品质量检验4.2 案例二：消费者偏好调查4.3 案例三：疾病与性别关系的分析第五章：总结与拓展5.1 独立性检验在实际问题中的应用范围5.2 独立性检验的局限性5.3 独立性检验与其他统计方法的比较教学方法：1. 讲授：讲解独立性检验的基本思想、原理及应用。

2. 案例分析：分析实际问题，引导学生运用独立性检验解决问题。

3. 小组讨论：分组讨论案例，培养学生的合作与交流能力。

4. 练习与反馈：布置课后习题，及时了解学生掌握情况，给予针对性的指导。

教学评估：1. 课后习题：检验学生对课堂内容的掌握程度。

2. 案例分析报告：评估学生在实际问题中运用独立性检验的能力。

3. 课堂表现：观察学生在课堂讨论、提问等方面的参与度。

教学资源：1. 教材：独立性检验相关章节。

2. 案例材料：产品质量检验、消费者偏好调查、疾病与性别关系等实际问题。

3. 计算器：用于计算卡方值及概率。

教学时数：1. 共计4课时，每课时45分钟。

2. 分配如下：第一章1课时，第二章1课时，第三章1课时，第四章1课时。

第六章：多组独立性检验6.1 多组独立性检验的定义6.2 多组独立性检验的方法6.3 多组独立性检验的应用案例第七章：非参数检验7.1 非参数检验的定义及意义7.2 非参数检验方法简介7.3 独立性检验与非参数检验的比较第八章：独立性检验的软件操作8.1 统计软件的选择与操作8.2 独立性检验的软件实现8.3 结果解读与分析第九章：独立性检验在实际问题中的应用案例分析9.1 案例一：市场调查与分析9.2 案例二：教育公平性研究9.3 案例三：医学研究中的应用第十章：总结与展望10.1 独立性检验在统计学中的地位与作用10.2 独立性检验的发展趋势10.3 独立性检验在未来的挑战与机遇教学方法：1. 讲授：讲解多组独立性检验、非参数检验及软件操作相关知识。

课题：独立性检验的基本思想及其初步应用班级：使用人姓名：编号：46 主编教师：张震审核人：自研课（时段：晚自习时间：10分钟）旧知链接：1、回归分析的基本思想、方法及初步应用2、常用函数的图象特点，选择不同的模型建模，比较相关指数对不同模型进行比较. 新知自研：课本第10-15页的内容。

展示课（时段：正课）一、学习目标（1分钟） 1．通过对典型案例的探究，了解独立性检验的基本思想、方法及初步应用。

2．经历由实际问题建立数学模型的过程，体会其基本方法。

3．通过创设情境激发学生学习数学的情感，在学生分析问题、解决问题的过程中培养其积极探索的精神。

二、【定向导学·互动展示·当堂反馈】课堂元素导学流程自研自探环节合作探究环节展示提升环节质疑评价环节总结归纳环节自学指导（内容·学法·时间）互动策略（内容·.学法·.时间）展示方案（内容·学法·时间）随堂笔记（成果记录·知识生成·同步演练）导学一动手操作规律生成（20min）【学法指导】自研教材第10～15页从中理解并掌握独立性检验的基本思想及其初步应用。

【自我探究】1．与列联表相关的概念：①分类变量：变量的不同“值”表示个体所属的____，像这样的变量称为分类量。

②列联表：列出的两个分类变量的_____称为列联表。

2．等高条形图：与表格相比，等高条形图更能直观地反映出两个分类变量间是否_________，常用它来展示列联表数据的_________。

3．独立性检验：（1）在2×2列联表中，随机变量K2的计算公式为__________________________，其中n=__________。

利用随机变量K2来判断“两个分类变量有关系”的方法称为。

当K2的观测值k0越大时，两个变量之间的关系越______，否则，关系越____。

（2）如何判断K2的观测值k0的大小？（3）临界值k0的判断规则是怎样的？P（K2≥k0）的含义是什么？（4）独立性检验的基本思想：①独立性检验的必要性（为什么不能只凭列联表的数据和图形下结论？）②师生共同总结“探究”的解决步骤：第一步：提出假设检验问题H0：吸烟与患肺癌没有关系 H1：吸烟与患肺癌有关系（H0：原假设 H1：备择假设）第二步：选择检验的指标22()K()()()()n ad bca b c d a c b d-=++++说明：它越小，原假设“H0：吸烟与患肺癌没有关系”成立的可能性越大；反之，它越大，备择假设“H1：吸烟与患肺癌有关系”成立的可能性越大.第三步：查表得出结论（10min）①小组之间相互交流学法指导中的问题，并迅速给出自己的看法和见解。

独立性检验的基本思想及初步应用教案教学目标：1. 了解独立性检验的基本思想及应用；2. 学会使用独立性检验进行数据分析；3. 能够解释独立性检验的结果及意义。

教学内容：第一章：独立性检验概述1.1 独立性检验的定义1.2 独立性检验的作用1.3 独立性检验与相关性检验的区别第二章：独立性检验的基本原理2.1 抽样分布2.2 零假设与备择假设2.3 检验统计量第三章：卡方检验3.1 卡方检验的定义3.2 卡方检验的计算方法3.3 卡方检验的判断准则第四章：独立性检验的应用4.1 应用场景介绍4.2 应用实例分析4.3 结果解释与分析第五章：独立性检验的局限性及改进5.1 独立性检验的局限性5.2 改进方法介绍5.3 案例分析教学方法：1. 讲授法：讲解独立性检验的基本概念、原理及应用；2. 案例分析法：分析实际案例，让学生更好地理解独立性检验的方法及意义；3. 讨论法：引导学生思考独立性检验的局限性及改进方法。

教学评价：1. 课堂问答：检查学生对独立性检验基本概念的理解；2. 案例分析报告：评估学生运用独立性检验解决实际问题的能力；3. 期末考试：考察学生对独立性检验的全面掌握程度。

教学资源：1. 教材：《统计学原理》；2. 课件：独立性检验的相关内容；3. 案例素材：用于分析的的实际案例。

教学进度安排：1. 第一章：2课时；2. 第二章：2课时；3. 第三章：3课时；4. 第四章：4课时；5. 第五章：2课时。

独立性检验的基本思想及初步应用教案（续）教学内容：第六章：虚拟变量与独立性检验6.1 虚拟变量的概念6.2 虚拟变量在独立性检验中的应用6.3 虚拟变量检验的实例分析第七章：多重检验问题7.1 多重检验的定义及问题7.2 多重检验的解决方案7.3 多重检验在独立性检验中的应用第八章：独立性检验的软件操作8.1 常用统计软件介绍8.2 独立性检验的操作步骤8.3 独立性检验结果的解读第九章：独立性检验在实际领域的应用9.1 营销领域的应用案例9.2 医学领域的应用案例9.3 社会科学领域的应用案例第十章：总结与展望10.1 独立性检验的重要性10.2 独立性检验的发展趋势10.3 独立性检验在未来的挑战与机遇教学方法：1. 讲授法：讲解虚拟变量、多重检验及软件操作的相关知识；2. 案例分析法：分析实际案例，让学生更好地理解独立性检验的方法及意义；3. 实操演示法：展示独立性检验的软件操作过程，引导学生动手实践。

精品导学案：1. 2 独立性检验的基本思想及其初步应用课前预习学案一、预习目标：能用所学的知识对实际问题进行回归分析，体会回归分析的实际价值与基本思想；了解判断刻画回归模型拟合好坏的方法――相关指数和残差分析。

二、预习内容1. 给出例3：一只红铃虫的产卵数y 和温度x 有关，现收集了7组观测数据列于下表中，试建立y 与x 之间的回归方程.温度/x C21 23 25 27 29 32 35 产卵数/y 个 71121 24 66115325（学生描述步骤，教师演示）2. 讨论：观察右图中的散点图，发现样本点并没有分布在某个带状区域内，即两个变量不呈线性相关关系，所以不能直接用线性回归方程来建立两个变量之间的关系.课内探究学案一、学习要求：通过对典型案例的探究，了解独立性检验的基本思想、方法及初步应用学习重点：对独立性检验的基本思想的理解.学习难点：独立性检验的基本思想的应用.二、学习过程：知识点详解知识点一：分类变量对于性别变量，其取值为男和女两种.这种变量的不同“值”表示个体所属的不同类别，像这样的变量称为分类变量.知识点二：列联表为调查吸烟是否对患肺癌有影响，某肿瘤研究所随机调查了9965人，得到如下结果（单位：人）：吸烟与患肺癌列联表不患肺癌 患肺癌 总计 不吸烟 7775 42 7817 吸烟 2099 49 2148 总计9874919965像上表这样列出的两个分类变量的频数表，称为列联表. 知识点三：独立性检验这种利用随机变量K 2来确定在多大程度上可以认为“两个分类变量有关系”的方法称为两个分类变量的独立性检验.知识点四：判断结论成立的可能性的步骤一般地，假设有两个分类变量X 和Y ，它们的值域分别为｛x 1，x 2｝和｛y 1，y 2｝，其样50100150200250300350010203040温度产卵数本频数列联表（称为2×2列联表）为：2×2列联表y1y2总计x1x b x＋bx2c d c＋d总计x＋c b＋d x＋b＋c＋d 若要推断的论述为H1：“X与Y有关系”，可以按如下步骤判断结论H1成立的可能性：（1）通过三维柱形图和二维条形图，可以粗略地判断两个分类变量是否有关系，但是这种判断无法精确地给出所得结论的可靠程度.①在三维柱形图中，主对角线上两个柱形高度的乘积xd与副对角线上的两个柱形高度的乘积bc相差越大，H1成立的可能性就越大.②在二维条形图中，可以估计满足条件X＝x1的个体中具有Y＝y1的个体所占的比例a a＋b ，也可以估计满足条件X＝x2的个体中具有Y＝y1的个体所占的比例cc＋d.两个比例的值相差越大，H1成立的可能性就越大.（2）可以利用独立性检验来考察两个分类变量是否有关系，并且能较精确地给出这种判断的可靠程度.具体做法是：根据观测数据计算由K2＝n（ad－bc）2（a＋b）（c＋d）（a＋c）（b＋d）给出的检验随机变量K2的值k，其值越大，说明“X 与Y有关系”成立的可能性越大.当得到的观测数据x，b，c，d都不小于5时，可以通过查阅下表来确定断言“X与Y有关系”的可信程度.P（K2≥k）0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001 k0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828 说明：当观测数据x，b，c，d中有小于5时，需采用很复杂的精确的检验方法.五、几个典型例题：例1 三维柱形图中柱的高度表示的是（A）A．各分类变量的频数B．分类变量的百分比C．分类变量的样本数D．分类变量的具体值例2 分类变量X和Y的列联表如下y1y2总计x1x b x＋bx2c d c＋d总计x＋c b＋d x＋b＋c＋d 则下列说法正确的是（C）X．xd－bc越小，说明X和Y关系越弱B．xd－bc越大，说明X和Y关系越强C．（xd－bc）2越大，说明X和Y关系越强D．（xd－bc）2越接近于0 ，说明X和Y关系越强例3 研究人员选取170名青年男女大学生的样本，对他们进行一种心理测验，发现有60名女生对该心理测验中的最后一个题目的反应是：作肯定的18名，不定的42名；男生110名在相同的项目上作肯定的有22名，否定的有88名.问：性别与态度之间是否存在某种关系？分别用图形和独立性检验的方法判断.解：根据题目所给数据建立如下列联表性别 肯定 否定 总计 男生 22 88 110 女生 18 42 60 总计40130170根据列联表中的数据得到K 2＝170×（22×42－18×88）2110×60×40×130≈2.158＜2.706因此没有充分的证据显示“性别与态度有关”.例 4 打鼾不仅影响别人休息，而且可能与患某种病症有关.下表是一次调查所得的数据，试问：每一晚都打鼾与患心脏病有关吗？患心脏病 未患心脏病总计 每一晚都打鼾 30 224 254 不打鼾 24 1355 1379 总计5415791633解：根据列联表中数据，得到，K 2＝1633×（30×1355－224×24）21379×254×54×1579＝68.033.因为68.033＞6.635，所以有99%的把握说，每一晚都打鼾与患心脏病有关课后练习与提高为了研究某种细菌随时间x 变化，繁殖的个数，收集数据如下：天数x /天 1 2 3 4 5 6繁殖个数y /个 612254995190（1）用天数作解释变量，繁殖个数作预报变量，作出这些数据的散点图；（2）试求出预报变量对解释变量的回归方程.（答案：所求非线性回归方程为0.69 1.112ˆy =e x .）。