杭州市萧山区2017年命题比赛试卷高中数学试卷(九)

2017年高考模拟试卷数学卷本试卷分选择题和非选择题两部份。

总分值150分，考试时刻120分钟。

选择题部份（共40分）一. 选择题（本大题共10小题，每题4分，共40分.在每题给出的四个选项中，只有一项为哪一项符合题目要求的.）1. [原创] 已知集合{|2}xP x R y =∈=，2{|1}Q y R y x =∈=-，那么P Q ⋂=（ ▲ ）A .[1,1]-B .[0,)+∞C .(,1][1,)-∞⋃+∞D .(0,1]2. [原创] 已知复数34i z i ⋅=+，其中i 为虚数单位，那么z =（ ▲ ）A .43i -+B .43i --C .43i -D .43i +3. [原创] 假设命题P ：关于任意的x ,有|1||21|x x a ++-≥恒成立，命题Q ：3a ≤，那么P 是Q 的（ ▲ ）A .充分没必要要条件B .必要不充分条件C .充要条件D .既不充分也没必要要条件4. [原创] 在平面直角坐标系XOY 中，曲线()ln f x a x x =+在x a =处的切线过原点，那么a =（ ▲ ）A .1B .eC . 1eD .05. [原创] 已知正整数,x y 知足不等式组2252x y x y y -≤⎧⎪+≥⎨⎪≤⎩，那么221x y x +++的取值范围为（ ▲ ）A .77[,]42B .7[2,]2C .7[,2]4D .57[,]226. [原创] 在三角形ABC ∆中，=4AB ，0AC λλ=>（），假设2CA CB ⋅≥-对任意的0λ>恒成立，那么角A 的取值范围为（ ▲ ）A .[]42ππ，B .3[]44ππ，C .3(0,]4πD .3[4ππ，）7. [原创] 浙江省高考制度改革以来，学生能够从7门选考科目中任意选取3门作为自己的选考科目。

目前C 学校的A 专业需要物理、技术、化学科目，B 专业需要技术、政治、历史科目，甲同窗想报考C 学校的A 和B 专业，其中A 、B 专业只要考生的选考科目中有一门知足条件即可报考，现请问甲同窗选择选考科目种类是（ ▲ ）种A .15B .35C .31D .198. [原创] 已知1(,0)F c -,2(,0)F c 别离为双曲线2222:1(,0)x y a b a bΓ-=>的左、右核心，过点1F 作直线l 切圆222()x c y r -+=于点P ,l 别离交Γ右支于A 、B 两点（A 、B 位于线段1F P 上），假设1||:||:||2:2:1F A AB BP =,那么双曲线Γ的离心率的值为（ ▲ ）A .5B .2655C .2623+D .263+ 9. [原创] 在四面体A BCD -中，,EF 别离为棱,AB CD 的中点，过EF 的平面α交,BC AD 于,GH ，那么,EGF EHF S S ∆∆知足以下哪一种关系（ ▲ ）A .EGF EHF S S ∆∆=B .EGF EHF S S ∆∆>C .EGF EHF S S ∆∆<D .,EGF EHF S S ∆∆随着平面α的转变而转变10、[原创]已知二次函数2(),,,f x ax bx c a b c N +=++∈,函数()f x 在11(,)44-上有两个零点，那么a b c ++的最小值为（）A .38B .39C .40D .41非选择题部份（共110分） 二. 填空题（本大题共7小题，多空题每题6分，单空题每题4分，共36分.） 11. [原创] 27log 83= ▲ ; 已知函数22()log (1)f x x x =++，那么221(log 3)(log )3f f += ▲ ; 12. [原创] 已知()2sin()cos 6f x x a x π=++的最大值为2，那么a = ▲ ;假设12,x x R ∀∈,12|()()|f x f x m -≤，那么m 的取值范围是 ▲13. [原创] 已知立体几何体的三视图如右图所示， 那么该立体几何体的体积是 ▲ ; 立体几何体的表面积是 ▲ .14. [原创] 已知数列{}n a 中，12a =，122(2)n a a na n n +++=≥，那么n a = ▲ ；假设数列1{}n n a a +的前n 项和为n S ，那么n S = ▲ .15. [原创] 已知函数()||f x x a m =-+，现规定1()()f x f x =，1()(())(1)n n f x f f x n +=≥，那么方程()0n f x =存在实数根的充要要条件是 ▲ （,,n a m 三者关系）16. [原创] 已知20c b >>,那么22(2)a b a c b -的最小值是 ▲17. [原创] 已知向量,,a b c 知足||1,||||,()()0a a b b a c b c =-=-⋅-=.关于确信的b ，记c 的长度的最大值和最小值别离为,m n ，那么当b 转变时，m n -的最小值是 ▲ .三. 解答题（本大题共5大题，共74分，解许诺写出文字说明、证明进程或演算步骤.） 18. [原创] 在ABC ∆中，角,,A B C 对应的边别离是,,a b c ，已知3B π∠=,4c =（Ⅰ）若3sin 5C =，求ABC ∆的面积. （Ⅱ）1CB CA ⋅=-，求b 的值.19. [原创] 如图，在底面是平行四边形的四棱锥P ABCD -中，,E F 别离是,AB PC 的中点，平面PDE ⊥平面PCD ,1PD DE ==,2PE AB ==（Ⅰ）证明：直线//BF 面PDE（Ⅱ）求直线PA 与平面PBC 所成角的正弦值.20. [原创] 已知函数2()xf x e ax x =--,2()231g x ax bx a =+-+.（Ⅰ）假设函数()f x 在R 上是单调递增的，求实数a 的值. （Ⅱ）当[4,4]x ∈-时，()0g x ≥恒成立，求5a b +的取值范围.21. [原创] 如图，在直角坐标系xoy 中，,A B 别离是椭圆22221x y a b +=2，P 是椭圆上的任意一点（异于左、右极点），直线AP 与直线l ：2a x c =相交于M 点，当P 在椭圆上的上极点时，3AP BP ==.（Ⅰ）求椭圆标准方程.（Ⅱ）设BP 的斜率为1k ,BM 的斜率为2k ,（i ）求证：12k k 为定值.（ii ）假设BP 平分ABM ∠，求2212k k +的值.22. [原创]对任意正整数n ，设n a 是关于x 的方程31x nx -=的最大实数根 （1）12n n n a a n +<<<+（2）、当4n ≥时，对任意的正整数m 2()n m n n m na a n m n ++-<-<+（3）、设数列21{}n a 的前n 项和为n S ，求证：2ln(1)133n n n S +<<2016年高考模拟试卷数学答卷一、选择题（每小题4分，共10小题，共40分）题号12345678910答案二、填空题（此题共有7小题，其中第1一、1二、13、14题每空3分，第1五、1六、17题每空4分，共36分）11． ,_____________. 12．___________ ，13．， 14．，15．____ _ _ 16， 17三、解答题（本大题共5小题，共74分．解许诺写出文字说明，证明进程或演算步骤）18．（本小题满分14分）19．（本小题满分15分）题号1-1011-171819202122总分得分2017年高考模拟试卷数学参考答案与评分标准1.【答案】B【解析】由{|}P x x R =∈，{|0}Q y y =≥，得{|0}P Q x x ⋂=≥.2.【答案】D【解析】由已知，得z =43i +,3443iz i i+==-. 3.【答案】A【解析】由|1||21|x x ++-恒成立，得min (|1||21|)a x x ≤++-，利用各绝对值的零点，别离画出函数的大致图像，即当32x =时，min 3(|1||21|)2x x ++-=，现在命题P ：32a ≤；又由于命题Q ：3a ≤，得P Q ⇒. 4.【答案】B【解析】由()ln f x a x x =+，得'()1a f x x =+，即'()2k f a ==。

说明1、本试卷的命题方向和命题意图主要从以下几点为出发点：（1）强化主干知识，强化知识之间的交叉，渗透和综合：基础知识全面考，重点知识重点考，注意信息的重组及知识网络的交叉点。

（2）淡化特殊技巧，强调数学思想方法。

考查与数学知识联系的基本方法、解决数学问题的科学方法。

（3）深化能力立意，突出考察能力与素质，对知识的考察侧重于理解和运用。

淡化繁琐、强调能力，提倡学生用简洁方法得出结论。

（4）控制难度. “易︰中︰难=3︰5︰2” .（5）新增知识考查力度及所占分数比例可略超课时比例。

基础题象“学考”，压轴题似“竞赛”.2、试卷结构与2016年12月份模拟卷保持一致⑴题型结构为， 10道选择、7道填空、5道解答的结构；⑵赋分设计为，选择每题4分、填空题单空体每题4分，多空题每题6分，解答题共74分（14+15+15+15+15）；⑶考查的内容，注重考查高中数学的主干知识：函数，三角函数和解三角形，立体几何，解析几何，数列等。

3、立足基础，突出主干命题把重点放在高中数学课程中最基础、最核心的内容上，充分关注考生在学习数学和应用数学解决问题中必须掌握的核心观念、思想方法、基本概念和常用技能。

对基础知识的考查主要集中在小题上，具体知识点分布在集合、向量、直线与圆、数列、函数图像、函数性质、线性规划、三视图、三角函数、圆锥曲线性质、空间角等内容上，而且小题的考查直接了当，大部分是直接考查单一知识点，试卷对中学数学的核心内容和基本能力，特别是对高中数学的主干知识进行较为全面地考查。

注重了知识之间的内在联系，重点内容重点考，没有片面追求知识及基本思想、方法的覆盖面，反映了新课程的理念。

4、试题难度适中，层次分明试卷在三种题型中体现出明显的层次感，选择题、填空题、解答题，层层递进。

试卷的入口题和每种题型的入口题较好的把握了难度。

试卷对较难的解答题利用分步给分的设计方法，在化解难度的同时，又合理区分不同层次的考生。

浙江省杭州市萧山区2017届高考模拟命题比赛数学试卷9一、选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1、已知集合{|}A x x R ==∈，},1{m B =，若B A ⊆，则m 的值为( )A . 2B . 1-C . 1-或2D . 2或22、复数34i23i+-对应的点落在（ ） A ．第一象限 B.第二象限 C ．第三象限 D ．第四象限3、”“}3,{a x ∈是不等式03522≥--x x 成立的一个充分不必要条件,则实数a 的范围是( )),3(.A +∞ [)1B.32，，⎛⎫-∞-+∞ ⎪⎝⎭⎥⎦⎤ ⎝⎛-∞-21,.C ),3(21,.+∞⎥⎦⎤ ⎝⎛-∞- D4、已知实数x ，y 满足0101x y y x b ≤≤⎧⎪≤≤⎨⎪≥+⎩，若z x y =-的最大值为1，则实数b 的取值范围是（ ） A ．1b ≥ B ．1b ≤ C ．1b ≥- D ．1b ≤- 5、已知直线l 、m 与平面α、β，βα⊂⊂m l ,，则下列命题中正确的是（ ）A ．若m l //，则必有βα//B ．若m l ⊥，则必有βα⊥C ．若β⊥l ，则必有βα⊥ D ．若βα⊥，则必有α⊥m6、一个几何体的三视图如图所示，其中正视图是一个正三角形，则这个几何体的（）A.外接球的半径为3B.C.1D.外接球的表面积为163π7、已知点P 是双曲线C ：)0,0(12222>>=-b a by a x 左支上一点，F 1，V 2是双曲线的左、右两个焦点，且PF 1⊥PF 2，PF 2与两条渐近线相交于M ，N 两点（如图），点N 恰好平分线段PF 2，则双曲线的离心率是（ ）8、已知)(x f 是定义在R 上的增函数，函数)1(-=x f y 的图象关于点（1,0）对称，若对任意的x ，y R ∈，等式0)34()3(2=--+-x x f y f 恒成立，则xy的取值范围是（ ）A .]3322,3322[+-B .]3322,1[+C .]3,3322[- D .]3,1[ 9、已知函数()()lg 03636x x f x f x x ⎧<⎪=⎨-<⎪⎩，，≤≤，设方程()()2xb x b f R -+∈=的四个实根从小到大依次为1234x x x x ，，，，对于满足条件的任意一组实根，下列判断中正确的个数为（ ）（1）()()1234100661x x x x <<--<<或；（2）()()123416061x x x x <--<>且； （3）123499125x x x x <<<<或；（4）1234925361x x x x <<<<且. A ．3 B ．2 C．1D ．010.过边长为2的正方形中心作直线l 将正方形分为两个部分，将其中的一个部分沿直线l翻折到另一个部分上.则两个部分图形中不重叠的面积的最大值为（ ） A.2B.2(3)C. 4(2D. 4(3－二、填空题：本大题共7小题，第9至12题每小题6分，第13至15题每题4分， 共36分.11、在ABC ∆中，角,,A B C 分别对应边,,a b c ，S 为ABC ∆的面积.已知4a =，5b =，2C A =，则c = ，S = .12、已知递增的等差数列}{n a 的首项11=a ，且1a 、2a 、4a 成等比数列.则数列}{n a 的通项公式为 ；则8313852+-++++++n n a a a a a 的表达式为____________. 13、已知x ，y 为正实数，且32=+y x .则xyyx +3的最小值为 ； 则)1(2+y x 的最大值为 .14、袋中有5个大小、质量相同的小球，每个小球上分别写有数字2,1,0摸出一个将其上的数字记为1a ，然后放回袋中，再次随机摸出一个，将其上的数字记为2a ，依次下去，第n 次随机摸出一个，将其上的数字记为n a 记n n a a a 21=ξ，则（1）随机变量3ξ的期望是_____； （2）当12-=n n ξ时的概率是______.15、已知直线l 的方程是60x y +-=，A ，B 是直线l 上的两点，且△OAB 是正三角形（O 为坐标原点），则△OAB 外接圆的方程是________ ．16、在正方形ABCD 中，E 为AB 的中点，P 为以A 为圆心，AB 为半径的圆弧上的任意一点，设向量μλ+=，则μλ+的最小值为 .17、球O 为边长为2的正方体1111D C B A ABCD -的内切球，P 为球O 的球面上动点，M 为11C B 中点，DP ⊥BM ，则点P 的轨迹长度为三、解答题：本大题共5个题，共74分，解答应写出文字说明、证明过程或演算步骤.18、（本题满分14分）已知函数f (x )=4tan x sin(2x π-)cos(3x π-(Ⅰ)求f (x )的定义域与最小正周期； （Ⅱ）讨论f (x )在区间[,44ππ-]上的单调性和最值.19.（本题满分14分）如图，在三棱台ABC DEF -中，2A B B C A C ===，1AD DF FC ===，N 为DF 的中点，二面角D AC B --的大小为23π. （Ⅰ）证明：AC BN ⊥；（Ⅱ）求直线AD 与平面BEFC 所成角的正弦值.（1）求动点P 的轨迹方程；（2）已知圆方程为222=+y x ，过圆上任意一点作圆的切线，切线与（1）中的轨迹交于A ，B 两点，O 为坐标原点，设Q 为AB 的中点，求||OQ 长度的取值范围.21、（本小题满分15分）已知函数f (x )=ln x ，g (x )=e x ． （1）若函数φ (x ) = f (x )－11x x +-，求函数φ (x )的单调区间； （2）设直线l 为函数 y ＝f (x ) 的图象上一点A (x 0，f (x 0))处的切线．证明：在区间(1，+∞)上存在唯一的x 0，使得直线l 与曲线y =g (x )相切．注：e 为自然对数的底数．22．（本小题满分15分）已知函数4()415f x x =+，（Ⅰ）求方程()0f x x -=的实数解；（Ⅱ）如果数列{}n a 满足11a =，1()n n a f a +=（n N *∈），是否存在实数c ，使得221n n a c a -<<对所有的n N *∈都成立？证明你的结论．（Ⅲ）在（Ⅱ）的条件下，设数列{}n a 的前n 项的和为n S ，证明：114n S n<≤．参考答案一、选择题二、填空题11. ① 6 12. ① ),1[∞+ ② ]1,2[- 13. ①3627+ ② 25 14. ①n a n = ② 2301932++n n 15. ]13,1[16.2117. ]21,2()2,21[+- 三、解答题 18．()II 解：令2,3z x π=-函数2sin y z =的单调递增区间是2,2,.22k k k Z ππ⎡⎤-+π+π∈⎢⎥⎣⎦由222232k x k πππ-+π≤-≤+π,得5,.1212k x k k Z ππ-+π≤≤+π∈ 设5,,,441212A B x k x k k Z ππ⎧ππ⎫⎡⎤=-=-+π≤≤+π∈⎨⎬⎢⎥⎣⎦⎩⎭，易知,124A B ππ⎡⎤=-⎢⎥⎣⎦.所以, 当,44x ππ⎡⎤∈-⎢⎥⎣⎦时,()f x 在区间,124ππ⎡⎤-⎢⎥⎣⎦上单调递增, 在区间412ππ⎡⎤--⎢⎥⎣⎦，上单调递减.19.（Ⅰ）证明：取AC 中点M ，连结NM BM 、. 易知：AC NM ⊥，AC BM ⊥，BM NM M =，所以AC ⊥平面NBM .又因为BN ⊂平面NBM ，所以AC BN ⊥.（Ⅱ）解：由三棱台结构特征可知，直线AD CF BE 、、的延长线交于一点，记为P ， 易知，PAC ∆为等边三角形.连结AE EC 、.由（Ⅰ）可知PMB ∠为二面角D AC B --的平面角，即23PMB π∠=. 因为2AB AP BC CP ====，E 为PB 中点， 所以PB ⊥平面AEC ，平面AEC ⊥平面PBC . 过点A 作AH EC ⊥于点H ，连结HP .由平面AEC ⊥平面PBC ，可知AH ⊥平面PBC ， 所以直线AD 与平面BEFC 所成角为APH ∠.易知AE CE ==，在AEC ∆中求得AH =所以sin 7AH APH AP ∠==. 20．解：（1）由题意知，点P 的轨迹为焦点在x 轴上的椭圆， 且6=a ，3=c ，3=b ，∴动点P 的轨迹方程为13622=+y x （2）若直线AB 斜率不存在，则直线AB 方程为2±=x ，此时，2||=OQ若直线AB 斜率存在，设直线AB 方程为b kx y +=，),(11y x A ，),(22y x B 联立⎩⎨⎧=++=6222y x b kx y ，得：0624)21(222=-+++b kbx x k ∴221214kkbx x +-=+ 22212162k b x x +-= ∴221212122)(k b b x x k y y +=++=+∴)21,212(22kbk kb Q ++- ∵直线AB 与圆O 相切，∴21||2=+k b ，即)1(222k b +=∴)1441(2144)154(2)21(4||2422424222222+++=++++=++=k k k k k k k k b b k OQ 当0=k 时，2||=OQ当0≠k 时，49)41411(2||222≤+++=kk OQ ， 当且仅当2214kk =时，等号成立 ∴]23,2[||∈OQ 21．解：（1）(),11ln 11)(-+-=-+-=x x x x x x f x ϕ 222,)1(1)1(21)(-⋅+=-+=x x x x x x ϕ,10≠>x x 且 0)(,>∴x ϕ)(x ϕ∴的单调递增区间为(0,1)和(1,+∞)（2）∵1()f x x'=，∴001()f x x '=，∴ 切线l 的方程为0001ln ()y x x x x -=-, 即001ln 1y x x x =+-, ① 设直线l 与曲线()y g x =相切于点11(,e )x x ，∵e ()x g x '=，∴101e x x =，∴10ln x x =-． ∴直线l 也为()00011ln y x x x x -=+， 即0000ln 11x y x x x x =++， ② 由①②得 0000ln 1ln 1x x x x -=+， ∴0001ln 1x x x +=-． 下证：在区间（1，+∞）上0x 存在且唯一. 由（1）可知，()x ϕ1ln 1x x x +=--在区间1,+∞（）上递增． 又1e e e e 2()ln 01e 1ϕ+-=-=<--，222222e e e e e 13()ln 011e ϕ+-=-=>--， 结合零点存在性定理，说明方程()0x ϕ=必在区间2(e,e )上有唯一的根，这个根就是所求的唯一0x ． 故结论成立．22.解：（Ⅰ）41()044154f x x x x x x -=⇔=⇒=-=+或；（Ⅱ）存在14c =使得22114n n a a -<<．证法1：因为4()415f x x =+，当(0,1]x ∈时，()f x 单调递减，所以40()15f x <<．因为11a =，所以由14415n n a a +=+得23476,19301a a ==且01n a <≤．下面用数学归纳法证明2211014n n a a -<<<≤． 因为2141011194a a <=<<=≤，所以当1n =时结论成立． 假设当n k =时结论成立，即2211014k k a a -<<<<．由于4()415f x x =+为(0,1]上的减函数，所以2211(0)()()()(1)4k k f f a f f a f ->>>>，从而21241415419k k a a +>>>>，因此212414()()()()()15419k k f f a f f a f +<<<<，即22214140()()115419k k f a a f ++<≤<<<≤．如对您有帮助，欢迎下载支持，谢谢！11 综上所述，对一切*n N ∈，2211014n n a a -<<<≤都成立， 即存在14c =使得22114n n a a -<<． 证法2：11114111415414444444415n n n n n n a a a a a a ++++---+==-++++，且11134420a a -=+ 144n n a a ⎧⎫-⎪⎪⎨⎬+⎪⎪⎩⎭是以320为首项，14-为公比的等比数列.所以113144204n n n a a --⎛⎫=⋅- ⎪+⎝⎭. 易知0n a >，所以当n 为奇数时，14n a >；当n 为偶数时，14n a < 即存在14c =，使得22114n n a a -<<. （Ⅲ）证明：由（2），我们有221411194n n a a -≤<<≤，从而12n a a a n +++≤. 设14n n b a =-，则由14415n n a a +=+得11114(1)433n n n n b b b a +==<++. 由于123333,,4761204b b b ==-=， 因此n =1，2，3时，120n b b b +++>成立，左边不等式均成立．当n >3时，有212132233376011412041()1()33n b b b b b b -+++>++=++≥--， 因此1214n a a a n +++>． 从而1214n n a a a n <+++≤．即114n S n <≤． 解法2: 由（Ⅱ）可知01n a <≤，所以113(,]444n n b a =-∈- 11144415416n n n n n b b a a b ++-=-==++，所以11(1,0)416n n n b b b +-=∈-+，所以2120n n b b -+> 所以当n 为偶数时，120n b b b +++>L ；所以当n 为奇数时，121()0n n b b b b -++++>L 即104n S n ->.。

浙江省杭州市萧山区2017届高考模拟命题比赛数学试卷1一、选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知R 为实数集，集合{}0A x x =>，{}220B x x x =-->，则C A B ⋂=R （ ）A ．（0，2]B ．（﹣1，2）C ．[﹣1，2]D ．[0，4]2、设a 为实数，直线12:1,:2l ax y l x ay a +=+=，则“1a =-”是“12//l l ”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件3．已知22nx ⎫⎪⎭展开式中只有第六项二项式系数最大,则n = ( )A ．9B ．10C ．11D ．124.已知随机变量ξ的分布列如下图所示，()1E ξ=则函数a = ( )A ．0.2B ．0.3C ．0.4D ．0.65．下列四个图中，哪个可能是函数10ln 11x y x +=+的图象 （ ）A ．B ．C ．D ．6．若直线2y x =上存在点(),x y 满足约束条件30230x y x y x m +-≤⎧⎪--≤⎨⎪≥⎩，则实数m 的最大值为（ ）A ．﹣1B ．1C ．D ．27．已知1F ，2F 分别是双曲线22221(,0)x y a b a b-=>P为双曲线右支上一点， 12F PF ∠的角平分线为l ，点1F 关于l 的对称点为Q ，22QF =则双曲线的方程为 （ ）A ．2212x y -= 4B ．2212y x -= C ．22124x y -= D ．22142x y -=8.已知向量,a b 是单位向量，若0a b ⋅=，且345c a c b -+-=,则c a +的取值范围是（ ）A ．[]3,4B ．16,45⎡⎤⎢⎥⎣⎦C ．165⎡⎢⎣ D ．⎡⎣9. 如图，在ABC ∆中，AB =BC ，90ABC ∠=，D 为AC 的中点，将ABD ∆沿BD 折起到PBD ∆的位置，使得PC =PD ，连接PC ,得到三棱锥P -BCD ，若三棱锥的所有顶点都在同一球面上，则该求得表面积为 ( )A ．7πB ． 5πC ．3πD ．π10．已知()f x 是定义域为（0，+∞）的单调函数，若对任意的x ∈（0，+∞），都有13()log 4f f x x ⎡⎤+=⎢⎥⎣⎦，且方程32()3694f x x x x a -=-+-+在区间（0，3]上有两解，则实数a 的取值范围是（ ） A ．0＜a ≤5B ．a ＜5C ．0＜a ＜5D ．a ≥5二、填空题:本大题共7小题，多空题每题6分，单空题每题4分，共36分. 11．若复数43i z =+，其中i 是虚数单位，则复数z 的模为 ，1iz+的值为 12．若某几何体的三视图 (单位：cm) 如图所示，则此几何体的体积是 cm 3表面积是 cm 2．13．已知sin 2α22cos 2α-=（02π<<α），则tan α= ，2sin sin 2αα+ = 14. 已知等差数列{}n a 前n 项和n S ，()*124,0,142,m m m S S S m m -+=-==≥∈N .n a = ，()362n n a -+的前n 项的和为15.已知圆C ：22()(2)4(0)x a y a -+-=>，若倾斜角为45°的直线l 过抛物线的212y x =-焦点，且直线l 被圆C 截得的弦长为a 等于16．某城市关系要好的A ，B ，C ，D 四个家庭各有两个小孩共8人，准备使用滴滴打车软件，分乘甲、乙两辆汽车出去游玩，每车限坐4名（乘同一辆车的4名小孩不考虑位置），其中A 户家庭的孪生姐妹需乘同一辆车，则乘坐甲车的4名小孩恰有2名来自于同一个家庭的乘坐方式共有17．已知直线y b =与函数()23f x x =+和()ln g x ax x =+分别交于A ，B 两点，若|AB |的最小值为2，则a +b = ．三．解答题: 本大题共5小题，共74分.解答应写出文字说明、证明过程或演算步骤. 18. ( 本小题满分14分)已知△ABC 的角A ，B ，C 的对边依次为a ，b ，c ，若满足tan tan tan A B A B ⋅--=（Ⅰ）求∠C 大小；（Ⅱ）若2c =，且△ABC 为锐角三角形，求22a b +取值范围.19.( 本小题满分15分)如图，在四棱锥P -ABCD 中，底面ABCD 是长方形，侧棱PD ⊥底面ABCD ,且PD =AD =1，DC =2，过D 作DF ⊥PB 于F ,过F 作FE ⊥PB 交PC 于E . （Ⅰ）证明：DE ⊥平面PBC ；（Ⅱ）求平面DEF 与平面ABCD 所成锐二面角的余弦值.20．( 本小题满分15分）已知函数()()3f x x x a a =+-∈R .(Ⅰ) 当1=a 时,求()x f 在()()0,0f 处的切线方程;(Ⅱ) 当()1,0∈a 时,求()x f 在区间[]1,1-上的最小值(用a 表示).图1GPFED CA21. ( 本小题满分15分)0y m -+=不过原点，且与椭圆22142y x +=有两个不同的公共点A ，B . (Ⅰ)求实数m 取值所组成的集合M ；(Ⅱ)是否存在定点P 使得任意的m M ∈，都有直线PA ，PB 的倾斜角互补？若存在，求出所有定点P 的坐标；若不存在，请说明理由.22. ( 本小题满分15分)设数列{}n a 满足()2*11n n n a a a n +=-+∈N ，n S 为{}n a 的前n 项和.证明：对任意*n ∈N ，（Ⅰ）当101a ≤≤时，01n a ≤≤； （Ⅱ）当11a >时，()1111n n a a a ->-；（Ⅲ）当112a =时，n n S n <.参考答案一、选择题：1-5 A ACBC 6-10 BBCAA 二、填空题: 11. 571i 55+ 12. 2π)62++π13.28514.26n -()()1*1122n n n --+∈N 15.116.24 17.2三． 解答题: 18.解：（I ）3C π=（II ）2262sin sin sin 23A a b c B A A B C A B π⎧<⎪⎪πππ⎪<⇒<<==⎨⎪π⎪+=⎪⎩，由正弦定理，222222162[sin sin ()]33168sin(2)336512sin(2)1,6266626208.3a b A A A A A A a b π+=+-π=+-ππππππ<<∴<-<∴<-≤<+≤，，即 19.解：法一：（Ⅰ）因为PD ⊥底面ABCD ，所以PD BC ⊥， 由底面ABCD 为长方形，有BC CD ⊥，而PDCD D =，所以BC PCD ⊥平面. 而DE PCD ⊂平面，所以BC DE ⊥.又因为DF PB ⊥， FE PB ⊥所以PB ⊥平面DEF . 而PB PBC ⊂平面，所以PB DE ⊥. 又BC DE ⊥，PBBC B =，所以DE ⊥平面PBC .（Ⅱ）如图1，在面PBC 内，延长BC 与FE 交于点G ，则DG 是平面DEF 与平面ABCD 的交线. 由（Ⅰ）知，PB DEF ⊥平面，所以PB DG ⊥. 又因为PD ⊥底面ABCD ，所以PD DG ⊥. 而PDPB P =，所以DG PBD ⊥平面.故BDF ∠是面DEF 与面ABCD 所成二面角的平面角， 在Rt △PDB 中, 由cos sin BDF PBD ∠=∠=, 故面DEF 与面ABCD法二：如图2, 由PD ABCD ⊥平面，所以(0 ,0 ,1)DP =是平面ABCD 的一个法向量； 由（Ⅰ）知，PB DEF ⊥平面，所以(1 , 2 , 1)PB =-是平面DEF 的一个法向量 设平面DEF 与平面ABCD 所成二面角为θ则1cos ||||6BP DP BP DP θ⋅==⋅， 故面DEF 与面ABCD图1GPFED C BA20.解: (Ⅰ) 当1,1<=x a 时,()(),13,123-='-+=x x f x x x f 所以()()10,10-='=f f ,所以()x f 在()()0,0f 处的切线方程1+-=x y .(Ⅱ) 当()1,0∈α时,由已知得()⎪⎩⎪⎨⎧≤≤-+-≤≤-+=.1,,1,33a x a x x x a a x x x f当1<<x a 时,由()0132>+='x x f ,知()x f 在()1,a 是上单调递增. 当a x <<-1时,由(),132-='x x f (1)当⎪⎪⎭⎫⎝⎛∈1,33a 时,()x f 在⎪⎪⎭⎫ ⎝⎛--33,1上递增,在⎪⎪⎭⎫⎝⎛-33,33上递减,在⎪⎪⎭⎫ ⎝⎛1,33上递增, 所以()()932932,min 33,1min min-=⎭⎬⎫⎩⎨⎧-=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎪⎭⎫ ⎝⎛-=a a a f f x f . (2)当⎪⎪⎭⎫ ⎝⎛∈33,0a 时,()x f 在⎪⎪⎭⎫ ⎝⎛--33,1上递增,在⎪⎪⎭⎫⎝⎛-a ,33上递增,在()1,a 上递增, 所以()()(){}{}.,min ,1min 33min a a a a f f x f ==-=综上所述, ()⎪⎪⎩⎪⎪⎨⎧⎥⎦⎤ ⎝⎛∈⎪⎪⎭⎫ ⎝⎛∈-=.33,0,,1,33,9323mina a a a x f21.解：（10y m -+= 不过原点，所以0m ≠，0y m -+=与22142y x +=联立，消去y 得：22440x m ++-=，因为直线与椭圆有两个不同的公共点,A B ，所以22816(4)0m m =-->，解得m -<<所以实数m 的范围组成的集合是()22,0(0,22)-⋃；（2）假设存在定点 00(,)P x y 使得任意的m M ∈,都有直线,PA PB 的倾斜角互补， 即0PA PB k k +=，令1122(),()A x m B x m ++,所以102010200m y m y x x x x +-+-+=--，整理得：12001200()()2()0x m y x x x y m +-++-=○1 由（1）知12,x x是22440x m ++-=的两个根，所以212124,24m x x x x -+=-=， 代入○1化简得0000()2(02y x m x y -+=，由题意0000020y x x y -=⎪⎨⎪-=⎩解得001x y =⎧⎪⎨=⎪⎩001x y =-⎧⎪⎨=⎪⎩所以定点的坐标为或，经检验，满足题意， 所以存在定点使得任意的,都有直线的倾斜角互补，坐标为(1P或(1,P -. 22.解:（Ⅰ）①当1n =时，显然成立； 设当()*n k k =∈N ，1k o a ≤≤， 则当1n k =+时，22113124k k k k a a a a +⎛⎫=-+=-+ ⎪⎝⎭[]3,10,14⎡⎤∈⊆⎢⎥⎣⎦.由①②，()*01n a n ∈N ≤≤.（Ⅱ）()()2211111n n n n n n n a a a a a a a +-=++-=-=-， 即1111n n n a a a a +-=-≥， 于是()11111n n a a a ---≥，即()()1*111n n a a a n ->-∈N ；（Ⅲ）当112a =时，由（Ⅰ），()*01n a n <<∈N ，故n S n >. 令()*1n n b a n =-∈N ，由（Ⅰ）（Ⅱ），()*10n n b b n +>>∈N . 由211n n n a a a +=-+，可得21n n n b b b +=-.从而()()222121223n b b b b b b b ++⋅⋅⋅+=-+-()111112n n n b b b b b +++⋅⋅⋅+-=-<=， 又222212n n b b b nb ++⋅⋅⋅+≥， 故212n nb <，即)*n b n <∈N .注意到n b <=<=，故12n b b b ++⋅⋅⋅+⎤++⋅⋅⋅+=⎦即n n S -n S n >.所以当112a =时，n n S n <.。

2017年高考模拟试卷数学卷本试卷分选择题和非选择题两部分。

满分150分，考试时间120分钟。

选择题部分（共40分）一. 选择题（本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1. [原创] 已知集合{|2}x P x R y =∈=，{|Q y R y =∈=，则P Q ⋂=（ ▲ ）A .[1,1]-B .[0,)+∞C .(,1][1,)-∞⋃+∞D .(0,1]2. [原创] 已知复数34i z i ⋅=+，其中i 为虚数单位，则z =（ ▲ ）A .43i -+B .43i --C .43i -D .43i +3. [原创] 若命题P ：对于任意的x ,有|1||21|x x a ++-≥恒成立，命题Q ：3a ≤，则P 是Q 的（ ▲ ）A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4. [原创] 在平面直角坐标系XOY 中，曲线()ln f x a x x =+在x a =处的切线过原点，则a =（ ▲ ）A .1B .eC .1eD .0 5. [原创] 已知正整数,x y 满足不等式组2252x y x y y -≤⎧⎪+≥⎨⎪≤⎩，则221x y x +++的取值范围为（ ▲ ）A .77[,]42B .7[2,]2C .7[,2]4D .57[,]226. [原创] 在三角形ABC ∆中，=4AB ，0AC λλ=>（），若2C A C B ⋅≥-对任意的0λ>恒成立，则角A 的取值范围为（ ▲ ）A .[]42ππ，B .3[]44ππ，C .3(0,]4πD .3[4ππ，）7. [原创] 浙江省高考制度改革以来，学生可以从7门选考科目中任意选取3门作为自己的选考科目。

目前C 学校的A 专业需要物理、技术、化学科目，B 专业需要技术、政治、历史科目，甲同学想报考C 学校的A 和B 专业，其中A 、B 专业只要考生的选考科目中有一门满足条件即可报考，现请问甲同学选择选考科目种类是（ ▲ ）种A .15B .35C .31D .198. [原创] 已知1(,0)F c -,2(,0)F c 分别为双曲线2222:1(,0)x y a b a bΓ-=>的左、右焦点，过点1F 作直线l 切圆222()x c y r -+=于点P ,l 分别交Γ右支于A 、B 两点（A 、B 位于线段1F P 上），若1||:||:||2:2:1F A AB BP =,则双曲线Γ的离心率的值为（ ▲ ）A .5BC .D .9. [原创] 在四面体A BCD -中，,EF 分别为棱,AB CD 的中点，过EF 的平面α交,BC AD 于,G H ，则,EGF EHF S S ∆∆满足下列哪种关系（ ▲ ）A .EGF EHF S S ∆∆=B .EGF EHF S S ∆∆>C .EGF EHF S S ∆∆<D .,EGF EHF S S ∆∆随着平面α的变化而变化10、[原创]已知二次函数2(),,,f x ax bx c a b c N +=++∈,函数()f x 在11(,)44-上有两个零点，则a b c ++的最小值为（）A .38B .39C .40D .41非选择题部分（共110分）二. 填空题（本大题共7小题，多空题每题6分，单空题每题4分，共36分.）11. [原创] 27log 83= ▲ ;已知函数2()log (f x x =+，则221(log 3)(log )3f f += ▲ ;12. [原创] 已知()2s i n ()c o s 6f x x ax π=++的最大值为2，则a = ▲ ;若12,x x R ∀∈,12|()()|f x f x m -≤，则m 的取值范围是 ▲13. [原创] 已知立体几何体的三视图如右图所示， 则该立体几何体的体积是 ▲ ; 立体几何体的表面积是 ▲ .14. [原创] 已知数列{}n a 中，12a =，122(2)n a a na n n +++=≥ ，则n a = ▲ ；若数列1{}n n a a +的前n 项和为n S ，则n S = ▲ .15. [原创] 已知函数()||f x x a m =-+，现规定1()()f x f x =，1()(())(1)n n f x f f x n +=≥，则方程()0n f x =存在实数根的充要要条件是 ▲ （,,n a m 三者关系）16. [原创] 已知20b >>,则22a +的最小值是 ▲17. [原创] 已知向量,,a b c 满足||1,||||,()()0a a b b a c b c =-=-⋅-= .对于确定的b ，记c的长度的最大值和最小值分别为,m n ，则当b变化时，m n -的最小值是 ▲ .三. 解答题（本大题共5大题，共74分，解答应写出文字说明、证明过程或演算步骤.） 18. [原创] 在ABC ∆中，角,,A B C 对应的边分别是,,a b c ，已知3B π∠=,4c =（Ⅰ）若3sin 5C =，求ABC ∆的面积. （Ⅱ）1CB CA ⋅=-，求b 的值.19. [原创] 如图，在底面是平行四边形的四棱锥P ABCD -中，,E F 分别是,AB PC 的中点，平面PDE ⊥平面PCD ,1PD DE ==,PE AB ==（Ⅰ）证明：直线//BF 面PDE（Ⅱ）求直线PA 与平面PBC 所成角的正弦值.20. [原创] 已知函数2()x f x e ax x =--,2()231g x ax bx a =+-+.（Ⅰ）若函数()f x 在R 上是单调递增的，求实数a 的值. （Ⅱ）当[4,4]x ∈-时，()0g x ≥恒成立，求5a b +的取值范围.21. [原创] 如图，在直角坐标系xoy 中，,A B 分别是椭圆22221x ya b+=的左、右顶点，离心率为2，P 是椭圆上的任意一点（异于左、右顶点），直线AP 与直线l ：2a x c =相交于M点，当P 在椭圆上的上顶点时，AP BP ==（Ⅰ）求椭圆标准方程.（Ⅱ）设BP 的斜率为1k ,BM 的斜率为2k ,（i ）求证：12k k 为定值.（ii ）若BP 平分ABM ∠，求2212k k +的值.22. [原创]对任意正整数n ，设n a 是关于x 的方程31x nx -=的最大实数根（1）1n n a a +<<<（2）、当4n ≥时，对任意的正整数m ，2n m n a a +<-<（3）、设数列21{}n a 的前n 项和为n S ，求证：ln(1)13n n S +<<2016年高考模拟试卷数学答卷一、选择题（每小题4分，共10小题，共40分）二、填空题（本题共有7小题，其中第11、12、13、14题每空3分，第15、16、17题每空4分，共36分）11．,_____________. 12．___________ ， 13． ，14． ， 15．______ 16， 17三、解答题（本大题共5小题，共74分．解答应写出文字说明，证明过程或演算步骤）2017年高考模拟试卷数学参考答案与评分标准1.【答案】B【解析】由{|}P x x R =∈，{|0}Q y y =≥，得{|0}P Q x x ⋂=≥. 2.【答案】D【解析】由已知，得z =43i +,3443iz i i+==-. 3.【答案】A【解析】由|1||21|x x ++-恒成立，得min (|1||21|)a x x ≤++-，利用各绝对值的零点，分别画出函数的大致图像，即当32x =时，min 3(|1||21|)2x x ++-=，此时命题P ：32a ≤；又由于命题Q ：3a ≤，得P Q ⇒. 4.【答案】B【解析】由()ln f x a x x =+，得'()1af x x=+，即'()2k f a ==。

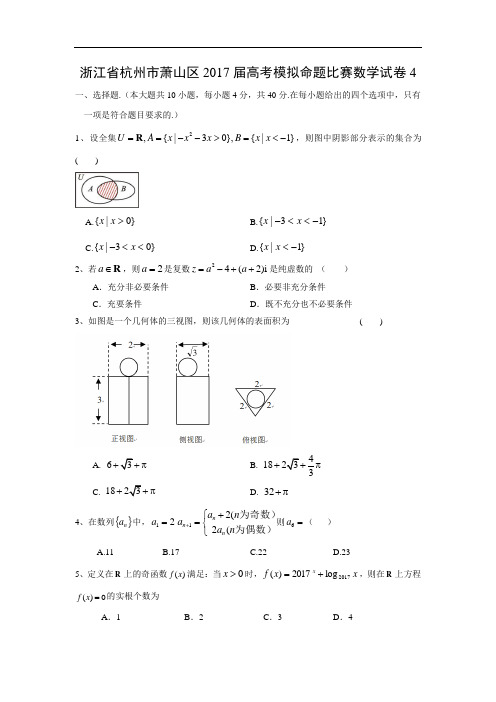
浙江省杭州市萧山区2017届高考模拟命题比赛数学试卷4一、选择题.（本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1、设全集2,{|30},{|1}U A x x x B x x ==-->=<-R ，则图中阴影部分表示的集合为 ( )A.B. C.D.2、若a ∈R ，则2=a 是复数24(2)i z a a =-++是纯虚数的 （ ） A ．充分非必要条件 B ．必要非充分条件C ．充要条件D ．既不充分也不必要条件3、如图是一个几何体的三视图，则该几何体的表面积为 ( )A. 6πB. 4183+πC. 18+πD. 32+π4、在数列{}n a 中，21=a ⎩⎨⎧+=+为偶数）为奇数）n a n a a n n n (2(21则=6a （ ）A.11B.17C.22D.235、定义在R 上的奇函数()f x 满足：当0>x 时，x x f x 2017log 2017)(+=，则在R 上方程()0f x =的实根个数为A ．1B ．2C ．3D ．4}0|{>x x }13|{-<<-x x }03|{<<-x x }1|{-<xx6、在1，2，3，4，5这五个数中，任取两个不同的数记作a,b ，则满足()f x x ax b =-+2有两个零点的概率是（ ）． A.52B.209C.109 D.21 7、已知定义在02π（，）上的函数)(x f ，其导函数为)(x f '，若对任意的(0,)2x π∈恒有0t an )()(<'-x x f x f 成立，则A ()()43ππ<B 、(1)2()sin16f f π<C ()()64f ππ>D ()()63f ππ>8、已知双曲线12222=+by a x ，圆222a y x =+，过双曲线第一象限内任意一点),(00y x P 作圆C 的两条切线，其切点分别为A 、B ，若AB 与x 轴、y 轴分别交于M 、N 两点，且3||||2222=-ON a OM b ，则双曲线的离心率为( ) A. 3 B. 2B. C.3D.29、三棱锥BCD A -的底面是正三角形，侧棱相等且两两垂直，点P 是该棱锥表面（包括棱）上一点，且P 到四个顶点的距离有且只有两个不同的值，则这样的点P 的个数有( )A. 5B. 6C. 8D. 1110、,P Q 是两个定点，点M 为平面内的动点，且MP MQλ=（0λ>且1λ≠），点M 的轨迹围成的平面区域的面积为S ，设()S f λ=（0λ>且1λ≠）则以下判断正确的是（ ）A ．)(λf 在)1,0(上是增函数，在），（∞+1上是减函数B ．)(λf 在)1,0(上是减函数，在），（∞+1上是减函数C ．)(λf 在)1,0(上是增函数，在），（∞+1上是增函数D ．)(λf 在)1,0(上是减函数，在），（∞+1上是增函数二、填空题:本大题共7小题，多空题每小题6分，单空题每小题4分，共36分. 11、已知函数()2sin(2)6f x x π=-，则)(x f 的最小正周期为 ；若[0,]3x π∈，则)(x f 的值域为12、已知直线01:1=-+y kx l ，01:2=++ky x l ，若21//l l ，则=k ；若不论k 为何实数，直线1l 与圆0422222=--+-+a a ax y x 恒有交点，则实数a 的取值范围是 .13、若随机变量A 在一次试验中发生的概率为p )10(<<p ，用随机变量ξ表示A 在1次试验中发生的次数.则方差ξD 的最大值为 ；ξξE D 12-的最大值为 . 14、设nx x )3(2131+的二项展开式中各项系数之和为t ，二项式系数之和为h ，则h t +用n 表示的表达式为__________.若272=+h t ，则其二项展开式中23x 项的系数为_______.15、设实数y x ,满足⎪⎩⎪⎨⎧≤-+≥≥02200y x y x ，则y x x -+1的取值范围是16、已知O 为ABC ∆的外心，C B C B ⋅⋅=⋅+⋅sin sin 322sin 2sin ,则A = 17、已知实数x 满足2||≥x 且022=-++b ax x ，则22)1(-+b a 的最小值为 三、解答题：：本大题共5小题，共72分.解答时应写出文字说明、证明过程或演算步骤. 18、在ABC ∆中，角C B A ,,所对的边分别为c b a ,,，已知B BC AC sin 23=，0<⋅， （1）求角A ；（2）若23cos )cos(=+-B C A ，6=a ，求ABC ∆的面积.19、如图，四边形ABCD 为矩形，DA ⊥平面ABE ,2AE EB BC ===，BF ⊥平面ACE 于点F ，且点F 在CE 上.（Ⅰ）求证：AE BE ⊥；（Ⅱ）设点M 在线段AB 上，且满足2AM MB =，试在线段CE 上确定一点N ，使得//MN 平面DAE .（Ⅲ）求二面角B EC D --余弦值；20、已知函数21()()e2xf x a x =-+.（a ∈R ）（Ⅰ）若)(x f 在区间)0(∞+，上单调递减，求实数a 的取值范围； （Ⅱ）若在区间),0(+∞上，函数)(x f 的图象恒在曲线2e x y a =下方，求a 的取值范围．21、已知椭圆椭圆：.椭圆的一个焦点为，其短轴上的一个端点到的距离为. （Ⅰ）求椭圆C 的方程;（Ⅱ）若点是以原点为圆心，2为半径的圆T 上一动点，过动点作直线使得与椭圆都只有一个交点，且分别交其圆T 于另一点N M ,两点.求证：为定值.22、已知各项均为正数的数列{}n a ，11=a ，前n 项和为n S ，且122-=-n n n S a a . (1) 求证：4212++<n n n a a S ；(2)求证：212121-<+⋯⋯++<+n n n S S S S SC )0(12222>>=+b a by a x C )0,2(F F 3P P 21,l l 21,l l C 21,l l MN参考答案一、选择题二、填空题11、π、]1,2[- 12、1、31≤≤-a 13、41、2－2214、nn42+、10815、),2()21,(+∞⋃--∞ 16、233ππ或 17、59三、解答题18、解：（1） B a b sin 23=，B A B sin sin 2sin 3=∴，0sin ≠B ，23sin =∴A ， 又0<⋅AC AB ，A ∴为钝角，23A π∴=. （2）由A B C ++=π知：)cos(cos C A B +-=，故23sin sin 2cos )cos(==+-C A B C A 23sin 3=∴C ，21sin =∴C ，得6C π=（舍去56π），6B π∴=，32==∴b c 3323323221sin 21=⨯⨯⨯==∴∆A bc S ABC19、（Ⅰ）证明：由AD ⊥平面ABE 及//AD BC 得BC ⊥平面ABE ，则AE BC ⊥ 而BF ⊥平面ACE ，则BF AE ⊥，又BC BF B =，则AE ⊥平面BCE ，又BE ⊂平面BCE ，故AE BE ⊥.（Ⅱ）在ABE ∆中过点M 作//MG AE 交BE 于点G ，在BEC ∆中过点G 作//GN BC 交BC 于点N ， 连接MN ，则由13CN BG MB CE BE AB ===得13CN CE = 由平面,ADE AE ⊂平面ADE ，则//MG 平面ADE再由//,//GN BC BC AD 得//GN 平面ADE ，又MN ⊂平面MGN ，则//MN 平面ADE . 故当点N 为线段CE 上靠近点C 的一个三等分点时，//MN 平面ADE .(Ⅲ)过点E 作DA 平行线，把几何体补全成三棱柱.由（Ⅰ）知BCE DH 平面⊥，故连接HF ，由BC =BE 知，CE HF ⊥,则连接DF ，可知二面角H CE D --的平面角即为DFH ∠.而二面角B EC D --的平面角即为DFH ∠的补角.故33cos =θ20、解：（Ⅰ）)(x f 在区间)0(∞+，上单调递减， 则2()(21)e 10x f x a '=-+≤在区间)0(∞+，上恒成立． 即2112e x a -≥，而当)0(∞+∈，x 时，211e x<，故121≥-a ． 所以0≤a ．（Ⅱ）令21()()2e ()e2e 2xxx g x f x a a a x =-=--+，定义域为R .在区间),0(+∞上，函数)(x f 的图象恒在曲线2e x y a =下方等价于0)(<x g 在区间),0(+∞上恒成立.∵2()(21)e 2e 1(e 1)[(21)e 1]x x x x g x a a a '=--+=--- ① 若21>a ，令0)(='x g ，得极值点01=x ，121ln 2-=a x ， 当012=>x x ，即121<<a 时，在（2x ，+∞)上有0)(>'x g ，此时)(x g 在区间),(2+∞x 上是增函数，并且在该区间上有)),(()(2+∞∈x g x g ，不合题意；当012=≤x x ，即1≥a 时，同理可知，)(x g 在区间),0(+∞上， 有)),0(()(+∞∈g x g ，也不合题意； ② 若21≤a ，则有012≤-a ，此时在区间),0(+∞上恒有0)(<'x g ，从而)(x g 在区间),0(+∞上是减函数；要使0)(<x g 在此区间上恒成立，只须满足021)0(≤--=a g 21-≥⇒a ， 此求得a 的范围是]21,21[-． 综合①②可知，当]21,21[-∈a 时，函数)(x f 的图象恒在直线2e x y a =下方. 21、解：（Ⅰ）.椭圆方程为， （Ⅱ）①当中有一条无斜率时，不妨设无斜率， 因为与椭圆只有一个公共点，则其方程为， 当方程为时，此时与准圆交于点，此时经过点（或）且与椭圆只有一个公共点的直线是（或），即为（或），显然直线垂直； 同理可证方程为时，直线垂直.②当都有斜率时，设点，其中.设经过点与椭圆只有一个公共点的直线为，则消去，得. 由化简整理得：因为，所以有. 设的斜率分别为，因为与椭圆只有一个公共点，1,3,2=∴==b a c ∴1322=+y x 21,l l 1l 1l 3±=x 1l 3=x 1l ()()1,3,1,3-()1,3()1,3-1=y 1-=y 2l 1=y 1-=y 21,l l 1l 3-=x 21,l l 21,l l ),(00y x P 42020=+y x ),(00y x P 00)(y x x t y +-=⎪⎩⎪⎨⎧=+-+=13)(2200y x tx y tx y y 03)(3)(6)312000022=--+-++tx y x tx y t x t （0=∆012)32000220=-++-y t y x t x （42020=+y x 0)3(2)32000220=-++-x t y x t x （21,l l 21,t t 21,l l所以满足上述方程， 所以，即垂直.综合①②知：因为经过点，又分别交其准圆于点，且垂直， 所以线段为准圆的直径，所以=4. 22、解：（1）在条件中，，又由条件有，上述两式相减，注意到得∴所以，，所以（2）因为，所以，所以；21,t t 0)3(2)32000220=-++-x t y x t x （121-=∙t t 21,l l 21,l l ),(00y x P N M ,21,l l MN 422=+y x MN。

2017年高考模拟试卷 数学本试卷分为选择题和非选择题两部分。

考试时间120分种。

请考生按规定用笔将所有试题的答案标号涂、写在答题纸上。

参考公式：球的表面积公式 柱体的体积公式24πS R = V=Sh球的体积公式 其中S 表示锥体的底面积，h 表示锥体的高34π3V R =台体的体积公式： 其中R 表示球的半径 V=31h （2211S S S S ++）棱锥的体积公式 其中21,s s 分别表示台体的上、下底面积，V=31Sh h 表示台体的高 其中S 表示锥体的底面积， 如果事件A B ，互斥，那么h 表示锥体的高 ()()()P A B P A P B +=+选择题部分一、选择题：本大题共10小题，每小题4分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 若a R ∈，则“0a >”是“||a a =”的（ ）A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分又不必要条件【命题意图】：主要考察充分条件与必要条件。

【预设难度系数】0.85【答案】A------------【原创】 2.已知复数Z 的共轭复数34=1iZ i-+,则复数Z 的虚部是（ ） A ．72 B ．72- C ．72i D ．72i -【命题意图】：主要考察复数的定义与运算。

【预设难度系数】0.85【答案】A------------【原创】3. 已知三条不同直线l m n 、、 ，三个不同平面αβγ、、，有下列命题： ①若m ∥α，n ∥α，则m ∥n ； ②若α∥β，l α⊂，则l ∥β；③若αγβγ⊥⊥，，则α∥β；④若,m n 为异面直线，m α⊂，n β⊂，m ∥β，n ∥α，则α∥β.其中正确的命题个数是( )A ．0B ．1C ．2D ．3 【命题意图】：本题主要考察了立体几何中线面之间的位置关系及其中的公理和判定定理，也蕴含了对定理公理综合运用能力的考察。

2017年浙江省高考模拟试卷 数学卷本试题卷分选择题和非选择题两部分．满分150分，考试时间120分钟。

请考生按规定用笔将所有试题的答案涂、写在答题纸上。

选择题部分（共40分）注意事项：1.答题前，考生务必将自己的姓名、准考证号用黑色的字迹的签字笔或钢笔填写在答题纸上。

2.每小题选出答案后，用2B 铅笔把答题纸上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。

答在试题卷上无效。

参考公式：如果事件A ，B 互斥，那么 棱柱的体积公式 ()()()P A B P A P B +=+ V Sh =如果事件A ，B 相互独立，那么 其中S 表示棱柱的底面积，h 表示棱柱的高 ()()()P A B P A P B ⋅=⋅ 棱锥的体积公式 如果事件A 在一次试验中发生的概率是p ，那么 13V S h =n 次独立重复试验中事件A 恰好发生k 次的概率 其中S 表示棱锥的底面积，h 表示棱锥的高()()()1,0,1,2,,n kk kn n P k C p k k n -=-= 棱台的体积公式球的表面积公式 24S R π= ()1213V h S S =球的体积公式 343V R π= 其中12,S S 分别表示棱台的上底、下底面积，其中R 表示球的半径 h 表示棱台的高一、选择题：（本大题共10小题，每小题4分，共40分。

）1、（原创）已知集合R U =，集合},2{R x y y M x∈==，集合)}3lg({x y x N -==，则()=N M C U （ ）A ．{}3≥y y B. {}0≤y y C. {}30<<y y D. ∅ 2、（原创）已知实数,,x y 则“2≥xy ”是“422≥+y x ”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件3、（引用十二校联考题）某几何体的三视图如图所示， 其中俯视图是半圆，则该几何体的表面积为（ ）A ．3π2 B ．πC ．3π2D ．5π24、（改编）袋中标号为1，2，3，4的四只球，四人从中各取一只，其中甲不取1号球，乙不取2号球，丙不取3号球，丁不取4号球的概率为（ ） A.41 B.83 C.2411 D.24235、（15年海宁月考改编）设变量y x ,满足约束条件⎪⎩⎪⎨⎧≥≤+-≥-a y y x y x 41，目标函数y x z 23-=的最小值为4-，则a 的值是( ) A ．1-B ．0C ．1D ．126、（改编）单位向量i a ，（4,3,2,1=i ）满足01=⋅+i i a a ,则1234a a a a +++ 可能值有( ) A ．2 个 B ．3 个 C ．4 个 D ．.5个7、（改编）如图，F 1,F 2分别是双曲线2222:1x y C a b-=（a,b ＞0）的左、右焦点，B 是虚轴的端点，直线F 1B 与C 的两条渐近线分别交于P,Q 两点，线段PQ 的垂直平分线与x 轴交于点M ，若|MF 2|=|F 1F 2|,则C 的离心率是( )A.3B.28、（引用余高月考卷）如图，α∩β＝l ，A∈α，C∈β，C ∉l ，直线AD∩l＝D ，A ，B ，C 三点确定的平面为γ，则平面γ、β的交线必过（ ）A.点AB.点BC.点C ，但不过点DD.点C 和点D9、若正实数y x ，满足xy y x 442=++，且不等式03422)2(2≥-+++xy a a y x 恒成立，则实数a 的取值范围是（ ）A ．]25,3[- B ．),25[]3,(+∞--∞ C ．]25,3(- D ．),25(]3,(+∞--∞10、（改编）已知2*11()2,()(),()(())(2,)n n f x x x c f x f x f x f f x n n N -=-+==≥∈，若函数()n y f x x =-不存在零点，则c 的取值范围是( ) A. 14c <B.34c ≥C.94c >D.94c ≤非选择题部分（共110分）二、填空题：（ 本大题共7小题, 单空题每题4分，多空题每题6分，共36分。

浙江省杭州市萧山区2017届高考模拟命题比赛数学试卷1一、选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知R 为实数集，集合{}0A x x =>，{}220B x x x =-->，则C A B ⋂=R （ ）A ．（0，2]B ．（﹣1，2）C ．[﹣1，2]D ．[0，4]2、设a 为实数，直线12:1,:2l ax y l x ay a +=+=，则“1a =-”是“12//l l ”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件3．已知22nx ⎫⎪⎭展开式中只有第六项二项式系数最大,则n = ( )A ．9B ．10C ．11D ．124.已知随机变量ξ的分布列如下图所示，()1E ξ=则函数a = ( )A ．0.2B ．0.3C ．0.4D ．0.65．下列四个图中，哪个可能是函数10ln 11x y x +=+的图象 （ ）A ．B ．C ．D ．6．若直线2y x =上存在点(),x y 满足约束条件30230x y x y x m +-≤⎧⎪--≤⎨⎪≥⎩，则实数m 的最大值为（ ）A ．﹣1B ．1C ．D ．27．已知1F ，2F 分别是双曲线22221(,0)x y a b a b-=>P为双曲线右支上一点， 12F PF ∠的角平分线为l ，点1F 关于l 的对称点为Q ，22QF =则双曲线的方程为 （ ）A ．2212x y -= 4B ．2212y x -= C ．22124x y -= D ．22142x y -=8.已知向量,a b 是单位向量，若0a b ⋅=，且345c a c b -+-=,则c a +的取值范围是（ ）A ．[]3,4B ．16,45⎡⎤⎢⎥⎣⎦C ．165⎡⎢⎣ D ．⎡⎣9. 如图，在ABC ∆中，AB =BC 90ABC ∠=，D 为AC 的中点，将ABD ∆沿BD 折起到PBD ∆的位置，使得PC =PD ，连接PC ,得到三棱锥P -BCD ，若三棱锥的所有顶点都在同一球面上，则该求得表面积为 ( )A ．7πB ． 5πC ．3πD ．π10．已知()f x 是定义域为（0，+∞）的单调函数，若对任意的x ∈（0，+∞），都有13()log 4f f x x ⎡⎤+=⎢⎥⎣⎦，且方程32()3694f x x x x a -=-+-+在区间（0，3]上有两解，则实数a 的取值范围是（ ） A ．0＜a ≤5B ．a ＜5C ．0＜a ＜5D ．a ≥5二、填空题:本大题共7小题，多空题每题6分，单空题每题4分，共36分. 11．若复数43i z =+，其中i 是虚数单位，则复数z 的模为 ，1iz+的值为 12．若某几何体的三视图 (单位：cm) 如图所示，则此几何体的体积是 cm 3表面积是 cm 2．13．已知sin 2α22cos 2α-=（02π<<α），则tan α= ，2sin sin 2αα+ = 14. 已知等差数列{}n a 前n 项和n S ，()*124,0,142,m m m S S S m m -+=-==≥∈N .n a = ，()362n n a -+的前n 项的和为15.已知圆C ：22()(2)4(0)x a y a -+-=>，若倾斜角为45°的直线l 过抛物线的212y x =-焦点，且直线l 被圆C 截得的弦长为a 等于16．某城市关系要好的A ，B ，C ，D 四个家庭各有两个小孩共8人，准备使用滴滴打车软件，分乘甲、乙两辆汽车出去游玩，每车限坐4名（乘同一辆车的4名小孩不考虑位置），其中A 户家庭的孪生姐妹需乘同一辆车，则乘坐甲车的4名小孩恰有2名来自于同一个家庭的乘坐方式共有17．已知直线y b =与函数()23f x x =+和()ln g x ax x =+分别交于A ，B 两点，若|AB |的最小值为2，则a +b = ．三．解答题: 本大题共5小题，共74分.解答应写出文字说明、证明过程或演算步骤. 18. ( 本小题满分14分)已知△ABC 的角A ，B ，C 的对边依次为a ，b ，c ，若满足tan tan tan A B A B ⋅--=（Ⅰ）求∠C 大小；（Ⅱ）若2c =，且△ABC 为锐角三角形，求22a b +取值范围.19.( 本小题满分15分)如图，在四棱锥P -ABCD 中，底面ABCD 是长方形，侧棱PD ⊥底面ABCD ,且PD =AD =1，DC =2，过D 作DF ⊥PB 于F ,过F 作FE ⊥PB 交PC 于E . （Ⅰ）证明：DE ⊥平面PBC ；（Ⅱ）求平面DEF 与平面ABCD 所成锐二面角的余弦值.20．( 本小题满分15分）已知函数()()3f x x x a a =+-∈R .(Ⅰ) 当1=a 时,求()x f 在()()0,0f 处的切线方程;(Ⅱ) 当()1,0∈a 时,求()x f 在区间[]1,1-上的最小值(用a 表示).图1GPFED CA21. ( 本小题满分15分)0y m -+=不过原点，且与椭圆22142y x +=有两个不同的公共点A ，B . (Ⅰ)求实数m 取值所组成的集合M ；(Ⅱ)是否存在定点P 使得任意的m M ∈，都有直线PA ，PB 的倾斜角互补？若存在，求出所有定点P 的坐标；若不存在，请说明理由.22. ( 本小题满分15分)设数列{}n a 满足()2*11n n n a a a n +=-+∈N ，n S 为{}n a 的前n 项和.证明：对任意*n ∈N ，（Ⅰ）当101a ≤≤时，01n a ≤≤； （Ⅱ）当11a >时，()1111n n a a a ->-；（Ⅲ）当112a =时，n n S n <.参考答案一、选择题：1-5 A ACBC 6-10 BBCAA 二、填空题: 11. 571i 55+ 12. 2π)62++π13.28514.26n -()()1*1122n n n --+∈N 15.116.24 17.2三． 解答题: 18.解：（I ）3C π=（II ）2262sin sin sin 23A a b c B A A B C A B π⎧<⎪⎪πππ⎪<⇒<<==⎨⎪π⎪+=⎪⎩，由正弦定理，222222162[sin sin ()]33168sin(2)336512sin(2)1,6266626208.3a b A A A A A A a b π+=+-π=+-ππππππ<<∴<-<∴<-≤<+≤，，即 19.解：法一：（Ⅰ）因为PD ⊥底面ABCD ，所以PD BC ⊥， 由底面ABCD 为长方形，有BC CD ⊥，而PD CD D =， 所以BC PCD ⊥平面. 而DE PCD ⊂平面，所以BC DE ⊥.又因为DF PB ⊥， FE PB ⊥所以PB ⊥平面DEF . 而PB PBC ⊂平面，所以PB DE ⊥. 又BC DE ⊥，PBBC B =，所以DE ⊥平面PBC .（Ⅱ）如图1，在面PBC 内，延长BC 与FE 交于点G ，则DG 是平面DEF 与平面ABCD 的交线. 由（Ⅰ）知，PB DEF ⊥平面，所以PB DG ⊥. 又因为PD ⊥底面ABCD ，所以PD DG ⊥. 而PDPB P =，所以DG PBD ⊥平面.故BDF ∠是面DEF 与面ABCD 所成二面角的平面角， 在Rt △PDB 中, 由cos sin BDF PBD ∠=∠, 故面DEF 与面ABCD法二：如图2, 由PD ABCD ⊥平面，所以(0 ,0 ,1)DP =是平面ABCD 的一个法向量； 由（Ⅰ）知，PB DEF ⊥平面，所以(1 , 2 , 1)PB =-是平面DEF 的一个法向量 设平面DEF 与平面ABCD 所成二面角为θ则1cos ||||6BP DP BP DP θ⋅===⋅， 故面DEF 与面ABCD图1GPFED CA20.解: (Ⅰ) 当1,1<=x a 时,()(),13,123-='-+=x x f x x x f所以()()10,10-='=f f ,所以()x f 在()()0,0f 处的切线方程1+-=x y .(Ⅱ) 当()1,0∈α时,由已知得()⎪⎩⎪⎨⎧≤≤-+-≤≤-+=.1,,1,33a x a x x x a a x x x f当1<<x a 时,由()0132>+='x x f ,知()x f 在()1,a 是上单调递增. 当a x <<-1时,由(),132-='x x f(1)当⎪⎪⎭⎫⎝⎛∈1,33a 时,()x f 在⎪⎪⎭⎫ ⎝⎛--33,1上递增,在⎪⎪⎭⎫⎝⎛-33,33上递减,在⎪⎪⎭⎫ ⎝⎛1,33上递增, 所以()()932932,min 33,1min min-=⎭⎬⎫⎩⎨⎧-=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎪⎭⎫ ⎝⎛-=a a a f f x f . (2)当⎪⎪⎭⎫ ⎝⎛∈33,0a 时,()x f 在⎪⎪⎭⎫ ⎝⎛--33,1上递增,在⎪⎪⎭⎫⎝⎛-a ,33上递增,在()1,a 上递增, 所以()()(){}{}.,min ,1min 33min a a a a f f x f ==-=综上所述, ()⎪⎪⎩⎪⎪⎨⎧⎥⎦⎤ ⎝⎛∈⎪⎪⎭⎫ ⎝⎛∈-=.33,0,,1,33,9323mina a a a x f21.解：（10y m -+= 不过原点，所以0m ≠，0y m -+=与22142y x +=联立，消去y 得：22440x m ++-=，因为直线与椭圆有两个不同的公共点,A B ，所以22816(4)0m m =-->，解得m -<<所以实数m 的范围组成的集合是()22,0(0,22)-⋃；（2）假设存在定点 00(,)P x y 使得任意的m M ∈,都有直线,PA PB 的倾斜角互补， 即0PA PB k k +=，令1122(),()A x m B x m ++,所以102010200m y m y x x x x +-+-+=--，整理得：12001200()()2()0x m y x x x y m +-++-=○1 由（1）知12,x x是22440x m ++-=的两个根，所以212124,24m x x x x -+=-=， 代入○1化简得0000()2(02y x m x y -+=，由题意0000020y x x y -=⎪⎨⎪-=⎩解得001x y =⎧⎪⎨=⎪⎩001x y =-⎧⎪⎨=⎪⎩所以定点的坐标为或，经检验，满足题意， 所以存在定点使得任意的,都有直线的倾斜角互补，坐标为(1P或(1,P -. 22.解:（Ⅰ）①当1n =时，显然成立； 设当()*n k k =∈N ，1k o a ≤≤，则当1n k =+时，22113124k k k k a a a a +⎛⎫=-+=-+ ⎪⎝⎭[]3,10,14⎡⎤∈⊆⎢⎥⎣⎦.由①②，()*01n a n ∈N ≤≤.（Ⅱ）()()2211111n n n n n n n a a a a a a a +-=++-=-=-， 即1111n n n a a a a +-=-≥， 于是()11111n n a a a ---≥，即()()1*111n n a a a n ->-∈N ；（Ⅲ）当112a =时，由（Ⅰ），()*01n a n <<∈N ，故n S n >. 令()*1n n b a n =-∈N ，由（Ⅰ）（Ⅱ），()*10n n b b n +>>∈N . 由211n n n a a a +=-+，可得21n n n b b b +=-.从而()()222121223n b b b b b b b ++⋅⋅⋅+=-+-()111112n n n b b b b b +++⋅⋅⋅+-=-<=， 又222212n n b b b nb ++⋅⋅⋅+≥， 故212n nb <，即)*n b n <∈N .注意到n b <=<=，故12n b b b ++⋅⋅⋅+<⎤++⋅⋅⋅+=⎦即n n S -n S n >所以当112a =时，n n S n <.。