当前位置：文档之家 › 第2讲 matlab的数值分析

第2讲 matlab的数值分析

  • 格式：doc
  • 大小：99.00 KB
  • 文档页数：10

下载文档原格式

  / 10

合集下载

使用MATLAB进行数学计算与数据分析

使用MATLAB进行数学计算与数据分析

使用MATLAB进行数学计算与数据分析第一章：MATLAB的基本介绍与使用MATLAB是一种强大的数学计算和数据分析工具，可用于解决各种数学问题和数据处理任务。

它提供了许多内置函数和工具箱，使得数学计算和数据分析变得简单快捷。

第一节：MATLAB的安装与基本配置要使用MATLAB，首先需要将其安装到电脑上。

下载并运行安装程序，按照指示完成安装过程即可。

安装完成后，还需要进行一些基本配置，例如设置工作目录和默认文件格式等。

第二节：MATLAB的基本操作打开MATLAB后，会看到一个命令窗口和一个编辑器窗口。

在命令窗口中，可以直接输入命令并执行，而编辑器窗口则用于编写、保存和运行MATLAB脚本文件。

还可以通过菜单栏和工具栏来调用MATLAB的各种功能和工具。

第二章：MATLAB中的数学计算MATLAB提供了丰富的数学函数和工具，可以实现各种数学计算。

第一节：基本的数学运算MATLAB可以进行基本的数学运算，如加减乘除、乘方、开方等。

只需简单地输入相应的命令，MATLAB就会自动进行计算并给出结果。

第二节：解方程与求根MATLAB提供了多种解方程和求根的方法，包括代数方程、非线性方程和微分方程的求解。

通过调用相应的函数，输入方程的形式和初始值等参数，MATLAB可以帮助我们找到相应的解或根。

第三节：数值积分与微分MATLAB可以实现数值积分和微分的计算。

通过调用相关函数，输入函数表达式和积分或微分区间等参数，MATLAB可以进行相应的数值计算，并给出结果。

第三章：MATLAB中的数据分析MATLAB不仅可以进行数学计算，还可以进行数据分析。

它提供了多种数据处理和分析的方法和工具。

第一节：数据导入与导出在MATLAB中，可以将各种数据文件导入到工作空间中进行处理和分析，也可以将处理后的数据导出到文件中保存。

可以通过调用相应的函数和工具来实现数据的导入和导出。

第二节：数据可视化MATLAB提供了强大的数据可视化功能，可以将数据以图表的形式展示出来。

数值分析第二讲MATLAB简介

数值分析第二讲MATLAB简介

MATLAB编程入门 MATLAB的编程风格与C语言相同。 常用流程控制语句 if if语句条件 elseif if语句条件 end 终止作用域 for 指定次数的循环 while 不指定次数的循环 break 终止循环 switch 开关语句 case 列出语句 otherwise否则语句 return 返回调用函数 function 函数定义语句
MATLAB常用函数名 数学函数（中文意义略） abs，acos，acosh，angle，asin，asinh，atan，atan2，atanh， ceil，conj，cos，cosh，exp，fix，floor，gcd，imag，lcm，log， log10，real，rem，round，sign，sin，sinh，sqrt，tan，tanh， 构造矩阵函数 eye(n)，ones(n)，zeros(n)：产生n阶单位、全1，全0矩阵 eye(m,n)，ones(m.n)，zeros(m.n)：产生m×n的单位、全1，全 0矩阵 Sparse：构造稀疏矩阵 Size(M)取矩阵M的各维大小(结果为向量) size (M,n) 取矩阵M的第n维大小
例1:构造两个可加减乘的矩阵A，B，C,求A+B，A*C， sin(A)+cos(B),以及取A,B,C的子矩阵作同样的运算。 解:A=[ 1,2,3,4;5 6 7 8; 9 10 11 12]; B=ones(3,4) C= pascal(3) ⑴ D=A+B ⑵ E=sin(A)+cos(B) (3) F=A*C 错误操作：A*B，A+C
MATLAB的基本用法 一、数与变量 MATLAB的内部本质上只有两种类型的数据：实数和字符。 一个实数占8个字节（64比特），一个字符占用1字节（8比特）。 复数由两个实数构成，矩阵元素由字符、实数、复数构成。由矩 阵再构成“struct”（结构）数据类型，字符串是以字符为变量的 行向量。所以表现形式有：字符、字符串、整数、实数、复数、 结构。 characters: ‘char’ 表有符号字符 8bits, ‘uchar’ 无符号字符 8bits. integers :‘short’ 短整数16 bits, ‘long’ 长整数 32 bits, floating-point: ‘single-‘ 表单精度浮点数32bits, ’double‘表双精度浮 点数:64bits

数值分析.Matlab简介

数值分析.Matlab简介
第二章 MATLAB简介 简介
一、Matlab使用入门 Matlab使用入门 二、数值计算 三、符号运算 四、图形处理 五、程序设计 六、在计算方法中的应用
1
内容讲解安排
目的意义：掌握Matlab的基本用法 1. 目的意义：掌握 的基本用法 2.重 数值计算、符号运算、 2.重 点：数值计算、符号运算、图形制作 及程序设计 3.难 3.难 点：程序设计 4.内容分配 内容分配： 4.内容分配： 第 2 次：§1 Matlab简介 简介
EISPACK的接口程序。Cleve Moler给这个接口程序取 的接口程序。 给这个接口程序取
名为MATLAB，意思是“矩阵实验室”。 ，意思是“矩阵实验室” 名为
9
不久以后， 受到了学生的普遍欢迎， 不久以后，MATLAB受到了学生的普遍欢迎，并 受到了学生的普遍欢迎 也成了应用数学界的一个术语。 且，MATLAB也成了应用数学界的一个术语。 也成了应用数学界的一个术语 1983年早春，Cleve Moler到斯坦福大学访问， 年早春， 到斯坦福大学访问， 到斯坦福大学访问 身为工程师的John Little意识到 意识到MATLAB潜在的广 身为工程师的 意识到 潜在的广 阔应用领域应在工程计算方面，于是在同年， 阔应用领域应在工程计算方面，于是在同年，他与 Moler、Steve Bangert一起合作开发了第二代专业版 、 一起合作开发了第二代专业版 MATLAB。从这一代开始，MATLAB的核心就采用 。从这一代开始， 的核心就采用 C语言编写。也是从这一代开始，MATLAB不仅具 语言编写。也是从这一代开始， 语言编写 不仅具 有数值计算功能，而且具有了数据可视化功能。 有数值计算功能，而且具有了数据可视化功能。
7
）．编程易 （4）．编程易、效率高 ）．编程易、

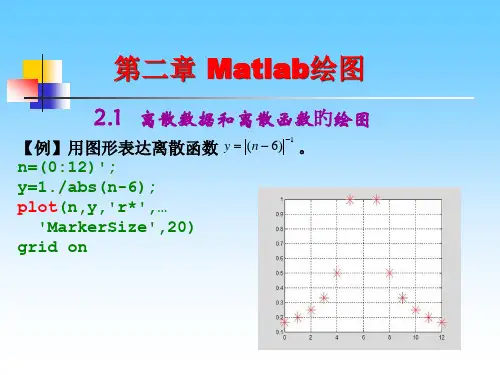
基于MATLAB的数值分析(2)

基于MATLAB的数值分析(2)
axis([0,pi,-1,1]),title('子图 (4)')
若干有用旳指令
clf：将图形窗口旳全部内容清除。 shg：显示图形窗口。 figure: 打开一种新旳图形窗口。 figure(n): 打开第n个图形窗口 cla: 将所绘曲线清除并重画坐标轴。 close(n):将关闭编号为n旳图形窗口， close all: 将关闭全部图形窗口.
pos取值0,1（缺省值）,2,3,4,-1 Legend off：擦出目前图上旳图例。
2.3 三维绘图旳基本操作
绘制二元函数基本环节： 1.生成二维网格点 2. 计算函数在网格点上旳值 3. 绘制函数图形
meshgrid指令：生成网格点
a=-0.98;b=0.98;c=-1;d=1;n=10; x=linspace(a,b,n); y=linspace(c,d,n); [X,Y]=meshgrid(x,y); plot(X,Y,'+')
分格线和坐标框
grid: grid on（画出分格线）, grid off （不画出分格线）
box : box on （坐标呈封闭形式）, box off （坐标呈开启形式）
【例】 n=(0:12)'; y=1./abs(n-6); Subplot(1,2,1),plot(n,y,'r*','MarkerSize',20),box on Subplot(1,2,2), plot(n,y,'r*','MarkerSize',20),box off
ylabel('\it{magnitude}');
title(' \it{sine wave and {\it{Ae}}^{-\alpha{\itt}}wave}');

第2讲 matlab的数值分析

第2讲 matlab的数值分析

第二讲MATLAB的数值分析2-1矩阵运算与数组运算矩阵运算和数组运算是MATLAB数值运算的两大类型，矩阵运算是按矩阵的运算规则进行的，而数组运算则是按数组元素逐一进行的。

因此，在进行某些运算（如乘、除）时，矩阵运算和数组运算有着较大的差别。

在MATLAB中，可以对矩阵进行数组运算，这时是把矩阵视为数组，运算按数组的运算规则。

也可以对数组进行矩阵运算，这时是把数组视为矩阵，运算按矩阵的运算规则进行。

1、矩阵加减与数组加减矩阵加减与数组加减运算效果一致，运算符也相同，可分为两种情况：（1）若参与运算的两矩阵（数组）的维数相同，则加减运算的结果是将两矩阵的对应元素进行加减，如A=[1 1 1;2 2 2;3 3 3];B=A;A+Bans=2 2 24 4 46 6 6（2）若参与运算的两矩阵之一为标量（1*1的矩阵），则加减运算的结果是将矩阵（数组）的每一元素与该标量逐一相加减，如A=[1 1 1;2 2 2;3 3 3];A+2ans=3 3 34 4 45 5 52、矩阵乘与数组乘（1）矩阵乘矩阵乘与数组乘有着较大差别，运算结果也完全不同。

矩阵乘的运算符为“*”，运算是按矩阵的乘法规则进行，即参与乘运算的两矩阵的内维必须相同。

设A、B为参与乘运算的=A m×k B k×n。

因此，参与运两矩阵，C为A和B的矩阵乘的结果，则它们必须满足关系C m×n算的两矩阵的顺序不能任意调换，因为A*B和B*A计算结果很可能是完全不一样的。

如：A=[1 1 1;2 2 2;3 3 3];B=A;A*Bans=6 6 612 12 1218 18 18F=ones(1,3);G=ones(3,1);F*Gans3G*Fans=1 1 11 1 11 1 1（2）数组乘数组乘的运算符为“.*”，运算符中的点号不能遗漏，也不能随意加空格符。

参加数组乘运算的两数组的大小必须相等（即同维数组）。

如何使用Matlab进行科学计算和数据分析

如何使用Matlab进行科学计算和数据分析

如何使用Matlab进行科学计算和数据分析Matlab（全称Matrix Laboratory）是一种常用的科学计算软件，在科学研究和数据分析中有着广泛的应用。

本文将针对如何使用Matlab进行科学计算和数据分析进行详细介绍，包括Matlab的基本操作、数据导入与处理、绘图与可视化、数值计算、统计分析等内容。

第一章：Matlab基本操作Matlab的基本操作包括环境设置、变量定义与操作、函数调用等。

首先，我们需要安装Matlab，并打开Matlab工作环境。

接下来，我们可以通过命令行界面或者脚本编辑器来输入和执行Matlab命令。

可以使用等号“=”来定义变量，并使用各种运算符进行数学运算。

此外，还可以通过调用Matlab的内置函数进行计算。

第二章：数据导入与处理在科学计算和数据分析中，我们经常需要从外部源导入数据并进行处理。

Matlab提供了多种方式来导入数据，包括读取文本文件、导入Excel文件、读取数据库等。

一旦数据被导入到Matlab 中，可以使用各种函数来进行数据处理，比如筛选、排序、合并等操作。

此外，还可以对数据进行清洗和转换，以便进一步分析。

第三章：绘图与可视化数据的可视化是科学计算和数据分析的重要环节之一。

Matlab提供了丰富的绘图函数，可以绘制二维和三维图形，包括散点图、线图、柱状图、等高线图等。

此外，Matlab还提供了自定义图形属性、添加标签、调整坐标轴等功能，使得绘图更加精美且易于理解。

通过可视化结果，我们可以更加直观地了解数据的分布和趋势。

第四章：数值计算Matlab具有强大的数值计算功能，可以进行各种数值运算和数值解析。

比如，可以求解线性方程组、进行数值积分、计算微分方程等。

Matlab内置了许多数值计算函数，可以极大地简化计算过程。

此外，Matlab还支持矩阵运算和向量化操作，提高计算效率。

第五章：统计分析数据分析常常需要进行统计分析，以获取数据的统计特征和推断性结论。

学习使用MATLAB进行数值计算和数据分析

学习使用MATLAB进行数值计算和数据分析

学习使用MATLAB进行数值计算和数据分析---第一章：MATLAB的基本介绍MATLAB是一种强大的数值计算和数据分析软件，广泛应用于科学研究、工程设计等领域。

它的主要特点是简洁直观的用户界面和丰富的数学函数库。

在本章中，我们将介绍MATLAB的基本特性和使用方法。

1.1 MATLAB的历史与发展MATLAB是由MathWorks公司于1984年首次推出的。

起初，它作为一个用于矩阵计算的工具被广泛使用。

随着时间的推移，MATLAB逐渐拓展了功能，加入了许多其他数学和工程计算的功能，如符号计算、数据统计和可视化。

如今，MATLAB已经成为一种非常受欢迎的工具。

1.2 MATLAB的安装和环境设置要开始使用MATLAB，首先需要从MathWorks官网下载并安装MATLAB软件。

安装完成后，打开MATLAB并设置工作目录和默认工作文件夹。

工作目录是指存储MATLAB代码和数据文件的文件夹，而默认工作文件夹是指MATLAB打开时默认选择的文件夹。

1.3 MATLAB的基本语法和命令MATLAB的基本语法和命令非常简单易懂。

它采用类似于其他编程语言的命令行交互方式，用户可以直接在命令行输入MATLAB语句并执行。

例如，可以输入"2+2"并按回车键得到结果4。

此外，MATLAB还具有许多内置的数学函数和运算符，可以进行各种数值计算和数据分析。

1.4 MATLAB脚本和函数在MATLAB中，可以使用脚本和函数来组织和执行一系列MATLAB命令。

脚本是一系列命令的集合，可以一次性运行。

函数是一段可以重复使用的代码，可以接受输入参数并返回输出结果。

通过编写脚本和函数，可以提高MATLAB代码的可重复性和可维护性。

第二章：数值计算MATLAB作为一种数值计算工具，提供了丰富的数学函数和算法，可以用于解决各种数值计算问题。

在本章中，我们将介绍MATLAB在数值计算方面的一些常用功能和技巧。

2.1 数值计算方法MATLAB中包含了许多数值计算方法，如数值积分、数值微分、线性代数求解等。

MATLAB在数值分析中的应用

MATLAB在数值分析中的应用

MATLAB在数值分析中的应用
matlab是一种高级计算及可视化软件，在数值分析方面有着广泛的应用。

其特点是完整的数学和统计功能，强大的可视化和计算能力，易于使用的环境和脚本语言，使得matlab在数值分析领域变得非常流行。

首先，matlab具有强大的符号计算功能，可以求解复杂的多项式及微分方程，进行多项式拟合和矩阵计算等，从而支持数值分析中的基本操作。

其次，matlab还提供了一系列的工具箱，如数值分析工具箱，控制系统工具箱和数据分析工具箱等，这些工具箱可以作为matlab的拓展工具，为数值分析提供支持，有助于研究者解决复杂的问题。

此外，matlab 在多种算法的支持上也拥有全面的支持，包括线性规划、非线性规划、自动微分、数值积分、拟合优化、最优化及矩阵分解，可以用于几乎所有的数值分析任务。

最后，matlab还提供了极强的可视化功能，可以处理矩阵、标量和向量的可视化，包括3D和4D图表，可以帮助研究者快速分析结果。

因此，matlab支持的数值分析功能强大，提供了非常丰富的工具箱和算法支持，并有强大的可视化功能，使其在数值分析领域得到了广泛应用。

使用MATLAB进行科学计算与数据分析教程

使用MATLAB进行科学计算与数据分析教程

使用MATLAB进行科学计算与数据分析教程第一章：介绍MATLABMATLAB是一种被广泛应用于科学计算和数据分析的高级编程语言和环境。

它是由MathWorks公司开发的，可以进行矩阵计算、绘图和数据可视化、符号计算、统计分析等功能。

本章将介绍MATLAB的基本概念和环境设置。

1.1 MATLAB的安装与启动首先，你需要从MathWorks官网下载并安装MATLAB。

安装完成后，你可以在电脑上找到MATLAB的快捷方式并打开。

MATLAB的启动界面提供了各种选项，包括创建新的脚本、打开已有的脚本、查看帮助文档等。

1.2 MATLAB的基本语法MATLAB使用类似英语的语法，可以进行数学运算、变量赋值、条件判断、循环等操作。

例如，你可以使用"+"进行加法运算，使用"="进行变量赋值，使用"if"和"for"进行条件判断和循环操作。

1.3 MATLAB的数据类型MATLAB支持各种数据类型，包括整数、浮点数、字符和逻辑值等。

它还可以处理矩阵和向量等数据结构。

你可以使用MATLAB提供的函数进行数据类型的转换和操作。

第二章：科学计算科学计算是MATLAB的一个重要应用领域。

本章将介绍MATLAB如何进行数值计算、数值求解和符号计算等操作。

2.1 数值计算MATLAB提供了丰富的数值计算函数，包括基本的数学函数、矩阵运算、统计函数等。

你可以使用这些函数进行数值的计算和处理。

2.2 数值求解MATLAB可以用于解决各种数值求解问题，比如方程求解、最优化问题、常微分方程等。

它提供了多种求解方法和函数，可以帮助我们快速准确地找到问题的解。

2.3 符号计算MATLAB的符号计算功能可以进行代数运算、微积分、方程求解等。

它可以处理符号表达式，精确计算结果。

符号计算在数学推理和理论研究中具有重要意义。

第三章：数据分析数据分析是MATLAB的另一个重要应用领域。

第二讲 MATLAB的数值计算 贵州大学(分析“矩阵”文档)共63张PPT

第二讲 MATLAB的数值计算 贵州大学(分析“矩阵”文档)共63张PPT
ans = x^4 + 2 x^3 + 3 x^2 + 4 x + 5
b=polyder(a)
b=4 6 6 4
poly2str(b,'x')
ans =4 x^3 + 6 x^2 + 6 x + 4
九、代数方程组求解
MATLAB中有两种除运算左除和右除。 对于方程ax+b，a 为an×m矩阵，有三种情 况： 当n=m时，此方程成为“恰定”方程 当n>m时，此方程成为“超定”方程 当n<m时，此方程成为“欠定”方程
例:a=[1 2 3;4 5 6;7 8 0]; p=poly(a)
p是多项式p(x)=x3-6x2-72x-27的 MATLAB描述方法，我们可用：
p1=poly2str(p,‘x’) — 函数文件，显示 数学多项式的形式
p1 =x^3 - 6 x^2 - 72 x - 27
2.roots —— 求多项式的根
X=A\B是方程AX=B的最小二乘意义上的解。
4. 矩阵乘方—— a^n,a^p,p^a
a ^ p —— a 自乘p次幂
方阵 >1的整数
对于p的其它值,计算将涉及特征值 和特征向量，如果p是矩阵，a是标量
a^p使用特征值和特征向量自乘到p次 幂；如a,p都是矩阵，a^p则无意义。
a=[1,2,3;4,5,6;7,8,9]; a^2 ans =30 36 42
{ } 构成单元数组
. 小数点或域访问符 .. 上级目录（父目录） … 续行标志 % 注释标志 ! 调用操作系统命令
= 赋值
几个重要操作符的用法
1. 冒号的用途
生成等间隔的行向量，默认间隔为1。

学会使用MATLAB进行数据分析与计算

学会使用MATLAB进行数据分析与计算

学会使用MATLAB进行数据分析与计算第一章：MATLAB的基础知识与环境搭建MATLAB是一种数据分析与计算的强大工具，使用它可以方便地进行数据处理、建模和分析。

在使用MATLAB之前，我们首先需要了解一些基本知识，并进行环境搭建。

在MATLAB中，我们可以通过命令行界面或者脚本来输入指令。

命令行界面可以提供即时的结果，而脚本则可以保存多个指令，方便重复执行。

我们可以使用MATLAB提供的帮助文档来查阅各种函数的使用方法和语法。

帮助文档中包含了详细的示例和解释，非常有助于学习和理解。

另外，在使用MATLAB之前，我们还需要进行环境搭建。

首先，我们需要下载和安装MATLAB软件，随后进行激活。

安装完成后，我们可以打开MATLAB并设置工作目录，以方便我们进行数据分析与计算的操作。

第二章：数据的导入与分析在进行数据分析与计算之前，首先需要将数据导入到MATLAB中。

MATLAB支持多种文件格式的数据导入，包括Excel、CSV、文本文件等。

一般情况下，我们可以使用MATLAB提供的importdata函数来导入数据。

这个函数可以根据不同的文件格式自动选择相应的导入方法，并将数据存储在一个结构体中。

导入数据后，我们可以利用MATLAB提供的各种函数进行数据分析。

例如，可以使用plot函数来绘制数据的曲线图，使用histogram函数来绘制数据的直方图，使用mean函数来计算数据的平均值等等。

除了基本的数据分析函数外，MATLAB还提供了一些高级的数据处理工具，如统计分布分析、回归分析、时间序列分析等。

这些工具可以方便地应用于各种数据处理任务中，并提供了可视化和报告的功能。

第三章：数值计算与优化问题MATLAB作为一种数值计算工具，提供了许多常用的数值计算与优化函数，可以方便地求解各种数学问题。

例如，我们可以使用solve函数来求解方程，使用integral函数来求解定积分，使用diff函数来求解导数，使用ode45函数来求解常微分方程等。

《数值分析及其MATLAB实现》第二篇MATLAB快速入门word第二章2.5

《数值分析及其MATLAB实现》第二篇MATLAB快速入门word第二章2.5

2.5 程序设计MATLAB提供了一个完善的程序设计语言环境，使我们能方便地编制复杂的程序，完成各种计算。

本节先简要介绍关系、逻辑运算和条件、循环语句等许多高级语言都具备的、编程的重要手段，再着重介绍MATLAB所特有的M文件。

2.5.1 关系和逻辑运算MATLAB的关系运算符有:<小于；>大于；<= 小于或等于；>= 大于或等于；== 等于；～= 不等于。

关系运算比较两个数值，当指出的关系成立时结果为1（表示真），否则为0（表示假）。

关系运算可以作用于两个同样大小的矩阵或数组，结果是一个0,1矩阵或数组，每个分量代表相应的矩阵或数组分量的关系运算结果，例如，在MATLAB工作窗口输入程序：》A=1:5,B=5:-1:1运行后输出结果如下：A =1 2 3 4 5B =5 4 3 2 1在MATLAB工作窗口输入程序：》C=A>=4运行后输出结果如下：C =0 0 0 1 1在MATLAB工作窗口输入程序：》D=A==B运行后输出结果如下：D =0 0 1 0 0下面举一个例子说明如何将关系运算和数值运算结合起来。

在MATLAB工作窗口输入程序：》x=(-3:3)/3运行后输出结果如下：x =-1.0000 -0.6667 -0.3333 0 0.3333 0.6667 1.0000在MATLAB工作窗口输入程序：》sin(x)./x运行后输出结果如下：Warning: Divide by zeroans =0.8415 0.9276 0.9816 NaN 0.9816 0.9276 0.8415在计算sinx/x时给出了警告信息，是因为第4个数据sin0/0没有定义，MATLAB返回NaN。

为了避免这种情况出现可以用最小浮点数eps来代替0，在MATLAB工作窗口输入程序：》x=(-3:3)/3；x=x+(x==0)*eps；sin(x)./x运行后输出结果如下：ans =0.8415 0.9276 0.9816 1.0000 0.9816 0.9276 0.8415 给出了sinx/x在x=0时正确的极限值。

MATLAB的基本知识与数值分析

MATLAB的基本知识与数值分析

MATLAB入门教程1．MATLAB的基本知识1-1、基本运算与函数在MATLAB下进行基本数学运算，只需将运算式直接打入提示号（>>）之後，并按入Enter 键即可。

例如：>> (5*2+1.3-0.8)*10/25ans =4.2000MATLAB会将运算结果直接存入一变数ans，代表MATLAB运算後的答案（Answer）并显示其数值於萤幕上。

小提示：">>"是MATLAB的提示符号（Prompt），但在PC中文视窗系统下，由於编码方式不同，此提示符号常会消失不见，但这并不会影响到MATLAB的运算结果。

我们也可将上述运算式的结果设定给另一个变数x：x = (5*2+1.3-0.8)*10^2/25x = 42此时MATLAB会直接显示x的值。

由上例可知，MATLAB认识所有一般常用到的加（+）、减（-）、乘（*）、除（/）的数学运算符号，以及幂次运算（^）。

小提示：MATLAB将所有变数均存成double的形式，所以不需经过变数宣告（Variable declaration）。

MATLAB同时也会自动进行记忆体的使用和回收，而不必像C语言,必须由使用者一一指定.这些功能使的MATLAB易学易用，使用者可专心致力於撰写程式，而不必被软体枝节问题所干扰。

若不想让MATLAB每次都显示运算结果，只需在运算式最後加上分号（；）即可，如下例：y = sin(10)*exp(-0.3*4^2);若要显示变数y的值，直接键入y即可：>>yy =-0.0045在上例中，sin是正弦函数，exp是指数函数，这些都是MATLAB常用到的数学函数。

下表即为MATLAB常用的基本数学函数及三角函数：小整理：MATLAB常用的基本数学函数abs(x)：纯量的绝对值或向量的长度angle(z)：复数z的相角(Phase angle)sqrt(x)：开平方real(z)：复数z的实部imag(z)：复数z的虚部conj(z)：复数z的共轭复数round(x)：四舍五入至最近整数fix(x)：无论正负，舍去小数至最近整数floor(x)：地板函数，即舍去正小数至最近整数ceil(x)：天花板函数，即加入正小数至最近整数rat(x)：将实数x化为分数表示rats(x)：将实数x化为多项分数展开sign(x)：符号函数(Signum function)。

matlab与数值分析课件：数值分析_(2)

matlab与数值分析课件：数值分析_(2)

u a u a u a u a u a u1 行 , , , ; , j 1, ,n
11
11
12
12
13
13
14
14
1j
1j
l a u l a u l a u l a u l 1 列
,
,
;
, i 2, ,n
21
21 11 31
31 11 41
41 11 i1
i1 11
u a l u u a l u u a l u u2 行
③ 消元
注：列交换改变了 xi 的顺序，须记录交换次序，解完后再 换回来。
列主元消去法
省去换列的步骤，每次仅选一列中最大的元。
| aik ,k
|
max
kin
|
aik
|
0
例：
109
1
1 1
1 2
1 109
1 1
2 1
1 0
1 1
2 1
x2 1 , x1 1 ✓
注：列主元法没有全主元法稳定。
例：11
109 1
109
2
1 0
109 109
109
109
x2 1 ,
x1
0
注意：这两个方程组在 数学上严格等价。
§ 2. 矩阵三角分解法
用矩阵理论分析消元法：
由 Gauss 消去法加上列主元 ( 或全主元）有 LU 分解：
A LU
1
l
21
1
l l L
31
1
32
l l
0
1
l 32 l 42
0 0 1
l 43
u 0

MATLAB数值分析

MATLAB数值分析

MATLAB数值分析MATLAB是一种强大的数值分析工具，它提供了许多函数和工具箱，用于解决各种数值分析问题。

本文将探讨MATLAB在数值分析领域的应用范围、常见的数值分析方法以及使用MATLAB进行数值分析的一般步骤。

首先，我们来看一下MATLAB在数值分析中的应用范围。

MATLAB可以用于解决各种数值分析问题，包括但不限于线性方程组的求解、函数插值、数值积分、数值微分、常微分方程的数值解法以及优化问题的求解等。

由于其易于使用、灵活性和高效性，MATLAB在科学计算和工程领域得到了广泛的应用。

接下来，我们将介绍一些常见的数值分析方法，在MATLAB中如何实现这些方法。

首先是线性方程组的求解。

MATLAB提供了许多函数和工具箱，用于求解线性方程组。

其中最常用的是使用LU分解或Cholesky分解进行直接求解，或使用迭代法（如共轭梯度法或Jacobi法）进行近似求解。

其次是函数插值。

MATLAB提供了许多插值函数，如多项式插值、样条插值等。

可以使用这些函数通过给定的离散数据点来近似计算函数的值和导数。

第三，数值积分在数值分析中也非常常见。

MATLAB提供了多种数值积分方法，如梯形法则、辛普森法则和高斯积分法。

用户可以根据具体需求选择适当的数值积分方法进行计算。

第四，数值微分也是数值分析的重要内容。

MATLAB提供了函数来计算函数的导数和高阶导数。

用户可以使用这些导数函数计算导数，并将其应用于其他数值计算，如方程求解或优化问题。

第五，对于常微分方程的求解，MATLAB提供了许多函数和工具箱。

用户可以使用MATLAB提供的常微分方程求解器来解决各种类型的常微分方程。

这些求解器提供了各种数值解法，如欧拉法、龙格-库塔法、Adams 法等。

最后，MATLAB还提供了许多用于解决优化问题的函数和工具箱。

用户可以使用这些函数和工具箱来解决线性规划、非线性规划、整数规划等各种类型的优化问题。

在使用MATLAB进行数值分析时，一般遵循以下步骤。

MATLAB 数值分析

MATLAB 数值分析

13.2
极小化
作图除了提供视觉信息外，还常常需要确定一个函数的其它更多的特殊属性。在许多 应用中，特别感兴趣的是确定函数的极值，即最大值（峰值）和最小值（谷值）。数学上， 可通过确定函数导数（斜率）为零的点，解析上求出这些极值点。检验 humps 的图形在峰 值和谷值点上的斜率就很容易理解这个事实。显然，如果定义的函数简单，则这种方法常 常奏效。然而，即使很多容易求导的函数，也常常很难找到导数为零的点。在这种情况下， 以及很难或不可能解析上求得导数的情况下，必须数值上寻找函数的极值点。MATLAB 提 供了两个完成此功能的函数 fmin 和 fmins。 这两个函数分别寻找一维或 n 维函数的最小值。 这里仅讨论 fmin。有关 fmins 的详细信息，参阅《MATLAB 参考指南》。因为 f(x)的最大 值等于-f(x)的最小值，所以，上述 fmin 和 fmins 可用来求最大值和最小值。如果还不清楚， 把上述图形倒过来看，在这个状态下，峰值变成了谷值，而谷值则变成了峰值。 为了解释求解一维函数的最小值和最大值， 再考虑上述例子。 从图 13.2 可知， 在 xmax=0.7 附 近 有 一 个 最 大 值 ， 并 且 在 xmin=4 附 近 有 一 个 最 小 值 。 而 这 些 点 的 解 析 值 为 ： x m a x / 4 0.785 和 x min 5 / 4 393 . 。为了方便，用文本编辑器编写一个脚本 M 文件，并用 fmin 寻出数值上极值点，给出函数主体如下： % ex_fmin.m fn=‘ 2*exp(-x)*sin(x) ‘; xmin=fmin(fn , 2 , 5)
% better approximation
自然地，上述两个结果不同。基于对图形的观察，粗略近似可能低估了实际面积。除 非特别精确，没有准则说明哪种近似效果更好。很明显，如果人们能够以某种方式改变单 个梯形的宽度，以适应函数的特性，即当函数变化快时，使得梯形的宽度变窄，这样就能 够得到更精确的结果。 MATLAB 的函数 quad 和 quad8 是基于数学上的正方形概念来计算函数的面积， 这些 积分函数的操作方式一样。为获得更准确的结果，两个函数在所需的区间都要计算被积函 数。 此外， 与简单的梯形比较， 这两个函数进行更高阶的近似， 而且 quad8 比 quad 更精确。 这两个函数的调用方法与 fzero 相同，即 >>area=quad(‘ humps ‘ , -1 , 2) % find area between -1 and 2

matlab 数值解

matlab 数值解

matlab 数值解Matlab 数值解Matlab 是一种强大的数学软件，它包含了很多数学工具箱，可以用于数值分析和求解数学问题。

在本文中，我们将介绍Matlab 中的数值解方法，包括数值积分、数值微分、非线性方程求解和常微分方程的数值解法。

数值积分数值积分是一种数学方法，用于求解函数的定积分。

在Matlab 中，可以使用 quad 和 quadl 函数进行数值积分。

其中，quad 函数用于计算一般积分，而 quadl 函数用于计算不定积分。

数值微分数值微分是一种数学方法，用于计算函数的导数。

在Matlab 中，可以使用diff 和gradient 函数进行数值微分。

其中，diff 函数用于计算一维函数的导数，而 gradient 函数用于计算多维函数的梯度。

非线性方程求解非线性方程是一种形式为 f(x)=0 的方程，其中 f(x) 是一个非线性函数。

在 Matlab 中，可以使用 fzero 和 fsolve 函数进行非线性方程求解。

其中，fzero 函数用于求解单变量非线性方程，而fsolve 函数用于求解多变量非线性方程。

常微分方程的数值解法常微分方程是一种形式为y'=f(t,y) 的方程，其中y 是未知函数，t 是自变量，f(t,y) 是已知函数。

在Matlab 中，可以使用ode45 和ode23 函数进行常微分方程的数值解法。

其中，ode45 函数是一种常用的数值解法，可以求解大部分常微分方程，而 ode23 函数则是一种高效的数值解法，适用于求解简单的常微分方程。

总结在本文中，我们介绍了Matlab 中的数值解方法，包括数值积分、数值微分、非线性方程求解和常微分方程的数值解法。

这些方法可以帮助我们快速、准确地求解数学问题，提高数学建模的效率和精度。

如何使用Matlab进行数值计算与数据分析

如何使用Matlab进行数值计算与数据分析

如何使用Matlab进行数值计算与数据分析第一章：Matlab的介绍与安装Matlab是一种广泛应用于科学研究和工程领域的计算机编程语言和环境。

它强大的数值计算能力和丰富的数据分析功能使得它成为了科学家和工程师们常用的工具。

本章将介绍Matlab的基本特点和安装方法。

Matlab的特点之一就是其强大的数值计算能力。

它支持各种各样的数值计算操作，例如矩阵运算、微分和积分、线性代数、符号计算等等。

此外，Matlab还拥有许多内置的数学函数和工具箱，可以帮助用户更方便地进行数值计算。

另一个Matlab的特点就是其优秀的数据分析功能。

Matlab可以处理各种类型的数据，包括数字、文本、图像和音频等等。

它提供了丰富的数据处理和统计分析函数，可以帮助用户从海量数据中提取有用的信息。

安装Matlab非常简单。

首先，你需要从MathWorks的官方网站下载Matlab安装程序。

在下载完成后，双击运行安装程序，按照提示进行安装。

安装过程中，你可以选择安装哪些工具箱和功能。

一般来说，初学者可以选择安装较为常用的工具箱，随后可以根据需要再安装其他工具箱。

安装完成后，你就可以开始使用Matlab进行数值计算和数据分析了。

第二章：Matlab基础知识在使用Matlab进行数值计算和数据分析之前，你需要掌握一些Matlab的基础知识。

本章将介绍一些常用的Matlab语法、变量和数据类型等等。

Matlab语法非常简洁和直观。

你可以在Matlab中直接执行各种数学运算，例如加法、减法、乘法和除法。

Matlab还支持各种控制流程语句，例如条件语句、循环语句和函数等等。

另外，Matlab的变量和数据类型也非常灵活。

你可以使用任意名称定义变量，并且Matlab会根据变量的赋值自动推断其数据类型。

Matlab支持各种常见的数据类型，包括整数、浮点数、字符和逻辑等等。

此外，Matlab还支持矩阵和向量等特殊的数据类型，使得它在矩阵计算方面具有天然的优势。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第二讲MATLAB的数值分析2-1矩阵运算与数组运算矩阵运算和数组运算是MATLAB数值运算的两大类型，矩阵运算是按矩阵的运算规则进行的，而数组运算则是按数组元素逐一进行的。

因此，在进行某些运算（如乘、除）时，矩阵运算和数组运算有着较大的差别。

在MATLAB中，可以对矩阵进行数组运算，这时是把矩阵视为数组，运算按数组的运算规则。

也可以对数组进行矩阵运算，这时是把数组视为矩阵，运算按矩阵的运算规则进行。

1、矩阵加减与数组加减矩阵加减与数组加减运算效果一致，运算符也相同，可分为两种情况：（1）若参与运算的两矩阵（数组）的维数相同，则加减运算的结果是将两矩阵的对应元素进行加减，如A=[1 1 1;2 2 2;3 3 3];B=A;A+Bans=2 2 24 4 46 6 6（2）若参与运算的两矩阵之一为标量（1*1的矩阵），则加减运算的结果是将矩阵（数组）的每一元素与该标量逐一相加减，如A=[1 1 1;2 2 2;3 3 3];A+2ans=3 3 34 4 45 5 52、矩阵乘与数组乘（1）矩阵乘矩阵乘与数组乘有着较大差别，运算结果也完全不同。

矩阵乘的运算符为“*”，运算是按矩阵的乘法规则进行，即参与乘运算的两矩阵的内维必须相同。

设A、B为参与乘运算的=A m×k B k×n。

因此，参与运两矩阵，C为A和B的矩阵乘的结果，则它们必须满足关系C m×n算的两矩阵的顺序不能任意调换，因为A*B和B*A计算结果很可能是完全不一样的。

如：A=[1 1 1;2 2 2;3 3 3];B=A;A*Bans=6 6 612 12 1218 18 18F=ones(1,3);G=ones(3,1);F*Gans3G*Fans=1 1 11 1 11 1 1（2）数组乘数组乘的运算符为“.*”，运算符中的点号不能遗漏，也不能随意加空格符。

参加数组乘运算的两数组的大小必须相等（即同维数组）。

数组乘的结果是将两同维数组（矩阵）的对应元素逐一相乘，因此，A.*B和B.*A的计算结果是完全相同的，如：A=[1 1 1 1 1;2 2 2 2 2;3 3 3 3 3];B=A;A.*Bans=1 1 1 1 14 4 4 4 49 9 9 9 9B.*Aans=1 1 1 1 14 4 4 4 49 9 9 9 9由于矩阵运算和数组运算的差异，能进行数组乘运算的两矩阵，不一定能进行矩阵乘运算。

如A=ones(1,3);B=A;A.*Bans=1 1 1A*A???Error using= =>Inner matrix dimensions must agree.3、矩阵除与数组除矩阵除分为矩阵右除和矩阵左除两种情况。

矩阵右除的运算符为“/”，设A、B为两矩阵，则“A/B”是指方程X*B=A的解矩阵X。

显然，矩阵右除运算对参与运算两矩阵的维数是有一定要求的，即矩阵A和B的列数必须相等。

如A=[1 1 1 1;2 2 2 2;3 3 3 3];B=[1 1 1 1];X=A/BX=12X*Bans=1 1 1 12 2 2 2矩阵右除允许参与右除运算的矩阵B为标量，这时矩阵右除运算的结果是将矩阵A的每一元素逐一与该标量进行除法运算。

如：A=[2 4 6 8；8 6 4 2]；B=2；A/Bans=1 2 3 44 3 2 1矩阵左除运算符为“\”，设A、B为两矩阵，则“A\B”是指方程B*X=A的解矩阵X。

显然，矩阵左除运算对参与运算两矩阵的维数也有一定要求的，即矩阵A和B的行数必须相等。

如数组右除的运算符为“./”，左除的运算符为“.\”。

数组右除和左除的运算结果是完全等效的。

设A、B为两同维矩阵，则“A./B”的运算结果是将矩阵A的每一个元素与矩阵B的对应元素相除。

应注意的是，参与数组运算的两矩阵（数组）的大小必须相等。

A=[2 2 3 3 4 4;1 1 2 2 3 3;4 4 5 5 6 6];B=[1 2 3 3 2 2;1 1 1 1 1 1;2 2 5 5 3 3];A./Bans=2 2 1 1 2 21 12 23 32 2 1 1 2 2B./Aans=0.5000 0.5000 1.0000 1.0000 0.5000 0.50001.0000 1.0000 0.5000 0.5000 0.3333 0.33330.5000 0.5000 1.0000 1.0000 0.5000 0.50004、常用的矩阵运算函数（1）用size()函数计算矩阵A 的维数，调用格式：d=size(A) %将矩阵A 的行数和列数赋给变量d[m,n]=size(A) %将矩阵A 的行数赋给变量m 、列数赋给变量n（2）用rand()函数产生随机矩阵，，调用格式：rand(n) %产生值在0~1之间随机分布的n*n 的随机方阵rand(m,n) %%生值在0~1之间随机分布的n*m 的随机矩阵（3）计算矩阵长度（列数）的函数length()，调用格式：a=length(B) %将矩阵B 的列数赋值给变量a（4）矩阵元素的求积运算函数prod()，调用格式：prod(A) %若A 为向量，将计算矩阵A 所有元素之积；若A 为矩阵，将产生一行向量，其元素分别为矩阵A 的各列元素之积。

prod(A,k) %将对矩阵A 按k 定义的方向进行示积运算，若k=1则按列的方向求积，若k=2则按行的方向求积。

（5）矩阵元素的求和运算函数sum()，调用格式同prod()函数。

2-2多项式及其运算MATLAB 提供了标准多项式的常用函数，包括求根、相乘、相除等。

1．多项式的表达与创建MATLAB 采用将多项式系数按幂次序排列形式的行向量来表征一多项式。

设多项式为：0111a s a s a s a s A n n n n ++++=-- )(则表征该多项式的行向量表示为：][011a a a a P n n-=。

因此，在MATLAB 中，创建多项式即可创用建行向量的方法，直接输入按顺序排序的多项式系数即可。

如，输入语句：A=[1 2 2 1];即表示创建多项式12223+++s s s ，并赋值给变量A 。

2．多项式求根函数roots()用于对多项式求根，调用格式：p=roots(A)其中A 为表征多项式的行向量，p 返回该多项式的根（用列向量表示）。

如B=[1 3 2]; %创建多项式232++s sroots(B) %求多项式的根ans=-2-1A=[1 2 2 1];roots(A)ans=-1.0000-0.5000+0.8660i-0.5000-0.8660i3．由指定根求多项式函数poly用于由给定根求多项式系数向量，调用格式为：A=poly(p)其中p为多项式根（行或列向量表示），A为返回的多项式系数（行向量表示）。

如：p=[2 1];poly (p)ans=1 -3 2可见roots()与poly()互为逆运算。

4．多项式相乘（卷积）函数conv()用于求两个多项式的乘积多项式，调用格式：R=conv(A,B)其中A、B分别为表征两个多项式的行向量，R为返回的每间积多项式的系数向量（按降幂次序排列）。

如A=[1 3 2]；B=[1 2 1]；R=conv(A,B)R=1 5 9 7 25．多项式相除（解卷）函数deconv()用于进行两个多项式的相除运算，它是相乘运算（conv）的逆运算，其调用格式为：[B,t]=deconv(R,A)其中R为被除多项式，A为除数多项式，B为商多项式，t为余多项式。

即多项式R除以多项式A后得商多项式B和余多项式t。

如：R=[1 5 9 7 2];A=[1 3 2];[B,t]=deconv(R,A)B=1 2 1t=0 0 0 0 0若多项式系数向量为零向量，则表示R能被A除尽。

2-3线性代数方程（组）求解我们习惯将上组方程式以矩阵方式表示如下：AX=B其中 A 为等式左边各方程式的系数项，X 为欲求解的未知项，B 代表等式右边之已知项，要解上述的联立方程式，我们可以利用矩阵左除\ 做运算，即是X=A\B。

如果将原方程式改写成XA=B其中A为等式左边各方程式的系数项，X 为欲求解的未知项，B 代表等式右边之已知项。

注意上式的X, B 已改写成列向量，A其实是前一个方程式中A 的转置矩阵。

上式的X 可以矩阵右除/ 求解，即是X=B/A。

若以反矩阵运算求解AX=B, X=B，即是X=inv(A)*B，或是改写成XA=B, X=B，即是X=B*inv(A)。

我们直接以下面的例子来说明这三个运算的用法：A=[3 2 -1; -1 3 2; 1 -1 -1]; % 将等式的左边系数键入B=[10 5 -1]'; % 将等式右边之已知项键入，B要做转置X=A\B % 先以左除运算求解X = % 注意X为行向量-256C=A*X % 验算解是否正确C = % C=B105-1A=A'; % 将A先做转置B=[10 5 -1];X=B/A % 以右除运算求解的结果亦同X = % 注意X为列向量10 5 -1X=B*inv(A); % 也可以反矩阵运算求解2-4 信号的MATLAB 表示举例1、指数信号at AeMATLAB 中表示：y=A*exp(a*t)%example2-1 decaying exponential signalA=1;a=-0.4;t=0:0.001:10;yt= A*exp(a*t);plot(t,yt)2、正弦信号)sin(ϕω+t A 0MATLAB 中表示：y=A*sin(w0*t+phi)%example2-2 sinusoidal signalA=1;w0=2*pi;phi=pi/6;t=0:0.001:8;yt= A*sin(w0*t+phi);plot(t,yt)3、抽样函数)(t SaMATLAB 中抽样函数用sinc 函数表示：y=sinc(t)%example2-3 Sample functiont=-3*pi:pi/100:3*pi;yt=sinc(t/pi);plot(t,yt)4、矩形脉冲信号MATLAB 中矩形脉冲信号用rectpuls 函数表示：y=rectpuls (t,width) %width 缺省值为1%example2-4 产生一幅度为1，宽度为width 以零点为对称的矩形波t=0:0.001:4;T=1;yt=rectpuls (t-2*T,T);plot(t,yt)axis([0,4,-0.5,1.5])5、三角波脉冲信号MATLAB中三角波脉冲信号用tripuls函数表示：y=tripuls (t,width,skew)用以产生一幅度最大为1，宽度为width的三角波，非零范围（-width/2, width/2）。