专题10 二次函数与圆综合问题(函数)-全国各地2019中考数学压轴题函数大题题型分类汇编(原卷版)(1)

2019学年度九年级数学二次函数综合题题型归类之与圆有关问题（附答案详解）1．如图，抛物线y=ax2-x+c（a≠0）的图象与x轴交于A、B两点，与y轴交于点C（0，-2），已知B点坐标为（4，0）（1）求抛物线的解析式；（2）试探究△ABC的外接圆的圆心位置，并求出圆心坐标；（3）若点M是线段BC下方的抛物线上一点，记点M到线段BC的距离为d，当d取最大值时，求出此时M点的坐标；（4）若点P是抛物线上一点，点E是直线y=-x+1上的动点，是否存在点P、E，使以点A，点B，点P，点E为顶点的四边形是平行四边形？若存在，请直接写出点E坐标；若不存在，请说明理由．2．如图，抛物线的图象经过点，对称轴为直线，一次函数的图象经过点，交轴于点，交抛物线于另一点，点、位于点的同侧．求抛物线的解析式；若，求一次函数的解析式；在的条件下，当时，抛物线的对称轴上是否存在点，使得同时与轴和直线都相切，如果存在，请求出点的坐标，如果不存在，请说明理由．3．如图，抛物线y=-x 2+bx+c 与直线AB 交于A(-4，-4)，B(0，4)两点，直线AC ：y=-x-6交y 轴与点C ．点E 是直线AB 上的动点，过点E 作EF ⊥x 轴交AC 于点F ，交抛物线于点G.（1）求抛物线y=-x 2+bx+c 的表达式；（2）连接GB 、EO ，当四边形GEOB 是平行四边形时，求点G 的坐标；（3）①在y 轴上存在一点H ，连接EH 、HF ，当点E 运动到什么位置时，以A 、E 、F 、H为顶点的四边形是矩形？求出此时点E 、H 的坐标；②在①的前提下，以点E 为圆心，EH 长为半径作圆，点M 为⊙E 上一动点，求AM+CM 的最小值.4．如图，二次函数2y ax bx c =++的图象关于y 轴对称且交y轴负半轴于点C ，与x 轴交于点A 、B ，已知AB=6，OC=4，⊙CP 为⊙C 上一动点．（1）求出二次函数的解析式；（2）是否存在点P ，使得△PBC 为直角三角形？若存在，求出点P 的坐标；若不存在，请说明理由；（3）连接PB ，若E 为PB 的中点，连接OE ，则OE 的最大值是多少？5．如图，在平面直角坐标系xoy 中，O 为原点，▱ABCD 的边AB 在x 轴上，点D 在y 轴上，点A 的坐标为（﹣2，0），AB=6，∠BAD=60°，点E 是BC 边上一点，CE=3EB ，⊙P 过A 、O、D三点，抛物线y=ax2+bx+c过点A、B、D三点．（1）求抛物线的解析式；（2）求证：DE是⊙P的切线；（3）若将△CDE绕点D顺时针旋转90°，点E的对应点E′会落在抛物线y=ax2+bx+c上吗？请说明理由；（4）若点M为此抛物线的顶点，平面上是否存在点N，使得以点B、D、M、N为顶点的四边形为平行四边形？若存在，请直接写出点N的坐标；若不存在，请说明理由．6．如图，O是平面直角坐标系的原点．在四边形OABC中，AB∥OC，BC⊥x轴于C，A（1，1），B（3，1），动点P从O点出发，沿x轴正方向以2个单位/秒的速度运动．设P点运动的时间为t秒（0＜t＜2）．（1）求经过O、A、B三点的抛物线的解析式；（2）过P作PD⊥OA于D，以点P为圆心，PD为半径作⊙P，⊙P在点P的右侧与x轴交于点Q．①则P点的坐标为_____，Q点的坐标为_____；（用含t的代数式表示）②试求t为何值时，⊙P与四边形OABC的两边同时相切；③设△OPD与四边形OABC重叠的面积为S，请直接写出S与t的函数解析式．7．如图①已知抛物线y=ax2﹣3ax﹣4a（a＜0）的图象与x轴交于A、B两点（A在B的左侧），与y的正半轴交于点C，连结BC，二次函数的对称轴与x轴的交点为E．（1）抛物线的对称轴与x轴的交点E坐标为_____，点A的坐标为_____；（2）若以E为圆心的圆与y轴和直线BC都相切，试求出抛物线的解析式；（3）在（2）的条件下，如图②Q（m，0）是x的正半轴上一点，过点Q作y轴的平行线，与直线BC交于点M，与抛物线交于点N，连结CN，将△CMN沿CN翻折，M的对应点为M′．在图②中探究：是否存在点Q，使得M′恰好落在y轴上？若存在，请求出Q的坐标；若不存在，请说明理由．答案详解：1．（1）；（2）外接圆的圆心为AB的中点，坐标为（，0）；（3）M（2，-3）；（4）,，（1）根据点B、C的坐标利用待定系数法即可求出抛物线的解析式；（2）令抛物线解析式中y=0得到关于x的一元二次方程，解方程求出x值，由此即可得出点A的坐标，根据两点间的距离公式即可求出AC、AB、BC，利用勾股定理得逆定理即可得出△ABC为直角三角形，由此即可得出△ABC的外接圆的圆心位置，再根据点A、B的坐标即可求出圆心坐标；（3）将直线AB往下平移得到直线l，直线l与抛物线只有一个交点M时，此时点M到直线AB的距离最远，根据点B、C的坐标利用待定系数法求出直线BC的解析式，设出直线l的解析式为y=x+m，将其代入抛物线解析式中令△=0，即可求出m值，再联立直线l和抛物线解析式成方程组，解方程组即可求出点M的坐标；（4）多种情况分类讨论：若AB线段为平行四边形的一条边；若AB线段为平行四边形的一条对角线，进而求解.解：(1)将B(4,0)、C(0,−2)代入y=a−x+c(a≠0)中，得：,解得：，∴抛物线的解析式为y=−x−2.(2)令y=−x−2中x=0,即−x−2=0，解得：=−1, =4，∴A(−1,0).∵B(4,0),C(0,−2)，∴AC=,BC=2，AB=5，∵，∴△ABC为直角三角形。

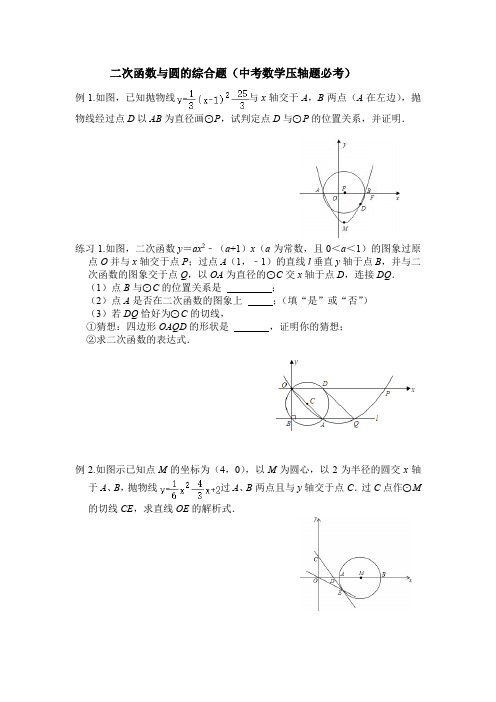
二次函数与圆的综合题（中考数学压轴题必考）例1.如图，已知抛物线与x轴交于A，B两点（A在左边），抛物线经过点D以AB为直径画⊙P，试判定点D与⊙P的位置关系，并证明．练习1.如图，二次函数y＝ax2﹣（a+1）x（a为常数，且0＜a＜1）的图象过原点O并与x轴交于点P；过点A（1，﹣1）的直线l垂直y轴于点B，并与二次函数的图象交于点Q，以OA为直径的⊙C交x轴于点D，连接DQ．（1）点B与⊙C的位置关系是；（2）点A是否在二次函数的图象上；（填“是”或“否”）（3）若DQ恰好为⊙C的切线，①猜想：四边形OAQD的形状是，证明你的猜想；②求二次函数的表达式．例2.如图示已知点M的坐标为（4，0），以M为圆心，以2为半径的圆交x轴于A、B，抛物线过A、B两点且与y轴交于点C．过C点作⊙M 的切线CE，求直线OE的解析式．练习2.平面直角坐标系中，已知A（﹣4，0），B（1，0），且以AB为直径的圆交y轴的正半轴，设平行于x轴的直线交抛物线y＝﹣x2﹣x+2于E，F两点，问：是否存在以线段EF为直径的圆，恰好与x轴相切？若存在，求出该圆的半径；若不存在，请说明理由．练习3.如图，抛物线y＝﹣x2﹣x+2与x轴交于A（﹣4，0），B（2，0），与y 轴交于点C（0，2）．以AB为直径作⊙M，直线经过点E（﹣1，﹣5），并且与⊙M相切，求该直线的解析式．练习4.如图，抛物线y＝﹣x2+x+2．经过A、B、C三点，A点坐标为（4，0），B点坐标为（﹣1，0），以AB的中点P为圆心，AB为直径作⊙P的正半轴交于点C，M为抛物线的顶点，试说明直线MC与⊙P的位置关系，并证明你的结论．练习5.如图，抛物线与x轴交于A、B两点，与y轴交于C点．以AB为直径作⊙M．（1）求出M的坐标并证明点C在⊙M上；（2）若P为抛物线上一动点，求出当CP与⊙M相切时P的坐标；练习6.在平面直角坐标系中，已知A（﹣4，0），B（1，0），且以AB为直径的圆交y轴的正半轴于点C，过点C作圆的切线交x轴于点D．（1）求点C的坐标和过A，B，C三点的抛物线的析式；（2）求点D的坐标：（3）设平行于x轴的直线交抛物线于E，F两点，问：是否存在以线段EF为直径的圆，恰好与x轴相切？若存在，求出该圆的半径，若不存在，请说明理由．练习7.如图，在平面直角坐标系中，已知OA＝n，OC＝m，⊙M与y轴相切于点C，与x轴交于A，B两点，∠ACD＝90°，抛物线y＝ax2+bx+c经过A，B，C三点．（1）求证：∠OCA＝∠OBC；（2）若A（x1，0），B（x2，0），且x1，x2满足x1+x2＝5，x1•x2＝4，求点C 的坐标和抛物线的解析式；（3）若△ACD≌△ABD，在四边形ABDC内有一点P，且点P到四边形四个顶点的距离之和P A+PB+PC+PD最小，求此时距离之和的最小值及P点的坐标（用含n的式子表示）．练习8.已知二次函数y＝mx2+（m﹣3）x﹣3（m＞0）（1）求证：它的图象与x轴必有两个交点；（2）这条抛物线与x轴交于两点A、B（A在B左），与y轴交于点C，顶点为D，sin∠ABD＝，⊙M过A、B、C三点，求⊙M的面积；（3）在（2）的条件下，抛物线上是否存在点P，使P A是⊙M的切线？若存在，求出P点的坐标，若不存在，说明理由．例3.如图，抛物线y＝ax2+bx+c（a，b，c是常数，a≠0）的对称轴为y轴，且经过（0，0）和（，）两点，点P在该抛物线上运动，以点P为圆心的⊙P总经过定点A（0，2）．（1）求a，b，c的值；（2）求证：在点P运动的过程中，⊙P始终与x轴相交；（3）设⊙P与x轴相交于M（x1，0），N（x2，0）（x1＜x2）两点，当△AMN 为等腰三角形时，求圆心P的纵坐标．练习9.已知：如图，抛物线y＝ax2+bx+1的图象关于y轴对称，且抛物线过点（2，2），点P为抛物线上的动点，以点P为圆心的⊙P与x轴相切，当点P运动对，⊙P始终经过y轴上的一个定点E．（1）求抛物线的解析式；（2）当⊙P的半径为时，⊙P与y轴交于M、N两点，求MN的长；（3）求定点E到直线y＝kx﹣8k的距离的最大值．练习10.已知：直线y＝﹣x﹣4分别交x、y轴于A、C两点，抛物线y＝ax2+bx （a＞0）经过A、O两点，且顶点B的纵坐标为﹣2（1）判断点B是否在直线AC上，并求该抛物线的函数关系式；（2）以点B关于x轴的对称点D为圆心，以OD为半径作⊙D，试判断直线AC与⊙D的位置关系，并说明理由；（3）若E为⊙D的优弧AO上一动点（不与A、O重合），连接AE、OE，问在抛物线上是否存在点P，使∠POA：∠AEO＝2：3？若存在，请求出所有满足条件的点P的坐标；若不存在，请说明理由．练习11.已知A是x轴正半轴上一个动点，以线段OA为直径作⊙B，圆心为点B，直径OA＝m，线段EF是⊙B的一条弦，EF∥x轴，点C为劣弧EF的中点，过点E作DE垂直于EF，交抛物线C1：y＝ax2+bx（a＞0）于点G，抛物线经过点O和点A．（1）求证：DG＝m；（2）拖动点A，如果抛物线C1与⊙B除点O和点A外有且只有一个交点，求b的值；（3）拖动点A，抛物线C1交⊙B于点O、E、F、A，①求证：DE＝m﹣；②直接写出FC2的值（用a，m的代数式表示）练习13.如图，在平面直角坐标系中，以点C（1，1）为圆心，2为半径作圆，交x轴于A．B两点，开口向下的抛物线经过点A，B，且其顶点P在⊙C上．（1）求∠ACB的大小；（2）写出A，B两点的坐标；（3）由圆与抛物线的对称性可知抛物线的顶点P的坐标为（1，3），求出抛物线的解析式；（4）在该抛物线上是否存在一点D点，使线段OP与CD互相平分？若存在，求出点D的坐标；若不存在，请说明理由．例4.如图1，抛物线y＝ax2+3ax（a为常数，a＜0）与x轴交于O，A两点，点B 为抛物线的顶点，点D是线段OA上的一个动点，连接BD并延长与过O，A，B三点的⊙P相交于点C，过点C作⊙P的切线交x轴于点E．（1）①求点A的坐标；②求证：CE＝DE；（2）如图2，连接AB，AC，BE，BO，当，∠CAE＝∠OBE时，①求证：AB2＝AC•BE；②求的值．练习14.如图1，已知圆O的圆心为原点，半径为2，与坐标轴交于A，C，D，E 四点，B为OD中点．（1）求过A，B，C三点的抛物线解析式；（2）如图2，连接BC，AC．点P在第一象限且为圆O上一动点，连接BP，交AC于点M，交OC于点N，当MC2＝MN•MB时，求M点的坐标；（3）如图3，若抛物线与圆O的另外两个交点分别为H，F，请判断四边形CFEH的形状，并说明理由．练习15.如图，二次函数与x轴的一个交点A的坐标为（﹣3，0），以点A为圆心作圆A，与该二次函数的图象相交于点B，C，点B，C的横坐标分别为﹣2，﹣5，连接AB，AC，并且满足AB⊥AC．过点B作BM⊥x轴于点M，过点C作CN⊥x轴于点N．（1）求该二次函数的关系式；（2）经过点B作直线BD，在A点右侧与x轴交于点D，与二次函数的图象交于点E，使得∠ADB＝∠ABM，连接AE，求证：AE＝AD；（3）若直线y＝kx+1与圆A相切，请求出k的值．例5.已知抛物线y＝ax2+bx+5（a≠0）经过A（5，0），B（6，1）两点，且与y 轴交于点C．（1）求抛物线y＝ax2+bx+5（a≠0）的函数关系式；（2）如图1，连接AC，E为线段AC上一点且横坐标为1，⊙P是△OAE外接圆，求圆心P点的坐标；（3）如图2，连接AC，E为线段AC上任意一点（不与A、C重合）经过A、E、O三点的圆交直线AB于点F；①点E在运动过程中四边形OEAF的面积是否为定值？如果是，请求出这个定值；如果不是，请说明理由；②求出当△AEF的面积取得最大值时，点E的坐标．练习16.如图1，已知抛物线y＝﹣x2+bx+c经过点A（1，0），B（﹣5，0）两点，且与y轴交于点C．（1）求b，c的值．（2）在第二象限的抛物线上，是否存在一点P，使得△PBC的面积最大？求出点P的坐标及△PBC的面积最大值．若不存在，请说明理由．（3）如图2，点E为线段BC上一个动点（不与B，C重合），经过B、E、O 三点的圆与过点B且垂直于BC的直线交于点F，当△OEF面积取得最小值时，求点E坐标．练习17.如图1，抛物线y＝+bx+c与x轴交于点A（﹣1，0），B（3，0），与y轴交于点C，顶点为D．（1）求抛物线的解析式；（2）如图2，以AB为直径在x轴上方画半圆交y轴于点E，圆心为G，P为半圆上一动点，连接DP，点Q为PD的中点．①判断点C、D与⊙G的位置关系，并说明原因；②当点P沿半圆从点B运动到点A时，求线段AQ的最小值．练习18.如图1，二次函数y＝ax2﹣3ax+b（a、b为参数，其中a＜0）的图象与x 轴交于A、B两点，与y轴交于点C，顶点为D．（1）若b＝﹣10a，求tan∠CBA的值（结果用含a的式子表示）；（2）若△ABC是等腰三角形，直线AD与y轴交于点P，且AP：DP＝2：3．求抛物线的解析式；（3）如图2，已知b＝﹣4a，E、F分别是CA和CB上的动点，且EF＝AB，若以EF为直径的圆经过点C，并交x轴于M、N两点，求MN的最大值．课后练习1.抛物线y＝ax2+bx﹣4交x轴于A（﹣2，0），B（4，0）两点，交y轴于点C，点P是介于B、C之间的抛物线上的动点（包括B、C两点），点E是△ABP 的外接圆圆心．（1）求抛物线的解析式；（2）如图1，当P为抛物线的顶点时，求圆心E的坐标；（3）如图2，作PH⊥x轴于点H，延长PH交⊙E于点Q，当P从C点出发，沿该抛物线运动到B点，求点Q在这个运动过程中的路径长．2.如图，在正方形OABC中，AB＝4，点E是线段OA（不含端点）边上一动点，作△ABE的外接圆交AC于点D．抛物线y＝ax2﹣x+c过点O，E．（1）求证：∠BDE＝90°；（2）如图1，若抛物线恰好经过点B，求此时点D的坐标；（3）如图2，AC与BE交于点F．①请问点E在运动的过程中，CF•AD是定值吗？如果是，请求出这个值，如果不是，请说明理由；②若，求点E坐标及a的值．。

【例1】.如图，点()40M ，，以点M 为圆心、2为半径的圆与x 轴交于点A B ，．已知抛物216y x bx c =++过点A 和B ，与y 轴交于点C ．⑴ 求点C 的坐标，并画出抛物线的大致图象．⑵ 点()8Q m ，在抛物线216y x bx c =++上，点P 为此抛物线对称轴上一个动点，求PQ PB + 最小值． ⑶ CE 是过点C 的M ⊙的切线，点E 是切点，求OE 所在直线的解析式．【巩固】已知抛物线2y ax bx c =++与y 轴的交点为C ，顶点为M ，直线CM 的解析式2y x =-+并且线段CM 的长为（1）求抛物线的解析式。

（2）设抛物线与x 轴有两个交点A （X 1 ，0）、B （X 2 ，0），且点A 在B 的左侧，求线段AB 的长。

（3）若以AB 为直径作⊙N ，请你判断直线CM 与⊙N 的位置关系，并说明理由。

【例2】如图，在平面直角坐标系中，以点(04)C ，为圆心，半径为4的圆交y 轴正半轴于点A ，AB 是C ⊙的切线．动点P 从点A 开始沿AB 方向以每秒1个单位长度的速度运动，点Q 从O 点开始沿x 轴正方向以每秒4个单位长度的速度运动，且动点P 、Q 从点A 和点O 同时出发，设运动时间为t (秒)．⑴当1t =时，得到1P 、1Q 两点，求经过A 、1P 、1Q 三点的抛物线解析式及对称轴l ；⑵当t 为何值时，直线PQ 与C ⊙相切？并写出此时点P 和点Q 的坐标；⑶在⑵的条件下，抛物线对称轴l 上存在一点N ，使NP NQ +最小，求出点N 的坐标并说明理由．提示：（1）先求出t=1时，AP 和OQ 的长，即可求得P 1，Q 1的坐标，然后用待定系数法即可得出抛物线的解析式．进而可求出对称轴l 的解析式．（2）当直线PQ 与圆C 相切时，连接CP ，CQ 则有Rt △CMP ∽Rt △QMC （M 为PG 与圆的切点），因此可设当t=a 秒时，PQ 与圆相切，然后用a 表示出AP ，OQ 的长即PM ，QM 的长（切线长定理）．由此可求出a 的值．（3）本题的关键是确定N 的位置，先找出与P 点关于直线l 对称的点P ′的坐标，连接P ′Q ，那么P ′Q 与直线l 的交点即为所求的N 点，可先求出直线P ′Q 的解析式，进而可求出N 点的坐标．【巩固】已知二次函数图象的顶点在原点O ，对称轴为y 轴．一次函数1y kx =+的图象与 二次函数的图象交于A B ，两点(A 在B 的左侧)，且A 点坐标为()44-，．平行于x 轴的直线l 过()01-，点．⑴ 求一次函数与二次函数的解析式；⑵ 判断以线段AB 为直径的圆与直线l 的位置关系，并给出证明；⑶ 把二次函数的图象向右平移2个单位，再向下平移t 个单位()0t >，二次函数的图象与x轴交于M N，，三点的圆的，两点，一次函数图象交y轴于F点．当t为何值时，过F M N面积最小？最小面积是多少？【例3】如图1,⊙O的半径为1，正方形ABCD顶点B坐标为()，，顶点D在⊙O上运动．50⑴当点D运动到与点A、O在同一条直线上时，试证明直线CD与⊙O相切；⑵当直线CD与⊙O相切时，求OD所在直线对应的函数关系式；⑶设点D的横坐标为x，正方形ABCD的面积为S，求S与x之间的函数关系式，并求出S 的最大值与最小值．【巩固】如图，已知点A 从()10，出发，以1个单位长度/秒的速度沿x 轴向正方向运动，以O A ，为顶点作菱形OABC ，使点B C ，在第一象限，且60AOC ∠=︒；以()03P ，为圆心，PC 为半径作圆．设点A 运动了t 秒，求： ⑴ 点C 的坐标（用含t 的代数式表示）；⑵ 当点A 在运动过程中，所有使P 与菱形OABC 的边所在直线相切的t 的值．【例4】已知：如图，抛物线213y x m =+与x 轴交于A B ，两点，与y 轴交于C 点，90ACB ∠=︒⑴ 求m 的值及抛物线顶点坐标；⑵ 过A B C ，，的三点的M ⊙交y 轴于另一点D ，连结DM 并延长交M ⊙于点E ，过E 点的M ⊙的切线分别交x 轴、y 轴于点F G ，，求直线FG 的解析式；⑶ 在条件⑵下，设P 为CBD 上的动点(P 不与C D ，重合)，连结PA 交y 轴于点H ，问是否存在一个常数k ，始终满足AH AP k ⋅=，如果存在，请写出求解过程；如果不存在，请说明理由．【巩固】如图，已知点A的坐标是()，，以AB为直径作O'，90-，，点B的坐标是()10交y轴的负半轴于点C，连接AC、BC，过A、B、C三点作抛物线．⑴求抛物线的解析式；⑵点E是AC延长线上一点，BCE∠的平分线CD交O'于点D，连结BD，求直线BD的解析式；⑶在⑵的条件下，抛物线上是否存在点P，使得PDB CBD∠=∠？如果存在，请求出点P的坐标；如果不存在，请说明理由．DCEA yxBO O'课后作业：1.如图，直角坐标系中，已知两点()A，，点B在第一象限且OAB2000O，，()∆为正三角形，OAB∆的外接圆交y轴的正半轴于点C，过点C的圆的切线交x轴于点D．⑴求B C，两点的坐标；⑵求直线CD的函数解析式；⑶设E F，分别是线段AB AD，上的两个动点，且EF平分四边形ABCD的周长．试探究：AEF∆的最大面积？参考答案例1【巩固】例2分析：（1）先求出t=1时，AP和OQ的长，即可求得P1，Q1的坐标，然后用待定系数法即可得出抛物线的解析式．进而可求出对称轴l的解析式．（2）当直线PQ与圆C相切时，连接CP，CQ则有Rt△CMP∽Rt△QMC（M为PG与圆的切点），因此可设当t=a秒时，PQ与圆相切，然后用a表示出AP，OQ的长即PM，QM的长（切线长定理）．由此可求出a的值．（3）本题的关键是确定N的位置，先找出与P点关于直线l对称的点P′的坐标，连接P′Q，那么P′Q与直线l的交点即为所求的N点，可先求出直线P′Q的解析式，进而可求出N点的坐标．【巩固】例3【巩固】例4【巩固】作业。

2019全国各地中考数学压轴大题函数综合八、二次函数含参数分类讨论综合问题1.（2019•宁波）如图，已知二次函数y＝x2+ax+3的图象经过点P（﹣2，3）．（1）求a的值和图象的顶点坐标．（2）点Q（m，n）在该二次函数图象上．①当m＝2时，求n的值；②若点Q到y轴的距离小于2，请根据图象直接写出n的取值范围．解：（1）把点P（﹣2，3）代入y＝x2+ax+3中，∴a＝2，∴y＝x2+2x+3，∴顶点坐标为（﹣1，2）；（2）①当m＝2时，n＝11，②点Q到y轴的距离小于2，∴|m|＜2，∴﹣2＜m＜2，∴2≤n＜11；2.（2019•杭州）设二次函数y＝（x﹣x1）（x﹣x2）（x1，x2是实数）．（1）甲求得当x＝0时，y＝0；当x＝1时，y＝0；乙求得当x＝时，y＝﹣．若甲求得的结果都正确，你认为乙求得的结果正确吗？说明理由．（2）写出二次函数图象的对称轴，并求该函数的最小值（用含x1，x2的代数式表示）．（3）已知二次函数的图象经过（0，m）和（1，n）两点（m，n是实数），当0＜x1＜x2＜1时，求证：0＜mn＜．解：（1）当x＝0时，y＝0；当x＝1时，y＝0；∴二次函数经过点（0，0），（1，0），∴x1＝0，x2＝1，∴y═x（x﹣1）＝x2﹣x，当x＝时，y＝﹣，∴乙说点的不对；（2）对称轴为x＝，当x＝时，y＝﹣是函数的最小值；（3）二次函数的图象经过（0，m）和（1，n）两点，∴m＝x1x2，n＝1﹣x1﹣x2+x1x2，∴mn＝[﹣][﹣]∵0＜x1＜x2＜1，∴0≤﹣≤，0≤﹣≤，∴0＜mn＜．3.（2019•温州）如图，在平面直角坐标系中，二次函数y＝﹣x2+2x+6的图象交x轴于点A，B（点A在点B的左侧）（1）求点A，B的坐标，并根据该函数图象写出y≥0时x的取值范围．（2）把点B向上平移m个单位得点B1．若点B1向左平移n个单位，将与该二次函数图象上的点B2重合；若点B1向左平移（n+6）个单位，将与该二次函数图象上的点B3重合．已知m＞0，n＞0，求m，n 的值．解：（1）令y＝0，则﹣，解得，x1＝﹣2，x2＝6，∴A（﹣2，0），B（6，0），由函数图象得，当y≥0时，﹣2≤x≤6；（2）由题意得，B1（6，m），B2（6﹣n，m），B3（﹣n，m），函数图象的对称轴为直线，∵点B2，B3在二次函数图象上且纵坐标相同，∴，∴n＝1，∴，∴m，n的值分别为，1．4.（2019•台州）已知函数y＝x2+bx+c（b，c为常数）的图象经过点（﹣2，4）．（1）求b，c满足的关系式；（2）设该函数图象的顶点坐标是（m，n），当b的值变化时，求n关于m的函数解析式；（3）若该函数的图象不经过第三象限，当﹣5≤x≤1时，函数的最大值与最小值之差为16，求b的值．解：（1）将点（﹣2，4）代入y＝x2+bx+c，得﹣2b+c＝0，∴c＝2b；（2）m＝﹣，n＝，∴n＝，∴n＝2b﹣m2，（3）y＝x2+bx+2b＝（x+）2﹣+2b，对称轴x＝﹣，当b≤0时，c≤0，函数不经过第三象限，则c＝0；此时y＝x2，当﹣5≤x≤1时，函数最小值是0，最大值是25，∴最大值与最小值之差为25；（舍去）当b＞0时，c＞0，函数不经过第三象限，则△≤0，∴0≤b≤8，∴﹣4≤x＝﹣≤0，当﹣5≤x≤1时，函数有最小值﹣+2b，当﹣5≤﹣＜﹣2时，函数有最大值1+3b，当﹣2＜﹣≤1时，函数有最大值25﹣3b；函数的最大值与最小值之差为16，当最大值1+3b时，1+3b+﹣2b＝16，∴b＝6或b＝﹣10，∵4≤b≤8，∴b＝6；当最大值25﹣3b时，25﹣3b+﹣2b＝16，∴b＝2或b＝18，∵2≤b≤4，∴b＝2；综上所述b＝2或b＝6；5.（2019•天门）在平面直角坐标系中，已知抛物线C：y＝ax2+2x﹣1（a≠0）和直线l：y＝kx+b，点A（﹣3，﹣3），B（1，﹣1）均在直线l上．（1）若抛物线C与直线l有交点，求a的取值范围；（2）当a＝﹣1，二次函数y＝ax2+2x﹣1的自变量x满足m≤x≤m+2时，函数y的最大值为﹣4，求m的值；（3）若抛物线C与线段AB有两个不同的交点，请直接写出a的取值范围．解：（1）点A（﹣3，﹣3），B（1，﹣1）代入y＝kx+b，∴，∴，∴y＝x﹣；联立y＝ax2+2x﹣1与y＝x﹣，则有2ax2+3x+1＝0，∵抛物线C与直线l有交点，∴△＝9﹣8a≥0，∴a≤且a≠0；（2）根据题意可得，y＝﹣x2+2x﹣1，∵a＜0，∴抛物线开口向下，对称轴x＝1，∵m≤x≤m+2时，y有最大值﹣4，∴当y＝﹣4时，有﹣x2+2x﹣1＝﹣4，∴x＝﹣1或x＝3，①在x＝1左侧，y随x的增大而增大，∴x＝m+2＝﹣1时，y有最大值﹣4，∴m＝﹣3；②在对称轴x＝1右侧，y随x最大而减小，∴x＝m＝3时，y有最大值﹣4；综上所述：m＝﹣3或m＝3；（3）①a＜0时，x＝1时，y≤﹣1，即a≤﹣2；②a＞0时，x＝﹣3时，y≥﹣3，即a≥，直线AB的解析式为y＝x﹣，抛物线与直线联立：ax2+2x﹣1＝x﹣，∴ax2+x+＝0，△＝﹣2a＞0，∴a＜，∴a的取值范围为≤a＜或a≤﹣2；6.（2019•大连）把函数C1：y＝ax2﹣2ax﹣3a（a≠0）的图象绕点P（m，0）旋转180°，得到新函数C2的图象，我们称C2是C1关于点P的相关函数．C2的图象的对称轴与x轴交点坐标为（t，0）．（1）填空：t的值为2m﹣1（用含m的代数式表示）（2）若a＝﹣1，当≤x≤t时，函数C1的最大值为y1，最小值为y2，且y1﹣y2＝1，求C2的解析式；（3）当m＝0时，C2的图象与x轴相交于A，B两点（点A在点B的右侧）．与y轴相交于点D．把线段AD原点O逆时针旋转90°，得到它的对应线段A′D′，若线A′D′与C2的图象有公共点，结合函数图象，求a的取值范围．解：（1）C1：y＝ax2﹣2ax﹣3a＝a（x﹣1）2﹣4a，顶点（1，﹣4a）围绕点P（m，0）旋转180°的对称点为（2m﹣1，4a），C2：y＝﹣a（x﹣2m+1）2+4a，函数的对称轴为：x＝2m﹣1，t＝2m﹣1，故答案为：2m﹣1；（2）a＝﹣1时，C1：y＝﹣（x﹣1）2+4，①当t＜1时，x＝时，有最小值y2＝，x＝t时，有最大值y1＝﹣（t﹣1）2+4，则y1﹣y2＝﹣（t﹣1）2+4﹣＝1，无解；②1≤t时，x＝1时，有最大值y1＝4，x＝时，有最小值y2＝﹣（t﹣1）2+4，y1﹣y2＝≠1（舍去）；③当t时，x＝1时，有最大值y1＝4，x＝t时，有最小值y2＝﹣（t﹣1）2+4，y1﹣y2＝（t﹣1）2＝1，解得：t＝0或2（舍去0），故C2：y＝（x﹣2）2﹣4＝x2﹣4x；（3）m＝0，C2：y＝﹣a（x+1）2+4a，点A、B、D、A′、D′的坐标分别为（1，0）、（﹣3，0）、（0，3a）、（0，1）、（﹣3a，0），当a＞0时，a越大，则OD越大，则点D′越靠左，当C2过点A′时，y＝﹣a（0+1）2+4a＝1，解得：a＝，当C2过点D′时，同理可得：a＝1，故：0＜a或a≥1；当a＜0时，当C2过点D′时，﹣3a＝1，解得：a＝﹣，故：a≤﹣；综上，故：0＜a或a≥1或a≤﹣．7.（2019•贵阳）如图，二次函数y＝x2+bx+c的图象与x轴交于A，B两点，与y轴交于点C，且关于直线x＝1对称，点A的坐标为（﹣1，0）．（1）求二次函数的表达式；（2）连接BC，若点P在y轴上时，BP和BC的夹角为15°，求线段CP的长度；（3）当a≤x≤a+1时，二次函数y＝x2+bx+c的最小值为2a，求a的值．解：（1）∵点A（﹣1，0）与点B关于直线x＝1对称，∴点B的坐标为（3，0），代入y＝x2+bx+c，得：，解得，所以二次函数的表达式为y＝x2﹣2x﹣3；（2）如图所示：由抛物线解析式知C（0，﹣3），则OB＝OC＝3，∴∠OBC＝45°，若点P在点C上方，则∠OBP＝∠OBC﹣∠PBC＝30°，∴OP＝OB tan∠OBP＝3，∴CP＝3；若点P在点C下方，则∠OBP′＝∠OBC+∠P′BC＝60°，∴OP′＝OB tan∠OBP′＝33，∴CP＝33；综上，CP的长为3或33；（3）若a+1＜1，即a＜0，则函数的最小值为（a+1）2﹣2（a+1）﹣3＝2a，解得a＝1（正值舍去）；若a＜1＜a+1，即0＜a＜1，则函数的最小值为1﹣2﹣3＝2a，解得：a＝﹣2（舍去）；若a＞1，则函数的最小值为a2﹣2a﹣3＝2a，解得a＝2（负值舍去）；综上，a的值为1或2．8.（2019•天津）已知抛物线y＝x2﹣bx+c（b，c为常数，b＞0）经过点A（﹣1，0），点M（m，0）是x轴正半轴上的动点．（Ⅰ）当b＝2时，求抛物线的顶点坐标；（Ⅱ）点D（b，y D）在抛物线上，当AM＝AD，m＝5时，求b的值；（Ⅲ）点Q（b+，y Q）在抛物线上，当AM+2QM的最小值为时，求b的值．解：（Ⅰ）∵抛物线y＝x2﹣bx+c经过点A（﹣1，0），∴1+b+c＝0，即c＝﹣b﹣1，当b＝2时，y＝x2﹣2x﹣3＝（x﹣1）2﹣4，∴抛物线的顶点坐标为（1，﹣4）；（Ⅱ）由（Ⅰ）知，抛物线的解析式为y＝x2﹣bx﹣b﹣1，∵点D（b，y D）在抛物线y＝x2﹣bx﹣b﹣1上，∴y D＝b2﹣b•b﹣b﹣1＝﹣b﹣1，由b＞0，得b＞＞0，﹣b﹣1＜0，∴点D（b，﹣b﹣1）在第四象限，且在抛物线对称轴x＝的右侧，如图1，过点D作DE⊥x轴，垂足为E，则点E（b，0），∴AE＝b+1，DE＝b+1，得AE＝DE，∴在Rt△ADE中，∠ADE＝∠DAE＝45°，∴AD＝AE，由已知AM＝AD，m＝5，∴5﹣（﹣1）＝（b+1），∴b＝3﹣1；（Ⅲ）∵点Q（b+，y Q）在抛物线y＝x2﹣bx﹣b﹣1上，∴y Q＝（b+）2﹣b（b+）﹣b﹣1＝﹣﹣，可知点Q（b+，﹣﹣）在第四象限，且在直线x＝b的右侧，∵AM+2QM＝2（AM+QM），∴可取点N（0，1），如图2，过点Q作直线AN的垂线，垂足为G，QG与x轴相交于点M，由∠GAM＝45°，得AM＝GM，则此时点M满足题意，过点Q作QH⊥x轴于点H，则点H（b+，0），在Rt△MQH中，可知∠QMH＝∠MQH＝45°，∴QH＝MH，QM＝MH，∵点M（m，0），∴0﹣（﹣﹣）＝（b+）﹣m，解得，m＝﹣，∵AM+2QM ＝，∴[（﹣）﹣（﹣1）]+2[（b +）﹣（﹣）]＝，∴b＝4．。

中考数学压轴题二次函数与圆二次函数与圆是中考数学中的一个重要知识点。

在考试中，通常会涉及到用二次函数的性质来解决与圆相关的问题。

下面我们就来详细介绍一下二次函数与圆的关系。

首先，我们先来回顾一下二次函数的基本知识。

二次函数的一般形式可以表示为y=ax²+bx+c，其中a、b、c是常数。

二次函数的图象是一个抛物线，具体的形状和位置取决于a、b、c的值。

在二次函数的图象上，有一些特殊点和特殊线。

特殊点包括顶点和零点，特殊线包括对称轴和切线。

顶点是抛物线的最高点或者最低点，对称轴是通过抛物线顶点的一条直线，切线是与抛物线相切的直线。

圆是一个平面上到一点距离固定的点的距离相等的所有点的轨迹。

圆的特点包括半径、直径、圆心、弧、弦和切线等。

圆心是圆上的任意一点，半径是圆心到圆上任意一点的距离，直径是通过圆心的一条线段，弧是圆上两个点之间的弯曲部分，弦是圆上任意两点之间的线段，切线是与圆只有一个交点的直线。

接下来，我们将通过一些例题来探究二次函数与圆的关系。

例题1：已知二次函数y=2x²-4x+3，求与y轴相切的圆方程。

解析：对于与y轴相切的圆，我们可以首先求出二次函数的切线，然后通过切线的斜率和截距求出圆心和半径。

首先，我们知道切线的斜率等于二次函数在切点处的导数。

求导得到y'=4x-4、接下来，我们利用二次函数和切线的性质，将二次函数和切线联立求解。

因为切线与y轴相切，所以切线在y轴上的截距为0。

代入切线方程，得到0=4x-4，解得x=1然后，我们将x=1带入二次函数的表达式中，得到y=2x²-4x+3=2*1²-4*1+3=1、所以切点坐标为(1,1)。

接着，我们通过圆心、半径、切点来确定圆的方程。

圆心的横坐标等于切点的横坐标，圆心的纵坐标等于切点的纵坐标加上半径。

因为切线与y轴相切，所以切线在y轴上的截距为半径。

所以圆心的坐标为(1,1+1)=(1,2)。

2019 初三数学中考专题复习二次函数和圆专题综合检测1. 以下关系式中，属于二次函数的是(x 为自变量 )()1 221 4 4A.y ＝8x＝－x －＝x2＝a x22 1 22. 抛物线 y＝2x ，y＝－ 2x ，y＝2x 的共同性质是 ( )A. 张口向上B.对称轴是y轴C.都有最高点随x的增大而增大3.若二次函数 y＝(x －m)2－1，当 x≤1时， y 随 x 的增大而减小，则 m的取值范围是 ( )＝＞1≥1≤14.如图， AB是⊙ O的直径 . 若∠ BAC＝35°，那么∠ ADC＝( )°°°°5.在同圆中，以下四个命题：①圆心角是极点在圆心的角；②两个圆心角相等，它们所对的弦也相等；③两条弦相等，它们所对的弧也相等；④等弧所对的圆心角相等 . 此中真命题有 ()A.4 个个个个6.如图，CD是⊙ O的直径，弦 AB⊥CD于 E，连结 BC、BD.以下结论错误的选项是( )＝BE B.C.OE ＝DE D. . ∠DBC＝90°7.如图， AD、AE、CB均为⊙ O的切线， D、E、F 分别是切点， AD＝8，则△ ABC的周长为 ()8. 假如二次函数y＝ax2＋bx＋c 的图象以下图，那么一次函数y＝bx＋c 和反比b例函数 y＝x在同一坐标系中的图象大概是( )9.如图，圆形薄铁片与直角三角尺、直尺紧靠在一同平放在桌面上 . 已知铁片的圆心为O，三角尺的直角极点 C 落在直尺的 10cm处，铁片与直尺的独一公共点 A 落在直尺的14cm处，铁片与三角尺的独一公共点为 B. 以下说法错误的选项是 ( )A. 圆形铁片的半径是 4cmB. 四边形 AOBC为正方形C. 弧 AB的长度为 4πcmD.扇形 OAB的面积是4πcm210.已知二次函数 y＝ax2＋bx＋c(a ≠0) 的图象以下图，而且对于 x 的一元二次方程ax2＋bx＋c－m＝0 有两个不相等的实数根，以下结论：①b2－4ac＜0；②abc＞0；③a－b＋c＜0；④ m＞－ 2，此中正确的个数有 ( )11. 如图，扇形 OAB的圆心角为 120°，半径为 3，则该扇形的弧长为( 结果保留π).2112. 已知抛物线 y＝x － 4x 上有两点 P1(3 ，y1) 、P2( －2，y2) ，则 y1与 y2的大小关系为： y1y2( 填“＞”“＜”或“＝”).13.如图，⊙ I 是△ ABC的内切圆， D、E、F 为三个切点，若∠ DEF＝52°，则∠ A 的度数为.14.某软件商铺销售一种益智游戏软件，假如以每盘 50 元的售价销售，一个月能售出 500 盘，依据市场剖析，若销售单价每涨价 1 元，月销售量就减少10 盘，当每盘的售价涨x 元 (x取整数)时，该商铺月销售额y( 元) 与 x 的函数关系式为，自变量 x 的取值范围是.15.设 A、B、C三点挨次分别是抛物线 y＝x2－2x－ 5 与 y 轴的交点以及与 x 轴的两个交点，则△ ABC的面积是.16.已知二次函数 y＝－ x2＋2x＋m的部分图象以下图，则对于 x 的一元二次方程－ x2＋2x＋m＝0 的解为.25117.已知抛物线 y＝2x ＋x－2.(1)用配方法求出它的极点坐标和对称轴；(2)若抛物线与 x 轴的两个交点为 A、B，求线段 AB的长 .18.如， AB是半 O的直径， C、D是半 O上的两点，且 OD∥BC，OD与 AC交于点E.(1)若∠ B＝70°，求∠ CAD的度数；(2)若 AB＝4，AC＝3，求 DE的 .19.已知二次函数 y＝ax2＋bx＋c 中，函数 y 与自量 x 的部分以下表：x⋯－101234⋯y⋯1052125⋯(1)求二次函数的关系式；(2)当 x 何， y 有最小，最小是多少？(3) 若 A(m，y1) 、B(m＋1，y2) 两点都在函数的象上，比y1与 y2的大小 .420.如图，已知 AB是⊙ O的直径，点 C、D在⊙ O上，∠ D＝60°且 AB＝6，过 O 点作 OE⊥AC，垂足为 E.(1) 求 OE的长；(2) 若 OE的延伸线交⊙ O于点 F，求弦 AF、AC和围成的图形(暗影部分)的面积.21.某企业经销一种绿茶，每千克成本为 50 元，市场检查发现，在一段时间内，销售量 w(千克 ) 随销售单价 x( 元/ 千克 ) 的变化而变化，详细关系为 w＝－ 2x＋240，且物价部门规定这类绿茶的销售单价不得高于90 元/ 千克 . 设这类绿茶在这段时间内的销售收益为y( 元) ，解答以下问题：(1)求 y 与 x 的函数关系式；(2)当 x 取何值时， y 的值最大？(3)假如企业想要在这段时间内获取 2250 元的销售收益，销售单价应定为多少元？22.如图，已知⊙ O是△ ABC的外接圆， AD是⊙ O的直径，且 BD＝BC，延伸 AD到 E，且有∠ EBD＝∠ CAB.(1)求证： BE是⊙ O的切线；(2)若 BC＝ 3，AC＝5，求圆的直径 AD及切线 BE的长 .23.如图，已知抛物线y＝ax2＋bx＋c(a≠0)经过A(－3,0)、B(5,0)、C(0,5)三点，O为坐标原点 .(1)求此抛物线的分析式；13(2)若把抛物线 y＝ax2＋bx＋c(a ≠0) 向下平移3个单位长度，再向右平移 n(n ＞0) 个单位长度获取新抛物线，若新抛物线的极点M在△ABC内，求 n 的取值范围；(3)设点 P 在 y 轴上，且知足∠ OPA＋∠ OCA＝∠ CBA，求 CP的长 .参照答案：1—10 ABCBB CCACB12.＜13.76 °14.y＝－ 10x2＋250000 ≤x≤50 且 x 为整数15.5616.x1＝－1，x2＝31217.解： (1)y ＝2(x ＋ 1)－3，它的极点坐标为 ( －1，－ 3)，对称轴为 x＝－ 1；1(2)令 y＝0，∴2(x ＋1) 2－3＝0，∴x1＝－ 1＋ 6，x2＝－ 1－ 6，∴ AB＝| －1＋ 6 －( －1－ 6)| ＝2 6.18.解：(1) ∵OD∥BC，∴∠ DOA＝∠ B＝70°，又∵ OA＝OD，∴∠ DAO＝∠ ADO＝55°，∵AB是直径，∴∠ ACB＝90°，∴∠ CAB＝20°，∴∠ CAD＝35°；BC77 (2) 在 Rt△ACB中，BC＝7，O是 AB中点，OD∥BC，∴OE＝2＝2，∴DE＝2－2 .19.解： (1) 依题意设 y＝a(x －2) 2＋1，把 (3,2) 代入得 a＝1，∴ y＝(x －2) 2＋1；(2)当 x＝2 时， y 有最小值，最小值为 1；(3)当 m≥2时， y2≥y1，当 m＜1 时， y1＞y2.20. 解：(1) 连结 OC，∵∠D和∠ AOC分别是所对的圆周角和圆心角，∠D＝60°，1∴∠ AOC＝2∠D＝120°，∵ OE⊥AC，∴∠ AOE＝∠ COE＝2∠AOC＝60°，∠OAE＝1330°. ∵AB 是⊙O的直径， AB＝6，∴ OA＝3，∴ OE＝2OA＝2；1(2) ∵OE ＝2OA，∴EF ＝ OE.∵OE⊥AC ，∴∠ AEF ＝∠CEO＝ 90°， AE ＝2CE.∴△ AEF≌△ CEO∴S.＝S＝60· π·3 3暗影＝π.扇形 COF36028与x 的关系式为： y＝－ 2x2＋340x－12000；(2)y ＝－ 2x2＋340x－12000＝－ 2(x －85) 2＋2450，∴当 x＝85 时， y 的值最大；(3) 当 y＝2250 时，可得方程－ 2(x －85) 2＋2450＝2250. 解这个方程，得x1＝ 75，x2＝95，依据题意， x2＝95 不合题意，应舍去 . ∴当销售单价为75 元/ 千克时，可获取销售收益2250 元.22.解：(1) 如图，连结 OB，∵BD＝ BC，∴∠ CAB＝∠ BAD，∵∠ EBD＝∠ CAB，∴∠ BAD ＝∠EBD，∵AD是⊙O的直径，∴∠ABD＝90°，OA＝BO，∴∠BAD＝∠ABO，∴∠EBD ＝∠ABO，∴∠OBE＝∠EBD＋∠OBD＝∠ABD＋∠OBD＝∠ABD＝90°，∵点 B 在⊙O上，∴ BE是⊙O的切线；(2)设圆的半径为 R，连结 CD，∵ AD为⊙O 的直径，∴∠ ACD＝90°，∵ BC＝ BD，15∴OB⊥CD，∴ OB∥AC，∵ OA＝ OD，∴ OF＝2AC＝2，∵四边形 ACBD是圆内接四边形，∴∠ BDE＝∠ ACB，∵∠ DBE＝∠ CAB，∴△ DBE∽△ CAB，∴3DE3＝，∴DE＝，∵∠ OBE 53552R3，∵R＞0，∴R＝ 3，∵BE是⊙O的切线，∴BE ＝∠ OFD＝90°，∴DF∥BE，∴R＝R＋533311＝DE×AE＝5×2×3＋5＝5.23. 解： (1) 把 A、B、C三点的坐标代入函数分析式可得，抛物线分析式为y＝－1 223x ＋3x＋5；16(2) ∵抛物线极点坐标为(1 ，3 ) ，新抛物线的极点M 坐标为 (1 ＋n,1) ，设直线 BC95k＋m＝0，解得k＝－ 1分析式为 y＝kx＋m，把 B、C 两点坐标代入可得，m＝5m＝5∴直线 BC的分析式为 y＝－ x＋5，令 y＝1，代入可得 1＝－ x＋5，解得 x＝4，∵新抛物线的极点 M在△ ABC内，∴ 1＋ n＜4，且 n＞0，解得 0＜n＜3，即 n 的取值范围为 0＜n＜3；(3)当点 P 在 y 轴负半轴上时，如图 1，过 P作 PD⊥AC，交 AC的延伸线于点 D，由题意可知 OB＝OC＝5，∴∠ CBA＝45°，∴∠ PAD＝∠ OPA＋∠ OCA＝∠ CBA＝45°，∴AD＝ PD，在 Rt△OAC中，OA＝3，OC＝5，可求得 AC＝34，设 PD＝AD＝m，则 CDCO AO ＝ AC＋AD＝34＋m，∵∠ ACO＝∠ PCD，∠COA＝∠ PDC，∴△ COA∽△ CDP，∴＝CD PD3＝AC533453334，∴33434，即＝＝PC，由＝可求得 m＝22＝PC，解得PC34＋m m34＋m mPC＝17；可求得 PO＝PC－OC＝17－5＝12，如图 2，在 y 轴正半轴上截取OP′＝ OP ＝12，连结 AP′，则∠ OP′A＝∠ OPA，∴∠ OP′A＋∠ OCA＝∠ OPA＋∠ OCA＝∠ CBA，∴P′也知足题目条件，此时 P′C＝OP′－ OC＝12－5＝7，综上可知 PC 的长为 7或17.10。

二次函数与圆的综合压轴题
一、题目描述
本题是一道综合性的数学题，涉及到二次函数和圆的相关知识。

具体要求如下：
给定一个二次函数 $y=ax^2+bx+c$ 和一个圆 $x^2+y^2=r^2$，其中 $a,b,c,r$ 均为已知常数，且 $a\neq0$。

请编写一个函数，判断该二次函数与圆是否有交点，并输出交点的坐标。

二、解题思路
1. 二次函数与圆的关系
首先，我们需要了解二次函数和圆之间的关系。

对于一个二次函数$y=ax^2+bx+c$ 和一个圆 $x^2+y^2=r^2$，它们之间可能存在以下三种情况：
（1）没有交点：当二次函数和圆分离时，它们没有交点。

（2）相切：当二次函数和圆相切时，它们只有一个交点。

（3）相交：当二次函数和圆相交时，它们有两个交点。

接下来，我们需要确定如何求出这些交点的坐标。

2. 求解交点坐标
对于一条直线和一个圆之间的交点坐标可以通过联立直线方程和圆方程求解。

但是对于一个二次函数而言，并不存在明确的直线方程。

因此，在本题中，我们可以通过以下步骤求解交点坐标：
（1）将二次函数和圆的方程联立，得到一个关于 $x$ 的二次方程。

（2）解出该二次方程的根，即为交点的横坐标。

（3）将横坐标代入二次函数或圆的方程中，求出相应的纵坐标。

最后，我们需要根据交点个数输出不同的结果。

如果没有交点，则输出“无交点”；如果有一个交点，则输出该交点坐标；如果有两个交点，则输出两个交点坐标。

三、代码实现
下面是本题的完整代码实现：。

备考2024中考二轮数学《高频考点冲刺》（全国通用）专题10 二次函数问题考点扫描☆聚焦中考二次函数问题是中考的重点内容，近几年各地中考题目主要以选择题与解答题的形式考查，也可能在填空题中出现，题目难度中高档；考查内容主要有：二次函数的性质与图象；用待定系数法确定函数解析式；二次函数的最值与平移问题；与方程、不等式、几何知识结合的综合题等；考查热点主要有：二次函数的性质与图象；通过具体问题情境学会用三种方式表示二次函数关系；通过在实际问题中应用二次函数的性质，发展应用二次函数解决实际问题的能力。

考点剖析☆典型例题（2022•株洲）已知二次函数y＝ax2+bx﹣c（a≠0），其中b＞0、c＞0，则该函数的图象可能为（）A．B．C．D．【答案】C【点拨】根据c＞0，可知﹣c＜0，可排除A，D选项，当a＞0时，可知对称轴＜0，可排除B选项，当a＜0时，可知对称轴＞0，可知C选项符合题意．【解析】解：∵c＞0，∴﹣c＜0，故A，D选项不符合题意；当a＞0时，∵b＞0，∴对称轴x＝＜0，故B选项不符合题意；当a＜0时，b＞0，故C选项符合题意，故选：C．【点睛】本题考查了二次函数的图象，熟练掌握二次函数的图象与系数的关系是解题的关键．2023•兰州）已知二次函数y＝﹣3（x﹣2）2﹣3，下列说法正确的是（）A．对称轴为直线x＝﹣2B．顶点坐标为（2，3）C．函数的最大值是﹣3D．函数的最小值是﹣3【答案】C【点拨】利用二次函数的性质进行判断即可．【解析】解：二次函数y＝﹣3（x﹣2）2﹣3的图象的开口向下，对称轴为直线x＝2，顶点坐标为（2，﹣3），x＝2时，y有最大值为y＝﹣3，故选：C．【点睛】本题考查二次函数的最值问题，解题关键是掌握二次函数的性质．2023•达州）如图，抛物线y＝ax2+bx+c（a，b，c为常数）关于直线x＝1对称．下列五个结论：①abc＞0；②2a+b＝0；③4a+2b+c＞0；④am2+bm＞a+b；⑤3a+c＞0．其中正确的有（）A．4个B．3个C．2个D．1个【答案】B【点拨】由抛物线开口方向以及与y轴的交点可知a＞0，c＜0，根据对称轴为直线x＝1得出b＝﹣2a＜0，即可判断①；由对称轴为直线x＝1得出2a+b＝0，即可判断②；由抛物线的对称性即可判断③；根据函数的最值即可判断④，由x＝﹣1时，y＞0，得出a﹣b+c＞0，由b＝﹣2a得出3a+c ＞0即可判断⑤．【解析】解：∵抛物线y＝ax2+bx+c（a，b，c为常数）关于直线x＝1对称，∴﹣＝1，∵a＞0，∴b＝﹣2a＜0，∵c＜0，∵b＝﹣2a，∴2a+b＝0，故②正确；∵x＝0时，y＜0，对称轴为直线x＝1，∴x＝2时，y＜0，∴4a+2b+c＜0，故③错误；∵抛物线开口向上，对称轴为直线x＝1，∴am2+bm+c≥a+b+c，即am2+bm≥a+b，故④错误；∵x＝﹣1时，y＞0，∴a﹣b+c＞0，∵b＝﹣2a，∴3a+c＞0．故⑤正确．故选：B．【点睛】本题考查二次函数图象与系数的关系，二次函数图象上点的坐标特征，熟练掌握二次函数的图象与性质是解题的关键．2023•西藏）将抛物线y＝（x﹣1）2+5平移后，得到抛物线的解析式为y＝x2+2x+3，则平移的方向和距离是（）A．向右平移2个单位长度，再向上平移3个单位长度B．向右平移2个单位长度，再向下平移3个单位长度C．向左平移2个单位长度，再向上平移3个单位长度D．向左平移2个单位长度，再向下平移3个单位长度【答案】D【点拨】先确定两个抛物线的顶点坐标，再利用点平移的规律确定抛物线平移的情况．【解析】解：抛物线y＝（x﹣1）2+5的顶点坐标为（1，5），抛物线y＝x2+2x+3＝（x+1）2+2的顶点坐标为（﹣1，2），而点（1，5）向左平移2个，再向下平移3个单位可得到（﹣1，2），【点睛】本题考查了二次函数图象与几何变换：由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．例5（2023•无锡）二次函数y＝x2+（2m﹣1）x+2m（m≠），有下列结论：①该函数图象过定点（﹣1，2）；②当m＝1时，函数图象与x轴无交点；③函数图象的对称轴不可能在y轴的右侧；④当1＜m＜时，点P（x1，y1），Q（x2，y2）是曲线上两点，若﹣3＜x1＜﹣2，﹣＜x2＜0，则y1＞y2．其中，正确结论的序号为①②④．【答案】①②④．【点拨】抛物线整理为y＝x2+（2m﹣1）x+2m＝x2+2mx﹣x+2m＝2m（x+1）+x2﹣x可判断①，将m＝1代入并计算b2﹣4ac即可判断②，计算抛物线对称轴并根据m≠可判断③，根据题意确定对称轴的范围后可确定P、Q的位置，再根据增减性可判断④．【解析】解：y＝x2+（2m﹣1）x+2m＝x2+2mx﹣x+2m＝2m（x+1）+x2﹣x，当x＝﹣1时，y＝2，∴该函数图象过定点（﹣1，2），故①正确；当m＝1时，y＝x2+x+2，∵b2﹣4ac＝1﹣4×2＝﹣7＜0，∴函数图象与x轴无交点，故②正确；抛物线的对称轴为：x＝，∵m≠，∴，∴当m＞时，对称轴在y轴左侧，当m＜时，对称轴在y轴右侧，故③错误；∵，∴﹣1＜﹣m＜﹣，∴P（x1，y1）在对称轴左侧，Q（x2，y2）在对称轴右侧，∵a＝1＞0，∴抛物线开口向上，在对称轴左侧，y随x增大而减小，在对称轴右侧，y随x增大而增大，∴当x＝﹣2时，y1最小＝y＝4﹣4m+2+2m＝﹣2m+6，当x＝0时，y2最大＝2m，此时，y1﹣y2＝﹣4m+6，∵，∴﹣4m+6＞0，∴y1＞y2，故④正确，故答案为：①②④．【点睛】本题考查的是二次函数的综合题，解题的关键是熟练理解并综合运用二次函数的各个特征．2023•丽水）已知点（﹣m，0）和（3m，0）在二次函数y＝ax2+bx+3（a，b是常数，a≠0）的图象上．（1）当m＝﹣1时，求a和b的值；（2）若二次函数的图象经过点A（n，3）且点A不在坐标轴上，当﹣2＜m＜﹣1时，求n的取值范围；（3）求证：b2+4a＝0．【答案】（1）a的值是﹣1，b的值是﹣2；（2）﹣4＜n＜﹣2；（3）证明见解析．【点拨】（1）当m＝﹣1时，二次函数y＝ax2+bx+3图象过点（1，0）和（﹣3，0），用待定系数法可得a的值是﹣1，b的值是﹣2；（2）y＝ax2+bx+3图象过点（﹣m，0）和（3m，0），可知抛物线的对称轴为直线x＝m，而y＝ax2+bx+3的图象过点A（n，3），（0，3），且点A不在坐标轴上，可得m＝，根据﹣2＜m＜﹣1，即得﹣4＜n＜﹣2；（3）由抛物线过（﹣m，0），（3m，0），可得﹣＝m，b＝﹣2am，把（﹣m，0），（3m，0）代入y＝ax2+bx+3变形可得am2+1＝0，故b2+4a＝（﹣2am）2+4a＝4a（am2+1）＝4a×0＝0．【解析】（1）解：当m＝﹣1时，二次函数y＝ax2+bx+3图象过点（1，0）和（﹣3，0），∴解得，∴a的值是﹣1，b的值是﹣2；（2）解：∵y＝ax2+bx+3图象过点（﹣m，0）和（3m，0），∴抛物线的对称轴为直线x＝m，∵y＝ax2+bx+3的图象过点A（n，3），（0，3），且点A不在坐标轴上，∴由图象的对称性得n＝2m，∴m＝，∵﹣2＜m＜﹣1，∴﹣2＜＜﹣1，∴﹣4＜n＜﹣2；（3）证明：∵抛物线过（﹣m，0），（3m，0），∴抛物线对称轴为直线x＝＝m，∴﹣＝m，∴b＝﹣2am，把（﹣m，0），（3m，0）代入y＝ax2+bx+3得：，①×3+②得：12am2+12＝0，∴am2+1＝0，∴b2+4a＝（﹣2am）2+4a＝4a（am2+1）＝4a×0＝0．【点睛】本题考查二次函数图象上点坐标的特征，涉及待定系数法，不等式，方程组等知识，解题的关键是整体思想的应用．2023•辽宁）商店出售某品牌护眼灯，每台进价为40元，在销售过程中发现，月销量y（台）与销售单价x（元）之间满足一次函数关系，规定销售单价不低于进价，且不高于进价的2倍，其部分对应数据如下表所示：销售单价x（元）…506070…月销量y（台）…908070…（1）求y与x之间的函数关系式；【答案】见解析【点拨】（1）设月销量y（台）与销售单价x（元）之间满足一次函数关系式为y＝kx+b，把（50，90）和（60，80）代入解方程组即可得到结论；（2）设每月出售这种护眼灯所获的利润为w元，根据题意得到二次函数解析式，根据二次函数的性质即可得到结论．【解析】解：（1）设月销量y（台）与销售单价x（元）之间满足一次函数关系式为y＝kx+b，把（50，90）和（60，80）代入得，解得，∴y＝﹣x+140；（2）∵规定销售单价不低于进价，且不高于进价的2倍，∴40≤x≤80，设每月出售这种护眼灯所获的利润为w元，根据题意得，w＝（x﹣40）y＝（x﹣40）（﹣x+140）＝﹣x2+180x﹣5600＝﹣（x﹣90）2+2500，∴当护眼灯销售单价定为80元时，商店每月出售这种护眼灯所获的利润最大，最大月利润为2400元．【点睛】本题主要考查了二次函数的应用，解题的关键是列出关系式，熟练掌握二次函数的性质，准确计算．2023•山西）综合与探究如图，二次函数y＝﹣x2+4x的图象与x轴的正半轴交于点A，经过点A的直线与该函数图象交于点B（1，3），与y轴交于点C．（1）求直线AB的函数表达式及点C的坐标；（2）点P是第一象限内二次函数图象上的一个动点，过点P作直线PE⊥x轴于点E，与直线AB 交于点D，设点P的横坐标为m．①当时，求m的值；②当点P在直线AB上方时，连接OP，过点B作BQ⊥x轴于点Q，BQ与OP交于点F，连接DF．设四边形FQED的面积为S，求S关于m的函数表达式，并求出S的最大值．【答案】（1）y＝﹣x+4，点C的坐标为（0，4）；（2）①2或3或；②，S的最大值为．【点拨】（1）利用待定系数法可求得直线AB的函数表达式，再求得点C的坐标即可；（2）①分当点P在直线AB上方和点P在直线AB下方时，两种情况讨论，根据PD＝2 列一元二次方程求解即可；②证明△FOQ∽△POE，推出FQ＝﹣m+4，再证明四边形FQED为矩形，利用矩形面积公式得到二次函数的表达式，再利用二次函数的性质即可求解．【解析】解：（1）由y＝﹣x2+4x得，当y＝0 时，﹣x2+4x＝0，解得x1＝0，x2＝4，∵点A在x轴正半轴上．∴点A的坐标为（4，0）．设直线AB的函数表达式为y＝kx+b（k≠0）．将A，B两点的坐标（4，0），（1，3）分别代入y＝kx+b，得，解得，∴直线AB的函数表达式为y＝﹣x+4．将x＝0代入y＝﹣x+4，得y＝4．∴点C的坐标为（0，4）；（2）①解：∵点P在第一象限内二次函数y＝﹣x2+4x的图象上，且PE⊥x轴于点E，与直线AB 交于点D，其横坐标为m．∴点P，D的坐标分别为P（m，﹣m2+4m），D（m，﹣m+4），∴PE＝﹣m2+4m．DE＝﹣m+4，OE＝m，∵点C的坐标为（0，4），∴OC＝4．，∴PD＝2．如图1，当点P在直线AB上方时，PD＝PE﹣DE＝﹣m2+4m﹣（﹣m+4）＝﹣m2+5m﹣4，∵PD＝2，∴﹣m2+5m﹣4＝2，解得m1＝2．m2＝3．如图2，当点P在直线AB下方时，PD＝DE﹣PE＝﹣m+4﹣（﹣m2+4m）＝m2﹣5m+4，∵PD＝2，∴m2﹣5m+4＝2，解得，∵0＜m＜1，m＝．综上所述，m的值为2或3或；②解：如图3，由（2）①得，OE＝m，PE＝﹣m2+4m，DE＝﹣m+4．∴OQ＝1，∵点P在直线AB上方，∴EQ＝m﹣1．∵PE⊥x轴于点E，∴∠OQF＝∠OEP＝90°，∴FQ∥DE，∠FOQ＝∠POE，∴△FOQ∽△POE，∴，∴，∴，∴FQ＝DE，∴四边形FQED为平行四边形，∵PE⊥x轴，∴四边形FQED为矩形．∴S＝EQ•FQ＝（m﹣1）（﹣m+4），即S＝﹣m2+5m﹣4＝，∵﹣1＜0，1＜m＜4，∴当m＝时，S的最大值为；【点睛】本题属于二次函数综合题，考查了二次函数的性质，一次函数的性质，特殊四边形的判定和性质等知识，解题的关键是学会用分类讨论的思想思考问题，学会利用参数构建二次函数解决问题，属于中考压轴题．考点过关☆专项突破类型一二次函数的图象与性质1．（2023•沈阳）二次函数y＝﹣（x+1）2+2图象的顶点所在的象限是（）A．第一象限B．第二象限C．第三象限D．第四象限【答案】B【点拨】首先确定二次函数的顶点坐标，然后根据点的坐标特点写出顶点的位置．【解析】解：∵y＝﹣（x+1）2+2，∴顶点在第二象限．故选：B．【点睛】本题考查了二次函数的性质，解题的关键是确定二次函数的顶点坐标．2．（2021•江西）在同一平面直角坐标系中，二次函数y＝ax2与一次函数y＝bx+c的图象如图所示，则二次函数y＝ax2+bx+c的图象可能是（）A．B．C．D．【答案】D【点拨】根据二次函数y＝ax2与一次函数y＝bx+c的图象，即可得出a＞0、b＞0、c＜0，由此即可得出：二次函数y＝ax+bx+c的图象开口向上，对称轴x＝﹣＜0，与y轴的交点在y轴负半轴，再对照四个选项中的图象即可得出结论．【解析】解：观察函数图象可知：a＞0，b＞0，c＜0，∴二次函数y＝ax2+bx+c的图象开口向上，对称轴x＝﹣＜0，与y轴的交点在y轴负半轴．故选：D．【点睛】本题考查了一次函数的图象以及二次函数的图象，根据二次函数图象和一次函数图象经过的象限，找出a＞0、b＞0、c＜0是解题的关键．3．（2023•陕西）在平面直角坐标系中，二次函数y＝x2+mx+m2﹣m（m为常数）的图象经过点（0，6），其对称轴在y轴左侧，则该二次函数有（）A．最大值5B．最大值C．最小值5D．最小值【答案】D【点拨】将（0，6）代入二次函数解析式，进而得出m的值，再利用对称轴在y轴左侧，得出m ＝3，再利用公式法求出二次函数最值．【解析】解：由题意可得：6＝m2﹣m，解得：m1＝3，m2＝﹣2，∵二次函数y＝x2+mx+m2﹣m，对称轴在y轴左侧，∴m＞0，∴m＝3，∴y＝x2+3x+6，∴二次函数有最小值为：＝＝．故选：D．【点睛】此题主要考查了二次函数的性质以及二次函数的最值，正确得出m的值是解题关键．4．（2023•衢州）已知二次函数y＝ax2﹣4ax（a是常数，a＜0）的图象上有A（m，y1）和B（2m，y2）两点．若点A，B都在直线y＝﹣3a的上方，且y1＞y2，则m的取值范围是（）A．B．C．D．m＞2【答案】C【点拨】根据已知条件列不等式即可得到结论．【解析】解：∵a＜0，∴y＝﹣3a＞0，∵A（m，y1）和B（2m，y2）两点都在直线y＝﹣3a的上方，且y1＞y2，∴4am2﹣8am＞﹣3a，∴4m2﹣8m+3＜0，∴＜m＜①，∵二次函数y＝ax2﹣4ax（a是常数，a＜0）的图象上有A（m，y1）和B（2m，y2）两点．∴am2﹣4am＞4am2﹣8am，∴3am2＜4am，∵a＜0，m＞0，∴am＜0，∴m＞②，由①②得＜m＜．故选：C．【点睛】本题考查了二次函数图象上点的坐标特征，一次函数图象上点的坐标特征，正确地列出不等式是解题的关键．5．（2023•大连）已知二次函数y＝x2﹣2x﹣1，当0≤x≤3时，函数的最大值为（）A．﹣2B．﹣1C．0D．2【答案】D【点拨】根据二次函数的图象，结合当0≤x≤3时函数图象的增减情况，即可解决问题．【解析】解：由二次函数的表达式为y＝x2﹣2x﹣1可知，抛物线开口向上，对称轴为直线x＝＝1．又1﹣0＜3﹣1，所以当x＝3时，函数取得最大值，y＝32﹣2×3﹣1＝2．故选：D．【点睛】本题考查二次函数的最值，能由二次函数的表达式得出抛物线的对称轴及开口方向是解题的关键．6．（2023•扬州）已知二次函数y＝ax2﹣2x+（a为常数，且a＞0），下列结论：①函数图象一定经过第一、二、四象限；②函数图象一定不经过第三象限；③当x＜0时，y随x的增大而减小；④当x＞0时，y随x的增大而增大．其中所有正确结论的序号是（）A．①②B．②③C．②D．③④【答案】B【点拨】由a的正负可确定出抛物线的开口方向，结合函数的性质逐项判断即可．【解析】解：∵a＞0时，抛物线开口向上，∴对称轴为直线x＝＝＞0，当x＜0时，y随x的增大而减小，当x＞时，y随x的增大而增大，∴函数图象一定不经过第三象限，函数图象可能经过第一、二、四象限．故选：B．【点睛】本题主要考查二次函数的性质，掌握a决定二次函数的开口方向，进一步能确定出其最值是解题的关键．7．（2021•福建）二次函数y＝ax2﹣2ax+c（a＞0）的图象过A（﹣3，y1），B（﹣1，y2），C（2，y3），D（4，y4）四个点，下列说法一定正确的是（）A．若y1y2＞0，则y3y4＞0B．若y1y4＞0，则y2y3＞0C．若y2y4＜0，则y1y3＜0D．若y3y4＜0，则y1y2＜0【答案】C【点拨】观察图象可知，y1＞y4＞y2＞y3，再结合题目一一判断即可．【解析】解：如图，由题意对称轴为直线x＝1，观察图象可知，y1＞y4＞y2＞y3，若y1y2＞0，如图1中，则y3y4＜0，选项A不符合题意，若y1y4＞0，如图2中，则y2y3＜0，选项B不符合题意，若y2y4＜0，如图3中，则y1y3＜0，选项C符合题意，若y3y4＜0，如图4中，则y1y2＞0，选项D不符合题意，故选：C．【点睛】本题考查二次函数的性质，二次函数图象上的点的坐标特征，解题的关键是学会利用图象法解决问题，属于中考常考题型．8．（2022•长春）已知二次函数y＝﹣x2﹣2x+3，当a≤x≤时，函数值y的最小值为1，则a的值为﹣1﹣．【答案】﹣1﹣．【点拨】函数配方后得y＝﹣x2﹣2x+3＝﹣（x+1）2+4，当y＝1时，﹣（x+1）2+4＝1，可得x＝﹣1±，因为﹣1+＞，所以﹣1﹣≤x≤时，函数值y的最小值为1，进而可以解决问题．【解析】解：∵y＝﹣x2﹣2x+3＝﹣（x+1）2+4，∴图象开口向下，顶点坐标为（﹣1，4），根据题意，当a≤x≤时，函数值y的最小值为1，当y＝1时，﹣（x+1）2+4＝1，∴x＝﹣1±，∵﹣1+＞，∴﹣1﹣≤x≤时，函数值y的最小值为1，∴a＝﹣1﹣．故答案为：﹣1﹣．【点睛】本题考查了二次函数的性质，二次函数的最值，熟练掌握二次函数的增减性质是解题的关键．9．（2023•福建）已知抛物线y＝ax2﹣2ax+b（a＞0）经过A（2n+3，y1），B（n﹣1，y2）两点，若A，B分别位于抛物线对称轴的两侧，且y1＜y2，则n的取值范围是﹣1＜n＜0．【答案】﹣1＜n＜0．【点拨】由题意可知：抛物线的对称轴为x＝1，开口向上，再分点A在对称轴x＝1的左侧，点B 在对称轴x＝1的右侧和点B在对称轴x＝1的左侧，点A在对称轴x＝1的右侧两种情况求解即可．【解析】解：抛物线的对称轴为：x＝﹣＝1，∵a＞0，∴抛物线开口向上，∵y1＜y2，∴若点A在对称轴x＝1的左侧，点B在对称轴x＝1的右侧，由题意可得：，不等式组无解；若点B在对称轴x＝1的左侧，点A在对称轴x＝1的右侧，由题意可得：，解得：﹣1＜n＜0，∴n的取值范围为：﹣1＜n＜0．故答案为：﹣1＜n＜0．【点睛】本题主要考查的是二次函数的性质以及二次函数图象上点的坐标的特征，能根据题意正确列出不等式组是解决本题的关键．10．（2023•北京）在平面直角坐标系xOy中，M（x1，y1），N（x2，y2）是抛物线y＝ax2+bx+c（a ＞0）上任意两点，设抛物线的对称轴为x＝t．（1）若对于x1＝1，x2＝2，有y1＝y2，求t的值；（2）若对于0＜x1＜1，1＜x2＜2，都有y1＜y2，求t的取值范围．【答案】（1）；（2）t≤．【点拨】（1）根据二次函数的性质求得对称轴即可，（2）根据题意判断出离对称轴更近的点，从而得出（x1，y1）与（x2，y2）的中点在对称轴的右侧，再根据对称性即可解答．【解析】解：（1）∵对于x1＝1，x2＝2，有y1＝y2，∴a+b+c＝4a+2b+c，∴3a+b＝0，∴＝﹣3．∵对称轴为x＝﹣＝，∴t＝．（2）∵0＜x1＜1，1＜x2＜2，∴，x1＜x2，∵y1＜y2，a＞0，∴（x1，y1）离对称轴更近，x1＜x2，则（x1，y1）与（x2，y2）的中点在对称轴的右侧，∴＞t，即t≤．【点睛】本题考查二次函数的性质，熟练掌握二次函数的对称性是解题关键．类型二二次函数的图象与系数的关系1．（2023•阜新）如图，二次函数y＝ax2+bx+c的图象与x轴的一个交点为（3，0），对称轴是直线x＝1，下列结论正确的是（）A．abc＜0B．2a+b＝0C．4ac＞b2D．点（﹣2，0）在函数图象上【答案】B【点拨】利用二次函数的图象与系数的关系可得出，a、b、c的正负，进而得出abc的正负；利用对称轴为直线x＝1，可得出2a+b与0的关系；由抛物线与x轴的交点情况，可得出b2与4ac的大小关系；由抛物线与x轴的一个交点坐标为（3，0），再结合对称轴为直线x＝1，可得出另一个交点坐标．【解析】解：A：由二次函数的图形可知：a＞0，b＜0，c＜0，所以abc＞0．故A错误．B：因为二次函数的对称轴是直线x＝1，则＝1，即2a+b＝0．故B正确．C：因为抛物线与x轴有两个交点，所以b2﹣4ac＞0，即4ac＜b2．故C错误．D：因为抛物线与x轴的一个交点坐标为（3，0），且对称轴为直线x＝1，所以它与x轴的另一个交点的坐标为（﹣1，0）．故D错误．故选：B．【点睛】本题考查二次函数图象与各项系数的关系，正确求得a，b，c的正负以及巧妙利用抛物线的对称轴是解决问题的关键．2．（2023•雅安）如图，二次函数y＝ax2+bx+c的图象与x轴交于A（﹣2，0），B两点，对称轴是直线x＝2，下列结论中，所有正确结论的序号为（）①a＞0；②点B的坐标为（6，0）；③c＝3b；④对于任意实数m，都有4a+2b≥am2+bm．A．①②B．②③C．②③④D．③④【答案】C【点拨】通过抛物线开口方向，对称轴，抛物线与y轴交点可判断①、②、③，通过x＝2时抛物线取得最大值判断4a+2b≥am2+bm，进而求解．【解析】解：∵抛物线开口向下，∴a＜0，①错误，∵A、B关于对称轴x＝2对称，∴B点的横坐标为6，②正确，∵二次函数y＝ax2+bx+c的对称轴为直线x＝2，∴﹣＝2，∴，把（﹣2，0）代入y＝ax2+bx+c，得：4a﹣2b+c＝0，∴﹣2b+c＝0，整理得：c＝3b，③正确，∵二次函数y＝ax2+bx+c的对称轴为直线x＝2，∴当x＝2时，抛物线取得最大值为y＝4a+2b+c，当x＝m时，y＝am2+bm+c，∴4a+2b+c≥am2+bm+c，即4a+2b≥am2+bm，④正确．∴所有正确结论的序号为②③④．故选：C．【点睛】本题考查二次函数图象与系数的关系，解题关键是灵活运用二次函数图象和性质．3．（2023•黄石）已知二次函数y＝ax2+bx+c（a≠0）的图象经过三点A（x1，y1），B（x2，y2），C （﹣3，0），且对称轴为直线x＝﹣1．有以下结论：①a+b+c＝0；②2c+3b＝0；③当﹣2＜x1＜﹣1，0＜x2＜1时，有y1＜y2；④对于任何实数k＞0，关于x的方程ax2+bx+c＝k（x+1）必有两个不相等的实数根．其中结论正确的有（）A．1个B．2个C．3个D．4个【答案】C【点拨】根据二次函数的对称轴为直线x＝﹣1和经过点C（﹣3，0），再结合抛物线的对称性即可解决问题．【解析】解：因为二次函数的图象过点C（﹣3，0），且对称轴为直线x＝﹣1，所以由抛物线的对称性可知，点（1，0）也在抛物线上．将（1，0）代入二次函数解析式得，a+b+c＝0．故①正确．因为抛物线的对称轴是直线x＝﹣1，所以，即b﹣2a＝0．又a+b+c＝0，则将a＝﹣b﹣c代入b﹣2a＝0得，2c+3b＝0．故②正确．因为﹣2＜x1＜﹣1，0＜x2＜1，所以点A离对称轴更近．则当a＞0时，y1＜y2；当a＜0时，y1＞y2．故③错误．由ax2+bx+c＝k（x+1）得，ax2+（b﹣k）x+c﹣k＝0．又a+b+c＝0，2c+3b＝0，得．则（b﹣k）2﹣4a（c﹣k）＝（）2﹣4×（）（c﹣k）＝．又k＞0，所以＞0．即该方程有两个不相等的实数根．故④正确．故选：C．【点睛】本题考查二次函数的图象与系数的关系及二次函数图象上点的坐标特征，能根据抛物线的对称轴及经过定点得出a，b，c的关系是解题的关键．4．（2023•遂宁）抛物线y＝ax2+bx+c（a≠0）的图象如图所示，对称轴为直线x＝﹣2．下列说法：①abc＜0；②c﹣3a＞0；③4a2﹣2ab≥at（at+b）（t为全体实数）；④若图象上存在点A（x1，y1）和点B（x2，y2），当m＜x1＜x2＜m+3时，满足y1＝y2，则m的取值范围为﹣5＜m＜﹣2，其中正确的个数有（）A．1个B．2个C．3个D．4个【答案】C【点拨】①分别判断a、b、c的符号，再判断abc的符号；②由对称轴为直线x＝﹣2，可知a与b的数量关系，消去b可得仅含a、c的解析式，找特定点可判断c﹣3a的符号．③用a与b的数量关系，可将原式化简得到关于t的不等式，再用函数的性质（t为全体实数）判断．④利用二次函数的性质及二次函数与一元二次方程的关系即可判断．【解析】解：①因图象开口向下，可知：a＜0；又∵对称轴为直线x＝﹣2，∴﹣＝﹣2，整理得：b＝4a，即a、b同号．由图象可知，当x＝4时，y＜0，又∵对称轴为直线x＝﹣2，可知：当x＝0时，y＜0；即c＜0；∴abc＜0，故①正确．②由①得：b＝4a．代入原解析式得：y＝ax2+4ax+c；由图象可知，当x＝﹣1时，y＞0．即：a•（﹣1）2+4a•（﹣1）+c＞0，整理得：c﹣3a＞0，故②正确．③设4a2﹣2ab≥at（at+b）则4a﹣2b≤at•t﹣bt，两边+c得到4a﹣2b+c≤at•t﹣bt+c，左侧为x＝﹣2时的函数值，右侧为x＝t时的函数值，显然不成立，故③错误．④由题意得，x1、x2是一元二次方程ax2+bx+c﹣y1＝0的两个根，从图象上看，因二次函数有对称性，x1、x2关于x＝﹣2对称，∴当且仅当m＜﹣2＜m+3时，存在点A（x1，y1）和点B（x2，y2），当m＜x1＜x2＜m+3时，满足y1＝y2，即当﹣5＜m＜﹣2时，满足题设，故④正确．故本题选：C．【点睛】本题考查了二次函数字母系数与图象的关系、二次函数与一元二次方程的关系等知识．需综合利用二次函数的性质，不等式的性质解题．5．（2023•湖北）抛物线y＝ax2+bx+c（a＜0）与x轴相交于点A（﹣3，0），B（1，0）．下列结论：①abc＜0；②b2﹣4ac＞0；③3b+2c＝0；④若点P（m﹣2，y1），Q（m，y2）在抛物线上，且y1＜y2，则m≤﹣1．其中正确的结论有（）A．1个B．2个C．3个D．4个【答案】B【点拨】根据二次函数的性质及数形结合思想进行判定．【解析】解：①由题意得：y＝ax2+bx+c＝a（x+3）（x﹣1）＝ax2+2ax﹣3a，∴b＝2a，c＝﹣3a，∵a＜0，∴b＜0，c＞0，∴abc＞0，故①是错误的；②∵抛物线y＝ax2+bx+c（a＜0）与x轴相交于点A（﹣3，0），B（1，0）．∴ax2+bx+c＝0有两个不相等的实数根，∴b2﹣4ac＞0，故②是正确的；③∵b＝2a，c＝﹣3a，∴3b+2c＝6a﹣6a＝0，故③是正确的；④∵抛物线y＝ax2+bx+c（a＜0）与x轴相交于点A（﹣3，0），B（1，0）．∴抛物线的对称轴为：x＝﹣1，当点P（m﹣2，y1），Q（m，y2）在抛物线上，且y1＜y2，∴m≤﹣1或，解得：m＜0，故④是错误的，故选：B．【点睛】本题考查了二次函数与系数的关系，掌握二次函数的性质及数形结合思想是解题的关键．6．（2023•南京）已知二次函数y＝ax2﹣2ax+3（a为常数，a≠0）．（1）若a＜0，求证：该函数的图象与x轴有两个公共点．（2）若a＝﹣1，求证：当﹣1＜x＜0时，y＞0．（3）若该函数的图象与x轴有两个公共点（x1，0），（x2，0），且﹣1＜x1＜x2＜4，则a的取值范围是a＞3或a＜﹣1．【答案】（1）证明见解析过程；（2）证明见解析过程；（3）a＞3或a＜﹣1．【点拨】（1）证明b2﹣4ac＞0即可解决问题．（2）将a＝﹣1代入函数解析式，进行证明即可．（3）对a＞0和a＜0进行分类讨论即可．【解析】证明：（1）因为（﹣2a）2﹣4×a×3＝4a2﹣12a，又因为a＜0，所以4a＜0，a﹣3＜0，所以4a2﹣12a＝4a（a﹣3）＞0，所以该函数的图象与x轴有两个公共点．（2）将a＝﹣1代入函数解析式得，y＝﹣x2+2x+3＝﹣（x﹣1）2+4，所以抛物线的对称轴为直线x＝1，开口向下．则当﹣1＜x＜0时，y随x的增大而增大，又因为当x＝﹣1时，y＝0，所以y＞0．（3）因为抛物线的对称轴为直线x＝，且过定点（0，3），又因为该函数的图象与x轴有两个公共点（x1，0），（x2，0），且﹣1＜x1＜x2＜4，所以当a＞0时，a﹣2a+3＜0，解得a＞3，故a＞3．当a＜0时，a+2a+3＜0，解得a＜﹣1，故a＜﹣1．综上所述，a＞3或a＜﹣1．故答案为：a＞3或a＜﹣1．【点睛】本题考查二次函数的图象和性质，熟知二次函数的图象和性质是解题的关键．类型三二次函数的图象变换1．（2022•泸州）抛物线y＝﹣x2+x+1经平移后，不可能得到的抛物线是（）A．y＝﹣x2+x B．y＝﹣x2﹣4 C．y＝﹣x2+2021x﹣2022D．y＝﹣x2+x+1【答案】D【点拨】根据抛物线的平移规律，可得答案．【解析】解：∵将抛物线y＝﹣x2+x+1经过平移后开口方向不变，开口大小也不变，∴抛物线y＝﹣x2+x+1经过平移后不可能得到的抛物线是y＝﹣x2+x+1．故选：D．【点睛】本题考查了二次函数图象与几何变换，由平移规律得出a不变是解题的关键．2．（2023•徐州）在平面直角坐标系中，将二次函数y＝（x+1）2+3的图象向右平移2个单位长度，再向下平移1个单位长度，所得抛物线对应的函数表达式为（）A．y＝（x+3）2+2 B．y＝（x﹣1）2+2C．y＝（x﹣1）2+4D．y＝（x+3）2+4【答案】B【点拨】直接利用二次函数的平移规律，左加右减，上加下减，进而得出答案．【解析】解：将二次函数y＝（x+1）2+3的图象向右平移2个单位长度，再向下平移1个单位长度，所得抛物线对应的函数表达式为y＝（x+1﹣2）2+3﹣1，即y＝（x﹣1）2+2．故选：B．【点睛】本题主要考查二次函数的几何变换，掌握“左加右减，上加下减”的法则是解题的关键．3．（2020•衢州）二次函数y＝x2的图象平移后经过点（2，0），则下列平移方法正确的是（）A．向左平移2个单位，向下平移2个单位B．向左平移1个单位，向上平移2个单位C．向右平移1个单位，向下平移1个单位D．向右平移2个单位，向上平移1个单位【答案】C【点拨】求出平移后的抛物线的解析式，利用待定系数法解决问题即可．【解析】解：A、平移后的解析式为y＝（x+2）2﹣2，当x＝2时，y＝14，本选项不符合题意．B、平移后的解析式为y＝（x+1）2+2，当x＝2时，y＝11，本选项不符合题意．C、平移后的解析式为y＝（x﹣1）2﹣1，当x＝2时，y＝0，函数图象经过（2，0），本选项符合题意．D、平移后的解析式为y＝（x﹣2）2+1，当x＝2时，y＝1，本选项不符合题意．故选：C．【点睛】本题考查二次函数图象与几何变换，二次函数图象上点的特征，解题的关键是熟练掌握基本知识，属于中考常考题型．4．（2020•陕西）在同一平面直角坐标系中，若抛物线y＝mx2+2x﹣n与y＝﹣6x2﹣2x+m﹣n关于x 轴对称，则m，n的值为（）A．m＝﹣6，n＝﹣3B．m＝﹣6，n＝3C．m＝6，n＝﹣3D．m＝6，n＝3【答案】D【点拨】根据关于x轴对称，函数y是互为相反数即可求得．【解析】解：∵抛物线y＝mx2+2x﹣n与y＝﹣6x2﹣2x+m﹣n关于x轴对称，∴﹣y＝﹣mx2﹣2x+n，∴y＝﹣mx2﹣2x+n与y＝﹣6x2﹣2x+m﹣n相同，∴﹣m＝﹣6，n＝m﹣n，解得m＝6，n＝3，故选：D．【点睛】本题考查了二次函数图象与几何变换，根据关于x轴对称的坐标特征把抛物线y＝mx2+2x ﹣n化成关于x轴对称的抛物线的解析式是解题的关键．5．（2022•黔东南州）在平面直角坐标系中，将抛物线y＝x2+2x﹣1先绕原点旋转180°，再向下平移5个单位，所得到的抛物线的顶点坐标是（1，﹣3）．【答案】（1，﹣3）．【点拨】先求出绕原点旋转180°的抛物线解析式，再求出向下平移5个单位长度的解析式，配成顶点式即可得答案．【解析】解：将抛物线y＝x2+2x﹣1绕原点旋转180°后所得抛物线为：﹣y＝（﹣x）2+2（﹣x）﹣1，即y＝﹣x2+2x+1，再将抛物线y＝﹣x2+2x+1向下平移5个单位得y＝﹣x2+2x+1﹣5＝﹣x2+2x﹣4＝﹣（x﹣1）2﹣3，∴所得到的抛物线的顶点坐标是（1，﹣3），故答案为：（1，﹣3）．【点睛】本题考查二次函数图象与几何变换，熟知二次函数的图象旋转及平移的法则是解答此题的关键．6．（2023•益阳）我们在学习一次函数、二次函数图象的平移时知道：将一次函数y＝2x的图象向上平移1个单位得到y＝2x+1的图象；将二次函数y＝x2+1的图象向左平移2个单位得到y＝（x+2）2+1的图象，若将反比例函数y＝的图象向下平移3个单位，如图所示，则得到的图象对应的函数表达式是y＝﹣3．【答案】y＝﹣3．【点拨】根据“上加下减，左加右减”的原则进行解答即可．【解析】解：由题意，将反比例函数y＝的图象向下平移3个单位，得到的图象对应的函数表达式为y＝﹣3．故答案为：y＝﹣3．【点睛】本题考查的是一次函数、二次函数、反比例函数的图象与几何变换，熟知“上加下减，左加右减”的原则是解答此题的关键．7．（2022•河北）如图，点P（a，3）在抛物线C：y＝4﹣（6﹣x）2上，且在C的对称轴右侧．（1）写出C的对称轴和y的最大值，并求a的值；（2）坐标平面上放置一透明胶片，并在胶片上描画出点P及C的一段，分别记为P′，C′．平移该胶片，使C′所在抛物线对应的函数恰为y＝﹣x2+6x﹣9．求点P′移动的最短路程．【答案】（1）对称轴是直线x＝6，y的最大值为4，a＝7；（2）5．【点拨】（1）根据抛物线的顶点式，判断出顶点坐标，令y＝3，转化为方程求出a即可；（2）求出平移前后的抛物线的顶点的坐标，可得结论．【解析】解：（1）∵抛物线C：y＝4﹣（6﹣x）2＝﹣（x﹣6）2+4，∴抛物线的顶点为Q（6，4），∴抛物线的对称轴为直线x＝6，y的最大值为4，当y＝3时，3＝﹣（x﹣6）2+4，∴x＝5或7，∵点P在对称轴的右侧，∴P（7，3），∴a＝7；（2）∵平移后的抛物线的解析式为y＝﹣（x﹣3）2，∴平移后的顶点Q′（3，0），∵平移前抛物线的顶点Q（6，4），∴点P′移动的最短路程＝QQ′＝＝5．【点睛】本题考查二次函数的性质，解题的关键是理解题意，求出平移前后的抛物线的顶点坐标，属于中考常考题型．类型四二次函数的图象与x轴的交点1．（2023•郴州）已知抛物线y＝x2﹣6x+m与x轴有且只有一个交点，则m＝9．。

二次函数(与圆有关)如图，在平面直角坐标系屮，正方形ABCD 和正方形DEFG 的边长分别为2a, 2b,点A, D, G 在y 轴上，坐 标原点0为AD 的中点，抛物线y=mx 2ac, F 两点，连接FD 并延长交抛物线于点M.(3)判断以FM 为直径的圆与AB 所在直线的位置关系，并说明理由.a如图，二次函数y二ax'+bx+c的图象交x轴于A(・l, 0), B (2, 0),交y轴于C (0, -2),过A, C画直线.(1)求二次函数的解析式；(2)点P在x轴正半轴上，且PA二PC,求OP的长；(3)点M在二次函数图象上，以M为圆心的圆与直线AC相切，切点为H.①若M在y轴右狈IJ,且厶CHMs/XAOC (点C与点A对应)，求点M的坐标；(备用图)如图，抛物线y二■一x2+mx+n的图象经过点A (2, 3),对称轴为直线x=l, —次函数y二kx+b的图象经过 4 点A,交x轴于点P,交抛物线于另一点B,点A、B位于点P的同侧.(1)求抛物线的解析式；(2)若PA： PB=3： 1,求一次函数的解析式；(3)在(2)的条件下，当k>0时，抛物线的对称轴上是否存在点C,使得OC同时与x轴和直线AP都相切，如果存在，请求出点C的坐标，如果不存在，请说明理由.(1) 求该二次函数的关系式；(2) 过y 轴上的一点M (0, m)作y 轴的垂线，若该垂线与AABC 的外接圆有公共点，求in 的取值范围；(3) 在该二次函数的图象上是否存在点D,使四边形ACBD 为直角梯形？若存在，求出点D 的坐标；若不存在，请说明理由。

1 7 如图，已知抛物线m： y二ax? - 6ax+c (a>0)的顶点A在x轴上，并过点B (0, 1),直线n： y二-2x+2与x 轴交于点D,与抛物线m的对称轴1交于点F,过B点的直线BE与直线n相交于点E (・7, 7).(1)求抛物线m的解析式；(2)P是1上的一个动点，若以B, E, P为顶点的三角形的周长最小，求点P的坐标；(3)抛物线m上是否存在一动点Q,使以线段FQ为直径的圆恰好经过点D?若存在，求点Q的坐标; 若不存在，请说明理由.如图，在平面直角坐标系中，点0为坐标原点，直线/与抛物线y=n^nx相交于A (1, 3 ), 〃(4, 0) 两点.(1)求出抛物线的解析式；(2)在坐标轴上是否存在点〃，使得△/!少是以线段为斜边的直角三角形？若存在，求出点〃的坐标; 若不存在，说明理由；(3)点P是线段川〃上一动点，(点戶不与点彳、g重合)，过点P作PM// OA,交第一象限内的抛物线于点MN 臥过点〃作MCLx轴于点Q,交AB于点N,若'BCN、側的面积S/^o、5\恥满足二2弘妙，求出——NC24. (2015荆州12分)如图，在平面直角坐标系中，O为原点，UABCD的边BC在兀轴上，D点在y 轴上，C 点坐标为(2, 0), BC=6, ZBCD=60。

专题10二次函数与圆存在性问题二次函数是初中数学代数部分最重要的概念之一，是中考数学的重难点；而圆是初中几何中综合性最强的知识内容，它与二次函数都在中考中占据及其重要的地位，两者经常作为压轴题综合考查，能够很好的考查学生的数学综合素养以及分析问题、解决问题的能力.圆心与抛物线的关系、圆上的点和抛物线的关系，其本质就是把位置关系向数量化关系转化.二次函数与圆的综合要数形结合，在读题之前要想到圆中的相关概念、性质及定理，比如圆的定义、垂径定理、圆周角、圆心角、内心、外心、切线、四点共圆的、隐藏圆等；对于二次函数，要熟练掌握解析式的求法和表达形式、顶点、最值、与方程之间的关系，线段长与点的坐标之间的数量转化等.【例1】（2022•闵行区二模）如图，在平面直角坐标系xOy中，抛物线y＝ax2+bx+4与x轴相交于点A（﹣1，0），B（3，0），与y轴交于点C．将抛物线的对称轴沿x轴的正方向平移，平移后交x轴于点D，交线段BC于点E，交抛物线于点F，过点F作直线BC的垂线，垂足为点G．（1）求抛物线的表达式；（2）以点G为圆心，BG为半径画⊙G；以点E为圆心，EF为半径画⊙E．当⊙G与⊙E内切时．①试证明EF与EB的数量关系；②求点F的坐标．【例2】（2022•福建模拟）如图，已知抛物线y＝ax2+bx+c与x轴相交于A，B两点，点C（2，﹣4）在抛物线上，且△ABC是等腰直角三角形．（1）求抛物线的解析式；（2）过点D（2，0）的直线与抛物线交于点M，N，试问：以线段MN为直径的圆是否过定点？证明你的结论．【例3】（2022•武汉模拟）已知抛物线y＝﹣2x2+bx+c（c＞0）．（1）如图1，抛物线与直线l相交于点M（﹣1，0），N（2，6）．①求抛物线的解析式；②过点N作MN的垂线，交抛物线于点P，求PN的长；（2）如图2，已知抛物线y＝﹣2x2+bx+c与x轴交于A、B两点，与y轴交于点C，点A，B，C，D（0，n）四点在同一圆上，求n的值．【例4】（2022•上海模拟）在平面直角坐标系xOy中，抛物线y＝ax2﹣3ax+2（a＜0）交y轴于点A，抛物线的对称轴交x轴于点P，联结PA．（1）求线段PA的长；（2）如果抛物线的顶点到直线PA的距离为3，求a的值；（3）以点P为圆心、PA为半径的⊙P交y轴的负半轴于点B，第一象限内的点Q在⊙P上，且劣弧＝2．如果抛物线经过点Q，求a的值．1．（2021•广元）如图1，在平面直角坐标系xOy中，抛物线y＝ax2+bx+c与x轴分别相交于A、B两点，与y轴相交于点C，下表给出了这条抛物线上部分点（x，y）的坐标值：x…﹣10123…y…03430…（1）求出这条抛物线的解析式及顶点M的坐标；（2）PQ是抛物线对称轴上长为1的一条动线段（点P在点Q上方），求AQ+QP+PC的最小值；（3）如图2，点D是第四象限内抛物线上一动点，过点D作DF⊥x轴，垂足为F，△ABD的外接圆与DF 相交于点E．试问：线段EF的长是否为定值？如果是，请求出这个定值；如果不是，请说明理由．2．（2021•张家界）如图，已知二次函数y＝ax2+bx+c的图象经过点C（2，﹣3），且与x轴交于原点及点B （8，0）．（1）求二次函数的表达式；（2）求顶点A的坐标及直线AB的表达式；（3）判断△ABO的形状，试说明理由；（4）若点P为⊙O上的动点，且⊙O的半径为2，一动点E从点A出发，以每秒2个单位长度的速度沿线段AP匀速运动到点P，再以每秒1个单位长度的速度沿线段PB匀速运动到点B后停止运动，求点E的运动时间t的最小值．3．（2021•宜宾）如图1，在平面直角坐标系中，抛物线与x轴分别交于A、B两点，与y轴交于点C（0，6），抛物线的顶点坐标为E（2，8），连结BC、BE、CE．（1）求抛物线的表达式；（2）判断△BCE的形状，并说明理由；（3）如图2，以C为圆心，为半径作⊙C，在⊙C上是否存在点P，使得BP+EP的值最小，若存在，请求出最小值；若不存在，请说明理由．4．（2020•雨花区校级一模）如图1，已知抛物线y＝ax2﹣12ax+32a（a＞0）与x轴交于A，B两点（A在B 的左侧），与y轴交于点C．（1）连接BC，若∠ABC＝30°，求a的值．（2）如图2，已知M为△ABC的外心，试判断弦AB的弦心距d是否有最小值，若有，求出此时a的值，若没有，请说明理由；（3）如图3，已知动点P（t，t）在第一象限，t为常数．问：是否存在一点P，使得∠APB达到最大，若存在，求出此时∠APB的正弦值，若不存在，也请说明理由．5．（2020•汇川区三模）如图，在平面直角坐标系上，一条抛物线y＝ax2+bx+c（a≠0）经过A（1，0）、B （3，0）、C（0，3）三点，连接BC并延长．（1）求抛物线的解析式；（2）点M是直线BC在第一象限部分上的一个动点，过M作MN∥y轴交抛物线于点N．1°求线段MN的最大值；2°当MN取最大值时，在线段MN右侧的抛物线上有一个动点P，连接PM、PN，当△PMN的外接圆圆心Q在△PMN的边上时，求点P的坐标．6．（2021•开福区模拟）如图，在平面直角坐标系中，抛物线y＝x2﹣bx+c交x轴于点A，B，点B的坐标为（4，0），与y轴于交于点C（0，﹣2）．（1）求此抛物线的解析式；（2）在抛物线上取点D，若点D的横坐标为5，求点D的坐标及∠ADB的度数；（3）在（2）的条件下，设抛物线对称轴l交x轴于点H，△ABD的外接圆圆心为M（如图1），①求点M的坐标及⊙M的半径；②过点B作⊙M的切线交于点P（如图2），设Q为⊙M上一动点，则在点运动过程中的值是否变化？若不变，求出其值；若变化，请说明理由．7．（2020•天桥区二模）如图，抛物线y＝ax2+bx+c（a≠0），与x轴交于A（4，0）、O两点，点D（2，﹣2）为抛物线的顶点．（1）求该抛物线的解析式；（2）点E为AO的中点，以点E为圆心、以1为半径作⊙E，交x轴于B、C两点，点M为⊙E上一点．①射线BM交抛物线于点P，设点P的横坐标为m，当tan∠MBC＝2时，求m的值；②如图2，连接OM，取OM的中点N，连接DN，则线段DN的长度是否存在最大值或最小值？若存在，请求出DN的最值；若不存在，请说明理由．8．（2020•百色）如图，抛物线的顶点为A（0，2），且经过点B（2，0）．以坐标原点O为圆心的圆的半径r＝，OC⊥AB于点C．（1）求抛物线的函数解析式．（2）求证：直线AB与⊙O相切．（3）已知P为抛物线上一动点，线段PO交⊙O于点M．当以M，O，A，C为顶点的四边形是平行四边形时，求PM的长．9．（2020•西藏）在平面直角坐标系中，二次函数y＝x2+bx+c的图象与x轴交于A（﹣2，0），B（4，0）两点，交y轴于点C，点P是第四象限内抛物线上的一个动点．（1）求二次函数的解析式；＝，求点P的坐标；（2）如图甲，连接AC，PA，PC，若S△P AC（3）如图乙，过A，B，P三点作⊙M，过点P作PE⊥x轴，垂足为D，交⊙M于点E．点P在运动过程中线段DE的长是否变化，若有变化，求出DE的取值范围；若不变，求DE的长．10．（2020•宜宾）如图，已知二次函数的图象顶点在原点，且点（2，1）在二次函数的图象上，过点F（0，1）作x轴的平行线交二次函数的图象于M、N两点．（1）求二次函数的表达式；（2）P为平面内一点，当△PMN是等边三角形时，求点P的坐标；（3）在二次函数的图象上是否存在一点E，使得以点E为圆心的圆过点F和点N，且与直线y＝﹣1相切．若存在，求出点E的坐标，并求⊙E的半径；若不存在，说明理由．11．（2021•嘉兴二模）定义：平面直角坐标系xOy中，过二次函数图象与坐标轴交点的圆，称为该二次函数的坐标圆．（1）已知点P（2，2），以P为圆心，为半径作圆．请判断⊙P是不是二次函数y＝x2﹣4x+3的坐标圆，并说明理由；（2）已知二次函数y＝x2﹣4x+4图象的顶点为A，坐标圆的圆心为P，如图1，求△POA周长的最小值；（3）已知二次函数y＝ax2﹣4x+4（0＜a＜1）图象交x轴于点A，B，交y轴于点C，与坐标圆的第四个交点为D，连结PC，PD，如图2．若∠CPD＝120°，求a的值．12．（2021•常州二模）如图1：抛物线y＝﹣x2+bx+c过点A（﹣1，0），点B（3，0），与y轴交于点C．动点E（m，0）（0＜m＜3），过点E作直线l⊥x轴，交抛物线于点M．（1）求抛物线的解析式及C点坐标；（2）连接BM并延长交y轴于点N，连接AN，OM，若AN∥OM，求m的值．（3）如图2．当m＝1时，P是直线l上的点，以P为圆心，PE为半径的圆交直线l于另一点F（点F在x 轴上方），若线段AC上最多存在一个点Q使得∠FQE＝90°，求点P纵坐标的取值范围．13．（2021•乐山模拟）如图，抛物线y＝ax2+bx+2与直线AB相交于A（﹣1，0），B（3，2），与x轴交于另一点C．（1）求抛物线的解析式；（2）在y上是否存在一点E，使四边形ABCE为矩形，若存在，请求出点E的坐标；若不存在，请说明理由；（3）以C为圆心，1为半径作⊙O，D为⊙O上一动点，求DA+DB的最小值14．（2021•河北区二模）如图，在平面直角坐标系中，抛物线y＝﹣x2+bx+3的对称轴是直线x＝2，与x 轴相交于A，B两点（点A在点B的左侧），与y轴交于点C．（Ⅰ）求抛物线的解析式及顶点坐标；（Ⅱ）M为第一象限内抛物线上的一个点，过点M作MN⊥x轴于点N，交BC于点D，连接CM，当线段CM＝CD时，求点M的坐标；（Ⅲ）以原点O为圆心，AO长为半径作⊙O，点P为⊙O上的一点，连接BP，CP，求2PC+3PB的最小值．15．（2021•长沙模拟）如图，在平面直角坐标系中，抛物线y＝ax2+bx+c（a＞0）的顶点为M，经过C（1，1），且与x轴正半轴交于A，B两点．（1）如图1，连接OC，将线段OC绕点O顺时针旋转，使得C落在y轴的负半轴上，求点C的路径长；（2）如图2，延长线段OC至N，使得ON＝，若∠OBN＝∠ONA，且，求抛物线的解析式；（3）如图3，抛物线y＝ax2+bx+c的对称轴为直线，与y轴交于（0，5），经过点C的直线l：y＝kx+m （k＞0）与抛物线交于点C、D，若在x轴上存在P1、P2，使∠CP1D＝∠CP2D＝90°，求k的取值范围．16．（2021秋•上城区校级期中）如图，已知抛物线y＝﹣x2+bx+c与x轴交于A、B两点（点A在点B左边），与y轴交于点C，⊙M是△ABC的外接圆．若抛物线的顶点D的坐标为（1，4）．（1）求抛物线的解析式，及A、B、C三点的坐标；（2）求⊙M的半径和圆心M的坐标；（3）如图2，在x轴上有点P（7，0），试在直线BC上找点Q，使B、Q、P三点构成的三角形与△ABC相似．若存在，请直接写出点坐标；若不存在，请说明理由．17．（2021秋•西湖区校级期中）我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”．如图所示，点A、B、C、D分别是“蛋圆”与坐标轴的交点，已知点D的坐标为（0，﹣3），AB为半圆的直径，半圆圆心M的坐标为（1，0），半圆半径为2．（1）求“蛋圆”抛物线部分的解析式及“蛋圆”的弦CD的长；（2）已知点E是“蛋圆”上的一点（不与点A，点B重合），点E关于x轴的对称点是点F，若点F也在“蛋圆”上，求点E坐标；（3）点P是“蛋圆”外一点，满足∠BPC＝60°，当BP最大时，直接写出点P的坐标．18．（2021•雨花区二模）如图1，已知圆O的圆心为原点，半径为2，与坐标轴交于A，C，D，E四点，B 为OD中点．（1）求过A，B，C三点的抛物线解析式；（2）如图2，连接BC，AC．点P在第一象限且为圆O上一动点，连接BP，交AC于点M，交OC于点N，当MC2＝MN•MB时，求M点的坐标；（3）如图3，若抛物线与圆O的另外两个交点分别为H，F，请判断四边形CFEH的形状，并说明理由．19．（2020•东海县二模）如图，△AOB的三个顶点A、O、B分别落在抛物线C1：y＝x2+x上，点A的坐标为（﹣4，m），点B的坐标为（n，﹣2）．（点A在点B的左侧）（1）则m＝，n＝．（2）将△AOB绕点O逆时针旋转90°得到△A'OB'，抛物线C2：y＝ax2+bx+4经过A'、B'两点，延长OB'交抛物线C2于点C，连接A'C．设△OA'C的外接圆为⊙M．①求圆心M的坐标；②试直接写出△OA'C的外接圆⊙M与抛物线C2的交点坐标（A'、C除外）．20．（2022•绿园区二模）在平面直角坐标系中，已知某二次函数的图象同时经过点A（0，3）、B（2m，3）、C（m，m+3）．其中，m≠0．（1）当m＝1时．①该二次函数的图象的对称轴是直线．②求该二次函数的表达式．（2）当|m|≤x≤|m|时，若该二次函数的最大值为4，求m的值．（3）若同时经过点A、B、C的圆恰好与x轴相切时，直接写出该二次函数的图象的顶点坐标．21．（2022•炎陵县一模）抛物线：y＝﹣x2+bx+c与y轴的交点C（0，3），与x轴的交点分别为E、G两点，对称轴方程为x＝1．（1）求抛物线的解析式；（2）如图1，过点C作y轴的垂线交抛物线于另一点D，F为抛物线的对称轴与x轴的交点，P为线段OC 上一动点．若PD⊥PF，求点P的坐标．（3）如图1，如果一个圆经过点O、点G、点C三点，并交于抛物线对称轴右侧x轴的上方于点H，求∠OHG的度数；（4）如图2，将抛物线向下平移2个单位长度得到新抛物线L，点B是顶点．直线y＝kx﹣k+4（k＜0）与抛物线L交于点M、N．与对称轴交于点G，若△BMN的面积等于2，求k的值．22．（2022•杨浦区二模）如图，已知在平面直角坐标系xOy中，抛物线y＝﹣+bx+c与x轴相交于点A （4，0），与y轴相交于点B（0，3），在x轴上有一动点E（m，0）（0＜m＜4），过点E作x轴的垂线交线段AB于点N，交抛物线于点P，过P作PM⊥AB，垂足为点M．（1）求这条抛物线的表达式；（2）设△PMN的周长为C1，△AEN的周长为C2，如果，求点P的坐标；（3）如果以N为圆心，NA为半径的圆与以OB为直径的圆内切，求m的值．【例1】（2022•闵行区二模）如图，在平面直角坐标系xOy中，抛物线y＝ax2+bx+4与x轴相交于点A（﹣1，0），B（3，0），与y轴交于点C．将抛物线的对称轴沿x轴的正方向平移，平移后交x轴于点D，交线段BC于点E，交抛物线于点F，过点F作直线BC的垂线，垂足为点G．（1）求抛物线的表达式；（2）以点G为圆心，BG为半径画⊙G；以点E为圆心，EF为半径画⊙E．当⊙G与⊙E内切时．①试证明EF与EB的数量关系；②求点F的坐标．【分析】（1）根据点A、B的坐标，设抛物线y＝a（x+1）（x﹣3），再将点C代入即可求出a的值，从而得出答案；（2）①分两种情形，当r⊙G＞r⊙E时，则GB﹣EF＝GE，则EF＝EB，当r⊙G＜r⊙E时，则EF﹣GB＝GE，设EF＝5t，FG＝3t，GE＝4t，则5t﹣GB＝4t，则GB＝t＜GE＝4t，从而得出矛盾；②由．设BD＝t，则DE＝，利用勾股定理得BE＝，则F坐标为（3﹣t，3t），代入抛物线解析式，从而解决问题．【解答】解：（1）∵点A坐标为（﹣1，0），点B坐标为（3，0）．设抛物线y＝a（x+1）（x﹣3）（a≠0），∵抛物线经过点C（0，4），∴4＝﹣3a．解得．∴抛物线的表达式是；（2）①由于⊙G与⊙E内切，当r⊙G＜r⊙E时，则EF﹣GB＝GE，设EF＝5t，FG＝3t，GE＝4t，则5t﹣GB＝4t，∴GB＝t＜GE＝4t，∴点E在线段CB的延长线上．又∵已知点E在线段BC上，∴矛盾，因此不存在．当r⊙G＞r⊙E时，则GB﹣EF＝GE，又∵GE＝GB﹣EB，∴EF＝EB；②∵OC⊥OB，FD⊥OB，∴∠COB＝∠EDB＝90°．∴．∴设BD＝t，则DE＝；在Rt△BED中，由勾股定理得，．∴，∴F坐标为（3﹣t，3t），∵F点在抛物线上，∴，∴解得，t＝0（点F与点B重合，舍去）．∴F坐标为（，）．【例2】（2022•福建模拟）如图，已知抛物线y＝ax2+bx+c与x轴相交于A，B两点，点C（2，﹣4）在抛物线上，且△ABC是等腰直角三角形．（1）求抛物线的解析式；（2）过点D（2，0）的直线与抛物线交于点M，N，试问：以线段MN为直径的圆是否过定点？证明你的结论．【分析】（1）等腰直角三角形斜边中线等于斜边一半，点的坐标，不难求出A、B两点坐标，把点A、B、C 代入二次函数解析式，解三元一次方程组就可得到函数解析式．（2））通过设过点D（2，0）的直线MN解析式为y＝k（x﹣2）＝kx﹣2k，得到关于x、关于y的方程，利用跟与系数的关系，再得到圆的解析式，待定系数法确定定点的x、y的值，确定定点的坐标．【解答】解：连接AC、BC，过点C作CP垂直于x轴于点P．在Rt△CAB中，AC＝BC，CP⊥AB，点C（2，﹣4），∴CP＝AP＝PB＝4，OP＝2，∴OA＝AP﹣OP＝4﹣2＝2，OB＝OP+PB＝4+2＝6，∴点A（﹣2，0），点B（6，0），把点A（﹣2，0），点B（6，0），点C（2，﹣4）代入函数解析式得，解得，∴抛物线的解析式为：y＝x2﹣x﹣3．故答案为：y＝x2﹣x﹣3．（2）设过点D（2，0）的直线MN解析式为y＝k（x﹣2）＝kx﹣2k，联立直线与抛物线解析式得关于x的等式：kx﹣2k＝x2﹣x﹣3，化简得＝0，x N+x M＝﹣＝4（k+1），x N x M＝＝8k﹣12..........①，联立直线与抛物线解析式得关于y的等式：y＝（+2）2﹣（+2）﹣3，化简得y2+（﹣﹣1）y﹣4＝0，y M+y N＝4k2，y M y N＝﹣16k2................②，线段MN的中点就是圆的圆心，∴x O＝（x N+x M）＝2（K+1），代入直线方程得y O＝2k2，∴圆心坐标为（2k+2，2k2），直径MN＝＝，把①、②代入上式化简整理得直径MN＝，设圆上某一点（x，y）到圆心的距离等于半径，∴＝，化简整理得16k2+12﹣8k＝x2﹣4kx﹣4x+y2﹣4k2y＝﹣4yk2﹣4kx+x2﹣4x+y2，圆过定点，所以与k值无关，看作是关于k的二次等式，k2、k的系数，常量对应相等，得﹣8＝﹣4x，x＝2，16＝﹣4y，y＝﹣4，由以上分析，所以以MN为直径的圆过定点（2，﹣4）．故答案为：以线段MN为直径的圆过定点（2，﹣4）．【例3】（2022•武汉模拟）已知抛物线y＝﹣2x2+bx+c（c＞0）．（1）如图1，抛物线与直线l相交于点M（﹣1，0），N（2，6）．①求抛物线的解析式；②过点N作MN的垂线，交抛物线于点P，求PN的长；（2）如图2，已知抛物线y＝﹣2x2+bx+c与x轴交于A、B两点，与y轴交于点C，点A，B，C，D（0，n）四点在同一圆上，求n的值．【分析】（1）①把点M（﹣1，0），N（2，6）代入到y＝﹣2x2+bx+c中，可得b和c的值．②设P（a，﹣2a2+4a+6），再利用M（﹣1，0），N（2，6），得到MN、PM、PN的表达式，最后利用勾股定理求得a的值．（2）令C（0，c），当y＝0时，代入抛物线得x A x B＝﹣，根据两角对应相等，可得△AOC∽△DOB，然后再找到对应线段成比例，即得到n的值．【解答】解：（1）①把M（﹣1，0）N（2，6）代入y＝﹣2x2+bx+c，得，解得，∴抛物线的解析式为y＝﹣2x2+4x+6；②由①，抛物线解析式为：y＝﹣2x2+4x+6，设P（a，﹣2a2+4a+6）∵M（﹣1，0），N（2，6），∴MN＝＝3，∴PM＝，PN＝，又∵PN⊥MN，则PM2＝MN2+PN2，（﹣1﹣a）2+（2a2﹣4a﹣b）2＝（3）2+（2﹣a）2+（2a2﹣4a）2．整理得：4a2﹣9a+2＝0，∴（a﹣2）（4a﹣1）＝0．∴a1＝2，a2＝．当a＝2时，P与N重合，∴a＝，PN＝．（2）证明：设OA＝﹣x A，OB＝x B，OD＝﹣n当y＝0时，﹣2x2+bx+c＝0，∴x A x B＝﹣，∴OA•OB＝﹣x A x B＝．∵∠CAO＝∠BDO，∠ACO＝∠DBO∴△AOC∽△DOB∴＝∴OA•OB＝OC•OD∴＝c•（﹣n）．∵c≠0∴n＝﹣．【例4】（2022•上海模拟）在平面直角坐标系xOy中，抛物线y＝ax2﹣3ax+2（a＜0）交y轴于点A，抛物线的对称轴交x轴于点P，联结PA．（1）求线段PA的长；（2）如果抛物线的顶点到直线PA的距离为3，求a的值；（3）以点P为圆心、PA为半径的⊙P交y轴的负半轴于点B，第一象限内的点Q在⊙P上，且劣弧＝2．如果抛物线经过点Q，求a的值．【分析】（1）分别求出P（，0），A（0，2），由两点间距离公式可求；＝×PM×OP＝×AP×3，可得a＝﹣；（2）抛物线的顶点为M（，2﹣a），由S△APM（3）连接PQ，BP，AM，设Q（t，at2﹣3at+2），求出M（﹣1，0），由垂径定理可得AM＝AQ，＝①，PQ＝AP，得②，联立①②可得a＝．【解答】解：（1）y＝ax2﹣3ax+2＝a（x﹣）2+2﹣a，∴抛物线的对称轴为x＝，∴P（，0），令x＝0，则y＝2，∴A（0，2），∴PA＝；（2）由（1）可知抛物线的顶点为M（，2﹣a），∵a＜0，∴2﹣a＞0，∴S △APM ＝×PM ×OP ＝×AP ×3，∴（2﹣a ）×＝×3，解得a ＝﹣；（3）连接PQ ，BP ，AM ，∵MP ⊥AB ，∴＝，∵＝2，∴＝，∴AM ＝AQ ，设Q （t ，at 2﹣3at +2），∵AP ＝，P （，0），∴M （﹣1，0），∴＝①，∵PQ ＝AP ，∴②，联立①②可得t ＝或t ＝﹣1（舍），将t ＝代入①，可得a ＝．1．（2021•广元）如图1，在平面直角坐标系xOy中，抛物线y＝ax2+bx+c与x轴分别相交于A、B两点，与y轴相交于点C，下表给出了这条抛物线上部分点（x，y）的坐标值：x…﹣10123…y…03430…（1）求出这条抛物线的解析式及顶点M的坐标；（2）PQ是抛物线对称轴上长为1的一条动线段（点P在点Q上方），求AQ+QP+PC的最小值；（3）如图2，点D是第四象限内抛物线上一动点，过点D作DF⊥x轴，垂足为F，△ABD的外接圆与DF 相交于点E．试问：线段EF的长是否为定值？如果是，请求出这个定值；如果不是，请说明理由．【分析】（1）运用待定系数法即可求出抛物线解析式，再运用配方法求出顶点坐标；（2）如图1，将点C沿y轴向下平移1个单位得C′（0，2），连接BC′交抛物线对称轴x＝1于点Q′，过点C作CP′∥BC′，交对称轴于点P′，连接AQ′，此时，C′、Q′、B三点共线，BQ′+C′Q′的值最小，运用勾股定理即可求出答案；（3）如图2，连接BE，设D（t，﹣t2+2t+3），且t＞3，可得DF＝t2﹣2t﹣3，BF＝t﹣3，AF＝t+1，运用圆内接四边形的性质可得∠DAF＝∠BEF，进而证明△AFD∽△EFB，利用＝，即可求得答案．【解答】解：（1）根据表格可得出A（﹣1，0），B（3，0），C（0，3），设抛物线解析式为y＝a（x+1）（x﹣3），将C（0，3）代入，得：3＝a（0+1）（0﹣3），解得：a＝﹣1，∴y＝﹣（x+1）（x﹣3）＝﹣x2+2x+3＝﹣（x﹣1）2+4，∴该抛物线解析式为y＝﹣x2+2x+3，顶点坐标为M（1，4）；（2）如图1，将点C沿y轴向下平移1个单位得C′（0，2），连接BC′交抛物线对称轴x＝1于点Q′，过点C作CP′∥BC′，交对称轴于点P′，连接AQ′，∵A、B关于直线x＝1对称，∴AQ′＝BQ′，∵CP′∥BC′，P′Q′∥CC′，∴四边形CC′Q′P′是平行四边形，∴CP′＝C′Q′，Q′P′＝CC′＝1，在Rt△BOC′中，BC′＝＝＝，∴AQ′+Q′P′+P′C＝BQ′+C′Q′+Q′P′＝BC′+Q′P′＝+1，此时，C′、Q′、B三点共线，BQ′+C′Q′的值最小，∴AQ+QP+PC的最小值为+1；（3）线段EF的长为定值1.如图2，连接BE，设D（t，﹣t2+2t+3），且t＞3，∵EF⊥x轴，∴DF＝﹣（﹣t2+2t+3）＝t2﹣2t﹣3，∵F（t，0），∴BF＝OF﹣OB＝t﹣3，AF＝t﹣（﹣1）＝t+1，∵四边形ABED是圆内接四边形，∴∠DAF+∠BED＝180°，∵∠BEF+∠BED＝180°，∴∠DAF＝∠BEF，∵∠AFD＝∠EFB＝90°，∴△AFD∽△EFB，∴＝，∴＝，∴EF＝＝＝1，∴线段EF的长为定值1．2．（2021•张家界）如图，已知二次函数y＝ax2+bx+c的图象经过点C（2，﹣3），且与x轴交于原点及点B （8，0）．（1）求二次函数的表达式；（2）求顶点A的坐标及直线AB的表达式；（3）判断△ABO的形状，试说明理由；（4）若点P为⊙O上的动点，且⊙O的半径为2，一动点E从点A出发，以每秒2个单位长度的速度沿线段AP匀速运动到点P，再以每秒1个单位长度的速度沿线段PB匀速运动到点B后停止运动，求点E 的运动时间t的最小值．【分析】（1）运用待定系数法即可求出答案；（2）运用配方法将抛物线解析式化为顶点式，得出顶点坐标，运用待定系数法求出直线AB的函数表达式；（3）方法1：如图1，过点A作AF⊥OB于点F，则F（4，0），得出△AFO、△AFB均为等腰直角三角形，即可得出答案，方法2：由△ABO的三个顶点分别是O（0，0），A（4，﹣4），B（8，0），运用勾股定理及逆定理即可得出答案；（4）以O为圆心，2为半径作圆，则点P在圆周上，根据t＝AP+PB＝PD+PB，可知当B、P、D三点共线时，PD+PB取得最小值，过点D作DG⊥OB于点G，由t＝DB＝即可求出答案．【解答】解：（1）∵二次函数y＝ax2+bx+c（a≠0）的图象经过C（2，﹣3），且与x轴交于原点及点B（8，0），∴c＝0，二次函数表达式可设为：y＝ax2+bx（a≠0），将C（2，﹣3），B（8，0）代入y＝ax2+bx得：，解得：，∴二次函数的表达式为；（2）∵＝（x﹣4）2﹣4，∴抛物线的顶点A（4，﹣4），设直线AB的函数表达式为y＝kx+m，将A（4，﹣4），B（8，0）代入，得：，解得：，∴直线AB的函数表达式为y＝x﹣8；（3）△ABO是等腰直角三角形．方法1：如图1，过点A作AF⊥OB于点F，则F（4，0），∴∠AFO＝∠AFB＝90°，OF＝BF＝AF＝4，∴△AFO、△AFB均为等腰直角三角形，∴OA＝AB＝4，∠OAF＝∠BAF＝45°，∴∠OAB＝90°，∴△ABO是等腰直角三角形．方法2：∵△ABO的三个顶点分别是O（0，0），A（4，﹣4），B（8，0），∴OB＝8，OA＝＝＝，AB＝＝＝，且满足OB2＝OA2+AB2，∴△ABO是等腰直角三角形；（4）如图2，以O为圆心，2为半径作圆，则点P在圆周上，依题意知：动点E的运动时间为t＝AP+PB，在OA上取点D，使OD＝，连接PD，则在△APO和△PDO中，满足：＝＝2，∠AOP＝∠POD，∴△APO∽△PDO，∴＝＝2，从而得：PD＝AP，∴t＝AP+PB＝PD+PB，∴当B、P、D三点共线时，PD+PB取得最小值，过点D作DG⊥OB于点G，由于，且△ABO为等腰直角三角形，则有DG＝1，∠DOG＝45°∴动点E的运动时间t的最小值为：t＝DB＝＝＝5．3．（2021•宜宾）如图1，在平面直角坐标系中，抛物线与x轴分别交于A、B两点，与y轴交于点C（0，6），抛物线的顶点坐标为E（2，8），连结BC、BE、CE．（1）求抛物线的表达式；（2）判断△BCE的形状，并说明理由；（3）如图2，以C为圆心，为半径作⊙C，在⊙C上是否存在点P，使得BP+EP的值最小，若存在，请求出最小值；若不存在，请说明理由．【分析】（1）运用待定系数法即可求得答案；（2）△BCE是直角三角形．运用勾股定理逆定理即可证明；（3）如图，在CE上截取CF＝（即CF等于半径的一半），连结BF交⊙C于点P，连结EP，则BF的长即为所求．【解答】解：（1）∵抛物线的顶点坐标为E（2，8），∴设该抛物线的表达式为y＝a（x﹣2）2+8，∵与y轴交于点C（0，6），∴把点C（0，6）代入得：a＝﹣，∴该抛物线的表达式为y＝x2+2x+6；（2）△BCE是直角三角形．理由如下：∵抛物线与x轴分别交于A、B两点，∴令y＝0，则﹣（x﹣2）2+8＝0，解得：x1＝﹣2，x2＝6，∴A（﹣2，0），B（6，0），∴BC2＝62+62＝72，CE2＝（8﹣6）2+22＝8，BE2＝（6﹣2）2+82＝80，∴BE2＝BC2+CE2，∴∠BCE＝90°，∴△BCE是直角三角形；（3）⊙C上存在点P，使得BP+EP的值最小且这个最小值为．理由如下：如图，在CE上截取CF＝（即CF等于半径的一半），连结BF交⊙C于点P，连结EP，则BF的长即为所求．理由如下：连结CP，∵CP为半径，∴＝＝，又∵∠FCP＝∠PCE，∴△FCP∽△PCE，∴＝＝，即FP＝EP，∴BF＝BP+EP，由“两点之间，线段最短”可得：BF的长即BP+EP为最小值．∵CF＝CE，E（2，8），∴由比例性质，易得F（，），∴BF＝＝．4．（2020•雨花区校级一模）如图1，已知抛物线y＝ax2﹣12ax+32a（a＞0）与x轴交于A，B两点（A在B 的左侧），与y轴交于点C．（1）连接BC，若∠ABC＝30°，求a的值．（2）如图2，已知M为△ABC的外心，试判断弦AB的弦心距d是否有最小值，若有，求出此时a的值，若没有，请说明理由；（3）如图3，已知动点P（t，t）在第一象限，t为常数．问：是否存在一点P，使得∠APB达到最大，若存在，求出此时∠APB的正弦值，若不存在，也请说明理由．【分析】（1）令y＝0，求得抛物线与x轴的交点A、B的坐标，令x＝0，用a表示C点的坐标，再由三角函数列出a的方程，便可求得a的值；（2）过M点作MH⊥AB于点H，连接MA、MC，用d表示出M的坐标，根据MA＝MC，列出a、d的关系式，再通过关系式求得结果；（3）取AB的中点T，过T作MT⊥AB，以M为圆心，MA为半径作⊙M，MT与直线y＝x交于点S，P′为直线y＝x上异于P的任意一点，连接AP′，交⊙M于点K，连接BK，MP，AP，BP，MB，MA，当P 为直线y＝x与⊙M的切点时，∠APB达到最大，利用圆圆周角性质和解直角三角形的知识求得结果便可．【解答】解：（1）连接BC，令y＝0，得y＝ax2﹣12ax+32a＝0，解得，x＝4或8，∴A（4，0），B（8，0），令x＝0，得y＝ax2﹣12ax+32a＝32a，∴C（0，32a），又∠ABC＝30°，∴tan∠ABC＝，解得，a＝；（2）过M点作MH⊥AB于点H，连接MA、MC，如图2，∴AH＝BH＝＝2，∴OH＝6，设M（6，d），∵MA＝MC，∴4+d2＝36+（d﹣32a）2，得2ad＝32a2+1，∴d＝16a+＝，∴当4时，有，即当a＝时，有；（3）∵P（t，t），∴点P在直线y＝x上，如图3，取AB的中点T，过T作MT⊥AB，以M为圆心，MA为半径作⊙M，MT与直线y＝x交于点S，P′为直线y＝x上异于P的任意一点，连接AP′，交⊙M于点K，连接BK，MP，AP，BP，MB，MA，当⊙M与直线y＝x相切时，有∠APB＝∠AKB＞∠AP′B，∴∠APB最大，此时相切点为P，设M（6，d），而T（6，0），∴S（6，6），∴∠PSM＝90°﹣∠SOT＝45°，又MP＝MB＝，∴MS＝＝，∵MS+MT＝ST＝6，∴，解得，d＝2（负根舍去），经检验，d＝2是原方程的解，也符合题意，∴M（6，2），∴MB＝2，∵∠AMB＝2∠APB，MT⊥AB，MA＝MB，∴∠AMT＝∠BMT＝∠AMB＝∠APB，∴sin∠APB＝sin∠BMT＝．5．（2020•汇川区三模）如图，在平面直角坐标系上，一条抛物线y＝ax2+bx+c（a≠0）经过A（1，0）、B （3，0）、C（0，3）三点，连接BC并延长．（1）求抛物线的解析式；（2）点M是直线BC在第一象限部分上的一个动点，过M作MN∥y轴交抛物线于点N．1°求线段MN的最大值；2°当MN取最大值时，在线段MN右侧的抛物线上有一个动点P，连接PM、PN，当△PMN的外接圆圆心Q在△PMN的边上时，求点P的坐标．【分析】（1）将三个已知点坐标代入抛物线的解析式中列出方程组求得a、b、c，便可得抛物线的解析式；（2）1°用待定系数法求出直线BC的解析式，再设M的横坐标为t，用t表示MN的距离，再根据二次函数的性质求得MN的最大值；2°分三种情况：当∠PMN＝90°时；当∠PNM＝90°时；当∠MPN＝90°时．分别求出符合条件的P点坐标便可．【解答】解：（1）把A、B、C三点的坐标代入抛物线y＝ax2+bx+c（a≠0）中，得，解得，，∴抛物线的解析式为：y＝x2﹣4x+3；（2）1°设直线BC的解析式为y＝mx+n（m≠0），则，解得，，∴直线BC的解析式为：y＝﹣x+3，设M（t，﹣t+3）（0＜t＜3），则N（t，t2﹣4t+3），∴MN＝﹣t2+3t＝﹣，∴当t＝时，MN的值最大，其最大值为；2°∵△PMN的外接圆圆心Q在△PMN的边上，∴△PMN为直角三角形，由1°知，当MN取最大值时，M（），N（），①当∠PMN＝90°时，PM∥x轴，则P点与M点的纵坐标相等，∴P点的纵坐标为，当y＝时，y＝x2﹣4x+3＝，解得，x＝，或x＝（舍去），∴P（）；②当∠PNM＝90°时，PN∥x轴，则P点与N点的纵坐标相等，∴P点的纵坐标为﹣，当y＝﹣时，y＝x2﹣4x+3＝﹣，解得，x＝，或x＝（舍去），∴P（，）；③当∠MPN＝90°时，则MN为△PMN的外接圆的直径，∴△PMN的外接圆的圆心Q为MN的中点，∴Q（），半径为，过Q作QK∥x轴，与在MN右边的抛物线图象交于点K，如图②，令y＝，得y＝x2﹣4x+3＝，解得，x＝＜（舍），或x＝，∴K（，），∴QK＝＞，即K点在以MN为直径的⊙Q外，设抛物线y＝x2﹣4x+3的顶点为点L，则l（2，﹣1），连接LK，如图②，则L到QK的距离为，LK＝，设Q点到LK的距离为h，则，∴＝，∴直线LK下方的抛物线与⊙Q没有公共点，∵抛物线中NL部分（除N点外）在过N点与x轴平行的直线下方，∴抛物线中NL部分（除N点外）与⊙Q没有公共点，∵抛物线K点右边部分，在过K点与y轴平行的直线的右边，∴抛物线K点右边部分与⊙Q没有公共点，综上，⊙Q与MN右边的抛物线没有交点，∴在线段MN右侧的抛物线上不存在点P，使△PMN的外接圆圆心Q在MN边上；综上，点P的坐标为（）或（）．6．（2021•开福区模拟）如图，在平面直角坐标系中，抛物线y＝x2﹣bx+c交x轴于点A，B，点B的坐标为（4，0），与y轴于交于点C（0，﹣2）．（1）求此抛物线的解析式；（2）在抛物线上取点D，若点D的横坐标为5，求点D的坐标及∠ADB的度数；（3）在（2）的条件下，设抛物线对称轴l交x轴于点H，△ABD的外接圆圆心为M（如图1），①求点M的坐标及⊙M的半径；②过点B作⊙M的切线交于点P（如图2），设Q为⊙M上一动点，则在点运动过程中的值是否变化？若不变，求出其值；若变化，请说明理由．【分析】（1）c＝﹣2，将点B的坐标代入抛物线表达式得：0＝﹣4b﹣2，解得：b＝﹣，即可求解；。