集合的基本运算资料讲解

集合的三种基本运算集合的三种运算分别是有交集、并集、补集。

集合，简称集，是数学中一个基本概念，也是集合论的主要研究对象。

集合论的基本理论创立于19世纪，关于集合的最简单的说法就是在朴素集合论（最原始的集合论）中的定义，即集合是“确定的一堆东西”，集合里的“东西”则称为元素。

现代的集合一般被定义为：由一个或多个确定的元素所构成的整体。

集合的基本运算：交集、并集、相对补集、绝对补集、子集。

（1）交集：集合论中，设A，B是两个集合，由所有属于集合A且属于集合B的元素所组成的集合，叫做集合A与集合B的交集（intersection），记作A∩B。

（2）并集：给定两个集合A，B，把他们所有的元素合并在一起组成的集合，叫做集合A与集合B的并集，记作A∪B，读作A并B。

（3）相对补集：若A和B是集合，则A在B中的相对补集是这样一个集合：其元素属于B但不属于A，B - A= { x| x∈B且x∉A}。

（4）绝对补集：若给定全集U，有A⊆U，则A在U中的相对补集称为A的绝对补集（或简称补集），写作∁UA。

（5）子集：子集是一个数学概念：如果集合A的任意一个元素都是集合B的元素，那么集合A称为集合B的子集。

符号语言：若∀a∈A，均有a∈B，则A⊆B。

基数：集合中元素的数目称为集合的基数，集合A的基数记作card(A)。

当其为有限大时，集合A称为有限集，反之则为无限集。

一般的，把含有有限个元素的集合叫做有限集，含无限个元素的集合叫做无限集。

假设有实数x < y：①[x，y] ：方括号表示包括边界，即表示x到y之间的数以及x和y；②(x，y)：小括号是不包括边界，即表示大于x、小于y的数。

集合的基本运算知识点在数学的广阔天地中，集合是一个非常基础且重要的概念。

而集合的基本运算，则是我们深入理解和运用集合的关键。

首先，让我们来了解一下什么是集合。

简单来说，集合就是把一些具有共同特征的对象放在一起组成的一个整体。

比如说，一个班级里所有的男生可以组成一个集合，一年中所有的月份也可以组成一个集合。

集合的表示方法有多种，常见的有列举法、描述法和图示法。

列举法就是把集合中的元素一一列举出来，像{1, 2, 3, 4, 5}就是用列举法表示的一个集合。

描述法呢，则是通过描述元素所具有的共同特征来表示集合，比如{x ｜ x 是小于 10 的正整数}。

图示法中，最常用的就是韦恩图，它能非常直观地展示集合之间的关系。

接下来，咱们重点说一说集合的基本运算。

集合的基本运算主要包括并集、交集和补集。

并集，用符号“∪”表示。

如果有两个集合 A 和 B，那么它们的并集A∪B 就是由属于 A 或者属于 B 的所有元素组成的集合。

举个例子，如果集合 A ＝｛1, 2, 3}，集合 B ＝｛3, 4, 5}，那么 A∪B ＝｛1, 2, 3, 4, 5}。

也就是说，把两个集合中的元素统统放到一起，去掉重复的，就是它们的并集。

交集，用符号“∩”表示。

集合 A 和集合 B 的交集A∩B 是由同时属于 A 和 B 的所有元素组成的集合。

还是上面的例子，集合 A ＝｛1, 2, 3}，集合 B ＝｛3, 4, 5}，那么A∩B ＝｛3}，只有 3 这个元素同时属于 A 和 B。

补集呢，相对来说稍微复杂一点。

设 U 是一个全集，集合 A 是 U的一个子集，那么 A 在 U 中的补集记作∁UA，是由属于 U 但不属于A 的所有元素组成的集合。

比如说，U ＝｛1, 2, 3, 4, 5}，A ＝｛1, 2, 3}，那么∁UA ＝｛4, 5}。

为了更好地理解这些运算，我们再来看几个实际的例子。

假设学校举办运动会，参加跑步比赛的同学组成集合 A ＝｛张三，李四，王五}，参加跳远比赛的同学组成集合 B ＝｛李四，赵六，孙七}。

集合的基本关系及运算【学习目标】1.理解集合之间包含与相等的含义，能识别一些给定集合的子集．在具体情境中，了解空集和全集的含义．2.理解两个集合的交集和并集的含义，会求两个简单集合的交集与并集．理解在给定集合中一个子集的补集的含义，会求给定子集的补集．【要点梳理】要点一、集合之间的关系1.集合与集合之间的“包含”关系集合A 是集合B 的部分元素构成的集合，我们说集合B 包含集合A ；子集：如果集合A 的任何一个元素都是集合B 的元素，我们说这两个集合有包含关系，称集合A 是集合B 的子集(subset).记作：A B(B A)⊆⊇或，当集合A 不包含于集合B 时，记作A B ，用Venn 图表示两个集合间的“包含”关系：A B(B A)⊆⊇或要点诠释：（1）“A 是B 的子集”的含义是：A 的任何一个元素都是B 的元素，即由任意的x A ∈，能推出x B ∈．（2）当A 不是B 的子集时，我们记作“A ⊆B (或B ⊇A )”，读作：“A 不包含于B ”（或“B 不包含A ”）． 真子集：若集合A B ⊆，存在元素x ∈B 且x A ∉，则称集合A 是集合B 的真子集(proper subset).记作：A B(或B A)规定：空集是任何集合的子集，是任何非空集合的真子集.2.集合与集合之间的“相等”关系A B B A ⊆⊆且，则A 与B 中的元素是一样的，因此A=B要点诠释：任何一个集合是它本身的子集，记作A A ⊆．要点二、集合的运算1.并集一般地，由所有属于集合A 或属于集合B 的元素所组成的集合，称为集合A 与B 的并集，记作：A ∪B 读作：“A 并B ”，即：A ∪B={x|x ∈A ，或x ∈B}Venn 图表示：要点诠释：（1）“x ∈A ，或x ∈B ”包含三种情况：“,x A x B ∈∉但”；“,x B x A ∈∉但”；“,x A x B ∈∈且”．（2）两个集合求并集，结果还是一个集合，是由集合A 与B 的所有元素组成的集合(重复元素只出现一次).2.交集一般地，由属于集合A 且属于集合B 的元素所组成的集合，叫做集合A 与B 的交集；记作：A ∩B ，读作：“A 交B ”，即A ∩B={x|x ∈A ，且x ∈B}；交集的Venn 图表示：要点诠释：（1）并不是任何两个集合都有公共元素，当集合A 与B 没有公共元素时，不能说A 与B 没有交集，而是A B =∅．（2）概念中的“所有”两字的含义是，不仅“A ∩B 中的任意元素都是A 与B 的公共元素”，同时“A 与B 的公共元素都属于A ∩B ”．（3）两个集合求交集，结果还是一个集合，是由集合A 与B 的所有公共元素组成的集合.3.补集全集：一般地，如果一个集合含有我们所研究问题中所涉及的所有元素，那么就称这个集合为全集，通常记作U.补集：对于全集U 的一个子集A ，由全集U 中所有不属于集合A 的所有元素组成的集合称为集合A 相对于全集U 的补集(complementary set)，简称为集合A 的补集，记作：U U A A={x|x U x A}∈∉；即且；补集的Venn 图表示：要点诠释：（1）理解补集概念时，应注意补集U A 是对给定的集合A 和()U A U ⊆相对而言的一个概念，一个确定的集合A ，对于不同的集合U ，补集不同．（2）全集是相对于研究的问题而言的，如我们只在整数范围内研究问题，则Z 为全集；而当问题扩展到实数集时，则R 为全集，这时Z 就不是全集．（3）U A 表示U 为全集时A 的补集，如果全集换成其他集合（如R ）时，则记号中“U ”也必须换成相应的集合（即R A ）．4.集合基本运算的一些结论A B A A B B A A=A A =A B=B A ⋂⊆⋂⊆⋂⋂∅∅⋂⋂，，，，A AB B A B A A=A A =A A B=B A ⊆⋃⊆⋃⋃⋃∅⋃⋃，，，，U U (A)A=U (A)A=⋃⋂∅，若A ∩B=A ，则A B ⊆，反之也成立若A ∪B=B ，则A B ⊆，反之也成立若x ∈(A ∩B)，则x ∈A 且x ∈B若x ∈(A ∪B)，则x ∈A ，或x ∈B求集合的并、交、补是集合间的基本运算，运算结果仍然还是集合，区分交集与并集的关键是“且”与“或”，在处理有关交集与并集的问题时，常常从这两个字眼出发去揭示、挖掘题设条件，结合Venn 图或数轴进而用集合语言表达，增强数形结合的思想方法.【典型例题】类型一、集合间的关系例1. 集合{}|2,A a a k k N ==∈，集合21|1(1)(1),8n B b b n n N ⎧⎫⎡⎤==--⋅-∈⎨⎬⎣⎦⎩⎭，那么,A B 间的关系是（ ）.A. A BB. B AC. A =BD.以上都不对【答案】B【解析】先用列举法表示集合A 、B ，再判断它们之间的关系.由题意可知，集合A 是非负偶数集，即{}0,2,4,6,8,A =⋅⋅⋅.集合B 中的元素211(1)(1)8n b n ⎡⎤=--⋅-⎣⎦0()1(1)(1)()4n n n n ⎧⎪=⎨+-⎪⎩为非负偶数时，为正奇数时.而1(1)(1)4n n +-（n 为正奇数时）表示0或正偶数，但不是表示所有的正偶数，即1,3,5,7,n =⋅⋅⋅.由1(1)(1)4n n +-依次得0,2,6,12，⋅⋅⋅，即{}0261220B =⋅⋅⋅，，，，，. 综上知，B A ，应选B .【总结升华】判断两个集合间的关系的关键在于：弄清两个集合的元素的构成，也就是弄清楚集合是由哪些元素组成的.这就需要把较为抽象的集合具体化（如用列举法来表示集合）、形象化（用Venn 图，或数形集合表示）.举一反三：【变式1】若集合{}{}|21,,|41,A x x k k z B x x l l z ==-∈==±∈，则（ ）.A. A BB. B AC. A =BD.A B Z =【答案】C例2. 写出集合{a ，b ，c}的所有不同的子集.【解析】不含任何元素子集为∅，只含1个元素的子集为{a}，{b}，{c}，含有2个元素的子集有{a ，b}，{a ，c}，{b ，c}，含有3个元素的子集为{a ，b ，c}，即含有3个元素的集合共有23=8个不同的子集.如果集合增加第4个元素d ，则以上8个子集仍是新集合的子集，再将第4个元素d 放入这8个子集中，会得到新的8个子集，即含有4个元素的集合共有24=16个不同子集，由此可推测，含有n 个元素的集合共有2n 个不同的子集.【总结升华】要写出一个集合的所有子集，我们可以按子集的元素个数的多少来分别写出.当元素个数相同时，应依次将每个元素考虑完后，再写剩下的子集.如本例中要写出2个元素的子集时，先从a 起，a 与每个元素搭配有{a ，b}，{a ，c}，然后不看a ，再看b 可与哪些元素搭配即可.同时还要注意两个特殊的子集：∅和它本身.举一反三：【变式1】已知{},a b A ⊆{},,,,a b c d e ，则这样的集合A 有 个.【答案】7个【变式2】（2016 湛江一模）已知集合A ={1，2，3}，平面内以（x ，y ）为坐标的点集合B ={（x ，y ）｜x ∈A ，y ∈A ，x +y ∈A }，则B 的子集个数为（ ）A ．3B ．4C ．7D ．8【答案】D【解析】∵ 集合A ={1，2，3}，平面内以（x ，y ）为坐标的点集合B ={（x ，y ）｜x ∈A ，y ∈A ，x +y ∈A }，∴B ={（1，1），（1，2），（2，1）}∴B 的子集个数为：23=8个．故选D ．例3．集合A={x|y=x 2+1}，B={y|y=x 2+1}，C={(x,y)|y=x 2+1}，D={y=x 2+1}是否表示同一集合？【答案】以上四个集合都不相同【解析】集合A={x|y=x 2+1}的代表元素为x ，故集合A 表示的是函数y=x 2+1中自变量x 的取值范围，即函数的定义域A=(,)-∞+∞；集合B={y|y=x 2+1}的代表元素为y ，故集合B 表示的是函数y=x 2+1中函数值y 的取值范围，即函数的值域B=[1,)+∞；集合C={(x,y)|y=x 2+1}的代表元素为点（x ，y ），故集合C 表示的是抛物线y=x 2+1上的所有点组成的集合；集合D={y=x 2+1}是用列举法表示的集合，该集合中只有一个元素：方程y=x 2+1．【总结升华】认清集合的属性，是突破此类题的关键.首先应当弄清楚集合的表示方法，是列举法还是描述法；其次对于用描述法表示的集合一定要认准代表元素，准确理解对代表元素的限制条件．举一反三：【变式1】 设集合{(,)|34}M x y y x ==+，{(,)|32}N x y y x ==--，则MN =（ ） A. {1,1}- B. {1,1}x y =-= C.(1,1)- D. {(1,1)}-【答案】D【解析】排除法：集合M 、N 都是点集，因此M N 只能是点集，而选项A 表示二元数集合，选项B 表示二元等式集合，选项C 表示区间(1,1)-（无穷数集合）或单独的一个点的坐标（不是集合），因此可以判断选D ．【变式2】 设集合{|21,}M x y x x Z ==+∈，{|21,}N y y x x Z ==+∈，则M 与N 的关系是（ ） A. N M B. M N C. N M = D. N M =∅ 【答案】A【解析】集合M 表示函数21,y x x Z =+∈的定义域，有{}M =整数；集合N 表示函数21,y x x Z =+∈的值域，有{}N =奇数，故选A.【高清课堂：集合的概念、表示及关系 377430 例2】【变式3】 设M={x|x=a 2+1，a ∈N +}，N={x|x=b 2-4b+5，b ∈N +}，则M 与N 满足( ) A. M=N B. M N C. N M D. M ∩N=∅【答案】B【解析】 当a ∈N +时，元素x=a 2+1，表示正整数的平方加1对应的整数，而当b ∈N +时，元素x=b 2-4b+5=(b-2)2+1，其中b-2可以是0，所以集合N 中元素是自然数的平方加1对应的整数，即M 中元素都在N 中，但N 中至少有一个元素x=1不在M 中，即M N ，故选B.【高清课堂：集合的概念、表示及关系 377430 例3】例4．已知},,,0{},,,{y x N y x xy x M =-=若M =N ，则+++2()(x y x )()1001002y x y +++ = ．A ．－200B ．200C ．－100D ．0【思路点拨】解答本题应从集合元素的三大特征入手，本题应侧重考虑集合中元素的互异性．【答案】D【解析】由M=N ，知M ，N 所含元素相同.由O ∈{0，|x|，y}可知O {x,xy,x-y}∈若x=0，则xy=0，即x 与xy 是相同元素，破坏了M 中元素互异性，所以x ≠0.若x ·y=0，则x=0或y=0，其中x=0以上讨论不成立，所以y=0，即N 中元素0，y 是相同元素，破坏了N 中元素的互异性，故xy ≠0 0x-y=，则x=y ，M ，N 可写为M={x ，x 2，0}，N={0，|x|，x}由M=N 可知必有x 2=|x|，即|x|2=|x|∴|x|=0或|x|=1若|x|=0即x=0，以上讨论知不成立若|x|=1即x=±1当x=1时，M 中元素|x|与x 相同，破坏了M 中元素互异性，故 x ≠1当x=-1时，M={-1，1，0}，N={0，1，-1}符合题意，综上可知，x=y=-1∴+++2()(x y x )()1001002y x y +++ =-2+2-2+2+…+2=0【总结升华】解答本题易忽视集合的元素具有的“互异性”这一特征，而找不到题目的突破口．因此，集合元素的特征是分析解决某些集合问题的切入点．举一反三：【变式1】设a ，b ∈R ，集合b {1,a+b,a}={0,,b}a，则b-a=( ) 【答案】2【解析】由元素的三要素及两集合相等的特征：b 1{0,,b},0{1,a+b,a}a 0a b=0a∈∈≠∴+，又， ∴当b=1时，a=-1，b {0,b}={0,-1,1}a∴， 当b =1a时，∴b=a 且a+b=0，∴a=b=0(舍) ∴综上：a=-1，b=1，∴b-a=2.类型二、集合的运算例 5. 设集合{}{}|3,,|31,A x x k k Z B y y k k Z ==∈==+∈，{}|32,C z z k k Z ==+∈，{}|61,D w w k k Z ==+∈，求,,,A B A C B C B D .【答案】A B A C B C ===∅,B D D =【解析】先将集合A 、B 、C 、D 转化为文字语言叙述，以便弄清楚它们的构成，再求其交集即可. 集合{}|3,A x x k k Z ==∈表示3的倍数所组成的集合；集合{}|31,B x x k k Z ==+∈表示除以3余1的整数所组成的集合；集合{}|32,C x x k k Z ==+∈表示除以3余2的整数所组成的集合；集合{}|61,D x x k k Z ==+∈表示除以6余1的整数所组成的集合；A B A C B C ∴===∅,B D D =.【总结升华】求两个集合的交集或并集，关键在于弄清两个集合由哪些元素所构成的，因而有时需要对集合进行转化，或具体化、形象化.如本例中转化为用自然语言来描述这些集合，有利于弄清集合的元素的构成.类似地，若一个集合元素的特征由不等式给出时，利用数轴就能使问题直观形象起来.举一反三：【变式】（2014 河南洛阳期中）已知集合{}2M x y x ==-，{}2N y y x==，则M ∩N ＝（ ） A ．∅ B ．(){}11, C ．{}0x x ≥ D ．{}0y y >【答案】C【解析】集合M 中的代表元素是x ，集合N 的代表元素是y ，表示构成相关函数的因变量取值范围，故可知：M ={x |x ∈R}，N ={y |y ≥0}，所以M ∩N ={x |x ≥0}，选C ．例6.（2016春 福建期中）已知全集U =R ，集合A ={x ∈R ｜x 2－3x －4＜0}，B ={x ∈R ｜2a ＜x ＜4a ，a ∈R }（1）当a =1时，求()U A B ；（2）若A ∪B =A ，求a 的取值范围．【思路点拨】（1）将a =1代入B ，求出B ，得到B 的补集，从而求出其和A 的交集即可；（2）根据A 、B 的包含关系，通过讨论B 得到关于a 的不等式组，解出即可．【答案】（1）(){|12}U A B x R x =∈-<≤；（2）102a -≤≤或a ≥4 【解析】A ={x ∈R ｜x 2－3x －4＜0}，（1）当a =1时，B ={x ∈R ｜2＜x ＜5}，∴(){|12}U A B x R x =∈-<≤（2）由已知A ∪B =A ，得B A ⊆；①当B =∅时2a ≥4+a ，即a ≥4，满足B A ⊆；②当B ≠∅时242144a a a a <+⎧⎪≥-⎨⎪+≤⎩，即102a -≤≤时，满足B A ⊆； 综上所述a 的取值范围为102a -≤≤或a ≥4． 举一反三：【变式1】（1）已知：M={x|x ≥2}，P={x|x 2-x-2=0}，求M ∪P 和M ∩P ；（2）已知：A={y|y=3x 2}， B={y|y=-x 2+4}， 求：A ∩B ，A ∪B ；（3）已知集合A={-3， a 2 ，1+a}， B={a-3， a 2+1， 2a-1}， 其中a ∈R ，若A ∩B={-3}，求A ∪B.【答案】（1）{x|x ≥2或x=-1}，{2}；（2）{y|0≤y ≤4}，R ；（3）{-4，-3，0，1，2}.【解析】（1）P={2，-1}，M ∪P={x|x ≥2或x=-1}，M ∩P={2}.（2）∵A={y|y ≥0}， B={y|y ≤4}， A ∩B={y|0≤y ≤4}， A ∪B=R .（3）∵A ∩B={-3}，-3∈B ，则有：①a-3=-3⇒a=0， A={-3，0，1}， B={-3，1，-1}⇒A ∩B={-3，1}，与已知不符，∴a ≠0；②2a-1=-3⇒a=-1， ∴ A={-3，1，0}， B={-4，2，-3}， 符合题设条件，∴A ∪B={-4，-3，0，1，2}.【总结升华】此例题既练习集合的运算，又考察了集合元素的互异性.其中（1）易错点为求并集时，是否意识到要补上孤立点-1；而（2）中结合了二次函数的值域问题；（3）中根据集合元素的互异性，需要进行分类讨论，当求出a 的一个值时，又要检验是否符合题设条件.【高清课堂：集合的运算 377474 例5】【变式2】设集合A={2，a 2-2a ，6}，B={2，2a 2，3a-6}，若A ∩B={2，3}，求A ∪B.【答案】｛2，3，6，18｝【解析】由A ∩B={2，3}，知元素2，3是A ，B 两个集合中所有的公共元素，所以3∈｛2，a 2-2a ，6｝，则必有a 2-2a=3，解方程a 2-2a-3=0得a=3或a=-1当a=3时，A={2，3，6}，B={2，18，3}∴A ∪B={2，3，6}∪｛2，18，3｝=｛2，3，6，18｝当a=-1时，A={2，3，6}，B={2，2，-9}这既不满足条件A ∩B={2，3}，也不满足B 中元素具有互异性，故a=-1不合题意，应舍去. 综上A ∪B=｛2，3，6，18｝例7.已知全集{}{}21,2,3,4,5,|40U A x x px ==++=，求C u A.【思路点拨】C u A 隐含了A U ⊆，对于A U ⊆，注意不要忘记A =∅的情形.【答案】 当44p -<<时，C u A={}1,2,3,4,5；当4p =-时，C u A={}1,3,4,5；当5p =-时，C u A={}2,3,5.【解析】当A =∅时，方程240x px ++=无实数解.此时2160,44p p ∆=-<-<<.C u A=U当A ≠∅时，二次方程240x px ++=的两个根12,x x ，必须属于U .因为124x x =，所以只可能有下述情形：当122x x ==时，4p =-，此时{}2,A = C u A={}1,3,4,5；当121,4x x ==时，5p =-，此时{}1,4,A = C u A={}2,3,5.综上所述，当44p -<<时，C u A={}1,2,3,4,5；当4p =-时，C u A={}1,3,4,5；当5p =-时，C u A={}2,3,5.【总结升华】求集合A 的补集，只需在全集中剔除集合A 的元素后组成一个集合即可.由于本题中集合A 的元素不确定，因此必须分类讨论才行.举一反三：【变式1】设全集U={x ∈N +|x ≤8}，若A ∩(C u B)={1，8}，(C u A)∩B={2，6}，(C u A)∩(C u B)={4，7}，求集合A ，B.【答案】{1，3，5，8}，{2，3，5，6}.【解析】全集U={1，2，3，4，5，6，7，8}由A ∩(C u B)={1，8}知，在A 中且不在B 中的元素有1，8；由(C u A)∩B={2，6}，知不在A 中且在B 中的元素有2，6；由(C u A)∩(C u B)={4，7}，知不在A 中且不在B 中的元素有4，7，则元素3，5必在A ∩B 中.由集合的图示可得A={1，3，5，8}，B={2，3，5，6}.类型三、集合运算综合应用例8．（2014 北京西城学探诊）已知集合A ={x |－4≤x ＜2}， B ={x |－1≤x ＜3}，C ={x |x ≥a ，a ∈R}．（1）若（A ∪B ）∩C =∅，求实数a 的取值范围；（2）若（A ∪B ）C ，求实数a 的取值范围．【思路点拨】（1）画数轴；（2）注意是否包含端点．【答案】（1）a ≥3 （2）a ≤－4【解析】（1）∵A ={x |－4≤x ＜2}， B ={x |－1≤x ＜3}，又（A ∪B ）∩C =∅，如图，a ≥3；（2）画数轴同理可得：a ≤－4．【总结升华】此问题从表面上看是集合的运算，但其本质是一个定区间，和一个动区间的问题．思路是，使动区间沿定区间滑动，数形结合解决问题．举一反三：【变式1】已知集合P=｛x ︱x 2≤1｝,M=｛a ｝.若P ∪M=P,则a 的取值范围是（ ）A ．(-∞, -1]B ．[1, +∞）C ．[-1，1]D ．（-∞，-1] ∪[1，+∞）【答案】C【解析】P =｛x ︱11x -≤≤｝又 P M P =， ∴M P ⊆，∴ 11a -≤≤故选C ．例9. 设集合{}{}222|40,|2(1)10,A x x x B x x a x a a R =+==+++-=∈.（1）若A B B =，求a 的值；（2）若A B B =，求a 的值.【思路点拨】明确A B B =、A B B =的含义，根据问题的需要，将其转化为等价的关系式B A ⊆和A B ⊆，是解决本题的关键.同时，在包含关系式B A ⊆中，不要漏掉B =∅的情况.【答案】（1）1a =或1a ≤-；（1）2．【解析】首先化简集合A ，得{}4,0A =-.（1）由A B B =，则有B A ⊆，可知集合B 为∅，或为{}0、{}4-，或为{}0,4-.①若B =∅时，224(1)4(1)0a a ∆=+--<，解得1a <-.②若0B ∈,代入得21011a a a -=⇒==-或.当1a =时，{}{}2|400,4,B x x x A =+==-=符合题意；当1a =-时，{}{}2|00,B x x A ===⊆也符合题意. ③若4B -∈，代入得2870a a -+=，解得7a =或1a =.当1a =时，已讨论，符合题意；当7a =时，{}{}2|1648012,4B x x x =++==--，不符合题意. 由①②③，得1a =或1a ≤-.（2）,A B B A B =∴⊆.又{}4,0A =-，而B 至多只有两个根，因此应有A B =，由（1）知1a =. 【总结升华】两个等价转化：,A B B A B A B B B A =⇔⊆=⇔⊆非常重要，注意应用.另外，在解决有条件A B ⊆的集合问题时，不要忽视A ≠∅的情况.举一反三：【变式1】已知集合{}{}222,|120A B x x ax a =-=++-=，若AB B =,求实数a 的取值范围. 【答案】4,a ≥或4a <-【解析】A B B =,B A ∴⊆.①当B =∅时，此时方程22120x ax a ++-=无解，由0∆<，解得4,a >或4a <-.②当B ≠∅时，此时方程22120x ax a ++-=有且仅有一个实数解-2， 0∴∆=，且22(2)2120a a --+-=，解得4a =.综上，实数a 的取值范围是4,a ≥或4a <-.【变式2】设全集U R =，集合{}{}|12,|40A x x B x x p =-≤≤=+<，若BC u A ，求实数p 的取值范围.【答案】4p ≥ 【解析】 C u A={}|1,2x x x <->或，|4p B x x ⎧⎫=<-⎨⎬⎩⎭. B C u A ，∴14p -≤-，即4p ≥.∴实数p 的取值范围是4p ≥.。

集合的基本概念与运算集合是数学中一个基本的概念，简单地说，集合是由元素构成的一种集合结构。

在数学中，集合和集合运算能够被应用到各种各样的领域，比如计算机科学、物理学、经济学等。

本文将深入探讨集合的基本概念和运算。

一、基本概念在集合的讨论中，我们需要先了解一些基本概念。

首先，元素是指集合中的一个个体。

例如，{1, 2, 3}中的1、2、3就是元素。

其次，集合可以用花括号{}来表示，例如{1, 2, 3}就是一个集合。

注意，集合中的元素是无序的，也就是说{1, 2, 3}和{3, 2, 1}是等价的。

另外，集合中的元素必须是不同的，例如{1, 1, 2}就不是一个合法的集合，因为其中有重复的元素。

集合的大小可以用“|S|”来表示，其中S是集合的名字。

比如{1, 2, 3}的大小是3。

二、集合运算在集合的讨论中，我们需要介绍一些集合运算。

这些集合运算包括并集、交集、补集等。

并集对于两个集合A、B，它们的并集是指由它们中的所有元素组成的集合，用“∪”表示。

例如，如果A={1, 2}，B={2, 3}，则它们的并集是{1, 2, 3}，即A∪B={1, 2, 3}。

需要注意的是，如果两个集合的元素有重复，重复的元素只会出现一次。

交集对于两个集合A、B，它们的交集是指它们中共同包含的元素所组成的集合，用“∩”表示。

例如，如果A={1, 2}，B={2, 3}，则它们的交集是{2}，即A∩B={2}。

补集对于一个集合A和它的一个父集合U，A的补集是指U中不包含A中所有元素的集合，用“A'”表示。

例如，如果U={1, 2, 3}，A={1, 2}，则A的补集是{3}，即A'={3}。

三、常用集合运算规则对于集合的运算，还有一些常用的规则。

结合律对于任意三个集合A、B、C，它们的并集和交集都满足结合律。

即(A∪B)∪C=A∪(B∪C)，(A∩B)∩C=A∩(B∩C)。

交换律对于任意两个集合A、B，它们的并集和交集都满足交换律。

集合的四种基本运算稿子一嘿，亲爱的小伙伴们！今天咱们来聊聊集合的四种基本运算，超有趣的哟！先说并集吧。

这就像是把两个篮子里的水果都放到一个大篮子里。

比如集合 A 里有苹果、香蕉，集合 B 里有橙子、草莓，那 A 和B 的并集就是苹果、香蕉、橙子、草莓，都在一块儿啦，是不是很简单？再讲讲交集。

这个呀，就好比找两个篮子里都有的水果。

还是刚才那两个集合，要是只有香蕉同时在 A 和 B 里，那香蕉就是它们的交集。

然后是差集。

比如说集合 A 减去集合 B，就是把集合 A 里属于集合 B 的那些东西拿掉，剩下的就是差集。

就好像从 A 篮子里把和B 篮子一样的水果拿走。

说说补集。

假如我们有个大的集合 U，还有个小集合 A，那 A 在U 里的补集，就是在 U 里但不在 A 里的那些东西。

怎么样，集合的这四种基本运算是不是还挺好玩的？多练习练习，咱们就能熟练掌握啦！稿子二嗨呀，朋友们！今天咱们来好好唠唠集合的四种基本运算。

并集呢，你就想象成两个帮派合并，把两边的人都算上。

比如说一个帮派有、，另一个帮派有、赵六，那并集就是、、、赵六都在一起。

交集呢，这就像是两个帮派里都有的共同成员。

假设一个帮派喜欢武术，另一个帮派喜欢书法，而同时喜欢武术和书法的就只有小明，那小明就是这两个帮派的交集。

差集呢，好比一个帮派开除一些人。

比如原来的帮派有小陈、小周，开除了小陈，剩下的小周就是差集。

补集呢，就像是整个江湖是个大集合，其中一个门派是个小集合。

门派之外的那些江湖人士就是这个门派在整个江湖里的补集。

集合的这四种运算呀，其实不难，只要咱们多琢磨琢磨，很快就能搞明白的！加油哦！。

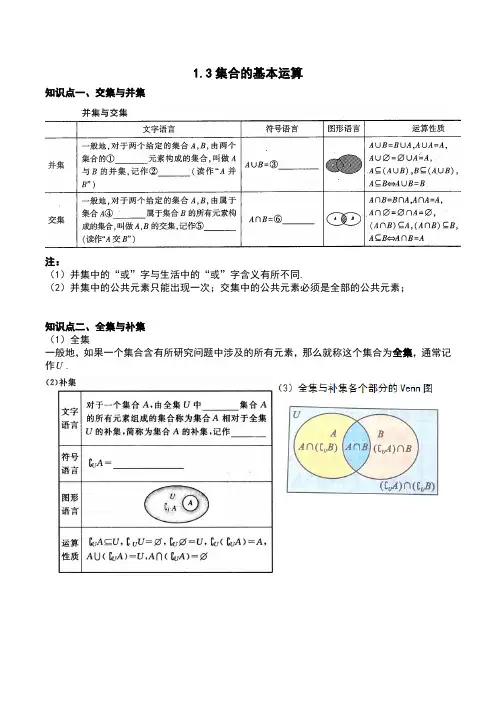
1.3集合的基本运算知识点一、交集与并集注：（1）并集中的“或”字与生活中的“或”字含义有所不同.（2）并集中的公共元素只能出现一次；交集中的公共元素必须是全部的公共元素；知识点二、全集与补集（1）全集一般地，如果一个集合含有所研究问题中涉及的所有元素，那么就称这个集合为全集，通常记作U.知识点三、德•摩根定律知识点四、集合中元素的个数我们用card 来表示有限集合A 中元素的个数，记作card (A).例如，A=｛a ，b ，c ｝，则card(A)=3.一般地，对任意两个有限集合A ，B ，C ，有：（1）card (A ⋃B)=card (A)+card (B)-card (A ⋂B).（2）card (A ⋃B ⋃C)=card (A)+card (B)+card (C)-card (A ⋂B)-card (A ⋂C)-card (B ⋂C)+ card (A ⋂B ⋂C).例题讲解一、交集、并集、补集的基本运算1、已知集合{}3,2,1=A ，{}A x x y y B ∈-==,12|，则=⋃B A （ ） A.{}321，， B.{}3211，，，- C.{}5321，，， D.{}5321，，，-2、已知集合{}21|<<-=x x A ，{}1|>=x x B ，则=⋃B A （ ）A.{}21|<<-x xB.{}21|<<x xC.{}1|->x xD.{}1|>x x3、已知集合{}6101，，，-=A ，{}R x x x B ∈>=，0|则=⋂B A .4、已知全集{}4,3,2,1=U ，集合{}2,1=A ，集合{}3,2=B ，则()B A C U ⋃=（ ） A.{}431，， B.{}43， C.{}3 D.{}45、(1)已知全集U ，集合A=｛1，3，5，7｝，C U A=｛2，4，6｝，C U B=｛1，4，6｝，则集合B= .(2)已知A ，B 均为集合U=｛1，3，5，7，9｝的子集，且A ⋂B=｛3｝，(C U B)⋂A=｛9｝，则A=（ ）A.｛1，3｝B.｛3，7，9｝C.｛3 ，5，9｝D.｛3，9｝6、设全集U=｛0，1，2，3，4｝，集合A={0，1，2，3}，B={2，3，4},则(C U A)⋃(C U B)= （ ）A. ｛0｝B.｛0，1｝C.｛0，1，4｝D.｛0，1，2,3，4｝二、利用集合的运算性质求参数的值或范围1、设集合A=｛x |x 2-2x =0｝，B=｛x |x 2-2a x +a 2-a =0｝.(1)若A ⋂B=B ，求实数a 的取值范围；(2)若A ⋃B=B ，求实数a 的值.2、设集合{}1,0,1-=M ，{}2,a a N =，若N N M =⋂,则实数a 的值是（ ）A.-1B.0C.1D.1或-13、已知集合T 是由关于x 的方程x 2+p x +q=0(p 2-4q ＞0)的解组成的集合，A=｛1，3，5，7，9｝，B=｛1，4，7，10｝，且T ⋂A=⍉，T ⋂B=T ，试求实数p 和q 的值.4、已知集合A=｛x |2a ≤x ≤a +3｝，B=｛x |x ＜-1或x ＞5｝，若A ⋂B=⍉，求实数a 的取值范围.三、补集思想1、已知集合A=｛y l y >a 2+1或y <a ｝，B=｛y |2≤y ≤4｝，若A ⋂B ≠⍉，则实数a 的取值范围为（ ）A.｛a l a ≥2｝B.｛a l-3＜a ＜3｝C.｛a l a >2或-3＜a ＜3｝D.｛a l a ≥2或-3≤a ≤3｝2、已知集合{}R x m mx x x A ∈=++-=,0624|2，{}R x x x B ∈<=,0|，若=⋂B A ⍉，求实数m 的取值范围.四、易错题型1、设M 和P 是两个非空集合，规定M-P=｛x l x ∈M ，且x ∉P ｝，根据这一规定，计算M-(M-P)等于( ).A.MB.PC.M ⋃PD.M ⋂P2、设全集S=｛2，3，a 2+2a -3｝，A=｛|2a -1|，2｝，C S A=｛5｝，求实数a 的值.基础巩固1、已知集合A ＝{0,2}，B ＝{－2，－1,0,1,2}，则A ∩B ＝( )A ．{0,2}B ．{1,2}C ．{0}D ．{－2，－1,0,1,2}2、已知集合A ＝{x |x －1≥0}，B ＝{0,1,2}，则A ∩B ＝( )A ．{0}B ．{1}C ．{1,2}D ．{0,1,2}3、已知集合A ＝{x ||x |<2}，B ＝{－2,0,1,2}，则A ∩B ＝( )A ．{0,1}B ．{－1,0,1}C ．{－2,0,1,2}D ．{－1,0,1,2}4、已知集合{}35A x x =-≤≤，{}141B x a x a =+≤≤+ A B B =，B ≠∅，则实数a 的取值范围是（ ）A ．1a ≤B ．01a ≤≤C ．0a ≤D ．41a -≤≤5、设{(,)|46}A x y x y =+=，{(,)|327}B x y x y =+=，则A ∩B ＝ ．6、已知集合A ＝{x |x ≤1}，B ＝{x |x ≥a }，且A ∪B ＝R ，则实数a 的取值范围为________．7、已知全集U ＝{1,2,3,4,5,6,7,8}，集合A ＝{2,3,5,6}，集合B ＝{1,3,4,6,7}，则集合A ∩(∁U B )＝( )A ．{2,5}B ．{3,6}C ．{2,5,6}D ．{2,3,5,6,8}8、已知集合U ={|0}x x >，{|02}U C A x x =<<，那么集合A =（ ）．A ． {|02}x x x ≤≥或B ． {|02}x x x <>或C ． {|2}x x ≥D ． {|2}x x > 9、设全集U ＝R ，M ＝{x |x <－2或x >2}，N ＝{x |1<x <3}，则图中阴影部分所表示的集合是( )A ．{x |－2≤x <1}B ．{x |－2≤x ≤2}C ．{x |1<x ≤2}D ．{x |x <2}10、已知A ，B 均为集合U ＝{1,3,5,7,9}的子集，且A ∩B ＝{3}，(∁U B )∩A ＝{9}，则A ＝() A ．{1,3} B ．{3,7,9}C ．{3,5,9}D ．{3,9}11、已知全集U =R ，集合A ={}220x x px ++=，{}250,B x x x q =-+= 若{}()2U C A B =，则p = ；q = ．12、设全集{}22,4,1U a a =-+，{}22,2A a a =--，且{}7U C A =，求实数a 的值．能力提升13、(1)设A ＝{4,5,6,8}，B ＝{3,5,7,8}，求A ∪B ．(2)设集合A ＝{x |－1<x <2}，集合B ＝{x |1<x <3}，求A ∪B ．(3)设集合A ＝{1,2}，求满足A ∪B ＝{1,2,3}的集合B ．14、(1)已知集合{}4,5,6,8A =，{}3,5,7,8B =，{}1,3C =，求()A B C ．(2)已知集合A ＝{x |－5≤x ≤5}，B ＝{x |x ≤－2或x >3}，则A ∩B ＝________．(3)设A ＝{等腰三角形}，B ＝{直角三角形}，求A B ．15、已知A ＝{x |x 2－a x ＋a 2－19＝0}，B ＝{x |x 2－5x ＋8＝2}，C ＝{x |x 2＋2x －8＝0}，若()A B ∅⊂，且A C =∅，求a 的值．16、已知集合{}0232=+-=x x x A ，{}20B x mx =+=，A B A =，求m 的取值范围．17、已知集合{}0232=+-=x x x A ，{}022=+-=mx x x B ，B B A = ，求m 的取值范围．18、已知集合A ＝{x |x <－1或x >4}，B ＝{x |2a ≤x ≤a ＋3}，若A ∩B ＝B ，求实数a 的取值范围．19、求下列集合的补集（1）设U ＝{x |x 是小于9的正整数}，A ＝{1,2,3}，B ＝{3,4,5,6}，求∁U A ，∁U B ．（2）设全集U ＝R ，M ＝{x |x <－2或x >2}，N ＝{x |1<x <3}，求∁U M ，∁U N ．20、已知全集U ＝{x |x ≤4}，集合A ＝{x |－2<x <3}，B ＝{x |－3<x ≤3}． 求A B ，A B ，U C A 、U C B ，()U C A B ，()U C A B ．21、试用集合,A B 的交集、并集、补集分别表示图中Ⅰ，Ⅱ，Ⅲ，Ⅳ四个部分所表示的集合．Ⅰ部分:______ ____Ⅱ部分:______ ____Ⅲ部分:____ ______Ⅳ部分:________ __或_________________．22、设全集U ＝{3,6，m 2－m －1}，A ＝{|3－2m |,6}，∁U A ＝{5}，求实数m ．23、设全集{}010,*U x x x N =<<∈，若{}3A B =，{}1,5,7U A C B =，()()U U C A C B ={}9，求A 、B ．24、已知集合A＝{x|x2－4x＋2m＋6＝0}，B＝{x|x<0}，若A B=∅，求实数m的取值范围．。

集合运算知识点总结一、集合的基本概念集合是数学中的一个基本概念，它是由一些确定的、互不相同的对象组成的。

这些对象称为集合的元素。

如果一个集合里有限个元素，称这个集合为有限集合；如果集合的元素可以用无穷个数来表达，称这个集合为无限集合。

集合用字母表示，大写字母A、B、C表示集合，小写字母a、b、c表示集合的元素。

当元素x属于集合A时，就记作x∈A，读作x属于A。

二、集合的表示方式1. 列举法：将集合中的元素用大括号{}括起来，用逗号隔开，写出来。

例如：集合A={1,2,3,4,5}，表示A是由元素1,2,3,4,5组成的集合。

2. 描述法：用一个符合逻辑条件的语句来描述该集合。

例如：集合A={x|x是自然数，0<x<6}，表示A是由大于0且小于6的自然数组成的集合。

三、集合之间的关系1. 相等关系：当两个集合具有完全相同的元素时，它们就是相等的。

例如：A={1,2,3,4,5}，B={5,4,3,2,1}，A和B是相等的集合。

2. 包含关系：当一个集合的所有元素都是另一个集合的元素时，称前一个集合包含于后一个集合。

例如：A={1,2,3,4}，B={1,2,3,4,5}，则A⊆B，表示A包含于B。

3. 交集：两个集合A和B的交集，是由所有既属于A又属于B的元素组成的集合。

例如：A={1,2,3,4}，B={3,4,5,6}，则A∩B={3,4}。

4. 并集：两个集合A和B的并集，是由所有属于A或属于B的元素组成的集合。

例如：A={1,2,3,4}，B={3,4,5,6}，则A∪B={1,2,3,4,5,6}。

5. 补集：若全集为U，集合A是U的一个子集，那么A对于U的补集是由A不在U中的元素组成的集合。

一般记作A'。

例如：U={1,2,3,4,5,6}，A={1,2,3,4}，则A'={5,6}。

四、集合的运算1. 交集运算：设A和B是两个集合，A∩B={x|x∈A且x∈B}，即A与B的交集是由既属于A又属于B的元素组成的集合。

集合的基本运算空集与全集集合的基本运算：空集与全集集合是数学中重要的概念之一，它是由一些特定对象或元素组成的，并且没有重复元素的事物的总体。

在集合的研究过程中，有一些基本的运算必须要掌握，其中包括空集与全集。

一、空集空集是指没有任何元素的集合。

用符号∅或 {} 来表示。

空集是集合论中最基本也是最简单的集合。

具体来说，对于任何给定的集合A，如果不存在任何一个元素 x，使得 x 属于 A，那么集合 A 就是一个空集。

举个例子，假设 A 是由正整数构成的集合，那么 A 中不包含任何负数和 0，因此 A 并不是一个空集。

空集的特点是没有元素，即其中不含任何对象。

空集的运算：1. 交集：对于任意集合 A，A 与空集的交集仍然是空集。

即A ∩ ∅= ∅。

2. 并集：对于任意集合 A，A 与空集的并集等于 A 本身。

即 A ∪∅ = A。

3. 差集：对于任意集合 A，A 与空集的差集等于 A 本身。

即 A - ∅= A。

二、全集全集是指包含了研究对象的所有元素的集合。

全集常用符号 U 来表示。

对于任何一个集合 A，如果 A 的所有元素都是全集 U 的子集，则称 A 为全集。

全集的运算：1. 交集：对于任意集合 A，A 与全集 U 的交集等于集合 A 本身。

即A ∩ U = A。

2. 并集：对于任意集合 A，A 与全集 U 的并集等于全集 U。

即 A ∪ U = U。

3. 差集：对于任意集合 A，A 与全集 U 的差集等于空集∅。

即 A - U = ∅。

需要注意的是，空集与全集是特殊的集合，它们在集合运算中具有一些特殊的性质。

比如，对于交集来说，任何集合与空集的交集都等于空集，而与全集的交集则等于原集合本身。

这是因为空集不包含任何元素，所以与任何集合的交集都是空集；而与全集的交集等于原集合本身，因为全集包含了所有元素。

对于并集来说，任何集合与空集的并集等于原集合本身，而与全集的并集则等于全集。

这是因为为空集不包含任何元素，所以与任何集合的并集都等于原集合；而与全集的并集等于全集，因为全集已经包含了所有元素。

集合间的基本运算一、知识概述1交集的定义一般地，由所有属于A且属于B的元素所组成的集合，叫做A, B的交集记作 A ' B （读作‘ A 交B'），即卩 A 1 B= {x|x 已A,且B} 2、并集的定义一般地，由所有属于集合A或属于集合B的元素所组成的集合，叫做A, B的并集.记作：A」B （读作’A并B'），即卩A」B ={x|x三A,或B}.3、补集：一般地，设S是一个集合，A是S的一个子集（即…=1 ）,由S中所有不属于A的元素组成的集合，叫做S中子集A的补集（或余集），记作。

貝, 即［/ ={小胡且入¥ 2}性质：％/）二月“J©乓0二用全集：如果集合S含有我们所要研究的各个集合的全部元素，这个集合就可以看作一个全集，全集通常用S, U表示+4、运算性质：（1） I I 「I 'I ；（2）I — -「'；（3）I . ；（4）T __「T 1 -；（5）、二一匚 _「丄一「* 二：.（6）「厂_「；：「：冷」'J'：,二、例题讲解例1、设集合A={ —4, 2m- 1, m2} , B={9, m-5, 1 —m},又A B={9}，求实数m的值.解：I A B={9}，二2m—1=9或m2=9,解得m=5或m=3或m=—3.若m=5 贝U A={—4, 9, 25} , B={9, 0,—4}与A B={9}矛盾；若m=3则B中元素m—5=1—m=—2,与B中元素互异矛盾；若m=-3,则A={ —4,—7, 9} , B={9,—8, 4}满足 A B={9}.二m=- 3.例2、设A={x|x 2+ ax+ b=0}, B={x|x 2+ ex + 15=0},又A B={3, 5} , A A B={3}, 求实数a , b , e的值.解：v A A B={3}，二3 € B，二32+ 3e+ 15=0,••• e= —8,由方程x2—8x+ 15=0 解得x=3 或x=5.••• B={3 , 5}.由A二（A」B）={3 , 5}知,3€ A, A （否则5€ A A B,与A G B={3}矛盾)故必有A={3},.••方程x2+ ax+ b=0有两相同的根3.由韦达定理得3+ 3=—a, 3 3=b,即a=—6, b=9, c=—8.例3、已知A={x|x 3+ 3x2+ 2x >0} , B={x|x 2+ ax+ b< 0},且A G B={x|0 v x< 2}, A U B={ x | x > —2},求a、b 的值.解：A={x| —2v x v—1 或x>0},设B= [x i, X2]，由A G B= (0, 2]知X2= 2,且—1<xW 0,①由A U B= (—2 ,+x)知一2w X1w —1. ②由①②知X i =—1, X2 = 2,a=—( X1+ X2)=—1, b= X1X2= —2.例4、已知A={x|x 2—ax+ a2—19=0}, B={x|x 2—5x + 8=2}, C={x|x 2+ 2x —8=0}. 若E =A G B,且A G C=] , 求a 的值.解：—3)(x —2)=0}={3 , 2},•- B={x|(xC={x|(x + 4)(x —2)=0}={ —4 , 2},又••• E =AG B,又••• A G C==,•可知-4^A, 2^A, 3€ A.• •由9—3a+ a —19=0 ,解得a=5或a=—2.①当a=5 时，A={2, 3}，此时A H C={2} ，矛盾，二a^ 5;②当a=—2时，A={—5, 3}，此时A H C山，A H B={3}工它，符合条件.综上①②知a=—2.例5、已知全集U={不大于20的质数} ,M N是U的两个子集，且满足MA （•门）={3，5},（「r）H N={7，19},（」'）H（ •「）={2，17}，求M N.解：用图示法表示集合U, M N （如图），将符合条件的元素依次填入图中相应的区域内，由图可知：M={3, 5, 11, 13}, N={7, 11, 13, 19}.点评：本题用填图的方法使问题轻松地解决，但要注意的是在填图时，应从已知区域填起，从已知区域推测未知区域的元素.特别提示：下列四个区域:对应的集合分别是:①一q : ::②一-r 二：③―_ 5 ■':④一I一、选择题1下列命题中，正确的是（）A. 若U=R 祐u,匸B. 若U为全集，①表示空集，则-①=①；C. 若A=｛1，①,｛2｝｝，则｛2｝二A;D. 若A=｛1，2，3｝，B=｛x|x 二A｝，则A€ B.3 IM= ｛工 |畝迄忑€ 血¥_｝= （x l 也｝『2、设数集 ' - …且MN都是集合｛x|0 < x< 1｝的子集，如果把b—a叫做集合｛x|a <x< b｝的“长度”，那么集合Mn N 的“长度”的最小值是（）1 2A. - B .」丄5C. 1- D .一3、设M N是两个非空集合，定义M与N的差集为M—N=｛x|x € M且x己N｝，则M—（M—N）等于（）A. N B . MA NC. MU N D . M 4、已知全集：=R，集合朴11"弔刀和严砂亠■“ L的关系的韦恩（Venn）图如下图所示，贝U阴影部分所示的集合的元素共有（）B . 2个 D .无穷个1、 - ••匚 I -①=U, {2} € A, {2}单独看是一个集合，但它又是A 中的一个元素.3 £2、集合M 的“长度”为-，集合N 的“长度”为」，而集合—+ — — 1{x|0 <x < 1}的“长度”为1,故MAN 的“长度”最小值为4」3、M-N={x|x €“且x^N}是指图（1）中的阴影部分.同样M-（ M- N ）是指图（2）中的阴影部分.4、t 图形中的阴影部分表示的是集合 =；，由；解得集合‘"一—二一，而N 是正奇数的集合；-「，故选B.二、填空题 5、已知集合A={x|x 2— 3x + 2=0}，集合B={x|ax — 2=0}（其中a 为实数），且A U B=A 则集合 C={a|a 使得 A U B=A}= ______________ . 5、｛0, 1, 2｝解析：A=｛1, 2｝，由 A U B=A 得 匪 A.••• 1€ A,即得 a=2;或 2€ A,即得 a=1 ;或 B=©，此时 a=0.••• C=｛0, 1, 2｝.A. 3个C. 1个⑴6、非空集合S^｛1 ,2,3,4,5｝，且若a€ S,则6-a€ S,这样的S共有________ 个.6、6解析：S=｛1, 5｝或｛2 , 4｝或⑶，或｛1 , 3, 5｝，或｛2 , 4 , 3｝，或｛1 , 5 , 2 , 4｝.三、解答题7、设集合卫=｛込加7-①，吕―^ —另1—^,9｝(1)若■■-丄)，求实数a的值.(2)若.''■,求实数a的值.7、解：(1)：9 三’1 '',二9 A.则a2=9或.解得a=±3或5.当时，'' ■' ■ ' - '-（舍）当a =—3时，卫={9,一兀一4},£=〔一出4,9〕(符合)当a = 5时，乂={25,9, —= {0,—4,9〕(符合).综上知一 ?或“一-.(2)由(1)知•，一二8已知全集U= R,叮•二•….丄v 0・，_ = “ V呗亠」或x >5 —「一：,，若- J，求实数⑴的取值范围8解：依题设可知全集】=三且打丨■■-0 =0月=缶1一2三工W5)，「月=仗冲+1=工w2喘_1}，由题设分类如下：①若'，贝U m^ 1>2mn 1= mV 2.②若加工0，则m^ i<2mn 1,且I®用一1« 5，解得2< 3.由①②可得：me 3.•••实数m的取值范围为{m|mc 3}.9、已知全集U={|a -1|，(a - 2)(a -1)，4，6}.(1)若-八「•求实数a的值;(2)若：4 '求实数a的值.9、解：(1)t L •厂一；' 且多U,•••|a - 1|=0,且(a - 2)(a - 1)=1 ,或|a -1|=1 ,且(a - 2)(a -1)=0 ;第一种情况显然不成立，在第二种情况中由|a -1|=1得a=0或a=2, --a=2.(2)依题意知|a - 1|=3 ,或(a - 2)(a - 1)=3,若|a -1|=3 ,则a=4, 或a=-2；若(a —2)(a —1)=3，贝U -经检验知a=4时，(4 —2)(4 —1)=6，与元素的互异性矛盾.二a=- 2或亠 .10、设集合A =｛：：广「二1｝, B 屮 | ...... - ,*｝，若A B=B求实数二的值.10、解：先化简集合A=J '.由A】B=B则F A,可知集合B可为二:，或为｛0｝，或｛- 4｝，或".(i) 若B』：，则贝:，解得立＜-：；(ii) 若- - B,代入得-- =0=应=1 或：'=一-,当丸=1时，B=A符合题意；当：』=-1时，B=｛0｝二A,也符合题意.（iii）若一4^B,代入得工上L = 口=7或“ =1,当：』=1时，已经讨论，符合题意；当屯=7时，B={- 12,—4}，不符合题意.综上可得，^ =1或立€-1.11、已知集合A={x|x —4m灶2计6=0}，B={x|x V 0}，若A A B M，求实数m的取值范围.= ^ | A = (-4jK)3-4(2^ 4-5)^ 0} = (/w | 或朋11、解：设全集 ' 」m皂U,< 珂4- x- = 4^ 鼻0,若方程X2—4mx+ 2m^ 6=0的两根x’，x?均非负，贝卩山忑八载以―D胆沖一••• {m|- }关于U的补集是{m|m<—1}，二实数m的取值范围是{m|m<—1}.1、（全国I，1）设集合A={4，5, 7,9}，B={3,4,乙8, 9}，全集U=A U B，则集合・⑺厂启）中的元素共有（）A. 3个B. 4个C. 5个D. 6个答案：A解析：2、（福建，2）已知全集U=R,集合A={x|x2—2x>0}，则干」等于（）A. {x|0 < x< 2}B. {x|0<x<2}C. {x|x<0 或x>2} D . {x|x < 0 或x > 2}答案：A解析：■/ x2—2x>0，二x（x —2）>0，得x<0 或x>2,••• A={x|x<0 或x>2}，[ 4 ；. ■ i•.3、（山东，1）集合A={0 , 2, a}, B={1 , a2}.若A U B={0, 1, 2, 4, 16}，则a 的值为（）A. 0B. 1C. 2D. 4答案：D解析：T A U B={0, 1, 2, a, a2}，又A U B={0, 1, 2, 4, 16}, • {a , a2}={4 , 16} , • a=4 ,故选D.集合中的交、并、补等运算，可以借助图形进行思考。

集合的基本运算是集合论中的重要内容，涉及到集合的交、并、差和补运算。

在数学和计算机科学中，集合的基本运算是解决问题和推理的基础。

本文将介绍集合的基本运算及其相关知识点。

一、集合的定义集合是由一些确定的事物组成的整体，这些事物称为集合的元素。

用大写字母表示集合，用小写字母表示集合的元素。

集合中的元素是无序的，且不重复。

例如，集合A={1, 2, 3}，表示A是由元素1、2和3组成的集合。

二、集合的基本运算1.交集交集运算是指给定两个集合，求出两个集合共有的元素所组成的集合。

用符号∩表示交集。

例如，集合A={1, 2, 3}，集合B={2, 3, 4}，则A∩B={2, 3}。

2.并集并集运算是指给定两个集合，求出两个集合所有元素的组合所组成的集合。

用符号∪表示并集。

例如，集合A={1, 2, 3}，集合B={2, 3, 4}，则A∪B={1, 2, 3, 4}。

3.差集差集运算是指给定两个集合，求出第一个集合减去与第二个集合交集后的元素所组成的集合。

用符号－表示差集。

例如，集合A={1, 2, 3}，集合B={2, 3, 4}，则A-B={1}。

4.补集补集运算是指给定一个全集和一个子集，求出子集相对于全集的差集所组成的集合。

用符号’表示补集。

例如，全集U={1, 2, 3, 4}，集合A={2, 3}，则A’={1, 4}。

三、集合运算的性质1.交换律集合的交集和并集满足交换律，即A∩B=B∩A，A∪B=B∪A。

2.结合律集合的交集和并集满足结合律，即(A∩B)∩C=A∩(B∩C)，(A∪B)∪C=A∪(B∪C)。

3.分配律集合的交集和并集满足分配律，即A∩(B∪C)=(A∩B)∪(A∩C)，A∪(B∩C)=(A∪B)∩(A∪C)。

4.互补律集合的补集满足互补律，即(A’)’=A。

四、集合运算的应用1.逻辑推理集合运算可以用于逻辑推理中。

通过对集合的交、并、差和补运算，可以分析给定条件的关系和推导出新的结论。

集合的基本运算集合是数学中的一个基本概念，它是由一组确定的元素所构成的整体。

集合的基本运算包括并集、交集、差集和补集。

本文将介绍集合的基本运算及其性质。

1. 并集：并集是指将两个或多个集合中的所有元素合并成一个集合的操作。

用符号"∪"表示。

假设集合A={a, b, c}，集合B={b, c, d}，则A∪B={a, b, c, d}。

并集的定义可以推广到多个集合的情况。

2. 交集：交集是指将两个或多个集合中共有的元素提取出来形成一个新的集合。

用符号"∩"表示。

假设集合A={a, b, c}，集合B={b, c, d}，则A∩B={b, c}。

交集运算同样适用于多个集合。

3. 差集：差集是指从一个集合中去除与另一个集合相同的元素，得到剩余的元素构成的新集合。

用符号"－"表示。

假设集合A={a, b, c}，集合B={b, c, d}，则A－B={a}。

差集运算同样适用于多个集合。

4. 补集：补集是指在给定的全集中去除一个集合中的所有元素，得到的剩余元素所构成的新集合。

全集是指包含所研究对象所有元素的集合。

用符号"′"或"'"表示补集运算。

假设全集为U，集合A={a, b, c}，则A′=U －A。

集合的基本运算具有以下性质：a) 结合律：对于任意集合A、B、C，有(A∪B)∪C=A∪(B∪C)，(A∩B)∩C=A∩(B∩C)。

b) 交换律：对于任意集合A和B，有A∪B=B∪A，A∩B=B∩A。

c) 分配律：对于任意集合A、B和C，有A∩(B∪C)=(A∩B)∪(A∩C)，A∪(B∩C)=(A∪B)∩(A∪C)。

d) 对偶律：对于任意集合A和B，有(A∪B)′=A′∩B′，(A∩B)′=A′∪B′。

除了基本运算，集合还具有其他相关概念和运算，如幂集、笛卡尔积等。

幂集是指一个集合的所有子集所构成的集合。

集合的基本关系及运算【学习目标】1.理解集合之间包含与相等的含义，能识别一些给定集合的子集．在具体情境中，了解空集和全集的含义．2.理解两个集合的交集和并集的含义，会求两个简单集合的交集与并集．理解在给定集合中一个子集的补集的含义，会求给定子集的补集．【要点梳理】要点一：集合之间的关系1.集合与集合之间的“包含”关系集合A 是集合B 的部分元素构成的集合，我们说集合B 包含集合A；子集：如果集合A 的任何一个元素都是集合B 的元素，我们说这两个集合有包含关系，称集合A 是集合B 的子集(subset).记作：A B(B A)⊆⊇或，当集合A 不包含于集合B 时，记作A B，用Venn 图表示两个集合间的“包含”关系：A B(B A)⊆⊇或要点诠释：（1）“A 是B 的子集”的含义是：A 的任何一个元素都是B 的元素，即由任意的x A ∈，能推出x B ∈．（2）当A 不是B 的子集时，我们记作“A ⊆B (或B ⊇A )”，读作：“A 不包含于B ”（或“B 不包含A ”）．真子集：若集合A B ⊆，存在元素x ∈B 且x A ∉，则称集合A 是集合B 的真子集(proper subset).记作：A B(或B A)规定：空集是任何集合的子集，是任何非空集合的真子集.2.集合与集合之间的“相等”关系A B B A ⊆⊆且，则A 与B 中的元素是一样的，因此A=B要点诠释：任何一个集合是它本身的子集，记作A A ⊆．要点二：集合的运算1.并集一般地，由所有属于集合A 或属于集合B 的元素所组成的集合，称为集合A 与B 的并集，记作：A∪B 读作：“A 并B”，即：A∪B={x|x ∈A，或x ∈B}Venn 图表示：要点诠释：（1）“x ∈A，或x ∈B”包含三种情况：“,x A x B ∈∉但”；“,x B x A ∈∉但”；“,x A x B ∈∈且”．（2）两个集合求并集，结果还是一个集合，是由集合A 与B 的所有元素组成的集合(重复元素只出现一次).2.交集一般地，由属于集合A 且属于集合B 的元素所组成的集合，叫做集合A 与B 的交集；记作：A∩B，读作：“A 交B”，即A∩B={x|x ∈A，且x ∈B}；交集的Venn 图表示：要点诠释：（1）并不是任何两个集合都有公共元素，当集合A 与B 没有公共元素时，不能说A 与B 没有交集，而是A B =∅ ．（2）概念中的“所有”两字的含义是，不仅“A∩B 中的任意元素都是A 与B 的公共元素”，同时“A 与B 的公共元素都属于A∩B”．（3）两个集合求交集，结果还是一个集合，是由集合A 与B 的所有公共元素组成的集合.3.补集全集：一般地，如果一个集合含有我们所研究问题中所涉及的所有元素，那么就称这个集合为全集，通常记作U.补集：对于全集U 的一个子集A，由全集U 中所有不属于集合A 的所有元素组成的集合称为集合A 相对于全集U 的补集(complementary set)，简称为集合A 的补集，记作：U U A A={x|x U x A}∈∉；即且；痧补集的Venn 图表示：要点诠释：（1）理解补集概念时，应注意补集U A ð是对给定的集合A 和()U A U ⊆相对而言的一个概念，一个确定的集合A ，对于不同的集合U，补集不同．（2）全集是相对于研究的问题而言的，如我们只在整数范围内研究问题，则Z 为全集；而当问题扩展到实数集时，则R 为全集，这时Z 就不是全集．（3）U A ð表示U 为全集时A 的补集，如果全集换成其他集合（如R ）时，则记号中“U”也必须换成相应的集合（即R A ð）．4.集合基本运算的一些结论：A B A A B B A A=A A =A B=B A ⋂⊆⋂⊆⋂⋂∅∅⋂⋂，，，，A A B B A B A A=A A =A A B=B A ⊆⋃⊆⋃⋃⋃∅⋃⋃，，，，U U (A)A=U (A)A=⋃⋂∅，痧若A∩B=A，则A B ⊆，反之也成立若A∪B=B，则A B ⊆，反之也成立若x ∈(A∩B)，则x ∈A 且x ∈B 若x ∈(A∪B)，则x ∈A，或x ∈B求集合的并、交、补是集合间的基本运算，运算结果仍然还是集合，区分交集与并集的关键是“且”与“或”，在处理有关交集与并集的问题时，常常从这两个字眼出发去揭示、挖掘题设条件，结合Venn 图或数轴进而用集合语言表达，增强数形结合的思想方法.【典型例题】类型一：集合间的关系例1.请判断①0{0}；②{}R R ∈；③{}∅∈∅；④∅{}∅；⑤{}0∅=；⑥{}0∈∅；⑦{}0∅∈；⑧∅{}0，正确的有哪些？【答案】②③④⑧【解析】①错误，因为0是集合{}0中的元素，应是{}00∈；②③中都是元素与集合的关系，正确；④⑧正确，因为∅是任何集合的子集，是任何非空集合的真子集，而④中的{}∅为非空集合；⑤⑥⑦错误，∅是没有任何元素的集合．【总结升华】集合的符号语言十分简洁，因而被广泛用于现代数学之中，但往往容易混淆，其障碍在于这些符号与具体意义之间没有直接的联系，突破方法是熟练地掌握这些符号的具体含义.举一反三：【变式1】用适当的符号填空：(1){x||x|≤1}{x|x 2≤1}；(2){y|y=2x 2}{y|y=3x 2-1}；(3){x||x|>1}{x|x>1}；(4){(x，y)|-2≤x≤2}{(x，y)|-1<x≤2}．【答案】(1)=(2)(3)(4)【总结升华】区分元素与集合间的关系，集合与集合间的关系.例2.（2015秋确山县期中）已知A ={x ｜x 2―4=0}，B ={x ｜ax ―6=0}，且B 是A 的子集．（1）求a 的取值集合M ；（2）写出集合M 的所有非空真子集．【思路点拨】对（1）根据A 集合中的元素，B A ⊆，分类讨论B 的可能情况，再注解a ，写出集合M ．根据含有n 个元素的集合的真子集个数是2n －1，求解（2）．【答案】（1）M ={0，3，－3}；（2）{0}，{3}，{－3}，{0，3}，{0，－3}，{3，－3}【解析】（1）A ={2，－2}．∵B 是A 的子集，∴B =∅，{2}，{－2}，①B =∅时，方程ax －6=0无解，得a =0；②B ={2}时，方程ax －6=0的解为x =2，得2a －6=0，所以a =3；③B ={－2}时，方程ax －6=0的解为x =－2，得－2a －6=0，所以a =－3．所以a 的取值集合M ={0，3，－3}．（2）M ={0，3，－3}的非空真子集为{0}，{3}，{－3}，{0，3}，{0，－3}，{3，－3}【总结升华】本题考查集合的子集问题，含有n 个元素的集合的子集个数是2n ，真子集个数是2n －1；非空真子集个数是2n －2．举一反三：【变式1】已知{},a b A ⊆{},,,,a b c d e ，则这样的集合A 有个.【答案】7个【变式2】同时满足：①{}1,2,3,4,5M ⊆；②a M ∈，则6a M -∈的非空集合M 有（）A.16个B.15个C.7个D.6个【答案】C【解析】3a =时，63a -=；1a =时，65a -=；2a =时，64a -=；4a =时，62a -=；5a =时，61a -=；∴非空集合M 可能是：{}{}{}{}{}{}3,1,5,2,4,1,3,5,2,3,4,1,2,4,5，{}1,2,3,4,5共7个.故选C.【变式3】已知集合A={1，3，a}，B={a 2}，并且B 是A 的真子集，求实数a 的取值.【答案】a=-1，a=3±或a=0【解析】∵，∴a 2∈A，则有：（1）a 2=1⇒a=±1，当a=1时与元素的互异性不符，∴a=-1；（2）a 2=3⇒a=3±（3）a 2=a ⇒a=0，a=1，舍去a=1，则a=0综上：a=-1，a=3±或a=0.注意：根据集合元素的互异性，需分类讨论.例3.设M={x|x=a 2+1，a ∈N +}，N={x|x=b 2-4b+5，b ∈N +}，则M 与N 满足()A.M=NB.M NC.N MD.M∩N=∅【答案】B【解析】当a ∈N +时，元素x=a 2+1，表示正整数的平方加1对应的整数，而当b ∈N +时，元素x=b 2-4b+5=(b-2)2+1，其中b-2可以是0，所以集合N 中元素是自然数的平方加1对应的整数，即M 中元素都在N 中，但N 中至少有一个元素x=1不在M 中，即M N，故选B.例4．已知},,,0{},,,{y x N y x xy x M =-=若M =N ，则+++2()(x y x )()1001002y x y +++ =．A ．－200B ．200C ．－100D ．0【思路点拨】解答本题应从集合元素的三大特征入手，本题应侧重考虑集合中元素的互异性．【答案】D【解析】由M=N，知M，N 所含元素相同.由0∈{0，|x|，y}可知0∈若x=0，则xy=0，即x 与xy 是相同元素，破坏了M 中元素互异性，所以x≠0.若x·y=0，则x=0或y=0，其中x=0以上讨论不成立，所以y=0，即N 中元素0，y 是相同元素，破坏了N 中元素的互异性，故xy≠00，则x=y，M，N 可写为M={x，x 2，0}，N={0，|x|，x}由M=N 可知必有x 2=|x|，即|x|2=|x|∴|x|=0或|x|=1若|x|=0即x=0，以上讨论知不成立若|x|=1即x=±1当x=1时，M 中元素|x|与x 相同，破坏了M 中元素互异性，故x≠1当x=-1时，M={-1，1，0}，N={0，1，-1}符合题意，综上可知，x=y=-1∴+++2()(x y x )()1001002y x y +++ =-2+2-2+2+…+2=0【总结升华】解答本题易忽视集合的元素具有的“互异性”这一特征，而找不到题目的突破口．因此，集合元素的特征是分析解决某些集合问题的切入点．举一反三：【变式1】设a，b ∈R ，集合b{1,a+b,a}={0,,b}a，则b-a=()【答案】2【解析】由元素的三要素及两集合相等的特征：b1{0,,b},0{1,a+b,a}a 0a b=0a∈∈≠∴+ ，又，∴当b=1时，a=-1，b{0,b}={0,-1,1}a∴，当b=1a时，∴b=a 且a+b=0，∴a=b=0(舍)∴综上：a=-1，b=1，∴b-a=2.类型二：集合的运算例5.（1）（2014湖北武汉期中）已知{}22A y y x ==-；{}22B y y x ==-+，则A ∩B ＝（）A ．()){}00,,,B ．⎡⎣C ．[－2，2]D ．{（2）设集合M ={3，a }，N ={x |x 2－2x ＜0，x ∈Z}，M ∩N ={1}，则M ∪N 为（）．A ．{1，2，a }B ．{1，2，3，a }C ．{1，2，3}D ．{1，3}【思路点拨】（1）先把集合A 、B 进行化简，再利用数轴进行相应的集合运算．（2）先把集合N 化简，然后再利用集合中元素的互异性解题．【答案】（1）C （2）D 【解析】（1）集合A 、B 均表示构成相关函数的因变量取值范围，故可知：A ={y |y ≥－2}，B ={y |y ≤2}，所以A ∩B ={y |－2≤y ≤2}，选C ．（2）由N ={x |x 2－2x ＜0，x ∈Z}可得：N ={x |0＜x ＜2，x ∈Z}={1}，又由M ∩N ={1}，可知1∈M ，即a =1，故选D ．举一反三：【变式1】设A、B 分别是一元二次方程2x 2+px+q=0与6x 2+(2-p)x+5+q=0的解集，且A∩B={21}，求A ∪B.【答案】{21，31，-4}【解析】∵A∩B={21}，∴21是方程2x 2+px+q=0的解，则有：0q p 2121(22=++(1)，同理有：6(21)2+(2-p)·21+5+q=0(2)联立方程(1)(2)得到：⎩⎨⎧-==.4q ,7p ∴方程(1)为2x 2+7x-4=0，∴方程的解为：x 1=21，x 2=-4，∴}4,21{A -=，由方程(2)6x 2-5x+1=0，解得：x 3=21，x 4=31，∴B={21，31}，则A∪B={21，31，-4}.【变式2】设集合A={2，a 2-2a，6}，B={2，2a 2，3a-6}，若A∩B={2，3}，求A∪B.【答案】｛2，3，6，18｝【解析】由A∩B={2，3}，知元素2，3是A，B 两个集合中所有的公共元素，所以3∈｛2，a 2-2a，6｝，则必有a 2-2a=3，解方程a 2-2a-3=0得a=3或a=-1当a=3时，A={2，3，6}，B={2，18，3}∴A∪B={2，3，6}∪｛2，18，3｝=｛2，3，6，18｝当a=-1时，A={2，3，6}，B={2，2，-9}这既不满足条件A∩B={2，3}，也不满足B 中元素具有互异性，故a=-1不合题意，应舍去.综上A∪B=｛2，3，6，18｝．例6.设全集U={x ∈N +|x≤8}，若A∩(C u B)={1，8}，(C u A)∩B={2，6}，(C u A)∩(C u B)={4，7}，求集合A，B.【答案】A={1，3，5，8}，B={2，3，5，6}【解析】全集U={1，2，3，4，5，6，7，8}由A∩(C u B)={1，8}知，在A 中且不在B 中的元素有1，8；由(C u A)∩B={2，6}，知不在A 中且在B 中的元素有2，6；由(C u A)∩(C u B)={4，7}，知不在A 中且不在B 中的元素有4，7，则元素3，5必在A∩B 中.由集合的图示可得A={1，3，5，8}，B={2，3，5，6}.类型三：集合运算综合应用例7．（2014北京西城学探诊）已知集合A ={x |－4≤x ＜2}，B ={x |－1≤x ＜3}，C ={x |x ≥a ，a ∈R}．（1）若（A ∪B ）∩C =∅，求实数a 的取值范围；（2）若（A ∪B ）ÜC ，求实数a 的取值范围．【思路点拨】（1）画数轴；（2）注意是否包含端点．【答案】（1）a ≥3（2）a ≤－4【解析】（1）∵A ={x |－4≤x ＜2}，B ={x |－1≤x ＜3}，又（A ∪B ）∩C =∅，如图，a ≥3；（2）画数轴同理可得：a ≤－4．【总结升华】此问题从表面上看是集合的运算，但其本质是一个定区间，和一个动区间的问题．思路是，使动区间沿定区间滑动，数形结合解决问题．举一反三：【变式1】已知集合P=｛x ︱x 2≤1｝,M=｛a ｝.若P ∪M=P,则a 的取值范围是（）A ．(-∞,-1]B ．[1,+∞）C ．[-1，1]D ．（-∞，-1]∪[1，+∞）【答案】C【解析】P =｛x ︱11x -≤≤｝又 P M P = ，∴M P ⊆，∴11a -≤≤故选C ．例8.设集合{}{}222|40,|2(1)10,A x x x B x x a x a a R =+==+++-=∈.（1）若A B B = ，求a 的值；（2）若A B B = ，求a 的值.【思路点拨】明确A B 、A B 的含义，根据的需要，将其转化为等价的关系式B A ⊆和A B ⊆，是解决本题的关键.同时，在包含关系式B A ⊆中，不要漏掉B =∅的情况.【答案】（1）1a =或1a ≤-；（2）1a =．【解析】首先化简集合A ，得{}4,0A =-.（1）由A B B = ，则有B A ⊆，可知集合B 为∅，或为{}0、{}4-，或为{}0,4-.①若B =∅时，224(1)4(1)0a a ∆=+--<，解得1a <-.②若0B ∈,代入得21011a a a -=⇒==-或.当1a =时，{}{}2|400,4,B x x x A =+==-=符合题意；当1a =-时，{}{}2|00,B x x A ===⊆也符合题意.③若4B -∈，代入得2870a a -+=，解得7a =或1a =.当1a =时，已讨论，符合题意；当7a =时，{}{}2|1648012,4B x x x =++==--，不符合题意.由①②③，得1a =或1a ≤-.（2）,A B B A B =∴⊆ .又{}4,0A =-，而B 至多只有两个根，因此应有A B =，由（1）知1a =.【总结升华】两个等价转化：,A B B A B A B B B A =⇔⊆=⇔⊆ 非常重要，注意应用.另外，在解决有条件A B ⊆的集合问题时，不要忽视A ≠∅的情况.举一反三：【变式1】（2015源汇区一模）设A ={x ｜x 2+4x =0}，B ={x ｜x 2+2(a +1)x +a 2－1=0}，其中x ∈R ，如果A ∩B =B ，求实数a 的取值范围．【答案】a =1或a ≤－1【解析】A ={x ｜x 2+4x =0}={0，－4}，∵A ∩B =B 知，B A ⊆，∴B ={0}或B ={－4}或B ={0，－4}或B =∅，若B ={0}时，x 2+2(a +1)x +a 2－1=0有两个相等的根0，则2002(1)001a a +=-+⎧⎨⨯=-⎩，∴a =－1，若B ={－4}时，x 2+2(a +1)x +a 2－1=0有两个相等的根－4，则24(4)2(1)4(4)1a a -+-=-+⎧⎨-⨯-=-⎩，∴a 无解，若B ={0，－4}时，x 2+2(a +1)x +a 2－1=0有两个不相等的根0和－4，则2402(1)401a a -+=-+⎧⎨-⨯=-⎩，∴a =1，当B =∅时，x 2+2(a +1)x +a 2－1=0无实数根，Δ=[2(a +1)]2－4(a 2－1)=8a +8＜0，得a ＜－1，综上，a =1或a ≤－1．。

集合的基本运算知识点总结与例题讲解本节知识点: （1）并集. （2）交集. （3）全集与补集. （4）德·摩根定律. 知识点一 并集自然语言 一般地,由所有属于集合A 或属于集合B 的元素组成的集合,称为集合A与集合B 的并集,记作B A ,读作“A 并B ”.符号语言 {}B x A x x B A ∈∈=或, .图形语言（用Venn 图表示并集） 图中阴影部分表示两个集合的并集.（1）A 与B 有公共元素,相互不包含 （2）A 与B 没有公共部分（3）B A ≠⊂ （4）A B ≠⊂（5）B A =对并集的理解（1）求两个集合的并集是集合的一种运算,结果仍是一个集合,它是由属于集合A 或集合B 的元素组成的.（2）并集概念中的“或”指的是只要满足其中一个条件即可.符号语言“B x A x ∈∈或,”分为三种情况:①A x ∈,但B x ∉; ②A x ∉,但B x ∈; ③A x ∈,且B x ∈.（3）根据集合元素的互异性,在求两个集合的并集时,两个集合中的公共元素在并集中只能出现一次.并集的性质求并集的方法（1）求两个有限集的并集 按照并集的定义进行计算,但要特别注意集合元素的互异性.（2）求两个无限集的并集 借助于数轴进行计算.注意两个集合的并集等于这两个集合在数轴上对应的图形所覆盖的全部范围.知识点二 交集自然语言 一般地,由属于集合A 且属于集合B 的所有元素组成的集合,称为集合A与集合B 的交集,记作B A ,读作“A 交B ”.符号语言 {}B x A x x B A ∈∈=且, .图形语言（用Venn 图表示交集） 图中阴影部分表示两个集合的并集.如下页图所示.（1）A 与B 有部分公共元素 （2）A 与B 无公共元素,∅=B A（3）若A B ≠⊂,则B B A = （4）若B A ≠⊂,则A B A = （5）B A B A ==对交集的理解（1）求两个集合的交集是集合的一种运算,结果仍是一个集合,它是由属于集合A 且属于集合B 的所有元素组成的集合,及两个集合的公共元素所组成的集合. （2）交集概念中的“所有”二字不能省略,否则会漏掉一些元素,一定要将两个集合中的相同元素（公共元素）全部找出来.（3）当集合A 与集合B 没有公共元素时,不能说集合A 与集合B 没有交集,而是交集为空集,.交集的性质AA B BA B求交集的方法（1）求两个有限集的交集 按照交集的定义进行计算,但要特别注意一定要找出两个集合中的所有公共元素.（2）求两个无限集的交集 借助于数轴进行计算.两个集合的交集等于这两个集合在数轴上对应的图形所覆盖的公共范围.知识点三 全集与补集全集 一般地,如果一个集合含有我们所研究问题中涉及的所有元素,那么就称这个集合为全集,记作U .补集 对于一个集合A ,由全集U 中不属于A 的所有元素组成的集合称为集合A相对于全集U 的补集,简称集合A 的补集,记作C U A ,即C U A {}A x U x x ∉∈=且,.用Venn 图表示为:对补集的理解（1）补集是相对于全集而言的,求一个集合的补集,结果因全集的不同而不同.所以求补集前,要先明确全集.（2）补集既是集合间的一种关系,同时也是集合之间的一种运算. （3）符号“C U A ”有三层意思: ① C U A {}A x U x x ∉∈=且,;② C U A 是U 的一个子集,及(C U A )U ⊆; ③ C U A 表示一个集合.补集的性质①(C U A )U A = ; ②(C U A )∅=A ; ③ C U (C U A )A =; ④ C U U ∅=; ⑤ C U U =∅.U4321B A 知识点四 德·摩根定律知识点五 重要结论如图所示,集合A , B 将全集U 分成了四部分,这四部分用集合表示如下: （1）①表示B A ; （2）②表示 A (C U B ); （3）③表示 B (C U A ); （4）④表示(C U A ) (C U B ).知识点六 集合中元素的个数若集合A 为有限集,则用card(A )表示集合A 中元素的个数. 如果集合A 中含有m 个元素,那么有card(A )m =. （1）一般地,对于任意两个有限集合A , B ,有 card ()=B A card(A )+card(B )－card ()B A . （2）一般地,对于任意三个有限集合A , B , C ,有card ()=C B A card(A )+card(B )－card ()B A －card ()C A －card ()C B ＋ card ()C B A .例题讲解题型一 并集运算一般地,由所有属于集合A 或属于集合B 的元素组成的集合,称为集合A 与集合B 的并集,记作B A ,读作“A 并B ”.即{}B x A x x B A ∈∈=或, .求并集的方法（1）求两个有限集的并集 按照并集的定义进行计算,但要特别注意集合元素的互异性.（2）求两个无限集的并集 借助于数轴进行计算.注意两个集合的并集等于这两个集合在数轴上对应的图形所覆盖的全部范围.例1. 已知集合{}31≤≤∈=x N x A ,{}5,4,3,2=B ,则=B A 【 】 （A ）{}2 （B ）{}3,2（C ）{}5,4,3,2 （D ）{}5,4,3,2,1 分析:将一个用描述法表示的集合转化为用列举法表示时,一定要弄清代表元素的含义或特征.求两个集合的并集运算时,可以按照并集的定义进行,也可以用Venn 图求解或借助于数轴求解.解:∵{}{}3,2,131=≤≤∈=x N x A1∴=B A {}{}{}5,4,3,2,15,4,3,23,2,1= . 选择【 D 】.例2. 已知集合{}1≥=x x A ,{}0322<--=x x x B ,则=B A ____________. 分析:先解一元二次不等式0322<--x x ,求出集合B ,然后把集合A 、B 在数轴上画出来,它们对应图形所覆盖的全部范围即为B A . 解:∵{}{}310322<<-=<--=x x x x x B ∴=B A {}{}{}1311->=<<-≥x x x x x x .例3. 已知集合{}m A ,3,1=,{}m B ,1=,若A B A = ,则m 等于【 】 （A ）0或3 （B ）0或3 （C ）1或3 （D ）1或3分析:{}m B ,1=,由集合元素的互异性,得1≠m ,排除C 、D 选项. 因为A B A = ,根据并集的性质,所以A B ⊆,这样就将两个集合的并集运算转化为了这两个集合之间的关系,从而可以确定参数的值或取值范围. 解:∵A B A = ,∴3=m 或m m =当m m =时,解之得:0=m （1=m 不符合题意,舍去） 综上,3=m 或0=m .例 4. 已知集合{}012≤-=x x P ,{}a M =,若P M P = ,则实数a 的取值范围是__________.分析:∵P M P = ,∴P M ⊆. 解:{}{}11012≤≤-=≤-=x x x x P ∵P M P = ,∴P M ⊆,∴P a ∈ ∴实数a 的取值范围是{}11≤≤-a a .例5. 已知集合{}x A ,3,2,1=,{}2,3x B =,且{}x B A ,3,2,1= ,求x 的值.分析:由题意可知:A B A = ,所以A B ⊆,从而A x ∈2,且32≠x . 解:分为三种情况:①当12=x 时,解之得:1-=x （1=x 不符合题意,舍去）; ②当22=x 时,解之得:2±=x ; ③当x x =2时,解之得:0=x . 综上所述,x 的值为0或2±或1-.注意:在求参数的值时,参数的值要满足集合元素的互异性.例6. 已知集合{}32>-=x x A ,{}a x x x B ->-=332,求B A . 分析:对于含参集合参与的集合运算,要注意分类讨论.解:{}{}532>=>-=x x x x A ,{}{}3332-<=->-=a x x a x x x B . 当3-a ≤5,即a ≤8时,{}53>-<=x a x x B A 或 ; 当53>-a 时,即8>a 时,=B A R .a例7.（易错题）已知集合{}1,1-=A ,{}1==mx x B ,且A B A = ,求由m 的取值构成的集合.分析:因为A B A = ,所以A B ⊆.由于集合B 是一个含参集合,所以要对集合B 分∅=B 和∅≠B 两种情况进行讨论. 解:∵A B A = ,∴A B ⊆. 当0=m 时,∅=B ,满足A B ⊆;当0≠m 时,{}11-=⎭⎬⎫⎩⎨⎧==m x x B 或{}1=B :①若{}1-=B ,则11-=m,解之得:1-=m ;②若{}1=B ,则11=m,解之得:1=m . 综上所述,m 的取值构成的集合为{}1,0,1-.例8. 设集合{}52<<-=x x M ,{}122+<<-=t x t x N ,若M N M = ,则实数t 的取值范围是__________.分析:先将并集运算的结果M N M = 转化为两个集合M , N 之间的关系M N ⊆,从而列出关于参数t 的不等式（组）求解.注意含参集合的分类讨论. 解:∵M N M = ,∴M N ⊆. 分为两种情况:①当∅=N 时,有t -2≥12+t ,解之得:t ≤31;②当∅≠N 时,则有:⎪⎩⎪⎨⎧≤+-≥-+<-51222122t t t t ,解之得:t <31≤2.综上所述,实数t 的取值范围是{}2≤t t .警示:在解决本题时,任意忽略∅=N 的情况,另外要注意端点值能否取到.例9. 已知集合{}2,1-=A ,{}01>+=mx x B ,若B B A = ,求实数m 的取值范围. 分析:注意本题与例7的区别. 解:∵B B A = ,∴B A ⊆. 分为三种情况:①当0=m 时,01>恒成立,∴{}=>+=01mx x B R ,满足B A ⊆;②当0>m 时,{}⎭⎬⎫⎩⎨⎧->=>+=m x x mx x B 101,有11-<-m ,解之得:1<m∴10<<m ;③当0<m 时,{}⎭⎬⎫⎩⎨⎧-<=>+=m x x mx x B 101,有21>-m ,解之得:21->m∴021<<-m .综上所述,实数m 的取值范围是⎭⎬⎫⎩⎨⎧<<-121m m .题型二 交集运算一般地,由属于集合A 且属于集合B 的所有元素组成的集合,称为集合A 与集合B 的交集,记作B A ,读作“A 交B ”.{}B x A x x B A ∈∈=且, .求交集的方法（1）求两个有限集的交集 按照交集的定义进行计算,但要特别注意一定要找出两个集合中的所有公共元素.（或可借助于Venn 图）（2）求两个无限集的交集 借助于数轴进行计算.两个集合的解集等于这两个集合在数轴上对应的图形所覆盖的公共范围.例10. 设集合{}01>+∈=x Z x A ,集合{}02≤-=x x B ,则=B A 【 】 （A ）{}21<<-x x （B ）{}21≤<-x x （C ）{}2,1- （D ）{}2,1,0分析:在进行集合的运算之前,要先弄清楚各个集合的本质.本题中集合A 的代表元素x 为整数,所以集合A 为1->x 范围内的整数集.解:∵{}{}101->∈=>+∈=x Z x x Z x A ,{}{}202≤=≤-=x x x x B ∴=B A {}{}2,1,021=≤<-∈x Z x . 选择【 D 】.例11. 设集合{}21<≤-=x x A ,{}a x x B <=,若∅≠B A ,则实数a 的取值范围是__________.分析:∅≠B A 说明集合A 、B 有公共元素,在数轴上集合A 、B 所对应的图形覆盖的区域有公共部分. 解:{}1->a a .1例12. 设集合{}52<<-=x x M ,{}122+<<-=t x t x N ,若N N M = ,求实数t 的取值范围.分析:若N N M = ,则由交集的性质知M N ⊆,在得到这两个集合之间的关系后借助于数轴就可以列出不等式（组）进行求解了. 解:∵N N M = ,∴M N ⊆. 分为两种情况:①当∅=N 时,满足M N ⊆,有t -2≥12+t ,解之得:t ≤31;②当∅≠N 时,则有:⎪⎩⎪⎨⎧≤+-≥-+<-51222122t t t t ,解之得:t <31≤2.综上所述,实数t 的取值范围是{}2≤t t .★例13.（易错题）设集合{}R x x y y A ∈+==,12,{}R x x y y B ∈+==,1,则B A 等于【 】（A ）{}1≥y y （B ）{}2,1 （C ）()(){}2,1,1,0 （D ）∅错解:解方程组⎩⎨⎧+=+=112x y x y 得:⎩⎨⎧==10y x 或⎩⎨⎧==21y x ,故选【 C 】.错因分析:这里好多学生认为是求抛物线12+=x y 和直线1+=x y 的交点坐标所构成的集合,根源在于没有搞清楚集合A , B 的本质,没有弄清楚集合的代表元素的特征.分析:本题中的两个集合都是由函数值构成的,它们的代表元素是函数值y .B A 表示函数12+=x y 和函数1+=x y 的函数值的交集. 解:∵{}{}1,12≥=∈+==y y R x x y y A ,{}=∈+==R x x y y B ,1R .∴{} 1≥=y y B A R {}1≥=y y . 选择【 A 】.变式: 设集合(){}1,2+==x y y x A ,(){}1,+==x y y x B ,则B A 等于【 】 （A ）{}1≥y y （B ）{}2,1 （C ）()(){}2,1,1,0 （D ）∅例14. 已知集合(){}1,22=+=y x y x A ,集合(){}x y y x B ==,,则B A 中元素的个数为【 】（A ）3 （B ）2 （C ）1 （D ）0解:解方程组⎩⎨⎧==+xy y x 122得:⎪⎪⎩⎪⎪⎨⎧==2222y x 或⎪⎪⎩⎪⎪⎨⎧-=-=2222y x ∴B A ⎭⎬⎫⎩⎨⎧⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛=22,22,22,22,共有2个元素.选择【 B 】. 方法二:由后面的学习可以知道,方程122=+y x 是单位圆的方程（以原点为圆心,以1为半径的圆）.集合A 是由圆122=+y x 上的所有点构成的,集合B 是由直线x y =上的所有点构成的,所以B A 就是由单位圆与直线的交点构成的,如图所示,交点有两个,故B A 中元素的个数为2.例15.（2018沈阳重点高中）设集合{}52≤≤-=x x A ,{}121-≤≤+=m x m x B . （1）若{}52≤≤-∈=x Z x A ,求A 的非空真子集的个数; （2）若B B A = ,求实数m 的取值范围. 分析:（1）子集、真子集个数的确定 若集合A 含有n 个元素,则集合A : （1）含有n 2个子集; （2）含有12-n 个非空子集; （3）含有12-n 个真子集; （4）含有22-n 个非空真子集.（2）若B B A = ,则A B ⊆,注意分类讨论. 解:（1）{}{}5,4,3,2,1,0,1,2-52-=≤≤-∈=x Z x A ∵集合A 中含有8个元素∴集合A 的非空真子集的个数为2542-28=; （2）∵B B A = ,∴A B ⊆. 分为两种情况:①当∅=B 时,满足A B ⊆,有121->+m m ,解之得:2<m ; ②当∅≠B 时,则有:⎪⎩⎪⎨⎧≤--≥+-≤+51221121m m m m ,解之得:2≤m ≤3. 综上所述,实数m 的取值范围是{}3≤m m .例16. 设{}042=+=x x x A ,(){}011222=-+++=a x a x x B ,其中∈x R ,如果B B A = ,求实数a 的取值范围. 解:{}{}4,0042-==+=x x x A ∵B B A = ,∴A B ⊆ 分为两种情况:①当∅=B 时,满足B B A =∴()[]()0141222<--+=∆a a ,解之得:1-<a ;②当∅≠B 时,{}0=B 或{}4-=B 或{}4,0-=B .若{}0=B 或{}4-=B ,则有()[]()0141222=--+=∆a a ,解之得:1-=a经检验,此时{}0=B ;若{}4,0-=B ,则由根与系数的关系定理可得:()⎩⎨⎧=--=+-014122a a ,解之得:1=a . 综上所述,实数a 的取值范围是{}11-≤=a a a 或.例17. 设集合{}3+≤≤=a x a x A ,{}51>-<=x x x B 或,若∅=B A ,求实数a 的取值范围.分析:对于任意实数a ,都有3+<a a ,所以本题中集合A 不会是空集. 解:∵3+<a a ,∴∅≠A . ∵∅=B A∴⎩⎨⎧≤+-≥531a a ,解之得:1-≤a ≤2.∴实数a 的取值范围是{}21≤≤-a a .★★例18.（综合性强）已知集合()(){}011222>++++-=a a y a a y y A ,集合⎭⎬⎫⎩⎨⎧≤≤+-==30,25212x x x y y B ,若∅=B A :（1）求实数a 的取值范围;（2）当ax x ≥+12恒成立时,求a 的最小值.分析:（1）求集合A 时要解含参一元二次不等式,可借助于因式分解:()()()()()()()()()[]11111122222222+--=-+--=++-+-=++++-a y a y a y a a y y a a ay a y y a a y a a y对于集合B ,代表元素是y ,所以集合B 是函数值的集合,通过配方得:()2121252122+-=+-=x x x y ∵0≤x ≤3,∴2≤y ≤4,∴{}42≤≤=y y B ;（2）这是与二次函数有关的恒成立问题,使用数形结合方法.解:（1）()(){}()()[]{}010112222>+--=>++++-=a y a y y a a y a a y y A∵04321122>+⎪⎭⎫ ⎝⎛-=-+a a a （这里作差比较12+a 与a 的大小）∴a a >+12∴{}12+><=a y a y y A 或.{}4230,25212≤≤=⎭⎬⎫⎩⎨⎧≤≤+-==y y x x x y y B∵∅=B A∴⎩⎨⎧≥+≤4122a a ,解之得:a ≤3-或3≤a ≤2. ∴实数a 的取值范围是{}233≤≤-≤a a a 或; （2）∵ax x ≥+12恒成立,即12+-ax x ≥0恒成立. ∴()42--=∆a ≤0,解之得:2-≤a ≤2.∴a 的最小值为2-.题型三 补集运算全集 一般地,如果一个集合含有我们所研究问题中涉及的所有元素,那么就称这个集合为全集,记作U .补集 对于一个集合A ,由全集U 中不属于A 的所有元素组成的集合称为集合A相对于全集U 的补集,简称集合A 的补集,记作C U A ,即C U A {}A x U x x ∉∈=且,.补集的性质①(C U A )U A = ; ②(C U A )∅=A ; ③ C U (C U A )A =; ④ C U U ∅=; ⑤ C U U =∅.例19. 已知全集{}60<<=x x U ,集合{}a x x A <<=1,若C U A U ≠,则实数a 的取值范围是__________.分析: C U A U ≠说明∅≠A ,且U A ⊆. 解:∵C U A U ≠,∴∅≠A ,且U A ⊆. ∴实数a 的取值范围是{}61≤<a a .例20. 已知全集{}5,4,3,2,1=U ,集合{}042=++=px x x A ,求C U A . 分析:集合A 是由方程042=++px x 的解构成的,而方程042=++px x 可能无解、有两个不相等的实数根或有两个相等的实数根,需要分类讨论. 解:由题意可知:U A ⊆. 分为两种情况:①当∅=A 时,方程无实数根,∴0162<-=∆p ,解之得:44<<-p ∴C U A =C U ∅{}5,4,3,2,1==U ;②当∅≠A 时,则有162-=∆p ≥0,解之得:p ≤4-或p ≥4. 设方程042=++px x 的两个实数根分别为21,x x 由根与系数的关系定理可得:421=x x :若4,121==x x ,则5-=p ,符合题意,此时{}4,1=A ,C U A {}5,3,2=; 若221==x x ,则4-=p ,符合题意,此时{}2=A ,C U A {}5,4,3,1=. 综上所述,当44<<-p 时,C U A ={}5,4,3,2,1;当5-=p 时,C U A {}5,3,2=;当4-=p 时,C U A {}5,4,3,1=.例21. 已知{}31≤<-=x x A ,{}m x m x B 31+<≤=. （1）当1=m 时,求B A ;（2）若⊆B C R A ,求实数m 的取值范围.分析:（1）求两个连续型实数集合的并集时,借助于数轴进行求解能将抽象的问题直观化,但要特别注意端点的实心和空心以及端点值的取舍;（2）求连续型实数集合的补集也是借助于数轴进行.解:（1）当1=m 时,{}{}4131<≤=+<≤=x x m x m x B ∴{}{}{}414131<<-=<≤≤<-=x x x x x x B A ; （2）∵{}31≤<-=x x A ,∴C R A {}31>-≤=x x x 或 ∵⊆B C R A ,∴分为两种情况:①当∅=B 时,有m ≥m 31+,解之得:m ≤21-; ②当∅≠B 时,则有:⎩⎨⎧-≤++<13131m m m 或⎩⎨⎧>+<331m mm解之得:无解或3>m .综上,实数m 的取值范围是⎭⎬⎫⎩⎨⎧>-≤321m m m 或.★例22. 设全集(){}R y R x y x I ∈∈=,,,()⎭⎬⎫⎩⎨⎧=--=123,x y y x A ,(){}1,+==x y y x B ,求C I A B .解:()(){}2,1,123,≠+==⎭⎬⎫⎩⎨⎧=--=x x y y x x y y x A ∴集合A 是由直线1+=x y 上除点()3,2外的所有点构成的集合 ∴C I A =(){}3,2 ∵(){}1,+==x y y x B∴集合B 是由直线1+=x y 上所有的点构成的集合 ∴C I A =B (){}3,2. 附:函数123=--x y ,即1+=x y ()2≠x 的图象如图所示.。

集合间的基本运算一、知识概述1、交集的定义一般地，由所有属于A且属于B的元素所组成的集合，叫做A，B的交集．记作A B（读作‘A交B’），即A B=｛x|x A，且x B｝．2、并集的定义一般地，由所有属于集合A或属于集合B的元素所组成的集合，叫做A，B的并集．记作：A B（读作‘A并B’），即A B ={x|x A，或x B}．3、补集：一般地，设S是一个集合，A是S的一个子集（即），由S中所有不属于A的元素组成的集合，叫做S中子集A的补集（或余集），记作，即=．性质：.全集：如果集合S含有我们所要研究的各个集合的全部元素，这个集合就可以看作一个全集，全集通常用S，U表示4、运算性质：（1）；（2）；（3）；（4）；（5）；（6）；．二、例题讲解例1、设集合A={－4，2m－1，m2}，B={9，m－5，1－m}，又A B={9}，求实数m的值．解：∵A B={9}，∴2m－1=9或m2=9，解得m=5或m=3或m=－3．若m=5，则A={－4，9，25}，B={9，0，－4}与A B={9}矛盾；若m=3，则B中元素m－5=1－m=－2，与B中元素互异矛盾；若m=－3，则A={－4，－7，9}，B={9，－8，4}满足A B={9}．∴m=－3．例2、设A={x|x2＋ax＋b=0}，B={x|x2＋cx＋15=0}，又A B={3，5}，A∩B={3}，求实数a，b，c的值．解：∵A∩B={3}，∴3∈B，∴32＋3c＋15=0，∴c=－8，由方程x2－8x＋15=0解得x=3或x=5．∴B={3，5}．由A（A B）={3，5}知，3∈A，5A（否则5∈A∩B，与A∩B={3}矛盾）.故必有A={3}，∴方程x2＋ax＋b=0有两相同的根3．由韦达定理得3＋3=－a，33=b，即a=－6，b=9，c=－8．例3、已知A={x|x3＋3x2＋2x＞0}，B={x|x2＋ax＋b≤0}，且A∩B={x|0＜x≤2}，A∪B＝｛x｜x＞－2｝，求a、b的值．解：A={x|－2＜x＜－1或x＞0}，设B=［x1，x2］，由A∩B=（0，2］知x2＝2，且－1≤x1≤0，①由A∪B=（－2，＋∞）知－2≤x1≤－1. ②由①②知x1＝－1，x2＝2，∴a＝－（x1＋x2）＝－1，b＝x1x2＝－2．例4、已知A={x|x2－ax＋a2－19=0}，B={x|x2－5x＋8=2}，C={x|x2＋2x－8=0}.若A∩B，且A∩C=，求a的值．解：∵B={x|(x－3)(x－2)=0}={3，2}，C={x|(x＋4)(x－2)=0}={－4，2}，又∵A∩B，∴A∩B≠．又∵A∩C=，∴可知－4A，2A，3∈A．∴由9－3a＋a2－19=0，解得a=5或a=－2．①当a=5时，A={2，3}，此时A∩C={2}≠，矛盾，∴a≠5；②当a=－2时，A={－5，3}，此时A∩C=，A∩B={3}≠，符合条件．综上①②知a=－2．例5、已知全集U={不大于20的质数}，M，N是U的两个子集，且满足M∩（）={3，5}，（）∩N={7，19}，（）∩（）={2，17}，求M、N．解：用图示法表示集合U，M，N（如图），将符合条件的元素依次填入图中相应的区域内，由图可知：M={3，5，11，13}，N={7，11，13，19}.点评：本题用填图的方法使问题轻松地解决，但要注意的是在填图时，应从已知区域填起，从已知区域推测未知区域的元素．特别提示：下列四个区域：对应的集合分别是：①—；②—；③—；④—．一、选择题1、下列命题中，正确的是（）A．若U=R，A U，；B．若U为全集，Φ表示空集，则Φ=Φ；C．若A={1，Φ，{2}}，则{2}A；D．若A={1，2，3}，B={x|x A}，则A∈B．2、设数集且M、N都是集合{x|0≤x≤1}的子集，如果把b－a叫做集合{x|a≤x≤b}的“长度”，那么集合M∩N 的“长度”的最小值是（）A． B．C． D．3、设M、N是两个非空集合，定义M与N的差集为M－N={x|x∈M且x N}，则M－（M－N）等于（）A．N B．M∩NC．M∪N D．M4、已知全集，集合M和的关系的韦恩（Venn）图如下图所示，则阴影部分所示的集合的元素共有（）A．3个 B．2个C．1个 D．无穷个1、Φ=U，{2}∈A，{2}单独看是一个集合，但它又是A中的一个元素．2、集合M的“长度”为，集合N的“长度”为，而集合{x|0≤x≤1}的“长度”为1，故M∩N的“长度”最小值为3、M－N={x|x∈M且x N}是指图（1）中的阴影部分．同样M－（M－N）是指图（2）中的阴影部分．4、∵图形中的阴影部分表示的是集合，由解得集合，而N是正奇数的集合，∴，故选B．二、填空题5、已知集合A={x|x2－3x＋2=0}，集合B={x|ax－2=0}（其中a为实数），且A ∪B=A，则集合C={a|a使得A∪B=A}=_____________．5、{0，1，2}解析：A={1，2}，由A∪B=A，得B A．∵1∈A，即得a=2；或2∈A，即得a=1；或B=Φ，此时a=0.∴C={0，1，2}．6、非空集合S{1，2，3，4，5}，且若a∈S，则6－a∈S，这样的S共有___________个．6、6解析：S={1，5}或{2，4}或{3}，或{1，3，5}，或{2，4，3}，或{1，5，2，4}．三、解答题7、设集合.（1）若，求实数a的值．（2）若，求实数a的值．7、解：（1）∵9，∴9 A.则a2=9或.解得a=±3或5.当时，（舍）；当时，（符合）；当时，（符合）.综上知或.（2）由（1）知.8、已知全集U＝R，＜0，＜或x＞，若，求实数的取值范围8、解：依题设可知全集且≥0≤≤5，≤≤，由题设可知.分类如下：①若，则m＋1＞2m－1m＜2.②若，则m＋1≤2m－1，且，解得2≤m≤3.由①②可得：m≤3.∴实数m的取值范围为{m|m≤3}.9、已知全集U={|a－1|，(a－2)(a－1)，4，6}．（1）若求实数a的值；（2）若求实数a的值．9、解：（1）∵且B U，∴|a－1|=0，且(a－2)(a－1)=1，或|a－1|=1，且(a－2)(a－1)=0；第一种情况显然不成立，在第二种情况中由|a－1|=1得a=0或a=2，∴a=2.（2）依题意知|a－1|=3，或(a－2)(a－1)=3，若|a－1|=3，则a=4，或a=－2；若(a－2)(a－1)=3，则经检验知a=4时，(4－2)(4－1)=6，与元素的互异性矛盾．∴a=－2或．10、设集合A ={|}，B ={|，}，若A B=B，求实数的值．10、解：先化简集合A=. 由A B=B，则B A，可知集合B可为，或为{0}，或{－4}，或．(i)若B=，则，解得＜；(ii)若B，代入得=0=1或=，当=1时，B=A，符合题意；当=时，B={0}A，也符合题意．(iii)若－4B，代入得=7或=1，当=1时，已经讨论，符合题意；当=7时，B={－12，－4}，不符合题意．综上可得，=1或≤．11、已知集合A={x|x2－4mx＋2m＋6=0}，B={x|x＜0}，若A∩B≠，求实数m 的取值范围．11、解：设全集．若方程x2－4mx＋2m＋6=0的两根x1，x2均非负，则解得．∵{m|}关于U的补集是{m|m≤－1}，∴实数m的取值范围是{m|m≤－1}．1、（全国I，1）设集合A={4，5，7，9}，B={3，4，7，8，9}，全集U=A∪B，则集合中的元素共有（）A．3个B．4个C．5个D．6个答案：A解析：2、（福建，2）已知全集U=R，集合A={x|x2－2x>0}，则等于（）A．{x|0≤x≤2} B．{x|0<x<2}C．{x|x<0或x>2} D．{x|x≤0或x≥2}答案：A解析：∵x2－2x>0，∴x(x－2)>0，得x<0或x>2，∴A={x|x<0或x>2}，.3、（山东，1）集合A={0，2，a}，B={1，a2}．若A∪B={0，1，2，4，16}，则a的值为（）A．0 B．1 C．2 D．4答案：D解析：∵A∪B={0，1，2，a，a2}，又A∪B={0，1，2，4，16}，∴{a，a2}={4，16}，∴a=4，故选D．集合中的交、并、补等运算，可以借助图形进行思考。