当前位置：文档之家 › 3第三章-地震学基础—地震波传播理论ppt课件

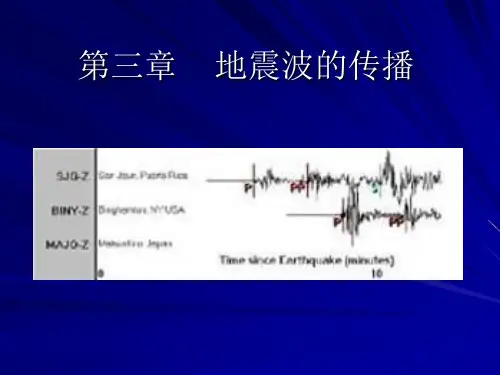
3第三章-地震学基础—地震波传播理论ppt课件

  • 格式：ppt
  • 大小：14.97 MB
  • 文档页数：18

下载文档原格式

  / 18

合集下载

地震勘探系列课件(中南大学)—第三章 地震波的时距关系

地震勘探系列课件(中南大学)—第三章 地震波的时距关系
2 x 2 Z 1 − (V1 / V2 ) = + V2 V1
�
当 x = 0 时，
2Z 1 − (V1 / V2 ) 2 t0 = V1
�
x ∴ t = t0 + V2
可见，折射波时距曲线也为 直线 ，其斜率 为1/V2 。 直线，其 斜率为 或截距时”，它是折射波时距曲线延伸 式中：t0 为“交叉时 交叉时或 到 t 轴与 t 轴的交点所对应的时间。因此，可以很方便地利用 直达波和折射波时距曲线的斜率求出 V1、V2，同时，将折射波 为： 时距曲线延伸到 t 轴求出交叉时 t0 ，则界面埋深 界面埋深为：
第三章 地震波的时距关系
本章重点：
★ 时距曲线的定义 ★ 不同介质、不同界面形态下的直达波、 折射波、反射波、特殊波的时距关系。 性 质：掌握 目 的：深入了解运动学特征，便于掌握勘探方法
� 地震波的时距关系 ：地震波在传播过程中，波前的空间位置与
其传播时间之间的几何关系(即地震波的时距关系)。
� 作用：通过研究地震波的时距关系，深入了解地震波的运动学特
依次排列在一起所形成的图形。
� 同相轴：地震记录中各地震道的波
形曲线上波峰(或波谷)的规则排列。
� 时距曲线：在一维测线上观测得到
的时距关系所构成的曲线。亦可描述 为：各道的同相轴时间 t 与其对应的 炮检距 x 所展现出的 t - x 关系曲线。
典型地震记录（ 1）
典型地震记录（ 2）
第一节 直达波及折射波时距曲线
，则在O点激发，OO'段接收时的折射波时距 � 采用相遇观测系统 相遇观测系统，则在 曲线为：
t= OM + PO′ MP + V1 V2 Z + Z 下 OQ − ( Z 上 + Z 下 )tgi = 上 + V1 cos i V2 x ⋅ cos ϕ Z 上 + Z 下 x ⋅ sin( i + ϕ ) 2 Z 上 = + cos i = + cos i V2 V1 V1 V1

3 第三章 地震波动方程wan

3 第三章 地震波动方程wan

第三章 地震波动方程现在，我们用前一章提出的应力和应变理论来建立和解在均匀全空间里弹性波传播的地震波动方程。

这章涉及矢量运算和复数，附录2对一些数学问题进行了复习。

3.1 运动方程（Equation of Motion ）前一章考虑了在静力平衡和不随时间变化情况下的应力、应变和位移场。

然而，因为地震波动是速度和加速度随时间变化的现象，因此，我们必须考虑动力学效应，为此，我们把牛顿定律（ma F =）用于连续介质。

3.1.1一维空间之振动方程式质点面上由于应力差的存在而使质点产生振动。

如图1-3所示，考虑一横截面为A ∆薄棒向x1轴延伸，任取以微元，沿x1的长度为1x ∆，其左端的应力为11σ，方向逆x1的方向，右端的应力为11111x σσ∂+∂，方向与x1方向相同，其位移量为u ：1D caseFigure 2.8x 1111111x ∂则其作用力为“应力” “其所在的质点面积”，所以其两边的作用力差为()()()()()111111111111111111111A x x x A x x x x Ax x σσσσσσ⎛⎫∂∂∆+∆-=∆+∆-=∆∆ ⎪∂∂⎝⎭惯量﹙inertia ﹚为212ux A tρ∂∆∆∂所以得出21121u t x σρ∂∂=∂∂ ……………………………………………………... （3-1）其中ρ为密度﹙density ﹚。

3-1式表示，物体因介质中的应力梯度﹙stress gradient ﹚而得到加速度。

如果ρ与E 为常数，1111uEx x σ∂∂=∂∂，这里考虑一维情况，将x 的角标去掉，则3-1式可写为 222221tu c x u ∂∂=∂∂ …………………………………………………… （3-2）其中ρEc =运用分离变量法求解（3-2）式，设u=X(x)T(t),(3-2)式可以变为T X cT X ''=''21设22ω-=''=''TT X X c 求解20T T ω''+=，其特征方程为220r ω+=，特征根为1,2r i ω=±，所以微分方程的解为：12i t i t T C e C e ωω-=+ 同理得到，220X X c ω''+=的解为12i xi x ccX D eD eωω-=+。

3第三章-地震学基础—地震波传播理论

3第三章-地震学基础—地震波传播理论

界面R上，因为波前与射线垂直，则波前面和界面R的夹角等于
α。设波前A´B´在t 时刻到达了分界面R上的A´点，按惠更斯原 理，A´点此时可以看成是一个新的点震源，由该点产生新的扰 动，向分界面两边的介质里传播。其中一部分扰动以V1速度在 W1介质中传播，另外一部分以V2速度在W2介质中传播。
第三章 地震波传播理论x) 1 dx V1
x h2 x2

1 V2
( L x) r 2 ( L x) 2
( L x) r 2 ( L x) 2
1 x 1 V1 h 2 x 2 V2
射线AOB的走时为：
t ( x) 1 1 h2 x2 r 2 ( L x) 2 V1 V2
地震学基础
（1） Fermat原理
A
inc
Snell定律
反射点 x 应使t达到最小值。即：
Fermat原理
B
ref
V1 V2
h
x
o
L x
r
L
dt( x) 1 x ( L x) 0 2 2 2 2 dx V1 h x r ( L x) x ( L x) h2 x2 r 2 ( L x) 2
1 t CB A C sin
' '
t s in ' AC 1
整理后：
1 t A D A C sin
' '
2 t A E A C sin
' '
第三章 地震波传播理论
t s in ' AC 1 t s in ' AC 2

地震概论第三章地震波讲义资料

地震概论第三章地震波讲义资料

六、地震波与地球内部结构
体波之所以对地球内部结构比较敏感，是因为在地球 内部的不同部分，地震波传播速度不同 ，在不同部分的 分界面上发生的反射、折射和波型转换，既影响体波的 “行走时间”，又影 响体波的振幅和形状。
把面波的波长延伸到整个地球的尺度，我们还有一个 专用的名词：地球自由振荡。这时，地 球好像是一口铜 钟被大地震重重地敲击一下，余音缭绕，经久不绝。不同 形状、不同结构的 铜钟具有不同的音色；类似地，不同 形状、不同结构的星球也具有不同的自由振荡的形 式。 地震学家就像一位钢琴调音师那样，通过倾听地球 的“音乐”，辨认出地球内部的结构。
P波和S波的速度表达式
P波，速度Vp = V (K+ 3/4µ)/ρ 花岗岩: Vp = 5.5千米/秒; 水: Vp = 1. 5千米/秒 ρ为密度
S波，速度Vs=V µ/ρ 花岗岩: Vs =3.0 千米/秒; 水: Vs = 0 千米/秒
P波速度
花岗岩 水
5.5千米/秒 1.5千米/秒
S波速度 3.0千米/秒
复习
一、波动 波动方程 波速、波长、周期、波频率、初相位、简 谐波与复杂波
2、S波
S波:S波跑的比P波慢，它只可以在固体传 播。在S波传播时，质点的运动方向与S波 的传播方向互相垂直，介质中产生剪切应 力。由于流体不能承受剪切应力，因此S波 不能在液体和气体中传播。
P波和S波的速度由介质的密度和弹性常数 决定。
内部圈层
深度 km
地震波速度
纵波 横波
Vp
Vs
密度ρ g·cm-
3
压力 P
MPa
重力 g
m·s-2
温度t C
附注
0 5.6 3.4 2.6

地震波ppt课件

地震波ppt课件
随着科技的不断进步，将发展更加先进的地震波观测技术和数据处理方 法，提高地震波研究的精度和可靠性。
未来地震波研究将更加注重应用实践，将研究成果应用于实际的地震监 测、预警和抗震减灾工作中，为人类创造更加安全、稳定的生存环境。
海啸预警
在地震引起的海啸预警中，地震波发挥着重要作用。通过分析地震波数据，可以快速判断是否可能发 生海啸，并及时发布预警信息，减少灾害损失。
04
地震波的挑战与未来发 展
地震波数据解析的挑战
数据处理难度大
地震波数据量大、复杂度高，需要高效、准确的处理方法才能提 取有用的信息。
噪声干扰严重
地震波传播过程中容易受到各种噪声的干扰，如何有效去除噪声、 提取真实信号是一大挑战。
我们应该如何利用地震波为人类服务
建立和完善地震监测网络，提 高地震预警的准确性和时效性 ，为灾害防范提供有力支持。
利用地震波数据开展工程抗震 设计和评估，提高建筑物和基 础设施的抗震能力。
通过研究地震波揭示地球内部 结构和性质，推动地球科学的 发展和人类对地球的认识。
对未来地震波研究的展望
未来地震波研究将更加注重跨学科合作，综合运用物理学、数学、地质 学等多学科理论和方法，深入揭示地震波的传播规律和地球内部结构。
分辨率和精度要求高
地震波数据需要高分辨率和高精度的解析，才能准确描述地层结构 和地质构造。
地震波探测技术的未来发展
智能化数据处理
利用人工智能和机器学习技术， 实现地震波数据的自动识别、分
类和解析。
多源信息融合
将不同来源的地震波数据融合，提 高探测精度和分辨率，为地质勘探 和资源开发提供更准确的信息。
提高地热能利用率
通过地震波探测技术了解地热田 的热传导特性和地温场分布，为 地热能的合理利用和提高利用率

地震波的特性和传播讲解38页PPT

地震波的特性和传播讲解38页PPT

16、业余生活要有意义，不要越轨。——华盛顿 17、一个人即使已登上顶峰，也仍要自强不息。——罗素·贝克 18、最大的挑战和突破在于用人，而用人最大的突破在于信任人。——马云 19、自己活着，就是为了使别人过得更美好。——雷锋 20、要掌握书，莫被书掌握；要为生而读，莫为读而生。——布尔沃
END

地震波的特性和传播讲解
6、法律的基础有两个，而且只有两个……公平和实用。——伯克 7、有两种和平的暴力，那就是法律和礼节。——歌德
8、法律就是秩序，有好的法律才有好的秩序。——亚里士多德 9、上帝把法律和公平凑合在一起，可是人类却把它拆开。——查·科尔顿 10、一切法律都是无用的，因为好人用不着它们，而坏人又不会因为它们而变得规矩起来。——德谟耶克斯

抗震PPT幻灯片课件

抗震PPT幻灯片课件
地下采空区属于危险地段。
不利于抗震的地段：软弱土，液化土，条状突出的山嘴，高耸孤立的山丘，陡 坡，陡坎，河岸和边坡的边缘，平面分布上成因、岩性、状态明显不均匀的土 层（含故河道、疏松的断层破碎带、暗埋的塘浜沟谷和半填半挖地基），高含 水量的可塑黄土，地表存在结构性裂缝等。
15
1.2 选择有利于抗震的场地 有利地段：一般是指位于开阔平坦地带的坚硬场地土或密实均匀中硬 场地土。 在选择高层建筑的场地时，应尽量建在基岩或薄土层上，或应建在具 有较大“平均剪切波速”的坚硬场地土上，以减少输入建筑物的地震 能量，从根本上减轻地震对建筑物的破坏作用。
楼层的最大弹性水平位移（或层间位移），大于该楼层两端弹性水平位 移（或层间位移）平均值的1.2倍
结构平面凹进的一侧尺寸，大于相应投影方向总尺寸的30%
楼板局部不连续 楼板的尺寸和平面刚度急剧变化，例如，有效楼板宽度小于该层楼板典
型宽度的50%,或开洞面积大于该层楼面面积的30%，或较大的楼层错层
b 0.5B
大大不足,率先破坏；3.水平地震作用下,柔而长的楼板产生可观的竖向运动等。
19
20
地震区的高层建筑，平面以方形、矩形、圆形为好；正六边 形、正八边形、椭圆形、扇形也可以。
不宜采用有较长翼缘的L形、T形、U形、H形、Y形等平面形状。 高层规程的规定：
设防烈度 L / B
６、７度 ≤6.0
l / Bmax
Ki3
Ki2 Ki1 Ki
Ki 0.7Ki1
Ki

0.8( Ki1

Ki2 3

Ki3 )
沿竖向的侧向刚度不规则（有柔软层） 竖向抗侧力构件不连续
25
立ห้องสมุดไป่ตู้不规则类型

第三章 地震波传播理论

第三章 地震波传播理论
数Nx=201 Nz=201; Nt=500； 步长dx=dz=dh=8 时间间隔dt=0.001; 波传播速度v=3000;
以二维声波方程为例进行地震波场模拟
2u x,z,t 2u x,z,t 1 2u x,z,t s（t） x 2 z 2 v2 t 2
含有低速层中的地震射线影区的产生模拟
3.1 地震波传播理论
地壳最上部的4km以每公里0.25km/s的速 度递增，下面2km以每公里1km/s的速度递 增，后面的12km仍然以每公里0.25km/s的速 度递增，我们研究其中的走时、震中距和p 参数的关系。
走 时 /s
12
10
8
逆
6
行
焦
散
点
顺
行
0
3.1.1 水平层状介质（反射、折射、时距曲线）
震源不在地表（h≠0）
A
c
V2>V1
c
B
V1 V2
V1
V1 sin( c ) 存在临界角 c , 满足: V2
o
B
A
o
V2
A
c
首波, 侧面波 （Head wave）
B
c
V1 V2
O
V2
P
球对称介质中Snell定律
i1
v1
sin(i1 ) sin( a1 ) v1 v2
3.1 地震波传播理论
3.1.1 水平层状介质（反射、折射、时距曲线） 3.1.2 倾斜介质时距曲线 3.1.3 多层水平介质 3.1.4 球状介质
3.2 体波各种震相和走时
第四章 地球内部结构 第五章 地震机制 第六章 地震仪和地震观测 第七章 地震统计分析 第八章 宏观地震学

地震勘探PPT课件

地震勘探PPT课件

3/6/2021 3:55 AM
21
GeoPen
地震勘探的基本原理
频率相同，幅值不同
频率相同，相位不同
地震波频谱特征的分析是地震勘探技术的一个重要方面， 根据有效波和干扰波的频段差异，可用来指导野外工作方法 的选择，并给数字滤波和资料解译等工作提供依据。
3/6/2021 3:55 AM
22
GeoPen
二、费马原理 费马原理又称射线原理或最小路径原理，它给出地震 波总是沿地震射线传播，以保证波到达某点所用的旅行时 间最少。显然，从一个等时面到另一个等时面，只有垂直 距离最短，因此波沿垂直于等时面的方向传播所用旅行时 间最少，故地震射线和等时面总是互相垂直的。有波前和 波射线的概念来描述波动是一种简便而清晰的方法。
工程物探根据波的特征，可分为折射波法、反射波法、 瞬态面波法、P，S波测井、弹性波CT、地脉动测试、桩基 完整性检测等。下面对其分别进行介绍。
3/6/2021 3:55 AM
25
GeoPen
浅层折射波地震勘探原理
设有两层介质，上层波速为Vl。下层为V2，且V2＞V1、 当入射波以临界角i(i＝arcsin(V1/V2))入射到界面时，透 射波将沿分界面以速度V2滑行。这种滑行波沿界面传播时， 必然引起界面上各质点的振动，根据惠更斯原理，滑行波 所经过的界面上的各点，都可看作是一个新的振源。由于 上下介质质点存在弹性联系，因此滑行波沿界面传播时， 在上覆介质中的质点也发生振动、并以波的形式返回地面， 这种波称为折射波(有时又叫首波)。
3/6/2021 3:55 AM
17
GeoPen
地震勘探的基本原理
若假设e是半径为r的球面波波前上单位面积的能量， 则整个球面的总能量E为：E = 4πr2e

地震与地震波-教育版PPT课件

地震与地震波-教育版PPT课件
一、地震 一种机械运动的传布，产生于地球介质的弹性。它的性质和声
波很接近，因此又称地声波。但普通的声波在流体中传播，而 地震波是在地球介质中传播，所以要复杂得多，在计算上地震 波和光波有些相似之处。波动光学在短波的情况下可以过渡到 几何光学，从而简化了计算;同样地，在一定条件下地震波的概 念可以用地震射线来代替而形成了几何地震学。不过光波只是 横波，地震波却纵、横两部分都有，所以在具体的计算中，地 震波要复杂得多。
22
授课：XXX
2021/3/9
地震波的概念
地下岩层断裂错位伴随产生大量的能 量释放，造成周围弹性介质的强烈振 动，这种振动以波的方式向外传播， 即为地震弹性波
23
授课：XXX
2021/3/9
地震波的种类
按波的本质形式大体可分为纵波和横 波
按波的传播区域大体可分为体波和面 波
24
授课：XXX
2021/3/9
震级 震源深度 震中距 场地条件 人口密度和经济发展程度 建筑物质量 发生地震的时间
16
授课：XXX
2021/3/9
地理分布——地震 带
地震的地理分布受一定的地质条件控制，具有一定的规律。地震 大多分布在地壳不稳定的部位，特别是板块之间的消亡边界，形成地震活动 活跃的地震带。全世界主要有三个地震带：
9
授课：XXX
2021/3/9
地震分类
◢ M<1级 的地震称为超微震 ◢ 1≤M<3级 的称为弱震或微震 ◢ 3≤M<4.5级 的称为有感地震 ◢ 4.5≤M<6级 的称为中强震 ◢ 6≤M<7级 的称为强震 ◢ 7≤M<8级 的称为大地震 ◢ 8≤M级 的称为巨大地震。
10
授课：XXX

《地震学总结》PPT课件

《地震学总结》PPT课件

a
5
a
2
§2.3 波动理论向射线理论的过渡 §2.4 球对称介质中的地震射线的特征 §2.5 近震地震射线与地壳构造 §2.6 远震地震射线与地球内部构造
程函方程及其物理意义，费马原理；
掌握球对称介质中参数方程形式的走时公式的推导，掌握球对称介质中地 震体波的射线参数方程与本多夫定律等的推导，不同的速率-深度分布曲线 情况下对应的地震射线，并了解正常及特殊情况下的走时曲线特征；
第四章 震源理论简介
§4.1 弹性回跳假设 §4.2 震源模型 §4.3 点源位移场及辐射图案 § 4.4 断层面解
掌握地震发震时间与震源位置的测定原理与基本方法；
了解并掌握常用地震震相的标示规则及其a 传播过程中的射线路径、走时；
4
பைடு நூலகம்
第五章 地震预报的地震学方法
地震空间活动图像 地震活动期和平静期 地震序列分析 波速异常的研究 震源机制与小震应力场的变化
地震学
第一章 概述
§1.1 地震学简介 §1.2 地震学的基本名词和概念 §1.3 地震的频度和地理分布及地震成因假说
天然地震的基本概念；地震烈度、等震线、震级等； 地震的分类。地震频度，G-R公式，地震分布。
a
1
第二章 地震波传播与地球内部构造
§2.1 波动方程及其基本解 §2.2 地震波的传播
§2.2.1 平面波在自由表面的反射 §2.2.2 平面波在平面上的反射和折射 §2.2.3 地震面波
波动方程及其解，平面波解和球面波解；地震波的主要简化 假设；自由表面的边界条件和自然边界条件；两个半无限空 间模型的边界条件；了解地震面波与地震体波在传播过程中 的异同点，掌握love面 波与瑞利面波的传播特征及在一些简 单模型下的波动方程和频散方程；了解地震面波的频散方程 及其所反映的地球内部构造，了解并掌握群速度与相速度的 基本概念及其相互关系推导与计算方法；

地震知识ppt课件

地震知识ppt课件

加强地震科普宣传
提高公众对地震的认识和应对 能力，加强地震预警信息的传 播和普及。
投资地震研究
加大对地震研究的投入，推动 地震监测、预测和减灾技术的
创新和发展。
04 地震案例分析
唐山大地震
唐山大地震是中国历史上一次非常严重的地震，造成了大量的人员伤亡 和财产损失。该地震发生在1976年，震级为7.8级，震中位于唐山市区附 近。
总结词
了解地震的分类和分布有助于更好地预 测和应对地震灾害。根据不同的分类标 准，地震可以分为多种类型，如浅源地 震、深源地震、构造地震等。同时，地 震的分布也有一定的规律，主要集中在 环太平洋地震带、欧亚地震带等地区。
VS
详细描述
根据不同的分类标准，地震可以分为多种 类型。根据震源深度，地震可以分为浅源 地震（震源深度小于60公里）、中源地 震（震源深度在60-300公里之间）和深 源地震（震源深度大于300公里）。根据 成因，地震可以分为构造地震、火山地震 、塌陷地震等类型。此外，根据地震的分 布规律，地震主要集中在环太平洋地震带 、欧亚地震带等地区，这些地区的地壳构 造活动较为活跃，容易发生地震灾害。
掌握应急避险技能
在地震发生时，应保持冷静，迅 速采取正确的避险姿势和避险措 施，如躲在桌子下、关闭火源等
。
学习自救互救知识
了解如何进行自救和互救，掌握 心肺复苏等基本的急救技能，以
便在地震后及时进行救援。
及时报警求助
在地震后应尽快报警求助，并告 知地震的地点、震级等信息，以 便专业救援队伍及时赶到现场进
唐山大地震造成了大量建筑物倒塌和损坏，道路、桥梁等基础设施也遭 到了严重破坏。由于当时的经济条件和科技水平有限，救援工作面临很
大的困难。

三章地震波

三章地震波

地球内部构造和板块构造
地球内部构造和板块构造
地球内部结构与速度分布图
二、地震波传播
地震波在地表面的传播 地震波在物质介面上传播 地震波在地壳内部传播（近震＼远震） 地震波走时曲线
地震的发生及地震波传播示意图
地 震 知 识 和 全 球 地 震 活 动
地震构造示意图
（一）地震波在地表面传播
地震波的波序
(二)地震波在介质界面上
由震源产生的地震波向四面八方传播，遇到 界面将发生反射和折射，经过证明,地震波 在完全弹性介质中的传播遵从波的反射、折 射（Snall）定律。
sin i P sin i P sin i P sin iS sin iS p v1P v1P v2 P v1S v2 S

花岗岩: Vs =3.0 千米/秒; 水: Vs = 0 千米/秒
花岗岩
P波速度 5.5千米/秒 S波速度 3.0千米/秒
水
1.5千米/秒 0
在同样条件下P波速度大于S波
体波之所以对地球内部结构比较敏感，是因为在地球内部的 不同部分，地震波传播速度不同，在不同部分的分界面上发生的 反射、折射和波型转换，既影响体波的“行走时间”，又影响体 波的振幅和形状。 把面波的波长延伸到整个地球的尺度，我们还有一个专用的 名词：地球自由振荡。这时，地球好像是一口铜钟被大地震重重 地敲击一下，余音缭绕，经久不绝。不同形状、不同结构的铜钟 具有不同的音色；类似地，不同形状、不同结构的星球也具有不 同的自由振荡的形式。地震学家就像一位钢琴调音师那样，通过 倾听地球的“音乐”，辨认出地球内部的结构。
地震时地面波动的描述
唐山地震发生在1976年7月28日凌晨3点多钟。当时笔者（陈颙）住在北京前 门附近一个非常破旧的二层木制结构的楼房里，楼房至少有五十年历史了， 除了外墙是砖砌的，地板和骨架都是木质的，一走起路来地板就发出”咯吱 咯吱”的呻吟声。那时正好是夏天，天气出奇的闷热，难以让人入睡。我刚 躺着一会儿，迷迷糊糊中就觉得床有些大幅度上下跳动，地板甚至整个楼房 都发出”嘎吱”的声音。我立刻意识到”有大地震发生了”。长年从事地震 工作的我被晃醒后没有立即下床，而是躺在床上开始数数，”一、二、 三，……”，数着数着床的晃动变小了。当数到第二十的时候，突然又来了一 次晃动，比第一次更厉害，整个楼层都在忍受剧痛似的”哗哗啦”乱响。这 短短的20秒钟间隔就是纵波和横波到达的时间差（地震通常会产生纵波和横 波，纵波在地球介质中传播得快，最先到达我们脚下，引起地表的上下运动； 横波跑得慢，我们感到的第二次强烈震动就是横波造成的，地面表现出水平 方向运动。由于横波携带了地震产生的大部分能量，因此它对地表建筑物的 破坏更为严重），反映了观测者和震源的距离，差1秒钟，表明约8公里远处 发生了地震，20秒钟则说明这次地震事件发生在约160公里处。于是，我有 了一个初步判断：地震不在北京–在距离北京160公里的地方有大地震发生了。 这和雷雨闪电的原理是一样的：天空两片雷雨云相遇时，发出闪电和雷声， 闪电（电磁波）跑得快，雷声（空气中得声波）跑得慢，我们先看见闪光， 后听见雷声，闪光和雷声之间的时间差，就表示发出闪光和雷电的云距我们 的距离。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

地震学基础
射线理论
在研究问题的尺度远大于地震波波长的情况下，可将地 震波传播当作射线来处理，从而使复杂的波动问题简化成为 射线问题。地震射线问题这和几何光学很相似。所谓地震射 线，就是地震波传播时，波阵面法线的轨迹，也即是震动由 一点传播到另一点所经过的途径。
射线地震学，也叫几何地震学，是波动地震学在波长很 短时的近似。它可以由波动地震学推演出来，但更直接的是 根据费马原理。这个原理说：当一个震动由介质中一点传播 到另一点时，它所经过的途径是使其传播时间为一稳定值(最 大、最小或拐点)。在一般的地震波计算中，地球介质可以做 为各向同性的完全弹性体来对待。
.
第三章 地震波传播理论
地震学基础
费马原理是从波射线的角度描述波的传播特点，在均匀介 质中，显然波射线应当是从震源发出的一系列直线。因为地震 波只有沿着这样的射线传播，路程最短，旅行时间才是最少。 在均匀层状介质中，地震波沿满足斯涅尔定律的射线方向传播 所用旅行时间才能最少短。
.
第三章 地震波传播理论
估算：1度约等于110千米。
.
第三章 地震波传播理论
地震学基础
第二节 地震波传播的基本理论
•
在地震波理论中，通常把地球介质当作均匀、各向同性和
完全弹性介质来处理，只是一种简化的假定。实践证明，这种
假定可以使分析大大简单，并且在多数情况下可以得到与观测
结果颇为符合的结果。
•
研究地震波在地球内部传论
地震学基础
传播定律定理： 用射线和波前来描述波的传播 位置和能量随时间变化的关系，这种关系是工程地 震勘察资料处理中的重要组成部分，是进行地震数 据资料处理和定性定量解释的依据。下面就地震波 传播中有关的运动学和动力学中的定律定理介绍给 大家。
.
第三章 地震波传播理论
地震学基础
1、惠更斯原理
在均匀弹性介质中，点振源产生球面波向周围传播，当距 离r 趋向无穷大时，球面波前的半径很大，曲率很小，此时球面 波蜕变成了平面波。若已知某时刻 t 在同一时刻波前面上的各 个点，可以把这些点看成该时刻产生子波新的点振源。经过任 意Δt 时间后，这些新子波的包络面，就是原波在 t+Δt 时刻 （或t-Δt）新的波前面(或波尾面)。
.
第三章 地震波传播理论
地震学基础
二、首波（或侧面波）
若介质是分层的，当地震波由低速的一方向高速的一方入 射时，还存在一种波，叫做侧面波(或叫首波、折射波、衍射波、 行走反射波，等等) 。
虽然首波的传播路径总是比直达波长，但是因为首波在分 界面上是以深层介质中的速度来传播的，因此超过一定临界距 离之后，首波就会比直达波率先到达台站。
.
第三章 地震波传播理论
地震波传播的定律、定理
地震学基础
波动本身的描述常使用T、λ、γ、φ等物理量，但要描述地 震波在介质中的传播过程，还需要使用波前和波射线等念。
波动是质点振动状态在介质里的传播过程，振动是在外力 作用下质点离开平衡位置附近作来回往复运动，但振动是波动 产生的根源。在弹性介质中，各个质点是以弹性力互相联系着 的。某质点A受到外界扰动离开平衡位置时，周围的质点对A产 生的作用力，使A回到平衡位置，并在平衡位置附近振动，同时 A点周围的质点也受到A的作用力，离开各自的平衡位置振动起 来。所以介质中一个质点的振动会引起临近质点的振动，周围 介质的振动又会引起较远质点一起振动，这样一来，振动就会 在弹性介质中由近及远的向各个方向传播，形成了波动。
表示能量消耗的另一个重要参数Q叫做品质因子，这是由
电路理论借用来的一个概念，定义 1 1 E Q 2 E
E是一定体积的介质在一周期时间内所存储的最大应变能，
.
第三章 地震波传播理论
地震学基础
四、震中距
震源在地表的垂直投影为震中。震中距就是震 中到观测台站之间的距离，单位是千米/km。
另一种震中距单位是度，就是震中—地球球心 连线与观测台站-球心连线的夹角，与千米制换算： 震中距（度）=（震中距（千米）×180）/（地球半 径×π）。
P波和S波都会有相应的首波。
.
第三章 地震波传播理论
地震学基础
三、地震波的吸收和衰减
将地球介质当作是完全弹性体是一种近似，实际上在波 动传播过程中，介质会吸收波动的能量转化为热能。
振幅随时间的衰减可用 AA0et表示，为衰减系数。
波传播 x距离后，因介质对能量的吸收而导致振幅的减
小，可用 AA0ex 表示, 称为吸收系数。
.
第三章 地震波传播理论
地震学基础
.
第三章 地震波传播理论
地震学基础
Δ
.
第三章 地震波传播理论
地震学基础
2、费马原理
上面已经讲到波前面，我们又把垂直于波前面的射线叫波
射线。地震波是沿波射线的方向上在介质中传播，地震波射线 永远是一系列垂直于波前面的直线。
费马原理是说地震波沿射线的旅行时间(传播)与沿其它任 何路径的旅行时间相比为最小。即波总是沿所使用旅行时间最 少的路径传播，又叫费马最小原理和射线原理。
学两种方法。动力学方法是直接求解波动方程，研究平面波在
平界面上的反射、折射，均匀半空间及平行分层空间中的地震 面波，以及球对称模型的地球的自由振荡。该方法相对繁琐，
本书不做介绍。我们介绍的是第二种方法：运动学方法，就是 将波动方程的求解简化成波传播的射线理论，用地震射线这一
概念，研究地震波在地球内部传播的运动学特征，同时获得地 球内部构造的情况。
地震学基础
第三章 地震波传播理论
第一节 地震波传播的基本概念 第二节 地震波传播的基本理论 第三节 体波各种震相和走时表
.
第三章 地震波传播理论
地震学基础
第一节 地震波传播的基本概念 一、地球介质和弹性波
• 地震波是地下传播的震动，必然与岩石 的弹性有关，一般都假定岩石是一种完全 弹性体。
• 在一般的地震波计算中，地球介质可以 做为各向同性的完全弹性体来对待。
在地震勘探中，弹性波已远离震源传播，其波前面已由球面波蜕化成平面波。
.
第三章 地震波传播理论
地震学基础
若已知某一时刻t波前面的位置，则根据惠更斯原理，可以 求出任意时刻新波前的位置。在非均匀介质中也适用。惠更斯 原理描述波前面的空间几何位置随时间变化的特征，是一种构 制任意时刻波前位置的几何方法，利用此原理，可以构划出反 射界面和折射界面。惠更斯是从波前面的角度来描述波在介质 空间中传播的规律，而费马原理则从波射线的角度来描述波的 传播规律。