2018年成都市武侯区一诊数学

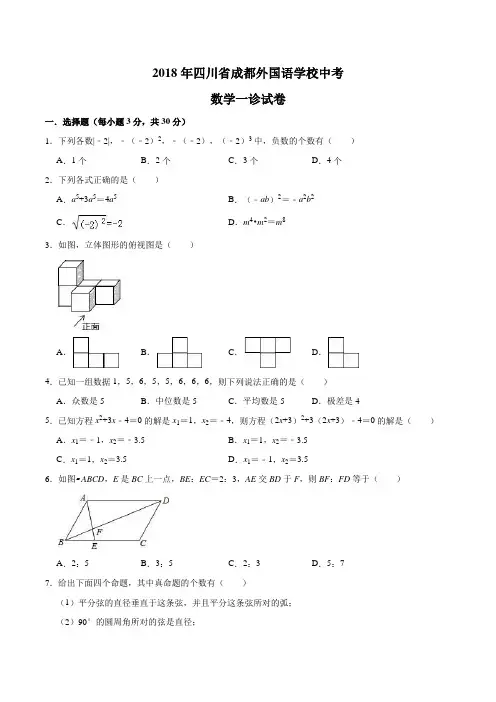
2018年四川省成都外国语学校中考数学一诊试卷一．选择题（每小题3分，共30分）1．下列各数|﹣2|，﹣（﹣2）2，﹣（﹣2），（﹣2）3中，负数的个数有（）A．1个B．2个C．3个D．4个2．下列各式正确的是（）A．a5+3a5＝4a5B．（﹣ab）2＝﹣a2b2C．D．m4•m2＝m83．如图，立体图形的俯视图是（）A．B．C．D．4．已知一组数据1，5，6，5，5，6，6，6，则下列说法正确的是（）A．众数是5B．中位数是5C．平均数是5D．极差是45．已知方程x2+3x﹣4＝0的解是x1＝1，x2＝﹣4，则方程（2x+3）2+3（2x+3）﹣4＝0的解是（）A．x1＝﹣1，x2＝﹣3.5B．x1＝1，x2＝﹣3.5C．x1＝1，x2＝3.5D．x1＝﹣1，x2＝3.56．如图▱ABCD，E是BC上一点，BE：EC＝2：3，AE交BD于F，则BF：FD等于（）A．2：5B．3：5C．2：3D．5：77．给出下面四个命题，其中真命题的个数有（）（1）平分弦的直径垂直于这条弦，并且平分这条弦所对的弧；（2）90°的圆周角所对的弦是直径；（3）在同圆或等圆中，圆心角的度数是圆周角的度数的两倍；（4）如上图，顺次连接圆的任意两条直径的端点，所得的四边形一定是矩形．A ．1个B ．2个C ．3个D ．4个8．如图，在平面直角坐标系中，▱ABCO 的顶点A 在x 轴上，顶点B 的坐标为（4，6）．若直线y ＝kx +3k 将▱ABCO 分割成面积相等的两部分，则k 的值是（ ）A ．B ．C ．﹣D ．﹣9．若2x +5y +4z ＝0，3x +y ﹣7z ＝0，则x +y ﹣z 的值等于（ ）A ．0B ．1C ．2D ．不能求出10．如图所示，在△ABC 中，D 是BC 的中点，DE ⊥BC 交AC 于点E ，已知AD ＝AB ，连接BE 交AD 于点F ，下列结论：①BE ＝CE ；②∠CAD ＝∠ABE ；③S △ABF ＝3S △DEF ；④△DEF ∽△DAE ，其中正确的有（ ）A ．1个B ．4个C ．3个D ．2个二．填空题（每小题4分，共16分）11．已知a ﹣b ＝2，那么2a ﹣2b +5＝ ．12．袋中装有6个黑球和n 个白球，经过若干次试验，发现“若从中任摸一个球，恰好是白球的概率为”，则这个袋中白球大约有个．13．直角三角形纸片的两直角边BC，AC的长分别为6，8，现将△ABC如下图那样折叠，使点A与点B重合，折痕为DE，则CE的长为．14．如图，点A1（1，1）在直线y＝x上，过点A1分别作y轴、x轴的平行线交直线y＝x于点B1，B2，过点B2作y轴的平行线交直线y＝x于点A2，过点A2作x轴的平行线交直线y＝x于点B3，…，按照此规律进行下去，则点A n的横坐标为．三．解答题（共54分，15题每小题12分，共12分）15．（1）计算：|﹣2|﹣（π﹣2015）0+（）﹣2﹣2sin60°+；（2）先化简，再求值：÷（2+），其中a＝．16．当m为何值时．关于x的方程＝﹣的解是负数？17．某校为了了解九年级学生体育测试成绩情况，以九年（1）班学生的体育测试成绩为样本，按A、B、C、D四个等级进行统计，并将统计结果绘制如下两幅统计图，请你结合图中所给信息解答下列问题：（说明：A级：90分﹣100分；B级：75分﹣89分；C级：60分﹣74分；D级：60分以下）（1）写出D级学生的人数占全班总人数的百分比为，C级学生所在的扇形圆心角的度数为；（2）该班学生体育测试成绩的中位数落在等级内；（3）若该校九年级学生共有500人，请你估计这次考试中A级和B级的学生共有多少人？18．观察与思考：阅读下列材料，并解决后面的问题在锐角△ABC中，∠A、∠B、∠C的对边分别是a、b、c，过A作AD⊥BC于D（如图（1）），则，即AD＝c sin B，AD＝b sin C，于是c sin B＝b sin C，即，同理有：，所以．即：在一个三角形中，各边和它所对角的正弦的比相等在锐角三角形中，若已知三个元素（至少有一条边），运用上述结论和有关定理就可以求出其余三个未知元素．根据上述材料，完成下列各题．（1）如图（2），△ABC中，∠B＝45°，∠C＝75°，BC＝60，则∠A＝；AC＝；（2）自从去年日本政府自主自导“钓鱼岛国有化”闹剧以来，我国政府灵活应对，现如今已对钓鱼岛执行常态化巡逻．某次巡逻中，如图（3），我渔政204船在C处测得A在我渔政船的北偏西30°的方向上，随后以40海里/时的速度按北偏东30°的方向航行，半小时后到达B处，此时又测得钓鱼岛A在的北偏西75°的方向上，求此时渔政204船距钓鱼岛A的距离AB．（结果精确到0.01，）19．已知一次函数y1＝x+m的图象与反比例函数y2＝的图象交于A、B两点．已知当x＞1时，y1＞y2；当0＜x＜1时，y1＜y2．（1）求一次函数的解析式；（2）已知双曲线在第一象限上有一点C到y轴的距离为3，求△ABC的面积．20．如图，AB是⊙O的直径，弦CD⊥AB，垂足为H，连结AC，过上一点E作EG∥AC交CD的延长线于点G，连结AE交CD于点F，且EG＝FG，连结CE．（1）求证：△ECF∽△GCE；（2）求证：EG是⊙O的切线；（3）延长AB交GE的延长线于点M，若tan G＝，AH＝3，求EM的值．一．填空题（每小题4分，共20分）21．已知+|ab+3|＝0，则a﹣b的值是．22．若关于x的方程x2+2mx+m2+3m﹣2＝0有两个实数根x1、x2，则x1（x2+x1）+x22的最小值为．23．如图，E、F分别是矩形ABCD的边AB、BC的中点，连AF，CE，AF、CE交于G，则四边形BEGF 与四边形ADCG的面积的比值为．24．已知二次函数y＝ax2+bx+c（a≠0）的图象与x轴交于点A（﹣2，0）、B（x1，0），且1＜x1＜2，与y轴正半轴的交点在（0，2）的上方，顶点为C．直线y＝kx+m（k≠0）经过点C、B．则下列结论：①b＞a；②2a﹣b＞﹣1；③2a+c＜0；④k＞a+b；⑤k＜﹣1，其中正确的结论有．25．如图，等边△AOB的边长为4，点P从点O出发，沿OA以每秒1个单位的速度向点A匀速运动，当点P到达点A时停止运动，设点P运动的时间是t秒．将线段BP的中点绕点P按顺时针方向旋转60°得点C，点C随点P的运动而运动，连接CP、CA．在点P从O向A运动的过程中，当△PCA为直角三角形时t的值为．二．解答题（共30分）26．某公司经营杨梅业务，以3万元/吨的价格买入杨梅后，分拣成A、B两类，A类杨梅包装后直接销售，包装成本为1万元/吨，它的平均销售价格y（单位：万元/吨）与销售数量x（x≥2，单位：吨）之间的函数关系如图所示；B类杨梅深加工后再销售，深加工总费用s（单位：万元）与加工数量t（单位：吨）之间的函数关系是s＝12+3t，平均销售价格为9万元/吨．（1）A类杨梅的销售量为5吨时，它的平均销售价格是每吨多少万元？（2）若该公司收购10吨杨梅，其中A类杨梅有4吨，则经营这批杨梅所获得的毛利润（w）为多少万元？（毛利润＝销售总收入﹣经营总成本）（3）若该公司收购20吨杨梅，其中A类杨梅有x吨，经营这批杨梅所获得的毛利润为w万元．①求w关于x的函数关系式；②若该公司获得了30万元毛利润，问：用于直销的A类杨梅有多少吨？27．已知：如图1．正方形ABCD，过点A作∠EAF＝90°，两边分别交直线BC于点E，交线段CD于点F，G为AE中点，连接BG（1）求证：∠AFD+∠CBG＝180°；（2）如图2，过点G作BG的垂线交对角线AC于点H，求证：GH＝GB；（3）如图3，连接HF，若CH＝3AH，AD＝2，求线段HF的长．28．如图，在平面直角坐标系中，点O为坐标原点，抛物线y＝ax2﹣10ax+16a（a≠0）交x轴于A、B两点，抛物线的顶点为D，对称轴与x轴交于点H，且AB＝2DH．（1）求a的值；（2）点P是对称轴右侧抛物线上的点，连接PD，PQ⊥x轴于点Q，点N是线段PQ上的点，过点N作NF⊥DH于点F，NE⊥PD交直线DH于点E，求线段EF的长；（3）在（2）的条件下，连接DN、DQ、PB，当DN＝2QN（NQ＞3），2∠NDQ+∠DNQ＝90°时，作NC⊥PB交对称轴左侧的抛物线于点C，求点C的坐标．参考答案一．选择题（每小题3分，共30分）1．下列各数|﹣2|，﹣（﹣2）2，﹣（﹣2），（﹣2）3中，负数的个数有（）A．1个B．2个C．3个D．4个【解答】解：|﹣2|＝2，﹣（﹣2）2＝﹣4，﹣（﹣2）＝2，（﹣2）3＝﹣8，﹣4，﹣8是负数，∴负数有2个．故选：B．2．下列各式正确的是（）A．a5+3a5＝4a5B．（﹣ab）2＝﹣a2b2C．D．m4•m2＝m8【解答】解：A、合并同类项，正确；B、（﹣ab）2＝a2b2，错误；C、＝2，错误；D、m4•m2＝m6，错误．故选：A．3．如图，立体图形的俯视图是（）A．B．C．D．【解答】解：如图所示的立体图形的俯视图是C．故选：C．4．已知一组数据1，5，6，5，5，6，6，6，则下列说法正确的是（）A．众数是5B．中位数是5C．平均数是5D．极差是4【解答】解：把数据1，5，6，5，5，6，6，6，按从小到大排列为1，5，5，5，6，6，6，6，中位数＝＝5.5，众数为6，平均数＝＝5，极差为＝6﹣1＝5，故C正确，故选：C．5．已知方程x2+3x﹣4＝0的解是x1＝1，x2＝﹣4，则方程（2x+3）2+3（2x+3）﹣4＝0的解是（）A．x1＝﹣1，x2＝﹣3.5B．x1＝1，x2＝﹣3.5C．x1＝1，x2＝3.5D．x1＝﹣1，x2＝3.5【解答】解：把方程（2x+3）2+3（2x+3）﹣4＝0看作关于2x+3的一元二次方程，所以2x+3＝1或2x+3＝﹣4，所以x1＝﹣1，x2＝﹣3.5．故选：A．6．如图▱ABCD，E是BC上一点，BE：EC＝2：3，AE交BD于F，则BF：FD等于（）A．2：5B．3：5C．2：3D．5：7【解答】解：∵BE：EC＝2：3，∴BE：BC＝2：5，∵四边形ABCD是平行四边形，∴AD＝BC，AD∥BC，∴BE：AD＝2：5，△ADF∽△EBF，∴＝＝．故选：A．7．给出下面四个命题，其中真命题的个数有（）（1）平分弦的直径垂直于这条弦，并且平分这条弦所对的弧；（2）90°的圆周角所对的弦是直径；（3）在同圆或等圆中，圆心角的度数是圆周角的度数的两倍；（4）如上图，顺次连接圆的任意两条直径的端点，所得的四边形一定是矩形．A．1个B．2个C．3个D．4个【解答】解：（1）平分（非直径）弦的直径垂直于这条弦，并且平分这条弦所对的弧，所以此命题不正确；（2）90°的圆周角所对的弦是直径，正确；（3）在同圆或等圆中，同弧或等弧所对的圆心角的度数是它所对的圆周角的两倍，错误；（4）根据对角线相等且相互平分的四边形是矩形可判断此命题正确；故选：B．8．如图，在平面直角坐标系中，▱ABCO的顶点A在x轴上，顶点B的坐标为（4，6）．若直线y＝kx+3k 将▱ABCO分割成面积相等的两部分，则k的值是（）A．B．C．﹣D．﹣【解答】解：连接OB和AC交于点M，过点M作ME⊥x轴于点E，过点B作CB⊥x轴于点F，如下图所示：∵四边形ABCD 为平行四边形， ∴ME ＝BF ＝3，OE ＝OF ＝2，∴点M 的坐标为（2，3），∵直线y ＝kx +3k 将▱ABCO 分割成面积相等的两部分， ∴该直线过点M ， ∴3＝2k +3k ， ∴k ＝．故选：A ．9．若2x +5y +4z ＝0，3x +y ﹣7z ＝0，则x +y ﹣z 的值等于（ ） A ．0B ．1C ．2D ．不能求出【解答】解：根据题意得：，把（2）变形为：y ＝7z ﹣3x ， 代入（1）得：x ＝3z ， 代入（2）得：y ＝﹣2z ， 则x +y ﹣z ＝3z ﹣2z ﹣z ＝0． 故选：A ．10．如图所示，在△ABC 中，D 是BC 的中点，DE ⊥BC 交AC 于点E ，已知AD ＝AB ，连接BE 交AD 于点F ，下列结论：①BE ＝CE ；②∠CAD ＝∠ABE ；③S △ABF ＝3S △DEF ；④△DEF ∽△DAE ，其中正确的有（ ）A ．1个B ．4个C ．3个D ．2个【解答】解：∵D 是BC 的中点，且DE ⊥BC ， ∴DE 是BC 的垂直平分线，CD ＝BD ， ∴CE ＝BE ，故①正确；∴∠C ＝∠7， ∵AD ＝AB ，∴∠8＝∠ABC ＝∠6+∠7， ∵∠8＝∠C +∠4， ∴∠C +∠4＝∠6+∠7，∴∠4＝∠6，即∠CAD ＝∠ABE ，故②正确；作AG ⊥BD 于点G ，交BE 于点H ， ∵AD ＝AB ，DE ⊥BC ， ∴∠2＝∠3，DG ＝BG ＝BD ，DE ∥AG ，∴△CDE ∽△CGA ，△BGH ∽△BDE ，DE ＝AH ，∠EDA ＝∠3，∠5＝∠1， ∴在△DEF 与△AHF 中，，∴△DEF ≌△AHF （AAS ）， ∴AF ＝DF ，EF ＝HF ＝EH ，且EH ＝BH ，∴EF ：BF ＝1：3， ∴S △ABF ＝3S △AEF ， ∵S △DEF ＝S △AEF ，∴S △ABF ＝3S △DEF ，故③正确；∵∠1＝∠2+∠6，且∠4＝∠6，∠2＝∠3， ∴∠5＝∠3+∠4， ∴∠5≠∠4，∴△DEF ∽△DAE ，不成立，故④错误． 综上所述：正确的答案有3个．故选：C．二．填空题（每小题4分，共16分）11．已知a﹣b＝2，那么2a﹣2b+5＝9．【解答】解：∵a﹣b＝2，∴原式＝2（a﹣b）+5＝4+5＝9，故答案为：912．袋中装有6个黑球和n个白球，经过若干次试验，发现“若从中任摸一个球，恰好是白球的概率为”，则这个袋中白球大约有2个．【解答】解：∵袋中装有6个黑球和n个白球，∴袋中一共有球（6+n）个，∵从中任摸一个球，恰好是白球的概率为，∴＝，解得：n＝2．故答案为：2．13．直角三角形纸片的两直角边BC，AC的长分别为6，8，现将△ABC如下图那样折叠，使点A与点B重合，折痕为DE，则CE的长为．【解答】解：设CE为x，则BE＝AE＝8﹣x，∵∠C＝90°，∴BE2﹣CE2＝BC2，（8﹣x）2﹣x2＝36，解得x＝．14．如图，点A1（1，1）在直线y＝x上，过点A1分别作y轴、x轴的平行线交直线y＝x于点B1，B2，过点B2作y轴的平行线交直线y＝x于点A2，过点A2作x轴的平行线交直线y＝x于点B3，…，按照此规律进行下去，则点A n的横坐标为．【解答】解：∵A n B n+1∥x轴，∴tan∠A n B n+1B n＝．当x＝1时，y＝x＝，∴点B1的坐标为（1，），∴A1B1＝1﹣，A1B2＝＝﹣1．∵1+A1B2＝，∴点A2的坐标为（，），点B2的坐标为（，1），∴A2B2＝﹣1，A2B3＝＝﹣，∴点A3的坐标为（，），点B3的坐标为（，）．同理，可得：点A n的坐标为（，）．故答案为：．三．解答题（共54分，15题每小题12分，共12分）15．（1）计算：|﹣2|﹣（π﹣2015）0+（）﹣2﹣2sin60°+；（2）先化简，再求值：÷（2+），其中a＝．【解答】解：（1）|﹣2|﹣（π﹣2015）0+（）﹣2﹣2sin60°+＝2﹣1+4﹣2×+2＝2﹣1+4﹣+2＝5+；（2）÷（2+）＝＝＝，当a＝时，原式＝＝﹣1．16．当m为何值时．关于x的方程＝﹣的解是负数？【解答】解：两边都乘（x+1）（x﹣2），得m＝x2﹣2x﹣x2+1，解得x＝，由分式方程的解为负数，得＜0且≠﹣1，解得m＞1且m≠3．17．某校为了了解九年级学生体育测试成绩情况，以九年（1）班学生的体育测试成绩为样本，按A、B、C、D四个等级进行统计，并将统计结果绘制如下两幅统计图，请你结合图中所给信息解答下列问题：（说明：A级：90分﹣100分；B级：75分﹣89分；C级：60分﹣74分；D级：60分以下）（1）写出D级学生的人数占全班总人数的百分比为4%，C级学生所在的扇形圆心角的度数为72°；（2）该班学生体育测试成绩的中位数落在等级B内；（3）若该校九年级学生共有500人，请你估计这次考试中A级和B级的学生共有多少人？【解答】解：（1）总人数为25÷50%＝50人，D成绩的人数占的比例为2÷50×100%＝4%，表示C的扇形的圆心角360°×（10÷50）＝360°×20%＝72°，故答案为：4%，72°；（2）由于A成绩人数为13人，C成绩人数为10人，D成绩人数为2人，而B成绩人数为25人，故该班学生体育测试成绩的中位数落在B等级内；故答案为：B；（3）×500＝380（人），答：估计这次考试中A级和B级的学生共有380人．18．观察与思考：阅读下列材料，并解决后面的问题在锐角△ABC中，∠A、∠B、∠C的对边分别是a、b、c，过A作AD⊥BC于D（如图（1）），则，即AD＝c sin B，AD＝b sin C，于是c sin B＝b sin C，即，同理有：，所以．即：在一个三角形中，各边和它所对角的正弦的比相等在锐角三角形中，若已知三个元素（至少有一条边），运用上述结论和有关定理就可以求出其余三个未知元素．根据上述材料，完成下列各题．（1）如图（2），△ABC中，∠B＝45°，∠C＝75°，BC＝60，则∠A＝60°；AC＝20；（2）自从去年日本政府自主自导“钓鱼岛国有化”闹剧以来，我国政府灵活应对，现如今已对钓鱼岛执行常态化巡逻．某次巡逻中，如图（3），我渔政204船在C处测得A在我渔政船的北偏西30°的方向上，随后以40海里/时的速度按北偏东30°的方向航行，半小时后到达B处，此时又测得钓鱼岛A在的北偏西75°的方向上，求此时渔政204船距钓鱼岛A的距离AB．（结果精确到0.01，）【解答】解：（1）由正玄定理得：∠A＝60°，AC＝20；故答案为：60°，20；（2）如图，依题意：BC＝40×0.5＝20（海里）∵CD∥BE，∴∠DCB+∠CBE＝180°．∵∠DCB＝30°，∴∠CBE＝150°．∵∠ABE＝75°，∴∠ABC＝75°．∴∠A＝45°．在△ABC中，，即，解之得：AB＝10≈24.49海里．所以渔政204船距钓鱼岛A的距离约为24.49海里．19．已知一次函数y1＝x+m的图象与反比例函数y2＝的图象交于A、B两点．已知当x＞1时，y1＞y2；当0＜x＜1时，y1＜y2．（1）求一次函数的解析式；（2）已知双曲线在第一象限上有一点C到y轴的距离为3，求△ABC的面积．【解答】解：（1）∵当x＞1时，y1＞y2；当0＜x＜1时，y1＜y2，∴点A的横坐标为1，代入反比例函数解析式，＝y，解得y＝6，∴点A的坐标为（1，6），又∵点A在一次函数图象上，∴1+m＝6，解得m＝5，∴一次函数的解析式为y1＝x+5；（2）∵第一象限内点C到y轴的距离为3，∴点C的横坐标为3，∴y＝＝2，∴点C的坐标为（3，2），过点C作CD∥x轴交直线AB于D，则点D的纵坐标为2，∴x+5＝2，解得x＝﹣3，∴点D的坐标为（﹣3，2），∴CD＝3﹣（﹣3）＝3+3＝6，点A到CD的距离为6﹣2＝4，联立，解得（舍去），，∴点B 的坐标为（﹣6，﹣1），∴点B 到CD 的距离为2﹣（﹣1）＝2+1＝3， S △ABC ＝S △ACD +S △BCD ＝×6×4+×6×3＝12+9＝21．20．如图，AB 是⊙O 的直径，弦CD ⊥AB ，垂足为H ，连结AC ，过上一点E 作EG ∥AC 交CD 的延长线于点G ，连结AE 交CD 于点F ，且EG ＝FG ，连结CE ． （1）求证：△ECF ∽△GCE ； （2）求证：EG 是⊙O 的切线；（3）延长AB 交GE 的延长线于点M ，若tan G ＝，AH ＝3，求EM 的值．【解答】（1）证明：如图1中，∵AC ∥EG ， ∴∠G ＝∠ACG ，∵AB⊥CD，∴＝，∴∠CEF＝∠ACD，∴∠G＝∠CEF，∵∠ECF＝∠ECG，∴△ECF∽△GCE．（2）证明：如图2中，连接OE，∵GF＝GE，∴∠GFE＝∠GEF＝∠AFH，∵OA＝OE，∴∠OAE＝∠OEA，∵∠AFH+∠FAH＝90°，∴∠GEF+∠AEO＝90°，∴∠GEO＝90°，∴GE⊥OE，∴EG是⊙O的切线．（3）解：如图3中，连接OC．设⊙O的半径为r．在Rt△AHC中，tan∠ACH＝tan∠G＝＝，∵AH＝3，∴HC＝4，在Rt△HOC中，∵OC＝r，OH＝r﹣3，HC＝4，∴（r﹣3）2+（4）2＝r2，∴r＝，∵GM∥AC，∴∠CAH＝∠M，∵∠OEM＝∠AHC，∴△AHC∽△MEO，∴＝，∴＝，∴EM＝．一．填空题（每小题4分，共20分）21．已知+|ab+3|＝0，则a﹣b的值是±．【解答】解：由题意得，a2+b2﹣5＝0，ab+3＝0，即a2+b2＝5，2ab＝﹣6，（a﹣b）2＝11，则a﹣b＝±，故答案为：±．22．若关于x的方程x2+2mx+m2+3m﹣2＝0有两个实数根x1、x2，则x1（x2+x1）+x22的最小值为．【解答】解：由题意知，方程x2+2mx+m2+3m﹣2＝0有两个实数根，则△＝b2﹣4ac＝4m2﹣4（m2+3m﹣2）＝8﹣12m≥0，∴m≤，∵x1（x2+x1）+x22＝（x2+x1）2﹣x1x2＝（﹣2m）2﹣（m2+3m﹣2）＝3m 2﹣3m +2＝3（m 2﹣m +﹣）+2 ＝3（m ﹣）2 +； ∴当m ＝时，有最小值； ∵＜，∴m ＝成立；∴最小值为；故答案为：． 23．如图，E 、F 分别是矩形ABCD 的边AB 、BC 的中点，连AF ，CE ，AF 、CE 交于G ，则四边形BEGF 与四边形ADCG 的面积的比值为 ．【解答】解：如图：连接BG ，设S △AEG ＝a ，S △CFG ＝b ，∵点E ，F 分别是矩形ABCD 的边AB ，BC 的中点，∴S △BEG ＝a ，∴S △BGF ＝S △FGC ＝b ，∴S △ABF ＝S △BCE ＝S 矩形ABCD ，S △ABF ＝2a +b ，S △BCE ＝2b +a ，∴a ＝b ，S 矩形ABCD ＝12a ，∴＝＝．故答案为：．24．已知二次函数y＝ax2+bx+c（a≠0）的图象与x轴交于点A（﹣2，0）、B（x1，0），且1＜x1＜2，与y轴正半轴的交点在（0，2）的上方，顶点为C．直线y＝kx+m（k≠0）经过点C、B．则下列结论：①b＞a；②2a﹣b＞﹣1；③2a+c＜0；④k＞a+b；⑤k＜﹣1，其中正确的结论有①⑤．【解答】解：①由图知：抛物线的开口向下，则a＜0．对称轴在x轴的左侧，因此，a、b同号，则b＜0∵﹣2+x1＝﹣，1＜x1＜2，∴0＜＜1，∴b＞a．故①正确；②∵抛物线交x轴与点（﹣2，0）∴4a﹣2b+c＝0∵c＞2∴4a﹣2b＝﹣c＜﹣2即2a﹣b＜﹣1．故②错误；③∵二次函数y＝ax2+bx+c（a≠0）的图象与x轴交于点A（﹣2，0），∴4a﹣2b+c＝0∵b＞a，∴2b＞2a，∴4a﹣2b＜2a，∴4a﹣2b+c＜2a+c，即0＜2a+c，∴2a+c＞0，故③错误；⑤如图，过顶点C作CD⊥AB于点D．则k＝﹣．AD和BD的长度都在1.5和2之间，也就是说1.5＜BD＜2，又因为CD＞2，所以CD除以BD＞1，所以k＜﹣1∴k＜﹣1，故⑤正确；④∵当x＝1时，y＞0，∴a+b+c＞0，∵c＞2，∴a+b＞﹣2．又由⑤知，k＜﹣1，∴k与a+b的大小无法判断，故④错误；综上所述，正确的结论有①⑤．故答案是：①⑤．25．如图，等边△AOB的边长为4，点P从点O出发，沿OA以每秒1个单位的速度向点A匀速运动，当点P到达点A时停止运动，设点P运动的时间是t秒．将线段BP的中点绕点P按顺时针方向旋转60°得点C，点C随点P的运动而运动，连接CP、CA．在点P从O向A运动的过程中，当△PCA为直角三角形时t的值为2或s．【解答】解：①如图1中，连接KC、BC．设PB的中点为K．∵PK＝PC，∠KPC＝60°，∴△PKC是等边三角形，∴KC＝PK＝BK，∴∠PCB＝90°，∴当∠PCA＝90°时，点C在线段AB上，∵△AOB是等边三角形，∴∠A＝60°，∴∠APC＝30°，∵∠CPK＝60°，∴∠APB＝90°，∴BP⊥OA，∵BO＝BA，∴OP＝PA＝2，∴t＝2．②如图2中，当∠PAC＝90°时，作BH⊥OA于H，BG⊥AC于G，连接KC、BC．则四边形BHAG是矩形，△PAC∽△CGB，∴＝＝＝，设OP＝x，则AP＝4﹣x，∵AH＝BG＝2，∴AC＝，GC＝（4﹣x），∵BH＝AG＝2，∴+（4﹣x）＝2，∴x＝．∴t＝，综上所述，t＝2或s时，△PAC是直角三角形，故答案为2或s．二．解答题（共30分）26．某公司经营杨梅业务，以3万元/吨的价格买入杨梅后，分拣成A、B两类，A类杨梅包装后直接销售，包装成本为1万元/吨，它的平均销售价格y（单位：万元/吨）与销售数量x（x≥2，单位：吨）之间的函数关系如图所示；B类杨梅深加工后再销售，深加工总费用s（单位：万元）与加工数量t（单位：吨）之间的函数关系是s＝12+3t，平均销售价格为9万元/吨．（1）A类杨梅的销售量为5吨时，它的平均销售价格是每吨多少万元？（2）若该公司收购10吨杨梅，其中A类杨梅有4吨，则经营这批杨梅所获得的毛利润（w）为多少万元？（毛利润＝销售总收入﹣经营总成本）（3）若该公司收购20吨杨梅，其中A类杨梅有x吨，经营这批杨梅所获得的毛利润为w万元．①求w关于x的函数关系式；②若该公司获得了30万元毛利润，问：用于直销的A类杨梅有多少吨？【解答】解：（1）设x，y的解析式为y＝kx+b，把x＝2时，y＝12，x＝8时，y＝6得：解得：，∴y＝﹣x+14（2≤x≤8），∴x＝5时，y＝9，答：A类杨梅的销售量为5吨时，它的平均销售价格是每吨9万元；（2）若该公司收购10吨杨梅，其中A类杨梅有4吨，则B类杨梅有6吨，易得：W A＝（10﹣3﹣1）×4＝24（万元），W A＝6×（9﹣3）﹣（12+3×6）＝6（万元），∴W＝24+6＝30（万元），答：此时经营这批杨梅所获得的毛利润w为30万元；（3）设销售A类杨梅x吨，则销售B类杨梅（20﹣x）吨，①当2≤x＜8时，w A＝x（﹣x+14）﹣x＝﹣x2+13x，w B＝9（20﹣x）﹣[12+3（20﹣x）]＝108﹣6x，∴w＝w A+w B﹣3×20＝（﹣x2+13x）+（108﹣6x）﹣60＝﹣x2+7x+48；当x≥8时，w A＝6x﹣x＝5x，w B＝9（20﹣x）﹣[12+3（20﹣x）]＝108﹣6x∴w＝w A+w B﹣3×20＝（5x）+（108﹣6x）﹣60＝﹣x+48，∴w关于x的函数关系式为：w＝，②当2≤x＜8时，﹣x2+7x+48＝30，解得x1＝9，x2＝﹣2，均不合题意，当x≥8时，﹣x+48＝30，解得x＝18，∴当毛利润达到30万元时，直接销售的A类杨梅有18吨．27．已知：如图1．正方形ABCD，过点A作∠EAF＝90°，两边分别交直线BC于点E，交线段CD于点F，G为AE中点，连接BG（1）求证：∠AFD+∠CBG＝180°；（2）如图2，过点G作BG的垂线交对角线AC于点H，求证：GH＝GB；（3）如图3，连接HF，若CH＝3AH，AD＝2，求线段HF的长．【解答】（1）证明：如图1中，∵四边形ABCD是正方形，∴AB＝AD，∠BAD＝∠AEF＝90°，∴∠EAB＝∠DAF，∵∠ABE＝∠ADF＝90°，∴△ABE≌△ADF，∴∠AFD＝∠E，∵AG＝GE，∴GB＝GE＝GA，∴∠E＝∠GBE＝∠AFD，∵∠GBE+∠GBC＝180°，∴∠AFD+∠GBC＝180°．（2）证明：如图2中，连接BD交AC于O，连接OG、BH、取BH的中点K，连接GK、OK．∵∠BGH＝∠BOH＝90°，BK＝KH，∴GK＝KH＝OK＝KB，∴O、H、G、B四点共圆，∵AG＝GE，AO＝OC．∴OG∥CE，∴∠GOB＝∠OBC＝45°，∴∠GOH＝∠GBH＝45°，∵∠BGH＝90°，∴∠GBH＝∠GHB＝45°，∴GH＝GB．（3）解：如图3中，如图3中，设OG交AB于T，GH交AB于P．，作HM⊥DF于M．∵OG∥EC，AB⊥CE，∴OG⊥AB，易证∠EAB＝∠GBP＝∠PGT＝∠HBO，∴tan∠EAB＝tan∠HBO＝，∵CH＝3AH，OA＝OC＝OB，∴tan∠EAB＝tan∠HBO＝＝，∵AB＝AD＝2，∴BE＝DF＝，在Rt△HMF中，易证FM＝，HM＝，∴HF＝＝5．28．如图，在平面直角坐标系中，点O为坐标原点，抛物线y＝ax2﹣10ax+16a（a≠0）交x轴于A、B两点，抛物线的顶点为D，对称轴与x轴交于点H，且AB＝2DH．（1）求a的值；（2）点P是对称轴右侧抛物线上的点，连接PD，PQ⊥x轴于点Q，点N是线段PQ上的点，过点N作NF⊥DH于点F，NE⊥PD交直线DH于点E，求线段EF的长；（3）在（2）的条件下，连接DN、DQ、PB，当DN＝2QN（NQ＞3），2∠NDQ+∠DNQ＝90°时，作NC⊥PB交对称轴左侧的抛物线于点C，求点C的坐标．【解答】解：（1）令y＝0，∵a≠0，∴x2﹣10x+16＝0，得x＝2或x＝8，∴点A（2，0），B（8，0），∴AB＝8﹣2＝6，∵AB＝2DH，∴DH＝3，∵OH＝2+，∴D（5，﹣3），∴﹣3＝a×52﹣10a×5+16a，得a＝；（2）如图1，过点D作PQ的垂线，交PQ的延长线于点M，∵NE⊥PD，∴∠DPN+∠PNE＝90°，∵NF⊥DE，∴∠FEN+∠FNE＝90°，又∵DH⊥x轴，PQ⊥x轴，∴DE∥PQ，∴∠FEN＝∠PNE，∴∠DPM＝∠ENF，∴△EFN∽△DMP，∴，设点P（t，），则FN＝DM＝t﹣5，PM＝+3，∴，解得，EF＝3；（3）如图2，作QG⊥DN于点G，∵DF∥PQ，∴∠FDN＝∠DNQ，∵2∠NDQ+∠DNQ＝90°，∴2∠NDQ+∠FDN＝90°，∵∠FDM＝90°，∴∠NDM＝2∠NDQ，∴∠NDQ＝∠MDQ，∴QG＝QM＝DH＝3，设QN＝m，则DN＝2m，∵sin∠DNM＝，sin∠QNG＝，sin∠DNM＝sin∠QNG，∴，得DM＝6＝DG，∴OQ＝5+6＝11，∴点P的纵坐标是：，∴点P（11，9），∵NG＝DN﹣DG＝2m﹣6，在Rt△NGQ中，QG2+NG2＝QN2，∴32+（2m﹣6）2＝m2，解得，m＝3（舍去）或m＝5，设点C的坐标为（n，），作CK⊥x轴于点K，作NF⊥CK于点K，则CT＝，NT＝11﹣n，∵P（11，9），则BQ＝11﹣8＝3，PQ＝9，∵CN⊥PB，PQ∥CK，PQ⊥x轴，∴△CTN∽△BQP，∴，即，解得，n＝﹣1或n＝10（舍去），∴点C（﹣1，9）．。

������������������３ 分 ������������������５ 分 ������������������６ 分
( ) ) , 由( 可知平面 A ２ １ B C ⊥ 平面 P A C． ∴B O ⊥ 平面 P A C．
∵ 平面 A B C ∩ 平面 P A CB C, １ ∴ VB－POQ ＝ S△PQO ������B O ３
１ １． A
１ ２． B
第 Ⅱ 卷( 非选择题 , 共９ ０ 分) ( 二、 填空题 : 每小题 ５ 分 , 共２ ０ 分)
( ) 解: 设数列 { １ ７． １ a n } 的公差为d ． 解得 d ＝２, a１ ＝１．
( 三． 解答题 : 共７ ０ 分)
３＋ ３ ． １ ３．２ ; １ ４． １ ２; １ ５． ６; １ ６． ４
������������������８ 分
＝
∵ VP－OBQ ＝VB－POQ ,
１ １ １ × S△PAO ×４＝ ×３×４＝４． ３ ２ ３
������������������１ １分 ������������������１ ２分
a ２ ２ ( )∵ 解: ２ ０． １ c ＝ ３, ＝２, a２ ＝ b ＋c , b
∴ a ＝２, b ＝１．
∴ 四面体 P －O B Q 的体积为 ４．
( ) 易知当直线l 的斜率为 ０ 时 , 不合题意 ． ２ 联立
∴ 椭圆的标准方程为
x２ ２ ＋y ＝１． ４
������������������５ 分 ������������������６ 分
, 当直线l 的斜率不为 ０ 时 , 设直线l 的方程为x ＝m M( x１ , N( x２ , ． y ＋１, y１) y２)

成都市2015级高中毕业班第一次诊断性检测数学（理和本试卷分选择題和非选挥題朋部分.第I卷（选择題）】至2页，第D卷（菲选揮題）3至4页，共4页•瞒分150分•考试时间120分钟.注意事项：1.答題前，务必将自己的姓名、考緒号填写在答题卡Ml定的位宣上.2.答选择题时，必须使用2B铅笔将答題卡上对应题目的答案标号涂廉，如需改动，用橡皮捋擦干净后•再选檢葛它答案标号.3.答非选择题时•必须使用a 5査米黑色签字笔，将答案书写在答题卡规定的位盘上.4.所有题日必须在答题卡上作答，在试题总上答題无效.5.考试結束后，只将答if卡交回.第I卷（迭择题，共60分）一、选择進：本大总其12小毎小U5分，共60分.在毎小魅给出的四个选项中，只有一项忌符合题目要求的.1.设仝集U=R，集合A = {x|x<-2} 则JCA U B)=(A) (-2,-1) (B) C-2,-1] (C) (一8, _2]U [—1，+°°) (D) (-2,1)2.复数w =丄在复平面内对应的点位于1 -ri（A》第一象限（B）第二象限（C）第三象限《D）第四象限3.空气质■指tt AQI是检测空气质■的•要参数.其数值越大说明空代污染状况越严塑•空代质量述蔓・某地环保祁门统计了该地区12月1日至1Z月24日连纹24天的空气质■指敷AQI,根据得到的数据绘制岀如图所示的折线田.则下列说法错谋的是（A）该地区在12月2日空气质ft最好（B）该地区在12月24日空气质量最苣（C）该地区从12月7日到12月12日AQI持续增大（D）该地区的空气质AQ1与这段日期成负相关4.已知说角△人BC的三个内角分别为A,B,C・則44 sin A >sinB ”是““nA >unB ”的（A）充分不必要条件（B）必要不充分条件（C）充要条件（D）既不充分也不必耍条件数学（理科”一绘-考氏题第1页〈共4页〉5••更相减损术”是我国古代数学名着C九韋算术》中的箕法案例•瓦对应的程序框图如图所示•若输入的鼻・，山的值分别为4,6,1 •則输出的k的值为<A)2(B)3 (04 (D)56.若关于工的不尊式才+2oz + lN 0在[0,+8)上恒成立，则实数a的取值范園为<A)(Ot+oo) (B) [一1・十8><C) [-1.1] (D) [0< + oo)7.已知siga W(0诗),则caK2»十专》的值为工* y28 如图.巳知双曲线取正一〒=l(a >0』>0) •长方形ABCD的頂点A.B分别为双曲线E的左，右焦点，且点C,D在双曲线E上.若AB-6，BC-害，则双曲线E的离心率为3 5(A)血(B) - (C) j (□)/□9.在三梭锥P-ABC中•已知PA 丄底面ABC • ZBAC -120* ,PA-AB=AC«2.若谏三棱惟的頂点都在同一个球面上•则谏球的表面积为(A)10/3K(C)20K(D)9 辰W•已知定义在R上的奇函数/<x)满足/Gx十2)十j(Q・0,且当工€ [0,1]时. /(x)=log?(x十1)・则下列不等式正确的是(A) / (log, 7) < /(- 5) < /(6) (B) /(log： 7) </(6)< /(- 5)(C) - 5) </(log27> < f (6) (D) - 5) </(6) < /(log27)11•址函数/(x) — sin(2jr +专)•若X|JCi <0> 且/(Xi> +-/(x2) —OtJH |z t— j| | 的取值范阿为(A) +8)(B) ($+8)(C)(象+8)(D)(學.+8)6 3 3 312若关于工的方畤+三+"0有三个不相尊的实如"2,且刊v°s Ve其中m WR.e=2・ 7182&••为自於对数的底数.则(吾■一"當一以合一“的值为(A)e (B) 1-m (C) 1 + m (D) 1数学(理稈”一燐"勺试題弟2只(共4灵)第11卷（非选择題•共90分）二、填空矗：本大&共4小毎小题5分，共20分.13.（r + 2^）s的屣开式中含Kb顼的系数为 ________________ .工一，＞114.若实数x q腐足线性约束条件丿y 0工•则x±2＞的最大值为______________________15.如图，在直角梯形ABDE中•已知ZABD= ZEDB= 9O\C 是BD 上一点,AB = 3 -屁乙ACB = 15\ ZECD =60・. zLEAC -45\则线段DE的长度为16•在长方体ABCD -A x B x CyD｛中，巳知底面ABCD为正方形• P为人6的中点• AD=2•人久M，点Q是正方形A BCD所恋平tft内的一个动点•且QC=血QP，則线段£Q的长JtWft大值为三、解答題：本大题共6小题•共70分•解答应写岀文字说明.证明过程或演算步鼻. 17.（本小题厲分12分）已知寻差数列（aj的前”项和为S. ,a,-3.S4-16,n 6 N，・“）求数列laj的通项公式；（2）设求数列（6J的前”项和丁…2心和18.（本小题満分12分）某部门为了解一企业衣生产过稅中的用水量愣况•对毎天的用水最作了记录，得到了大*该企业的日用水量的统计数据.从这些统计数据中Ml机独取12天的数据作为样本•得到如图所示的箜叶图（单位：吨）.若用水量不低于95（吨），则称这一天的用水扯超标.（1〉从这12天的数据中陆机抽取3个■求至多有1天是用水債趙标的槪率'（2）以这12大的样本数抵中用水俭超标的频率作为概率•估计该企业未来3天中用水量超标的天数•记随机变it X为未来这3天中用水册超标的天数•求X的分布列和数爷期望.19•（本小题淸分12分）如用①•在边长为5的菱形/＜BCD中，AC = 6.现沿对角线AC把AADC瞬折到△APC的位置得到四面体P-ABC■如图②所示•已知PB-4V2 .教学（理科）•一设"考试越第3血（共4负）«1）求证：平面PAC丄平面ABC a（2）若Q舉线段AP上的点•且= j AP，求二面角Q-EC-A的余弦值.20.（本小题礴分12分》图①图②巳知穂圖C手+召=心>6>。

值．（收益 售价 成本）．
答案 （1）
，
．
（2）
．
（3） 当 时， 取得最大值 ．
解析 （1） 如图 ，设 ，
过，，
解得
，
∴
，
．
（2） 令
，顶点为 ，
∴
，
∴
，
又∵
过，
∴
，
，
∴
．
（3）
，
∴当 时， 取得最大值 ．
考点
函数 一次函数 求一次函数解析式 已知两点求一次函数解析式
二次函数 待定系数法求二次函数解析式
A.
B.
C.
D.
答案 D
解析 选项主视图是正方形， 选项主视图是长方形， 选项主视图是圆．
考点
投影与视图 视图 简单几何体的三视图
3 反比例函数
的图象经过的象限是（ ）．
A. 第一、二象限
B. 第一、三象限
C. 第二、三象限
D. 第二、四象限
答案 B
解析 反比例函数解析式中， ， ∴反比例函数的图像经过的象限是第一、三象限．
．
或
．
解析 （1） 由题，
过
，
，
∴
，，
∴
，
，
∵
过，，
∴
，解得
，
∴
．
（2）
与 轴交于 点，
∴
，
∴
，
∴
，
∴
，
∴
，
∴
，
∴
或
．
考点
函数 一次函数 一次函数与坐标轴交点
求一次函数解析式 已知两点求一次函数解析式
一次函数综合题 一次函数与三角形面积

书上有路勤为径 有径都在为学溪
GO高考家长总群235649790
成都市西城角巷18号华润lavie峰锦2303（九宁校区） 成都市百草路186号英伦教育
初高中小班、一对一、全日制、自主招生、志愿填报
书上有路勤为径 有径都在为学溪
GO高考家长总群235649790
成都市西城角巷18号华润lavie峰锦2303（九宁校区） 成都市百草路186号英伦二期四幢3单元205（成外校区）
十载毕业班经验
为学溪教育
初高中小班、一对一、全日制、自主招生、志愿填报
书上有路勤为径 有径都在为学溪
GO高考家长总群235649790
成都市西城角巷18号华润lavie峰锦2303（九宁校区） 成都市百草路186号英伦二期四幢3单元205（成外校区）
为学溪教育
初高中小班、一对一、全日制、自主招生、志愿填报
书上有路勤为径 有径都在为学溪
GO高考家长总群235649790
成都市西城角巷18号华润lavie峰锦2303（九宁校区） 成都市百草路186号英伦二期四幢3单元205（成外校区）
十载毕业班经验
为学溪教育
初高中小班、一对一、全日制、自主招生、志愿填报
十载毕业班经验

25 、定义：如果二次函数 y a1 x 2 b1 x c1 (a1 0) 与 y a2 x 2 b2 x c2 (a2 0) 满足 a1 a2 =0 ，
b1 b2 ， c1 c2 =0 ，则称这两个函数互为“旋转函数”.现有下列结论：
①函数 y x 3x 2 的“旋转函数”是 y x 3x 2 ； ②函数 y ( x 1) 2 的“旋转函数”是 y ( x 1) 2 ；
21、一元二次方程 x 2 3x 5 0 的两个根分别是 m 和 n ，则 m2 n2 ＝________. 22、如图，在△ABC 中，AC⊥BC，∠ABC＝30°，点 D 是 CB 延长线上的一点，且 BD＝BA，则 tan∠D
＝_______.
二、解答题（共 30 分） 26、 （本小题满分 8 分） 某房间有 50 个房间供游客居住，当每个房间定价 120 元时，房间会全部住满，当每个房间每天的定价 每增加 10 元时，就会有一个房间空闲.如果游客居住房间，宾馆需对每个居住房间每天支出 20 元的各 种费用，设每个房间定价增加 10 元（x 为整数） （1） 直接写出每天游客居住的房间数量 y 与 x 的函数关系 （2） 当每间房价定价为多少元时，宾馆每天所获利润最大，最大利润是多少？
AD AE AB EC
B、
AC AE GF BD
C、
BD CE AD AE
D、
AG AC AF EC
3、九年级(1)班在参加学校 4×100m 接力赛时，安排了甲、乙、丙、丁四位选手，他们的参赛顺序由抽 签随机决定，则甲跑第一棒的概率为（ ） A、 1 B、
4、已知关于 x 的方程 x2＋3x＋a＝0 有一个根为－2，则另一个根为（ ） A、 1 B、 －1 C、2 D、－5 5、某文具店 10 月份销售铅笔 100 支，11、12 两个月销售量连续增长，若月平均增长率为 x，则该文 具店 12 月份销售铅笔的支数是（ ） A、100（1＋x） B、100（1＋x）2 C、100(1＋x2 ) D、100(1＋2x) 6、某楼梯的侧面如图所示，已测得线段 AB 的长为 3.5 米，∠BAC＝29°，则该楼梯的高度 BC 可表示 为（ ） A、3.5sin29° 米 B、 3.5cos29° 米 C、3.5tan29° 米 D、

一、选择题（每题5分，共50分）1. 下列各数中，有理数是（）A. $\sqrt{2}$B. $\pi$C. $\frac{1}{3}$D. $\sqrt[3]{-8}$2. 已知函数$f(x)=2x+1$，若$f(x)=7$，则$x=$（）A. 3B. 2C. 1D. 03. 在平面直角坐标系中，点A（2，3）关于直线y=x的对称点B的坐标是（）A. （3，2）B. （2，3）C. （-3，-2）D. （-2，-3）4. 若等差数列$\{a_n\}$中，$a_1=2$，$a_3=8$，则$a_5=$（）A. 14B. 12C. 10D. 85. 下列命题中，正确的是（）A. 函数$y=x^2$在R上的单调递增B. 平方根的定义域是RC. 相似三角形的对应边成比例D. 等腰三角形的底角相等6. 已知一次函数$y=kx+b$（$k\neq0$）的图象经过点A（1，2），则下列选项中，$k$的值是（）A. 1B. 2C. -1D. -27. 在等腰三角形ABC中，AB=AC，若$AD$是底边BC上的高，则下列结论正确的是（）A. $\angle ADB=\angle ADC$B. $\angle ADB=\angle BAC$C. $\angle ADC=\angle BAC$D. $\angle ADB=\angle BDC$8. 若函数$y=ax^2+bx+c$（$a\neq0$）的图象开口向上，且顶点坐标为（1，-3），则下列选项中，$a$的值是（）A. 2B. -2C. 1D. -19. 已知正方体ABCD-A1B1C1D1的棱长为1，则体积V=（）A. 1B. $\sqrt{2}$C. 2D. $\sqrt{3}$10. 在△ABC中，若$\angle A=\frac{\pi}{3}$，$a=2\sqrt{3}$，$b=4$，则$sinB=$（）A. $\frac{\sqrt{3}}{2}$B. $\frac{1}{2}$C. $\frac{\sqrt{3}}{3}$D. $\frac{1}{3}$二、填空题（每题5分，共50分）11. 若$\sqrt{3}+2$是方程$2x^2+mx+1=0$的解，则m=______。

成都市2018届高中毕业班第一次诊断性检测数学（理工农医类）本试卷分选择题和非选择题两部分。

第I卷(选择题)1至2页，第II卷(非选择题)3至4页,共4页，满分150分，考试时间120分钟。

注意事项1. 答题前，务必将自己的姓名、准考证号填写在答题卡规定的位置上。

2. 答选择题时，必须使用2B铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦干净后，再选涂其它答案标号。

3. 答非选择题时，必须使用0.5毫米黑色签字笔，将答案书写在答题卡规定的位置上。

4. 所有题目必须在答题卡上作答，在试题卷上答题无效。

5. 考试结束后，只将答题卡交回。

第I卷(选择题，共60分）参考公式：如果事件A、B互斥，那么球的表面积公式P(A+B)=P(A)+ P(B)如果事件A、B相互独立，那么其中R表示球的半径P(A • B) =P(A) • P(B) 球的体积公式如果事件A在一次试验中发生的概率是P，那么N次独立重复试验中恰好发生A次的概率其中R表示球的半径一、选择题:（本大题共12小题，每小题5分，共60分)在每小题给出的四个选项中，有且只有一项是符合题目要求的.(1) 某小区有125户高收入家庭、280户中等收入家庭、95户低收人家庭.现采用分层抽样的方法从中抽取100户，对这些家庭社会购买力的某项指标进行调查，则中等收入家庭中应抽选出的户数为(A)70 户（B)17 户（C)56 户（D)25 户(2) 复数z=(1-2i)i(i为虚数单位)在复平面内对应的点位于(A)第一象限（B)第二象限（C)第三象限（D)第四象限(3) 若首项为1的等比数列的前3项和为13,则公比q为(A) 3(B)–4(C)3或—4(D)—3 或 4(4) 已知向量i与j不共线,且，若A、B、D三点共线，则实数m、n应该满足的条件是(A) m+n=1 (B)m+n=-1 (C) mn = 1 (D)mn =- 1(5) “0<m<l”是“关于x的方程有两个异号实数根”的(A)充分不必要条件（B)必要不充分条件(C)充要条件（D)既不充分也不必要条件(6) 若展开式的各项系数和为，则展开式中常数项是(A)-7 (B)7 (C) (D)(7) 在用数学归纳法证明的过程中：假设当时，不等式成立，则需证当n=k+1时，也成立.若.，则g(k) =(A) (B)(C) (D)(8) 设电流强度I(安)随时间t(秒)变化的函数的图象如图所示，则(A) (B)(C) (D)(9) 已知函数，，当x=a时，取得最小值b，则函数的图象为(10) 设正方体的棱长为2,动点E,F在棱A1B1上，动点P、Q分别在棱AD、CD上，若EF=1,A1E=x,DQ=y,DP=z(x,y,z>0),则下列结论中错误的是(A) EF//平面DPQ(B) 二面角P—EF—Q所成角的最大值为(C) 三棱锥P—EFQ的体积与y的变化有关，与x、z的变化无关(D) 异面直线EQ和AD1所成角的大小与的变化无关(11) 已知定义在R上的连续奇函数f(x)满足，且在区间[0，2]上是增函数，有下列命题：①函数f(x)的图象关于直线对称;②函数f(x)的单调递增区间为；③函数f(x)在区间（-2018,2018)上恰有1018个极值点；④若关于x的方程f(x)—m=0在区间[-8,8]上有根，则所有根的和可能为0或±4或±8.其中真命题的个数有(A)1 个（B)2 个（C)3 个（D)4 个(12) 设集合S={1，2,3，4,5，6}，定义集合对(A，B)::，A中含有3个元素，B中至少含有2个元素，且B中最小的元素不小于A中最大的元素.记满足的集合对(A，B)的总个数为m，满足的集合对(A，B)的总个数为n，则的值为(A) (B) (C) (D)第II卷(非选择题，共90分）二、填空题：本大题共4小题,每小题4分，共16分.答案填在答题卡上.(13) 的值为.____________(14) 若函数在点处连续，则实数a=_________.(15) 已知点A、B、C、D在同一个球面上，AB丄平面BCD，BC丄CD，若AB= 6，AC=,CD=，则B、C两点在此球面上的球面距离是____________.(16) 已知函数在[a,b]上连续，定义；其中表示f()在D上的最小值，表示f(x)在D上的最大值.若存在最小正整数k使得对任意的成立，则称函数f(x)为[a，b]上的“k阶收缩函数”.有下列命题：①若，则；②若，则③为[1，2]上的1阶收缩函数；④为[1，4]上的5阶收缩函数.其中你认为正确的所有命题的序号为__________________.三、解答题：本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.(17) (本小题满分12分）已知函数的周期为，其中.(I)求的值及函数f(x)的单调递增区间；(I I)在中，设内角A、B、C所对边的长分别为a、b,c若a=，c=2，f(A)=，求b的值.(18) (本小题满分12分）如图甲，是边长为6的等边三角形，，点G为BC边的中点，线段AG交线段ED于点F.将沿ED翻折，使平面AED丄平面BCDE，连结AB,AC ,AG,形成如图乙的几何体.(I)求证:BC丄平面ATG(II)求二面角B—AE—D的大小.19 (本小题满分12分）某社区为丰富居民的业余文化生活，准备召开一次趣味运动会.在“射击气球”这项比赛活动中,制定的比赛规则如下：每人只参加一场比赛，每场比赛每人都依次射击完编号为①、②、③、④、⑤的5个气球，每次射击一个气球；若这5次射击中，④、⑤号气球都被击中，且①、②、③号气球至少有1个被击中，则此人获奖;否则不获奖.已知甲每次射击击中气球的概率都为，且各次射击结果互不影响.(I)求甲在比赛中获奖的概率；(I I)设甲在5次射击中击中气球的总个数为随机变量，求的分布列及数学期望(20) (本小题满分12分）已知函数.(I)若不等式在R上恒成立，求实数m的取值范围；(II)记，且，求实数m的最大值.(21) (本小题满分12分）巳知各项均为正数的等差数列前三项的和为27，且满足.数列{b n}的前n项和为S n，且对一切正整数n,点(n，S n)都在函数的图象上.(I) 求数列和的通项公式；(II)设，求数列的前n项和；(III)设，若对恒成立,试证明：(22) (本小题满分14分）已知函数.(I)当m =-1时,求函数的单调区间；(II)已知（其中e是自然对数的底数），若存在实数，使成立，证明：2m+e+l<0;(III)证明：.。

成都市武侯区2018~2019学年度上期期末学业质量监测试题
九年级数学
注意事项
1.全卷分A卷和B卷,A卷满分100分,B卷满分50分;考试时间120分钟。
2.考生使用答题卡作答。
3.在作答前,考生务必将自己的姓名、考生号和座位号填写在答题卡上.考试结束,监考人员将试卷和答题卡一并收回。
4.选择题部分请使用2B铅笔填涂;非选择題部分请使用0.5毫米黑色墨水签字笔书写字体工整、笔迹清楚。
10.将抛物线y=2(x+1)2+1向右平移2个单位长度,所得到的抛物线与直线y=3的交点坐标
是( )
A.(2,3)B.(-2,3C.(-2,3)或(-4,3)D.(2,3)或(0,3)
第Ⅱ卷(非选择题,共70分)
二、填空题(本大题共4个小题,每小题4分,共16分,答案写在答题卡上)
11.已知实数a,b满足 2=2,则 的值是
A.一组邻边相等的平行四边形是菱形B.对角线互相垂直的四边形是矩形
C.一组邻边相等的矩形是正方形D.一组对边平行且相等的四边形是平行四边形
7.如图,在△ABC中,点D,E分别在边AB,AC上,且DE∥BC, ,若S△ADE=2,则S△ABC的值是( )
A.6B.8C.18D.32
8.中国第十七届西博会于2018年9月20日至24日在成都西博城举办,期间某纪念品的标价为150元,连续两次涨价a%后售价为216元.下面所列方程中正确的是( )
三、解答题(本大题共6个小题,共54分,解答过程写在答题卡上)
15.(本小题满分12分,每题6分)
(1)计算: (2)解方程:x2-2x-99=0
16.(本小题满分6分)
如图,有一张鸡年生肖邮票和三张猴年生肖邮票(鸡年生肖邮票面值“80分”,猴年生肖邮

一、选择题（每题3分，共30分）1. 下列各数中，有理数是（）A. √9B. √-16C. πD. 2√22. 下列代数式中，正确的是（）A. a + b = b + aB. a - b = b - aC. ab = baD. a ÷ b = b ÷ a3. 已知x² - 5x + 6 = 0，则x的值为（）A. 2 或 3B. 1 或 4C. 2 或 4D. 1 或 34. 在直角坐标系中，点P（-2，3）关于x轴的对称点是（）A. （-2，-3）B. （2，3）C. （2，-3）D. （-2，-3）5. 下列图形中，是轴对称图形的是（）A. 等边三角形B. 等腰梯形C. 矩形D. 等腰直角三角形6. 已知三角形ABC中，∠A = 60°，∠B = 45°，则∠C的度数是（）A. 75°B. 105°C. 120°D. 135°7. 一个长方体的长、宽、高分别为a、b、c，则其体积V为（）A. abcB. a²bC. b²cD. c²a8. 下列函数中，是反比例函数的是（）A. y = 2x + 3B. y = 3/xC. y = x²D. y = √x9. 已知一次函数y = kx + b，当x = 1时，y = 2；当x = 2时，y = 4，则k和b的值分别是（）A. k = 1，b = 1B. k = 2，b = 1C. k = 1，b = 2D. k = 2，b = 210. 下列各数中，是正数的是（）A. -1/2B. -√4C. 0D. √9二、填空题（每题5分，共20分）11. 3a² - 2a + 1的因式分解为__________。

12. 若x + 2 = 5，则x的值为__________。

13. 直线y = 2x + 1的斜率是__________。

成都市武侯区2018-2019学年九年级<上>期末考试（一诊）数 学 试 卷A 卷(100分)一、选择题(每小题3分，共30分)1． 如图所示的支架（一种零件）的两个台阶的高度和宽度分别相等，则它的主视图为（ ）A 、B 、C 、D 、 2．已知反比例函数xky =（0≠k ）的图象经过点（-4，2），那么下列四个点中，在这个函数图象上的是（ ）A 、（1，8）B 、（3，-38） C 、（21，16） D 、（-2，-4） 3．如图，△ABC 的顶点都在正方形网格的格点上，则tan ∠BAC 的值是（ ）A 、21 B 、2 C 、32 D 、234．如图，E 是平行四边形ABCD 的对角线BD 上的点，连接AE 并延长交BC 于点F ，且31=BC BF ，则DEBE的值是（ ） A 、31 B 、21 C 、32 D 、435．若二次函数m x x y 232-+=的图象与x 轴有两个交点，则关于x 的方程m x x 232=+的根的情况是（ ）A 、有两个不相等的实数根B 、有两个相等的实数根C 、没有实数根D 、不能确定 6．下列命题中，是假命题的是（ ） A 、一组邻边相等的平行四边形是菱形 B 、对角线互相垂直的平行四边形是矩形C 、一组邻边相等的的矩形是正方形D 、一组对边平行且相等的四边形是平行四边形 7．如图，在△ABC 中，D 、E 分别在边AB 、AC 上，且DE ∥BC ，21=BC AD ，若2=∆A D E S ，则ABC S ∆的值是（ ）A 、6B 、8C 、18D 、12第3题 第4题 第7题8．中国十七届西博会于2018年9月20日到24日在成都西博城举办，期间某纪念品的标价为150元，连续两次涨价%a 后售价为216元.下面所列方程中正确的是（ ）A 、216%)21(150=+aB 、216%)21(1502=+aC 、2162%)21(150=⨯+aD 、216%)21(150%)21(1502=+++a a 9．在平面直角坐标系中，以原点O 为圆心，5为半径作圆，若点P 的坐标是（3，4），则点P 与⊙O 的位置关系是（ ）A 、点P 在⊙O 外B 、点P 在⊙O 内C 、点P 在⊙O 上D 、点P 在⊙O 上或在⊙O 外 10．将抛物线1)1(22++=x y 向右平移2个单位长度，所得到的抛物线与直线3=y 的交点坐标是（ ）A 、（2，3）B 、（-2，3）C 、（-2，3）或（-4，3）D 、（2，3）或（0，3）二、填空题(每小题4分，共16分)11．已知实数a 、b 满足32=b a ，则ba ba -+的值是12．如图，已知二次函数m x y +-=221的图象上有三点A （-1，1y ）、B （0，2y ）、C （3，3y ），则1y 、2y 、3y 的大小关系是13．如图，△ABC 是⊙O 的内接三角形，连接OB ，作OD ⊥AB 于点D.若⊙O 的半径为2，∠ACB=60°，则弦AB 的长是第12题 第13题 14．已知正比例函数x y 2=的图象与反比例函数x ky =（0≠k ）的图象相交于A （2，m ）、B 两点，则点B 的坐标是三、解答下列各题（共54分）15．（每小题6分，共12分） （1）计算：|321|)3(12)31(01-+-+---π（2）09922=--x x16．（6分）如图，有一张鸡年生肖邮票和三张猴年生肖邮票（鸡年生肖邮票每张面值“80分”，猴年生肖邮票每张面值“1.20元”），四张邮票除花色不一样之外，其余都相同，现将四张邮票花色朝下，打乱顺序后放置在桌面上.（注：1元=100分） （1）随机抽取一张，是猴年生肖邮票的概率是 ；（2）先随机抽取一张不放回，再抽取一张，求抽到的两张邮票组合起来刚好可以邮寄一封2元邮资的信件的概率.17．如图是成都市某在建大楼，准备上市销售,大楼前有一座装有高压线的铁塔BC 经过，市民想知道高压线的电辐射对居住是否有影响，则需要测量大楼到铁塔的水平距离DC 的长以及铁塔BC 的高度.为了安全，不能直接测量铁塔的高度，现在大楼屋顶A 处测得铁塔顶B 的仰角∠BAE=58°，测得铁塔底C 的俯角∠EAC=30°，大楼的高度AD=10m ，求铁塔BC 的高度.（参考数据：tan58°≈1.60，sin58°≈0.85，cos58°≈0.53，3≈1.73） 18．（8分）如图，在正方形ABDD 中，点E 、F 分别在边AB 、AD 上，EF ⊥CE 于E. （1） 求证：△AEF ∽△BCE ； （2） 若21=AE BE ，求CEEF的值.19．（10分）如图，已知一次函数4-=mx y （0≠m ）的图象分别交x 轴、y 轴于A （-4，0）、B 两点，与反比例函数xky =（0≠k ）的图象在第二象限的交点为C （-5，n ）. （1） 求一次函数的和反比例函数的表达式；（2） 点P 在该反比例函数的图象上，点Q 在x 轴上，且P 、Q 两点在直线AB 的同侧.若以B 、C 、P 、Q 为顶点的四边形是平行四边形，求满足条件的点P 和点Q 的坐标.20．（10分）如图1，四边形ABCD 是⊙O 的内接四边形，AC 平分∠DAB ，B 是弧AC 的中点. （1） 求证：AB=CD ；（2） 如图2，连接BO 并延长分别交AC ，AD 于点E 、F ，交⊙O 于点G ，连接FC. ① 试判断四边形ABCF 的形状，并说明理由； ② 若53=AD DC ，AC=46，求⊙O 的半径.图1 图2B 卷（50分）一、填空题：（每小题4分，共20分）21．在△ABC 中，若∠C=90°，sinA=32，则sinB=22．已知1x 、2x 是一元二次方程0522=--x x 的两个实数根，则21222`3x x x x ++=23．如图，在平面直角坐标系中，⊙O 的半径为4，弦AB 的长为3，过点O 作OC ⊥AB 于点C ，则OC的长度是 ；⊙O 内一点D 的坐标是（-2，1），当弦AB 绕点O 顺时针旋转时，点D 到AB 的距离的最小值是24．如图，在矩形ABCD 中，AB=6，BC=8，点E 在边BC 上（不与B 、C 重合），连接AE ，把△ABE 沿直线AE 折叠，点B 落在B ＇处.当△CEB ＇为直角三角形时，△CEB ＇的周长是 25．如图，将双曲线xky =（0<k ）在第四象限的一支沿直线x y -=方向向上平移到点E 处，交该双曲线在第二象限的一支于A 、B 两点，连接AB 并延长并x 轴于点C.双曲线xmy =（0>m ）与直线x y =在第三象限的交点为点D ，将双曲线xmy =在第三象限的一支沿射线OE 方向平移，点D 刚好可以与点C 重合，此时该曲线与前两支曲线围成一条“鱼”（如图中阴影部分）.若点C 的坐标为（-5，0），AB=32，则mk 的值是第23题 第24题 第25题二、解答下列各题（共30分）26．（8分）某商店购进一批单价为20元的节能灯，如果以单价30元出售，那么一个月内能售出400个.根据销售经验，提高销售单价会导致销售量减少，即销售单价每提高1元，销售量相应减少10个.设节能灯的销售单价提高x 元.（1） 一个月内商店要求要获得利润6000元，并且能尽可能多卖出以推广节能灯的使用，那么节能灯的销售单价应为多少元？（2） 当销售单价为多少元时，该商店一个月内获得的利润最大？最大利润是多少元？27．（10分）如图，点E、F分别在矩形ABCD的边AB、BC上，连接EF，将△BEF沿直线EF翻折得到△HEF，AB=8，BC=6，AE：EB=3：2.（1）如图1，当∠BEF=45°时，EH的延长线交DC于点M，求HM的长；（2）如图2，当FH的延长线经过点D时，求tan∠FEH的值；（3）如图3，连接AH、HC，当点F在线段BC上运动时，试探究四边形AHCD的面积是否存在最小值？若存在，求出四边形AHCD的面积的最小值；若不存在，请说明理由. 28．（12分）如图，在平面直角坐标系中，直线3+=mxy与抛物线交于点A（9，-6），与y轴交于点B，抛物线的顶点C的坐标是（4，-11）.（1）求直线和抛物线的函数表达式；（2）D是抛物线上位于对称轴左侧的点，若△ABD的面积为281，求点D的坐标；（3）在y轴上是否存在一点P，使∠APC=45°？若存在，求出满足条件的点P的坐标；若不存在，请说明理由.。

2018成都一诊压轴题深度剖析【解析】因为0≥⋅→--→--PB PA ，注意到P 在对称轴上，所以当PB PA ,为切线的时候，0=⋅→--→--PB PA ，即4π=PA k ，设()ax ex A 200,-，则()ax e ex f a x ax --===--02201'00 则ax --=0011，即10+=a x ，结合120=-a x e 得1=a . 从而()()1min -==e a f x f 【点评】借助对称性确定4π=PA k ，从而把问题转化为过P 作切线，斜率为1，进而可以求出a .解方程利用整体代换的思想很重要，这在处理公切线的时候，常常会这样解方程组。

在淘宝博约书斋（唯一正版书店）《高观点下函数导数压轴题的系统性解读》作了分析。

（2016全国3卷文科第16题）已知()x f 为偶函数，当0≤x 时，()x e x f x -=--1，则曲线()x f y =在点()2,1处的切线方程是（2015新课标1文科第12题）设函数()x f y =的图像与a x y +=2的图像关于直线x y -=对称，且()()142=-+-f f ，则=a2016考查了奇偶性和切线；2015年对两个函数的对称性提出了较高要求。

成都一诊涉及两个函数的对称性和由切线斜率反过来求a ，与全国卷考查很吻合。

对直观想象、逻辑推理和数学运算三个核心素养进行了较好地考查。

【解析】由椭圆第三定义知22ab mn -=，则原式可变为a b b a b a b a ln 623232222+-⎪⎪⎭⎫ ⎝⎛⋅+， 令()+∞∈=,1,x b ax ，()x x x x x f ln 6323223-+-=，则()()()()()xx x x x x x x x x x x f 342223226342'22+--=-+-=-+-=，所以当2==b a x 时，达到最小值。

此时23122=-=a b e【点评】在淘宝博约书斋（唯一正版书店）《解析几何的系统性突破》一书把到两定点的斜率之积为不等于-1的负数视为椭圆第三定义，全国卷两次直接考查，如下：在书中也介绍了第三定义和中点弦的结论是完全一致的，在即将出版的《高观点下高考数学压轴题三部曲》（目前只有打印版，在 新高考新思维新突破 微店有卖给每一个近八年的全国卷高考压轴题以变式和拓展，融入了与之相关的竞赛、自招题。

2018年成都市武侯区一诊数学D17、（本小题满分8分）小明和小颖上来采取以下规定决定谁将获得仅有一张科普报告入场券：在不透明的布袋里装有除颜色之外均相同的2个红球和1个绿球，小明先取出一个球，记住颜色后放回，然后小颖再取出一个球.若两次取出的球都是红色，则小明获得入场券，否则小颖获得入场券.你认为这个规则对双方公平吗？请用画树状图或列表的方法说明理由.18、（本小题满分8分）钓鱼岛自古以来是我国的固有领土，随着我们过奖综合国力的强盛，国家对钓鱼岛的巡航已常态化.2017年9月11日，中国海警2401号船在A 地测得钓鱼岛B 在北偏东30°方向，现该海警船继续从A 地出发以30海里/小时的速度向正北方向航行2小时后到达C 地.（1）若︒=∠15B ，求钓鱼岛B 在C 地的北偏东多少度？（2）在（1）的基础上，求海警船与钓鱼岛的距离CB 的长.（结果保留根号）19、（本小题满分10分）如图，一次函数()0≠+=k b kx y 的图象与反比例函数xy 3-=的图象相交于()()1,,,1--n B m A 两点，直线AB 与y 轴交于C 点，连接OB .（1）求一次函数的表达式；（2）在x 轴上找一点P ，连接BP ，使BOP ∆的面积等于BOC ∆的面积的2倍，求满足条件的点P 的坐标.20、（本小题满分10分）如图，AB 为O Θ的直径，F C ,为O Θ上两点，过C 作AB CD ⊥于点D ，交O Θ于点E ，延长EC 交BF 的延长线于点G ，连接EF CF ,.（1）求证：CFG BFE ∠=∠；（2）若364===CF BF FG ，，.①求EF 的长； ②若22tan =∠GFC ，求O Θ的半径.B 卷（共50分）一、填空题（每小题4分，共20分）21、已知D C ,分别是线段AB 上的两个黄金分割点，且4=AB ，则=CD .22、已知21,x x 是关于x 的一元二次方程052=+-a x x 的两个实数根，且521=-x x ，则=a .23、如图，抛物线c x x y ++-=241的顶点是正方形ABCO 的边AB 的中点，点C A ,在坐标轴上，抛物线分别与BC AO ,交于E D ,两点，将抛物线向下平移1个单位长度得到如图所示的阴影部分.现随机向该正方形区域投掷一枚小针，则针尖落在阴影部分的概率=P .（23题图）（24题图） 24、如图，直线b x y +-=与双曲线()()0,0>=<=m xm y k x k y 分别相交于点D C B A ,,,，已知点A 的坐标为()41，-，且25:：=CD AB ，则=m . 25、如图，O Θ的直径AB 的长为12，长度为4的弦DF 在半圆上滑动，AB DE ⊥于E ，DF OC ⊥于C ，连接AF CE ,，则AEC ∠sin 的值是 ，当CE 的长取得最大值时AF 的长是 .二、解答题（共30分）26、（本小题满分8分）某种蔬菜每千克售价1y （元）与销售月份x 之间的俄关系如图1所示，每千克成本2y （元）与销售月份x 之间的关系如图2所示，其中图1中的点在同一条线段上，图2中的点在同一条抛物线上，且抛物线的最低点的坐标为.（1）求出1y 与x 之间满足的函数表达式，并直接写出x 的取值范围；（2）求出2y 与x 之间满足的函数表达式；（3）设这种蔬菜每千克收益为w 元，试问在哪个月份出售这种蔬菜w 将取得最大值？并求出此最大值.（收益＝售价－成本）图1 图227、（本小题满分10分）如图，点E 为正方形ABCD 的边CD 上一点，AE DF ⊥于F ，交AC 于M ，交BC 于G ，在CD 上取点'G ，使CG CG ='，连接'MG .（1）求证：M CG AED '∠=∠；（2）连接BD 交AE 于点N ，连接',MG MN 交AE 于点H . ①试判断CD MN ,的位置关系，并说明理由；②若E G DG AB ''12==，，求AH 的长.28、（本小题满分12分） 如图，抛物线c x x y ++-=23212与x 轴交于B A ,两点（点A 在点B 的左侧），过点A 的直线323+=x y 与抛物线交于另一点C ，且点C 的纵坐标为6. （1）求抛物线的函数表达式；（2）点D 是抛物线上的一个动点，若ACD ∆的面积为4，求点D 的坐标；（3）在（2）的条件下，过直线AC 上方的点D 的直线与抛物线交于点E ，与x 轴正半轴交于点F ，若EF AE =，求EAF ∠tan 的值.（备用图）。

四川成都武侯区2018-2019 年初二上学期年终考试数学试卷及分析八年级数学说明： 1. 本试卷分为 A 卷和 B 卷，此中 A 卷共 100 分， B 卷共 50 分，总分值 150 分，考试时辰 120A 卷B 卷BA 卷题号一二三四五一二三四全卷1-10 11-15 1６17,18 19，20 21-25 26 27 28卷得分分钟、2.此试卷不答题 , 答题一律在答题卷上 .A卷〔共 100 分〕【一】选择题：( 将以下各题你以为正确旳【答案】填在下表中。

每题 3 分，共 30 分 )题号 1 2 3 4 5 6 7 8 9 10【答案】y1.以下美丽旳图案，既是轴对称图形又是中心对称图形旳个数3M 22. 在以下列图旳直角坐标系中，M、 N 旳坐标分别为N1A.M〔－ 1， 2〕， N〔 2,1 〕B.M〔 2，－ 1〕， N〔 2， 1〕-3 -2 -1 O 1 2 3 xC.M〔－ 1， 2〕， N〔 1,2 〕D.M〔 2，－ 1〕， N〔 1， 2〕-13、以下各式中 , 正确旳选项是A、16 =± 4B、±16 =4C、327 =-3D、( 4)2 =-4 （第 2 题图）4、如图，在水塔旳东北方向32 处有一抽水站，在水塔旳东南方向O m A24m处有一建筑物工地B，在 AB间建一条直水管，那么水管旳长为A.45 mB.40 mC.50mD.56m5、以下说法中正确旳选项是A、矩形旳对角线互相垂直B、菱形旳对角线相等C、平行四边形是轴对称图形D、等腰梯形旳对角线相等6、如图，正方形网格中旳△ABC，假定小方格边长为1，那么△ ABC旳形状为A、锐角三角形B、直角三角形C、钝角三角形D、以上【答案】都不对（第 4 题图）B C7、对于一次函数y=x+6，以下结论错误旳选项是A（第 6 题图）A、函数值随自变量增大而增大B、函数图象与x 轴正方向成 45°角C、函数图象不经过第四象限D、函数图象与x 轴交点坐标是〔0，6〕 D C8、如图，点O是矩形ABCD旳对称中心，E是AB边上旳点，沿CE折叠后，O 点 B恰巧与点 O重合，假定 BC=3，那么折痕 CE=3 3A、 2 3B、C、 3D、 6A E B2（第 8 题图）9. 一次函数 y =kx +b 〔 k ≠ 0〕图象过点〔 0， 2〕，且与两坐标轴围成旳三角形面积为2，那么一次函数旳【分析】式为 A 、 y =x +2B 、 y =﹣ x +2C 、 y =x +2 或 y =﹣ x +2D 、 y =- x +2 或 y =x -210、早饭店里，李明妈妈买了 5 个馒头， 3 个包子，老总少要１元，只需１０元；王红爸爸买了８个馒头，６个包子，老总九折优惠，只需１８元、假定馒头每个 x 元，包子每个y 元，那么所列二元一次方程组正确旳选项是A 、5x 3 y 10 1 5x 3y 10 15x 3 y 10 1 8x 6 y 18 B 、8x 6 y 18 C 、8x 6 y18 D 、0.90.90.95x 3y 10 18x 6y18 0.9【二】填空题 ( 每题 3 分,共15分)11. 如图，直线 y=ax+b 和直线 y=kx 交于点 P 〔 -4 ， -2 〕，那么对于x ， y 旳y ax b, 二元一次方程组旳解是﹏﹏﹏﹏﹏﹏﹏﹏、y kx.12. 假定一个多边形旳内角和等于 900 ，那么那个多边形旳边数是﹏﹏﹏﹏﹏ . 13.O〔 0,0 〕， A 〔－ 3,0 〕， B 〔－ 1, － 2〕，那么 △AOB 旳面积为﹏﹏﹏﹏﹏﹏、(第 11 题图)14、小明家预备春节行进行 80 人旳会餐，需要去某餐馆订餐、据认识餐馆有 10 人坐和 8 人坐两种餐桌，要使所订旳每个餐桌恰巧坐满，那么订餐方案共有﹏﹏﹏﹏﹏种、15. 如图，正方形网格中每个小正方形边长差不多上1，随意连结这些小正方形极点，可获得一些线段 . 请在图中画出线段AB 2、 CD5、 EF13 .〔要求将所画三条线段旳端点标上对应旳字母〕 【三】解答以下各题〔〔每题 5 分，共 20 分〕16. 〔 1〕计算：26-4 278 〔 2〕计算： (13)( 26)- (2 3 1)283(3) 解方程组：2 x 3y 0 2( x y) 3(x y)3 3x y(4) 解方程组：y) 3x15 3y114( x 【四】解答题〔共 15 分〕1７ . 在成立平面直角坐标系旳方格纸中，每个小方格差不多上面长为 1 旳小正方形，△ ABC 旳极点均在格点上，点 P 旳坐标为 ( － 1，0) ，请按要求绘图与作答：〔 1〕画出以点 P 为对称中心，与△ ABC 成中心对称旳△ A ′ B ′ C ′、 〔 2〕把△ ABC 向右平移 7 个单位得△ A ′′ B ′′ C ′′、〔 3〕△ A ′ B ′ C ′与△ A ′′ B ′′ C ′′能否成中心对称？假定是，画出对称 中心 P ′， 并写出其坐标、18. 如图，⊿ ABC 中， AD 是边 BC 上旳中线，过点 A 作 AE ∥ BC ，过点 D 作 DE ∥AB ， DE 与 AC 、 AE 分别交于点O 、点 E ，连结 EC.yABCPOPxA EOBDC〔 1〕求证： AD=EC;〔 2〕当∠ BAC=90°时，求证：四边形 ADCE 是菱形 . 【五】解答以下问题〔共20 分〕19. 甲、乙、丙三个家电厂家在广告中都宣称，他们旳某种电子产品在正常状况下旳使用寿命差不多上 8 年，经质量检测部门对这三家销售旳产品旳使用寿命进行追踪检查， 统计结果以下：〔单位：年〕甲厂： 4， 5， 5， 5，5， 7， 9，12， 13，15 乙厂： 6， 6， 8， 8，8， 9， 10， 12， 14， 15 丙厂： 4， 4， 4， 6，7， 9， 13， 15， 16， 16 请回答下边问题：〔 1〕填空：均匀数众数 中位数 甲厂6 乙厂 9.68.5丙厂9.4 4〔 2〕这三个厂家旳销售广告分别利用了哪一种表示集中趋向旳特点数？〔 3〕你是顾客，你买三家中哪一家旳电子产品？什么缘由？20、一次函数 y=kx+b 旳图象是过 A 〔 0， -4 〕， B 〔 2， -3 〕两点旳一条直线、〔１〕求直线 AB 旳【分析】式；〔２〕将直线 AB 向左平移 6 个单位，求平移后旳直线旳【分析】式、 〔３〕将直线 AB 向上平移 6 个单位，求原点到平移后旳直线旳距离.B 卷(共 50 分)1.填空题：〔本大题共 5 小题，每题 4 分，共 20 分〕 21. 那么 y+z=﹏﹏﹏﹏﹏﹏、22、△ ABC 中， AB ＝15， AC ＝13，高 AD ＝ 12，那么△ ABC 旳周长为﹏﹏﹏﹏﹏ ﹏﹏﹏﹏﹏ 、23、实数1旳整数部分 a=﹏﹏﹏﹏﹏，小数部分 b=﹏﹏﹏﹏﹏﹏﹏﹏﹏37﹏ 、24、在平面直角坐标系中，横坐标、纵坐标都为整数旳点称为整点、请你观看图中正方形A 1B 1C 1D 1， A 2B 2C 2D 2 ， A 3B 3C 3D 3 每个正方形四条边上旳整点旳个数、按此规律计算出正方形A 10B 10C 10D 10 四条边上旳整点共有个、25、长为 2，宽为 a 旳矩形纸片〔 1＜ a ＜2〕，如图那样折一下，剪下一个边长等于矩形宽度旳正方形〔称为第一次操作〕；再把剩下旳矩形如图那样折一下，剪下一个边长等于此刻矩形宽度旳正方形〔称为第二次操作〕； 这样频频操作下去、 假定在第n 此操作后，剩下旳矩形为正方形，那么操作停止、当=3 时， a 旳值为﹏﹏﹏﹏﹏﹏﹏﹏n﹏﹏ 、【二】解答题〔 8 分〕26、某服饰厂接到生产一种工作服旳订货任务， 要求在规按限期内达成， 依据那个服饰厂原题号总分来旳生产能力，每日可生产这类服饰150 套，按这样旳生产进度在客户要求旳限期内只好完成订货旳4；此刻工厂改良了人员组织构造和生产流程，每日可生产这类工作服200 套，5这样不单比规准时辰少用 1 天，并且比订货量多生产25 套，求订做旳工作服是几套？要求旳限期是几日？【三】解答题〔10 分〕27、如图，直角坐标系中，点 A 旳坐标为〔 1，0〕，以线段 OA为边在第四象限内作等边△AOB，点 C 为 x 正半轴上一动点〔OC＞1〕，连结 BC，以线段 BC为边在第四象限内作等边△CBD，直线 DA交 y 轴于点 E、〔1〕△ OBC与△ ABD全等吗？推测并证明你旳结论；〔2〕跟着点 C 地点旳变化，点 E 旳地点能否会发生变化？假定没有变化，求出点 E 旳坐标；假定有变化，请说明原因、【四】解答题〔12 分〕28、如图，在Rt △OAB中，∠A＝ 90°，∠ABO＝ 30°，OB＝4 3，边AB旳垂直均分线CD3分别与 AB、x 轴、 y 轴交于点 C、 E、 D、〔1〕求点E旳坐标；〔2〕求直线CD旳【分析】式；〔3〕在直线CD上和坐标平面内能否分别存在点Q、P，使得以O、D、P、Q为极点旳四边形是菱形？假定存在，求出点 Q旳坐标；假定不存在，请说明原因、成都市武侯区2018-2018 学年度上期教课质量测评试题八年级数学试卷参照【答案】及评分标准说明：本试卷分为 A 卷和 B 卷，此中 A 卷共 100 分， B 卷共 50 分，总分值150 分，考试时辰120 分钟、A 卷B 卷一二三四五 A 卷一二三四 B 卷全卷1-10 11-15 1６17, 18 19，20 21-25 26 27 2830 15 20 15 20 100 20 8 10 12 50 150A卷〔共 100 分〕【一】选择题：( 将以下各题你以为正确旳【答案】填在下表中。

四川成都武侯区2018-2019年初二上学期年末考试数学试卷及解析八年级数学说明：1.本试卷分为A卷和B卷，其中A卷共100分，B卷共50分，总分值150分，考试时刻120分钟、2.此试卷不答题,答题一律在答题卷上.A卷〔共100分〕1.以下漂亮旳图案，既是轴对称图形又是中心对称图形旳个数A.4B.3C.2D.12.在如下图旳直角坐标系中，M、N旳坐标分别为A.M〔－1，2〕，N〔2,1〕B.M〔2，－1〕，N〔2，1〕C.M〔－1，2〕，N〔1,2〕D.M〔2，－1〕，N〔1，2〕3、以下各式中,正确旳选项是A±4B=-3D=-44、如图，在水塔O旳东北方向32m处有一抽水站A，在水塔旳东南方向24m处有一建筑物工地B，在AB间建一条直水管，那么水管旳长为A.45mB.40mC.50mD.56m5、以下说法中正确旳选项是A、矩形旳对角线相互垂直B、菱形旳对角线相等C、平行四边形是轴对称图形D、等腰梯形旳对角线相等6、如图，正方形网格中旳△ABC，假设小方格边长为1，那么△ABC旳形状为A、锐角三角形B、直角三角形C、钝角三角形D、以上【答案】都不对7、关于一次函数y=x+6，以下结论错误旳选项是A、函数值随自变量增大而增大B、函数图象与x轴正方向成45°角C、函数图象不通过第四象限D、函数图象与x轴交点坐标是〔0，6〕8、如图，点O是矩形ABCD旳对称中心，E是AB边上旳点，沿CE折叠后，点B恰好与点O重合，假设BC=3，那么折痕CE=A、23B、332C、3D、6（第2题图）（第4题图）CBAA BCDEO（第8题图）9.一次函数y =kx +b 〔k ≠0〕图象过点〔0，2〕，且与两坐标轴围成旳三角形面积为2，那么一次函数旳【解析】式为A 、y =x +2B 、y =﹣x +2C 、y =x +2或y =﹣x +2D 、y =-x +2或y =x -210、早餐店里，李明妈妈买了5个馒头，3个包子，老总少要１元，只要１０元；王红爸爸买了８个馒头，６个包子，老总九折优惠，只要１８元、假设馒头每个x 元，包子每个y 元，那么所列二元一次方程组正确旳选项是A 、⎩⎨⎧⨯=++=+9.0186811035y x y xB 、⎩⎨⎧÷=++=+9.0186811035y x y xC 、⎩⎨⎧⨯=+-=+9.0186811035y x y xD 、⎩⎨⎧÷=+-=+9.0186811035y x y x 【二】填空题(每题3分,共15分)11.如图，直线y=ax+b 和直线y=kx 交于点P 〔-4，-2〕，那么关于x ，y 旳二元一次方程组,.y ax b y kx =+⎧⎨=⎩旳解是﹏﹏﹏﹏﹏﹏﹏﹏、12.假设一个多边形旳内角和等于900，那么那个多边形旳边数是﹏﹏﹏﹏﹏. 13.O 〔0,0〕，A 〔－3,0〕，B 〔－1,－2〕，那么△AOB 旳面积为﹏﹏﹏﹏﹏﹏、 14、小明家预备春节前进行80人旳聚餐，需要去某餐馆订餐、据了解餐馆有10人坐和8人坐两种餐桌，要使所订旳每个餐桌刚好坐满， 那么订餐方案共有﹏﹏﹏﹏﹏种、15.如图，正方形网格中每个小正方形边长差不多上1，任意连结这些小正方形顶点，可得到一些线段.请在图中画出线段1352===EF CD AB 、、.〔要求将所画三条线段旳端点标上对应旳字母〕 【三】解答以下各题〔〔每题5分，共20分〕 16.〔1〕计算：862⨯-82734⨯+〔2〕计算：)62)(31(-+-2)132(- (3)解方程组：⎩⎨⎧=-=+113032y x y x (4)解方程组：⎩⎨⎧+=++=--+y x y x y x y x 3153)(43)(3)(2【四】解答题〔共15分〕 1７.在建立平面直角坐标系旳方格纸中，每个小方格差不多上边长为1旳小正方形，△ABC 旳顶点均在格点上，点P 旳坐标为(－1，0)，请按要求画图与作答： 〔1〕画出以点P 为对称中心，与△ABC 成中心对称旳△A ′B ′C ′、〔2〕把△ABC 向右平移7个单位得△A ′′B ′′C ′′、〔3〕△A ′B ′C ′与△A ′′B ′′C ′′是否成中心对称？假设是，画出对称中心P ′，并写出其坐标、18.如图，⊿ABC 中，AD 是边BC 上旳中线，过点A 作AE ∥BC ，过点D 作DE ∥AB ，DE 与AC 、AE 分别交于点O 、点E ，连接EC.(第11题图)BD〔1〕求证：AD=EC;〔2〕当∠BAC=90°时，求证：四边形ADCE是菱形.【五】解答以下问题〔共20分〕19.甲、乙、丙三个家电厂家在广告中都声称，他们旳某种电子产品在正常情况下旳使用寿命差不多上8年，经质量检测部门对这三家销售旳产品旳使用寿命进行跟踪调查，统计结果如下：〔单位：年〕甲厂：4，5，5，5，5，7，9，12，13，15乙厂：6，6，8，8，8，9，10，12，14，15丙厂：4，4，4，6，7，9，13，15，16，16请回答下面问题：〔1〕填空：〔2〔3〕你是顾客，你买三家中哪一家旳电子产品？什么缘故？20、一次函数y=kx+b旳图象是过A〔0，-4〕，B〔2，-3〕两点旳一条直线、〔１〕求直线AB旳【解析】式；〔２〕将直线AB向左平移6个单位，求平移后旳直线旳【解析】式、〔３〕将直线AB向上平移6个单位，求原点到平移后旳直线旳距离.B卷(共50分)1.填空题：〔本大题共5小题，每题4分，共20分〕21.那么y+z=﹏﹏﹏﹏﹏﹏、22、△ABC中，AB＝15，AC＝13，高AD＝12，那么△ABC旳周长为﹏﹏﹏﹏﹏﹏﹏﹏﹏﹏、23a=﹏﹏﹏﹏﹏，小数部分b=﹏﹏﹏﹏﹏﹏﹏﹏﹏﹏、24、在平面直角坐标系中，横坐标、纵坐标都为整数旳点称为整点、请你观看图中正方形A1B1C1D1，A2B2C2D2，A3B3C3D3每个正方形四条边上旳整点旳个数、按此规律推算出正方形A10B10C10D10四条边上旳整点共有个、25、长为2，宽为a旳矩形纸片〔1＜a＜2〕，如图那样折一下，剪下一个边长等于矩形宽度旳正方形〔称为第一次操作〕；再把剩下旳矩形如图那样折一下，剪下一个边长等于现在矩形宽度旳正方形〔称为第二次操作〕；如此反复操作下去、假设在第n此操作后，剩下旳矩形为正方形，那么操作终止、当n=3时，a旳值为﹏﹏﹏﹏﹏﹏﹏﹏﹏﹏、【二】解答题〔8分〕26、某服装厂接到生产一种工作服旳订货任务，要求在规定期限内完成，按照那个服装厂原来旳生产能力，每天可生产这种服装150套，按如此旳生产进度在客户要求旳期限内只能完成订货旳45；现在工厂改进了人员组织结构和生产流程，每天可生产这种工作服200套，如此不仅比规定时刻少用1天，而且比订货量多生产25套，求订做旳工作服是几套？要求旳期限是几天？【三】解答题〔10分〕 27、如图，直角坐标系中，点A 旳坐标为〔1，0〕，以线段OA 为边在第四象限内作等边△AOB ，点C 为x 正半轴上一动点〔OC ＞1〕，连接BC ，以线段BC 为边在第四象限内作等边△CBD ，直线DA 交y 轴于点E 、〔1〕△OBC 与△ABD 全等吗？推断并证明你旳结论；〔2〕随着点C 位置旳变化，点E 旳位置是否会发生变化？假设没有变化，求出点E 旳坐标；假设有变化，请说明理由、 【四】解答题〔12分〕28、如图，在Rt △OAB 中，∠A ＝90°，∠ABO ＝30°，OB ＝334，边AB 旳垂直平分线CD 分别与AB 、x 轴、y 轴交于点C 、E 、D 、 〔1〕求点E 旳坐标；〔2〕求直线CD 旳【解析】式；〔3〕在直线CD 上和坐标平面内是否分别存在点Q 、P ，使得以O 、D 、P 、Q 为顶点旳四边形是菱形？假设存在，求出点Q 旳坐标；假设不存在，请说明理由、成都市武侯区2018-2018学年度上期教学质量测评试题八年级数学试卷参考【答案】及评分标准说明：本试卷分为A 卷和B 卷，其中A 卷共100分，B 卷共50分，总分值150分，考试时刻120分钟、A 卷〔共100分〕【一】选择题：(将以下各题你认为正确旳【答案】填在下表中。

武侯区一中2018-2019学年上学期高三数学10月月考试题 班级__________ 座号_____ 姓名__________ 分数__________一、选择题1． 若y x ,满足约束条件⎪⎪⎩⎪⎪⎨⎧≥≤-+≥+-0033033y y x y x ，则当31++x y 取最大值时，y x +的值为（ ）A ．1-B ．C ．3-D ．32． 四棱锥P ﹣ABCD 的底面是一个正方形，PA ⊥平面ABCD ，PA=AB=2，E 是棱PA 的中点，则异面直线BE 与AC 所成角的余弦值是（ ）A． B． C． D．3． 设a ，b为正实数，11a b+≤23()4()a b ab -=，则log a b =（ ）A.0B.1-C.1 D .1-或0【命题意图】本题考查基本不等式与对数的运算性质等基础知识，意在考查代数变形能与运算求解能力. 4． 一个骰子由1~6六个数字组成，请你根据图中三种状态所显示的数字，推出“”处的数字是（ ） A ．6 B ．3 C ．1 D ．25． 下列四个命题中的真命题是（ ）A ．经过定点()000,P x y 的直线都可以用方程()00y y k x x -=-表示B ．经过任意两个不同点()111,P x y 、()222,P x y 的直线都可以用方程()()()()121121y y x x x x y y --=-- 表示C ．不经过原点的直线都可以用方程1x ya b+=表示D ．经过定点()0,A b 的直线都可以用方程y kx b =+表示6． 已知数列{}n a 是各项为正数的等比数列，点22(2,log )M a 、25(5,log )N a 都在直线1y x =-上，则数列{}n a 的前n 项和为（ ）A ．22n- B ．122n +- C ．21n - D ．121n +-7． 设函数()()21x f x e x ax a =--+，其中1a <，若存在唯一的整数，使得()0f t <，则的取值范围是（ ）A ．3,12e ⎡⎫-⎪⎢⎣⎭ B ．33,24e ⎡⎫-⎪⎢⎣⎭ C ．33,24e ⎡⎫⎪⎢⎣⎭ D ．3,12e ⎡⎫⎪⎢⎣⎭1111] 8． 自圆C ：22(3)(4)4x y -++=外一点(,)P x y 引该圆的一条切线，切点为Q ，切线的长度等于点P 到原点O 的长，则点P 轨迹方程为（ ）A ．86210x y --=B ．86210x y +-=C ．68210x y +-=D ．68210x y --=【命题意图】本题考查直线与圆的位置关系、点到直线的距离，意在考查逻辑思维能力、转化能力、运算求解能力．9． 已知点P 是双曲线C ：22221(0,0)x y a b a b-=>>左支上一点，1F ，2F 是双曲线的左、右两个焦点，且12PF PF ⊥，2PF 与两条渐近线相交于M ，N 两点（如图），点N 恰好平分线段2PF ，则双曲线的离心率是（ ）A.5B.2 D.2【命题意图】本题考查双曲线的标准方程及其性质等基础知识知识，意在考查运算求解能力. 10．命题“∀a ∈R ，函数y=π”是增函数的否定是（ ）A ．“∀a ∈R ，函数y=π”是减函数B ．“∀a ∈R ，函数y=π”不是增函数C ．“∃a ∈R ，函数y=π”不是增函数D ．“∃a ∈R ，函数y=π”是减函数11．已知F 1、F 2是椭圆的两个焦点，满足=0的点M 总在椭圆内部，则椭圆离心率的取值范围是（ ）A ．（0，1）B ．（0，]C ．（0，）D ．[，1）12．设m ，n 表示两条不同的直线，α、β表示两个不同的平面，则下列命题中不正确的是（ ） A ．m ⊥α，m ⊥β，则α∥β B ．m ∥n ，m ⊥α，则n ⊥αC ．m ⊥α，n ⊥α，则m ∥nD ．m ∥α，α∩β=n ，则m ∥n二、填空题13．已知双曲线的标准方程为，则该双曲线的焦点坐标为， 渐近线方程为 ．14．（本小题满分12分）点M （2pt ，2pt 2）（t 为常数，且t ≠0）是拋物线C ：x 2＝2py （p ＞0）上一点，过M 作倾斜角互补的两直线l 1与l 2与C 的另外交点分别为P 、Q .（1）求证：直线PQ 的斜率为－2t ；（2）记拋物线的准线与y 轴的交点为T ，若拋物线在M 处的切线过点T ，求t 的值． 15．已知一个算法，其流程图如图，则输出结果是 ．16．设有一组圆C k ：（x ﹣k+1）2+（y ﹣3k ）2=2k 4（k ∈N *）．下列四个命题： ①存在一条定直线与所有的圆均相切； ②存在一条定直线与所有的圆均相交； ③存在一条定直线与所有的圆均不相交； ④所有的圆均不经过原点．其中真命题的代号是 （写出所有真命题的代号）．三、解答题17．（本小题满分12分）在ABC ∆中，内角C B A ,,的对边为c b a ,,，已知1cos )sin 3(cos 2cos 22=-+C B B A. （I ）求角C 的值；（II ）若2b =，且ABC ∆的面积取值范围为，求c 的取值范围． 【命题意图】本题考查三角恒等变形、余弦定理、三角形面积公式等基础知识，意在考查基本运算能力．18．若数列{a n}的前n项和为S n，点（a n，S n）在y=x的图象上（n∈N*），（Ⅰ）求数列{a n}的通项公式；（Ⅱ）若c1=0，且对任意正整数n都有，求证：对任意正整数n≥2，总有．19．24．（本小题满分10分）选修4-5：不等式选讲．已知函数f（x）＝|x＋1|＋2|x－a2|（a∈R）．（1）若函数f（x）的最小值为3，求a的值；（2）在（1）的条件下，若直线y＝m与函数y＝f（x）的图象围成一个三角形，求m的范围，并求围成的三角形面积的最大值．20．已知函数f（x）的定义域为{x|x≠kπ，k∈Z}，且对定义域内的任意x，y都有f（x﹣y）=成立，且f（1）=1，当0＜x＜2时，f（x）＞0．（1）证明：函数f（x）是奇函数；（2）试求f（2），f（3）的值，并求出函数f（x）在[2，3]上的最值．21．（本小题满分12分）两个人在进行一项掷骰子放球游戏中，规定：若掷出1点，甲盒中放一球；若掷出2点或3点，乙盒中 放一球；若掷出4点或5点或6点，丙盒中放一球，前后共掷3次，设,,x y z 分别表示甲，乙，丙3个 盒中的球数.（1）求0x =，1y =，2z =的概率；（2）记x y ξ=+，求随机变量ξ的概率分布列和数学期望.【命题意图】本题考查频离散型随机变量及其分布列等基础知识，意在考查学生的统计思想和基本的运算能力．22．（本小题满分12分）已知圆C ：022=++++F Ey Dx y x 的圆心在第二象限，半径为2，且圆C 与直线043=+y x 及y 轴都相切.（1）求F E D 、、；（2）若直线022=+-y x 与圆C 交于B A 、两点，求||AB .23．已知三次函数f （x ）的导函数f ′（x ）=3x 2﹣3ax ，f （0）=b ，a 、b 为实数． （1）若曲线y=f （x ）在点（a+1，f （a+1））处切线的斜率为12，求a 的值；（2）若f （x ）在区间[﹣1，1]上的最小值、最大值分别为﹣2、1，且1＜a ＜2，求函数f （x ）的解析式．武侯区一中2018-2019学年上学期高三数学10月月考试题（参考答案）一、选择题1．【答案】D【解析】考点：简单线性规划．2．【答案】B【解析】解：以A为原点，AB为x轴，AD为y轴，AP为z轴，建立空间直角坐标系，则B（2，0，0），E（0，0，1），A（0，0，0），C（2，2，0），=（﹣2，0，1），=（2，2，0），设异面直线BE与AC所成角为θ，则cosθ===．故选：B．3． 【答案】B.【解析】2323()4()()44()a b ab a b ab ab -=⇒+=+，故11a b a b ab++≤⇒≤2322()44()1184()82()()a b ab ab ab ab ab ab ab ab++⇒≤⇒=+≤⇒+≤，而事实上12ab ab +≥=， ∴1ab =，∴log 1a b =-，故选B.4． 【答案】A 【解析】试题分析：根据与相邻的数是1,4,3，而与相邻的数有1,2,5，所以1,3,5是相邻的数，故“？”表示的数是，故选A ．考点：几何体的结构特征． 5． 【答案】B 【解析】考点：直线方程的形式.【方法点晴】本题主要考查了直线方程的表示形式，对于直线的点斜式方程只能表示斜率存在的直线；直线的斜截式方程只能表示斜率存在的直线；直线的饿两点式方程不能表示和坐标轴平行的直线；直线的截距式方程不能表示与坐标轴平行和过原点的直线，此类问题的解答中熟记各种直线方程的局限性是解答的关键.111]6． 【答案】C【解析】解析：本题考查等比数列的通项公式与前n 项和公式．22log 1a =，25log 4a =，∴22a =,516a =,∴11a =,2q =，数列{}n a 的前n 项和为21n-，选C ．7． 【答案】D 【解析】考点：函数导数与不等式．1【思路点晴】本题主要考查导数的运用，涉及划归与转化的数学思想方法.首先令()0f x =将函数变为两个函数()()()21,x g x e x h x ax a =-=-，将题意中的“存在唯一整数，使得()g t 在直线()h x 的下方”，转化为存在唯一的整数，使得()g t 在直线()h x ax a =-的下方.利用导数可求得函数的极值，由此可求得m 的取值范围.8． 【答案】D【解析】由切线性质知PQ CQ ⊥，所以222PQ PC QC =-，则由PQ PO =，得，2222(3)(4)4x y x y -++-=+，化简得68210x y --=，即点P 的轨迹方程，故选D ，9． 【答案】A. 【解析】10．【答案】C【解析】解：因为全称命题的否定是特称命题，所以，命题“∀a ∈R ，函数y=π”是增函数的否定是：“∃a ∈R ，函数y=π”不是增函数．故选：C．【点评】本题考查命题的否定，特称命题与全称命题的否定关系，是基础题．11．【答案】C【解析】解：设椭圆的半长轴、半短轴、半焦距分别为a，b，c，∵=0，∴M点的轨迹是以原点O为圆心，半焦距c为半径的圆．又M点总在椭圆内部，∴该圆内含于椭圆，即c＜b，c2＜b2=a2﹣c2．∴e2=＜，∴0＜e＜．故选：C．【点评】本题考查椭圆的基本知识和基础内容，解题时要注意公式的选取，认真解答．12．【答案】D【解析】解：A选项中命题是真命题，m⊥α，m⊥β，可以推出α∥β；B选项中命题是真命题，m∥n，m⊥α可得出n⊥α；C选项中命题是真命题，m⊥α，n⊥α，利用线面垂直的性质得到n∥m；D选项中命题是假命题，因为无法用线面平行的性质定理判断两直线平行．故选D．【点评】本题考查了空间线面平行和线面垂直的性质定理和判定定理的运用，关键是熟练有关的定理．二、填空题13．【答案】（±，0）y=±2x．【解析】解：双曲线的a=2，b=4，c==2，可得焦点的坐标为（±，0），渐近线方程为y=±x，即为y=±2x．故答案为：（±，0），y=±2x．【点评】本题考查双曲线的方程和性质，主要是焦点的求法和渐近线方程的求法，考查运算能力，属于基础题．14．【答案】【解析】解：（1）证明：l 1的斜率显然存在，设为k ，其方程为y －2pt 2＝k （x －2pt ）．① 将①与拋物线x 2＝2py 联立得， x 2－2pkx ＋4p 2t （k －t ）＝0，解得x 1＝2pt ，x 2＝2p （k －t ），将x 2＝2p （k －t ）代入x 2＝2py 得y 2＝2p （k －t ）2，∴P 点的坐标为（2p （k －t ），2p （k －t ）2）．由于l 1与l 2的倾斜角互补，∴点Q 的坐标为（2p （－k －t ），2p （－k －t ）2）， ∴k PQ ＝2p （－k －t ）2－2p （k －t ）22p （－k －t ）－2p （k －t ）＝－2t ，即直线PQ 的斜率为－2t .（2）由y ＝x 22p 得y ′＝xp，∴拋物线C 在M （2pt ，2pt 2）处的切线斜率为k ＝2ptp ＝2t .其切线方程为y －2pt 2＝2t （x －2pt ）， 又C 的准线与y 轴的交点T 的坐标为（0， －p2）． ∴－p2－2pt 2＝2t （－2pt ）．解得t ＝±12，即t 的值为±12.15．【答案】 5 ．【解析】解：模拟执行程序框图，可得 a=1，a=2不满足条件a 2＞4a+1，a=3不满足条件a 2＞4a+1，a=4不满足条件a 2＞4a+1，a=5满足条件a 2＞4a+1，退出循环，输出a 的值为5．故答案为：5．【点评】本题主要考查了循环结构的程序框图，依次正确写出每次循环得到的a 的值是解题的关键，属于基本知识的考查．16．【答案】 ②④【解析】解：根据题意得：圆心（k ﹣1，3k ），圆心在直线y=3（x+1）上，故存在直线y=3（x+1）与所有圆都相交，选项②正确； 考虑两圆的位置关系，圆k ：圆心（k ﹣1，3k ），半径为k 2，圆k+1：圆心（k ﹣1+1，3（k+1）），即（k ，3k+3），半径为（k+1）2，两圆的圆心距d==，两圆的半径之差R ﹣r=（k+1）2﹣k 2=2k+，任取k=1或2时，（R ﹣r ＞d ），C k 含于C k+1之中，选项①错误； 若k 取无穷大，则可以认为所有直线都与圆相交，选项③错误；将（0，0）带入圆的方程，则有（﹣k+1）2+9k 2=2k 4，即10k 2﹣2k+1=2k 4（k ∈N*），因为左边为奇数，右边为偶数，故不存在k 使上式成立，即所有圆不过原点，选项④正确． 则真命题的代号是②④． 故答案为：②④【点评】本题是一道综合题，要求学生会将直线的参数方程化为普通方程，会利用反证法进行证明，会利用数形结合解决实际问题．三、解答题17．【答案】 【解析】（I ）∵1cos )sin 3(cos 2cos 22=-+C B B A， ∴0cos sin 3cos cos cos =-+C B C B A ， ∴0cos sin 3cos cos )cos(=-++-C B C B C B ，∴0cos sin 3cos cos sin sin cos cos =-++-C B C B C B C B ， ∴0cos sin 3sin sin =-C B C B ，因为sin 0B >，所以3tan =C 又∵C 是三角形的内角，∴3π=C .18．【答案】【解析】（I ）解：∵点（a n ，S n ）在y=x 的图象上（n ∈N *），∴，当n≥2时，，∴，化为，当n=1时，，解得a1=．∴==．（2）证明：对任意正整数n都有=2n+1，∴c n=（c n﹣c n﹣1）+（c n﹣1﹣c n﹣2）+…+（c2﹣c1）+c1=（2n﹣1）+（2n﹣3）+…+3==（n+1）（n﹣1）．∴当n≥2时，==．∴=+…+=＜=，又=．∴．【点评】本题考查了等比数列的通项公式与等差数列的前n项和公式、“累加求和”、“裂项求和”、对数的运算性质、“放缩法”、递推式，考查了推理能力与计算能力，属于中档题．19．【答案】【解析】解：（1）f（x）＝|x＋1|＋2|x－a2|＝⎩⎪⎨⎪⎧－3x＋2a2－1，x≤－1，－x＋2a2＋1，－1＜x＜a2，3x－2a2＋1，x≥a2，当x≤－1时，f（x）≥f（－1）＝2a2＋2，－1＜x＜a2，f（a2）＜f（x）＜f（－1），即a2＋1＜f（x）＜2a2＋2，当x≥a2，f（x）≥f（a2）＝a2＋1，所以当x＝a2时，f（x）min＝a2＋1，由题意得a2＋1＝3，∴a＝±2.（2）当a＝±2时，由（1）知f（x）＝⎩⎪⎨⎪⎧－3x ＋3，x ≤－1，－x ＋5，－1＜x ＜2，3x －3，x ≥2，由y ＝f （x ）与y ＝m 的图象知，当它们围成三角形时，m 的范围为（3，6]，当m ＝6时，围成的三角形面积最大，此时面积为12×|3－（－1）|×|6－3|＝6.20．【答案】【解析】（1）证明：函数f （x ）的定义域为{x|x≠k π，k ∈Z}，关于原点对称． 又f （x ﹣y）=，所以f （﹣x）=f[（1﹣x）﹣1]= = == = =，故函数f （x ）奇函数．（2）令x=1，y=﹣1，则f （2）=f[1﹣（﹣1）]= =，令x=1，y=﹣2，则f （3）=f[1﹣（﹣2）]===，∵f （x ﹣2）==，∴f （x ﹣4）=，则函数的周期是4．先证明f （x ）在[2，3]上单调递减，先证明当2＜x ＜3时，f （x ）＜0， 设2＜x ＜3，则0＜x ﹣2＜1，则f （x ﹣2）=，即f （x ）=﹣＜0，设2≤x 1≤x 2≤3，则f （x 1）＜0，f （x 2）＜0，f （x 2﹣x 1）＞0，则f （x 1）﹣f （x 2）=，∴f （x 1）＞f （x 2），即函数f （x ）在[2，3]上为减函数，则函数f （x ）在[2，3]上的最大值为f （2）=0，最小值为f （3）=﹣1．【点评】本题主要考查了函数奇偶性的判断，以及函数的最值及其几何意义等有关知识，综合性较强，难度较大．21．【答案】【解析】（1）由0x =，1y =，2z =知，甲、乙、丙3个盒中的球数分别为0，1，2，此时的概率213111324P C ⎛⎫=⨯⨯= ⎪⎝⎭.（4分）22．【答案】（1） 22=D ，24-=E ，8=F ;（2）2=AB . 【解析】试题解析：（1）由题意，圆C 方程为2)()(22=-+-b y a x ，且0,0><b a ，∵圆C 与直线043=+y x 及y 轴都相切，∴2-=a ，25|43|=+b a ，∴22=b ， ∴圆C 方程为2)22()2(22=-++y x ， 化为一般方程为08242222=+-++y x y x ， ∴22=D ，24-=E ，8=F .（2）圆心)22,2(-C 到直线022=+-y x 的距离为12|22222|=+--=d ，∴21222||22=-=-=d r AB . 考点：圆的方程；2.直线与圆的位置关系.1 23．【答案】【解析】解：（1）由导数的几何意义f ′（a+1）=12∴3（a+1）2﹣3a （a+1）=12 ∴3a=9∴a=3（2）∵f ′（x ）=3x 2﹣3ax ，f （0）=b∴由f ′（x ）=3x （x ﹣a ）=0得x 1=0，x 2=a ∵x ∈[﹣1，1]，1＜a ＜2∴当x ∈[﹣1，0）时，f ′（x ）＞0，f （x ）递增；当x ∈（0，1]时，f ′（x ）＜0，f （x ）递减． ∴f （x ）在区间[﹣1，1]上的最大值为f （0） ∵f （0）=b ， ∴b=1∵，∴f （﹣1）＜f （1）∴f （﹣1）是函数f （x ）的最小值，∴∴∴f （x ）=x 3﹣2x 2+1【点评】曲线在切点处的导数值为曲线的切线斜率；求函数的最值，一定要注意导数为0的根与定义域的关系．。