高等数学Ⅱ(专科类)第2阶段练习题 江南大学 考试题库及答案 一科共有三个阶段,这是其中一个阶段。

装 ---------------------------------订 ---------------------------------线 ------------------------------------------------装 订 线 左 侧 不 要 书 写 内 容1．与向量{3,0,3}a =-平行的单位向量为 .2. 判断级数1n ∞=∑的收敛性（填收敛或者发散） .3. 交换二次积分的积分次序2 1(,)xxdx f x y dy ⎰⎰= .4. 设函数()y f x =由方程221x y +=确定 ，则dydx.5. 如果级数∑∞=0n n u 收敛，则lim n n u →∞= .10 分，共 60 分）1. 求以(1,2,3),(3,4,5),(2,4,7)A B C 为顶点的ABC ∆的面积。

2. 一个平面通过两点(1,1,1)A 和(0,1,1)B -且垂直于平面0x y z ++=，求此平面的方程。

3. 将直线的一般方程32402350x y z x y z +--=⎧⎨-+-=⎩化为点向式方程及参数方程。

4. 设22sin ,,uz e v u x y v xy ==+=，求,z z x y∂∂∂∂。

------------------------------------------------ 装 ---------------------------------订 ---------------------------------线 ------------------------------------------------装 订 线 左 侧 不 要 书 写 内 容5. 计算二重积分DI xydxdy =⎰⎰，其中:D 由2yx =和2y x =-所围成区域。

6. 求幂级数11(1)2nnn x n ∞=-⋅∑的收敛域。

三.解答题（每题10分，共 20 分）1．求由旋转抛物面22z x y =+和222z x y =--围成的立体的体积。

江南大学现代远程教育2015年第一阶段测试卷考试科目:《高等数学》专升本 第一章至第三章（总分100分） 时间：90分钟__________学习中心（教学点） 批次： 层次：专业： 学号： 身份证号： 姓名： 得分：一、选择题 (每题4分) 1. 函数y =的定义域是 ( a ). (a) (2,6)- (b) (2,6] (c)[2,6) (d)[2,6]- 2. 10lim(13)xx x →+ ( c )(a)e (b) 1 (c) 3e (d) ∞3.要使函数()f x x=在0x =处连续, 应给(0)f 补充定义的数值是( d ).(a) 1 (b) 2(c) (d)54. 设 sin 3xy -=, 则 y ' 等于 ( b ).(a)sin 3(ln3)cos xx - (b) sin 3(ln3)cos x x -- (c) sin 3cos x x -- (d) sin 3(ln3)sin x x --5. 设函数 ()f x 在点 0x 处可导, 则 000(3)()limh f x h f x h→+-等于 ( b ).(a) 03()f x '- (b) 03()f x ' (c) 02()f x '- (d) 02()f x ' 二.填空题(每题4分)6. 设 2(1)3f x x x -=++, 则 ()f x = 235x x ++7. 2sin(2)lim2x x x →-++=__1___.8. 设 1,0,()5,0,1,0x x f x x x x -<⎧⎪==⎨⎪+>⎩, 则 0lim ()x f x +→=___1___.9. 设 ,0(),2,0x e x f x a x x -⎧≤=⎨+>⎩ 在点 0x = 处连续, 则常数 a =___1/2___10. 曲线 54y x-= 在点 (1,1) 处的法线方程为11. 由方程 2250xy x y e -+=确定隐函数 ()y y x =, 则 y '=222222xy xy e y xy x xye--12. 设函数 2()ln(2)f x x x =, 则 (1)f ''=___2ln2+3_____三. 解答题(满分52分) 13. 求 45lim()46xx x x →∞--. 解： 1(4x -6+6)x x x 411111444x-664444x-54x-6+111lim ()=lim ()=lim (1+)=lim (1+)4x-64x-64x-64x-611 =lim (1+)+lim (1+)=e .1=e 4x-64x-6x x x x x x →∞→∞→∞→∞→∞→∞⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦ 14. 求x →.解：利用等价无穷小2x=x 2S i n 3x 3x则0x 1=3x 3x x →→ 15. 确定A 的值, 使函数 62cos ,0(),tan ,0sin 2x e x x f x Ax x x-⎧-≤⎪=⎨>⎪⎩ 在点 0x = 处连续。

江南大学现代远程教育第二阶段测试卷考试科目:《管理会计》第四章至第八章（总分100分）时间：90分钟学习中心（教学点）批次：层次：专业：学号：身份证号：姓名：得分：一、填空（把答案填在题中的横线上。

每空1分，共10分。

）1、预测分析法一般可分为定性预测分析法和定量预测分析法。

2、货币的时间价值是指货币经过一定时间的投资与再投资后，所增加的价值。

3、建立最佳安全库存量政策时，必须考虑两项成本，即安全库存量的储存成本和库存耗竭成本。

4、只有在相关范围内，增加一个单位产量的单位变动成本才能和边际成本相一致。

5、最优生产批量指一次投产的最优经济批量，在这个投产批量下，生产成本最低。

二、单选（选出一个正确答案填入题中的括号里。

每题1分，共10分。

）1、（B）决策不属于短期经营决策。

A、接受追加订货；B、购买固定资产；C、亏损产品停产；D、开发新产品。

2、通过比较各备选方案贡献毛益的大小确定最优方案的分析方法，称为（C）。

A、差量成本法；B、概率分析法；C、贡献毛益法；D、成本无差别分析法。

3、按各观察值与预测值不同的相关程度分别规定适当权数，是运用（D）进行预测销关键。

A、算术平均法；B、对数直线法；C、回归直线法；D、加权平均法。

4、现值指数（C）就表明该项目具有正的净现值，对企业有利。

A、大于0；B、小于0；C、大于1；D、小于1。

5、在确定两种产品生产的最优组合时，运用线性规划法，得到产品组合（x1，x2）的可行解区域：A（25，35）、B（0，60）、C（40，0）、D（0，0），这样边际贡献S＝3x1＋x2的最大值为（A）。

A、120；B、150；C、175；D、145。

6、递延年金的特点是（B）。

A、没有终值；B、没有第一期的支付额；C、没有现值；D、上述说法都对。

7、设某厂需零件甲，其外购价为10元，若自行生产，单位变动成本为6元，且需要为此每年追加10000元的固定成本，通过计算可知，当该零件的年需要量为（A）件时，两种方案等效。

专科起点升本科《高等数学（二）》入学考试题库（共180题）1．函数、极限和连续（53题）1.1函数（8题）1.1.1函数定义域1．函数lg arcsin 23x x y x =+-的定义域是（）。

A A.[3,0)(2,3]-；B.[3,3]-；C.[3,0)(1,3]-；D.[2,0)(1,2)-. 211(。

D 3. A.(0,4]；B.,0)(0,2]；D.4．如果函数()f x 的定义域是A .1[,0)(0,3]3-⋃；B .1[,3]3；C .1[,0)9-⋃5．如果)(x f 的定义域是[0，1]，则(arcsin )f x A.[0,1]；B.1[0,2；C.[0,]2π；D.[0,]π. 1.1.2函数关系 6.设()()22221,1x f x x x x ϕϕ+⎡⎤==⎣⎦-，则()f x =()．A A ．211x x +-；B.211x x -+；C.121x x -+；D.121x x +-. 7．函数331xx y =+的反函数y =（）。

B A ．3log ()1x x +；B.3log ()1x x -；C.3log ()1x x -；D.31log (x x-. 8．如果2sin (cos )cos 2x f x x=，则()f x =()．CA ．22121x x +-；B.22121x x -+；C.22121x x --；D.22121x x ++. 1.2极限（37题）1.2.1数列的极限9．极限123lim (2n n n n →+∞++++-=()．B A ．1；B.12；C.13；D.∞. 10．极限2123lim 2n n n→∞++++=()．A A ．14；B.14-；C.15；D.15- 11(1)nn +++122(1)2113n n ++-++9；D.9-13．极限lim x x→∞=()．C A ．12；B.12-；C.1；D.1-. 14．极限01lim x x →=()．A A ．12；B.12-；C.2；D.2-. 15．极限01lim x x →-=（）．B A.32-；B.32；C.12-；D.12. 16．极限11lim 1x x →=-（）．C A.-2；B.0；C.1；D.2.17．极限4x →=()．B A ．43-；B.43；C.34-；D.34. 18．极限x →∞=()．DA ．∞；B.2；C.1；D.0.19．极限2256lim 2x x x x →-+=-()．D A ．∞；B.0；C.1；D.-1.20．极限3221limx x →-=()．A 212223．极限01lim sin x x x →=()．B A ．1-；B.0；C.1；D.2.24．极限020sin 1lim xx t dt t x →-=⎰()．BA ．12；B.12-；C.13；D.13-. 25．若232lim 43x x x k x →-+=-，则k =（）．A A ．3-；B.3；C.13-；D.13. 26．极限2323lim 31x x x x →∞++=-()．B A ．∞；B.0；C.1；D.-1.1.2.3无穷小量与无穷大量27．当0x →时，2ln(12)x +与2x 比较是（）。

高数II-2一、单项选择1、级数为( )• A、发散• B、条件收敛但不绝对收敛• C、绝对收敛但不条件收敛• D、绝对收敛且条件收参考答案 B2、曲线在t=2处的切向量是（）。

• A、(2,1, 4)•B、(4,3, 4)•C、0•D、(−4,3, 4)参考答案 A3、在)处均存在是在处连续的（）条件。

• A、充分• B、必要• C、充分必要• D、既不充分也不必要参考答案 D4、设a为常数，则级数( )• A、绝对收敛• B、条件收敛• C、发散• D、敛散性与a的值有关参考答案 A5、二元函数的定义域是（）。

• A、• B、• C、• D、参考答案 A6、方程表示的曲面是（）。

• A、圆• B、椭球• C、抛物面• D、球面参考答案 D7、有且仅有一个间断点的函数是（）。

• A、• B、• C、• D、参考答案 B8、下列级数中,收敛级数是()• A、• B、• C、• D、参考答案 A9、按牛顿冷却定律：物体在空气中冷却的速度与物体的温度和空气的温度之差成正比。

已知空气温度为300C,而物体在15分钟内从1000C冷却到700C，求物体冷却到400C所需的时间为（）分钟。

• A、50•B、51•C、52•D、53参考答案 C10、平面4y－7z=0的位置特点是（）• A、平行于z轴• B、垂直于x轴• C、平行于y轴• D、通过x轴参考答案 D11、若满足，则交错级数。

• A、一定发散• B、一定收敛• C、可收敛也可发散• D、难以确定参考答案 C12、下列无穷级数中发散的是（）。

• A、• B、• C、• D、参考答案 C13、下列说法正确的是（）。

• A、两直线之间的夹角范围在• B、两平面之间的夹角范围在• C、两向量之间的夹角范围在• D、直线和平面之间的夹角范围在参考答案 C14、级数收敛，则参数a满足条件（）• A、a>e•B、a<e•C、a=e•D、a为任何实数参考答案 A15、下列方程中( )是表示母线平行于y轴的双曲柱面。

模拟试卷一―――――――――――――――――――――――――――――――――― 注意：答案请写在考试专用答题纸上，写在试卷上无效。

（本卷考试时间100分）一、单项选择题（每题3分，共24分）1、已知平面π：042=-+-z y x 与直线111231:-+=+=-z y x L 的位置关系是（ ） （A ）垂直 （B ）平行但直线不在平面上（C ）不平行也不垂直 （D ）直线在平面上 2、=-+→→1123lim0xy xy y x （ ）（A ）不存在 （B ）3 （C ）6 （D ）∞3、函数),(y x f z =的两个二阶混合偏导数y x z ∂∂∂2及xy z∂∂∂2在区域D 内连续是这两个二阶混合偏导数在D 内相等的（ ）条件.（A ）必要条件 （B ）充分条件（C ）充分必要条件 （D ）非充分且非必要条件 4、设⎰⎰≤+=ay x d 224πσ，这里0 a ，则a =（ ）（A ）4 （B ）2 （C ）1 （D ）0 5、已知()()2y x ydydx ay x +++为某函数的全微分，则=a （ ）（A ）-1 （B ）0 （C ）2 （D ）16、曲线积分=++⎰L z y x ds222（ ），其中.110:222⎩⎨⎧==++z z y x L（A ）5π（B ）52π （C ）53π （D ）54π7、数项级数∑∞=1n na发散，则级数∑∞=1n nka（k 为常数）（ ）（A ）发散 （B ）可能收敛也可能发散（C ）收敛 （D ）无界 8、微分方程y y x '=''的通解是（ ）（A ）21C x C y += （B ）C x y +=2（C ）221C x C y += （D ）C x y +=221 二、填空题（每空4分，共20分）1、设xyez sin =，则=dz 。

2、交换积分次序：⎰⎰-222xy dy e dx = 。

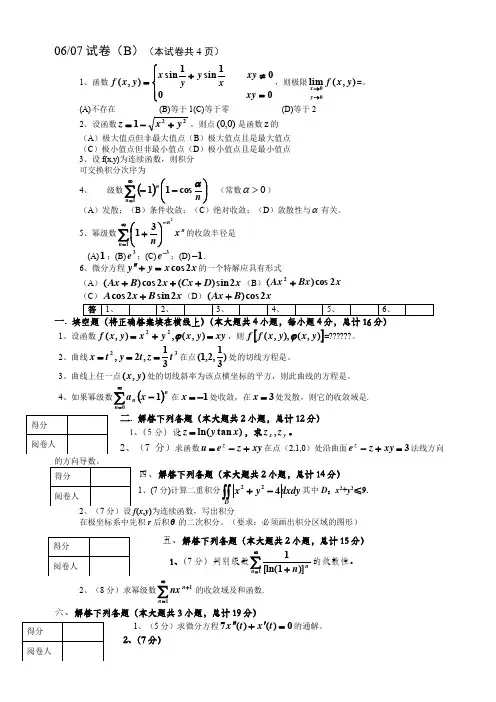
06/07试卷（B ）（本试卷共4页）1、函数⎪⎩⎪⎨⎧=≠+=0001sin 1sin ),(xy xy x y y x y x f ，则极限),(lim 00y x f y x →→=。

(A)不存在(B)等于1(C)等于零 (D)等于2 2、设函数221y x z +-=，则点(,)00是函数z 的（A ）极大值点但非最大值点（B ）极大值点且是最大值点（C ）极小值点但非最小值点（D ）极小值点且是最小值点3、设f (x ,y )为连续函数，则积分可交换积分次序为4、 级数()∑∞=⎪⎭⎫ ⎝⎛--1cos 11n n n α（常数0>α）（A ）发散；（B ）条件收敛；（C ）绝对收敛；（D ）敛散性与α有关。

5、幂级数n n n x n 2131-∞=∑⎪⎭⎫ ⎝⎛+的收敛半径是 (A)1；(B)3e ；(C)3-e ；(D)1-.6、微分方程x x y y 2cos =+''的一个特解应具有形式（A ）x D Cx x B Ax 2sin )(2cos )(+++（B ）x Bx Ax 2cos )(2+（C ）x B x A 2sin 2cos +（D ）x B Ax 2cos )(+一. 1、设函数xy y x y x y x f =+=),(,),(22ϕ，则[]),(),,(y x y x f f ϕ=??????。

2、曲线3231,2,t z t y t x ===在点)31,2,1(处的切线方程是。

3、曲线上任一点),(y x 处的切线斜率为该点横坐标的平方，则此曲线的方程是。

4、如果幂级数()∑∞=-01n n n x a 在1-=x 处收敛，在3=x 处发散，则它的收敛域是. 二. 解答下列各题（本大题共2小题，总计12分） 1、（5分）设)tan ln(x y z =，求y x z z ,。

2、（7分）求函数xy z e u z +-=在点（2,1,0）处沿曲面3=+-xy z e z 法线方向四、解答下列各题（本大题共2小题，总计14分） 1、(7分)计算二重积分224+-⎰⎰D xy dxdy 其中D ：x2+y 2≤9.f (x ,y )为连续函数，写出积分在极坐标系中先积r 后积θ的二次积分。