7b1 第七章 力法 结构力学电子教案

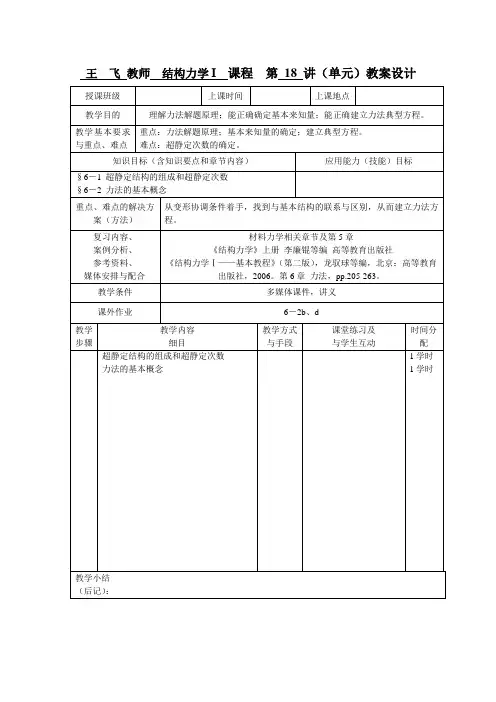
王飞教师结构力学І课程第18 讲（单元）教案设计第六章力法力法计算超静定结构主要是利用静定结构内力计算和位移计算来解决超静定结构的内力计算，因此静定结构的内力计算和位移计算是本章的基础；由于力法的计算量较大，本章的学习重点应是力法的基本方程的理解和应用，主要是不超过三次超静定结构。

§6-1 超静定结构的组成和超静定次数6.1.1 超静定结构的组成静定结构:结构的反力和各截面的内力都可以用静力平衡条件唯一确定(图6-1a)。

超静定结构:结构的反力和各截面的内力不能完全由静力平衡条件唯一的加以确定(图6-1b)。

图6-1从几何组成分析中可知：静定结构和超静定结构都是几何不变体体系，而静定结构没有多余的约束，超静定结构存在多余约束，将图6-1b中支座C去掉结构仍为几何不变体系(图6-1c)。

结论：满足平衡方程的内力解不唯一，几何上有多余约束，这就是超静定结构区别于静定结构的基本特点。

6.1.2 超静定次数超静定次数：超静定结构中多余约束的个数；也可以认为多余未知力的数目。

将超静定结构中多余约束去掉，可变为相应的静定结构，则去掉多余约束的个数n即为原结构的超静定次数。

结构去掉多余约束的方式有以下几种：1.去掉一根支座链杆或切断一根链杆，等于去掉一个约束(图6-2)。

2.去掉一个固定铰支座或撤去一个单铰，等于去掉两个约束。

3.将刚性连接改为单铰，相当于去掉一个约束(图6-3)。

4.去掉一个固定端或切断一个梁式杆，等于去掉三个约束(图6-4)。

图6-2图6-3图6-4对于一个超静定结构，去掉多余约束的方式可能有几种，但必须注意：去掉多余约束后，一般应是几何不变的、静定的结构。

图6-2a、图6-3a、图6-4a结构的超静定次数分别为1、1、3。

§6-2 力法的基本概念6.2.1 基本思路(1)力法是计算超静定结构的最基本方法。

力法的基本思路是把超静定结构的计算问题转化为静定结构的计算问题。

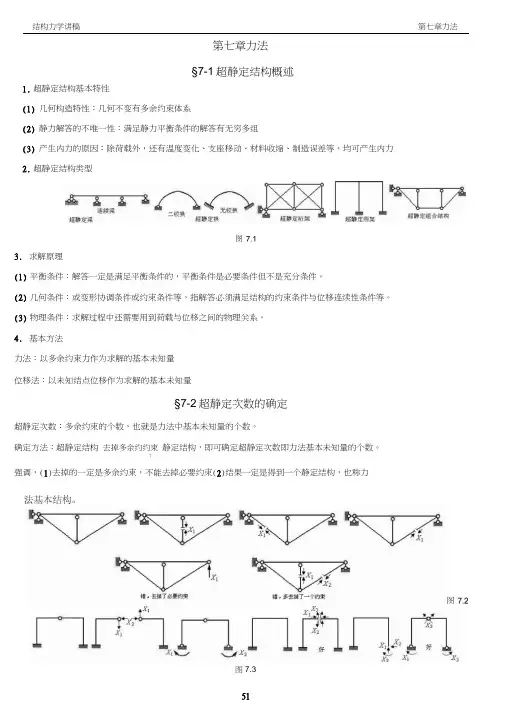
1. 超静定结构基本特性(1) 几何构造特性：几何不变有多余约束体系(2) 静力解答的不唯一性：满足静力平衡条件的解答有无穷多组(3) 产生内力的原因：除荷载外，还有温度变化、支座移动、材料收缩、制造误差等，均可产生内力 2. 超静定结构类型3. 求解原理(1) 平衡条件：解答一定是满足平衡条件的，平衡条件是必要条件但不是充分条件。

(2) 几何条件：或变形协调条件或约束条件等，指解答必须满足结构的约束条件与位移连续性条件等。

(3) 物理条件：求解过程中还需要用到荷载与位移之间的物理关系。

4. 基本方法力法：以多余约束力作为求解的基本未知量 位移法：以未知结点位移作为求解的基本未知量§7-2超静定次数的确定超静定次数：多余约束的个数，也就是力法中基本未知量的个数。

确定方法：超静定结构 去掉多余约约束 静定结构，即可确定超静定次数即力法基本未知量的个数。

T强调，(1)去掉的一定是多余约束，不能去掉必要约束(2)结果一定是得到一个静定结构，也称力第七章力法 §7-1超静定结构概述图7.3力法基車堀构IP一次超静定，去掉支座B ,得到力法基本未知量与基本结构;(2)要使基本结构与原结构等价，则要求，荷载与X i共同作用下，1=0(3)由叠加原理，有，宀一站•冷p =X 「ii =0，力法典型方程，即多余约束处的位移约束条件(4)柔度系数W与自由项"MP均为力法基本结构上(静定结构)的位移，由图乘法，得(5)X i已知，可作出原结构M图，如图示§7-4力法典型方程由上节知，力法典型方程就是多余约束处的位移方程。

下面讨论一般情况下力法方程的形式。

图7.4图7.6§7-3力法基本概念F面用力法对一单跨超静定梁进行求解，以说明力法基本概念, 对力法有一个初步了解^1=136 =丄丄4 ,l 2 J^也ii III , ipEI 2 3 3EI4i i I i |2 3| ql 、，l ql l , X iEI 3 2 4 8EI=fqi-'ii 8图7.5形式上完全相同，只是各符号的具体物理含义有所不同依此类推，n 次超静定结构，有n 个多余约束力时，力法典型方程为■「n X n ■“1P八：1 = 0+ ^2nX n + 也2P =6 =0' nnXn ^nP 二"n = 0A P '-2P:_i=0,卜］{X} { P } =0UnP为线性代数方程组，由位移互等定理， r =13次超静定，去掉一个固定支座，得到力法基本结构。

一、力（一）课前思虑（二）力1．力的定义：。

察看以下图理解力的定义。

2．对力的认识1）施力物体与受力物体：一个物体对另一个物体施加推、拉、提、压等作用时，施加这类作用的物体叫，遇到这类作用的物体叫。

（2）力不可以离开物体独自存在：力起码跟两个物体相关（一个施力物体、一个受力物体），单唯一个物体不可以产生力的作用，即力是物体对物体的运动。

3）力的产生与能否接触没关：相互接触的物体不必定发生力的作用，没有接触的物体之间也不必定没有力的作用（如磁铁吸引小铁钉），所以“接触与否不可以成为发生力的作用的依照”。

【例题一】在发生力的作用时，以下说法正确的选项是（）A．能够没有物体，既没有施力物体，也没有受力物体B．只需有受力物体就行，能够没有施力物体C．只需存在施力物体就行，有没有受力物体是没相关系的D．必定既有受力物体，又有施力物体，走开物体谈不上作用，就没有力了3．力的单位力一般用字母F表示，在国际单位制中，力的单位是牛顿，简称牛，用符号N表示。

（牛顿是伟大的物理学家、天文家和数学家，经典力学系统的奠定人，以后人们为纪念他，就用他的名字作为力的单位。

）以下图展现了一些力的大小，从图中能看出：托起两个鸡蛋所用的力约为1N。

【例题二】托起以下哪一个物体所用的力最靠近1N（）A．一袋方便面B．一张学生用板凳C．一枚大头针D．一块砖（二）力的作用成效在物理学中，人们往常经过力的作用成效来认识和描绘力。

1．改变物体的形状；2．改变物体的运动状态。

结论：力的作用成效的两个方面能够同时发生，也能够独自发生。

一个物体的运动状态或形状发生变化，则这个物体必定遇到了力的作用。

【例题三】以下现象中，物体的运动状态不发生改变的是（）A．自行车匀速转弯B．水平路面上加快运动的小轿车C．人造卫星绕着地球运动D．小车在桌面上做匀速直线运动【例题四】跳板跳水是我国传统的体育项目，水平居世界前列。

运动员对跳板施力的同时，也遇到跳板对他的作使劲，但这两个力的作用成效却不一样，前者主要改变了跳板的，后者主要改变了运动员的。