一、线性变换的矩阵表示式.

线性变换的矩阵表示与相似矩阵线性代数是数学中一个重要的分支，研究向量空间和线性变换的性质以及相应的代数结构。

在线性代数中，线性变换是其中一个重要的概念，它可以用矩阵表示，并且与相似矩阵有着密切的关系。

一、线性变换的矩阵表示线性变换是指保持向量空间中的线性结构不变的变换。

在二维或三维向量空间中，线性变换可以用一个矩阵来表示。

以二维向量空间为例，设有向量v=(v₁, v₂)，线性变换v将其映射为向量v=(v₁, v₂)，则可以使用矩阵v来表示v的线性变换，即：[v₁] [v₁₁, v₁₂] [v₁][v₂] = [v₂₁, v₂₂] × [v₂]其中，矩阵v=[v₁₁, v₁₂; v₂₁, v₂₂]表示线性变换v的矩阵表示。

这种矩阵表示的好处在于可以简化线性变换的计算，尤其是在高维向量空间中。

二、相似矩阵的定义相似矩阵是指具有相同特征值的矩阵。

设有两个v×v矩阵v和v，如果存在一个可逆矩阵v使得v=v⁻¹vv成立，则称矩阵v和v相似，矩阵v称为相似变换矩阵。

三、线性变换的矩阵表示与相似矩阵的联系线性变换的矩阵表示与相似矩阵有着密切的联系。

以二维向量空间为例，设有一个线性变换v的矩阵表示为v=[v₁₁, v₁₂; v₂₁, v₂₂]，我们希望找到一个矩阵v使得v=v⁻¹vv中的矩阵v与v相似。

根据相似矩阵的定义，我们可以得到v=v⁻¹vv的形式。

对于二维向量空间来说，v为一个2×2的可逆矩阵，假设v=[v₁₁, v₁₂; v₂₁, v₂₂]，则v可表示为：[v₁₁, v₁₂][v₂₁, v₂₂]若要使得v=v⁻¹vv成立，只需令v⁻¹=[v₁₁, v₁₂; v₂₁, v₂₂]即可。

则v的形式为：[v₁₁, v₁₂][v₂₁, v₂₂]通过矩阵相乘的运算可以得到：[v₁₁, v₁₂] [v₁₁, v₁₂][v₂₁, v₂₂] × [v₂₁, v₂₂]由此可以得到v=[v₁₁, v₁₂; v₂₁, v₂₂]与v=[v₁₁, v₁₂;v₂₁, v₂₂]相似的条件为：[v₁₁, v₁₂] [v₁₁, v₁₂][v₂₁, v₂₂] = [v₂₁, v₂₂]也就是说，要使得两个矩阵相似，只需保证其对应位置上的元素相等即可。

线性变换的相关知识点总结一、线性变换的定义线性变换是指一个向量空间V到另一个向量空间W的一个函数T，满足以下两条性质：1.加法性质：对于向量空间V中的任意两个向量x和y，有T(x+y)=T(x)+T(y)。

2.数乘性质：对于向量空间V中的任意向量x和标量a，有T(ax)=aT(x)。

根据以上的定义，我们可以得出线性变换的几个重要性质：1. 线性变换保持向量空间中的原点不变；2. 线性变换保持向量空间中的直线和平面不变；3. 线性变换将线性相关的向量映射为线性相关的向量；4. 线性变换将线性无关的向量映射为线性无关的向量。

二、线性变换的矩阵表示在研究线性变换时，我们通常会使用矩阵来表示线性变换。

设V和W分别是n维和m维向量空间，选择它们的一组基{v1, v2, ..., vn}和{w1, w2, ..., wm}。

线性变换T可以用一个m×n的矩阵A来表示，假设向量x在基{v1, v2, ..., vn}下的坐标为[x]，向量T(x)在基{w1, w2, ..., wm}下的坐标为[T(x)]，则有[T(x)]=[A][x]。

由此可见，矩阵A中的每一列都是T(vi)在基{w1, w2, ..., wm}下的坐标，而T(vi)可以写成基{w1, w2, ..., wm}的线性组合，所以矩阵A的列向量就是线性变换T对基{v1, v2, ..., vn}下的坐标系的映射。

另外，矩阵A的行空间也是线性变换T的像空间，而零空间是T的核空间。

线性变换的基本性质在矩阵表示下也可以得到进一步的解释，例如线性变换的复合、逆变换等都可以在矩阵表示下进行研究。

因此，矩阵表示是研究线性变换的重要工具。

三、特征值和特征向量特征值和特征向量是线性代数中的一个非常重要的概念，它们在研究线性变换的性质时有非常重要的应用。

设T是一个n维向量空间V上的线性变换，那么存在一个标量λ和一个非零向量v，使得Tv=λv。

这里的λ就是T的特征值，v就是T的特征向量。

线性变换的矩阵表示线性变换是数学中的重要概念，它在许多领域都有广泛应用。

线性变换可以通过矩阵表示，这种表示形式方便计算和讨论线性变换的性质。

本文将介绍线性变换的矩阵表示以及相关概念和性质。

1. 线性变换的定义线性变换是指满足以下两个条件的映射：(1) 对于任意向量u和v以及实数a和b，线性变换T满足T(a*u +b*v) = a*T(u) + b*T(v)。

(2) 线性变换T对于向量的加法和数乘运算封闭，即T(u + v) = T(u) + T(v)，T(k*u) = k*T(u)（k为实数）。

2. 矩阵表示的意义线性变换的矩阵表示可以将线性变换转化为矩阵的乘法运算，从而方便计算和分析线性变换的性质。

对于任意线性变换T，可以找到一个矩阵A，使得对于任意向量u，有T(u) = A*u。

矩阵A被称为线性变换T的矩阵表示。

3. 线性变换的矩阵表示方法线性变换的矩阵表示可以通过以下步骤得到：(1) 选择标准基下的基向量，分别记作e1, e2, ..., en。

(2) 对于每个基向量ei，计算线性变换T(ei)的坐标表示，得到矩阵A的第i列。

(3) 将所有计算得到的列向量排列起来，得到矩阵A。

4. 矩阵表示的性质线性变换的矩阵表示具有以下性质：(1) 线性变换的合成对应于矩阵的乘法。

对于线性变换T1和T2，它们的矩阵表示分别为A和B，则它们的合成线性变换对应的矩阵表示为A*B。

(2) 线性变换的逆对应于矩阵的逆。

若线性变换T存在逆变换，它们的矩阵表示分别为A和A^-1，则逆变换对应的矩阵表示为A^-1。

(3) 线性变换的像空间和核空间可以通过矩阵表示进行刻画。

像空间对应于矩阵的列空间，而核空间对应于矩阵的零空间。

5. 矩阵表示的例子考虑一个二维平面上的旋转变换，将向量绕原点逆时针旋转θ度。

选择标准基下的基向量为e1 = (1, 0)和e2 = (0, 1)。

对于基向量e1，旋转变换后的坐标表示为cosθ*e1 - sinθ*e2。

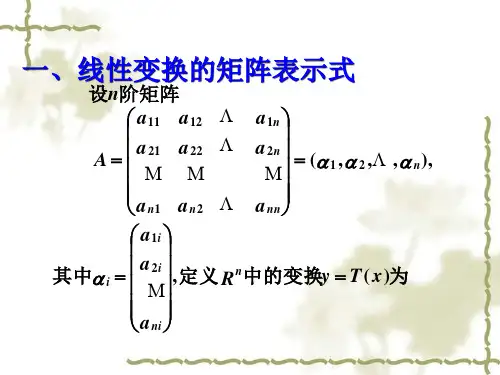
§5 线性变换的矩阵表示式上节例10中，关系式()T x Ax =()n x R ∈ 简单明了地表示出中的一个线性变换. 我们自然希望中任何一个线性变换都能用这样的关系式来表示. 为此，考虑到n n Ae Ae ==αα,,11 （n e e ,,1 为单位坐标向量），即()n i Ae i i ,,2,1 ==α，可见如果线性变换有关系式()Ax x T =，那么矩阵应以()i e T 为列向量. 反之，如果一贯个线性变换使()()n i e T i i ,,2,1 ==α，那么必有关系式()11122(),,()n n n T x T e e x T x e x e x e ==+++⎡⎤⎣⎦1122()()()n n x T e x T e x T e =+++()11(),,()(,,)n n T e T e x x Ax αα===总之，中任何线性变换，都能用关系式()()nR x Ax x T ∈=表示，其中1((),,())n A T e T e =.把上面的讨论推广到一般的线性空间，我们有定义7 设是线性空间中的线性变换，在中取定一个基n αα,,1 ，如果这个基在变换下的象（用这个基线性表示）为11112121212122221122(),(),(),n n n n n n n nn n T a a a T a a a T a a a αααααααααααα=+++⎧⎪=+++⎪⎨⎪⎪=+++⎩记()()()()n n T T T αααα,,,,11 = ，上式可表示为11(,,)(,,)n n T A αααα=， （5）其中1111n n nn a a A a a ⎛⎫ ⎪= ⎪ ⎪⎝⎭，那么，就称为线性变换在基n αα,,1 下的矩阵 .显然，矩阵由基的象()()n T T αα,,1 唯一确定.如果给出一个矩阵作为线性变换在基n αα,,1 下的矩阵，也就是给出了这个基在变换下的象，那么根据变换保持线性关系的特性，我们来推导变换必须满足的关系式：中的任意元素记为in i i x αα∑==1，有 11()()n n i i i i i i T x x T ααα====∑∑121((),,())n n x x T T x αα⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭121(,,)n n x x A x αα⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭， 即112211(,,)(,,)n n n n x x x x T A x x αααα⎡⎤⎛⎫⎛⎫⎢⎥ ⎪ ⎪⎢⎥ ⎪ ⎪=⎢⎥ ⎪ ⎪⎢⎥ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ （6）这个关系式唯一地确定一个变换，可以验证所确定的变换是以为矩阵的线性变换.总之。

线性变换的矩阵表⽰千⾥之⾏始于⾜下，重视基础才是本质。

在矩阵论中提到的线性变换是⼀个相对抽象的概念，先给出相关定义定义：设V 是数域K 上的线性空间，T 是V 到⾃⾝的⼀个映射，使对任意向量x ∈V ，V 中都有唯⼀的向量y 与之对应，则称T 是V 的⼀个变换或者算⼦，记Tx =y ，称y 为x 在T 下的象，⽽x 是y 的原象（象源）这个T 类似于数学分析中的函数y =f (x )，不过那⾥是数量函数，这⾥是向量函数。

如果变换T 满⾜⼀定的线性变换要求T (kx +ly )=kT (x )+lk (y )，则T 为V 的⼀个线性变换。

概念类⽐到数量函数，线性变换T 的也是很好理解的。

但是在具体计算过程中，我们怎么把抽象的概念具体化？这就涉及到线性变换的矩阵表⽰。

从定义⼊⼿的话，如果需要确定线性变换T ，则需要找到V 中所有向量在T 下的象。

事实上不需要这么⿇烦的。

V 中所有向量都可以由V 的基向量组(x 1,x 2,……,x n )线性表⽰，加上T 是V 的线性变换，则V 中所有象都可以由基象组(Tx_1,Tx_2,……,Tx_n)线性表⽰。

设T 是线性空间V n 的线性变换，x ∈V n ,且x 1,x 2,……,x n 是V n 的⼀个基，则x =a 1x 1+a 2x 2+……+a n x n Tx =a 1(Tx 1)+a 2(Tx 2)+……+a n T (x n )令Tx 1=a 11x 1+a 21x 2+……+a n 1x n Tx 2=a 12x 1+a 22x 2+……+a n 2x n ……Tx n =a 1n x 1+a 2n x 2+……+a nn x n 在处理具体问题时，采⽤矩阵乘法的形式表⽰上述公式组：T (x 1,x 2,……,x n )=(Tx 1,Tx 2,……,Tx n )=(x 1,x 2,……,x n )A 这个A 称为线性变换T 在V n 的基x 1,x 2,……,x n 下的矩阵，简称A 为T 的矩阵。

第七章 线性变换§7.1 线性变换的定义与判别一、线性变换的定义：定义1 设V 为数域P 上线性空间，A 为V 的一个变换(即V ⟶V 的映射)，若A 保持加法和数乘运算，即A (α+β)=A (α)+ A (β),∀α,β∈V ，A (kα)=k A (α),∀k ∈P ，则称A 为V 的一个线性变换.注记： 以后我们用花体拉丁字母A,B,C,...表示V 的线性变换，除了特别说明外，本章节中V 均指数域P 上有限维线性空间.例1.说明下列变换均为线性变换： (1)把V 中任一向量都映射为0（称为零变换，记作0）； (2)把V 中任一向量α映射为本身（恒等变换，记作E ）； (3)取定k ∈P ，把V 中的每一个向量α映射为kα（数乘变换，记作k ）.例2.判定下列规则σ是否为指定线性空间的线性变换： (1)ℝ,x -:σ(f (x ))=f′(x );(2)C ,a,b -: σ(f (x ))=∫f (t )dt x0;(3)P n×n : σ(A )=A +A ′,σ2(A )=SAT ，S,T 为固定二个n ×n 矩阵. (4)ℝ,x -n : σ1(f (x ))=xf (x ),σ2(f (x ))=f (x )+1. 解：可验证(1)-(3)均为线性变换，下面证明(1)： ∀ f (x )∈ℝ,x -，其导函数唯一确定，且f (x )∈ℝ,x -，因而σ为V ⟶V 的变换，即V 的一个变换，σ(f (x )+g (x ))=(f (x )+g (x ))′=f ′(x )+g ′(x )= σ(f (x ))+ σ(g (x )), ∀k ∈ℝ,σ(kf (x ))=(kf (x ))′=kf ′(x )=kσ(f (x )).(4): σ1与σ2均不是线性变换，取f (x )=x n−1+1=ℝ,x -n ，但σ1(f (x ))=xf (x )=x n +x ∉ℝ,x -n ， 因而σ1不是ℝ,x -n 的一个变换， σ2是ℝ,x -n 的一个变换，但运算不保持，因而不是线性变换.习题：P320、1例3.设α为通常几何空间ℝ3中固定的向量，把空间中每个向量η映射为η在α上的内映射（正投影），即Πα: η⟶(α∙η)(α∙α)α是ℝ3的线性变换，这里(α∙η),(α∙α)表示通常向量的内积.证：如图，Πα(η)=OD ⃗⃗⃗⃗⃗ =ηcos (η∙α)α|α|=(α∙η)(α∙α)α，唯一确定， 从而Πα为ℝ3的一个变换，如图，AC ⊥W(垂足为C)，OCD LA Wα1α2η因此L 与W 为ℝ3的子空间且ℝ3=W ⊕L ，令 η=α1+α2,α1=OD⃗⃗⃗⃗⃗ =Πα(η),α2∈W , δ=β1+β2,β1=Πα(δ)∈L,β2∈W ，则η+δ=(α1+β1)+(α2+β2),α1+β1∈L,α2+β2∈W ， 从而Πα(η+δ)=α1+β1=Πα(η)+Πα(δ)， 同理，Πα(kη)=kΠα(η).二、线性变换的性质： 设A 为V 的线性变换，则： (1) A (0)=0, A (−α)=−A (α),∀α∈V ; (2) A (k 1α1+k 2α2+⋯+k t αt )=k 1A (α1)+k 2A (α2)+⋯+k t A (αt ); (3) A 把线性相关的向量组映射为线性相关的向量组（反之不真）.2011-04-02A : V ⟶V 线性变换性质： (3) A 为V 中线性相关的向量组，映为V 中线性相关的向量组，即α1,α2,…,αs 相关⟹A (α1), A (α2),…, A (αs )相关;但A (α1), A (α2),…, A (αs )线性相关⇒α1,α2,…,αs 相关. 如A =0,∀ α∈V,α≠0, A (α)=0.(4)设α1,α2,…,αn 为V 的一个基，∀ α∈V,α=x 1α1+x 2α2+⋯+x n αn ⟹A (α)=A (x 1α1+x 2α2+⋯+x n αn ) 线性变换A 由V 中一个基中的像唯一确定;(5)设α1,α2,…,αn 为V 的一个基，则对V 中任一向量组β1,β2,…,βn 必存在一个线性变换 A : V ⟶V ，使得：A (αi )=βi ,1≤i ≤n ;证：作V ⟶V 映射：A (α)= x 1β1+x 2β2+⋯+x n βn ，其中：α=x 1β1+x 2β2+⋯+x n βn ,则A (αi )=βi ,1≤i ≤n ; 下证：A 为V 的线性变换：∀ α=x 1α1+x 2α2+⋯+x n αn ∈V,β=y 1α1+y 2α2+⋯+y n αn ∈V,A (α+β)= A .(x 1+y 1)α1+(x 2+y 2)α2+⋯+(x n +y n )αn /=(x 1+y 1)β1+(x 2+y 2)β2+⋯+(x n +y n )βn=(x 1β1+x 2β2+⋯+x n βn )+(y 1β1+y 2β2+⋯+y n βn ) = A (x 1α1+x 2α2+⋯+x n αn )+ A (y 1α1+y 2α2+⋯+y n αn )= A (α)+A (β)同理，∀k ∈P ，A (kα)=k A (α).§7.2 线性变换的运算为方便，引入记号：Hom (V,V )，它表示数域P 上线性空间V 的所有线性变换的集合。

线性变换的矩阵表示与坐标变换线性变换是线性代数中非常重要的概念之一。

它是指将一个向量空间中的向量按照一定的规则进行变换的操作。

线性变换可以通过矩阵进行表示，并且与坐标变换之间存在着紧密的联系。

一、线性变换的定义与性质线性变换是指满足以下两个性质的向量空间之间的映射：1. 对于任意的两个向量u和v，线性变换T(u+v) = T(u) + T(v)；2. 对于任意的标量k和向量u，线性变换T(ku) = kT(u)。

线性变换具有一些重要的性质：1. 零向量的线性变换结果仍为零向量：T(0) = 0；2. 线性变换保持向量空间中向量间的线性组合关系；3. 线性变换将向量空间中所有向量的零向量映射到目标向量空间的零向量。

二、矩阵表示线性变换线性变换可以通过矩阵来表示。

假设V和W是两个向量空间，维数分别为n和m，线性变换T: V→W可以表示为一个m×n的矩阵A。

对于向量v∈V，其在基底B={b1,b2,...,bn}下的坐标表示为[v]B =[x1,x2,...,xn]^T，T(v)在基底B'={b1',b2',...,bm'}下的坐标表示为[T(v)]B'= [y1,y2,...,ym]^T，则矩阵A表示了从基底B到基底B'的坐标变换关系。

具体而言，矩阵A的第j列为T(bj)在基底B'下的坐标表示的列向量。

通过矩阵向量乘法，可以得到变换后向量的坐标表示。

即：[T(v)]B' = A[v]B三、从坐标变换到线性变换以上我们讨论了线性变换如何通过矩阵表示，现在我们来看看如何从给定的坐标变换得到对应的线性变换矩阵。

考虑二维向量空间的坐标变换示例。

假设向量空间V的基底为B={e1,e2}，向量空间W的基底为B'={e1',e2'}。

将V中的向量v表示为[v]B = [x1,x2]^T，W中的向量T(v)表示为[T(v)]B' = [y1,y2]^T。

线性变换与矩阵表示
线性变换是线性代数中的重要概念，可以用来描述向量空间中的变换关系。

而矩阵表示则是将线性变换表示为矩阵的形式，便于计算和分析。

线性变换
线性变换是指保持向量空间中向量加法和数乘的运算规则不变的变换。

具体地，对于向量空间V中的两个向量u和v，以及标量c，线性变换T满足以下条件：
1. T(u + v) = T(u) + T(v)
2. T(cu) = cT(u)
这意味着线性变换保持向量加法和数乘的运算结果不变。

矩阵表示
线性变换可以通过矩阵表示来进行计算和分析。

对于向量空间V中的一个线性变换T，选择向量空间V的一组基{e1, e2, ..., en}，对于每个向量ei，线性变换T(ei)可以表示为一个线性组合：
T(ei) = a1i * e1 + a2i * e2 + ... + ani * en
其中aij为标量。

将向量空间V的基按列组成一个矩阵A：
A = [e1, e2, ..., en]
那么对于向量空间V中的任意向量x，线性变换T(x)可以表示为：
T(x) = A * x
其中x为列向量。

通过选择合适的基和矩阵A，可以将线性变换T表示为矩阵的形式，通过矩阵乘法进行计算和分析。

总结
线性变换是保持向量空间中向量加法和数乘的运算规则不变的变换，矩阵表示则是将线性变换表示为矩阵形式。

通过选择合适的基和矩阵，线性变换可以方便地用矩阵乘法进行计算和分析。

对于线性代数的学习和应用，理解线性变换和矩阵表示是非常重要的基础知识。

向量空间中的线性变换和矩阵变换在线性代数中，向量空间是一个重要的概念，它是一组元素的集合，这些元素可以相加和相乘，满足一些特定的规则。

线性变换和矩阵变换则是向量空间中的基本操作，它们有着重要的应用，例如在机器学习和物理学等领域中。

一、线性变换的定义和性质线性变换是指将一个向量空间中的向量映射到另一个向量空间中的向量的变换。

严格地说，线性变换应该满足以下两个性质：1. 对于任意向量a和b，有T(a+b) = T(a) + T(b)；2. 对于任意向量a和标量k，有T(ka) = kT(a)。

这两个性质分别对应向量的加法和乘法。

线性变换不仅用于向量空间中，还可以应用于其他数学领域，例如微积分和拓扑学等。

线性变换有很多重要的性质，例如：1. 线性变换可以用矩阵表示；2. 线性变换保持向量空间的结构不变；3. 线性变换可以有逆变换，逆变换也是线性变换。

这些性质使得线性变换成为了一个非常常见的数学工具。

二、矩阵变换的定义和性质矩阵变换是指将一个向量空间中的向量用矩阵相乘的方式进行变换。

矩阵变换的定义可以表示为：T(x) = Ax其中T表示矩阵变换，A表示一个矩阵，x表示一个向量。

矩阵变换中的矩阵A具有很多特殊的性质，例如：1. 矩阵A可以表示线性变换；2. 矩阵A的行列式为0时，矩阵A不可逆，否则可逆；3. 矩阵A的秩表示变换后空间的维度；4. 矩阵A的特征值和特征向量可以用于描述变换的性质。

矩阵变换可以方便地进行计算，并且可以应用于很多实际问题中。

三、线性变换与矩阵变换的关系线性变换和矩阵变换有着密切的关系。

事实上，线性变换可以用矩阵表示，也可以通过矩阵变换来实现。

具体来说，任何一个线性变换T都可以表示成矩阵变换的形式：T(x) = Ax其中x表示一个向量，A表示一个矩阵。

如果我们在一个标准基下进行求解，那么矩阵A的每一列就是变换后的基向量的坐标。

同时，任何一个矩阵变换也可以表示成线性变换的形式。

对于任意矩阵A，可以定义一个线性变换T，使得：T(x) = Ax这里的x同样表示一个向量。