当前位置：文档之家 › 离散数学--几种特殊的图

离散数学--几种特殊的图

  • 格式：ppt
  • 大小：910.01 KB
  • 文档页数：26

下载文档原格式

  / 26

合集下载

离散数学课件第十章 几种图的介绍

离散数学课件第十章 几种图的介绍

前言
在图论的历史中，还有一个最著名的问题——四色猜想。这个猜想说 ，在一个平面或球面上的任何地图能够只用四种颜色来着色，使得没 有两个相邻的国家有相同的颜色。每个国家必须由一个单连通域构成 ，而两个国家相邻是指它们有一段公共的边界，而不仅仅只有一个公 共点。四色猜想有一段有趣的历史。每个地图可以导出一个图，其中 国家都是点，当相应的两个国家相邻时这两个点用一条线来连接。所 以四色猜想是图论中的一个问题。它对图的着色理论、平面图理论、 代数拓扑图论等分支的发展起到推动作用。
10.2 哈密尔顿图
定理10.7 设图 G是具有n（≥3）个结点的无向简单图，如果 G中每一 对结点度数之和大于等于n-1，则在 G 中存在一条哈密尔顿路。 定理10.8 若G是具有n（≥3）个结点的无向简单图，对于G中每一对不
相邻的结点 u , v 均有 d(u)d(v)≥n，则G是一个哈密尔顿图。
图10.6
10.2 哈密尔顿图
定义10.3 给定无向图G，图G中包含其所有顶点的简单开路径称为图G 的哈密尔顿路径，图G中包含其所有顶点的简单闭路径称为G的哈密尔顿 回路。具有哈密顿回路的图称为哈密尔顿图。
由定义可知哈密尔顿圈与哈密尔顿路通过图G中的每个结点一次且仅 一次，例如图10.6（b）就是哈密尔顿图（哈密尔顿圈用实线标出）。
10.2 哈密尔顿图
例10.4 图10.8（a）不是哈密尔顿图。
图10.8
图10.8（a）中共有9个结点，如果取结点集S={3个白点}，即 S 3 。而
这时 (GS)4（如图（b））。这说明图10.8（a）不是哈密尔顿图。但要注
意若一个图满足定理10.6的条件也不能保证这个图一定是哈密尔顿图，如图10.8 （c）。
定理10.7和10.8都是充分条件，即满足这些条件的图一定是哈密尔顿图。但不是所 有的哈密尔顿图都满足这些条件。例如图10.9是哈密尔顿图,但它不满足上述定理的 条件。

武汉大学《离散数学》课件-第5章

武汉大学《离散数学》课件-第5章
(1) 若i(1il), vi1, vi是ei的端点(对于有向图, 要求vi1是始点,
vi是终点), 则称为通路, v0是通路的起点, vl是通路的终点, l为通路的长度. 又若v0=vl，则称为回路.
(2) 若通路(回路)中所有顶点(对于回路, 除v0=vl)各异，则称为 初级通路(初级回路).初级通路又称作路径, 初级回路又称 作圈.
32
通路与回路(续)
定理 在n阶图G中，若从顶点u到v（uv）存在通 路，则从u到v存在长度小于等于n1的通路. 推论 在n阶图G中，若从顶点u到v（uv）存在通 路，则从u到v存在长度小于等于n1的初级通路.
定理 在一个n阶图G中，若存在v到自身的回路，则 一定存在v到自身长度小于等于n的回路. 推论 在一个n阶图G中，若存在v到自身的简单回 路，则存在v到自身长度小于等于n的初级回路.
D
D[{e1,e3}]
D[{v1,v2}]
26
补图
定义 设G=<V,E>为n阶无向简单图，以V为顶点集, 所有使G成为完全图Kn的添加边组成的集合为边集 的图，称为G的补图，记作 G . 若G G , 则称G是自补图.
例 对K4的所有非同构子图, 指出互为补图的每一对 子图, 并指出哪些是自补图.
图论
1
图论部分
第5章 图的基本概念 第6章 特殊的图 第7章 树
2
第5章 图的基本概念
5.1 无向图及有向图 5.2 通路, 回路和图的连通性 5.3 图的矩阵表示 5.4 最短路径, 关键路径和着色
3
5.1 无向图及有向图
▪ 无向图与有向图 ▪ 顶点的度数 ▪ 握手定理 ▪ 简单图 ▪ 完全图 ▪ 子图 ▪ 补图
27
5.2 通路、回路、图的连通性

离散数学课件15欧拉图与哈密顿图

离散数学课件15欧拉图与哈密顿图
证明 若G是平凡图，结论显然成立。
下面设G为非平凡图，设G是m条边的n阶无 向图，
并设G的顶点集V＝{v1,v2,…,vn}。 必要性。因为G为欧拉图，所以G中存在欧 拉回路，
设C为G中任意一条欧拉回路，vi,vj∈V， v2i0,2v0/7j/都23 在C上，
定理15.1的证明
充分性。由于G为非平凡的连通图可知，G中边数 m≥1。
2020/7/23
半欧拉图的判定定理
定理15.2 无向图G是半欧拉图当且仅当G是连通的 ，且G中恰有两个奇度顶点。
证明 充分性。设G的两个奇度顶点分别为u0和v0， 对G加新边（u0,v0），得G ＝G∪(u0,v0)， 则G 是连通且无奇度顶点的图， 由定理15.1可知，G 为欧拉图， 因而存在欧拉回路C ，而C＝C -(u0,v0)为G中一 条欧拉通路， 所以G为半欧拉图。
并2行从020/7遍/C23 上G 的i中某的顶欧点拉vr回开路始C行遍i，，i＝每1遇,2,到…v,s*j，i，最就后
半欧拉图的判定定理
定理15.2 无向图G是半欧拉图当且仅当G是连通的 ，且G中恰有两个奇度顶点。
证明 必要性。设G是m条边的n阶无向图，因为G为 半欧拉图， 因而G中存在欧拉通路(但不存在欧拉回路)， 设Г＝vi0ej1vi1…vim-1ejmvim为G中一条欧拉通路， vi0≠vim。 v∈V(G)，若v不在Г的端点出现，显然d(v)为偶 数， 若v在端点出现过，则d(v)为奇数，
欧拉对物理力学、天文学、弹道学、航海学、建筑学、音 乐都有研究！有许多公式、定理、解法、函数、方程、常数等 是以欧拉名字命名的。欧拉写的数学教材在当时一直被当作标 准教程。19世纪伟大的数学家高斯曾说过“研究欧拉的著作永 远是了解数学的好方法”。欧拉还是数学符号发明者，他创设 的许多数学符号，例如π，i，e，sin，cos，tg，Σ，f (x)等等， 至今202沿0/7/2用3 。

离散数学图论

离散数学图论

图的同构
对于两个图G和G,如果它们的顶点之间存在一一对应关系，而 且这种关系保持了两顶点间的邻接关系（在有向图中，还保 持了边的方向）和边的重数，则这两个图是同构的。
同构的图除了点和边的名称不同外，实际上代表同样的组织结 构。 由于图形的顶点位置和连线长度都可任意选择，同一个图可能 画出不同的形状来，因而引出图同构的概念。 如下面两个图同构:
32

Zhengjin,Central South University
33
8.3 图的矩阵表示
定义 1 设 G=<V,E> 是无向图，且无平行边，其中 V={v1,v2,…,vn}, 定义一个nn的矩阵A,其中各元素aij为：
1 如果<vi,vj>E aij=
0 如果<vi,vj>E
称这样的矩阵为图 G 的邻接矩阵。（即若两点间有边相连，则对应 的为1，无边相连，则对应的为0）
Zhengjin,Central South University
23
Zhengjin,Central South University
24
Zhengjin,Central South University
25
Zhengjin,Central South University
26
Zhengjin,Central South University
连通图
定义3 设G=<V,E>，且vi,vjV.如果存在从vi到vj的路径，则 称从vi可达vj. (因vi 可看作长度为 0的路径，即从vi可达vi, 即任何顶点都是自己可达)。
定义4 在无向图中，如果任何两个顶点都可达，则称之为连通图。 如果G的子图是连通图，称之为连通子图。 一个无向图如果不是连通图，就是由若干个连通子图构成。 定义5 在有向图G中，如果在任两个顶点中，存在从一个顶点到 另一个顶点的路径，则称图 G为单向连通的。如果在 G中，任 何两个顶点都互相可达，则称G为强连通的。如果它的基础图 （底图）是连通的，则称之为弱连通的。 显然，强连通的，也是单向连通的，也是弱连通的。

离散数学--第十五章 欧拉图和哈密顿图

离散数学--第十五章 欧拉图和哈密顿图
13
实例
在上图中， (1),(2) 是哈密顿图; (3)是半哈密顿图; (4)既不是哈密顿图，也不是半哈密顿图，为什么？
14
无向哈密顿图的一个必要条件
定理15.6 设无向图G=<V,E>是哈密顿图，对于任意V1V且 V1，均有 p(GV1) |V1|
证 设C为G中一条哈密顿回路。
当V1顶点在C上均不相邻时， p(CV1)达到最大值|V1|，
求图中1所示带权图k29主要内容欧拉通路欧拉回路欧拉图半欧拉图及其判别法哈密顿通路哈密顿回路哈密顿图半哈密顿图带权图货郎担问题基本要求深刻理解欧拉图半欧拉图的定义及判别定理深刻理解哈密顿图半哈密顿图的定义
第十五章 欧拉图与哈密顿图
主要内容
➢ 欧拉图 ➢ 哈密顿图 ➢ 带权图与货郎担问题
1
15.1 欧拉图
大时，计算量惊人地大
27
例6 求图中(1) 所示带权图K4中最短哈密顿回路.
(1)
(2)
解 C1= a b c d a,
W(C1)=10
C2= a b d c a,
W(C2)=11
C3= a c b d a,
W(C3)=9
可见C3
(见图中(2))
是最短的，其权为9. 28
第十五章 习题课
主要内容 欧拉通路、欧拉回路、欧拉图、半欧拉图及其判别法 哈密顿通路、哈密顿回路、哈密顿图、半哈密顿图 带权图、货郎担问题
点.
由vi 的任意性，结论为真. 充分性 对边数m做归纳法（第二数学归纳法）. (1) m=1时，G为一个环，则G为欧拉图. (2) 设mk（k1）时结论为真，m=k+1时如下证明：
5
从以上证明不难看出：欧拉图是若干个边不重的圈之 并，见示意图3.

《离散数学》图论 (上)

《离散数学》图论 (上)
12
无向图与有向图
v2
e1
e2
e3
v3
e4
v1
e5 (e1)={( v42, v24 )}
v4
(e2)={( v32, v23 )} (e3)={( v3, v4 )}
(e4)=({ v43, v34 )}
(e5)=({ v4,}v4 )
13
无向图与有向图
A B C
D E F
14
无向图与有向图
第八章 图论
第八章 图论
§8.1 基本概念
§8.1.1 无向图、有向图和握手定理 §8.1.2 图的同构与子图 §8.1.3 道路、回路与连通性 §8.1.4 图的矩阵表示
§8.2 欧拉图 §8.3 哈密尔顿图 §8.4 平面图 §8.5 顶点支配、独立与覆盖
2
无向图与有向图
3
无向图与有向图
一个无向图（undirected graph, 或graph） G 指一个三元组 (V, E, )，其中
vV
vV
24
特殊的图
假设 G=(V, E, ) 为无向图，若 G 中所有 顶点都是孤立顶点，则称 G 为零图（null graph）或离散图（discrete graph）；若 |V|=n，|E|=0，则称 G 为 n 阶零图 所有顶点的度数均相等的无向图称为正 则图（regular graph），所有顶点的度数 均为 k 的正则图称为k度正则图，也记作 k-正则图 注：零图是零度正则图
19
握手定理
定理（图论基本定理/握手定理）
假设 G=(V, E, ) 为无向图，则deg(v) 2 E ， vV
即所有顶点度数之和等于边数的两倍。
推论
在任何无向图中，奇数度的顶点数必是偶 数。

离散数学欧拉图

离散数学欧拉图

欧拉图的判断方法
在计算机科学中，欧拉图还可用于描述有向图（Directed Graph） 的路径问题，例如，欧拉路径（Euler Path）和欧拉回路 （Eulerian Circuit） 欧拉路径是指一条路径包含图中所有的边恰好一次。而欧拉回路 是指一条闭合路径包含图中所有的边恰好一次。一个图存在欧拉 回路当且仅当该图的每条边的权值都是偶数 在复杂网络理论中，欧拉图可以用于描述网络的结构和行为，例 如社交网络、互联网、脑科学等领域的网络。在这些网络中，节 点代表个体或事件，边代表它们之间的联系或互动。通过对这些 网络进行分析，可以发现它们的结构和行为规律，从而更好地理 解和预测网络的行为 此外，欧拉图还可以用于构建和分析化学分子的结构。在化学中， 欧拉图是一种用于表示分子结构的图形，其中顶点代表原子，边 代表化学键。通过分析欧拉图，可以了解分子的结构、性质和反 应行为等信息
在这个图中，每个顶点都有偶数条边连接，并且存在一条路径（A---B---C---D---E---F--A）包含所有顶点，且每个边都只经过一次
欧拉图的性质
欧拉图的性质
欧拉图具有以下性质 欧拉图的边数一定是偶数 欧拉图一定是连通的（即所有顶点之间都有路径相连） 欧拉图中的任何两个顶点之间都有偶数条边相连 如果一个图是欧拉图：那么它的每个子图都是欧拉图
欧拉图的判断方法
对于一个连通图：如果它的所有边都可以被一个2-因子覆盖（即每个顶点都在两个2因子中出现），那么这个图是欧拉图。否则，这个图不是欧拉图 对于一个连通图：如果它可以被分解成两个子图，每个子图都包含所有的顶点并且所 有边的数量相同，那么这个图是欧拉图。否则，这个图不是欧拉图
对于一个连通图：如果它可以被分解成两个子图，每个子图的边数相同并且所有顶点 的度数相同（即每个顶点的度数都是偶数），那么这个图是欧拉图。否则，这个图不 是欧拉图。除了以上方法，还有一些复杂的方法可以判断一个图是否为欧拉图，例如 通过检查图的子图或者通过编程实现图的遍历算法。这些方法需要更深入的图论知识 和计算机科学知识，但它们可以提供更准确和高效的结果

离散数学平面图

离散数学平面图
则满足欧拉公式 v – e + r = 2 即：6-9+r=2，解得r=5
又因为任取K3,3中三个结点，至少有两个点不邻接， 所以不能组成一个面，即K3,3中任何 一个面至少由四条边围成，即：所有面 的次数之和deg(r) >=4r=20 又由定理1知：deg(r)=2|E|=18 即18>=20矛盾不。论怎所么以画，K总3,有3不交是叉点平面图。
❖ 平面图基本性质
设G是一个有v个结点e条边的连通简单平面图，若v3, 则：e<=3v-6。等价于: 若不满足e<=3v-6，则G不是连通平面图。
例题：证明k5图不是平面图。
K5图中,v=5,e=10,10 3*v-6=35-6=9
但定理的条件只是必要条件。
如K3,3中v= 6,e =9, e<3v-6=12 满足条件，但K3,3不是平面图。
离散数学
❖ 图论
1 图的基本概念 2 路与回路 3 图的矩阵表示 4 欧拉图与汉密尔顿图 5 平面图 6 对偶图与着色 7 树与生成树
❖ 平面图基本概念
定义1：设G=<V,E>是一个无向图，如果能把G的所有结点和
边画在平面上，且使得任何两条边除了端点外没有其他的交点， 就称G是一个平面图。
(1)
G为k条边，再添加一条边，只有下述两种情况：
面数不变 点树加1 边数加1
点数不变 面数加1 边数加1
(Vk+1)-(ek+1)+rk=2成立
(Vk)-(ek+1)+(rk+1)=2成立
通过上述归纳法证明欧拉公式v-e+r=2成立。
❖ 平面图基本性质
例1：证明K3,3不是平面图
证：假设K3,3是平面图，

离散数学图的概念与表

离散数学图的概念与表
离散数学图的概念与表
本课件PPT仅供大家学习使用 学习完请自行删除，谢谢！ 本课件PPT仅供大家学习使用 学习完请自行删除，谢谢！ 本课件PPT仅供大家学习使用 学习完请自行删除，谢谢！ 本课件PPT仅供大家学习使用 学习完请自行删除，谢谢！
16.1 图的根本概念
什么是图?可用一句话概括，即：图是用点 和线来刻划离散事物集合中的每对事物间以某 种方式相联系的数学模型。
(1) 如果V2 V1和E2 E1，那么称G2为G1的子 图，记为G2 G1。
(2) 如果V2 V1，E2 E1且E2≠E1，那么称G2 为G1的真子图，记为G2 G1。
(3) 如果V2=V1，E2 E1，那么称G2为G1的生
成子图，记为G2
G1。
v2 v1
定义16.1.9 设图G2=<V2，E2>是图G1=<V1， E1> 的 子 图 。 假 设 对 任 意 结 点 u 和 v ， 如 果 〔u ， v〕 ∈E1，有〔u，v〕∈E2，那么G2由V2唯一地确定， 并 称 G2 是结 点 集 合 V2 的 诱导子 图 ， 记作 <V2>或 G 〔V2〕；如果G2无孤立结点，且由E2所唯一确定，那 么称G2是边集E2的诱导子图，记为<E2>或G〔E2〕。
如果把图G中的弧或边总看作联结两个结点，那么 图G可简记为G=<V，E>，其中V是非空结点集，E是 联结结点的边集或弧集。
定义16.1.2 在图G=<V，E>中，如果每条边都 是弧，该图称为有向图；假设每条边都是无向边，该图 G称为无向图；如果有些边是有向边，另一些边是无向 边，图G称为混合图。
定义16.1.3 在图G=<V，E>中，如果任何两结 点间不多于一条边(对于有向图中，任何两结点间不多 于一条同向弧)，并且任何结点无环，那么图G称为简单 图；假设两结点间多于一条边(对于有向图中，两结点 间多于一条同向弧)图G称为多重图，并把联结两结点之 间的多条边或弧，称为平行边或弧，平行边或弧的条数 称为重数。

离散数学离散数学第8章 一些特殊的图 PPT课件

离散数学离散数学第8章 一些特殊的图 PPT课件

在23岁时，他发表了他还是一个17岁的孩子时作出的“奇怪的发 现”，…即《光线系统理论》第一部分，这是一篇伟大的杰作，它对于 光学，就象拉格朗日的《分析力学》之于力学。
哈密尔顿最深刻的悲剧既不是酒精，也不是他的婚姻，而是他顽固地
相信，四元数是解决物质宇宙的数学关键。…从来没有一个伟大的数学
家这样毫无希望地错误过。
2
1
3
4
(2) 有限面与无限面：面积有限的区域称为有 限面(或内部面)，否则为无限面(或外部面) 。 上图中，面4是无限面。
7/1/2020 9:05 PM
第四部分：图论（授课教师：向胜军）
24
(3) 面的次数等于面边界的边数(注意：悬挂边算2 次)，记为deg(R).
(4) 平面图中面的次数之和等于边数m的两倍，即
d(u)+d(v)≥n-1 则G是半哈密尔顿图。
注意:
此定理条件显然不是必要条件，如n≥6的n边形，对于 任意不相邻的顶点u, v, d(u)+d(v)=4，4<n-1，而n边形显 然有哈密尔顿通路。
7/1/2020 9:05 PM
第四部分：图论（授课教师：向胜军）
18
哈密尔顿图的充分条件
❖ 设G是n(n≥3)阶无向简单图，若G中 任意不相邻的顶点对u,v均满足： d(u)+d(v)≥n 则G是哈密尔顿图。
a
bc
d
e
f g
h
i j
k
l
ba
d
g
e j
f
l
b
a
c
d
g
j
i
e
h
f
k
7/1/2020 9:05 PM

离散数学及其应用课件：特殊图

离散数学及其应用课件：特殊图

特殊图
图6-7 基于用户的协同过滤
特殊图
基于物品的协同过滤算法与基于用户的协同过滤算法类 似,只是将商品和用户互换。通过计算不同用户对不同物品 的评分获得物品间的关系,基于物品间的关系对用户进行相 似物品的推荐。举个例子:若用户A 购买了商品a 和b,那么说 明a 和b 的相关度较高。当用户B 也购买了商品a,就可以推 断用户 B 也有购买商品b 的需求。该算法可描述如图 6-8所示。
特殊图
图6-6-题设对应的二部图
特殊图
基于用户的协同过滤算法是通过用户的历史行为(如商 品购买、收藏、内容评价或分享)数据发现用户对商品或内 容的喜欢程度,并对这些喜好进行度量和打分,然后根据不同 用户对相同商品或内容的偏好程度计算用户之间的关系,在 有相同喜好的用户之间进行商品推荐。比如:若A,B 两个用户 都购买了x,y,z 三本图书,并且给出了5星好评,那么A,B 属于同 一类用户,可以将A 看过的书w 推荐给用户B,也可以将B 买过 的商品β推荐给用户A。该算法可描述如图6-7所示。
特殊图
特殊图
解 表6-1中的关系可以用一个二部图G=<V1,V2,E>表示, 如图6-6所示,其中V1={A1,A2,A3,A4,A5}表示5名应届毕业 生,V2={C1,C2,C3,C4,C5}表示五座西部城市。因为A1、A2、A3、 A4、A5 关联的边数分别为2、2、2、3、3,所以每个顶点至少 关联t=2条边,而C2、C3 关联了4条边,4>2,所以不满足t条件,于 是找不到合适的匹配,使得每个人都能去到自己想去的城市。
特殊图 例6.6-考虑图6-16,判断它们是否是欧拉图或半欧拉图,为
什么?
图6-16-有向图的欧拉图判定
特殊图

离散数学-几种特殊图

离散数学-几种特殊图

第四讲几种特殊图一、小结本讲主要介绍欧拉图与汉密尔顿图、平面图与着色以及一些相关的概念与结论等。

1．欧拉图的概念给定无孤立结点图G ，若存在一条路经过图G的每条边一次且仅一次，则该路称为欧拉路；若存在一条回路经过图G的每条边一次且仅一次，在该回路称为欧拉回路；具有欧拉回路的图称为欧拉图；具有欧拉路但无欧拉回路的图称为半欧拉图。

规定平凡图为欧拉图。

2．欧拉路与回路存在的充要条件无向图G具有一条欧拉路，当且仅当G是连通的，且有零个或2个奇数度数的结点。

无向图G具有一条欧拉回路，当且仅当G是连通的，并且它的结点度数都是偶数的。

3．汉密尔顿图的概念给定图G ，若存在一条路经过图G的每个结点一次且仅一次，则该路称为汉密尔顿路；若存在一条回路经过图G的每个结点一次且仅一次，则该回路称为汉密尔顿回路；具有汉密尔顿回路的图称为汉密尔顿图；具有汉密尔顿路但无汉密尔顿回路的图称为半汉密尔顿图。

4．汉密尔顿回路存在的必要条件若图G=<V,E>中具有一条汉密尔顿回路，则对于结点集V的每个非空子集S均有W(G-S)￡|S|成立，其中W(G-S)是（G-S）中连通分支数。

5．汉密尔顿路存在的充分条件设G=<V，E>是具有n个结点的简单图，若在G中每一对结点度数之和大于等于n - 1，则在G中存在一条汉密尔顿路。

6．平面图的概念设G=<V，E>是一个无向图，如果能把G的所有结点与边画在平面上，并且使得任何两条边除端点外没有其他的交点，则称G是一个平面图（也称可平面图）.显然平面图的边与边只在结点处相交。

将平面图“图示在平面上”，有时也说成“将平面图嵌入一平面”。

7．平面图的面、边界、面的次数等概念设G是一个连通平面图，如果由图中的边所包围的一个区域内既不包含图的结点，也不包含图的边，则这个区域称为G的一个面，包围该面的所有边所构成的回路称为这个面的边界。

面r的边界的回路长度称为该面的次数，记为deg(r)。

离散数学 第4-5章

离散数学 第4-5章

例题6： 1 2 带权图如右，求图的最小生成树 6 5 e 4 解：选取含最大边(c,d)的回路cdec， 3 删去其中权数最大的边(c,d)，然后 b 1 c 再选取含最大边(a,b)的回路abea，删去其中权数最 大的边(a,b)，再选取含最大边(c,e)的回路bceb，删 去其中权数最大的边(c,e)，再选取含最大边(a,d)的 回路adea，删去其中权数最大的边(a,d)，即得最小 a 生成树。 d 1 T=<{a,b,c,d,e},{(c,b),(b,e),(e,a),(e,d)}>。 e 2
汉密尔顿图的判定：
必要条件但不是充分条件定理： 1。在汉密尔顿图G中删除结点集V1后，G－V1的 连通分支数W (G V1 ) | V 1|。不满足这一条件的图一 定不是汉密尔顿图。 充分条件但不是必要条件定理： 2。如果无向简单图G中任何一对结点的度数之和 都大于等于结点数，则G中存在一条汉密尔顿回路。
例题4： 下列结论不正确的是（ D ）。 A）无向连通图G是欧拉图的充分必要条件是G不 含奇数度结点 B）非平凡连通图G有欧拉通路的充分必要条件是 G最多有两个奇数度结点 C）有向连通图D是欧拉图的充分必要条件是D的 每个结点的入度等于出度 D）有向连通图D是有向欧拉图的充分必要条件是 除两个结点外，每个结点的入度等于出度
例题3： 设G是无向图如右(彼得森图)， 说明G不是欧拉图。 解：因为无向图G中所有的 结点的度数全为奇数，所以 G不是欧拉图。 2。无向连通图存在欧拉通路的充分必要条件是图 中只有两个奇数度的结点。 3。当n为奇数时，完全无向图Kn是欧拉图。例 如K3、K5等。 4。当n为偶数时，完全无向图Kn不是欧拉图，也 不存在欧拉通路。
g
例题8： 设图G如右，作图G 的嵌入图，说明图G是 平面图。 解： 图G的嵌入图如下， 故图G是平面图。

离散数学PPT【共34张PPT】

离散数学PPT【共34张PPT】
15
18.4 点着色
定义17.9 (1) 图G的一种点着色——给图G的每个顶点涂上一种颜色，
使相邻顶点具有不同颜色 (2) 对G进行k着色（G是k-可着色的）——能用k种颜色给G
的顶点着色 (3) G的色数(G)=k——G是k-可着色的，但不是(k1)-可着色
的.
16
关于顶点着色的几个简单结果
定理17.19 (G)=1当且仅当G为零图 定理17.20 (Kn)=n 定理17.21 若G为奇圈或奇阶轮图，则(G)=3，若G为偶阶轮 图，则(G)=4. 定理17.22 若G的边集非空，则(G)=2当且仅当G为二部图.
路径 (7) M的交错圈——由M与EM中的边交替出现构成的G中圈
上图中，只有第一个图存在完美匹配
8
可增广路径及交错圈
(1)
(2)
(3)
设红色边在匹配M中，绿色边不在M中，则图(1)中的两条路 径均为可增广的交错路径；(2)中的全不是可增广的交错路 径；(3)中是一个交错圈. 不难看出，可增广交错路径中，不在M中的边比在M中的边 多一条. 交错圈一定为偶圈.
立集 (3) 最大点独立集——元素最多的点独立集 (4) 点独立数——最大点独立集中的元素个数，记为0
(1)
(2)
在图中，点独立数依次为2, 2, 3.
(3)
2
极大独立集与极小支配集
定理18.1 设G=<V,E>中无孤立点，则G的极大点独立集都是 极小支配集. 证明线索： (1) 设V*为G的极大点独立集，证明它也是支配集.
定理17.28 偶圈边色数为2，奇圈边色数为3. 定理17.29 (Wn) = n1, n4. 定理17.30 二部图的边色数等于最大度. 定理17.31 n为奇数（n1）时，(Kn)=n；
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
例如 当r≠s时, Kr,s不是哈密顿图
推论 有割点的图不是哈密顿图
15
实例
例2 证明下述各图不是哈密顿图:
(a)
(b)
(c) 中存在哈密顿通路
(c)
16
实例
例3 证明右图不是哈密顿图 证 假设存在一条哈密顿回路, a,f,g是2度顶点, 边(a,c), (f,c)和 (g,c)必在这条哈密顿回路上, 从而点c出现3次, 矛盾.
说明： 哈密顿通路是初级通路 哈密顿回路是初级回路 有哈密顿通路不一定有哈密顿回路 环与平行边不影响图的哈密顿性
14
哈密顿图的必要条件
定理6.10 若无向图G=<V,E>是哈密顿图, 则对于V的任意 非空真子集V1均有 p(GV1)|V1|. 证 设C为G中一条哈密顿回路, 有p(CV1) |V1|. 又因为 CG, 故 p(GV1) p(CV1) |V1|.
6.4 几种特殊的图
• 6.4.1 二部图
– 二部图的充要条件
• 6.4.2 欧拉图
– 欧拉回路(通路)及其存在的充要条件
• 6.4.3 哈密顿图
– 哈密顿回路(通路)及其存在的必要条件和充 分条件
• 6.4.4 平面图
1
二部图
定义6.19 设无向图 G=<V,E>, 若能将V 分成V1 和 V2 使得 V1V2=V, V1V2=, 且G中的每条边的两个端点都一个 属于V1, 另一个属于V2, 则称G为二部图, 记为<V1,V2,E>, 称V1和V2为互补顶点子集. 又若G是简单图, 且V1中每个顶 点均与V2中每个顶点都相邻, 则称G为完全二部图, 记为 Kr,s, 其中r=|V1|, s=|V2|.
8
欧拉图判别定理
定理6.8 无向图G具有欧拉回路当且仅当G是连通的且无 奇度顶点. 无向图G具有欧拉通路、但没有欧拉回路当且仅当G是连 通的且有2个奇度顶点, 其余顶点均为偶度数的. 这2个奇 度顶点是每条欧拉通路的端点.
推论 无向图G是欧拉图当且仅当G是连通的且无奇度顶点
9
实例
无欧拉通路
欧拉图
K23
K33
2
二部图的判别定理
定理6.7 无向图G=<V,E>是二部图当且仅当G中无奇长度 的回路
证 必要性. 设G=<V1,V2,E>是二部图, 每条边只能从V1到 V2, 或从V2到V1, 故任何回路必为偶长度. 充分性. 不妨设G至少有一条边且连通. 取任一顶点u, 令
V1={v | vV d(v,u)为偶数}, V2={v | vV d(v,u)为奇数} 则V1V2=V, V1V2=. 先证V1中任意两点不相邻. 假设存 在s,tV1, e=(s,t)E. 设Γ1, Γ2分别是u到s,t的短程线, 则 Γ1eΓ2是一条回路, 其长度为奇数, 与假设矛盾. 同理可 证V2中任意两点不相邻.
3
实例
非二部图
非二部图
4
实例
例1 某中学有3个课外活动小组:数学组, 计算机组和生物 组. 有赵,钱,孙,李,周5名学生, 问分别在下述3种情况下, 能 否选出3人各任一个组的组长? (1) 赵, 钱为数学组成员, 赵,孙,李为计算机组成员, 孙,李, 周为生物组成员. (2) 赵为数学组成员, 钱,孙,李为计算机组成员, 钱,孙,李,周 为生物组成员. (3) 赵为数学组和计算机组成员, 钱,孙,李,周为生物组成员.
5
实例(续)
解
数计生
数计生
数计生
赵钱孙李周 赵钱孙李周 赵钱孙李周
(1)
(2)
(3)
(1),(2)有多种方案, (3) 不可能
6
欧拉图
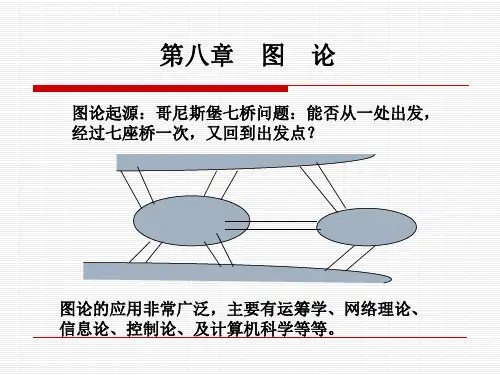
哥尼斯堡七桥
7
欧拉图
欧拉通路:经过所有边且每条边恰好经过一次的通路 欧拉回路:经过所有边且每条边恰好经过一次的回路 欧拉图:有欧拉回路的图
说明： 上述定义对无向图和有向图都适用 规定平凡图为欧拉图 欧拉通路是简单通路, 欧拉回路是简单回路 环不影响图的欧拉性
推论 有向图D是欧拉图当且仅当D是连通的且所有顶点的 入度等于出度.
11
实例
欧拉图
无欧拉通路
无欧拉通路
有欧拉通路 无欧拉回路
无欧拉通路
有欧拉通路 无欧拉回路
12
周游世界问题(W.Hami路与哈密顿通路
哈密顿通路: 经过图中所有顶点一次且仅一次的通路. 哈密顿回路: 经过图中所有顶点一次且仅一次的回路. 哈密顿图: 具有哈密顿回路的图.
19
推论 设G是n(n3)阶无向简单图, 若(G)n/2, 则G是哈密
顿图
当n3时, Kn是哈密顿图; 当r=s2时, Kr,s是哈密顿图.
定理6,12 设D是n(n2)阶有向图, 若略去所有边的方向后 所得无向图中含子图Kn, 则D中有哈密顿通路.
18
应用
例4 有7个人, A会讲英语, B会讲英语和汉语, C会讲英语、
d f
a
b c
g e
此外, 该图满足定理6.10的条件, 这表明此条件是必要、 而不充分的.
又, 该图有哈密顿通路.
17
存在哈密顿回路(通路)的充分条件
定理6.11 设G是n(n3)阶无向简单图, 若任意两个不相邻 的顶点的度数之和大于等于n1, 则G中存在哈密顿通路; 若任意两个不相邻的顶点的度数之和大于等于n, 则G中 存在哈密顿回路, 即G为哈密顿图.
意大利语和俄语, D会讲日语和汉语, E会讲德语和意大利
语, F会讲法语、日语和俄语, G会讲法语和德语. 问能否将
他们沿圆桌安排就坐成一圈, 使得每个人都能与两旁的人
交谈?
解 作无向图, 每人是一个顶点,
GA
2人之间有边他们有共同的语言. F
B
ACEGFDBA是一条哈密顿回路,
E
D
C
按此顺序就坐即可.
欧拉图
有欧拉通路 非欧拉图
有欧拉通路 非欧拉图
无欧拉通路
10
欧拉图判别定理(续)
定理6.9 有向图D有欧拉回路当且仅当D是连通的且所有 顶点的入度等于出度. 有向图D有欧拉通路、但没有欧拉回路当且仅当D是连通 的且有一个顶点的入度比出度大1、一个顶点的入度比出 度小1, 其余的顶点的入度等于出度.