离散数学习题课图论

习 题 六1．设G 是一个无回路的图, 求证：若G 中任意两个顶点间有惟一的通路, 则G 是树. 证明：由假设知，G 是一个无回路的连通图，故G 是树。

2．证明：非平凡树的最长通路的起点和终点均为悬挂点. 分析：利用最长通路的性质可证。

证明：设P 是树T 中的极长通路。

若P 的起点v 满足1)(>v d ，则P 不是T 中极长的通路。

对终点u 也可同理讨论。

故结论成立。

3．证明：恰有两个悬挂点的树是一条通路.分析：因为树是连通没有回路的，所以树中至少存在一条通路P 。

因此只需证明恰有两个悬挂点的树中的所有的点都在这条通路P 中即可。

证明：设v u ,是树T 中的两个悬挂点，即1)()(==v d u d 。

因T 是树，所以存在),(v u -通路P ：0,1≥k v w uw k 。

显然，2)(≥i w d 。

若2)(>i w d ，则由T 恰有两个悬挂点的假设，可知T 中有回路；若T 中还有顶点x 不在P 中，则存在),(x u -通路，显然u 与x 不邻接，且2)(≥x d 。

于是，可推得T 中有回路，矛盾。

故结论成立。

4．设G 是树, ()k G ≥∆, 求证：G 中至少有k 个悬挂点.分析：由于()k G ≥∆，所以G 中至少存在一个顶点v 的度≥k ，于是至少有k 个顶点与邻接，又G 是树，所以G 中没有回路，因此与v 邻接的点往外延伸出去的分支中，每个分支的最后一个顶点必定是一个悬挂点，因此G 中至少有k 个悬挂点。

证明：设)(G V u ∈，且k m u d ≥≥)(。

于是，存在)(,,1G V v v m ∈ ，使m i G E uv i ,,1),( =∈。

若i v 不是悬挂点，则有),(G V v i ∈'使。

如此下去，有)()(G V v l i ∈，满足,,)(j i v v j l i≠≠且1)()(=l i v d , m i ,,1 =。

故G 中至少有k 个悬挂点。

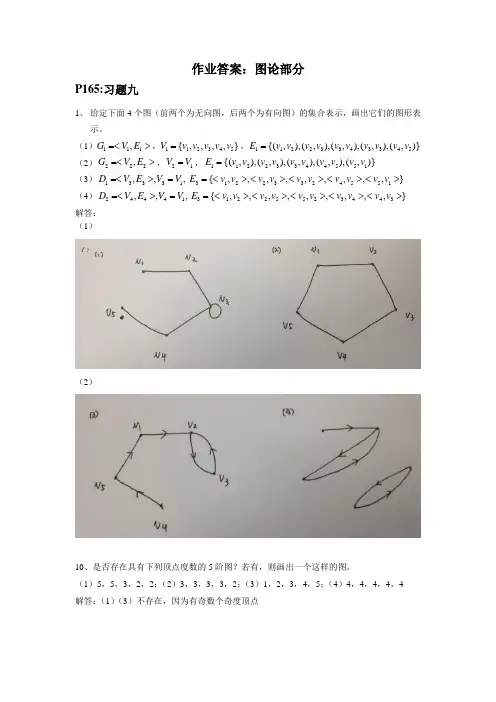
作业答案：图论部分P165:习题九1、 给定下面4个图（前两个为无向图，后两个为有向图）的集合表示，画出它们的图形表示。

（1）111,G V E =<>，112345{,,,,}V v v v v v =，11223343345{(,),(,),(,),(,),(,)}E v v v v v v v v v v = （2）222,G V E =<>，21V V =，11223344551{(,),(,),(,),(,),(,)}E v v v v v v v v v v = （3）13331,,,D V E V V =<>=31223324551{,,,,,,,,,}E v v v v v v v v v v =<><><><><> （4）24441,,,D V E V V =<>=31225523443{,,,,,,,,,}E v v v v v v v v v v =<><><><><> 解答： （1）（2）10、是否存在具有下列顶点度数的5阶图？若有，则画出一个这样的图。

（1）5，5，3，2，2；（2）3，3，3，3，2；（3）1，2，3，4，5；（4）4，4，4，4，4 解答：（1）（3）不存在，因为有奇数个奇度顶点。

14、设G 是(2)n n ≥阶无向简单图，G 是它的补图，已知12(),()G k G k δ∆==，求()G ∆，()G δ。

解答：2()1G n k ∆=--；1()1G n k δ=--。

15、图9.19中各对图是否同构？若同构，则给出它们顶点之间的双射函数。

解答：（c ）不是同构，从点度既可以看出，一个点度序列为4，3，3，3，3而另外一个为4，4，3，3，1（d ）同构，同构函数为12()345x a x bf x x c x d x e=⎧⎪=⎪⎪==⎨⎪=⎪=⎪⎩ 16、画出所有3条边的5阶简单无向图和3条边的3阶简单无向图。

离散数学习题解答 习题六 （第六章 图论）1．从日常生活中列举出三个例子，并由这些例子自然地导出两个无向图及一个向图。

[解] ①用V 代表全国城市的集合，E 代表各城市间的铁路线的集合，则所成之图G=（V ，E ）是全国铁路交通图。

是一个无向图。

②V 用代表中国象棋盘中的格子点集，E 代表任两个相邻小方格的对角线的集合，则所成之图G=（V ，E ）是中国象棋中“马”所能走的路线图。

是一个无向图。

③用V 代表FORTRAN 程序的块集合，E 代表任两个程序块之间的调用关系，则所成之图G+（V ，E ）是FORTRAN 程序的调用关系图。

是一个有向图。

2．画出下左图的补图。

[解] 左图的补图如右图所示。

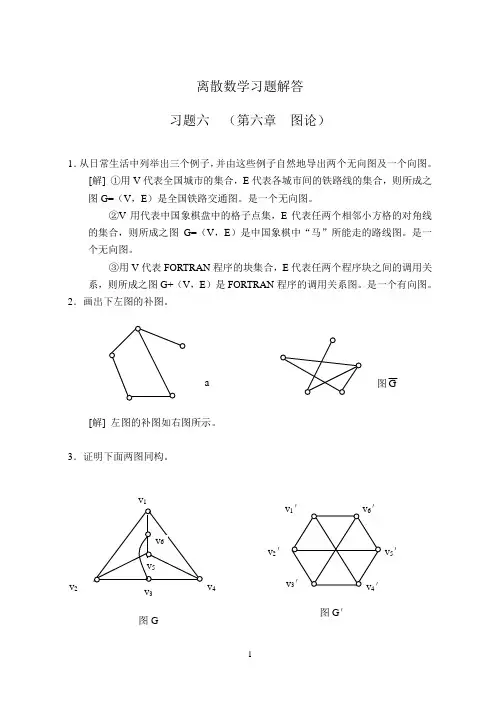
3．证明下面两图同构。

a v 2 v 3 v 4图G图G ′[证] 存在双射函数ϕ:V →V ′及双射函数ψ : E →E ′ϕ (v 1)=v 1′ ϕ (v 1，v 2)=(v 1′，v 2′) ϕ (v 2)=v 2′ ϕ (v 2，v 3)=(v 2′，v 3′) ϕ (v 3)=v 3′ ϕ (v 3，v 4)=(v 3′，v 4′) ϕ (v 4)=v 4′ ϕ (v 4，v 5)=(v 4′，v 5) ϕ (v 5)=v 5′ ϕ (v 5，v 6)=(v 5′，v 6′) ϕ (v 6)=v 6′ϕ (v 6，v 1)=(v 6′，v 1′) ϕ (v 1，v 4)=(v 1′，v 4′) ϕ (v 2，v 5)=(v 2′，v 5′) ϕ (v 3，v 6)=(v 3′，v 6′)显然使下式成立：ψ (v i ，v j )=(v i ,v j ′)⇒ ϕ (v i )=v i ′∧ϕ (v j )=v j ′ (1≤i ·j ≤6) 于是图G 与图G ′同构。

4．证明（a ），（b ）中的两个图都是不同构的。

图G 中有一个长度为4的圈v 1v 2v 6v 5v 1，其各顶点的度均为3点，而在图G ′中却没有这样的圈，因为它中的四个度为3的顶点v 1'，v 5'，v 7'，v 3'不成长度的4的圈。

第4章图论综合练习一、单项选择题1．设L是n阶无向图G上的一条通路，则下面命题为假的是( )．(A) L可以不是简单路径，而是基本路径(B) L可以既是简单路径,又是基本路径(C) L可以既不是简单路径，又不是基本路径(D) L可以是简单路径，而不是基本路径答案：A2．下列定义正确的是( )．(A) 含平行边或环的图称为多重图 (B) 不含平行边或环的图称为简单图(C) 含平行边和环的图称为多重图 (D) 不含平行边和环的图称为简单图答案：D3．以下结论正确是 ( )．(A) 仅有一个孤立结点构成的图是零图(B) 无向完全图K n每个结点的度数是n(C) 有n(n>1)个孤立结点构成的图是平凡图(D) 图中的基本回路都是简单回路答案：D4．下列数组中，不能构成无向图的度数列的数组是( )．(A) (1,1,1,2,3) (B) (1,2,3,4,5) (C) (2,2,2,2,2) (D) (1,3,3,3)答案：B5．下列数组能构成简单图的是( )．(A) (0,1,2,3) (B) (2,3,3,3) (C) (3,3,3,3) (D) (4,2,3,3)答案：C6．无向完全图K3的不同构的生成子图的个数为（）．(A) 6 (B) 5 (C) 4 (D) 3答案：C7．n阶无向完全图K n中的边数为（）．(A)2)1(+nn(B)2)1(-nn(C) n (D)n(n+1)答案：B8．以下命题正确的是( )．(A) n (n1)阶完全图K n都是欧拉图(B) n(n 1)阶完全图K n都是哈密顿图(C) 连通且满足m=n－1的图<V,E>(V=n,E=m)是树(D) n(n5)阶完全图K n都是平面图答案：C10．下列结论不正确是( )．(A) 无向连通图G是欧拉图的充分必要条件是G不含奇数度结点(B) 无向连通图G有欧拉路的充分必要条件是G最多有两个奇数度结点(C) 有向连通图D是欧拉图的充分必要条件是D的每个结点的入度等于出度(D) 有向连通图D有有向欧拉路的充分必要条件是除两个结点外，每个结点的入度等于出度 答案：D11．无向完全图K 4是（ ）．（A ）欧拉图 （B ）哈密顿图 （C ）树 答案：B12．有4个结点的非同构的无向树有 ( )个． (A) 2 (B) 3 (C) 4 (D) 5 答案：A13．设G 是有n 个结点，m 条边的连通图，必须删去G 的( )条边，才能确定G 的一棵生成树．(A) 1+-n m (B) m n - (C) 1++n m (D) 1+-m n 答案：A14．设G 是有6个结点的完全图，从G 中删去( )条边，则得到树． (A) 6 (B) 9 (C) 10 (D) 15 答案：C二、 填空题1．数组{1，2，3，4，4}是一个能构成无向简单图的度数序列， 此命题的真值是 . 答案：02．无向完全图K 3的所有非同构生成子图有 个． 答案：43．设图G V ,E ，其中V n ,E m ．则图G 是树当且仅当G 是连通的，且m ． 答案：n －14．连通图G 是欧拉图的充分必要条件是 ． 答案：图G 无奇数度结点5．连通无向图G 有6个顶点9条边，从G 中删去 条边才有可能得到G 的一棵生成树T ． 答案：46．无向图G 为欧拉图，当且仅当G 是连通的，且G 中无 结点． 答案：奇数度7．设图>=<E V G ,是简单图，若图中每对结点的度数之和 ，则G 一定是哈密顿图．答案：V ≥8．如图1所示带权图中最小生成树的权是 ．答案：12三、化简解答题1．设无向图G ＝<V ,E >，V ={v 1，v 2，v 3，v 4，v 5，v 6}， E ={( v 1，v 2), ( v 2，v 2), ( v 4，v 5), ( v 3，v 4), ( v 1，v 3),( v 3，v 1), ( v 2，v 4)}． 1 v 2 v 6 v 53 v 4图2•2 23 • 1 • 7 9 2• 8 • 6 图1(1) 画出图G 的图形；(2) 写出结点v 2, v 4，v 6的度数； (3) 判断图G 是简单图还是多重图． 解：(1) 图G 的图形如图5所示．(2) 0)deg(,3)deg(,4)deg(642===v v v ．(3) 图G 是多重图．作图如图2. 2．设图G ＝<V ，E >，其中V ＝{a ,b ,c ,d ,e }, E ={(a ,b ),(b ,c ),(c ,d ), (a ,e )}试作出图G 的图形，并指出图G 是简单图还是多重图？是连通图吗？说明理由. 解：图G 如图8所示．. 图G 中既无环，也无平行边，是简单图． 图G 是连通图．G 中任意两点都连通.所以，图G 有9个结点．作图如图3．四、计算题1．设简单连通无向图G 有12条边，G 中有2个1度结点，2个2度结点，3个4度结点，其余结点度数为3．求G 中有多少个结点．试作一个满足该条件的简单无向图．解：设图G 有x 个结点，由握手定理21+22+34+3（x 223）＝122 271821243=-+=x x ＝9 故图G 有9个结点．满足该条件的简单无向图如图4所示2．设图G (如图5表示)是6个结点a ,b ,c , d ,e ,f的图，试求，图G 的最小生成树，并计算它的权．解：构造连通无圈的图，即最小生成树，用克鲁斯克尔算法：第一步： 取ab ＝1；第二步： 取af =4 第三步： 取fe ＝3；第四步： 取ad =9 第五步： 取bc =23如图6．权为1+4+3+9+23=403．一棵树T 有两个2度顶点，1个3度顶点；3个4度顶点， 问它有几片树叶？解：设T 有n 顶点，则有n －1条边．T 中有2个 2度顶点，1个3度顶点，3个4度顶点， 其余n －2－1-3个1度顶点．由握手定理： 2·2+1·3+3·4+ (n －2－1-3)=2(n －1) 解得 n =15．于是T 有15-6=9片树叶五、证明题1．若无向图G 中只有两个奇数度结点，则这两个结点一定是连通的．证：用反证法．设G 中的两个奇数度结点分别为u 和v ．假若u 和v 不连通．即它们之间无任何通路，则G 至少有两个连通分支G 1，G 2，且u 和v 分别属于G 1和G 2，于是G 1和G 2各含有一个奇数度结点．这与握手定理的推论矛盾．因而u 和v 一定是连通的．a b ec d 图3图4b • 23 1c • • a 4 • f 9 3d • •e 图6b •23 1 15 c • 25 •a 4 • f 28 9 16 3 d • 15 • e 图5。

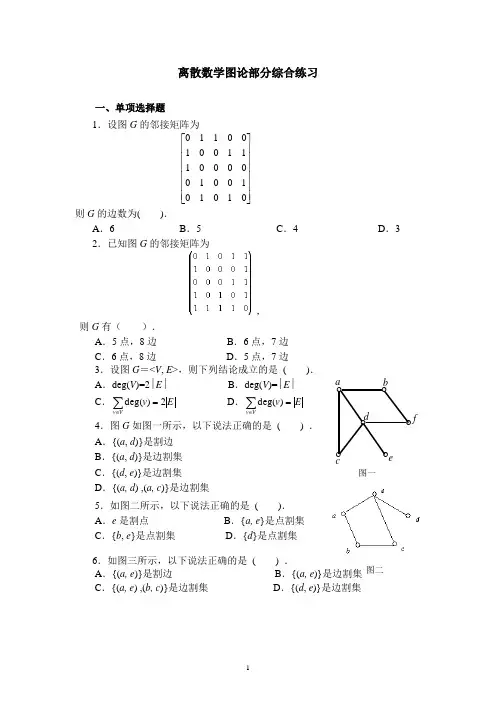
离散数学图论部分综合练习一、单项选择题1．设图G 的邻接矩阵为⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡0101010*******11100100110则G 的边数为( )．A ．6B ．5C ．4D ．32．已知图G 的邻接矩阵为， 则G 有（ ）．A ．5点，8边B ．6点，7边C ．6点，8边D ．5点，7边3．设图G ＝<V , E >，则下列结论成立的是 ( )．A ．deg(V )=2∣E ∣B ．deg(V )=∣E ∣C ．E v Vv 2)deg(=∑∈ D ．E v Vv =∑∈)deg(4．图G 如图一所示，以下说法正确的是 ( ) ． A ．{(a , d )}是割边 B ．{(a , d )}是边割集 C ．{(d , e )}是边割集 D ．{(a, d ) ,(a, c )}是边割集5．如图二所示，以下说法正确的是 ( )． A ．e 是割点 B ．{a, e }是点割集 C ．{b , e }是点割集 D ．{d }是点割集6．如图三所示，以下说法正确的是 ( ) ．A ．{(a, e )}是割边B ．{(a, e )}是边割集C ．{(a, e ) ,(b, c )}是边割集D ．{(d , e )}是边割集οο ο ο οca b edο f图一图二图三7．设有向图（a ）、（b ）、（c ）与（d ）如图四所示，则下列结论成立的是 ( )．图四A ．（a ）是强连通的B ．（b ）是强连通的C ．（c ）是强连通的D ．（d ）是强连通的 应该填写：D8．设完全图K n 有n 个结点(n ≥2)，m 条边，当（ ）时，K n 中存在欧拉回路．A ．m 为奇数B ．n 为偶数C ．n 为奇数D ．m 为偶数 9．设G 是连通平面图，有v 个结点，e 条边，r 个面，则r = ( )．A ．e －v ＋2B ．v ＋e －2C ．e －v －2D ．e ＋v ＋2 10．无向图G 存在欧拉通路，当且仅当( )． A ．G 中所有结点的度数全为偶数 B ．G 中至多有两个奇数度结点 C ．G 连通且所有结点的度数全为偶数 D ．G 连通且至多有两个奇数度结点11．设G 是有n 个结点，m 条边的连通图，必须删去G 的( )条边，才能确定G 的一棵生成树．A ．1m n -+B ．m n -C ．1m n ++D ．1n m -+ 12．无向简单图G 是棵树，当且仅当( )．A ．G 连通且边数比结点数少1B ．G 连通且结点数比边数少1C ．G 的边数比结点数少1D ．G 中没有回路．二、填空题1．已知图G 中有1个1度结点，2个2度结点，3个3度结点，4个4度结点，则G 的边数是 ． 2．设给定图G (如图四所示)，则图G 的点割ο οο οc a b f集是 ．3．若图G=<V , E>中具有一条汉密尔顿回路， 则对于结点集V 的每个非空子集S ，在G 中删除S 中的所有结点得到的连通分支数为W ，则S 中结点 数|S|与W 满足的关系式为 ．4．无向图G 存在欧拉回路，当且仅当G 连通 且 ．5．设有向图D 为欧拉图，则图D 中每个结点的入度 ． 应该填写：等于出度6．设完全图K n 有n 个结点(n 2)，m 条边，当 时，K n 中存在欧拉回路．7．设G 是连通平面图，v , e , r 分别表示G 的结点数，边数和面数，则v ，e 和r 满足的关系式 ．8．设连通平面图G 的结点数为5，边数为6，则面数为 ． 9．结点数v 与边数e 满足 关系的无向连通图就是树．10．设图G 是有6个结点的连通图，结点的总度数为18，则可从G 中删去 条边后使之变成树．11．已知一棵无向树T 中有8个结点，4度，3度，2度的分支点各一个，T 的树叶数为 ．12．设G ＝<V , E >是有6个结点，8条边的连通图，则从G 中删去 条边，可以确定图G 的一棵生成树．13．给定一个序列集合{000，001，01，10，0}，若去掉其中的元素 ，则该序列集合构成前缀码．三、判断说明题1．如图六所示的图G 存在一条欧拉回路．2．给定两个图G 1，G 2（如图七所示）：（1）试判断它们是否为欧拉图、汉密尔顿图？并说明理由． （2）若是欧拉图，请写出一条欧拉回路．v 123图六图七3．判别图G (如图八所示)是不是平面图， 并说明理由．4．设G 是一个有6个结点14条边的连 通图，则G 为平面图．四、计算题1．设图G =<V ，E >，其中V ={a 1, a 2, a 3, a 4, a 5},E ={<a 1, a 2>，<a 2, a 4>，<a 3, a 1>，<a 4, a 5>，<a 5, a 2>}（1）试给出G 的图形表示； （2）求G 的邻接矩阵；（3）判断图G 是强连通图、单侧连通图还是弱连通图？2．设图G =<V ，E >，V ={ v 1，v 2，v 3，v 4，v 5}，E ={ (v 1, v 2)，(v 1, v 3)，(v 2, v 3)，(v 2, v 4)，(v 3, v 4)，(v 3, v 5)，(v 4, v 5) }，试（1）画出G 的图形表示； （2）写出其邻接矩阵；（2）求出每个结点的度数； （4）画出图G 的补图的图形． 3．设G =<V ，E >，V ={ v 1，v 2，v 3，v 4，v 5}，E ={ (v 1,v 3)，(v 2,v 3)，(v 2,v 4)，(v 3,v 4)，(v 3,v 5)，(v 4,v 5) }，试（1）给出G 的图形表示； （2）写出其邻接矩阵； （3）求出每个结点的度数； （4）画出其补图的图形． 4．图G =<V , E >，其中V ={ a , b , c , d , e }，E ={ (a , b ), (a , c ), (a , e ), (b , d ), (b , e ), (c , e ), (c , d ), (d , e ) }，对应边的权值依次为2、1、2、3、6、1、4及5，试（1）画出G 的图形； （2）写出G 的邻接矩阵；（3）求出G 权最小的生成树及其权值．5.用Dijkstra 算法求右图中A 点到其它各点的最短路径。