数线段 (一年级数学思维拓展训练)

数线段练习题数线段练习题在数学中，线段是指两个端点之间的连续部分。

它是几何学中的基本概念，广泛应用于各个领域。

今天，我们来通过一些练习题来加深对线段的理解和运用。

1. 给定线段AB，长度为5cm，C是AB的中点，求线段AC的长度。

解析：由于C是AB的中点，所以AC的长度等于AB的一半。

即AC = 5cm / 2 = 2.5cm。

2. 线段DE的长度是线段BC长度的3倍，而线段DE的长度是12cm，求线段BC的长度。

解析：设线段BC的长度为x，则线段DE的长度为3x。

根据题目中的信息，我们可以列出方程3x = 12。

解这个方程得到x = 4，所以线段BC的长度为4cm。

3. 线段FG和线段HI的长度之和是10cm，线段FG的长度是线段HI长度的2倍，求线段FG和线段HI的长度。

解析：设线段HI的长度为x，则线段FG的长度为2x。

根据题目中的信息，我们可以列出方程2x + x = 10。

解这个方程得到x = 2，所以线段FG的长度为4cm，线段HI的长度为6cm。

4. 线段JK和线段LM的长度之比是2:3，线段JK的长度是6cm，求线段LM的长度。

解析：设线段LM的长度为x，则线段JK的长度为2x。

根据题目中的信息，我们可以列出方程2x = 6。

解这个方程得到x = 3，所以线段LM的长度为9cm。

5. 线段NO的长度是线段PQ长度的1/4，线段PQ的长度是线段RS长度的2倍，线段RS的长度是10cm，求线段NO的长度。

解析：设线段PQ的长度为x，则线段RS的长度为2x。

根据题目中的信息，我们可以列出方程2x = 10。

解这个方程得到x = 5，所以线段PQ的长度为5cm，线段NO的长度为5cm / 4 = 1.25cm。

通过以上的练习题，我们可以发现线段之间的关系可以通过方程来表示和求解。

在实际应用中，线段的长度和比例关系经常出现，因此掌握线段的相关知识和运用方法对我们的数学学习和实际问题解决都有很大的帮助。

数图形1 A01-1提示你上学以前，爸爸妈妈一定教你数过数，如：数一数你家共有几口人，数苹果、数糖果、数手指头、数小棒等等。

我们在数物体个数时，要从1开始数，1、2、3、4、5、6、7、8、9……每个物体都要数到，最后一个物体所对应的数，就是数物体的结果。

我们通过数物体的个数，画一定数量的图形，找出图数对应进行匹配，按顺序数数等练习，能感觉到数字在生活中是无处不在的，也能体会到数数中的一些乐趣。

像1、2、3、4、5、6、7、8、9……这些数，不仅可以按照顺序一个一个地数，也可以从小到大几个几个地数，只要大家多观察，勤动脑，就一定能发现许多有趣的数学问题。

举例1你能数出下面的物体各是多少吗？（ ） （ ） （ ） （ ）【创造力思维】数物体时，小朋友要注意每个物体都要数到，并且只数1次，数到最后一个物体所对应的那个数，就是数的结果。

（1只鹿）从1开始数数，1、2、3、4、5、6（6朵花）从1开始数数，1、2、3、4、5、6、7（7个三角形）从1开始数数，1、2、3、4、5、6、7、8、9、10（10个气球）快练11.看图写数。

（ ） （ ） （ ） （ ）（ ） （ ） （ ） （ ）2.举例2数出下列物体的个数。

（）【创造力思维】我们平时在数物体的个数时，可以一个一个地数，也可以两个两个、五个五个地数，这样数，可以数得又对又快。

两个两个地数，2、4、6、8，共8粒。

五个五个地数，5、10，共10颗。

快练21.数一数，下面这群小鸡共有多少条腿？共有（）条腿2.数一数，下面图中共有多少个手指头？共有（）个手指头举例3看数画○。

A01-2【创造力思维】小朋友一定会画圆、三角形、正方形这些图形。

今天我们来看数画图，画的图形的个数要与数相等。

在画图的时候，先看清所写的数是几，再按照1、2、3、4、5、6、画圆圈的时候，边画边数1、2、3。

画圆圈的时候，边画边数1、2、3、4、5、6、7、8、9、10。

快练31.2.看图画□。

数线段的方法回顾：
①如图（1）直线l上有2个点，则图中有条线段
②如图（2）直线l上有3个点，则图中有条
线段。

③直线上有4个点，则图中有条线段。

④直线上有n个点，则图中有条线段。

借助上面找线段的方法，解决下列四个问题：
1.找角：（1）从一个顶点出发，引出两条射线，得个角；
（2）从一个顶点出发，引出3条射线，得个角；
（3）从一个顶点出发，引出4条射线，得个角；
（4）从一个顶点出发，引出n条射线，得个角；
2.踢比赛问题：某校七年级共有6个班进行足球比赛，准备进行单循环赛（即每两队之间赛一场），
预计全部赛完共需场比赛。

要是n个班呢？共踢场
3.握手问题：某校9年级七班毕业生有50人，大家握手告别，全班共握手次。

要是有n个人呢？共握手次；
4.送贺卡或者发短信问题：元旦快到了，同学们相互发短信送祝福，班里一共有53人，则一共需要
发条短信。

5.直线分平面问题：一个西瓜放在桌子上用刀切下去，一刀可以切成2块，2刀最多可以切成4块；3刀最多可以切成7块，4刀最多可以切成11块（如图）．
上述问题转化为数学模型实际上就是n条直线最多把平面分成几块的问题，有没有规律
呢？
试验，填写
下表，。

思维拓展训练1一、每种水果都表示一个数，你能知道这个数是几吗？— 6 = 15， = 12 — = 8 ， =+ 12 = 35 ， = 25 — = 11 ， =二、每个图形代表一个数，你能算出这个数是多少吗？？(1) △一7=５ o+△=１7 (2)☆+☆=12 ☆一△=6△=( ) o=( ) ☆=( ) △=( ) （3）△一4=11 o+△=１6 (4)☆+☆=24 ☆一△=6 △=( ) o=( ) ☆=( ) △=( ) （5）5+o=12 △+o=10 (6) o 一☆=5 12一☆=8o=( ) △=( ) o =( ) ☆=( )(7)5+o=12 △+o=10 (8) o 一☆=5 12一☆=8o=( ) △=( ) o =( ) ☆=( )（9）△+△=18 △=( ) （10）口+口+△+△=14 ☆+ o =13 o =( ) △+△+口=10△+ o =15 ☆=( ) △=( ) 口=( )三、每个图形代表一个数，你能算出这个数是多少吗？（ 1 ）△＋□=9 ○-△=1 △＋△＋△＝9△=（）□=（）○=（）（ 2 ）△ + ○ = 12 ○ + ☆ = 8 △ + ○ + ☆ = 21△ =( ) ○= ( ) ☆=( )（ 3 ）你 + 我 = 7 你 + 他 = 18 你 + 我 + 他 = 24你 = （）我 = （）他 = （）（ 4 ）○+□=10，□+△=12，○+□+△=15。

○=（），□=（），△=（）。

（5）△+○=9 △+△+○+○+○=25△=（）○=（）四、每个图形代表一个数，你能算出这个数是多少吗？（1）△＋△＋△＋△＝28 △＝（）△＋△＋□＝20 □＝（）（2）○＋○＋○＝6 ○＝（）△＋△＋△＝12 △＝（）（3）△－○＝1 △＝（）△＋△－○＝9 ○＝（）△＋○－□＝10 □＝（）五、下图中每种水果各代表一个数，算一算，它们各代表几?＋ = 7，＋= 10，＋= 9=（）=（）=（）六、1.已知：☆+☆+☆=6，△+△+△+△=20，则△－☆=( )2.已知：△＋○＝14，△－○＝2 ，则△＝( ) ○＝( )3.已知：▲＝●＋●＋●，▲＋●＝12，则●＝（），▲＝（）4.已知：△ + ○ = 5，○ + ☆ = 9，△ + ○ + ☆ = 13△ =( ) ○= ( ) ☆=( )七、张老师把红、白、蓝各一个气球分别送给三位小朋友。

数数线段
10+1= 14+5= 18-7= 10+2= 10+6= 16-6= 10+9= 10+3= 11+2= 19-5=
11+4= 15-3= 11+5= 18-5= 11+7=
小明有一根旺旺碎冰冰，他准备和自己的小伙伴一起分着吃，要怎么分呢？
一、计算小能手
二、当堂小启发
三. 经典例题
例1、数一数，下图中有几条线段？
小试牛刀
数数看，下图中共有多少条线段？
例2、数一数，下图中有几条线段？
小试牛刀
请数出右图中线段的条数，并用算式表示出来。

四. 举一反三
数一数，下列图中各有多少条线段？
（1）（2）
五.大显身手
A：你能数一数下图中线段的条数吗？
B：下图中的线段你能全部找出来吗？
六.知识小总结
课堂笔记：
七.课后作业
1、数出下图线段的总条数。

2、数出下图线段的总条数。

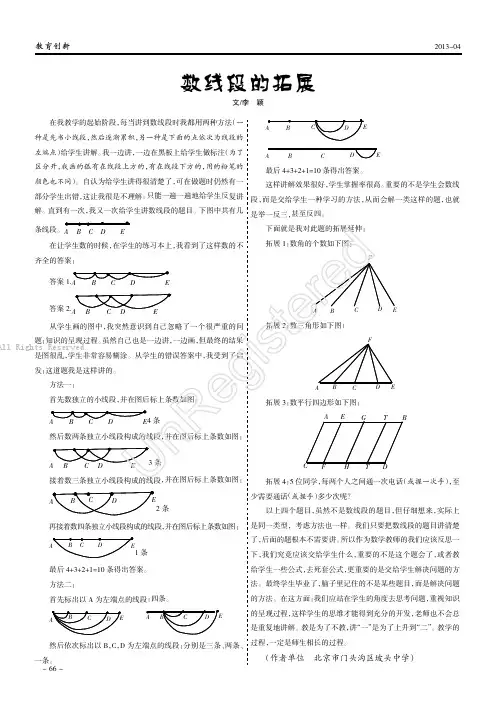
教育创新2013-04在我教学的起始阶段，每当讲到数线段时我都用两种方法（一种是先书小线段，然后逐渐累积，另一种是下面的点依次为线段的左端点）给学生讲解。

我一边讲，一边在黑板上给学生做标注（为了区分开，我画的弧有在线段上方的，有在线段下方的，用的粉笔的颜色也不同）。

自认为给学生讲得很清楚了，可在做题时仍然有一部分学生出错，这让我很是不理解。

只能一遍一遍地给学生反复讲解。

直到有一次，我又一次给学生讲数线段的题目。

下图中共有几ABC DE在让学生数的时候，在学生的练习本上，我看到了这样数的不齐全的答案：答案答案2.从学生画的图中，我突然意识到自己忽略了一个很严重的问题：知识的呈现过程。

虽然自己也是一边讲，一边画，但最终的结果是图很乱，学生非常容易糊涂。

从学生的错误答案中，我受到了启发：这道题我是这样讲的。

方法一：首先数独立的小线段，并在图后标上条数如图：条然后数两条独立小线段构成的线段，并在图后标上条数如图：条接着数三条独立小线段构成的线段，并在图后标上条数如图：2条再接着数四条独立小线段构成的线段，并在图后标上条数如图：条最后4+3+2+1=10条得出答案。

方法二：首先标出以A 为左端点的线段：四条。

然后依次标出以B ，C ，D 为左端点的线段：分别是三条、两条、一条。

最后4+3+2+1=10条得出答案。

这样讲解效果很好，学生掌握率很高。

重要的不是学生会数线段，而是交给学生一种学习的方法，从而会解一类这样的题，也就是举一反三，甚至反四。

下面就是我对此题的拓展延伸：拓展1：数角的个数如下图：拓展2：数三角形如下图：拓展3：数平行四边形如下图：拓展4：5位同学，每两个人之间通一次电话（或握一次手），至少需要通话（或握手）多少次呢？以上四个题目，虽然不是数线段的题目，但仔细想来，实际上是同一类型，考虑方法也一样。

我们只要把数线段的题目讲清楚了，后面的题根本不需要讲。

所以作为数学教师的我们应该反思一下，我们究竟应该交给学生什么，重要的不是这个题会了，或者教给学生一些公式，去死套公式，更重要的是交给学生解决问题的方法。

巧数线段题目
这是一道关于巧数线段的题目，题目给出了一个由n个点构成的点集，其中任意三个点都不共线。

题目要求我们找出这些点可以构成的线段数量。

解题思路：
1. 首先，我们可以观察到，对于任意一个点，它都可以与其它n-1个点构成线段。

因此，如果我们从每个点出发，都可以构造出n-1条线段。

2. 但是，这样计算会导致每条线段被计算两次，因为每条线段是由两个点确定的。

所以我们需要将上述结果除以2，以消除重复计数。

用数学公式，我们可以表示为：
线段数量 = (n (n - 1)) / 2
这是一个经典的组合问题，可以通过组合数学中的公式来解决。

使用这个公式，我们可以快速计算出给定点集可以构成的线段数量。

欧阳美创编 2021.01.01
欧阳美创编 2021.01.01
时间：2021.01.01 笔直的桌子边缘向两边无限延伸一直线；直线由挨的非常紧密的点组成，直线上任何两点之间（包 括两点）构成线段，这两点叫做线段的端点；
由直线上一点向宜线的英中一个方向无限延伸构成射线，这个点叫作射线的端点；
端点，射线有一个端点，线段有两个端点；
线段是由其两个端点的位置决泄的。

例一、数一数，下而中共有多少条线段？
练习L 数一数.卜恤|!菇张名小条线＞.?■.£用四种•扮法解，并写出各条线段） 规律卜若线创所含"掖木线&数为n,则这条线段 皿线段总数为1+2+3+.、、
数线段
创作：欧阳美 所以，直线没有
、+n 例二八数一躺下ifiQ 」共有®少条线段?
欧阳美创编2021.01.01 欧阳美创编2021.01.01 例三、下而图中有多少条线段?
欧阳美创编2021.01.01 欧阳美创编2021.01.01。

第十二章　数线段知识导航线段是直线的一部分，它有两个端点，有一定的长度，可以用刻度尺量出线段的长度。

我们把相邻两个端点之间的线段叫作基本线段，很容易发现，在数线段的过程中，线段图上有几条基本线段，线段总数量就是从几倒数加到1。

图解思维训练题例1　数一数，算一算图中一共有多少条线段？图解思路规范解答如左图所示，共有3条线段。

例2　数一数，算一算图中一共有多少条线段？图解思路要想准确数出线段的条数，我们应该按一定的顺序数，按什么顺序呢？思路一：我们可以采用以线段左端点分别数的方法。

以A点为左端点的线段有：AB、AC、AD共3条；以B点为左端点的线段有：BC、BD共2条；以C点为左端点的线段有：CD共1条。

思路二：我们还可以这样想，把图中线段AB、BC、CD看作基本线段来数。

由1条基本线段构成的线段：AB、BC、CD共3条；由2条基本线段构成的线段：AC、BD共2条；由3条基本线段构成的线段：AD只有1条。

规范解答图中共有线段3+2+1=6（条）。

例3　数一数，算一算图中一共有多少条线段？图解思路数线段的关键是做到不重复、不遗漏，而有条理地数线段，是不遗漏不重复的重要保证。

数线段时用图示法比较好。

如图（1）所示，给线段上的每个点标上字母，首先从第一个字母A出发，数出以A点为一个端点的六条线段AB、AC、AD、AE、AF、AG。

如图（2）所示，再从第二个字母B出发数出以B点为一个端点的五条线段BC、BD、BE、BF、BG，需要注意的是，要按照同一个方向数，避免重复。

同理，依次从C点、D点、E点、F点、G点出发，可以分别数出4条线段CD、CE、CF、CG，3条线段DE、DF、DG，2条线段EF、EG和1条线段FG。

规范解答图中线段共有6+5+4+3+2+1=21（条）。

例4　数一数，算一算图中一共有多少条线段？图解思路如图所示，给线段上每个端点标上字母。

线段AB、CG两条线段分别数。

（1）线段AB上有AE、AB、EB三条线段。

怎样数线段？
数线段、数角是低年级几何计数入门内容，首先还是对线段和角概念要理解。

怎么才算一个不同的线段和角，特征理解了，数起来才能不遗漏。

比如有线段有两个端点，两个端点变化就会产生一条新的线段。

我是王老师，致力于小学数学的精品问答！目的是不重复，不遗漏，方法要结合孩子年龄阶段。

这个问题，如果一年级我会采用比较形象的方法（投铅球法），帮助孩子有序计数，如果二年级我会引导他找到规律和归纳（不是记公式），更高年级我会让他根据图形构造用排列组合来算。

当然你也可以直接数！
下面我还是介绍孩子比较容易理解的方法，供您参考。

数线段
一年级数线段方法（选自王老师一年级趣味数学专栏）
认知基础~线段概念
【例题】如下图，小朋友们数一下，一共有多少条线段？
直接数的话由于点线重复，不像图形计数那么清晰，对于一年级孩子能数正确难度是有的。

所以为了辅助孩子去数，用投铅球这种比较形象易联想情景的思路，引导孩子建立有序概念。

如下图
→ 从A点投可以投到B,C,D点，对应3条线段
→ 从B点投可以投到C,D点，对应2条线段
→ 从C点投只能投到D点，对应1条线段。

3+2+1=6条
以上！数线段方法很多，要找对孩子能理解接受的，才是正确有效的。

高年级学过排列数组合数的话，根据两个点构成一个线段特点，直接4选2的组合数即可解题。

一年级数学练习题数线段数学是一门非常重要的学科，也是培养学生逻辑思维和数学能力的关键学科之一。

对于一年级的学生来说，数学练习题是巩固知识和锻炼能力的重要途径。

本文将介绍一些适合一年级学生的数学练习题，其中主题为数线段。

一、认识数线段数线段是数学中的基本概念之一。

数线段是由两个端点确定的线段，我们可以用字母表示数线段，例如AB代表由端点A和端点B所确定的线段。

在数线段上，我们可以用长度来表示线段的大小，长度是线段上的两个端点之间的距离。

示例练习题1：画一个长度为3的数线段CD。

示例练习题2：若数线段EF的长度为5，画出数线段EF。

二、比较数线段的大小在数学中，我们经常需要对数线段的大小进行比较。

为了比较数线段的大小，我们可以利用数线段的长度来判断。

示例练习题3：比较数线段GH和数线段IJ的大小，已知数线段GH的长度为4，数线段IJ的长度为6。

示例练习题4：在数线上，标记出数线段KL和数线段MN，已知数线段KL的长度为3，数线段MN的长度为4，比较数线段KL和数线段MN的大小。

三、练习题请根据题目要求完成以下练习题：练习题1：在数线上标记出数线段PQ，已知数线段PQ的长度为2。

练习题2：在数线上标记出数线段RS和数线段TU，已知数线段RS的长度为4，数线段TU的长度为5。

练习题3：比较数线段VW和数线段XY的大小，已知数线段VW的长度为3，数线段XY的长度为2。

练习题4：在数线上标记出数线段YZ和数线段AB，已知数线段YZ的长度为6，数线段AB的长度为7，比较数线段YZ和数线段AB的大小。

练习题5：在数线上标记出数线段CD、数线段EF和数线段GH，已知数线段CD的长度为2，数线段EF的长度为4，数线段GH的长度为6，比较三个数线段的大小。

通过以上练习题，一年级的学生可以巩固对数线段的认识和理解，并通过比较数线段的大小来锻炼数学能力和思维逻辑。

希望同学们能够通过练习，掌握数线段的基本概念和比较大小的方法，为接下来的学习打下坚实的基础。

知识要点：数图形时我们要按照一定的顺序、有条理、有计划、有方法的去解答题目，可由单个图形数起，再数两个图形合成的图形，依此规律一个一个往下数。

教学目标：能够用多种方法准确的数出图形个数
教学难点：准确，且方法正确
｛例1｝数一数图中共有几条线段？
D
A B
C
这样想：数之前，先将每条线段写上字母，写好后，先数AB这条线段上有4条小线段，再数两条合并成的有3条，再数三条合并成的有2条，最后数四条合并成的有1条，
4+3+2+1=10条。

同样CD这条线段上也有10条，和起来一共有20条。

｛例2｝数一数图中共有几个小长方体？
这样想：从上面先数，第一排有2个小长方体，再数第二排有4个小长方体，最后数第三排有6个小长方体，所以
2+4+6=12，有12个小长方体。

｛例3｝数一数图中共有几个三角形？
这样想：数之前，先将每个图形编号，编好后，先数单个三角形共10个。

再数两个图形合成的三角形，按顺序两个两个合并，共8个三角形。

所以10+8=18，共18个三角形。

｛例4｝数一数图中共有几个三角形？
练习讨论：先数单个三角形共4个。

再数两个三角形合成的三角形，按顺序两个两个合并，共2个三角形。

最后数由3个小三角形组成的大三角形，有1个。

所以4+2+1=7，共7个三角形。

｛例5｝数一数图中共有几个三角形？
练习，讨论：先数每个角上三角形共5个，再数由两个不靠着的角和中间五边形合成的三角形，按顺序数共3个三角形，所以5+3=8，共8个三角形。

数线段A06-1提示我们知道，许多图形都是由线段组成的。

1.·这叫“点”，用笔在纸上画一个“点”，可以画大些，也可以画小些，“点”在纸上占一个位置。

2. 这叫“线段”，沿着直尺把两点用笔连起来，就能画出一条线段，图上的这两点就是线段的端点，线段有两个端点。

线段必须是直的，而且要有两个端点。

可以用若干条线段组成简单的或复杂的图形。

通过练习，要掌握在图形中数线段的方法，但在数的时候，要仔细观察，注意有条理、有次序地数，做到既不重复又不遗漏。

这将对以后的数图形有很大的帮助。

举例1观察，谁是线段？在线段下打“√”。

（）（）（）（）（）（）【创造力思维】线段的特点有两个：1.是直的，2.有两个端点。

我们在判断谁是线段时，必须满足这两个特点，缺一不可。

是直的而且有两个端点，是线段。

不是直的，不是线段。

只有一个端点，不是线段。

是直的而且有两个端点，是线段。

（√）（）（）（）（）（√）快练11.在线段下打“√”。

（）（）（）（）（）（）（）2.不是线段的打“×”。

（）（）（）（）（）（）（）举例2想一想，在下图三点之间，你能连几条线段？···【创造力思维】在两点之间用笔沿直尺连接起来，就可以形成一条线段。

现在有三个点，应在每两个点之间画一条线段，试试看，你能连几条线段。

在三点之间，可以连3条线段。

···快练21.先画两个点，再用直尺把这两个点连起来，看看，这是什么？2.有四个点，你能在它们之间连几条线段？····举例3数一数，下面这个图形中共有几条线段。

【创造力思维】这是一条线段。

在一个图形中可以包含许多条这样的线段，A06-2这就要求小朋友们仔细观察，做到数的时候不重复、不遗漏。

这个图形中共有5条线段。

我们可以照下面的方法数。

快练31.数一数，图中有几条线段。

2.你能数出下图中共有几条线段吗？举例4一共有几条线段？【创造力思维】这是一条线段，而且只有一条。