下载文档原格式
必修一第三章指数函数与对数函数复习教案一、教学目标1.了解指数函数和对数函数的定义及性质；2.掌握指数函数和对数函数的图像和性质；3.熟练运用指数函数和对数函数解决实际问题。
二、教学重点1.指数函数的定义与性质；2.对数函数的定义与性质；3.指数函数和对数函数的图像和性质。
三、教学内容1.指数函数1.指数函数的定义：$y=a^x$，其中a>0且a≠1，x是任意实数。
2.指数函数图像：-当0<a<1时，函数图像呈递减趋势，经过点(0,1)；-当a>1时，函数图像呈递增趋势，经过点(0,1)；3.指数函数的性质：-函数图像经过点(0,1)；-当x=0时，y=1；-指数函数在0<a<1时，取值范围为(0,+∞)，在a>1时，取值范围为(0,+∞)；-函数图像在经过点(0,1)时，若a>1，则过(1，a)；若0<a<1，则过(a,1)；-当x→+∞时，y→+∞；当x→-∞时，y→0。
2.对数函数1. 对数函数的定义：$y=log_{a}{x}$，其中 a > 0 且a≠1，x > 0。
2.对数函数图像：-当0<a<1时，函数图像呈递减趋势，过点(1,0)；-当a>1时，函数图像呈递增趋势，过点(1,0)。
3.对数函数的性质：-函数图像过点(1,0)；-对数函数取值范围为(-∞,+∞)；-函数图像在过点(1,0)时，若a>1，则过点(a,1)；若0<a<1，则过点(1/a,1)；-当x→+∞时，y→+∞；当x→0+时，y→-∞。
四、教学方法1.教师讲解结合示例引入指数函数和对数函数的定义及性质；2.布置题目，让学生互相讨论，并与学生一起解答问题；3.利用电子白板展示指数函数和对数函数的图像，让学生观察特点。
五、教学过程1.引入指数函数和对数函数的定义及性质，与学生一起讨论和提问；2.利用示例分别介绍指数函数和对数函数的图像和性质，解释每个关键点的含义；3.设计问题让学生自主思考并与同学讨论解决；4.利用电子白板展示指数函数和对数函数的图像，与学生进行互动讨论。
指数函数与对数函数复习课一. 复习目标1. 掌握指数函数与对数函数的函数性质及图象特征.2. 加深对图象法，比较法等一些常规方法的理解.3. 体会分类讨论，数形结合等数学思想.二．指数函数1．指数函数定义：地，函数xy a =（0a >且1a ≠）叫做指数函数，其中x 是自变量，函数定义域是R ．2．指数函数xy a =在底数及这两种情况下的图象和性质：1a > 01a <<图象性质（1）定义域：R （2）值域：(0,)+∞（3）过点(0,1)，即0x =时1y =（4）在R 上是增函数（4）在R 上是减函数例1．求下列函数的定义域、值域： （1）1218x y -= （2）11()2x y =-（3）3xy -= （4）1(0,1)1x xa y a a a -=>≠+ 练习1．当1a >时，证明函数11x x a y a +=- 是奇函数练习2．设a 是实数，2()()21x f x a x R =-∈+， （1）试证明：对于任意,()a f x 在R 为增函数； （2）试确定a 的值，使()f x 为奇函数。
分析：此题虽形式较为复杂，但应严格按照单调性、奇偶性的定义进行证明。
还应要求学生注意不同题型的解答方法。
三 对数函数1．对数函数的定义：函数 x y a log =)10(≠>a a 且叫做对数函数。
2．对数函数的性质：（1）定义域、值域：对数函数x y a log =)10(≠>a a 且的定义域为),0(+∞，值域为),(+∞-∞．（2）图象：由于对数函数是指数函数的反函数，所以对数函数的图象只须由相应的指数函数图象作关于x y =的对称图形，即可获得。
同样：也分1>a 与10<<a 两种情况归纳，以x y 2log =（图1）与x y 21log =（图2）为例。
（3）对数函数性质列表：图 象1a >01a <<性 质（1）定义域：(0,)+∞ （2）值域：R（3）过点(1,0)，即当1=x 时，0=y（4）在（0，+∞）上是增函数（4）在(0,)+∞上是减函数例1．求下列函数的定义域：（1）2log x y a =； （2）)4(log x y a -=； （3）)9(log 2x y a -=．分析：此题主要利用对数函数x y a log =的定义域(0,)+∞求解。
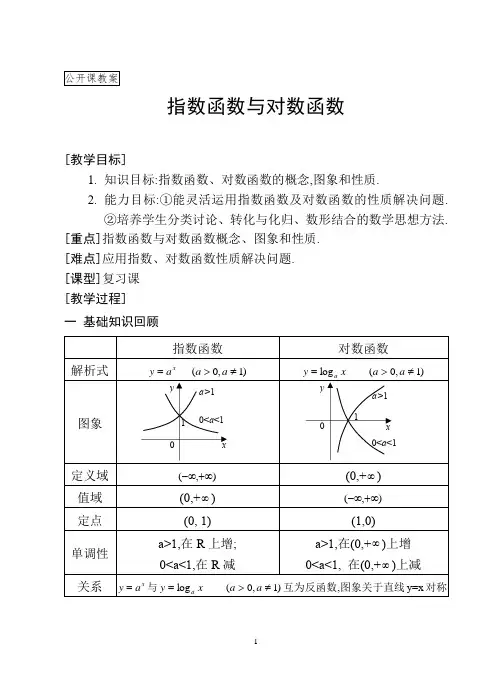
公开课教案指数函数与对数函数[教学目标]1. 知识目标:指数函数、对数函数的概念,图象和性质.2. 能力目标:①能灵活运用指数函数及对数函数的性质解决问题.②培养学生分类讨论、转化与化归、数形结合的数学思想方法.[重点]指数函数与对数函数概念、图象和性质. [难点]应用指数、对数函数性质解决问题. [课型]复习课 [教学过程] 一 基础知识回顾指数函数对数函数解析式x a y = )1,0(≠>a a)1,0(log ≠>=a a xy a图象定义域 ),(+∞-∞ (0,+∞)值域 (0,+∞) ),(+∞-∞定点 (0, 1) (1,0) 单调性 a>1,在R 上增; 0<a<1,在R 减a>1,在(0,+∞)上增 0<a<1, 在(0,+∞)上减关系 x a y =与)1,0(log ≠>=a a xy a 互为反函数,图象关于直线y=x 对称xy1a>1 0<a <1xy1a>10<a <1二 注意:1.指数函数的底数及对数函数的真数和底数应满足的条件,应予以重视.2.指数函数与对数函数性质直接受底数影响,所以分类讨论思想表现得尤为突出.3.研究指数、对数问题尽量化为同底.4.充分利用指数函数、对数函数的图象和性质解决相关问题,特别是它们的单调性应用. 三 例题讲解例 1.函数)(x f y =的图象与x y )31(=的图象关于直线y=x 对称.则)2()(2x x f x F -=的单调增区间为( ).A.[1,+∞)B.(- ∞, 1]C. (0, 2)D. [1, 2)例2.(2000京皖春招)已知),()(,0.lg )(b f a f b a x x f ><<=且若证明ab<1. 法一: 平方法. 法二: 图象法例3.比较下列各组数大小.(1))1,0(1.12.1≠>a a a a 且与 分析:按a 分类讨论. (2)3log 3log 54与 分析:换底,化为同底. (3)3.0322,2log ,3.0 分析:插入中间桥梁 “1”，“0”.(4)若0<x <1, a>0,且a ≠1,比较:p=||)1(log ||)1(log x q x a a +=-与的大小. 分析:①分类讨论;②作差比较;③作商比较. 例4.(2002高考)设y=)0,0](1)(2[21log 22>>+-+b a b ab a x x x 求使y 为负值时,x 的取值范围. 分析:利用指数、对数函数的单调性,解不等式.[小结]1.指数、对数函数是中学数学中重点内容,在高考中考查力度大,特别是它们的图象,性质的应用,都有全面的考查.解决问题时多注意底数、真数的取值范围以及对底数进行讨论。
高中数学北师大版必修1第三章《指数函数、幂函数、对数函数增长的比较》优质课教案省级比赛获奖教案公开课教师
面试试讲教案
【名师授课教案】
1教学目标
1.借助信息技术,利用函数图像及数据表格,比较指数函数、对数函数以及幂函数的增长差异.
2.恰当运用函数的三种表示方法(解析式、表格、图像),并借助信息技术解决一些实际问题.
3.让学生体会数学在实际问题中的应用价值,培养学生学习兴趣.
2重点难点
教学重点:认识指数函数、对数函数、幂函数等函数模型的增长差异,体会直线上升、指数爆炸与对数增长的不同.
教学难点:应用函数模型解决简单问题.
3学情分析
1.知识储备方面
学习本课之前,学生在初中已经掌握了一次函数,二次函数、正比例函数、反比例函数几类基本初等函数;并且在高中阶段独立探究过指数函数与对数函数的图象与性质,基本掌握了研究函数的一般方法与过程。
本节课通过对对指数函数、对数函数、幂函数等函数模型的增长差异,体会直线上升、指数爆炸与对数增长的不同。
课本对几种不同增长的函数模型的认识及应用,都是通过实例来实现的。
由于指数函数、对数函数、幂函数等函数模型的增长情况比较复杂,学生在对图象共性的归纳与概括方面可能遇到困难,因此在教学中尽量多使用多媒体技术进行教学。
2.思维水平方面
所授课班级是理科实验班学生,学生有较高的数学素养和较强的数学思维能力,对数学充满探索精神,同时对课堂教学有较高需求。
3.技术使用方面
学生能够熟练掌握图形计算器的操作,并具有利用信息技术进行自主探究的意识。
