直接积分法(课堂PPT)

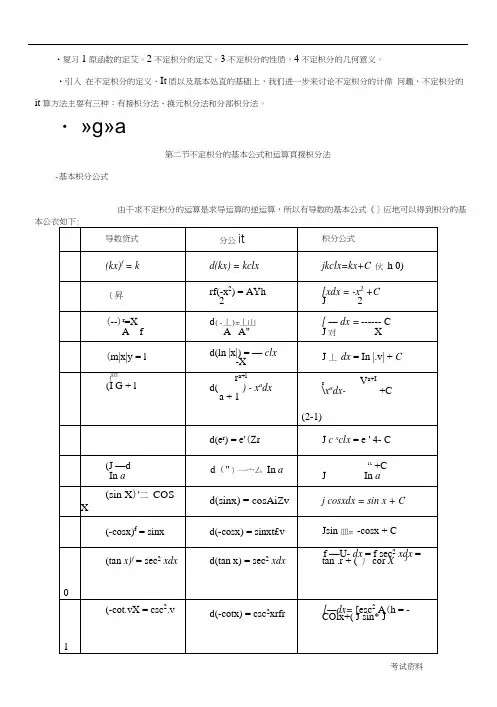
•复习1原函数的定艾。

2不定枳分的定艾。

3不定枳分的性质。

4不定枳分的几何意义。

•引入在不定枳分的定义、It质以及基本处直的基础上，我们进一步来讨论不定枳分的计偉冋趣，不定枳分的it算方法主耍有三种：有接枳分法、换元枳分法和分部枳分法。

・ »g»a第二节不定枳分的基本公式和运算頁接枳分法-基本枳分公式由干求不定枳分的运算是求导运算的逆运算，所以有导数的基本公式《］应地可以得到枳分的基2(secx/= secxtanx d(secx) = secAtairxz/v J sec x tan xdx = secx + C3(-csc.r^cscACOtx d(-cscx)=cscxcotxrfr ^cscxcotxdx = -cscx + C4 (arctan x)r = —1 + .Ld(arctan x) = —1 + x?Zv [ —dx = arc tan.v + C5 (arcsin xY =,丨= d( arcsin A*)=―.=■2 x/l+ .V2l.\ f 严1 .. dx = arcs in x +CJ vr+x2以上十五个公述是求不定枳分的U t t,恋须熟记，不仅要记右端的结果，连要熟悉左端被枳函数的的形式。

求因数的不定枳分的方法叫枳分法。

(2 ) j xjxdx此例表明，对某些分式或根式函数求不定枳分时，可先把它们化力x"的形氏，然后应用显函数的枳分公式求枳分。

二不定枳分的基本运算法则a«i两个因数代数和的枳分，等干各因数枳分的代数和，即J [/W 土g(x)肚=J/(A>/A± j g(x\LxSi 1对于有限多个函数的和也成立的.违则2被枳因数中不为零的常数因子可提到枳分号外，即J kf(x\l.x = kj* f(x\lx( " 0 )M 2 求J (2x' 4-1-e x }dx解J(2x3+\—e x)dx =21x3dx + jdx-j e x dx二—X” + x — 0' + C o例1 •求下列不定枳分.(1)ii貝中毎一項的不定枳分虽然都应当有一个枳分常数，但是逹里并不需要在毎一頂后面则上一个枳分常数，因为代意常釵之利if是任意常数，所以迪里只把它的和C写在末尾，以后仿此。

不定积分的基本公式和直接积分法第二节不定积分的基本公式和直接积分法（Basic Formula of UndefinedIntegral and Direct Integral）课题：1.不定积分的基本公式2.不定积分的直接积分法课堂类型：讲授教学目的：熟练掌握不定积分的基本公式，对简单的函数能用直接积分法进行积分。

教学重点：不定积分的基本公式教学难点: 直接积分法教具：多媒体课件教学方法：教学内容：一、不定积分的基本公式由于不定积分是求导的逆运算，所以由导数的基本公式对应地可以得到不定积分的基本公式。

二、不定积分的直接积分法利用不定积分的性质和基本公式，可以求出一些简单函数的不定积分，通常把这种求不定积分的方法叫做直接积分法。

例１ 求32x dx ⎰导数的基本公式 ()1222()01()1()()ln 1(ln )(sin )cos (cos )sin (tan )sec (cot )csc (sec )sec tan (csc )csc cot (arcsin )1(arctan )1(arccos )1(cot )1x xx x C x xxe e a a ax xx x x x x x x x x x x x x x x x x x arc x ααα+'='='=+'='='='='=-'='=-'='=-'='=+'='=-+21(log )ln a x x x a'=不定积分的基本公式 ()1222011ln ln ||cos sin sin cos sec tan csc cot sec tan sec csc cot csc arcsin arctan 1x x xxdx Cdx x Cx x dx C a e dx e C a a dx C a dxx Cx xdx x C xdx x C xdx x C xdx x C x xdx x C x xdx x Cx Cdxx C xααα+==+=+≠-+=+=+=+=+=-+=+=-+=+=-+=+=++⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰2arccos arc cot 11log ln a x C dxx C x dx x Cx a =-+=-++=+⎰⎰⎰解 31333412222312x x dx x dx x dx C x C +===⨯+=++⎰⎰⎰例２求(23cos x x dx -+⎰ 解(32322233233cos 3cos 3sin 5310sin 3xx dx x dx xdx x x x Cx x x C -+=-+=⨯-++=-++⎰⎰⎰⎰例３ 求dx x x ⎰-23)1( 解Cx x x x Cx x dxxx x dx xx x x dx x x +++-=+-=-+-=-+-=-⎰⎰⎰1||ln 332 31072 )133( 133)1(22327222323 例４ 求221sin cos dx x x⎰ 解22222222221sin cos 11sin cos sin cos cos sin sec csc tan cot x x dx dx dx dx x x x x x x xdx xdx x x C+==+=+=-+⎰⎰⎰⎰⎰⎰例５ 求2x x e dx ⎰解 ()()()2222ln 21ln 2xxxx x e e e dx e dx C C e==+=++⎰⎰例６ 求2sin 2xdx ⎰ 解 21cos sin 22x x-=21cos 11sin sin 2222x x dx dx x x C -==-+⎰⎰ 例７ 求()221dxx x +⎰ 解()222211111x x x x =-++ ()222222111111111arctan dx dx dx dx x x x x x x x Cx⎛⎫=-=- ⎪+++⎝⎭=--+⎰⎰⎰⎰例８ 已知物体以速度()221/v t m s =+沿Ox 轴作直线运动，当1t s =时，物体经过的路程为3m ，求物体的运动方程。

直接积分法
直接积分法（Direct Integration）是一种使用无穷多项式（Infinite Series）作为求取积分的数学方法。

它在解决复杂积分方程时有着不可替代的优势。

这种方法的基础是多项式（Polynomial）展开定理，说明函数可以利用无穷多个项表达，而不需要考虑数学上的复杂推导。

例如，使用函数y=x^2的积分的话，将其平方展开后，得到的多项式结果形式为：y=1/3*x^3 + C。

这里的对应项就是一次多项式，求取某个范围内的积分只要求出两个多项式项之间的差值即可。

而采用直接积分方法求取积分时，首先需要将函数分解为无限多项式，即将函数平方展开，得到一系列项和系数，再把这些项应用到函数中进行积分，比如将求得函数积分后的项代入运算结果中。

该方法虽然能够有效求解复杂的积分方程，但也存在一些问题和局限性，比如一般情况下难以计算求取到的值的准确性，而且用时较长，因此并不能满足一些复杂的积分任务的要求。

因此，直接积分法虽然有其特殊优势，但也同样有一定的局限性，因此如何有效求解复杂的积分问题，仍有待进一步探索。