清华大学 钢结构 5章例题

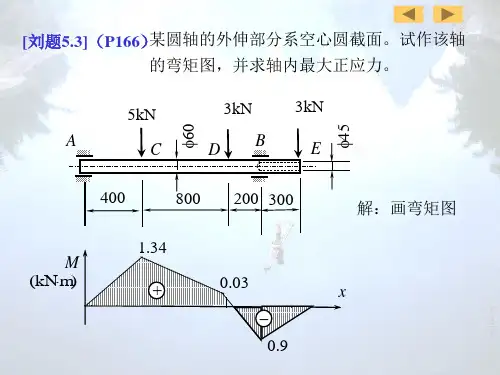
5-1 把直径1d mm =的钢丝绕在直径为2m 的卷筒上，试计算该钢丝中产生的最大应力。

设200E GPa =解：钢丝绕在直径为D 的卷筒上后产生弯曲变形，其中性层的曲率半径为22D d Dρ+=≈（因D d >>） 该钢丝中产生的最大应力为39maxmax/211020010100/22y d d E E E Pa MPa D D σρ-⨯====⨯⨯=5.4 矩形截面悬臂梁如图所示。

已知4l m =，23b h =，10/q kN m =，[]10MPa σ=，试确定此梁横截面的尺寸。

解：作梁的弯矩图如图所示。

梁的最大弯矩发生在固定端截面上。

22max 111048022M ql kN m ==⨯⨯=⋅ 由强度条件，有max maxmax 26[]z M M W bhσσ==≤ 将23b h =代入上式，得0.416416h m mm ≥=== 22773b h mm =≥ 5.5 20a 工字钢梁的支承和受力情况如图所示。

若[]160MPa σ=，试求许可载荷F 。

解：（1）求支座反力。

选整个梁为研究对象，受力分析如图所示。

列平衡方程，有0yF =∑，0A B F F F F ++-=()0AM=∑F ，6240B F F F ⨯-⨯+⨯=解得：13A F F =，13B F F =-M O212qlM O（2）作梁的弯矩图如图所示。

由图可知该梁的最大弯矩为max 23C M M F ==查表得No.20a 工字钢的抗弯截面系数为3237z W cm =，由强度条件，有max max 2/3[]z zM F W W σσ==≤ 解得663[]3237101601056.922z W F kN σ-⨯⨯⨯⨯≤==所以许可载荷56.9F kN =。

5.8 压板的尺寸和载荷情况如图所示。

材料为45钢，380s MPa σ=，取安全因数1.5n =。

试校核压板的强度。

解：由受力分析可知最大弯矩发生在m m -截面处，且其值为3max 10.0215.4100.02308M P N m =⨯=⨯⨯=⋅m m -截面的抗弯截面系数z W 为333max11302030121212156810zz I W mm y ⨯⨯-⨯⨯=== 压板的最大应力为max max 9308197156810z M MPa W σ-===⨯ 而许用应力为380[]2531.5sMPa nσσ===截面m-m因最大应力小于许用应力，所以压板的强度足够。

eBook工程力学习题详细解答教师用书(第5章)2011-10-1范 钦 珊 教 育 教 学 工 作 室FAN Qin-Shan ,s Education & Teaching Studio习题5－1 习题5－2 习题5－3 习题5－4 习题5－5 习题5－6工程力学习题详细解答之五第5章 杆件的内力分析与内力图5－1 试用截面法计算图示杆件各段的轴力，并画轴力图。

5－2 圆轴上安有5个皮带轮，其中轮2为主动轮，由此输入功率80 kW ；1、3、4、5均为从动轮，它们输出功率分别为25 kW 、15 kW 、30 kW 、10 kW ，若圆轴设计成等截面的，为使设计更合理地利用材料，各轮位置可以互相调整。

1． 请判断下列布置中哪一种最好？(A) 图示位置最合理；(B) 2轮与5轮互换位置后最合理； (C) 1轮与3轮互换位置后最合理； (D) 2轮与3轮互换位置后最合理。

2． 画出带轮合理布置时轴的功率分布图。

30kN 20kN10kN20kN10kN 5kNBAD CB A DC BACBA C(a)(b)(c)(d)F NF ACBF N xDACB102030ACF N x210ADCF N -10习题5－1图解： 1. D2. 带轮合理布置时轴的扭矩图如图（b ）所示。

5－3 一端固定另一端自由的圆轴承受4个外力偶作用，如图所示。

各力偶的力偶矩数值均示于图中。

试画出圆轴的扭矩图。

固定固定(kN.m)习题5－3图P x (kW)2540(b)习题5－2图5－4 试求图示各梁中指定截面上的剪力、弯矩值。

（a）题解：取1-1截面左段为研究对象，1-1截面处的剪力和弯矩按正方向假设：22222211qa qa qa a qa M M qaF Q =−=⎟⎠⎞⎜⎝⎛⋅−=−= 取2-2截面左段为研究对象，2-2截面处的剪力和弯矩按正方向假设：222222222qa qa qa a qa M M qaqa qa F Q =−=⎟⎠⎞⎜⎝⎛⋅−=−=−−= （b）题解：取1-1截面右段为研究对象，1-1截面处的剪力和弯矩按正方向假设：21P 12322qa a qa a qa M qa qa qa qa F F Q −=⋅−⋅−==+=+= 取2-2截面右段为研究对象，2-2截面处的剪力和弯矩按正方向假设：2222222qa qa a qa a qa M qaF Q −=+⋅−⋅−== （c）题解：（1）考虑整体平衡，可解A 、C 支座约束力0m kN 5.4124m kN 4,0)(=⋅××−×+⋅=∑C i A F F M得 kN 25.1=C F0kN 12,0=×−+=∑C A iyF F F得 kN 75.0=A F（2）取1-1截面左段为研究对象，1-1截面处的剪力和弯矩按正方向假设：BB5kN1 m34AAB(b)(a)(c)(d)习题5－4图0,01=−=∑Q A iyF F F得 kN 75.01=Q F02,0)(11=+×−=∑M F F MQ i A得 m kN 5.11⋅=M(3) 取2-2截面左段为研究对象，2-2截面处的剪力和弯矩按正方向假设：0,02=−=∑Q A iyF F F得 kN 75.02=Q F0m kN 42,0)(22=+⋅+×−=∑M F F M Q i A得 m kN 5.22⋅−=M(4) 取3-3截面右段为研究对象，3-3截面处的剪力和弯矩按正方向假设：0kN 12,03=×−+=∑C Q iyF F F得 kN 75.03=Q F0m kN 1221,0)(23=⋅××−−=∑M F M i C得 m kN 13⋅−=M (5) 取4-4截面右段为研究对象，4-4截面处的剪力和弯矩按正方向假设：0kN 12,04=×−=∑Q iyF F得 kN 24=Q F0m kN 1221,0)(24=⋅××−−=∑M F Mi C得 m kN 14⋅−=M （d）题解：（1）考虑整体平衡，可解A 、B 支座约束力03m kN 2m kN 15,0)(=×+⋅+⋅×−=∑B i A F F M 得 kN 1=B F0kN 5,0=+−=∑B A iyF F F得 kN 4=A F（2）取1-1截面左段为研究对象，1-1截面处的剪力和弯矩按正方向假设：0,01=−=∑Q A iyF F F得 kN 41=Q F01,0)(11=+×−=∑M FF M Ai得 m kN 41⋅=M(3) 取2-2截面左段为研究对象，2-2截面处的剪力和弯矩按正方向假设：0kN 5,02=−−=∑Q A iyF F F得 kN 12−=Q F01,0)(22=+×−=∑M F F M A i得 m kN 42⋅=M(4) 取3-3截面右段为研究对象，3-3截面处的剪力和弯矩按正方向假设：0,03=+=∑B Q iyF F F得 kN 13−=Q F1m kN 2,0)(33=×+⋅+−=∑B iF M F M得 m kN 33⋅=M(5) 取4-4截面右段为研究对象，4-4截面处的剪力和弯矩按正方向假设：0,04=+=∑B Q iyF F F得 kN 14−=Q F1,0)(44=×+−=∑B i F M F M得 m kN 14⋅=M5－5 试写出以下各梁的剪力方程、弯矩方程。

第五章 轴心受力构件5.1 验算由2635L ⨯组成的水平放置的轴心拉杆的强度和长细比。

轴心拉力的设计值为270KN ，只承受静力作用，计算长度为3m 。

杆端有一排直径为20mm 的孔眼，钢材为Q235钢。

如截面尺寸不够，应改用什么角钢？注：计算时忽略连接偏心和杆件自重的影响。

解：查型钢表2635L ⨯角钢，221.94, 2.82,215/,6.142x y i cm i cm f N mm A cm ====⨯ 确定危险截面如图1—1截面净截面面积2(6.1420.5)210.28n A cm =-⨯⨯=验算强度： 322227010262.65/215/10.2810n N N mm f N mm A ⨯==>=⨯ （说明截面尺寸不够） 验算长细比：[]0300154.63501.94x x l i λλ===<= 所以，刚度满足要求需用净截面面积322701012.56215n N A cm f ⨯≥== 改用2755L ⨯角钢，22.32,3.29,7.412x y i cm i cm A cm ===⨯此时净截面面积22(7.4120.5)212.8212.56n A cm cm =-⨯⨯=> （满足强度要求）[]030091.183503.29y y l i λλ===<= （满足刚度要求） 5．2 一块—400×20的钢板用两块拼接板—400×12进行拼接。

螺栓孔径为22mm ，排列如图5．30所示。

钢板轴心受拉，N ＝135KN （设计值）。

钢材为Q235钢，解答下列问题：（1）钢板1－1截面的强度够否？ （2）是否还需要验算2—2截面的强度？假定N 力在13个螺栓中平均分配，2—2截面应如何验算？（3）拼接板的强度够否？ 解：（1）验算钢板1—1截面的强度：A n =40×2－3×2.2×2＝66.8cm 2（2）2－2截面虽受力较小，但截面消弱较多，尚应进行验算。

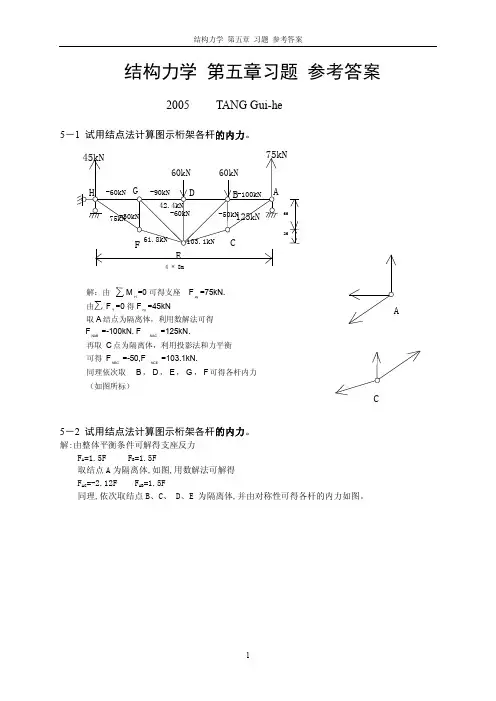
结构力学 第五章习题 参考答案2005级 TANG Gui-he （整理）5－1 试用结点法计算图示桁架各杆的内力。

5－2 试用结点法计算图示桁架各杆的内力。

解:由整体平衡条件可解得支座反力 F A =1.5F F B =1.5F 取结点A 为隔离体,如图,用数解法可解得 F A C =-2.12F F A B =1.5F 同理,依次取结点B 、C 、 D 、E 为隔离体,并由对称性可得各杆的内力如图。

4 * 8m60k N60k N6M 2MA B C D E FG H 解：由 M H =0 可得支座F a y=75kN.由 F Y=0 得 F h y=45kN 取 A 结点为隔离体，利用数解法可得 F N AB=-100kN. F NAC=125kN. 再取 C 点为隔离体，利用投影法和力平衡 可得 F N BC=-50,F NCE=103.1kN.同理依次取 B ， D ， E ， G ， F 可得各杆内力（如图所标）AC-60k N -90k N -100k N 45k N75k N125k N 75k N 42.4k N61.8k N 103.1k N -60k N -50k N -30k N55－4试判断图示桁架中的零杆。

解：图中红色的杆件为零杆在杆中标有 为零杆其中用到K 型和T 型结构判断原理5－5试用截面法计算图示桁架中指定杆件的内力。

2解:（1）求出支座竖向反力为2.5F (↑),（2）作截面I -I ，由∑M A=0得: 2.5F ×15-10F -5F +6F N 1=0 → F N 1=-3.75F （3）由∑M B=0得: 2.5F ×10-F ×5-F N 2×6=0 → F N 2=3.33F （4）利用勾股定理求出A B 杆长7.8F N 4x =5F N 4/3.84 由∑M C=0得: 2.5F ×10-5F +F N 1×6+6×5F N 4/7.8=0 → F N 4=0.65F （5）取结点B 为分析对象,由∑F Y=0得: F N 4×6/7.8+F N 3=0 → F N 3=-0.5F5－6试用截面法计算图示桁架中指定杆件的内力。

第五章 受弯构件正截面承载力计算《建筑结构》第五章习题：共用条件：一类环境使用，结构安全等级为二级。

5-25 一钢筋混凝土矩形梁截面尺寸200m m ×500mm ，弯矩设计值M=120kN ·M 。

混凝土强度等级C25，试计算其纵向受力钢筋截面面积：①当选用HPB235级钢筋时；②改用HRB400级钢筋时；最后画出相应配筋截面图。

解：依题意查得参数：γ0=1，fc=11.9N/mm 2，ft=1.27N/mm 2，c=25mm ，○1fy=210N/mm 2，ξb =0.614；a s =65mm 。

h 0=500-65=435mm 先按单筋矩形截面计算，266.04352009.111012026201=⨯⨯⨯==bh f M c s αα 614.032.0266.0211211=<=⨯--=--=b s ξαξAs=M/[fyh 0（1-0.5ξ）]=1560.65mm 2， 选5ø20，As=1571mm 2＞ρmin =0.45ftbh/fy=0.45×1.27×200×500*210=272mm 2＞0.02bh=0.002×200×500=200mm 2,○2 fy=360N/mm 2，ξb =0.517；a s =40mm ，h 0=500-40=460mm 先按单筋矩形截面计算，238.04602009.111012026201=⨯⨯⨯==bh f M c s αα517.028.0238.0211211=<=⨯--=--=b s ξαξAs=M/[fyh 0（1-0.5ξ）]=120×106/[360×460×（1-0.5×0.28）]=842.61mm 2， 选3#20，As=941mm 2，或4#18，As=1018mm 2＞ρmin =272 mm 2 ○1 ○25-26 某大楼中间走廊单跨简支板，计算跨度 2.18m ，承受均布荷载设计值g ＋q=6kN/m 2（包括自重），混凝土强度等级C20，HPB235级钢筋。

第5章 受弯构件14. 一简支梁，梁跨为7m,焊接组合工字形对称截面150mm 450mm 18mm 12mm ×××（图5-57），梁上作用有均布恒载（标准值，未含梁自重）17.1kN/m ，均布活荷载6.8kN/m ，距梁端2.5m 处，尚有集中恒荷载标准值60kN ，支承长度200mm ，荷载作用面距离钢梁顶面为120mm ，钢材抗拉强度设计值为2215N/mm ，抗剪强度设计值为2125N/mm ，荷载分项系数对恒载取1.2，对活载取1.4。

试验算钢梁截面是否满足强度要求（不考虑疲劳）。

解：截面积2A=1501824141210368mm ××+×=334150450138414323046144mm 1212××=−=x I3x W 1440000mm 2==xI h梁自重 32-67850kg/m 10368mm 10=81.4kg/m=0.814kN/m ××简支梁承受的均布恒载荷载标准值k (0.814+17.1)kN/m=17.9kN/m q =均布线荷载设计值y 1.217.9+1.4 6.8=31kN/m q =××集中荷载设计值y 1.26072kN p =×=（1）验算该简支梁的抗弯强度按y xx nx y ny+γW γW M M f ≤计算，取y 0M =。

集中恒荷载作用处有2x 317 4.512.572 2.531 2.5290.1kN m 272M ×=×+××−××=⋅ 跨中处2x 317 4.513.572 3.531 3.5721279.9kN m 272M ×=×+××−××−×=⋅受压翼缘的宽厚比：w 1b-t b 15012= 3.8t 2t 36−==取x 1.05γ=截面模量6y 22xx nx y ny 290.110+192.3N/mm 215N/mm 1.051440000γγ×==<=×M M f W W （满足） （2）验算抗剪强度 支座处剪力最大且317 4.572108.546.3154.8kN 27V ×=+×=+= 320715018(2079)20712840294mm 2S =××++××=322v w 154.810840294=33.5N/mm 125N/mm 32304614412VS f It τ××==<=×（满足） （3）局部承压强度集中力沿腹板平面作用于梁上翼缘，该荷载作用处未加加劲肋，应验算该处腹板计算高度上边缘的局部承压强度。

钢结构设计原理第五章习题参考答案钢结构设计原理第五章习题参考答案P196：5-7解：（一）计算截面参数222000101000240015mm A =?+??=493310924.3121000390121030400mm I x ?=?-?= 4833106.11210100021240015mm I y ?=?+??= 3610295.4250500105.50740015mm S c ?=??+??=3610045.35.50740015mm S b ?=??=（二）梁自重计算单位长度梁自重标准值：m KN g k /727.15.7810220006=??=- 单位长度梁自重设计值（因题意不明，假设2.1=G γ）m KN g /07.2727.12.1=?=（三）抗弯强度验算计算位置：危险截面：跨中截面，危险点：a 点跨中截面弯矩： m KN M /73.104381307.25.24002max =?+?= 296max /215/47.130********.305.11073.1043mm N f m N W M nx x x ==== γσ抗弯强度满足要求。

（四）抗剪强度验算计算位置：危险截面：支座截面，危险点：c 点支座截面剪力：KN V 46.4131307.221400max =??+= P a2963max /26.451010924.310295.41046.413mm N It VS w ===τ （五）局部承压强度验算计算位置：因支座支承情况不明，故计算集中力作用截面b 点。

223/215/320)15550(10104000.1mm N f mm N l t F z w c ==?+== ψσ 局部承压强度满足要求。

（六）折算应力验算计算位置：集中力作用截面b 点集中力作用截面弯矩：m KN M .22.102725.207.25.246.4132=?-?= b 点由弯矩产生的正应力：296/66.12450010924.305.11022.1027mm N W M nx x x ===γσ 集中力作用截面剪力：KN V 29.4085.207.246.413=?-=b 点由剪力产生的剪应力：2963/68.311010924.310045.31029.408mm N It VS w ===τ 折算应力验算：212222222/5.2362151.1/71.28468.31332066.12432066.124 3mm N f mm N c c =?==?+?-+=+-+βτσσσσ 折算应力满足要求。

5.1一平台的梁格布置如图5.53所示，铺板为预制钢筋混凝土板，焊于次梁上，设平台恒荷载的标准值（不包括梁自重）为 2.0kN/m 2，活荷载的标准值为20kN/m 2。

试选择次梁截面，钢材为Q345钢。

解：平台板与次梁连牢，所以不必计算整体稳定。

假设次梁自重为m kN 1，次梁间距为3m ，故次梁承受的线荷载标准值为：()mm N 67m kN 67320130.2k ==⨯++⨯=q 线荷载设计值为：[可以判定是活载起控制作用，故恒载分项系数为1.2，活载分项系数为1.3]： ()m kN 4.863.13202.1130.2=⨯⨯+⨯+⨯=q 最大弯矩设计值：m kN 8.38864.86818122x ⋅=⨯⨯==ql M 根据抗弯强度选择截面，需要的截面模量为： 36x x nx cm1194)31005.1/(108.388)/(=⨯⨯==f r M W 选用HN 446199812⨯⨯⨯，3x 1217cm W =验算强度： 跨中无孔眼削弱，此nx W 大于3nx cm 1194=W 。

由于型钢的腹板较厚，一般不必验算抗剪强度；若将次梁连于主梁的加劲肋上也不必验算次梁支座处的局部承压强度。

其他截面特性：4X 27146cm I =，自重65.1㎏/m=0.651kN m ，小于假设自重，不必重新计算抗弯强度。

由附表2，验算刚度：()k 2.030.65120366.651kN m 66.651N mm q =⨯++⨯==在全部荷载标准值作用下：()[]33T k 34x T 66.65160005538438420610271001011294250v q l l EI v l ⨯=⋅=⨯⨯⨯⨯=<=在可变荷载标准值作用下：Q Q 12031129466.651323300v v l l ⎡⎤⨯⎣⎦=⨯=<= 5.3 图5.54(a)所示的简支梁，其截面为不对称工字型[图5.54(b)]，材料为Q235-B 钢；梁的中点和两端均有侧向支撑；在集中荷载（未包括梁自重）F =160kN （设计值）的作用下，梁能否保证稳定性？解：该简支梁的稳定性系数b ϕ应按附3.1计算y b 21y x 2y b b 2354.41.4320f h t W Ah ⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫ ⎝⎛+=ηλλβϕ该梁的跨度中点有侧向支撑m 61=l ，且主要承受集中荷载的作用，查附表3.1，得75.1b =β；()()4333y cm 8.23361018.080301121=⨯+⨯+⨯=I 2cm 1048.080110130=⨯+⨯+⨯=Acm 74.41048.2336y y ===A I i 6.12674.4600y 1y ===i l λ 964.0101121301121301121333211b =⨯⨯+⨯⨯⨯⨯=+=I I I α截面不对称影响系数b η（加强受压翼缘）()()7424.01964.028.0128.0b b =-⨯⨯=-=αη求形心，设形心到上翼缘外边缘的距离为d ，则： d⨯=⨯⨯+⨯⨯+⨯⨯1045.81110418.0805.0130cm 2.33=∴d ()()()4232323x cm934405.0811*******1418.080808.01215.0130130121=+-⨯⨯+⨯⨯+-⨯⨯+⨯⨯+-⨯⨯+⨯⨯=d d d I 上翼缘：3x 1x cm 28102.3393440===d I W 下翼缘：x13X x2cm 8.19148.489344082W d I W <==-=()2352356.05.27424.0824.416.12612810821046.126432075.12354.41.432022yb 1y x12y b b >=⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯⨯⨯=⎥⎦⎤⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛+=f h t W Ah ηλλβϕ得：由bb 282.007.1ϕϕ-='∴0.1957.05.2282.007.1b <=-='ϕ 梁单位长度自重标准值（钢材重量集度为 77kN/m 3）： m kN 8.010104774k =⨯⨯==-A q ρmkN 3.4971216041122.18.081418122x ⋅=⨯⨯+⨯⨯⨯=+=Fl ql M236x1b x N/mm 9.184102810957.0103.497=⨯⨯⨯='W M ϕ2mm N 215=<f故梁可以保证其整体稳定性。

P 1073.3试设计如图所示双角钢和节点板间的角焊缝连接。

钢材Q235-B ，焊条E43型，手工焊，轴心拉力设计值N=500kN （静力荷载）。

①采用侧焊缝；②采用三面围焊。

解：角焊缝的强度设计值2160/w f f N mm =，焊缝内力分配系数为120.70,0.30K K ==。

焊角尺寸：max min min max (1~2)8(1~2)7~61.5 1.510 4.74f f h t mm mm mmh t mm=-=-==== 取6f h mm =①采用两边侧焊缝（转角处做绕角焊）： 110.7500350N K N kN =⋅=⨯=，220.3500150N K N kN =⋅=⨯= 肢背计算长度：31135010260.420.720.76160w w f f N l mm h f ⨯===⨯⨯⨯⨯⨯⨯，取1270w l mm =； 肢尖计算长度：31215010111.6120.720.76160w w f f N l mm h f ⨯===⨯⨯⨯⨯⨯⨯，取2120w l mm =； ②采用三面围焊缝：正面角焊缝的长度等于相连角钢肢的宽度，即390w l b mm ==。

3320.720.7690 1.22160147.57w f w f f N h l f kN β=⨯⨯⋅⋅⋅=⨯⨯⨯⨯⨯=1132231147.570.750035073.79276.21221147.570.350015073.7976.2122N K N N kN N K N N kN =-=⨯-=-==-=⨯-=-= 311276.21106205.516211.5120.720.76160w f w f f N l h mm h f ⨯=+=+=+=⨯⨯⨯⨯⨯⨯，取1220w l mm =； 32276.2110656.70662.7020.720.76160w f w f f N l h mm h f ⨯=+=+=+=⨯⨯⨯⨯⨯⨯，取270w l mm =。

第二章（最后一题）解：吊车的计算模型如图（b）所示，横梁上A点受力情况如图（c）所示。

根据力的平衡方程；有：由吊车的几何尺寸得：故有由型钢结构表查得50mmX50mmX5mm的等边角钢的截面积为4.80cm2，10号槽钢的截面积为12.74cm 2。

则AC 杆所受拉应力为由此求得AB 梁所受压应力为 由此求得取两者中较小值即为吊车允许的最大起吊重量。

解：1.因在A 、B 点处均有集中荷载作用，故AB 、BC 段的轴力各不相同。

分别在AB 、BC 段的任一截面处将杆截开。

假定AB 段的轴力为对截开的两部分分别应用平衡方程(a)30(b)即可确定AB、BC段杆横截面上的轴力，分别为于是在坐标系上即可画出轴力图，如图（b）所示。

2.各段杆横截面上的工作应力为AB段：BC段：3.各段杆的变形量分别为AB段：BC段：故得杆的变形总量解：1. AB段所受轴力为BD段所受轴力为取钢杆的弹性模量为200GPa，铜的弹性模量为110GPa。

则，AB段杆的轴向伸长量为BC段杆的轴向伸长量为CD段杆的轴向伸长量为故C截面的铅垂位移为1.474+1.474=2.948mmD截面的铅垂位移为1.474+1.474+2.233=5.181mm2. 杆的总伸长为从而得出解：求出铝筒在F P作用下的压缩变形，钢杆在F P作用下的伸长变形，然后将两者相加即为C端向下移动的距离。

解：A点为坐标原点，x轴方向垂直向下。

则故AC段的应变为：解:旋紧螺栓受压，固定螺栓受拉。

根据力矩的平衡，求出所受的拉压应力即可。

解：2-8解：分别求出每个杆件的载荷，最后确定出整个结构的需用载荷。

2-9解：因铝板跟钢板的变形量相同，故有：2-10解：同2-9题。

解：第三章BAADD C第四章习题4-3解：1.两轴传递的扭矩实心圆轴所受最大剪应力为空心圆轴所受最大剪应力为上述计算结果表明，实心圆轴与空心圆轴横截面上的最大剪应力都正好等于许用剪应力。

因此，实心圆轴与空心圆轴的强度都是安全的。