2016-2017年四川省成都外国语学校高一(上)数学期中试卷和答案

成都外国语学校2016～2017学年上期高2016级高一10月月考数学试题满分:150分 时间：120分钟。

第Ⅰ卷(60分）一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中,只有一项是符合题目要求的. 1.设全集{1,2,3,4,5}U =，集合{1,3,5}M =,{2,5}N =，则Venn 图中阴影部分表示的集合是（ ）A 。

{5} B. {1,3} C 。

{2,4} D 。

{2,3,4}2。

已知:f A B→为从集合A 到集合B 的一个映射,{(,)|,},:(,)(,)A B x y x R y R f x y x y x y ==∈∈→+-,若A 中元素(1,)a 的象是(,4)b ,则实数,a b 的值分别为（ ）A.2,3-B 。

2,3-- C. 3,2-- D. 1,43．若函数()|1|||f x x x a =---是奇函数而不是偶函数,且()f x 不恒为0，则2016(1)a +的值（）A. 0 B 。

1 C 。

20162 D 。

201634。

已知21,(0)()(1)1,(0)x x f x f x x ⎧->=⎨+-≤⎩，则(1)f -=（)A 。

2- B. 1-C 。

0 D. 15。

设全集{|||4}U x Z x =∈<,集合{2,1,3}S =-,若UC P S⊆，则这样的集合P 的个数共有( ） A ．5 B ．6 C ．7 D ．86。

若集合2{|210}A x kx x =--=的元素至多一个，则实数k 的取值集合为（ ）A.1k ≤-B.1k ≤-或者0k =C.(,1){0}-∞-D.(,1]{0}-∞-7．已知函数21(2016)(0)2x f x x x++=>，则函数()f x 的最小值是（）A 。

2 B.2016 C.2015- D. 1 8. 下列五种说法正确的个数有（ ） ①若,,ABC 为三个集合，满足AB BC=，则一定有A C ⊆；②函数的图像与垂直于x 轴的直线的交点有且仅有一个； ③若,A U B U ⊆⊆，则()()UA AB AC B =；④若函数()f x 在[,]a b 和[,]b c 都为增函数，则()f x 在[,]a c 为增函数。

成都外国语学校 高一 上期半期考试数学试卷满分150分，测试时间：120分钟 命题人：全 鑫 审题人：全 鑫 第Ⅰ卷（选择题共60分）一．选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.设集合{}1,2,4A =，{}240x x x m B =-+=．若{}1AB =，则B =（ ）A ．{}1,3-B ．{}1,0C ．{}1,3D ．{}1,5。

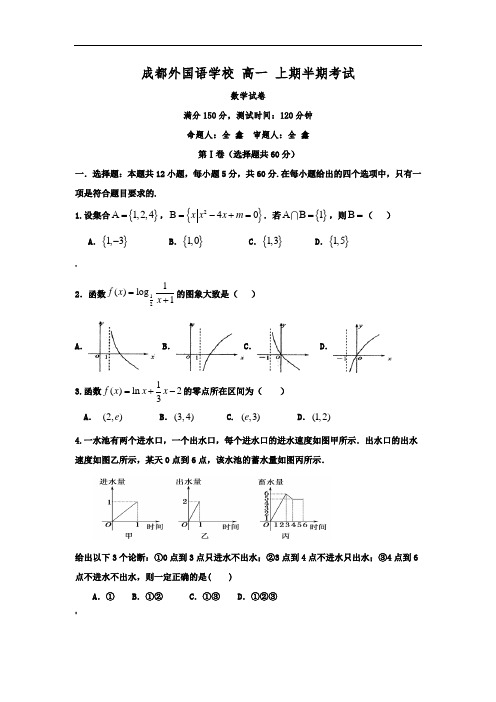
2．函数121()log 1f x x =+的图象大致是（ ）A ．B ．C ．D ．3.函数1()ln 23f x x x =+-的零点所在区间为（ ） A ． (2,)e B ．(3,4) C. (,3)e D ．(1,2)4.一水池有两个进水口，一个出水口，每个进水口的进水速度如图甲所示．出水口的出水速度如图乙所示，某天0点到6点，该水池的蓄水量如图丙所示．给出以下3个论断：①0点到3点只进水不出水；②3点到4点不进水只出水；③4点到6点不进水不出水，则一定正确的是( )A ．①B ．①②C ．①③D ．①②③:5.已知123515,12,3x og y og z -===，则下列关系正确的是（ ）A ．x y z >>B ．y x z >>C ．z y x >>D ．x z y >>6. 函数23()()2x f x x =-的零点的个数为（ ） B. 2 D. 47．方程()24250x m x m +-+-=的一根在区间()1,0-内，另一根在区间()0,2内，则m的取值范围是（ ） A ．5,53⎛⎫ ⎪⎝⎭ B ．7,53⎛⎫- ⎪⎝⎭ C ．()5,5,3⎛⎫-∞+∞ ⎪⎝⎭ D ．5,3⎛⎫-∞ ⎪⎝⎭8.若数()2)3f x x =+，且(log 2019)5a f =，则1(log )2019af =（ ） …A. 5-B. 4C. 3D. 19.已知函数2()|l g |,(2)f x o x x =≤,若a b ≠，且()()f a f b =，则a b +的取值范围是（ ） A. 5(1,]2 B. 5(2,]2C. (2,)+∞D. [1,2] 10．已知max{,}a b 表示,a b 两数中的最大值，若|||2|()max{,}x x f x e e +=，则()f x 的最小值为（ ）A. eB. 1C. 2eD. 2 11.给出下列命题，其中正确的命题的个数（ ） ①函数()122log 23y x x =-+图象恒在x 轴的下方；?②将2xy =的图像经过先关于y 轴对称，再向右平移1个单位的变化后为12xy -=的图像；③若函数()()22log 21f x x ax =-+的值域为R ，则实数a 的取值范围是()1,1-； ④函数()x f x e =的图像关于y x =对称的函数解析式为ln .y x = B. 2C. 3D. 4 12.若函数9()log (91)2xxf x =+-，则使不等式()0f x m -≤有解时，实数m 的最小值为（ ） A. 0 B. 3log 2- C. 3log 2 D. 3log二、填空题（本大题共4小题，每小题5分，共20分）13．函数log (25)1a y x =--恒过定点的坐标为__________.14．若5(21)2xf x x -=+，则(3)f -=________.15．若函数12()2xx m f x n +-=+是奇函数．则实数m n +=_______.:16.已知函数3,()8log ,a x x af x x x a⎧≤=⎨>⎩若存在实数1212,,x x x x ≠且使得函数12()()f x f x =成立，则实数a 的取值范围为_________.三、解答题：（本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤） 17.（本小题满分10分）已知全集U R =，集合{}02|>+=a x x A ，集合B是()f x =.（Ⅰ）当2a =时，求集合A B ；（Ⅱ）若()U B C A B =，求实数a 的取值范围.]18. 求下列各式的值（Ⅰ）2311log 222)22(21(2)3[(1]log 4-+-+；（II ）已知11223a a -+=，求332222a aa a--++值.&19.设函数()3,()9xxg x h x ==（I ）解关于x 的方程()11()2(1)0h x g x h -+=；（II ）令()F x =，求1220182019()()()()2020202020202020F F F F ++++的值.；20. 已知函数222()()mm f x x m Z -++=∈为偶函数，且(3)(2)f f >.（Ⅰ）求m 的值，并确定()f x 的解析式；（Ⅱ）若()log [()5](0,1)a g x f x ax a a =-+>≠且,是否存在实数a ，使得()g x 在区间[1,2]上为减函数.21．已知()f x 是定义在[1,1]-上的奇函数，且(1)1f =，若对于任意的,[1,1]a b ∈-且0,a b +≠有()()0f a f b a b+>+恒成立.：（I ）判断()f x 在[1,1]-上的单调性，并证明你的结论；（II ）若函数()[24]1xxF x f a =⋅++有零点,求实数a 的取值范围.22．已知函数2()(0,1)x xa tf x a a a +=>≠是奇函数．（I ）求实数t 的值；（II ）若(1)0f <，对任意[0,1]x ∈有21(2)f x kx k a a-->-恒成立，求实数k 取值范围； ！（III ）设22()log [()],(0,1)xx m g x aa mf x m m -=+->≠,若3(1)2f =，问是否存在实数m 使函数()g x 在2[1,log 3]上的最大值为0 若存在，求出m 的值；若不存在，说明理由.]高一数学试卷(参考答案)一、 选择题 1～6, CDCADC 7～12, BDBACD二、 填空题： 13. (3,1)- 14. 1-215. 3± 16. (0,1)(2,)+∞ 三、解答题：17.解：（Ⅰ）{|1}A x x =>-， 1{|0}2B x x =-<≤ 则A B B = （Ⅱ） {|}2U a C A x x =≤- ，U B C A ⊆, 所以0a ≤18.解：（Ⅰ）53 （Ⅱ） 1847，19.解：（Ⅰ）3log 2,2x x == （Ⅱ）2019220.解：（1）(3)(2)f f >，所以()f x 在(0,)+∞上增函数，所以，2220m m -++>即：11m <<+m Z ∈故0,1,2m =，当0,2m =时，2222m m -++=此时，2()f x x =满足条件当1m =时，3()f x x =不满足条件 综上：0,2m =，2()f x x =（2）由（1）可知2()log [5](0,1)a g x x ax a a =-+>≠且假设存在实数a 使得2()log [5](0,1)a g x x ax a a =-+>≠且在[1,2]上为减函数.…①当01a <<时，25u x ax =-+在[1,2]上增函数， 即：12a≤，60a ->，得到01a <<②当1a >时，同理：9[4,)2综上：存在a 满足9(0,1)[4,)221.解（1）设任意12,[1,1]x x ∈-，且12x x <、令12,a x b x ==-，因为对于任意的,[1,1]a b ∈-且0,a b +≠有()()0f a f b a b+>+恒成立.所以1212()()0f x f x x x +->-，又因为()f x 是定义在[1,1]-上的奇函数 1212()()0f x f x x x ->-，120x x -< ， 所以12()()f x f x <故()f x 在[1,1]-上是增函数（2）因为()[24]1xxF x f a =⋅++有零点，所以方程[24]1xxf a ⋅+=-有解又因为(1)(1)1f f -=-=-，所以[24](1)x xf a f ⋅+=- 即 241x x a ⋅+=-有解即1(2)2xxa =-+，即2a ≤- 22.解：（1）因为f (f )的定义域为f，且f (f )为奇函数，^所以f (f )=f +ff=f ，解得f =−f .检验：当f =−f 时，f (f )=f ff −f f f=f f −f −f ，对任意f ∈f，都有f (−f )=f −f −f f =−f (f )，即f (f )是奇函数，所以f =−f 成立。

一、选择题1．(0分)[ID ：11822]函数()2312x f x x -⎛⎫=- ⎪⎝⎭的零点所在的区间为（ ） A ．()0,1B ．()1,2C ．()2,3D ．()3,42．(0分)[ID ：11819]在下列区间中，函数()43xf x e x =+-的零点所在的区间为（ ） A ．1,04⎛⎫-⎪⎝⎭B ．10,4⎛⎫ ⎪⎝⎭C ．11,42⎛⎫⎪⎝⎭D ．13,24⎛⎫⎪⎝⎭3．(0分)[ID ：11799]已知(31)4,1()log ,1a a x a x f x x x -+<⎧=⎨≥⎩是(,)-∞+∞上的减函数，那么a的取值范围是（ ）A ．(0,1)B ．1(0,)3C ．11[,)73D ．1[,1)74．(0分)[ID ：11779]已知()f x 是定义域为(,)-∞+∞的奇函数,满足(1)(1)f x f x -=+.若(1)2f =，则(1)(2)(3)(50)f f f f ++++=（ ）A ．50-B ．0C ．2D ．505．(0分)[ID ：11773]如图，U 为全集，M 、P 、S 是U 的三个子集，则阴影部分所表示的集合是（ ）A ．()M P S ⋂⋂B ．()M P S ⋂⋃C ．()()UM P S ⋂⋂D ．()()UM P S ⋂⋃6．(0分)[ID ：11749]设x 、y 、z 为正数，且235x y z ==，则 A ．2x <3y <5z B ．5z <2x <3y C ．3y <5z <2xD ．3y <2x <5z7．(0分)[ID ：11745]已知函数(),1log ,1x a a x f x x x ⎧≤=⎨>⎩（1a >且1a ≠），若()12f =，则12f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭（ ） A ．1-B ．12-C ．12D 28．(0分)[ID ：11737]已知奇函数()f x 在R 上是增函数，若21log 5a f ⎛⎫=- ⎪⎝⎭，()2log 4.1b f =，()0.82c f =，则,,a b c 的大小关系为( )A ．a b c <<B ．b a c <<C ．c b a <<D ．c a b <<9．(0分)[ID ：11734]已知函数()f x =2log (1),(1,3)4,[3,)1x x x x ⎧+∈-⎪⎨∈+∞⎪-⎩，则函数[]()()1g x f f x =-的零点个数为（ ）A ．1B ．3C ．4D ．610．(0分)[ID ：11733]设0.60.3a =，0.30.6b =，0.30.3c =，则a ，b ，c 的大小关系为（ ） A ．b a c <<B ．a c b <<C ．b c a <<D ．c b a <<11．(0分)[ID ：11732]方程 4log 7x x += 的解所在区间是（ ） A ．(1,2)B ．(3,4)C ．(5,6)D ．(6,7)12．(0分)[ID ：11817]函数y =）A ．(41)--，B ．(41)-，C ．(11)-，D ．(11]-， 13．(0分)[ID ：11803]设0.13592,ln ,log 210a b c ===，则,,a b c 的大小关系是 A ．a b c >>B ．a c b >>C ．b a c >>D ．b c a >>14．(0分)[ID ：11783]函数()(1)f x x x =-在[,]m n 上的最小值为14-，最大值为2，则n m -的最大值为（ ）A ．52B．522+C ．32D ．215．(0分)[ID ：11760]设函数3()f x x x =+ ，. 若当02πθ<<时，不等式(sin )(1)0f m f m θ+-> 恒成立，则实数m 的取值范围是（ ）A ．1(,1]2B ．1(,1)2C ．[1,)+∞D ．(,1]-∞二、填空题16．(0分)[ID ：11911]已知函数2()121()f x ax x ax a R =+++-∈的最小值为0，则实数a =_________.17．(0分)[ID ：11906]1232e 2(){log (1)2x x f x x x ，，-<=-≥，则f （f （2））的值为____________．18．(0分)[ID ：11896]函数()f x 的定义域是__________．19．(0分)[ID ：11883]已知函数()f x 是定义在 R 上的奇函数，且当0x >时，()21x f x =-，则()()1f f -的值为______．20．(0分)[ID ：11876]函数y =lg (x +1)+12−x 的定义域为___．21．(0分)[ID ：11867]已知函数1)4f x +=-，则()f x 的解析式为_________. 22．(0分)[ID ：11866]已知函数()f x 满足对任意的x ∈R 都有11222⎛⎫⎛⎫++-= ⎪ ⎪⎝⎭⎝⎭f x f x 成立，则 127...888f f f ⎛⎫⎛⎫⎛⎫+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭＝ ． 23．(0分)[ID ：11861]已知函数()()212log 22f x mx m x m ⎡⎤=+-+-⎣⎦，若()f x 有最大值或最小值，则m 的取值范围为______．24．(0分)[ID ：11844]有15人进家电超市，其中有9人买了电视，有7人买了电脑，两种均买了的有3人，则这两 种都没买的有 人.25．(0分)[ID ：11841]某班有36名同学参加数学、物理、化学竞赛小组，每名同学至多参加两个小组，已知参加数学、物理、化学小组的人数分别为26，15，13，同时参加数学和物理小组的有6人，同时参加物理和化学小组的有4人，则同时参加数学和化学小组的有__________人．三、解答题26．(0分)[ID ：11981]已知函数()212ax f x x b +=+是奇函数，且()312f =.（1）求实数a ，b 的值；（2）判断函数()f x 在(],1-∞-上的单调性，并用定义加以证明． （3）若[]2,1x ∈--，求函数的值域27．(0分)[ID ：11972]求关于x 的方程2210ax x ++=至少有一个负根的充要条件. 28．(0分)[ID ：11971]设集合A ＝{x ∈R|x 2＋4x ＝0}，B ＝{x ∈R|x 2＋2(a ＋1)x ＋a 2－1＝0，a ∈R }，若B ⊆A ，求实数a 的值．29．(0分)[ID ：11956]已知函数()lg(2)lg(2)f x x x =++-. （1）求函数()y f x =的定义域； （2）判断函数()y f x =的奇偶性； （3）若(2)()f m f m -<，求m 的取值范围.30．(0分)[ID ：11935]已知集合{}24xA x R =∈<，(){}lg 4B x R y x =∈=-.（1）求集合,A B ；（2）已知集合{}11C x m x m =-≤≤-，若集合()C A B ⊆⋃，求实数m 的取值范围.【参考答案】2016-2017年度第*次考试试卷参考答案**科目模拟测试一、选择题1．B2．C3．C4．C5．C6．D7．C8．C9．C10．B11．C12．C13．A14．B15．D二、填空题16．【解析】【分析】设计算可得再结合图象即可求出答案【详解】解：设则则由于函数的最小值为0作出函数的大致图象结合图象得所以故答案为：【点睛】本题主要考查分段函数的图象与性质考查转化思想考查数形结合思想属17．2【解析】【分析】先求f（2）再根据f（2）值所在区间求f（f（2））【详解】由题意f（2）=log3（22–1）=1故f（f（2））=f（1）=2×e1–1=2故答案为：2【点睛】本题考查分段函数18．【解析】由得所以所以原函数定义域为故答案为19．【解析】由题意可得：20．(-12)∪(2+∞)【解析】【分析】根据式子成立的条件对数式要求真数大于零分式要求分母不等于零即可求得函数的定义域【详解】要使函数有意义则x+1>012-x≠0解得x>-1且x≠2所以函数的定义域21．【解析】【分析】利用换元法求解析式即可【详解】令则故故答案为【点睛】本题考查函数解析式的求法换元法是常见方法注意新元的范围是易错点22．7【解析】【分析】【详解】设则因为所以故答案为723．或【解析】【分析】分类讨论的范围利用对数函数二次函数的性质进一步求出的范围【详解】解：∵函数若有最大值或最小值则函数有最大值或最小值且取最值时当时由于没有最值故也没有最值不满足题意当时函数有最小值没24．【解析】【分析】【详解】试题分析：两种都买的有人所以两种家电至少买一种有人所以两种都没买的有人或根据条件画出韦恩图：(人)考点：元素与集合的关系25．8【解析】【分析】画出表示参加数学物理化学竞赛小组集合的图结合图形进行分析求解即可【详解】由条件知每名同学至多参加两个小组故不可能出现一名同学同时参加数学物理化学竞赛小组设参加数学物理化学竞赛小组的三、解答题26．27．28．29．30．2016-2017年度第*次考试试卷 参考解析【参考解析】**科目模拟测试一、选择题 1．B 解析：B 【解析】 【分析】判断函数()2312x f x x -⎛⎫=- ⎪⎝⎭单调递增，求出f （0）=-4，f （1）=-1，f （2）=3＞0，即可判断．【详解】∵函数()2312x f x x -⎛⎫=- ⎪⎝⎭单调递增，∴f（0）=-4，f （1）=-1， f （2）=7＞0，根据零点的存在性定理可得出零点所在的区间是()1,2， 故选B ． 【点睛】本题考查了函数的单调性，零点的存在性定理的运用，属于容易题．2．C解析：C 【解析】 【分析】先判断函数()f x 在R 上单调递增，由104102f f ⎧⎛⎫< ⎪⎪⎪⎝⎭⎨⎛⎫⎪> ⎪⎪⎝⎭⎩,利用零点存在定理可得结果.【详解】因为函数()43xf x e x =+-在R 上连续单调递增，且114411221143204411431022f e e f e e ⎧⎛⎫=+⨯-=-<⎪ ⎪⎪⎝⎭⎨⎛⎫⎪=+⨯-=-> ⎪⎪⎝⎭⎩, 所以函数的零点在区间11,42⎛⎫⎪⎝⎭内，故选C.【点睛】本题主要考查零点存在定理的应用，属于简单题.应用零点存在定理解题时，要注意两点：（1）函数是否为单调函数；（2）函数是否连续.3．C解析：C 【解析】 【分析】要使函数()f x 在(,)-∞+∞上为减函数，则要求①当1x <，()(31)4f x a x a =-+在区间(,1)-∞为减函数，②当1x ≥时，()log a f x x =在区间[1,)+∞为减函数，③当1x =时，(31)14log 1a a a -⨯+≥，综上①②③解方程即可.【详解】令()(31)4g x a x =-+，()log a h x x =.要使函数()f x 在(,)-∞+∞上为减函数，则有()(31)4g x a x =-+在区间(,1)-∞上为减函数，()log a h x x =在区间[1,)+∞上为减函数且(1)(1)g h ≥,∴31001(1)(31)14log 1(1)a a a g a a h -<⎧⎪<<⎨⎪=-⨯+≥=⎩,解得1173a ≤<. 故选：C. 【点睛】考查分段函数求参数的问题.其中一次函数y ax b =+，当0a <时，函数y ax b =+在R 上为减函数，对数函数log ,(0)a y x x =>，当01a <<时，对数函数log ay x =在区间(0,)+∞上为减函数.4．C解析：C 【解析】分析：先根据奇函数性质以及对称性确定函数周期，再根据周期以及对应函数值求结果. 详解：因为()f x 是定义域为(,)-∞+∞的奇函数，且(1)(1)f x f x -=+， 所以(1)(1)(3)(1)(1)4f x f x f x f x f x T +=--∴+=-+=-∴=, 因此(1)(2)(3)(50)12[(1)(2)(3)(4)](1)(2)f f f f f f f f f f ++++=+++++，因为(3)(1)(4)(2)f f f f =-=-，，所以(1)(2)(3)(4)0f f f f +++=，(2)(2)(2)(2)0f f f f =-=-∴=，从而(1)(2)(3)(50)(1)2f f f f f ++++==，选C.点睛：函数的奇偶性与周期性相结合的问题多考查求值问题，常利用奇偶性及周期性进行变换，将所求函数值的自变量转化到已知解析式的函数定义域内求解．5．C解析：C 【解析】 【分析】先根据图中的阴影部分是M∩P 的子集，但不属于集合S ，属于集合S 的补集，然后用关系式表示出来即可． 【详解】图中的阴影部分是： M∩P 的子集，不属于集合S ，属于集合S 的补集,即是C U S 的子集则阴影部分所表示的集合是（M∩P ）∩(∁U S). 故选C ． 【点睛】本题主要考查了Venn 图表达集合的关系及运算，同时考查了识图能力，属于基础题．6．D解析：D 【解析】令235(1)x y zk k ===>，则2log x k =，3log =y k ，5log =z k∴22lg lg 3lg 913lg 23lg lg8x k y k =⋅=>，则23x y >， 22lg lg5lg 2515lg 25lg lg32x k z k =⋅=<，则25x z <，故选D. 点睛:对于连等问题，常规的方法是令该连等为同一个常数，再用这个常数表示出对应的,,x y z ，通过作差或作商进行比较大小.对数运算要记住对数运算中常见的运算法则，尤其是换底公式以及0与1的对数表示.7．C解析：C 【解析】 【分析】由()12f =，求得2a =，得到函数的解析式，进而可求解1(())2f f 的值，得到答案． 【详解】由题意，函数(),1(1log ,1x a a x f x a x x ⎧≤=>⎨>⎩且1)a ≠，()12f =，所以()12f a ==，所以()22,1(1log ,1x x f x a x x ⎧≤=>⎨>⎩且1)a ≠，所以121()22f ==所以211(())log 22f f f ===，故选C ． 【点睛】本题主要考查了函数解析式的求解，以及函数值的运算问题，其中解答中根据题意准确求得函数的解析式，合理利用解析式求解是解答的关键，着重考查了运算与求解能力，属于基础题．8．C解析：C 【解析】由题意：()221log log 55a f f ⎛⎫=-= ⎪⎝⎭， 且：0.822log 5log 4.12,122>><<，据此：0.822log 5log 4.12>>，结合函数的单调性有：()()()0.822log 5log 4.12f f f >>，即,a b c c b a >><<. 本题选择C 选项.【考点】 指数、对数、函数的单调性【名师点睛】比较大小是高考常见题，指数式、对数式的比较大小要结合指数函数、对数函数，借助指数函数和对数函数的图象，利用函数的单调性进行比较大小，特别是灵活利用函数的奇偶性和单调性数形结合不仅能比较大小，还可以解不等式.9．C解析：C 【解析】 【分析】令[]()()10g x f f x =-=,可得[]()1f f x =,解方程()1f x =,结合函数()f x 的图象,可求出答案. 【详解】令[]()()10g x f f x =-=,则[]()1f f x =,令()1f x =,若2log (1)1x +=,解得1x =或12x =-,符合(1,3)x ∈-;若411x =-,解得5x =,符合[3,)x ∈+∞.作出函数()f x 的图象,如下图,(]1,0x ∈-时,[)()0,f x ∈+∞;()0,3x ∈时,()()0,2f x ∈;[3,)x ∈+∞时,(]()0,2f x ∈. 结合图象,若()1f x =,有3个解;若1()2f x =-,无解;若()5f x =,有1个解. 所以函数[]()()1g x f f x =-的零点个数为4个. 故选:C.【点睛】本题考查分段函数的性质,考查了函数的零点,考查了学生的推理能力,属于中档题.10．B解析：B 【解析】 【分析】根据指数函数的单调性得出0.60.30.30.3<，而根据幂函数的单调性得出0.30.30.30.6<，从而得出a ，b ，c 的大小关系． 【详解】 解：0.3x y =在定义域上单调递减，且0.360.<，0.60.30.30.3∴<，又0.3y x∴=在定义域上单调递增，且0.360.<，0.30.30.30.6∴<， 0.60.30.30.30.30.6∴<<，a cb ∴<<故选：B ． 【点睛】考查指数函数和幂函数的单调性，以及增函数和减函数的定义．11．C解析：C 【解析】 【分析】令函数4()log 7xf x x =+-，则函数()f x 是()0,∞+上的单调增函数，且是连续函数，根据(5)(6)0f f ⋅<，可得函数4()log 7xf x x =+-的零点所在的区间为()5,6，由此可得方程4log 7x x +=的解所在区间． 【详解】令函数4()log 7xf x x =+-，则函数()f x 是()0,∞+上的单调增函数，且是连续函数.∵(5)0f <，(6)0>f ∴(5)(6)0f f ⋅<∴故函数4()log 7xf x x =+-的零点所在的区间为()5,6∴方程4log 7x x +=的解所在区间是()5,6 故选C. 【点睛】零点存在性定理：利用定理不仅要函数在区间[,]a b 上是连续不断的曲线，且()()0f a f b ⋅<，还必须结合函数的图象与性质（如单调性、奇偶性）才能确定函数有多少个零点.12．C解析：C 【解析】要使函数有意义，需使210{340x x x +>--+>，即1{41x x >--<<，所以1 1.x -<<故选C13．A解析：A 【解析】 试题分析：，，即，，．考点：函数的比较大小．14．B解析：B 【解析】 【分析】根据二次函数的图象和性质，求出最大值和最小值对应的x 的取值，然后利用数形结合即可得到结论． 【详解】当x≥0时，f （x ）=x （|x|﹣1）=x 2﹣x=（x ﹣12）2﹣1144≥-，当x＜0时，f（x）=x（|x|﹣1）=﹣x2﹣x=﹣（x+12）2+14，作出函数f（x）的图象如图：当x≥0时，由f（x）=x2﹣x=2，解得x=2．当x=12时，f（12）=14-．当x＜0时，由f（x）=）=﹣x2﹣x=14 -．即4x2+4x﹣1=0，解得x=24444432248-±+⨯-±=⨯=4421282-±-±=，∴此时x=122--，∵[m，n]上的最小值为14-，最大值为2，∴n=2，12122m--≤≤，∴n﹣m的最大值为2﹣122--=5222+，故选：B．【点睛】本题主要考查函数最值的应用，利用二次函数的图象和性质是解决本题的关键，利用数形结合是解决本题的基本数学思想．15．D解析：D【解析】【分析】【详解】易得()f x是奇函数，2()310()f x x f x '=+>⇒在R 上是增函数，不等式(sin )(1)0f m f m θ+-> 恒成立. 可得11(sin )(1)sin 1,0sin 111sin 1sin f m f m m m m m θθθθθ>-⇒>-⇒<<<⇒⇒≤--， 故选D.二、填空题16．【解析】【分析】设计算可得再结合图象即可求出答案【详解】解：设则则由于函数的最小值为0作出函数的大致图象结合图象得所以故答案为：【点睛】本题主要考查分段函数的图象与性质考查转化思想考查数形结合思想属 解析：±1. 【解析】 【分析】设2()()1()()21g x h x ax g x h x x ax +=+⎧⎨-=+-⎩，计算可得2(),()()()2(),()()g x g x h x f x h x g x h x ≥⎧=⎨<⎩，再结合图象即可求出答案． 【详解】解：设2()()1()()21g x h x ax g x h x x ax +=+⎧⎨-=+-⎩，则22()()1g x x ax h x x ⎧=+⎨=-⎩， 则()()()()()f x g x h x g x h x =++-2(),()()2(),()()g x g x h x h x g x h x ≥⎧=⎨<⎩，由于函数()f x 的最小值为0，作出函数()g x ，()h x 的大致图象，结合图象，210x -=，得1x =±， 所以1a =±， 故答案为：±1． 【点睛】本题主要考查分段函数的图象与性质，考查转化思想，考查数形结合思想，属于中档题．17．2【解析】【分析】先求f （2）再根据f （2）值所在区间求f （f （2））【详解】由题意f （2）=log3（22–1）=1故f （f （2））=f （1）=2×e1–1=2故答案为：2【点睛】本题考查分段函数解析：2 【解析】 【分析】先求f （2），再根据f （2）值所在区间求f （f （2））. 【详解】由题意，f （2）=log 3（22–1）=1，故f （f （2））=f （1）=2×e 1–1=2，故答案为：2． 【点睛】本题考查分段函数求值，考查对应性以及基本求解能力.18．【解析】由得所以所以原函数定义域为故答案为 解析：(],0-∞【解析】由120x -≥，得21x ≤，所以0x ≤，所以原函数定义域为(],0-∞，故答案为(],0-∞.19．【解析】由题意可得： 解析：1-【解析】由题意可得：()()()()()111,111f f ff f -=-=--=-=-20．(-12)∪(2+∞)【解析】【分析】根据式子成立的条件对数式要求真数大于零分式要求分母不等于零即可求得函数的定义域【详解】要使函数有意义则x+1>012-x≠0解得x>-1且x≠2所以函数的定义域 解析：(−1,2)∪(2,+∞)【解析】 【分析】根据式子成立的条件，对数式要求真数大于零，分式要求分母不等于零，即可求得函数的定义域. 【详解】要使函数有意义，则{x +1>012−x≠0，解得x >−1且x ≠2，所以函数的定义域为：(−1,2)∪(2,+∞)， 故答案是：(−1,2)∪(2,+∞). 【点睛】该题考查的是有关函数的定义域的求解问题，在求解的过程中，注意对数式和分式成立的条件即可，属于简单题目.21．【解析】【分析】利用换元法求解析式即可【详解】令则故故答案为【点睛】本题考查函数解析式的求法换元法是常见方法注意新元的范围是易错点解析：2()23(1)f x x x x =--≥【解析】 【分析】利用换元法求解析式即可 【详解】 令11t x =+≥，则()21x t =-故()()214f t t =--=223(1)t t t --≥ 故答案为2()23(1)f x x x x =--≥ 【点睛】本题考查函数解析式的求法，换元法是常见方法，注意新元的范围是易错点22．7【解析】【分析】【详解】设则因为所以故答案为7解析：7 【解析】 【分析】 【详解】 设， 则，因为11222⎛⎫⎛⎫++-= ⎪ ⎪⎝⎭⎝⎭f x f x ， 所以，,故答案为7.23．或【解析】【分析】分类讨论的范围利用对数函数二次函数的性质进一步求出的范围【详解】解：∵函数若有最大值或最小值则函数有最大值或最小值且取最值时当时由于没有最值故也没有最值不满足题意当时函数有最小值没解析：{|2m m >或2}3m <- 【解析】 【分析】分类讨论m 的范围，利用对数函数、二次函数的性质，进一步求出m 的范围. 【详解】解：∵函数()()212log 22f x mx m x m ⎡⎤=+-+-⎣⎦，若()f x 有最大值或最小值，则函数2(2)2y mx m x m =+-+-有最大值或最小值，且y 取最值时，0y >.当0m =时，22y x =--，由于y 没有最值，故()f x 也没有最值，不满足题意. 当0m >时，函数y 有最小值，没有最大值，()f x 有最大值，没有最小值.故y 的最小值为24(2)(2)4m m m m ---，且 24(2)(2)04m m m m--->，求得 2m >；当0m <时，函数y 有最大值，没有最小值，()f x 有最小值，没有最大值.故y 的最大值为24(2)(2)4m m m m---，且 24(2)(2)04m m m m --->，求得23m <-. 综上，m 的取值范围为{|2m m >或2}3m <-. 故答案为：{|2m m >或2}3m <-. 【点睛】本题主要考查复合函数的单调性，二次函数、对数函数的性质，二次函数的最值，属于中档题.24．【解析】【分析】【详解】试题分析：两种都买的有人所以两种家电至少买一种有人所以两种都没买的有人或根据条件画出韦恩图：(人)考点：元素与集合的关系 解析：【解析】 【分析】 【详解】试题分析：两种都买的有人，所以两种家电至少买一种有人.所以两种都没买的有人.或根据条件画出韦恩图：(人).考点：元素与集合的关系.25．8【解析】【分析】画出表示参加数学物理化学竞赛小组集合的图结合图形进行分析求解即可【详解】由条件知每名同学至多参加两个小组故不可能出现一名同学同时参加数学物理化学竞赛小组设参加数学物理化学竞赛小组的解析：8 【解析】 【分析】画出表示参加数学、物理、化学竞赛小组集合的Venn 图，结合图形进行分析求解即可． 【详解】由条件知，每名同学至多参加两个小组，故不可能出现一名同学同时参加数学、物理、化学竞赛小组，设参加数学、物理、化学竞赛小组的人数构成的集合分别为A ，B ，C ， 则()0card A B C ⋂⋂=，()6card A B ⋂=，()4card B C ⋂=， 由公式()card A B C ⋃⋃()()()()()()card A card B card C card A B card A C card B C =++-⋂-⋂-⋂知()3626151364card A C =++---⋂，故()8card A C ⋂=即同时参加数学和化学小组的有8人， 故答案为8．【点睛】本小题主要考查Venn 图表达集合的关系及运算、Venn 图的应用、集合中元素的个数等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想，属于基础题．三、解答题 26．（1）2,0a b ==；（2）()f x 在(],1-∞-上为增函数，证明见解析；（3）93,42⎡⎤--⎢⎥⎣⎦. 【解析】 【分析】（1）由函数为奇函数可得()312f =,()312f -=-，再联立解方程组即可得解； （2）利用定义法证明函数()f x 在(],1-∞-上为增函数即可； （3）由函数()f x 在[]2,1--上为增函数，则可求得函数的值域. 【详解】解：（1）由函数()212ax f x x b+=+是奇函数，且()312f =,则()312f -=-，即22113212(1)132(1)2a b a b ⎧⨯+=⎪⨯+⎪⎨⨯-+⎪=-⎪⨯-+⎩ ，解得：20a b =⎧⎨=⎩ ； （2）由（1）得：()2212x f x x+=，则函数()f x 在(],1-∞-上为增函数； 证明如下： 设121x x <≤-，则12()()f x f x -=211212x x +222212x x +-=2212212112222x x x x x x x x +--121212()(21)2x x x x x x --=，又因为121x x <≤-，所以120x x -<，12210x x ->，120x x >， 即12())0(f x f x -< ，即12()()f x f x <， 故()f x 在(],1-∞-上为增函数；（3）由（2）得：函数()f x 在[]2,1--上为增函数，所以(2)()(1)f f x f -≤≤-，即93()42f x -≤≤-，故[]2,1x ∈--，函数的值域为：93,42⎡⎤--⎢⎥⎣⎦. 【点睛】本题考查了函数的奇偶性及增减性，重点考查了利用函数的性质求函数的值域问题，属中档题.27．充要条件是1a ≤． 【解析】 【分析】当0a ≠时，根据根为“1正1负”、“2负根”进行讨论，由此求得a 的范围.当0a =时，直接解出方程的根.由此求得a 的取值范围. 【详解】①0a ≠时，显然方程没有等于零的根．若方程有两异号实根，则0a <；若方程有两个负的实根，则必有102{001440aa aa >-<∴≤∆=-≥＜．．②若0a =时，可得12x =-也适合题意．综上知，若方程至少有一个负实根，则1a ≤．反之，若1a ≤，则方程至少有一个负的实根，因此，关于x 的方程2210ax x ++=至少有一负的实根的充要条件是1a ≤． 【点睛】本小题主要考查根据含有参数的一元二次方程根的分布求参数，考查分类讨论的数学思想方法，属于基础题.28．a ≤－1或a ＝1. 【解析】 【分析】先解方程得集合A ，再由 B ⊆A 得B 为A 子集，根据子集四种情况分类讨论，解出实数a 的值．注意对结果要验证 【详解】解 ∵A ＝{0，－4}，B ⊆A ，于是可分为以下几种情况． (1)当A ＝B 时，B ＝{0，－4}， ∴由根与系数的关系，得22(1)410a a -+=-⎧⎨-=⎩解得a ＝1. (2)当B ≠A 时，又可分为两种情况． ①当B ≠∅时，即B ＝{0}或B ＝{－4}， 当x ＝0时，有a ＝±1； 当x ＝－4时，有a ＝7或a ＝1. 又由Δ＝4(a ＋1)2－4(a 2－1)＝0， 解得a ＝－1，此时B ＝{0}满足条件； ②当B ＝∅时，Δ＝4(a ＋1)2－4(a 2－1)<0， 解得a <－1.综合(1)(2)知，所求实数a 的取值为a ≤－1或a ＝1.29．（1）{|22}x x -<<（2）偶函数（3）01m << 【解析】 【分析】 【详解】（Ⅰ）要使函数有意义，则，得.函数的定义域为. （Ⅱ）由（Ⅰ）可知，函数的定义域为，关于原点对称，对任意，.由函数奇偶性可知，函数为偶函数.（Ⅲ）函数由复合函数单调性判断法则知，当时，函数为减函数又函数为偶函数，不等式等价于，得.30．(1) ()4,B =+∞(),2A =-∞;(2) m 的取值范围是()-3∞，. 【解析】试题分析：（1）由题意，根据指数幂的运算性质，可得(),2A =-∞，根据函数()lg 4y x =- 可解得4x >，得到集合B ；（2）由（1）可得()()(),24,AB =-∞+∞，根据()C A B ⊆⋃，再分C =∅和C ≠∅两种情况分类讨论，即可求得实数m 的取值范围.试题解析： （1）∵x 222<∴()A ,2∞=-又∵()y lg x 4=-可知x 4> ∴()B 4,∞=+（2）∵()()()A B ,24,∞∞⋃=-⋃+，又∵()C A B ⊆⋃ （i ）若C ∅=，即1m m 1->-， 解得m 1<，满足：()C A B ⊆⋃ ∴m 1<符合条件（ii ）若C ∅≠，即m m 1-≤-， 解得m 1≥，要保证：()C A B ⊆⋃1m 4->或m 12-<，解得m 3<-（舍）或m 12-<解得[)m 1,3∈,综上：m 的取值范围是()-3∞， .。

成都外国语学校2017-2018学年上期半期考试高一数学试题满分：150分， 时间：120分钟一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的. 1.设集合(){}(410A x Z x x =∈-+）＜，集合{}2,3,4B =，则B A =( ) A.（2,4） B.{2.4} C.{3} D.{2,3}2.已知 1.30.20.20.7,3,log 5a b c ===，则,,a b c 的大小关系（ ） A. a c b << B. c a b << C. b c a << D. c b a <<3.若函数1()lg(f x x x +=+，则55()()22f f -+的值（ ）A. 2B. lg 5C. 0D. 34.函数31()()2x f x x =-的零点所在的区间（ ）A.(0,1)B. (1,2)C. (2,3)D. (3,4) 5.下列四种说法正确的个数有（ ）①若,,A B C 为三个集合，满足A B B C =，则一定有A C ⊆； ②函数的图像与垂直于x 轴的直线的交点有且仅有一个； ③若,A U B U ⊆⊆,则()()U A A B A C B =；④若函数()f x 在[,]a b 和[,]b c 都为增函数，则()f x 在[,]a c 为增函数.A. 1个B. 2个C. 3 个D. 4个6.设全集{|||4}U x Z x =∈<，集合{2,1,3}S =-，若U C P S ⊆，则这样的集合P 的个数共有()A ．5B ．6C ．7D ．87. 为了得到函数43log 4x y -=的图像，只需把函数21log 2y x =图像上所有的点（ ）A. 向左平移3个单位长度，再向上平移1个单位长度；B. 向右平移3个单位长度，再向上平移1个单位长度；C. 向右平移3个单位长度，再向下平移1个单位长度；D.向左平移3个单位长度，再向下平移1个单位长度；8. 函数21(2017)(0)x f x x x++=>的最小值为（ ） A. 2017 B. 2 C. -2017 D. 20199．如图，在AOB ∆中，点(2,1),(3,0)A B ，点E 在射线OB 上自O 开始移动，设OE x =,过E 作OB 的垂线l ，记AOB ∆在直线l 左边部分的面积S ，则函数()S f x =的图象是（ ）A. B.C.D.10. 已知函数2()1(0)f x a x x a =-+≠，若任意12,[1,)x x ∈+∞且12x x ≠都有1212()()1f x f x x x ->-，则实数a 的取值范围（ ）A. [1,)+∞B. (0,1]C. [2,)+∞D. (0,)+∞11.根据有关资料，围棋状态空间复杂度的上限M 约为3612，而可观测宇宙中普通物质的原子总数N 约为8010.则下列各数中与M N最接近的是（ ）（参考数据：lg2≈0.30）（A ）3010（B ）2810 （C ）3610 （D ）931012.若函数16()log (161)2xxf x m =+--有零点,则实数m 的取值范围（ ） A. 1[,)4+∞ B. 1[,)16+∞ C. (,16)-∞ D. 1(,16]4第Ⅱ卷二、填空题：本大概题共4小题，每小题5分。

2016-2017学年第一学期高一数学上册期中试题(含答案)2016-2017学年第一学期期中考试高一数学试题第Ⅰ卷（选择题共60分）一、选择题：（本大题共12小题，每小题分，共60分，在每个小题给出的四个选项中，只有一项是符合题目要求的）1设集合U={1,2,3,4,},A={1,2,3},B={2,},则A U B等于( )A{2} B{2,3} {3} D{1,3}2已知且，则A的值是（）A7 B D 983若a&gt;0且a≠1，且，则实数a的取值范围是（）A．0&lt;a&lt;1 B．．D．或a&gt;14函数（&gt;0且≠1）的图象必经过点（）A（0,1） B (1,1) (2,3) D(2,4)三个数之间的大小关系是（）A B D6函数= 在[1,3]上的最大值与最小值的和为1，则a =（）A B 2 3 D7下列函数中，在区间（0，2）上不是增函数的是（）A B D8函数与（）在同一坐标系中的图像只可能是( ）9 下列各式:①＝a;②(a2－3a＋3)0＝1③＝其中正确的个数是()A 0B 12 D 310计算()A BD 111 f(x)= 则f =()A -2B -39 D12 已知幂函数的图象经过点(9,3),则( )A 1 BD第Ⅱ卷（非选择题共90分）二、填空题：（每小题分，共20分）13 已知f(x)是定义在R上的奇函数,当x&gt;0时,f(x)=1+ ,则f(-2)=14若函数在区间内单调递减,则a的取值范围是______________ 1函数的定义域是．16求值：＝________ _．三、解答题：（本题共包含个大题，共70分）17 求值:（10分）(1) ;(2)求lg2．6．2+lg +ln + 的值．18 已知={x| -2≤x≤}, N={x| a+1≤x≤2a-1},若N，求实数a的取值范围（12分）19 已知函数f(x)=lga(3+2 x),g(x)=lga(3-2x)(a&gt;0,且a≠1)（12分）(1)求函数=f(x)-g(x)的定义域(2)判断函数=f(x)-g(x)的奇偶性,并予以证明20 已知函数且（12分）(1)判断的奇偶性,并证明;(2)求使的的取值范围21已知函数f(x)＝lg(1＋x)＋lg(1－x)．（12分）(1)求函数f(x)的定义域；(2)判断函数f(x)的奇偶性；(3)若f(x)＝lg g( x)，判断函数g(x)在(0,1)内的单调性并用定义证明．22设函数（12分）(1)设,用表示,并指出的取值范围;(2)求的最值,并指出取得最值时对应的x的值2016-2017学年第一学期期中考试高一数学试卷答案一、选择题（60）1-12 DBDD ABA B二、填空（20）13 -14116 49 B【解析】令a=-1，n=2时，＝1，①错;因为a2－3a＋3&gt;0,所以②正确; = ，③显然错误所以选项B错误10 A【解析】&#8226; lg23&#8226; ,故选A11 【解析】因为f =lg3 =-2,所以f =f(-2)= =9,故选12 B【解析】设f(x)= 由幂函数的图象经过点(9,3)，则f(9)= ，所以f(x)= ，故选B三、（70分）17（10分）(1) 原式(2) 解：原式＝2－2＋ln ＋＝＋6＝18（12分）解：①当N=Φ时，即a＋1＞2a－1，有a＜2；②当N≠Φ，则，解得2≤a≤3，综合①②得a的取值范围为a≤319 （12分）(1) =f(x)-g(x)= lga(3+2x)-lga(3-2x),要使该函数有意义,则有,解得&lt;x&lt;所以函数=f(x)-g(x)的定义域是(2) 由第1问知函数=f(x)-g(x)的定义域关于原点对称f(-x)-g(-x)=lga(3-2x)-lga(3+2x)= -[lga(3+2x)-lga(3-2x)]=-[f(x)-g(x)],所以函数=f(x)-g(x)是奇函数20 （12分）(1) 由,得故的定义域为∵,∴是奇函数(2) 当时,由,得,所以,当时,由,得,所以故当时, 的取值范围是;当时, 的取值范围是21 （12分）22 （1 2分）(1) 设,因为,所以此时, ，即,其中(2) 由第1问可得,因为,函数在单调递增,在单调递减,所以当,即,即时, 取得最大值;当,即,即时, 取得最小值。

2016-2017年第一学期高一数学上册期中试题（有答案）高一第一学期期中考试数学试卷本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分共1 0分，考试时间120分钟。

注意事项：答题前考生务必将考场、姓名、班级、学号写在答题纸的密封线内。

选择题每题答案涂在答题卡上，非选择题每题答案写在答题纸上对应题目的答案空格里，答案不写在试卷上。

考试结束，将答题卡和答题纸交回。

第Ⅰ卷（选择题，共60分）一、选择题：本大题共12小题，每小题分，共60分在每小题给出的四个选项中，只有一项是符合题目要求的1．已知集合A＝{－1,1}，B＝{x|ax＋1＝0}，若B&#8838;A，则实数a的所有可能取值的集合为()A．{－1} B．{1} ．{－1,1} D．{－1,0,1}2．函数＝1ln&#61480;x－1&#61481;的定义域为()A．(1，＋∞)B．[1，＋∞)．(1,2)∪(2，＋∞) D．(1,2)∪[3，＋∞)3．已知f(x)＝f&#61480;x－&#61481;，x≥0，lg2&#61480;－x&#61481;，x&lt;0，则f(2 016)等于()A．－1 B．0 ．1 D．24、若α与β的终边关于x轴对称，则有()A．α＋β＝90° B．α＋β＝90°＋&#8226;360°，∈Z．α＋β＝2&#8226;180°，∈Z D．α＋β＝180°＋&#8226;360°，∈Z、设1＝409，2＝8048，3＝(12)－1，则()A．3＞1＞2B．2＞1＞3．1＞2＞3D．1＞3＞26．在一次数学试验中，运用图形计算器采集到如下一组数据：x－20－100100新标x b1 200300024011202398802则x，的函数关系与下列哪类函数最接近？(其中a，b为待定系数)()A．＝a＋bxB．＝a＋bx．＝ax2＋bD．＝a＋bx7．定义运算a⊕b＝a，a≤b，b，a＞b则函数f(x)＝1⊕2x的图象是()8、设偶函数f(x)满足f(x)＝2x－4(x≥0)，则不等式f(x－2)&gt;0的解集为()A．{x|x&lt;－2，或x&gt;4}B．{x|x&lt;0，或x&gt;4}．{x|x&lt;0，或x&gt;6} D．{x|x&lt;－2，或x&gt;2}9．函数＝lg12(x2－x＋3)在[1,2]上的值恒为正数，则的取值范围是()A．22&lt;&lt;23B．22&lt;&lt;72．3&lt;&lt;72D．3&lt;&lt;2310 已知1＋sinxsx＝－12，那么sxsinx－1的值是()A12 B．－12 ．2 D．－211．设∈R，f(x)＝x2 －x＋a(a＞0)，且f()＜0，则f(＋1)的值() A．大于0 B．小于0 ．等于0D．不确定12、已知函数f(x)＝1ln&#61480;x＋1&#61481;－x，则＝f(x)的图象大致为()第Ⅱ卷（非选择题共90分）二、填空题：本大题4小题，每小题分，共20分13．已知集合A＝{x∈R||x＋2|&lt;3}，集合B＝{x∈R|(x－)(x－2)&lt;0}，且A∩B＝(－1，n)，则＋n＝________14 函数f(x)＝x＋2x在区间[0,4]上的最大值与最小值N的和为__ 1．若一系列函数解析式相同，值域相同，但定义域不同，则称这些函数为“同族函数”，那么函数解析式为＝x2，值域为{1,4}的“同族函数”共有________个．16 已知f(x)＝ax2＋bx＋3a＋b是偶函数，且其定义域为[a－1,2a]，则＝f(x)的值域为________．三、解答题：本大题共6小题，共70分，解答应写出字说明，证明过程或演算步骤17．（本小题10分）已知集合A＝{x|x2－3x＋2＝0}，B＝{x|x2－ax＋a－1＝0}，若A∪B ＝A，求实数a的值．18．(本小题满分12分)已知扇形的圆心角是α，半径为R，弧长为l(1)若α＝60°，R＝10 ，求扇形的弧长l(2)若扇形的周长是20 ，当扇形的圆心角α为多少弧度时，这个扇形的面积最大？(3)若α＝π3，R＝2 ，求扇形的弧所在的弓形的面积．19．（本小题满分12分）已知定义域为R的函数f(x)＝－2x＋b2x＋1＋a是奇函数．(1)求a，b的值；(2)若对任意的t∈R，不等式f(t2－2t)＋f(2t2－)＜0恒成立，求的取值范围．20、（本小题满分12分）已知函数f(x)＝4x＋&#8226;2x＋1有且仅有一个零点，求的取值范围，并求出该零点．21．（本小题满分12分）如图，建立平面直角坐标系x，x轴在地平面上，轴垂直于地平面，单位长度为1千米．某炮位于坐标原点．已知炮弹发射后的轨迹在方程＝x－120(1＋2)x2(＞0)表示的曲线上，其中与发射方向有关．炮的射程是指炮弹落地点的横坐标．(1)求炮的最大射程；(2)设在第一象限有一飞行物(忽略其大小)，其飞行高度为32千米，试问它的横坐标a不超过多少时，炮弹可以击中它？请说明理由．22．(本小题满分12分)设函数f(x)＝ax－a－x(a&gt;0且a≠1)是定义域为R的奇函数．(1 )若f(1)&gt;0，试求不等式f(x2＋2x)＋f(x－4)&gt;0的解集；(2)若f(1)＝32，且g(x)＝a2x＋a－2x－4f(x)，求g(x)在[1，＋∞)上的最小值．高一数学期中测试卷参考答案1．解析：由题意知集合B的元素为1或－1或者B为空集，故a＝0或1或－1，选D答案：D2 解析由ln(x－1)≠0，得x－1&gt;0且x－1≠1由此解得x&gt;1且x≠2，即函数＝1ln&#61480;x－1&#61481;的定义域是(1,2)∪(2，＋∞)．答案3 解析f(2 016)＝f(1)＝f(1－)＝f(－4)＝lg24＝2答案 D4 解析：根据终边对称，将一个角用另一个角表示，然后再找两角关系．因为α与β的终边关于x轴对称，所以β＝2&#8226;180°－α，∈Z，故选答案：解析：1＝409＝218，2＝8048＝2144，3＝(12)－1＝21由于指数函数f(x)＝2x在R上是增函数，且18＞1＞144，所以1＞3＞2，选D 答案：D6 解析：在坐标系中将点(－2,024)，(－1,01)，(0,1)，(1,202)，(2,398)，(3,802)画出，观察可以发现这些点大约在一个指数型函数的图象上，因此x与的函数关系与＝a＋bx最接近．答案：B7 解析：f(x)＝1⊕2x＝1，x≥0，2x，x＜0故选A答案：A8 解析：当x≥0时，令f(x)＝2x－4&gt;0，所以x&gt;2又因为函数f(x)为偶函数，所以函数f(x)&gt;0的解集为{x|x&lt;－2，或x&gt;2}．将函数＝f(x)的图象向右平移2个单位即得函数＝f(x－2)的图象，故f(x －2)&gt;0的解集为{x|x&lt;0，或x&gt;4}．答案：B9 解析：∵lg12(x2－x＋3)&gt;0在[1,2]上恒成立，∴0&lt;x2－x＋3&lt;1在[1, 2]上恒成立，∴&lt;x＋3x&gt;x＋2x在[1,2]上恒成立又当1≤x≤2时，＝x＋3x∈[23，4]，＝x＋2x∈[22，3]．∴3&lt;&lt;23答案：D10 解析：设sxsinx－1＝t，则1＋sinxsx&#8226;1t＝1＋sinxsx&#8226;sinx－1sx＝sin2x－1s2x＝－1，而1＋sinxsx＝－12，所以t＝12故选A答案：A11 解析：函数f(x)＝x2－x＋a的对称轴为x＝12，f(0)＝a，∵a＞0，∴f(0)＞0，由二次函数的对称性可知f(1)＝f(0)＞0∵抛物线的开口向上，∴由图象可知当x＞1时，恒有f(x)＞0∵f()＜0，∴0＜＜1∴＞0，∴＋1＞1，∴f(＋1)＞0答案：A12 解析：(特殊值检验法)当x＝0时，函数无意义，排除选项D中的图象，当x＝1e－1时，f(1e－1)＝1ln&#61480;1e－1＋1&#61481;－&#61480;1e－1&#61481;＝－e&lt;0，排除选项A、中的图象，故只能是选项B中的图象．(注：这里选取特殊值x＝(1e－1)∈(－1,0)，这个值可以直接排除选项A、，这种取特值的技巧在解题中很有用处)答案：B13 答案0 解析由|x＋2|&lt; 3，得－3&lt;x＋2&lt;3，即－&lt;x&lt;1又A∩B＝(－1，n)，则(x－)(x－2)&lt;0时必有&lt;x&lt;2，从而A∩B＝(－1,1)，∴＝－1，n＝1，∴＋n＝014 解析：令t＝x，则t∈[0,2]，于是＝t2＋2t＝(t＋1)2－1，显然它在t∈[0,2]上是增函数，故t＝2时，＝8；t＝0时N＝0，∴＋N＝8答案：81 解析：值域为{1,4}，则定义域中必须至少含有1，－1中的一个且至少含有2，－2中的一个．当定义域含有两个元素时，可以为{－1，－2}，或{－1,2}，或{1，－2}，或{1,2}；当定义域中含有三个元素时，可以为{－1,1，－2}，或{－1，1,2}，或{1，－2,2}，或{－1，－2,2}；当定义域含有四个元素时，为{－1,1，－2,2}．所以同族函数共有9个．答案：916 解析：∵f(x)＝ax2＋bx＋3a＋b是偶函数，∴其定义域[a－1,2a]关于原点对称，即a－1＝－2a，∴a＝13∵f(x)＝ax2＋bx＋3a＋b是偶函数，即f(－x)＝f(x)，∴b＝0，∴f(x)＝13x2＋1，x∈[－23，23]，其值域为{|1≤≤3127}．答案：{|1≤≤3127}17 答案a＝2或a＝3解析A＝{1,2}，∵A∪B＝A，∴B&#8838;A，∴B＝&#8709;或{1}或{2}或{1,2}．当B＝&#8709;时，无解；当B＝{1}时，1＋1＝a，1×1＝a－1，得a＝2；当B＝{2}时，2＋2＝a，2×2＝a－1，无解；当B＝{1,2}时，1＋2＝a，1×2＝a－1，得a＝3综上：a＝2或a＝318 【解析】(1)α＝60°＝π3，l＝10×π3＝10π3(2)由已知得，l＋2R＝20，所以S＝12lR＝12(20－2R)R＝10R－R2＝－(R－)2＋2所以当R＝时，S取得最大值2，此时l＝10，α＝2(3)设弓形面积为S弓．由题知l＝2π3S弓＝S扇形－S三角形＝12×2π3×2－12×22×sin π3＝(2π3－3) 2 【答案】(1)10π3 (2)α＝2时，S最大为2(3)2π3－3 219 解：(1)因为f(x)是定义在R上的奇函数，所以f(0)＝0，即b－1a＋2＝0&#868;b＝1，所以f(x)＝1－2xa＋2x＋1，又由f(1)＝－f(－1)知1－2a＋4＝－1－12a＋1&#868;a＝2(2)由(1)知f(x)＝1－2x2＋2x＋1＝－12＋12x＋1，易知f(x)在(－∞，＋∞)上为减函数．又因f(x)是奇函数，从而不等式：f(t2－2t)＋f(2t2－)＜0等价于f(t2－2t)＜－f(2t2－)＝f(－2t2)，因f(x)为减函数，由上式推得：t2－2t＞－2t2，即对t∈R有：3t2－2t－＞0，从而Δ＝4＋12＜0&#868;＜－1320 解：∵f(x)＝4x＋&#8226;2x＋1有且仅有一个零点，即方程(2x)2＋&#8226;2x＋1＝0仅有一个实根．设2x＝t(t＞0)，则t2＋t＋1＝0当Δ＝0时，即2－4＝0∴＝－2时，t＝1；＝2时，t＝－1(不合题意，舍去)，∴2x＝1，x＝0符合题意．当Δ＞0时，即＞2或＜－2时，t2＋t＋1＝0有两正或两负根，即f(x)有两个零点或没有零点．∴这种情况不符合题意．综上可知：＝－2时，f(x)有唯一零点，该零点为x＝021 解：(1)令＝0，得x－120(1＋2)x2＝0，由实际意义和题设条知x＞0，＞0，故x＝201＋2＝20＋1≤202＝10，当且仅当＝1时取等号．所以炮的最大射程为10千米．(2)因为a＞0，所以炮弹可击中目标&#8660;存在＞0，使32＝a－120(1＋2)a2成立&#8660;关于的方程a22－20a＋a2＋64＝0有正根&#8660;判别式Δ＝(－20a)2－4a2(a2＋64)≥0&#8660;a≤6所以当a不超过6(千米)时，可击中目标．22 答案(1) {x|x&gt;1或x&lt;－4}(2)－2解析∵f(x)是定义域为R的奇函数，∴f(0)＝0，∴－1＝0，∴＝1(1)∵f(1)&gt;0，∴a－1a&gt;0又a&gt;0且a≠1，∴a&gt;1∵＝1，∴f(x)＝ax－a－x当a&gt;1时，＝ax和＝－a－x在R上均为增函数，∴f(x)在R上为增函数．原不等式可化为f (x2＋2x)&gt;f(4－x)，∴x2＋2x&gt;4－x，即x2＋3x－4&gt;0∴x&gt;1或x&lt;－4∴不等式的解集为{x|x&gt;1或x&lt;－4}．(2)∵f(1)＝32，∴a－1a＝32，即2a2－3a－2＝0∴a＝2或a＝－12(舍去)．∴g(x)＝22x＋2－2x－4(2x－2－x)＝(2x－2－x)2－4(2x－2－x)＋2令t＝h(x)＝2x－2－x(x≥1)，则g(t)＝t2－4t＋2∵t＝h(x)在[1，＋∞)上为增函数(由(1)可知)，∴h(x)≥h(1)＝32，即t≥32∵g(t)＝t2－4t＋2＝(t－2)2－2，t∈[32，＋∞)，∴当t＝2时，g(t)取得最小值－2，即g(x)取得最小值－2，此时x＝lg2(1＋2)．故当x＝lg2(1＋2)时，g(x)有最小值－2。

成都外国语学校高一数学半期试卷一、选择题（每小题5分，共50分）1．设全集U={1,2,3,4,5}，集合M={1,3,5}，N={2,5}则Venn图中阴影部分表示的集合是（）A.{1,3}B.{2}C.{3,5}D.{5}2．函数3+=x ay（a＞0，a≠1）的图象经过的定点坐标是（）A.(0,1)B.(2,1)C.(3-,1) D.(3-,0)3．已知⎩⎨⎧-≤-=)0()3()0(1)(2x＞xfxxxf，则)]1([ff的值是（）A.1- B.3 C.2 D.54．设a＞0，将322aaa⋅写成分数指数幂，其结果是（）A.23a B.21a C.65a D.67a5．函数1||1+=xy的大致图象为（）A B C D6．设24.0=a，4.02=b，4.02log=c，则（）A.a＞c＞bB.b＞a＞cC.b＞c＞aD.a＞b＞c7．若0＜3loga＜1（a＞0，a≠1），则a的取值范围是（）A.)31,0( B.(0,3) C.(3,+∞) D.(1,3)8．已知xxf2log)(=，则)1(xfy-=的图象是（）A B C D9 .已知)(xf是奇函数，当0≥x时，1)(+=x exf（e为自然对数的底数），则)21(lnf=（） A.3- B. 2 C. 3 D. 0⊂≠10 .已知)1(32≠==k k b a 且ab b a =+2，则实数k 的值为（ ）A. 6B. 9C. 12D. 18二、填空题。

（每小题5分，共25分）11 满足Ф A ⊆{1,2,3}的集合A 的个数是 。

13 已知偶函数)(x f 满足)( )()2(R x x f x x f ∈⋅=+，则)1(f = 。

14 若)3(log +=ax y a （a ＞0且a ≠1）在区间),1(+∞-上是增函数，则a 的取值范围是15 若函数a ax x x f 2)(2--=在区间[0,2]上的最大值为1，则实数a 等于三、解答题。

成都外国语学校2016－2017学年度上期期末考试高一数学试卷注意事项：1、 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分2、 本堂考试时间120分钟，满分150分3、 答题前，请考生务必先将自己的姓名、考号填写在答题卷上，并用2B 铅笔填涂4、 考试结束后，请考生将答题卷交回第Ⅰ卷（选择题 共60分）一、选择题：本大题共12小题，每小题5分共60分，在每小题所给出的四个选项中，只有一项是符合题目要求的，并将正确选项的序号填涂在答题卷。

1.已知集合{}21110,24,2x M x x N x x Z +⎧⎫=-≤=<<∈⎨⎬⎩⎭，则M N = ( )A.{}1B.{}1,0-C.{}1,0,1-D.∅2.下列函数图像与x 轴均有公共点，其中能用二分法求零点的是 ( )3．已知2()3f x ax bx a b =+++是偶函数，定义域为[1,2]a a -，则a b += ( ) A. 31-B. 1C.0D.314.下列说法中正确的是 （ ）A.若a b a c ⋅=⋅ ，则b c = ，B.若0a b ⋅= ，则0a = 或0b =C.若不平行的两个非零向量,满足||||=，则0)()(=-⋅+D.若与平行，则||||a b a b ⋅=⋅5.若角θ是第四象限的角，则角2θ-是 （ ）A.第一、三象限角B.第二、四象限角C.第二、三象限角D.第一、四象限角6.已知函数(1)f x +的定义域为[－2, 3]，则(32)f x -的定义域为 ( )A.]5,5[-B.]9,1[-C.1[,2]2-D.]3,21[ 7.右图是函数sin()()y A x x R ωϕ=+∈在区间5,66ππ⎡⎤-⎢⎥⎣⎦上的图象，为了得到这个函数的图像，只要将()sin y x x R =∈的图象上所有的点 ( ) A.向左平移6π个单位长度，再把所得各点的横坐标缩短到原来的12倍，纵坐标不变 B.向左平移6π个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变C.向左平移3π个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变D.向左平移3π个单位长度，再把所得各点的横坐标缩短到原来的12倍，纵坐标不变8.已知奇函数)(x f 满足)()2(x f x f =+，当()1,0∈x 时，函数x x f 2)(=，则)23(log 21f = ( )A. 2316-B. 1623-C.2316D.16239.在ABC ∆中，若||2AB = ，||3AC = ，||4BC = ，O 为ABC ∆的内心，且AO AB BC λμ=+，则λμ+= ( )A.34 B. 59 C. 79D. 57 10.若实数,,a b c 满足log 3log 3log 3a b c <<，则下列关系中不可能．．．成立的 （ ） A.a b c << B.b a c << C.c b a << D.a c b <<11.不存．．在．函数()f x 满足，对任意x R ∈都有 （ ） A. x x x f 2|)1(|2+=+ B. x x f cos )2(cos = C. xx f 2cos )(sin =D. x x f 2cos )(cos =12.已知()2sin cos f x x x =+，若函数()()g x f x m =-在()0,x π∈上有两个不同零点 αβ、，则=+)cos(βα （ ） A.54 B. 53C. 54-D.53-第Ⅱ卷（非选择题 共90分）二、填空题(本大题共4个小题，每小题5分，共20分)13.在二分法求方程()0f x =在[0,4]上的近似解时，最多经过_________次计算精确度可以达到0.001.14.若=(λ，2)，=(3，4)，且与的夹角为锐角，则λ的取值范围是_______ 15.已知函数)42ln()(2-+=a x f x 的定义域、值域都为R ，则a 取值的集合为__________ 16.已知R m ∈，函数⎩⎨⎧>-<+=1),1ln(1|,12|)(x x x x x f ，122)(22-+-=m x x x g ，若函数m x g f y -=))((有6个零点则实数m 的取值范围是_______三、解答题：解答应写出文字说明，证明过程或演算步骤 17.（本题满分10分，每小题5分）化简求值. （1）1320311()(1.03)(42--+⋅⋅（2）()2lg 2lg 20lg 5+⨯+3log 2log 49⋅18.（本题满分12分）求值.（1）已知2tan =α，求αα2cos 2sin 1++的值； （2.19.（本题满分12分）已知函数23()2sin ()2)2f x x x ππ=+- （1）若]2,0[π∈x ，求()f x 的取值范围；（2）求函数12log ()y f x =的单调增区间.20.（本题满分12分）已知,是两个不共线的向量，且)sin,(cos ),sin ,(cos ββαα==（1）求证：b a +与b a -垂直； （2）若)4,4(ππα-∈，4πβ=且516||=+，求αsin .21.（本题满分12分）函数()f x 的定义域为R,并满足以下条件:①对任意x R ∈,有()f x >0;②对任意,x y R ∈,有()[()]y f xy f x =;③1()13f >. （1）求证: ()f x 在R 上是单调增函数;（2）若12(422)1x x f a a ++⋅-+≥对任意x R ∈恒成立，求实数a 的取值范围.22.（本题满分12分）若在定义域内存在实数0x 使得)1()()1(00f x f x f +=+成立则称函数)(x f 有“溜点0x ”（1）若函数2)21()(mx x f x +=在)1,0(上有“溜点”，求实数m 的取值范围； （2）若函数)1lg()(2+=x ax f 在)1,0(上有“溜点”，求实数a 的取值范围.成都外国语学校2016－2017学年度上期期末高一数学考试参考答案一、选择题：BCDCA CDBCA BD 二、填空题13. 12； 14.2338≠->λλ且； 15.}2,2{-； 16.)43,0( 三、解答题：解答应写出文字说明，证明过程或演算步骤17.（本题满分10分，每小题5分）化简求值. （1）1320311()(1.03)(42--+++⋅⋅2163625616=+++=-（2）()2lg 2lg 20lg 5+⨯+3log 2log 49⋅45415lg 2lg 415lg )5lg 2(lg 2lg 3log 212log 215lg )2lg 1()2(lg 232=++=+++=⋅+⋅++=18.（本题满分12分）（1）已知2tan =α，求αα2cos 2sin 1++的值；3241t a n 2t a n t a n c o s s i n c o s 2c o s s i n 2s i n 222222+=+++=+++=ααααααααα （2.50cos 50sin )50cos 50(sin 250cos 50sin )3010sin(250sin 250cos 50sin 250cos 50sin )10sin 310(cos 50sin 222++=+++=++++=19.（本题满分12分）已知函数23()2sin ()2)2f x x x ππ=+- （1）若]2,0[π∈x ，求()f x 的取值范围；（2）求函数12log ()y f x =的单调增区间.[详细分析]2()2cos 2cos2212sin(2)16f x x x x x x π==+=++（1）当]2,0[π∈x 时，67626πππ≤+≤x ，故1)62sin(21≤+≤-πx02sin(2)136x π≤++≤则)(x f 的取值范围是]3,0[.（2）由题意有⎪⎪⎩⎪⎪⎨⎧∈+≤+≤+>+Z k k x k x ,22362220)62sin(ππππππ解得函数12log ()y f x =的单调增区间为Z k k k ∈++],125,6[ππππ20.（本题满分12分）已知,是两个不共线的向量，且)sin ,(cos ),sin ,(cos ββαα== （1）求证：+与-垂直； （2）若)4,4(ππα-∈，4πβ=且516||=+b a ，求αsin . [详细分析]（1）证明：,是两个不共线的向量，则+与-为非零向量)sin sin ,cos (cos βαβα++=+，)sin sin ,cos (cos βαβα--=-0)sin (cos )sin (cos )sin (sin )cos (cos 22222222=+-+=-+-=+ββααβαβα所以b a +与b a -垂直（2）)sin sin cos (cos 22)sin (sin )cos (cos |222βαβαβαβα++=+++=+b)cos(22βα-+= 则516)cos(22=-+βα，又4πβ=所以53)4cos(=-πα又)4,4(ππα-∈，所以)0,2(4ππα-∈-于是54)4sin(-=-πα102225322544sin )4cos(4cos )4sin(]4)4sin[(sin -=+-=-+-=+-=ππαππαππαα故102sin -=α 21.（本题满分12分）函数()f x 的定义域为R,并满足以下条件:①对任意x R ∈,有()f x >0;②对任意,x y R ∈,有()[()]y f xy f x =;③1()13f >. （1）求证: ()f x 在R 上是单调增函数;（2）若12(422)1x x f a a ++⋅-+≥对任意x R ∈恒成立，求实数a 的取值范围.（1）证明：由题可知1()13f >，故1[()]3xy f =为增函数对任意R x x ∈21,且21x x <，有2133x x <则123311[()][()]33x x f f <)331()331()()(2121x f x f x f x f ⋅-⋅=-)]31([)]31([2133<-=x x f f 故 ()f x 在R 上是单调增函数;（2）()[()]y f xy f x =中令2,0==y x 有2(0)[(0)]f f =，对任意x R ∈,有()f x >0 故1)0(=f12(422)1x x f a a ++⋅-+≥即12(422)(0)x x f a a f ++⋅-+≥，由（1）有()f x 在R 上是单调增函数，即：124220xx a a ++⋅-+≥任意x R ∈恒成立令0,2>=t t x则02222≥+-+a at t 在),0(+∞上恒成立） i ）0≤∆即0)2(4422≤--a a 得11≤≤-aii ）⎪⎩⎪⎨⎧≥+-<->∆02002a a 得21≤<a综上可知21≤≤-a22.（本题满分12分）若在定义域内存在实数0x 使得)1()()1(00f x f x f +=+成立则称函数)(x f 有“溜点0x ”（1）若函数2)21()(mx x f x +=在)1,0(上有“溜点”，求实数m 的取值范围； （2）若函数)1lg()(2+=x ax f 在)1,0(上有“溜点”，求实数a 的取值范围.（1）2)21()(mx x f x+=在)1,0(上有“溜点” 即)1()()1(f x f x f +=+在)1,0(上有解，即m mx x m x x +++=+++21)21()1()21(221在)1,0(上有解整理得xmx )21(14=-在)1,0(上有解从而14)(-=mx x h 与xx g )21()(=的图象在)1,0(上有交点故)1()1(g h >，即2114>-m ，得83>m（2）由题已知0>a ，且)2lg()1lg(]1)1(lg[22ax a x a ++=++在)1,0(上有解 整理得22)1(222++++=x x x a ，又)22121(222)1(2222+++-=+++x x x x x x设22122+++=x x x y ，令12+=x t ，由)1,0(∈x 则)3,1(∈t于是2545242++=++=t t t t t y825252<++≤+t t 则2152212212-≤+++<x x x从而122)1(25322<+++≤-x x x故实数a 的取值范围是)1,53[-。

2016-2017学年上学期四川省成都外国语学校高三年级第一次月考 测试卷文科数学一、选择题（本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．已知集合{|33}A x x =-<<，{|lg(1)}B x y x ==+，则集合A B 为（ ） A ．[0,3)B ．[1,3)-C ．(1,3)-D ．(3,1]--2．已知复数z 的实部为1-，虚部为2，则5iz=（ ） A ．2i -B ．2i +C ．2i --D ．2i -+3．下列说法正确的是（ ）A ．R a ∈，“11<a”是“1>a ”的必要不充分条件B ．“q p ∧为真命题”是“q p ∨为真命题”的必要不充分条件C ．命题“R x ∈∃，使得0322<++x x ”的否定是：“R x ∈∀，0322>++x x ” D ．命题p ：“R x ∈∀，2cos sin ≤+x x ”，则p ⌝是真命题4．若函数[)[]⎪⎩⎪⎨⎧∈-∈=1,0,40,1,41)(x x x f x x ）（，则411log 33f f ⎧⎫⎛⎫=⎨⎬ ⎪⎝⎭⎩⎭（ ）A ．31B ．3C ．41 D ．45．已知)(log ax y a -=2在[]0,1上是x 的减函数，则a 的取值范围是（ ） A ．()0,1B ．()1,2C ．()0,2D ．[2,)+∞6．函数x e x f x-=)(在区间]1,1[-上的值域为（ ） A ．]1,1[-eB ．]1,11[-+e eC ．]2,11[+eD ．]1,0[-e7．执行如图的程序框图，若程序运行中输出的一组数是(),12x -，则x 的值为（ ）A ．27B ．81C ．243D ．7298．将函数)64sin(3)(π+=x x f 图象上所有点的横坐标伸长到原来的2倍，再向右平移6π个单位长度，得到函数)(x g y =的图象，则)(x g y =图象的一条对称轴是（ ） A ．12π=xB ．6π=xC ．3π=xD ．32π=x 9．若5,412x ππ⎡⎤∈⎢⎥⎣⎦，则()sin 4sin 2x x f x xπ⎛⎫+ ⎪⎝⎭=的最大值为（ ）A ．1B ．2C ．3D ．410．齐王与田忌赛马，田忌的上等马优于齐王的中等马，劣于齐王的上等马，田忌的中等马优于齐王的下等马，劣于齐王的中等马，田忌的下等马劣于齐王的下等马，现从双方的马匹中随机选一匹进行一场比赛，则田忌马获胜的概率为（ ） A ．13B ．14C ．15D ．1611．函数()f x 的定义域是R ，(0)2f =，对任意x R ∈，'()()1f x f x +>，则不等式()1x xe f x e >+的解集为（ ） A ．{|0}x x >B ．{|0}x x <C ．{|11}x x x <->或D ．{|11}x x x <-<<或012．已知函数3,3||)(2≥---=a a a x x x x f ．若函数)(x f 恰有两个不同的零点21,x x ，则|11|21x x -的取值范围是（ ） A ．)(1,+∞B ．),31(+∞C ．]1,31(D ．]31,21(二、填空题（本大题共4小题，每题5分，满分20分．）13．已知31)125cos(=+απ，且2παπ-<<-，则=-)12cos(απ_______________． 14．已知函数1)391ln()(2+-+=x x x f ，则=+)21(lg )2(lg f f _______．15．直线l的参数方程是x y ⎧=⎪⎪⎨⎪=+⎪⎩(其中t 为参数)，圆C 的极坐标方程为)4cos(2πθρ+=，过直线上的点向圆引切线，则切线长的最小值是_________________． 16．设函数2()2f x kx x =+（k 为实常数）为奇函数，函数()() 1(01)f x g x aa a =->≠且．当a =时，2()21g x t mt ≤-+对所有的[1,1]x ∈-及[1,1]m ∈-恒成立，则实数t 的取值范围________．三、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．）17．（本小题满分10分）计算：（Ⅰ）2log 351log 25lg 2100++； (Ⅱ) 已知()11223a a a R -+=∈，求值：22111a a a a --++++．18．(本小题满分12分) 已知函数ππ1()cos()cos()sin cos 334f x x x x x =+--+ （1）化简)(x f 的解析式，并写出)(x f 的最小正周期；（2）求当]2,0[π∈x 时，求函数()f x 的值域．19．（本小题满分12分）已知函数212ln )(2+--=x x x x f ．（1）求函数()f x 的单调递增区间；（2）证明：当1x >时，()1f x x <-．20．（本小题满分12分）周立波主持的《壹周·立波秀》节目以其独特的视角和犀利的语言，给观众留下了深刻的印象．央视鸡年春晚组为了了解观众对《壹周·立波秀》节目的喜爱程度，随机调查了观看了该节目的140名观众，得到如下2×2的列联表：（单位：名）（Ⅰ）从这60名男观众中按对《壹周·立波秀》节目是否喜爱采取分层抽样，抽取一个容量为6的样本，问样本中喜爱与不喜爱的观众各有多少名？（Ⅱ）根据以上列联表，问能否在犯错误的概率不超过0．025的前提下认为观众性别与喜爱《壹周·立波秀》节目有关．（精确到0．001）（Ⅲ）从（Ⅰ）中的6名男性观众中随机选取两名作跟踪调查，求选到的两名观众都喜爱《壹周·立波秀》节目的概率． 附：临界值表参考公式：()()()()()22n ad bc K a b c d a c b d -=++++，n a b c d =+++．21．（本小题满分12分）在ABC ∆中，已知5524==B A cos ,π． (I)求C cos 的值；(Ⅱ)若D BC ,52=为AB 的中点，求CD 的长．22．（本小题满分12分）已知函数2()ln f x x x mx =-，（m 为常数）． （Ⅰ）当0m =时，求函数()f x 的单调区间；（Ⅱ）若21()x xf x ->对任意2]x e ∈恒成立，求实数m 的取值范围；（Ⅲ）若121,(,1)x x e∈，121x x +<，求证：41212()x x x x <+．2016-2017学年上学期四川省成都外国语学校高三年级第一次月考 测试卷文科数学答案一、选择题（本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．【答案】C【解析】因}1|{->=x x B ，故}31|{<<-=x x B A ，应选C ． 考点：集合的交集运算． 2．【答案】A 12z i =-+，()()()5125510521212125i i i i ii z i i i ---====--+-+-- 3．【解析】对于A ，由于当1>a 时一定有11<a ，所以“11<a ”是“1>a ”的必要条件，又因为11<a 时不能推出1>a ，如1a =-，所以所以“11<a ”是“1>a ”的不充分条件，综上可知“11<a”是“1>a ”的必要不充分条件，故可知选A ． 考点：充分条件必要条件与命题的否定．4．【解析】因为[)[]⎪⎩⎪⎨⎧∈-∈=1,0,40,1,41)(x x x f x x）（，因为[]41log 1,03∈-，所以41log 3411f(log )()334==，1411f(log )1,(1)4433f ∴===，所以411log 33f f ⎧⎫⎛⎫=⎨⎬ ⎪⎝⎭⎩⎭4，答案为D ．考点：分段函数的应用．5．【解析】由题已知0,2a t ax >=-为减函数，又()2log ax a y -=在[]0,1为减函数，则可得：120a a >⎧⎨->⎩，解得a 的取值范围是（1，2） 考点：复合函数的单调性．6．【解析】'()1xf x e =-，'(0)0f =，当[1,0)x ∈-时，'()0f x <，()f x 递减，当(0,1]x ∈时，'()0f x >，()f x 递增，0(0)01f e =-=，1(1)1f e -=+，1(1)11f e e=->+，所以()f x 值域为[1,1]e -．故选A ．考点：用导数求函数的值域． 7．【解析】考点：算法流程图的识读理解和运用． 8．【解析】将函数)64sin(3)(π+=x x f 图象上所有点的横坐标伸长到原来的2倍得到函数3sin 26y x π⎛⎫=+ ⎪⎝⎭的图象，再向右平移6π个单位长度，得到函数3sin 266y x ππ⎡⎤⎛⎫=-+ ⎪⎢⎥⎝⎭⎣⎦3sin 26x π⎛⎫=- ⎪⎝⎭，即)(x g y =的图象，而33g π⎛⎫= ⎪⎝⎭，则)(x g y =图象的一条对称轴是3π=x ，故选C ．考点：三角函数的图象和性质及其变换． 9．【答案】A 【解析】试题分析：()sin cos (sin cos )sin cos 114sin 22sin cos 2sin 2tan 2x x x x x x x f x x x x x x π⎛⎫+ ⎪++⎝⎭====+，5,412x ππ⎡⎤∈⎢⎥⎣⎦，∴1tan 2x ≤≤121tan x ∴-≤，∴当1=1tan x时，()1max f x =．故选A ． 考点：三角函数的最值．10．【解析】考点：古典概型的计算公式及运用．【易错点晴】概率是高中数学中的重要内容，也高考和各级各类考试的重要内容和考点．解答本题时要充分利用题设中提供的有关信息，充分借助题设中提供有效信息，运用列举法列举出赛马所有可能Cc Cb Ca Bc Bb Ba Ac Ab Aa ,,,,,,,,，共九种可能，依据题设其中Bc Ac Ab ,,是胜局共三种可能，然后运用古典概型的概率公式求出田忌胜的概率是3193==P ．列举法也就简单枚举法一直是中学数学中重要而简单的数学方法之一，考查基础知识基本方法是高考的要求，这需扎实掌握并引起足够的重视．11．【解析】令函数1)()(--=x x e x f e x F ，因0]1)()([)()()(///>-+=-+=x f x f e e x f e x f e x F x x x x ， 故函数1)()(--=xxe xf e x F 是单调递增函数，且0112)0(=--=F ，所以不等式()1x x e f x e >+等价于)0()(F x F >，故0>x ，应选A ． 考点：导数的有关知识及综合运用．【易错点晴】导数是研究函数的单调性和极值问题的重要工具，也高考和各级各类考试的重要内容和考点．解答本题时要充分利用题设中提供的有关信息，先构造出函数1)()(--=x x e x f e x F ，再运用求导法则求函数1)()(--=x x e x f e x F 的导数，判断该函数的单调性为增函数，将不等式()1x x e f x e >+等价转化为)0()(F x F >．最后借助函数的单调性从而使得问题获解，本题具有一定的难度，难点在于如何构造函数)(x f y =的解析表达式，这里题设中的条件起到了的重要作用． 12．考点：分段函数，函数的零点．第Ⅱ卷（非选择题共90分）二、填空题（本大题共4小题，每题5分，满分20分．）13．【答案】322-【解析】55cos()cos(())sin()1221212ππππααα-=-+=+=． 14．【答案】2【解析】()()()()221ln 2391ln 391ln 22=+=+-++++=+-x x x x x f x f ，()()()22lg 2lg 21lg 2lg =-+=⎪⎭⎫⎝⎛+f f f f考点：函数的性质 15．【答案】【解析】ρθθ=，2cos sin ρθθ∴=，∴圆C的直角坐标方程为220x y +-=，即22((1x y ++=， ∴圆心直角坐标为． ∴直线l的普通方程为0x y -+=，圆心C 到直线l5，∴直线l 上的点向圆C=． 16．【答案】(,2]{0}[2,)t ∈-∞-+∞【解析】由()()f x f x -=-得2222kx x kx x -=--，∴0k =．∵()22() 11()1f x x x g x a a a =-=-=-①当21a >，即1a >时，2() ()1x g x a =-在[1,2]-上为增函数，∴()g x 最大值为4(2)1g a =-．②当21a <，即01a <<时，∴2() ()xg x a =在[1,2]-上为减函数，∴()g x 最大值为21(1)1g a -=-．∴4max 21,1()11,01a a g x a a⎧->⎪=⎨-<<⎪⎩ 由（2）得()g x 在[1,1]x ∈-上的最大值为2(1)11g =-=，∴2121t mt ≤-+即220t mt -≥在[1,1]-上恒成立分令2()2h m mt t =-+，∴22(1)20,(1)20,h t t h t t ⎧-=+≥⎪⎨=-≥⎪⎩ 即20,0 2.t t ≤-≥⎧⎨≤≥⎩或t 或t所以(,2]{0}[2,)t ∈-∞-+∞ ． 考点：（1）函数的奇函数．（2）指数函数的性质．（3）恒成立问题及函数思想．【名师点睛】本题考查函数的奇偶性，单调性，考查不等式恒成立问题．解决不等式恒成立问题关键是进行问题的转化，象本题不等式2()21g x t mt ≤-+对所有的[1,1]x ∈-恒成立，则有max (())221g x t mt ≤-+，这样我们只要求得()g x 的最大值，不等式就可消去变量x ，同样新不等式对[1,1]m ∈-恒成立，也可象刚才一样转化为求函数最值，也可转化为关于m 的一次函数问题．三、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．）17．【答案】（Ⅰ）72； (Ⅱ)6．【解析】（Ⅰ）原式=172(2)322+-++=；(Ⅱ)11122223,7,47,a aa a a a ---+=∴+=∴+= 22114716171a a a a --+++∴==+++ 18．【答案】(Ⅰ)ππ11()cos()cos()sin 23324f x x x x =+--+1111(cos )(cos )sin 22224x x x x x =+-+ 221311cos sin sin 24424x x x =--+1cos 233cos 211sin 28824x x x +-=--+ 1(cos 2sin 2)2x x =-24x π⎛⎫=+ ⎪⎝⎭ 函数)(x f 的最小正周期为 T π=，(II)由]2,0[π∈x ，得]45,4[42πππ∈+x ，]22,1[)42cos(-∈+πx 所以当]2,0[π∈x 时，求函数()f x 的值域为]21,22[-19．【答案】（1）⎛ ⎝⎭；（2）证明见解析． 【解析】（1）()f x 的定义域为()0,+∞，()211'1,x x f x x x x-++=-+=令()'0f x >，得2010x x x >⎧⎨-++>⎩，解得102x +<<，所以函数()f x的单调递增区间是⎛ ⎝⎭． （2）令()()()()1,1,g x f x x x =--∈+∞，则()21'0x g x x-=<在()1,+∞上恒成立， 所以()g x 在()1,+∞上单调递减，所以当1x >时，()()10g x g <=， 即当1x >时，()1f x x <-．20．【答案】(Ⅰ)2,4；(Ⅱ)不能在犯错误的概率不超过0.025的前提下认为观众性别与喜爱《壹周·立波秀》节目有关；(Ⅲ)4.0．【解析】试题分析：(Ⅰ)借助题设条件运用比例关系求解；(Ⅱ)借助题设条件运用卡方系数进行推证；(Ⅲ)运用列举法和古典概型的计算公式求解． 试题解析： （Ⅰ）抽样比为616010=，则样本中喜爱的观众有40×110=4名；不喜爱的观众有6﹣4=2名． …………………3分(Ⅱ)假设观众性别与喜爱《壹周·立波秀》节目无关，由已知数据可求得：024********2244010060802040206014022..)(<≈=⨯⨯⨯⨯-⨯⨯=k所以不能在犯错误的概率不超过0250.的前提下认为观众性别与喜爱《壹周·立波秀》节目有关……8分（Ⅲ）设喜爱《壹周·立波秀》节目的4名男性观众为a ，b ，c ，d ， 不喜爱《壹周·立波秀》节目的2名男性观众为1，2；则基本事件分别为：（a ，b ），（a ，c ），（a ，d ），（a ，1），（a ，2），（b ，c ），（b ，d ），（b ，1），（b ，2），（c ，d ），（c ，1），（c ，2），（d ， 1），（d ，2），（1，2）．其中选到的两名观众都喜爱《壹周·立波秀》节目的事件有6个， 故其概率为P （A ）=60.415=…………… 12分 考点：22⨯列联表、古典概型的概率等有关知识的综合运用． 21．【答案】解:(Ⅰ)552cos =B 且(0,)B π∈，∴55cos 1sin 2=-=B B ， )43cos()cos(cos B B A C -=--=ππ1010552255222sin 43sin cos 43cos -=⋅+⋅-=+=B B ππ，(Ⅱ)由(Ⅰ)可得10103)1010(1cos 1sin 22=--=-=C C ， 由正弦定理得sin sin BC AB A C =，即101032252AB=，解得6=AB ， 在BCD ∆中，55252323)52(222⨯⨯⨯-+=CD 5=， 所以5=CD ．22．【答案】(Ⅰ)单调递增区间为1(,)e +∞，单调递减区间为1(0,)e ；(Ⅱ) 2212m e e-<<；(Ⅲ)证明见解析． 【解析】(Ⅱ) 已知2]x e ∈，于是21()x xf x ->变形为11ln x x mx ->-， 从而11ln 1x mx x >--，即0ln 1x mx x <-<-，整理得ln 1ln x x xm x x-+<<．令ln 1()x x g x x -+=，则'2ln ()0x g x x-=<，即()gx 在2]e 上是减函数， ∴max ()1g x g ==-，令ln ()x h x x =，则'21ln ()x h x x -=， x e <时，'()0h x >， 即此时()h x 单调递增； 当2ex e <<时，'()0h x <， 即此时()h x 单调递减， 而222()h h e e =>=，∴min22()h x e =，∴2212m e e -<<．考点：导数的有关知识的综合运用．【易错点晴】导数是研究函数的单调性和极值最值问题的重要而有效的工具．本题就是以含参数m 的函数解析式为背景，考查的是导数知识在研究函数单调性和极值等方面的综合运用和分析问题解决问题的能力．本题的第一问是求函数)(x f 单调区间问题，求解时直接对函数2()ln f x x x mx =-求导，求出了函数2()ln f x x x mx =-的单调区间；第二问运用则借助不等式恒成立将其巧妙变形为11ln 1x mx x >--，将不等式问题进一步逐步转化为ln 1ln x x xm x x-+<<，然后通过构造函数2()e ()()e ek xxx k g x x k -'=--，再运用导数知识求得两函数的最值使得问题获解；第三问借助第一问中结论将欲证的不等式进行分析转化，然后借助基本不等式分析推证，从而使得不等式简捷巧妙获证．本题具有一定的难度和区分度，是一道难得的好题．。

成都外国语学校 高一 上期半期考试数学试卷满分150分，测试时间：120分钟 命题人：全 鑫 审题人：全 鑫 第Ⅰ卷（选择题共60分）一．选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.设集合{}1,2,4A =，{}240x x x m B =-+=．若{}1AB =，则B =（ ）A ．{}1,3-B ．{}1,0C ．{}1,3D ．{}1,5 2．函数121()log 1f x x =+的图象大致是（ ） A ． B ．C ． D ．3.函数1()ln 23f x x x =+-的零点所在区间为（ ） A ． (2,)e B ．(3,4) C. (,3)e D ．(1,2)4.一水池有两个进水口，一个出水口，每个进水口的进水速度如图甲所示．出水口的出水速度如图乙所示，某天0点到6点，该水池的蓄水量如图丙所示．给出以下3个论断：①0点到3点只进水不出水；②3点到4点不进水只出水；③4点到6点不进水不出水，则一定正确的是( )A ．①B ．①②C ．①③D ．①②③ 5.已知123515,12,3x og y og z -===，则下列关系正确的是（ ）A ．x y z >>B ．y x z >>C ．z y x >>D ．x z y >>6. 函数23()()2x f x x =-的零点的个数为（ ） A.1 B. 2 C.3 D. 47．方程()24250x m x m +-+-=的一根在区间()1,0-内，另一根在区间()0,2内，则m的取值范围是（ ） A ．5,53⎛⎫ ⎪⎝⎭ B ．7,53⎛⎫- ⎪⎝⎭ C ．()5,5,3⎛⎫-∞+∞ ⎪⎝⎭ D ．5,3⎛⎫-∞ ⎪⎝⎭8.若数()2)3f x x =+，且(log 2019)5a f =，则1(log )2019af =（ ） A. 5- B. 4 C. 3 D. 19.已知函数2()|l g |,(2)f x o x x =≤,若a b ≠，且()()f a f b =，则a b +的取值范围是（ ） A. 5(1,]2 B. 5(2,]2C. (2,)+∞D. [1,2] 10．已知max{,}a b 表示,a b 两数中的最大值，若|||2|()max{,}x x f x e e +=，则()f x 的最小值为（ ）A. eB. 1C. 2eD. 2 11.给出下列命题，其中正确的命题的个数（ ） ①函数()122log 23y x x =-+图象恒在x 轴的下方；②将2x y =的图像经过先关于y 轴对称，再向右平移1个单位的变化后为12xy -=的图像；③若函数()()22log 21f x x ax =-+的值域为R ，则实数a 的取值范围是()1,1-； ④函数()xf x e =的图像关于y x =对称的函数解析式为ln .y x = A.1 B. 2C. 3D. 4 12.若函数9()log (91)2xxf x =+-，则使不等式()0f x m -≤有解时，实数m 的最小值为（ ） A. 0 B. 3log 2- C. 3log 2 D. 3log 二、填空题（本大题共4小题，每小题5分，共20分）13．函数log (25)1a y x =--恒过定点的坐标为__________.14．若5(21)2xf x x -=+，则(3)f -=________.15．若函数12()2xx m f x n +-=+是奇函数．则实数m n +=_______.16.已知函数3,()8log ,a x x af x x x a⎧≤=⎨>⎩若存在实数1212,,x x x x ≠且使得函数12()()f x f x =成立，则实数a 的取值范围为_________.三、解答题：（本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤） 17.（本小题满分10分）已知全集U R =，集合{}02|>+=a x x A ，集合B是()f x =.（Ⅰ）当2a =时，求集合A B ；（Ⅱ）若()U BC A B =，求实数a 的取值范围.18. 求下列各式的值（Ⅰ）2311log 222)22(21(2)3[(1]log 4-+-++；（II ）已知11223a a -+=，求332222a aa a--++值.19.设函数()3,()9x xg x h x ==（I ）解关于x 的方程()11()2(1)0h x g x h -+=； （II）令()F x =，求1220182019()()()()2020202020202020F F F F ++++的值.20. 已知函数222()()mm f x x m Z -++=∈为偶函数，且(3)(2)f f >.（Ⅰ）求m 的值，并确定()f x 的解析式；（Ⅱ）若()log [()5](0,1)a g x f x ax a a =-+>≠且,是否存在实数a ，使得()g x 在区间[1,2]上为减函数.21．已知()f x 是定义在[1,1]-上的奇函数，且(1)1f =，若对于任意的,[1,1]a b ∈-且0,a b +≠有()()0f a f b a b+>+恒成立.（I ）判断()f x 在[1,1]-上的单调性，并证明你的结论；（II ）若函数()[24]1xxF x f a =⋅++有零点,求实数a 的取值范围.22．已知函数2()(0,1)x xa tf x a a a+=>≠是奇函数． （I ）求实数t 的值；（II ）若(1)0f <，对任意[0,1]x ∈有21(2)f x kx k a a-->-恒成立，求实数k 取值范围； （III ）设22()log [()],(0,1)x xm g x a a mf x m m -=+->≠,若3(1)2f =，问是否存在实数m 使函数()g x 在2[1,log 3]上的最大值为0？ 若存在，求出m 的值；若不存在，说明理由.高一数学试卷(参考答案)一、 选择题 1～6, CDCADC 7～12, BDBACD二、 填空题： 13. (3,1)- 14. 1-215. 3± 16. (0,1)(2,)+∞ 三、解答题：17.解：（Ⅰ）{|1}A x x =>-， 1{|0}2B x x =-<≤ 则A B B = （Ⅱ） {|}2U a C A x x =≤- ，U B C A ⊆, 所以0a ≤18.解：（Ⅰ）53 （Ⅱ） 184719.解：（Ⅰ）3log 2,2x x == （Ⅱ）2019220.解：（1）(3)(2)f f >，所以()f x 在(0,)+∞上增函数，所以，2220m m -++>即：11m <<+m Z ∈故0,1,2m =，当0,2m =时，2222m m -++=此时，2()f x x =满足条件 当1m =时，3()f x x =不满足条件 综上：0,2m =，2()f x x =（2）由（1）可知2()log [5](0,1)a g x x ax a a =-+>≠且假设存在实数a 使得2()log [5](0,1)a g x x ax a a =-+>≠且在[1,2]上为减函数.①当01a <<时，25u x ax =-+在[1,2]上增函数， 即：12a≤，60a ->，得到01a <<②当1a >时，同理：9[4,)2综上：存在a 满足9(0,1)[4,)221.解（1）设任意12,[1,1]x x ∈-，且12x x <令12,a x b x ==-，因为对于任意的,[1,1]a b ∈-且0,a b +≠有()()0f a f b a b+>+恒成立.所以1212()()0f x f x x x +->-，又因为()f x 是定义在[1,1]-上的奇函数1212()()0f x f x x x ->-，120x x -< ， 所以12()()f x f x <故()f x 在[1,1]-上是增函数（2）因为()[24]1xxF x f a =⋅++有零点，所以方程[24]1xxf a ⋅+=-有解又因为(1)(1)1f f -=-=-，所以[24](1)x xf a f ⋅+=- 即 241x x a ⋅+=-有解即1(2)2xxa =-+，即2a ≤- 22.解：（1）因为f(x)的定义域为R ，且f(x)为奇函数， 所以f(0)=1+t 1=0，解得t =−1.检验：当t =−1时，f(x)=a2x −1a x=a x −a −x ，对任意x ∈R ，都有f(−x)=a −x −a x =−f(x)，即f(x)是奇函数，所以t =−1成立。