河南大学附属中学七年级上册数学期末试卷及答案

2020-2021河南大学附属中学七年级数学上期末模拟试卷(附答案)一、选择题1．下列计算中：①325a b ab +=；②22330ab b a -=；③224246a a a +=；④33532a a -=；⑤若0,a ≤a a -=-，错误．．的个数有 （ ） A ．1个 B ．2个 C ．3个 D ．4个 2．整式23x x -的值是4，则2398x x -+的值是（ ）A ．20B ．4C ．16D ．-43．按一定规律排列的单项式：x 3，－x 5，x 7，－x 9，x 11，……第n 个单项式是( )A ．(－1)n －1x 2n －1B ．(－1)n x 2n －1C ．(－1)n －1x 2n ＋1D ．(－1)n x 2n ＋14．“校园足球”已成为灵武市第四张名片，这一新闻获得2400000的点击率，2400000这个数用科学记数法表示，结果正确的是( ) A ．30.2410⨯ B ．62.410⨯ C ．52.410⨯ D ．42410⨯ 5．钟表在8：30时，时针与分针的夹角是（ ）度．A ．85B ．80C ．75D ．706．已知线段AB=10cm ，点C 是直线AB 上一点，BC=4cm ，若M 是AC 的中点，N 是BC 的中点，则线段MN 的长度是（ ） A ．7cmB ．3cmC ．7cm 或3cmD ．5cm7．如图，把六张形状大小完全相同的小长方形卡片（如图①）不重叠的放在一个底面为长方形（长为7cm ，宽为6cm ）的盒子底部（如图②），盒子底面未被卡片覆盖的部分用阴影表示，则图②中两块阴影部分的周长和是（ ）A ．16cmB ．24cmC ．28cmD ．32cm8．下列比较两个有理数的大小正确的是（ ） A ．﹣3＞﹣1B ．1143> C ．510611-<-D ．7697->- 9．如图所示，C 、D 是线段AB 上两点，若AC=3cm ，C 为AD 中点且AB=10cm ，则DB=（ ）A ．4cmB ．5cmC ．6cmD ．7cm10．下列说法： ①若|a|=a ，则a=0；②若a ，b 互为相反数，且ab≠0，则ba=﹣1； ③若a 2=b 2，则a=b ；④若a ＜0，b ＜0，则|ab ﹣a|=ab ﹣a ． 其中正确的个数有（ ） A ．1个B ．2个C ．3个D ．4个11．观察下列各式：133=，239=，3327=，4381=，53243=，63729=，732187=，836561=……根据上述算式中的规律，猜想20193的末位数字是（ ）A ．3B ．9C ．7D ．112．如图，C ，D ，E 是线段AB 的四等分点，下列等式不正确的是（ ）A ．AB ＝4ACB ．CE ＝12AB C ．AE ＝34AB D ．AD ＝12CB 二、填空题13．某市有一天的最高气温为2℃，最低气温为﹣8℃，则这天的最高气温比最低气温高 ________．14．如果方程2x +a ＝x ﹣1的解是﹣4，那么a 的值为_____． 15．观察下列算式：222222222210101;21213;32325;43437;54549;-=+=-=+=-=+=-=+=-=+=L L若字母n 表示自然数，请把你观察到的规律用含有n 的式子表示出来： 16．小强在解方程时，不小心把一个数字用墨水污染成了x=1﹣•5x -，他翻阅了答案知道这个方程的解为x=1，于是他判断●应该是_______． 17．若当x ＝1时，多项式12ax 3﹣3bx +4的值是7，则当x ＝﹣1时，这个多项式的值为_____．18．已知一个角的补角比这个角的余角的3倍小20︒，则这个角是______度． 19．现在的时间是9时20分，此时钟面上时针与分针夹角的度数是_____度． 20．已知关于x 的一元一次方程1999（x +1）﹣3＝2（x +1）+b 的解为x ＝9，那么关于y 的一元一次方程1999y ﹣3＝2y +b 的解y ＝_____． 三、解答题21．解方程：1231337x x -+=-22．某淘宝商家计划平均每天销售某品牌儿童滑板车100辆，但由于种种原因，实际每天的销售量与计划量相比有出入。

2024年七年级上册数学期末测试试卷及答案一、选择题（每题4分，共40分）1. 下列数中是无理数的是：A. √2B. 3C. 0.5D. -7答案：A2. 下列等式中，正确的是：A. √8 = 2√2B. √8 = √2C. √8 = 2√4D. √8 = √16答案：A3. 下列哪个数是七年级上册数学所学的立方根：A. ∛27B. √27C. 27^(1/2)D. 27^(1/3)答案：A4. 下列哪个数是七年级上册数学所学的平方根：A. √9B. ∛9C. 9^(1/2)D. 9^(1/3)答案：C5. 下列哪个数是有理数：A. √3B. πC. 3/2D. √-1答案：C6. 下列哪个数是无理数：A. √4B. 3/4C. √2D. 2√2答案：C7. 下列哪个数是整数：A. -3/4B. 2.5C. -2D. 3/2答案：C8. 下列哪个数是分数：A. -3B. 2C. -3/2D. 2√2答案：C9. 下列哪个数是正数：A. -3B. 0C. 3D. -3/2答案：C10. 下列哪个数是负数：A. 3B. 0C. -3D. -3/2答案：D二、填空题（每题4分，共40分）11. 2 × 2 × 2 = _______答案：812. 3 × 3 × 3 = _______答案：2713. 4 × 4 × 4 = _______答案：6414. 5 × 5 × 5 = _______答案：12515. 6 × 6 × 6 = _______答案：21616. 7 × 7 × 7 = _______答案：34317. 8 × 8 × 8 = _______答案：51218. 9 × 9 × 9 = _______答案：72919. 10 × 10 × 10 = _______答案：100020. 11 × 11 × 11 = _______ 答案：1331三、解答题（共20分）21. 计算下列各题：a. √9 + √16b. √25 - √64c. √81 + √121答案：a. 3 + 4 = 7b. 5 - 8 = -3c. 9 + 11 = 2022. 计算下列各题：a. √(49 - 16)b. √(36 + 49)c. √(16 - 9)答案：a. √33b. √85c. √723. 计算下列各题：a. √(121 - 64)b. √(49 + 64)c. √(16 + 25)答案：a. √57b. √113c. √4124. 判断下列各题：a. √25 + √16 = 5 + 4 = 9b. √81 - √64 = 9 - 8 = 1c. √100 - √100 = 10 - 10 = 0答案：a. 正确b. 错误c. 错误25. 计算下列各题：a. √(16 + 9)b. √(25 - 16)c. √(49 - 25)答案：a. √25 = 5b. √9 = 3c. √24 = 4√6以上是2024年七年级上册数学期末测试试卷及答案，希望对您有所帮助。

七年级上册河南大学附属中学数学期末试卷测试与练习（word解析版）一、初一数学上学期期末试卷解答题压轴题精选（难）1．如图1，已知∠MON=140°，∠AOC与∠BOC互余，OC平分∠MOB，（1）在图1中，若∠AOC=40°，则∠BOC=°，∠NOB=°.（2）在图1中，设∠AOC=α，∠NOB=β，请探究α与β之间的数量关系（必须写出推理的主要过程，但每一步后面不必写出理由）；（3）在已知条件不变的前提下，当∠AOB绕着点O顺时针转动到如图2的位置，此时α与β之间的数量关系是否还成立？若成立，请说明理由；若不成立，请直接写出此时α与β之间的数量关系.【答案】（1）解：如图1，∵∠AOC与∠BOC互余，∴∠AOC+∠BOC=90°，∵∠AOC=40°，∴∠BOC=50°，∵OC平分∠MOB，∴∠MOC=∠BOC=50°，∴∠BOM=100°，∵∠MON=40°，∴∠BON=∠MON-∠BOM=140°-100°=40°，（2）解：β=2α-40°，理由是：如图1，∵∠AOC=α，∴∠BOC=90°-α，∵OC平分∠MOB，∴∠MOB=2∠BOC=2（90°-α）=180°-2α，又∵∠MON=∠BOM+∠BON，∴140°=180°-2α+β，即β=2α-40°；（3）解：不成立，此时此时α与β之间的数量关系为：2α+β=40°，理由是：如图2，∵∠AOC=α，∠NOB=β，∴∠BOC=90°-α，∵OC平分∠MOB，∴∠MOB=2∠BOC=2（90°-α）=180°-2α，∵∠BOM=∠MON+∠BON，∴180°-2α=140°+β，即2α+β=40°，答：不成立，此时此时α与β之间的数量关系为：2α+β=40.【解析】【分析】（1）先根据余角的定义计算∠BOC=50°，再由角平分线的定义计算∠BOM=100°，根据角的差可得∠BON的度数；（2）同理先计算∠MOB=2∠BOC=2（90°-α）=180°-2α，再根据∠BON=∠MON-∠BOM列等式即可；（3）同理可得∠MOB=180°-2α，再根据∠BON+∠MON=∠BOM列等式即可.2．如图，线段AB=20cm．（1）点P沿线段AB自A点向B点以2cm/秒运动，同时点Q沿线段BA自B点向A点以3cm/秒运动，几秒后，点P、Q两点相遇？（2）如图，AO=PO=2cm，∠POQ=60°，现点P绕着点O以30°/秒的速度顺时针旋转一周后停止，同时点Q沿直线BA自B点向A点运动，若P、Q两点也能相遇，求点Q运动的速度．【答案】（1）解：设x秒点P、Q两点相遇根据题意得：2x+3x=20，解得x=4答：4秒后，点P、Q两点相遇。

七年级上册河南大学附属中学数学期末试卷测试与练习（word解析版）一、初一数学上学期期末试卷解答题压轴题精选（难）1．如图下图所示,已知AB//CD, ∠B=30°，∠D=120°;（1）若∠E=60°，则∠F=________;（2）请探索∠E与∠F之间满足的数量关系?说明理由.（3）如下图所示,已知EP平分∠BEF,FG平分∠EFD,反向延长FG交EP于点P,求∠P的度数;【答案】（1）90°（2）解：如图，分别过点E，F作EM∥AB，FN∥AB∴EM∥AB∥FN∴∠B=∠BEM=30°，∠MEF=∠EFN又∵AB∥CD，AB∥FN∴CD∥FN∴∠D+∠DFN=180°又∵∠D =120°∴∠DFN=60°∴∠BEF=∠MEF+30°，∠EFD=∠EFN+60°∴∠EFD=∠MEF +60°∴∠EFD=∠BEF+30°（3）解：如图，过点F作FH∥EP由（2）知，∠EFD=∠BEF+30°设∠BEF=2x°，则∠EFD=（2x+30）°∵EP平分∠BEF，GF平分∠EFD∴∠PEF= ∠BEF=x°，∠EFG= ∠EFD=（x+15）°∵FH∥EP∴∠PEF=∠EFH=x°，∠P=∠HFG ∵∠HFG=∠EFG-∠EFH=15°∴∠P=15°【解析】【解答】解：（1）分别过点E、F作EM∥AB，FN∥AB，则有AB∥EM∥FN∥CD.∴∠B=∠BEM=30°，∠MEF=∠EFN，∠DFN=180°-∠CDF=60°，∴∠BEF=∠MEF+30°，∠EFD=∠EFN+60°，∴∠EFD=∠BEF+30°=90°.【分析】（1）分别过点E、F作AB的平行线，根据平行线的性质即可求解；（2）根据平行线的性质可得∠DFN=60°，∠BEM=30°，∠MEF=∠NFE，即可得到结论；（3）过点F作FH∥EP，设∠BEF=2x°，根据（2）中结论即可表示出∠BFD，根据角平分线的定义可得∠PEF=x°，∠EFG=（x+15）°，再根据平行线的性质即可得到结论.2．如图，直线SN与直线WE相交于点O，射线ON表示正北方向，射线OE表示正东方向．已知射线OB的方向是南偏东m°，射线OC的方向是北偏东n°，且m+n=90°．（1）①若m=50，则射线OC的方向是________，②图中与∠BOE互余的角有________，与∠BOE互补的角有________．（2）若射线OA是∠BON的角平分线，则∠SOB与∠AOC是否存在确定的数量关系？如果存在，请写出你的结论以及计算过程；如果不存在，请说明理由．【答案】（1）北偏东40°；∠BOS，∠EOC；∠BOW（2）解：∠AOC= ∠SOB．理由如下：∵OA平分∠BON，∴∠NOA= ∠NOB，又∵∠BON=180°-∠SOB，∴∠NOA= ∠BON=90°- ∠SOB，∵∠NOC=90°-∠EOC，由（1）知∠BOS=∠EOC，∴∠NOC=90°-∠SOB，∠AOC=∠NOA-∠NOC=90°- ∠SOB-（90°-∠SOB），即∠AOC= ∠SOB.【解析】【解答】解：（1）①∵m+n=90°，m=50°，∴n=40°，∴射线OC的方向是北偏东40°；②∵∠BOE+∠BOS=90°，∠BOE+∠EOC=90°，∴图中与∠BOE互余的角有∠BOS，∠EOC；∠BOE+∠BOW=180°，∴图中与∠BOE互补的角有∠BOW，故答案为：①北偏东40°；②∠BOS，∠EOC；∠BOW.【分析】（1）①由m+n=90°，m=50°可求得n值，从而可得射线OC的方向.②根据余角定义可知∠BOE+∠BOS=90°，∠BOE+∠EOC=90°，从而可得图中与∠BOE互余的角；由补角定义可得∠BOE+∠BOW=180°，从而可得图中与∠BOE互补的角.（2）∠AOC=∠SOB．理由如下：由角平分线定义和领补角定义可得∠NOA= ∠BON=90°-∠SOB，结合（1）中条件可得∠NOC=90°-∠SOB；由∠AOC=∠NOA-∠NOC即可求得它们之间的数量关系.3．如图1，平面内一定点A在直线MN的上方，点O为直线MN上一动点，作射线OA、OP、OA′，当点O在直线MN上运动时，始终保持∠MOP=90°、∠AOP=∠A′OP，将射线OA 绕点O顺时针旋转60°得到射线OB（1）如图1，当点O运动到使点A在射线OP的左侧，若OB平分∠A′OP，求∠AOP的度数．（2）当点O运动到使点A在射线OP的左侧，∠AOM=3∠A′OB时，求的值．（3）当点O运动到某一时刻时，∠A′OB=150°，直接写出∠BOP=________度．【答案】（1）解：由题意可得：∠AOB=60°，∠AOP=∠A′OP，∵OB平分∠A′OP，∴∠A′OP=2∠POB，∴∠AOP=∠A′OP=2∠POB，∴∠AOB=∠AOP+∠POB=3∠POB=60°，∴∠POB=20°，∴∠AOP=2∠POB=40°（2）解：①当点O运动到使点A在射线OP的左侧，且射线OB在在∠A′OP的内部时，如图1，设∠A′OB=x，则∠AOM=3∠A′OB=3x，∠AOA′= ，∵OP⊥MN，∴∠AON=180°-3，∠AOP=90°-3x，∴，∵∠AOP=∠A′OP，∴∠AOP=∠A′OP=∴，解得：，∴；②当点O运动到使A在射线OP的左侧，但是射线OB在∠A′ON内部时，如图2，设∠A′OB=x，则∠AOM=3x，∠AON= ，∠AOA′= ，∵∠AOP=∠A′OP，∴∠AOP=∠A′OP= ，∵OP⊥MN，∴∠AOP=90-∠AOM=90-3x，∴，解得：，∴；（3）解：①如图3，当∠A′OB=150°时，由图可得：∠A′OA=∠A′OB-∠AOB=150°-60°=90°，又∵∠AOP=∠A′OP，∴∠AOP=45°，∴∠BOP=60°+45°=105°；②如图4，当∠A′OB=150°时，由图可得∠A′OA=360°-150°-60°=150°，又∵∠AOP=∠A′OP，∴∠AOP=75°，∴∠BOP=60°+75°=135°；综上所述：∠BOP的度数为105°或135°.【解析】【分析】（1）由角平分线的性质和∠ AOP=∠A′OP可得∠POB= ∠AOB，∠AOP=∠AOB，则∠POA的度数可求解；（2）由题意可分两种情况：①当点O运动到使点A在射线OP的左侧，且射线OB在在∠A′OP的内部时，由角的构成易得∠AOP= -∠AOM= -3∠A′OB，∠AOA′=+∠A′OB，由角平分线的性质可得∠AOP=∠A′OP，于是可得关于∠A′OB的方程，解方程可求得∠A′OB的度数，则可求解；②当点O运动到使A在射线OP的左侧，但是射线OB在∠A′ON内部时，同理可求解；（3）由题意可分两种情况讨论求解：①当∠A′OB沿顺时针成150°时，结合已知条件易求解；②当∠A′OB沿时针方向成 150°时，结合题意易求解。

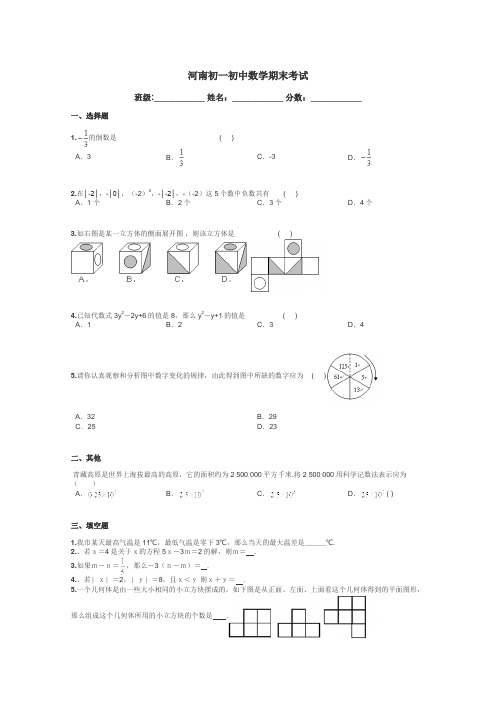
河南初一初中数学期末考试班级:___________ 姓名：___________ 分数：___________一、选择题1.的倒数是 ( )A．3B．C．-3D．2.在│-2│，-│0│，（-2）5，-│-2│，-（-2）这5个数中负数共有 ( )A．1 个B．2个C．3个D．4个3.如右图是某一立方体的侧面展开图，则该立方体是 ( )4.已知代数式3y2－2y+6的值是8，那么y2－y+1的值是 ( )A．1B．2C．3D．45.请你认真观察和分析图中数字变化的规律，由此得到图中所缺的数字应为 ( )A．32B．29C．25D．23二、其他青藏高原是世界上海拔最高的高原，它的面积约为2 500 000平方千米.将2 500 000用科学记数法表示应为（）A．B．C．D． ( )三、填空题1.我市某天最高气温是11℃，最低气温是零下3℃，那么当天的最大温差是＿＿＿℃.2.、若ｘ＝4是关于ｘ的方程5ｘ－3ｍ＝2的解，则ｍ＝ .3.如果ｍ－ｎ＝，那么－3（ｎ－ｍ）＝ .4.、若∣ｘ∣＝2，∣ｙ∣＝8，且ｘ＜ｙ则ｘ＋ｙ＝ .5.一个几何体是由一些大小相同的小立方块摆成的，如下图是从正面、左面、上面看这个几何体得到的平面图形，那么组成这个几何体所用的小立方块的个数是 .从正面看从左面看从上面看6.某日历上一竖列的相邻三个数的和为63，则中间一个的日期是 .7.标价为ｘ元的某件商品，按标价八折出售仍盈利ｂ元，已知该件商品的进价是ａ元，则ｘ＝ .8.已知线段AB＝10cm，点D是线段AB的中点，直线AB上有一点C，并且BC＝2 cm，则线段DC＝ .9.当ｘ＝1，ｙ＝－1时代数式ａｘ＋ｂｙ－3的值为0，那么当ｘ＝－1，ｙ＝1时代数式ａｘ＋ｂｙ－3的值为 .四、计算题1.（8分）计算：－13－（1－0.5）××［2－（－3）2］.2.（10分）计算：.五、解答题1.（9分）先化简，再求值：×（－4ｘ2＋2ｘ－8）－（ｘ－1），其中ｘ＝.2.（9分）解方程：－＝1.3.（9分）下图是由一些相同的小立方块搭成的几何体，请画出从三个不同方向看这个几何体得到的平面图形。

5 y 2x-3－2 2 x51 –4 –23 202X 河南省七年级上学期期末考试数学试题七（ ）班 分数：一、选择题：（第小题3分，共24分）1、下列四个算式中，有一个算式与其他三个算式的计算结果不同，则该算式是（ ）A ．()21-B ．21-C ．()31- D ．1--2、现在网购越来越多地成为人们的一种消费方式，刚刚过去的202X 年的“双11”网上促销活动中，天猫的支付交易额突破570亿元，将570亿元用科学记数法表示为（ ） A. 81070.5⨯ B. 101070.5⨯ C. 9100.57⨯ D. 1110570.0⨯3、a 、b 为有理数，a<0，b<0，且|a|>|b|，如果a ，b ，－a ，－b 在数轴上所对应的点分别为A 、B 、C 、D ，那么这四个点在数轴上从左到右的顺序依次为： （ ） A. A B D C B. C D B A C. B A C D D. B D C A4、如图是一个正方体的平面展开图，正方体中相对的面上的数字或代数式互为相反数，则2x ＋y 的值为 ( ) A. 0 B. －１ C. －２ D. 15、下列判断错误的是 （ ）A ．多项式4252+-x x 是二次三项式B ．单项式432c b a -的系数是－1，次数是9 C ．式子m + 5，ab ，x=1，－2，vs都是代数式D.当k=3时，关于x ，y 的代数式(－3kxy + 3y)+(9xy － 8x + 1)中 不含二次项 6、方程131212=---x x 去分母得62236=---x x ，其中错误的原因是( )A. 分母的最小公倍数找错B. 去分母时，漏乘了分母为1的数C. 去分母时，分子部分多项式未添括号，造成符号错误D. 去分母时，分子未乘相应的数7、已知某商店有两个进价不同的计算器，都卖了100元，其中一个盈利60％，另一个亏损20％，在这次买卖中，这家商店（ ）A. 不盈不亏B. 盈利37.5元C. 亏损25元D. 盈利12.5元 8、下列语句正确的是 （ ）A ．线段AB 是点A 与点B 的距离B ．过n 边形的每一个顶点有（n -3）条对角线C ．各边相等的多边形是正多边形D ．两点之间的所有连线中，直线最短 二、填空题：（第小题3分，共21分）9、两个同样大小的正方体积木，每个正方体相对两个面上写的数字之 和都等于0．现将两个正方体并排放置，看得见的5个面上的数如图所示，则看不见的7个面上所写的数字之和等于 ．10、已知a+b=-7，ab=10，则代数式(3ab+6a+4b)-(2a-2ab)的值为 ．11、9时45分时,时钟的时针与分针的夹角度数是 .12、如图所示，O 是直线AC 上一点，OB 是一条射线，OD 平分AOB ∠，OE 在BOC ∠内，EOC BOE ∠=∠31，︒=∠60DOE ，则EOC ∠的度数是 .13、点C 在直线AB 上，AC = 10 cm ，CB =8 cm ，点M 、N 分别是AC 、BC 的中点, 则线段MN 的长为 ．14、一圆柱形容器的内半径为3厘米，内壁高30厘米，容器内盛有18厘米高的水，现将一个底面半径为2厘米，高15厘米的金属圆柱竖直放入容器内，问容器内的水将升高 厘米．15、已知：1＋3＝4＝22；1＋3＋5＝9＝32；1＋3＋5＋7＝16＝42；1＋3＋5＋7＋9＝25＝52，…，根据前面各式的规律，以下等式（n 为正整数），①1＋3＋5＋7＋9＋…＋（2n -1）=2n ；②1＋3＋5＋7＋9＋…＋（2n +3）=()23+n ；③ 1＋3＋5＋7＋9＋…＋2013=21007 ；④101＋…＋2013=21007-250其中正确的有 个.三、解答题:(共8个小题，共75分)16、（６分）画出右面由11个小正方体搭成的几何体从不同角 度看得到的图形。

河南初一初中数学期末考试班级:___________ 姓名：___________ 分数：___________一、选择题1.如图所示的圆柱体，其主视图、左视图和俯视图中至少有一个是（）．A．三角形B．四边形C．五边形D．六边形2.设a是最小的自然数，b是最大的负整数，c是绝对值最小的有理数，则等于( )．A．1B．0C．-1D．23.若-5x a yz b与 2x3y c z2是同类项，则abc的值是（）A．-35B．35C．6D．-64.一条船停留在海面上，从船上看灯塔位于北偏东30°，那么从灯塔看船位于灯塔的( )A．南偏西60° B．西偏南50° C．南偏西30° D北偏东30°5.下列说法错误的是( )A．射线OA与射线AO是不同的两条射线B．两直线相交，只有一个交点C．相等的两个角的余角相等D．相等的两个角是对顶角6.若四个不等于0的数相乘所得积的符号为负，那么，这四个数中正数的个数是（）A．1个B．2个C．3个D．1个或3个7.如果用A表示1个立方体，用B表示两个立方体叠加，用C表示三个立方体叠加，那么右图中由7个立方体叠成的几何体，正视图为( )8.下列判断的语句不正确的是（）Ａ．若点C在线段BA的延长线上，则BA=AC－BCＢ．若点Ｃ在线段ＡＢ上，则ＡＢ＝ＡＣ＋ＢＣＣ．若ＡＣ＋ＢＣ>ＡＢ，则点Ｃ一定在线段ＢＡ外D．若Ａ、Ｂ、Ｃ三点不在一直线上，则ＡＢ<AC+BC9.线段AB上有任一点C，点E和点F分别是线段AC和线段CB的中点，若EF=4，则AB的长是（）。

A．6B．8C．10D．1210.计算：，，，，，·····归纳各计算结果中的个位数字规律，则的个位数字是（）。

A．1B．3C．7D．5二、填空题1.若代数式的值与的取值无关，则2.已知直线AB和CD、EF相交于O点，CD⊥AB，∠COE=27°18′，则∠DOF=___；∠AOF=_____.3.绝对值大于2而小于9的数中，最小的整数是，最大的整数是，满足条件的全部整数的和是 .4.把多项式按字母b降幂排列为；5.已知∠α的余角等于38°12′，则∠α=__________；∠α的补角=____________.6.已知一条射线OA，若从点O再引两条射线OB和OC，使∠AOB=60°，∠BOC=20°，则∠AOC=_____7.为了节约用水，某市规定，每户居民每月用水不超过20立方米，按每立方米2元收费，超过20立方米，则超过部分按每立方米4元收费。

河南初一初中数学期末考试班级:___________ 姓名：___________ 分数：___________一、单选题1.下列是二元一次方程的是（）A．3x﹣6=x B．3x=2y C．x﹣y2=0D．2x﹣3y=xy2.下列交通标志中，是轴对称图形但不是中心对称图形的是（）A．B．C．D．3.若关于x的方程x﹣2+3k=的解是正数，则k的取值范围是（）A．k＞B．k≥C．k＜D．k≤4.为了搞活经济，某商场将一种商品A按标价9折出售，仍获利润10%，若商品A标价为33元，那么商品进货价为（）A．31元B．30.2元C．29.7元D．27元5.根据不等式的性质，下列变形正确的是（）A．由a＞b得ac2＞bc2B．由ac2＞bc2得a＞bC．由-a＞2得a＜2D．由2x+1＞x得x＞16.已知等腰三角形的两边长分別为a、b，且a、b满足+（2a+3b-13）2=0，则此等腰三角形的周长为（）A．7或8B．6或10C．6或7D．7或107.我国古代数学名著《孙子算经》中记载了一道题，大意是：100匹马恰好拉了100片瓦，已知1匹大马能拉3片瓦，3匹小马能拉1片瓦，问有多少匹大马、多少匹小马？若设大马有x匹，小马有y匹，那么可列方程组为（）A．B．C．D．8.已知三角形的三边长为3，8，x．若周长是奇数，则x的值有（）A．6个B．5个C．4个D．3个9.选用下列某一种形状的瓷砖密铺地面，不能做到无缝隙，不重叠要求的（）A．正方形B．任意三角形C．正六边形D．正八边形10.关于x 的不等式组的整数解共有5个，则a 的取值范围（ ） A ．a=﹣3B ．﹣4＜a ＜﹣3C ．﹣4≤a ＜﹣3D ．﹣4＜a≤﹣3二、填空题1.若关于x 的方程（k ﹣2）x |k ﹣1|+5k+1="0" 是一元一次方程，则k+x=_____．2.方程3x ﹣y=4中，有一组解x 与y 互为相反数，则3x+y=_____．3.一个多边形的每一个外角都等于72°，则这个多边形是_____边形．4.一个三角形有两条边相等，周长为18cm ，三角形的一边长为4cm ，则其他两边长分别为_____cm ，_____cm ．5.书店举行购书优惠活动：①一次性购书不超过100元，不享受打折优惠；②一次性购书超过100元但不超过200元一律打九折； ③一次性购书200元一律打七折．小丽在这次活动中，两次购书总共付款229.4元，第二次购书原价是第一次购书原价的3倍，那么小丽这两次购书原价的总和是 元．三、解答题1.﹣=1.2．2.解方程组：．3.解不等式组：把解集表示在数轴上并求出它的整数解的和．4.如图，已知△ABC ≌△DEF ，∠A=32°，∠B=48°，BF=3，求∠DFE 的度数和EC 的长．5.如图，在所给网格图（ 每小格均为边长是1的正方形）中完成下列各题： （1）将△ABC 向下平移5个单位得△A 1B 1C 1，画出平移后的△A 1B 1C 1． （2）画出△ABC 关于点B 成中心对称的图形．（3）在直线l 上找一点P ，使△ABP 的周长最小．6.如图，在△ABC 中，点D 是BC 边上的一点，∠B=50°，∠BAD=30°，将△ABD 沿AD 折叠得到△AED ，AE 与BC 交于点F ．（1）填空：∠AFC=_____度；（2）求∠EDF 的度数．7.某中学计划购买A 型和B 型课桌凳共200套．经招标，购买一套A 型课桌凳比购买一套B 型课桌凳少用40元，且购买4套A 型和5套B 型课桌凳共需1820元．（1）求购买一套A 型课桌凳和一套B 型课桌凳各需多少元？（2）学校根据实际情况，要求购买这两种课桌凳总费用不能超过40880元，并且购买A 型课桌凳的数量不能超过B 型课桌凳数量的，求该校本次购买A 型和B 型课桌凳共有几种方案？哪种方案的总费用最低？8.如图，取一副三角板按图1拼接，固定三角板ADE（含30°），将三角板ABC（含45°）绕点A顺时针方向旋转一个大小为α的角（0°＜α≤45°），试问：（1）当∠α=_____度时，能使图2中的AB∥DE；（2）当旋转到AB与AE重叠时（如图3），则∠α=_____度；（3）当△ADE的一边与△ABC的某一边平行（不共线）时，直接写出旋转角α的所有可能的度数；（4）当0°＜α≤45°时，连接BD（如图4），探求∠DBC+∠CAE+∠BDE的值的大小变化情况，并说明理由．河南初一初中数学期末考试答案及解析一、单选题1.下列是二元一次方程的是（）A．3x﹣6=x B．3x=2y C．x﹣y2=0D．2x﹣3y=xy【答案】B【解析】A、是一元一次方程，故错误；B、正确；C、未知数的项的最高次数是2，故错误；D、未知数的项的最高次数是2，故错误．故选B．【点睛】主要对二元一次方程的条件(①只含有两个未知数；②未知数的项的次数都是1；③整式方程)进行分析.2.下列交通标志中，是轴对称图形但不是中心对称图形的是（）A．B．C．D．【答案】A【解析】根据轴对称图形与中心对称图形的概念求解．A、是轴对称图形，不是中心对称图形，符合题意；B、不是轴对称图形，也不是中心对称图形，不符合题意；C、不是轴对称图形，也不是中心对称图形，不符合题意；D、是轴对称图形，也是中心对称图形，不符合题意．【考点】（1）中心对称图形；（2）轴对称图形3.若关于x的方程x﹣2+3k=的解是正数，则k的取值范围是（）A．k＞B．k≥C．k＜D．k≤【解析】解方程x﹣2+3k=得：x=-4k+3，∵方程得解为正数，∴-4k+3＞0，解得：k＜.故选C.4.为了搞活经济，某商场将一种商品A按标价9折出售，仍获利润10%，若商品A标价为33元，那么商品进货价为（）A．31元B．30.2元C．29.7元D．27元【答案】D【解析】设进货价为x元．那么根据题意可得出：（1+10%）x=33×90%，解得：x=27，故选：D．5.根据不等式的性质，下列变形正确的是（）A．由a＞b得ac2＞bc2B．由ac2＞bc2得a＞bC．由-a＞2得a＜2D．由2x+1＞x得x＞1【答案】B【解析】根据不等式的基本性质可知：选项A、C、D错误；故选B.【考点】不等式的基本性质.6.已知等腰三角形的两边长分別为a、b，且a、b满足+（2a+3b-13）2=0，则此等腰三角形的周长为（）A．7或8B．6或10C．6或7D．7或10【答案】A【解析】先根据非负数的性质求出a，b的值，再分两种情况确定第三边的长，从而得出三角形的周长．∵+（2a+3b﹣13）2=0，∴解得，当a为底时，三角形的三边长为2，3，3，则周长为8；当b为底时，三角形的三边长为2，2，3，则周长为7；综上所述此等腰三角形的周长为7或8．【考点】(1)、等腰三角形的性质；(2)、非负数的性质：偶次方；(3)、非负数的性质：算术平方根；(4)、解二元一次方程组；(5)、三角形三边关系．7.我国古代数学名著《孙子算经》中记载了一道题，大意是：100匹马恰好拉了100片瓦，已知1匹大马能拉3片瓦，3匹小马能拉1片瓦，问有多少匹大马、多少匹小马？若设大马有x匹，小马有y匹，那么可列方程组为（）A．B．C．D．【答案】C【解析】设有x匹大马，y匹小马，根据100匹马恰好拉了100片瓦，已知一匹大马能拉3片瓦，3匹小马能拉1片瓦，列方程组:8.已知三角形的三边长为3，8，x．若周长是奇数，则x的值有（）A．6个B．5个C．4个D．3个【答案】D【解析】解：根据三角形的三边关系可得：8-3＜x＜8+3，即：5＜x＜11，∵三角形的周长为奇数，∴x=6，8，10，共3个．故选D．9.选用下列某一种形状的瓷砖密铺地面，不能做到无缝隙，不重叠要求的（）A．正方形B．任意三角形C．正六边形D．正八边形【答案】D【解析】A选项:正方形的每个内角是90°，能整除360°，能密铺；B选项:任意三角形的内角和是180°，能整除360°，能密铺；C选项:正六边形每个内角是120°，能整除360°，能密铺；D选项:正八边形每个内角是135°，不能整除360°，不能密铺；故选D．【点睛】一种正多边形的镶嵌应符合一个内角度数能整除360°．10.关于x的不等式组的整数解共有5个，则a的取值范围（）A．a=﹣3B．﹣4＜a＜﹣3C．﹣4≤a＜﹣3D．﹣4＜a≤﹣3【答案】D【解析】不等式组解得：a≤x<2，∵不等式组的整数解有5个为1，0，-1，-2，-3∴-4＜a≤-3．故选D．【点睛】此题考查了一元一次不等式组的整数解，弄清题意是解本题的关键．二、填空题1.若关于x的方程（k﹣2）x|k﹣1|+5k+1="0" 是一元一次方程，则k+x=_____．【答案】k="0," x=【解析】根据题意得：k-2≠0且|k-1|=1，解得：k=0．把k=0代入方程得-2x+1=0，解得：x=∴k+x=.故答案是:.2.方程3x﹣y=4中，有一组解x与y互为相反数，则3x+y=_____．【答案】2【解析】依题意得：x=-y．∴3x-y=3x+x=4x=4，∴x=1，则y=-1．∴3x+y=2．故答案是：2.3.一个多边形的每一个外角都等于72°，则这个多边形是_____边形．【答案】5【解析】边数n=360°÷72°=5．故答案为：5．4.一个三角形有两条边相等，周长为18cm，三角形的一边长为4cm，则其他两边长分别为_____cm，_____cm．【答案】 7 7【解析】（1）若4cm为底边，则另外两边均为（18-4）=7厘米；（2）若4cm为腰长，则另一腰为4厘米，底边为18-4×2=10厘米∵4+4＜10，∴此时不能构成三角形，舍去．因此其他两边的长分别为7cm、7cm．故答案是：7，7．【点睛】此题主要考查学生对等腰三角形的性质及三角形的三边关系的掌握；做题时注意分情况讨论，并注意是否能构成三角形．5.书店举行购书优惠活动：①一次性购书不超过100元，不享受打折优惠；②一次性购书超过100元但不超过200元一律打九折；③一次性购书200元一律打七折．小丽在这次活动中，两次购书总共付款229.4元，第二次购书原价是第一次购书原价的3倍，那么小丽这两次购书原价的总和是元．【答案】248或296【解析】设第一次购书的原价为x元，则第二次购书的原价为3x元．根据x的取值范围分段考虑，根据“付款金额=第一次付款金额+第二次付款金额”即可列出关于x的一元一次方程，解方程即可得出结论．设第一次购书的原价为x元，则第二次购书的原价为3x元，依题意得：①当0＜x≤时，x+3x=229.4，解得：x=57.35（舍去）；②当＜x≤时，x+×3x=229.4，解得：x=62，此时两次购书原价总和为：4x=4×62=248；③当＜x≤100时，x+×3x=229.4，解得：x=74，此时两次购书原价总和为：4x=4×74=296．综上可知：小丽这两次购书原价的总和是248或296元【考点】一元一次方程的应用三、解答题1.﹣ =1.2．【答案】6.4【解析】试题分析:先将分母化成整数后,再去分母,去括号,移项,系数为1的步骤解方程即可;试题解析:-=50x-50-30x-60="18"20 x="128"x="6.4"2.解方程组：．【答案】【解析】试题分析:先对方程组进行化简后,再用代入消元法解.试题解析:解:由④得： x="5y" -3代入③得： 25y -15 -11y =-1 14y =14 y=1则：x ="5-3" =2 综上：3.解不等式组：把解集表示在数轴上并求出它的整数解的和．【答案】-7【解析】试题分析:先求两个不等式的解集,再求公共解,并数轴上表示,写出整数解和求整数解的和. 试题解析:不等式①，得x ＜3， 解不等式②，得x≥﹣4．在同一数轴上表示不等式①②的解集，得∴这个不等式组的解集是﹣4≤x ＜3，∴这个不等式组的整数解的和是﹣4﹣3﹣2﹣1+0+1+2="﹣7．"4.如图，已知△ABC ≌△DEF ，∠A=32°，∠B=48°，BF=3，求∠DFE 的度数和EC 的长．【答案】∠DFE=1000 EC=3【解析】试题分析:根据全等三角形的性质得出∠D=∠A=48°，∠E=∠B=32°，BC=EF ，求出BF=EC ，即可求出答案． 试题解析: ∵ ≌∴∠D=∠A=480∠E=∠B=320 在中∠D+∠E+∠DFE=1800 解得 ∠DFE=1000 ∵ ≌ ∴ BC="EF" BF+FC=EC+CF ∴ BF="EC" ∵ ∴EC=35.如图，在所给网格图（ 每小格均为边长是1的正方形）中完成下列各题： （1）将△ABC 向下平移5个单位得△A 1B 1C 1，画出平移后的△A 1B 1C 1． （2）画出△ABC 关于点B 成中心对称的图形．（3）在直线l 上找一点P ，使△ABP 的周长最小．【答案】【解析】试题分析:（1）直接利用平移的性质得出对应点位置进而得出答案； （2）直接利用中心对称图形的性质得出对应点位置； （3）利用轴对称求最短路线的方法得出答案． 试题解析:(1)如图所示: △A 1B 1C 1即为所求 (2) 如图所示: △DEF 即为所求(3) 如图所示: P 点位置,使△ABP 的周长最小.6.如图，在△ABC 中，点D 是BC 边上的一点，∠B=50°，∠BAD=30°，将△ABD 沿AD 折叠得到△AED ，AE 与BC 交于点F ．（1）填空：∠AFC=_____度；（2）求∠EDF 的度数．【答案】(1) 1100. (2) 20°【解析】试题分析:（1）根据折叠的特点得出∠BAD=∠DAF ，再根据三角形一个外角等于它不相邻两个内角之和，即可得出答案；（2）根据已知求出∠ADB 的值，再根据△ABD 沿AD 折叠得到△AED ，得出∠ADE=∠ADB ，最后根据∠EDF=∠EDA+∠BDA-∠BDF ，即可得出答案． 试题解析:（1）∵△ABD 沿AD 折叠得到△AED ， ∴∠BAD=∠DAF ， ∵∠B=50°∠BAD=30°，∴∠AFC=∠B+∠BAD+∠DAF=110°； 故答案为110． （2）∵∠B=50°，∠BAD=30°， ∴∠ADB=180°-50°-30°=100°， ∵△ABD 沿AD 折叠得到△AED ， ∴∠ADE=∠ADB=100°，∴∠EDF=∠EDA+∠BDA-∠BDF=100°+100°-180°=20°．【点睛】此题考查了三角形的内角和定理、三角形的外角的性质、翻折变换等问题，解答的关键是沟通外角和内角的关系．7.某中学计划购买A 型和B 型课桌凳共200套．经招标，购买一套A 型课桌凳比购买一套B 型课桌凳少用40元，且购买4套A 型和5套B 型课桌凳共需1820元．（1）求购买一套A 型课桌凳和一套B 型课桌凳各需多少元？（2）学校根据实际情况，要求购买这两种课桌凳总费用不能超过40880元，并且购买A 型课桌凳的数量不能超过B 型课桌凳数量的，求该校本次购买A 型和B 型课桌凳共有几种方案？哪种方案的总费用最低？ 【答案】(1) 购买一套A 型课桌凳和一套B 型课桌凳各需180元和220元. (2) 共有3种方案,总费用最低方案是购买A 型80套，购买B 型120套【解析】试题分析: （1）根据购买一套A型课桌凳比购买一套B型课桌凳少用40元，以及购买4套A型和5套B型课桌凳共需1820元，得出等式方程求出即可；（2）利用要求购买这两种课桌凳总费用不能超过40880元，并且购买A型课桌凳的数量不能超过B型课桌凳数量的，得出不等式组，求出a的值即可，再利用一次函数的增减性得出答案即可．试题解析:（1）设A型每套元，B型每套（）元∴∴即购买一套A型课桌凳和一套B型课桌凳各需180元和220元。

河南大学附属中学七年级上学期数学压轴题期末复习试卷及答案-百度文库一、压轴题1．如图1，O为直线AB上一点，过点O作射线OC，∠AOC＝30°，将一直角三角板（其中∠P＝30°）的直角顶点放在点O处，一边OQ在射线OA上，另一边OP与OC都在直线AB的上方．将图1中的三角板绕点O以每秒3°的速度沿顺时针方向旋转一周．（1）如图2，经过t秒后，OP恰好平分∠BOC．①求t的值；②此时OQ是否平分∠AOC？请说明理由；（2）若在三角板转动的同时，射线OC也绕O点以每秒6°的速度沿顺时针方向旋转一周，如图3，那么经过多长时间OC平分∠POQ？请说明理由；（3）在（2）问的基础上，经过多少秒OC平分∠POB？（直接写出结果）．2．已知长方形纸片ABCD，点E在边AB上，点F、G在边CD上，连接EF、EG．将∠BEG 对折，点B落在直线EG上的点B′处，得折痕EM；将∠AEF对折，点A落在直线EF上的点A′处，得折痕EN．（1）如图1，若点F与点G重合，求∠MEN的度数；（2）如图2，若点G在点F的右侧，且∠FEG＝30°，求∠MEN的度数；（3）若∠MEN＝α，请直接用含α的式子表示∠FEG的大小．3．如图，已知数轴上有三点A，B，C ，若用AB 表示A，B 两点的距离，AC 表示A ，C 两点的距离，且BC = 2 AB ，点A 、点C 对应的数分别是a 、c ，且| a - 20 | + | c +10 |= 0 .（1）若点P，Q 分别从A，C 两点同时出发向右运动，速度分别为 2 个单位长度/秒、5个单位长度/ 秒，则运动了多少秒时，Q 到B 的距离与P 到B 的距离相等？（2）若点P ，Q 仍然以（1）中的速度分别从A ，C 两点同时出发向右运动，2 秒后，动点R 从A点出发向左运动，点R 的速度为1个单位长度/秒，点M 为线段PR 的中点，点N为线段RQ的中点，点R运动了x 秒时恰好满足MN +AQ = 25，请直接写出x的值.4．已知AOD α∠=，OB 、OC 、OM 、ON 是AOD ∠内的射线．(1)如图1，当160α=︒，若OM 平分AOB ∠，ON 平分BOD ∠，求MON ∠的大小；(2)如图2，若OM 平分AOC ∠，ON 平分BOD ∠，20BOC ∠=︒，60MON ∠=︒，求α．5．如图，已知数轴上点A 表示的数为8，B 是数轴上位于点A 左侧一点，且AB =22，动点P 从A 点出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t （t ＞0）秒．（1）出数轴上点B 表示的数 ；点P 表示的数 （用含t 的代数式表示）（2）动点Q 从点B 出发，以每秒3个单位长度的速度沿数轴向右匀速运动，若点P 、Q 同时出发，问多少秒时P 、Q 之间的距离恰好等于2？（3）动点Q 从点B 出发，以每秒3个单位长度的速度沿数轴向左匀速运动，若点P 、Q 同时出发，问点P 运动多少秒时追上点Q ？（4）若M 为AP 的中点，N 为BP 的中点，在点P 运动的过程中，线段MN 的长度是否发生变化？若变化，请说明理由，若不变，请你画出图形，并求出线段MN 的长．6．如图，从左到右依次在每个小方格中填入一个数，使得其中任意三个相邻方格中所填数之和都相等．6 a b x -1 -2 ... （1）可求得 x =______，第 2021 个格子中的数为______；（2）若前 k 个格子中所填数之和为 2019，求 k 的值；（3）如果m ，n 为前三个格子中的任意两个数，那么所有的|m -n | 的和可以通过计算|6-a |+|6-b|+|a -b|+|a -6| +|b -6|+|b -a| 得到．若m ，n 为前8个格子中的任意两个数，求所有的|m-n|的和.7．已知数轴上两点A 、B ，其中A 表示的数为-2，B 表示的数为2，若在数轴上存在一点C ，使得AC+BC=n ，则称点C 叫做点A 、B 的“n 节点”．例如图1所示：若点C 表示的数为0，有AC+BC=2+2=4，则称点C 为点A 、B 的“4节点”．请根据上述规定回答下列问题：（1）若点C 为点A 、B 的“n 节点”，且点C 在数轴上表示的数为-4，求n 的值；（2）若点D 是数轴上点A 、B 的“5节点”，请你直接写出点D 表示的数为______；（3）若点E 在数轴上（不与A 、B 重合），满足BE=12AE ，且此时点E 为点A 、B 的“n 节点”，求n 的值．8．结合数轴与绝对值的知识解决下列问题：探究：数轴上表示4和1的两点之间的距离是____，表示－3和2两点之间的距离是____；结论：一般地，数轴上表示数m 和数n 的两点之间的距离等于∣m-n ∣．直接应用：表示数a 和2的两点之间的距离等于____，表示数a 和－4的两点之间的距离等于____；灵活应用：(1)如果∣a+1∣=3，那么a=____；(2)若数轴上表示数a 的点位于－4与2之间，则∣a-2∣+∣a+4∣=_____；(3)若∣a-2∣+∣a+4∣=10，则a =______；实际应用：已知数轴上有A 、B 、C 三点，分别表示-24，-10，10，两只电子蚂蚁甲、乙分别从A 、C 两点同时相向而行，甲的速度为4个单位长度/秒，乙的速度为6个单位长度/秒.(1)两只电子蚂蚁分别从A 、C 两点同时相向而行，求甲、乙数轴上相遇时的点表示的数。

河南省七年级数学上册期末试卷姓名： 计分：一、精心选一选(每小题3分，共30分)1．下列说法中，不正确的是（ ）A ．0既不是正数，也不是负数 B ．1是绝对值最小的数C ．0的相反数是0D ．0的绝对值是02．已知数轴上C 、D 两点的位置如图1所示，那么下列说法错误的是（ ）A ．D 点表示的数是正数B ．C 点表示的数是负数C ．D 点表示的数比0小D ．C 点表示的数比D 点表示的数小3．下列变形正确的是（ ）A ．从7+x =13，得到x =13+7 B ．从5x =4x +8，得到5x -4x =8C ．从94x =-，得到94x=-D ．从02x=，得x = 2. 4．下面的说法正确的是（ ）A ．2-不是单项式 B ．a -表示负数 C ．b a 232π-的系数是32-．D 、1ax x++不是多项式5．今年，参加“全省课改实验区初中毕业学生考试”的同学约有15万人． 其中男生约有a 万人， 则女生约有 （ ） A ．(15)a +万人B ．(15)a -万人C ．15a 万人D ．15a万人 6．-12300000用科学记数法 应记做：A 、71023.1⨯ B 、81023.1⨯- C 、71023.1⨯- D 、6103.12⨯- 7．下列各式中运算错误的是（ ）A ．523x x x -= B ．550ab ba -= C ．22245xy xy x y -=-D ．222325x x x +=8．若有理数满足110a b+=，则下列说法不正确的是（ ）A ．a 与b 的差是正数 B ．a 与b 的和为0C ．a 与b 的积为负数D ．a 与b 的商为-19．已知233122102n m +⎛⎫-++= ⎪⎝⎭，则2m n -的值是（）A ．13 B ．11 C ．9 D ．1510、46.23的余角的补角是： A 、14.66 B 、 46.113 C 、 44.157 D 、54.47 二、耐心填一填(每小题3分，共30分) 1．请你写出一个比零小的数： ． 2．平方得81的数有 个， （填“有”或“没有”）立方得-8的有理数．3．112-的相反数是 ，倒数是 ． 54.26=__________'''. 4．比较大小：0 12-；34- 56-．（填“<”、“>”或“=”）.6．20XX 年，兄妹两人的年龄分别是16岁和10岁，当哥哥的年龄是妹妹的年龄的2倍时，应是 年． 7．数轴上，将表示-1的点向右移动 3 个单位后，对应点表示的数是 ． 8．产量由m 千克增长15%后，达到 千克．9．为了解某市初中生视力情况，有关部门进行抽样调查，数据如下表，若该市有15万人，则全市视力不良的初中生约有 万人．10．已知4215na b 与3162m a b +是同类项，则m = ，n = ．三、用心想一想(共60分)1．计算（本题8分，每小题4分）： (1)、[]2(2)18(3)24-+--⨯÷． （2）、()()x xy y x xy y x -+--+--2232322222．解方程（本题10分）：（1）43(2)5x x --=； （2）2233236x x x -+-=-．3．（本题10分）某商场在元旦期间，开展商品促销活动．将某型号的电视机按进价提高35%后，打9折另送50元路费的方式销售，结果每台电视机仍获利208元，问每台电视机的进价是多少元？4．（本题10分）某村有10块小麦田，今年收成与去年相比（增产为正，减产为负）的情况如下：55kg ，77kg ，-40kg ，-25kg ，10kg ，-16kg ，27kg ，-5kg ，25kg ，10kg ．问今年小麦的总产量与去年相比是增产还是减产？增（减）产多少kg ？5．（本题11分）有这样一道题：“计算(2x 3-3x 2y -2xy 2)-(x 3-2xy 2+y 3)+(-x 3+3x 2y -y 3)的值，其中12x=，1y =-”．甲同学把“12x =”错抄成“12x =-”，但他计算的最后结果，与其他同学的结果都一样．试说明理由，并求出这个结果．6．（本题11分）某生物课外活动小组的同学举行植物标本制作比赛，结果统计如下：人数 1 2 4 3 2 每人所作标本数246810根据表中提供的信息，回答下列问题： （1）该组共有学生多少人？（2）制作标本数在6个及以上的人数在全组人数中所占比例？ （3）平均每人制作多少个标本？（4）补全图4的条形统计图．答案一、1．B 2．C 3．B 4．D 5．B 6．D 7．C 8．B 9．A 10．A 二、1．略 2．两，有 3．112，23- 4．>，> 5．7 6．2001 7．2 8．2320m9．7.2 10．1，3 三、1．10．2．（1）1x =-；（2）3x =-． 3．1200元．4．今年小麦的总产量与去年相比是增产了，增产了118千克． 5．代数式化简结果为32y -，与x 无关，结果是2． 6．（1）12；（2）34；（3）6.5；（4）略． 教师的职务是‘千教万教，教人求真’;学生的职务是‘千学万学，学做真人’。