下载文档原格式
玻璃等效厚度计算公式玻璃的等效厚度在很多领域都有着重要的应用，比如建筑设计、汽车制造等等。
那什么是玻璃的等效厚度呢？简单来说，就是把玻璃的复杂结构或者性能用一个等效的单一厚度来表示，方便我们进行计算和设计。
要搞清楚玻璃等效厚度的计算公式，咱们先得了解一下玻璃的特性。
玻璃这东西，看起来挺简单，就是透明的、硬邦邦的，但实际上它的物理性质可不简单。
比如说，它的强度、导热性、隔音效果等等，都和厚度有关系。
我记得有一次去一个建筑工地，看到工人们正在安装玻璃幕墙。
那一块块巨大的玻璃在阳光下闪闪发光，特别好看。
我就好奇地问其中一个师傅，这玻璃的厚度怎么选啊？师傅笑着说，这可大有讲究，不仅要看建筑的高度、风压，还得考虑隔热、隔音的要求。
这让我更加意识到，玻璃的厚度可不是随便定的，得经过精心计算。
那玻璃等效厚度的计算公式到底是啥呢？一般来说，它是基于玻璃的力学性能、热学性能或者声学性能来确定的。
对于力学性能，比如说抗压强度，等效厚度可以通过下面这个公式来计算：Te = (K * t^n) / f ，这里的 Te 就是等效厚度，K 是一个与玻璃材料相关的常数，t 是实际的玻璃厚度，n 是一个指数，f 是所要求的强度值。
再来说说热学性能。
在考虑玻璃的隔热效果时，等效厚度可能会用这样的公式：Te = (λ1 * t1 + λ2 * t2) / λe ，其中λ1、λ2 是不同玻璃层的热导率，t1、t2 是对应的厚度，λe 是等效热导率。
声学性能方面呢，等效厚度的计算可能就更复杂一些啦。
但大致的思路也是类似的，要考虑玻璃的隔音系数、声波频率等等因素。
比如说，在汽车车窗的设计中，为了降低车内噪音，就得精确计算玻璃的等效厚度，以达到最佳的隔音效果。
要是算错了，那开车的时候可就吵得要命啦！总之，玻璃等效厚度的计算公式虽然看起来有点复杂，但只要我们理解了其中的原理，再结合实际的需求，就能准确地算出合适的厚度，让玻璃在各种应用中发挥出最好的性能。
课后习题《材料物理性能》第一章材料的力学性能1-1一圆杆的直径为2.5 mm 、长度为25cm 并受到4500N 的轴向拉力，若直径拉细至 2.4mm ，且拉伸变形后圆杆的体积不变,求在此拉力下的真应力、真应变、名义应力和名义应变，并比较讨论这些计算结果。
解：由计算结果可知：真应力大于名义应力，真应变小于名义应变。
1-5一陶瓷含体积百分比为95%的Al 2O 3 (E = 380 GPa)和5%的玻璃相(E = 84 GPa)，试计算其上限和下限弹性模量。
若该陶瓷含有5 %的气孔，再估算其上限和下限弹性模量。
解：令E 1=380GPa,E 2=84GPa,V 1=0.95,V 2=0.05。
则有当该陶瓷含有5%的气孔时，将P=0.05代入经验计算公式E=E 0(1-1.9P+0.9P 2)可得，其上、下限弹性模量分别变为331.3 GPa 和293.1 GPa 。
0816.04.25.2ln ln ln 22001====A A l l T ε真应变)(91710909.4450060MPa A F =⨯==-σ名义应力0851.0100=-=∆=A A l l ε名义应变)(99510524.445006MPa A F T =⨯==-σ真应力)(2.36505.08495.03802211GPa V E V E E H =⨯+⨯=+=上限弹性模量)(1.323)8405.038095.0()(112211GPa E V E V E L =+=+=--下限弹性模量1-11一圆柱形Al 2O 3晶体受轴向拉力F ，若其临界抗剪强度τf 为135 MPa,求沿图中所示之方向的滑移系统产生滑移时需要的最小拉力值，并求滑移面的法向应力。
解：1-6试分别画出应力松弛和应变蠕变与时间的关系示意图，并算出t = 0,t = ∞ 和t = τ时的纵坐标表达式。
解：Maxwell 模型可以较好地模拟应力松弛过程：Voigt 模型可以较好地模拟应变蠕变过程：).1()()(0)0()1)(()1()(10//0----==∞=-∞=-=e EEe e Et t t στεσεεεσεττ；；则有：其蠕变曲线方程为：./)0()(;0)();0()0((0)e (t)-t/e στσσσσσστ==∞==则有：：其应力松弛曲线方程为0123450.00.20.40.60.81.0σ(t )/σ(0)t/τ应力松弛曲线0123450.00.20.40.60.81.0ε(t )/ε(∞)t/τ应变蠕变曲线)(112)(1012.160cos /0015.060cos 1017.3)(1017.360cos 53cos 0015.060cos 0015.053cos 82332min 2MPa Pa N F F f =⨯=︒︒⨯⨯=⨯=︒⨯︒⨯=⇒︒⨯︒=πσπτπτ：此拉力下的法向应力为为：系统的剪切强度可表示由题意得图示方向滑移以上两种模型所描述的是最简单的情况，事实上由于材料力学性能的复杂性，我们会用到用多个弹簧和多个黏壶通过串并联组合而成的复杂模型。
字体大小：大| 中| 小2007-08-02 14:02 - 阅读：734 - 评论：0第一节概述1．物质的玻璃态自然界中，物质存在着三种聚集状态，即气态，液态和固态。
固态物质又有两种不同的形式存在，即晶体和非晶体（无定形态）。
玻璃态属于无定形态，其机械性质类似于固体，是具有一定透明度的脆性材料，破碎时往往有贝壳状断面。
但从微观结构看，玻璃态物质中的质点呈近程有序，远程无序，因而又有些象液体。
从状态的角度理解，玻璃是一种介于固体和液体之间的聚集状态。
对于“玻璃”的定义，二十世纪四十年代以来曾有过几种不同的表述。
1945年，美国材料试验学会将玻璃定义为“熔化后，冷却到固化状态而没有析晶的无机产物”。
也有将玻璃定义扩展为“物质（包括有机物，无机物）经过熔融，在降温冷却过程中因粘度增加而形成的具有固体机械性质的无定形物体”。
我国的技术词典中把“玻璃态”定义为；从熔体冷却，在室温下还保持熔体结构的固体物质状态。
其实，在上世纪八十年代，有人提出上述定义‘是多余的限制’。
因为，无机物可以形成玻璃，有机物也可以形成玻璃，显然早期的表述并不合适。
另外，经过熔融可以形成玻璃，不经过熔融也可以形成玻璃，例如，经过气相沉积，溅射可得到非晶态材料，采用溶胶-凝胶法也可以得到非晶态材料，可见后期的表述也并不妥当。
现代科学技术的发展已使玻璃的含义有了很大的扩展。
因此，有人把具有下述四个通性的物质不论其化学性质如，均称为玻璃。
这四个通性是；（1）各相同性。
玻璃的物理性质，如热膨胀系数，导热系数，导电性，折射率等在各个向都是一致的。
表明物质部质点的随机分布和宏观的均匀状态。
（2）介稳性。
熔体冷却成玻璃体时并没有处于能量最低的状态，仍然有自发转变为晶体的倾向，因而，从热力学的观点看，处于介稳状态。
但常温下玻璃的粘度非常大，自发转变为晶体的速度非常慢，所以，从动力学的观点看，它又是非常稳定的。
（3）固态和熔融态间转化的渐变性和可逆性。
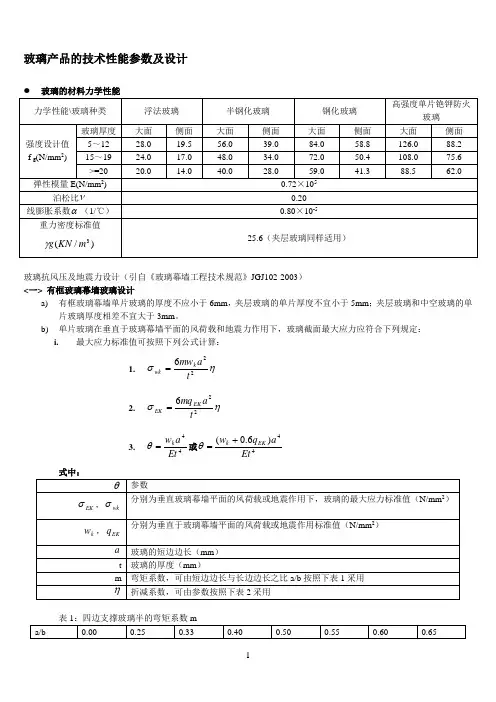
玻璃产品的技术性能参数及设计玻璃抗风压及地震力设计（引自《玻璃幕墙工程技术规范》JGJ102-2003） <一> 有框玻璃幕墙玻璃设计a) 有框玻璃幕墙单片玻璃的厚度不应小于6mm ，夹层玻璃的单片厚度不宜小于5mm ；夹层玻璃和中空玻璃的单片玻璃厚度相差不宜大于3mm 。
b) 单片玻璃在垂直于玻璃幕墙平面的风荷载和地震力作用下，玻璃截面最大应力应符合下列规定： i. 最大应力标准值可按照下列公式计算：1.ησ226t a mw k wk=2.ησ226ta mq EK EK= 3. 44Et a w k =θ或44)6.0(Eta q w EK k +=θ表2：折减系数ηc) 单片玻璃的刚度和跨中挠度应符合以下规定：1. 单片玻璃的刚度D ，按照：)1(1223v Et D -=计算。
2. 玻璃跨中挠度u 可按照下式计算：ημDa w u k 4=四边支撑板的挠度系数：3. 在风荷载标准值作用下，四边支撑玻璃的最大挠度u 不宜大于其短边尺寸的1/60d ） 夹层玻璃可按照下列规定进行计算：1. 作用于夹层玻璃上的风荷载和地震作用可按下列公式分配到两片玻璃上：3231311t t t w w kk +=（1）3231322t t t w w kk +=（2）3231311t t t q q Ek EK +=（3）3231322t t t q q EkEK +=（4）2. 两片玻璃可各自按照第1，2条的规定分别进行单片玻璃的应力计算；3. 夹层玻璃的挠度可按照第1，3条的规定进行计算，但在计算刚度D 时，应采用等效厚度t et e 可按照下式计算：32313t t t e +=（5）其中：t 1,t 2分别为各单片玻璃的厚度（mm ）e) 中空玻璃可按照下列规定进行计算1． 作用于中空玻璃上的风荷载标准值可按下列公式分配到两片玻璃上：i. 直接承受风荷载作用的单片玻璃：32313111.1t t t W W k k +=（1.5-1）ii.不直接承受风荷载作用的单片玻璃：32313221.1t t t W W k k +=（1.5-2）2. 作用于中空玻璃上的地震作用标准值，可根据各单片玻璃的自重计算。
